人教版初一数学下册6.1第一课时算数平方根(20210128051833)

新课标人教版数学七年级下册第六章平方根（一）6．1《算术平方根》说课稿尊敬的各位评委、各位老师：你们好！我今天说课的内容是:义务教育教科书人教版数学教材七年级下册第六章第一节《算术平方根》。

我准备从教材分析、学情分析、教法学法、教学过程、课后反思等五个方面来谈谈我对本节课的教学构想.一、教材分析算术平方根是人教版七年级下册第六章第一节的第一课时的教学内容。

本章内容主要包括算术平方根、平方根、立方根以及实数的概念和运算。

学习算数平方根是为以后学习平方根做铺垫，通过学习，学生对数的认识就由有理数范围扩大到实数范围，完成了初中阶段对所有数的扩展。

，因此本节课是今后学习实数、根式、分式、函数等知识的重要基础。

二、学情分析学生通过上个学期的数学学习，能基本从具体事例中通过观察、类比等活动抽象出问题的规律，并且学生在上学期的数学已经学习了乘方这个运算，具备了用所学知识来算术平方根的基础。

三、教学目标：新课标明确提出，义务教育阶段的教学课程，要从数学本身的特点出发，从学生学习数学的心理规律和学生已有的知识经验出发，让学生经历一个实践、思考、探索、交流、解释、应用的学习过程，在获得对教学理解的同时，在思维能力、情感态度和价值观等多方面都得到进步和发展。

所以我设计的教学目标是：知识与技能：了解算术平方根的概念，会用根号表示正数的算术平方根，并了解算术平方根的非负性。

过程与方法：通过学习算术平方根，建立初步的数感和符号感，发展抽象思维。

情感态度与价值观：通过解决实际生活中的问题，让学生体验数学与现实生活是紧密联系的，提高学习兴趣。

四、教学重难点：重点：了解算术平方根的概念难点：根据算术平方根的概念正确求出或用根号表示一个正数的算术平方根。

五、教学方法结合本课特点，我主要采用了以下教学方法：1讲练结合法——理论加练习，由难化简；2提问法——逐步引导，逐渐深入；3点拨法——展开联想，拓展思路；4经验交流法——与人交流，与人合作六、说教学流程：为了达成教学目标，在设计思路上，我设计了这么几个活动：1、创设情境，导入新课；2、自主探究，合作交流；3、师生互动，归纳新知；4、巩固练习，加深理解；5、课堂小结，整体感悟。

第六章实数6.1平方根第1课时算术平方根4教字目畅【知识与技能】1•了解算术平方根的概念，会用根号表示正数的算术平方根•2•了解算术平方根的非负性.【过程与方法】通过学习算术平方根，建立初步的数感和符号感，发展抽象思维•【情感态度】通过对实际生活中问题的解决，让学生体验数学与生活实际是紧密联系着的通过探究活动培养动手能力和学习兴趣.【教学重点】理解算术平方根的概念和求法•【教学难点】根据算术平方根的概念正确求出非负数的算术平方根•时于-占这个数惣有文数的平7/等于它・故平力为-夕的文数彳％伉< 丄 k 3 )2±1.3.问题3学校要举行美术比赛，小壮想裁一块面积为25dm 2的正方形画布画 一幅画，这块画布的边长应取多少？分析：本题实质是要求一个平方后得 25的数,由上面的讨论可知这个数为土 5, 但考虑正方形的边长不能为负数，所以正方形边长应取5dm.、思考探究，获取新知教师归纳出新定义：般地,如果一个正数x 的平方等于a,即 x2=a 那么这个正数x 叫做a 的算术 平方根，记作(5,读作 根号a ”，a 叫作被开方数.规定:0的算术平方根是0.三、例题讲解例1求下列各数的算术平方根.(1) ( -3 凡⑵ I 券(3)0；(4)分析：正数的算术平方根是正数，零的算术平方根是零，负数没有算术平方根 解：(1 )内为护二9二〔—3尸.所以(一3严的算术平方根是3▼即7( -3)2 =3, ⑵因为&「存］為所以唔的算术平方根是斗』卩 7 V 49 7(3) M 为U 的算术平方根建0 ,故Q = (L(4) M 为擔门^糾的算术平方根9,而9的算术平方根址九听以阿■的算术平方根址王1 + 一12425 2二苕故平方为去的数占忌平办为击的数为丄告 =I . &9 , 平方为1. 69白勺数足【教学说明】(1)算术平方根是非负数，要注意不要弄错算术平方根的符号•如: 不要把(-3 2 =3写成(-3 2 =-3；(2)要审清题意不要被表面现象迷惑.如求81的算术平方根，错误地理解为求81的算术平方根,81.探究:当a为负数时,a2有没有算术平方根？其算术平方根与a有什么关系？举例说明所得结论•【教学指导】当a为负数时,a2为正数,故a2有算术平方根,如a=-5 时,a2=(-5)2=25, a2 - 25 =5,5是-5的相反数，故a<0时,a2的算术平方根与a互为相反数，表示为-a.当a2为正数时,a的算术平方根表示为心2其值为a,即a2 =a.当a=0时, a2 =0.a a >0 h综上所述、- I«I = a= 0,- a < 0.L【教学说明】应用上述结论解题时，可如例题的解答写出过程，熟练后再直接写出结果.对• a2结果的讨论，可以检验学生是否真正理解了算术平方根的含义. 学生中出现的问题，可由学生间交流讨论.教师向学生介绍用计算器求算术平方根的方法，并由学生实际运用，体会方法.四、运用新知，深化理解】•冷的算术平方根是于川数学式子表示为2.汁算41 -5)2的结果是( )A.5B. -5C, *5 1).25N卜「列各式屮尤总义的足( >A -辽 B.(：* 7( -2)2I) V-324.求下列各式:的值.(I ) V1.44:(2 ) 7( -(K J )2；(3 ) \/n78T - ^yfT04；(4 ) J1 2 缶【教学说明】学生自主探究，教师巡视，了解学生对本节课知识的掌握情况, 及时予以指导，帮助学生巩固新知•【答案】1.A 2.A 3.D4. ( |) V'K44= L2(2) 7( -0. I )2 = VOT = 0.】(3) 7(). 81 - /(). 04=0. 9-(L2=0. 75■被开方数的大小与对应的算术平方根的大小之间有什么关系呢？四、探究算术平方根的非负性1、a可以取任何数吗？2、v是什么数？归纳：1. a表示a的算术平方根;2.双重的非负性：a为八a淘;3...是算术平方根的运算符。

6.1平方根(\)学习目标：1、了解数的算术平方根的概念。

2、会求禁些非负数的算术平方根。

学习重点：会求禁些非负数的算术平方扌艮。

学习堆点：对数的算术平方根概念的理解。

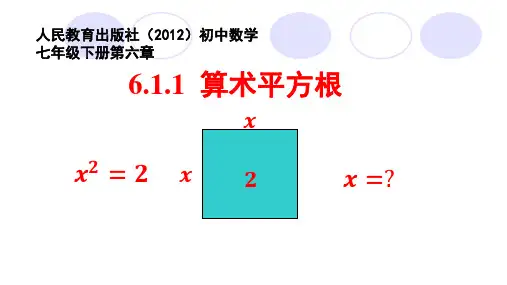
情景问題:学校要举行美术作品比赛，小鸥很高兴，他想裁出一块面积为25血2的正方形画布，画上自己的得意之作参加比赛，这块正方形画布的边长应取多少?因为「=25,所以这个正方形画框的边长应取5dm填写下表IiT1346I■fi总结概4念"一般地，如果一个正数^的平方等于r<a,即「电那么这个正数x叫做a的算术平方根。

a的算术平方根记为亦, 读作“根号「, a叫做被开方数。

即：x2 =a (x>0),x叫做a的算术平方根,记作：x =特殊：0的算术平方根是0。

记作：则=0判断:(1) 5是25的算术平方根;(2)-6是36的算术平方根;(3)0的算术平方根是0；(4)0. 01是0. 1的算术平方根;(5)-5是-25的算术平方根。

例題解析例1求下列各数的算术平方根:49(1) 100 (3) 0. 0001解飞黑防呗所以】。

的算术平方根为1。

,(7 节49 jo T(2)因为.-=—,所以了的算术平方根是亍(3)因为0.012 =0. 0001,所以0. 0001的算术平方根为0.01,即JO.OOOl =0.01o提出问題被开方数的大小与对应的算术平方根的大小之间有什么关系呢？结论：被开方数大的数算术平方根也大.试i试你能根据等式：12 2二144说出144的算术平方根是多少吗? 并用等式表示出来。

怨一想下列式子表示什么意思？你能求出它们的值吗？V25" Volf 衣补克练习：1.8的算术平方根是；屈踊算术平方根是O3.V360tJ4后矛的算术平方根等于o课臺小结1.什么是算术平方根?2.如何求一个正数的算术平方根?作如习题6」第1題。

单元教学设计
科目数学七年级下册
6.1平方根（第一课时）教学设计
6.1平方根（1）随堂检测题
1、下列命题中,正确的个数有( )
①1的算术平方根是1;②(-1)2的算术平方根是-1;③一个数的算术平方根等于它本身,这个数只能是零；④-4没有算术平方根.毛
A.1个
B.2个
C.3个
D.4个
2、一个自然数的算术平方根是x,则下一个自然数的算术平方根是( )
A.+1
B.
C.
D.x+1
3、x是16的算术平方根,那么x的算术平方根是( )
A.4
B.2
C.
D.±4
4、36的算术平方根是______,36的算术平方根是_____.
5、算术平方根等于它本身的数是_______.
6、 =_______, -=_______.±=______,=________.
7、的算术平方根是________.
8、求下列各式的值:
(1)- ； (2)+； (3) +
9、若 =2,求2x+5的算术平方根.
10、已知a为的整数部分,b-1是400的算术平方根,求.。

算术平方根教材分析:《算术平方根》是人教版初中数学七年级下第六章第一节第一课时。

在此之前，学生已经学习了有理数、有理数的乘方、用字母表示数等知识，这为过渡到本节起着铺垫作用。

本节主要学习算术平方根的概念和性质，在运算方面，引入了开方运算，使学生掌握的代数运算由原来的加、减、乘、除、乘方五种扩展到六种，建立起较完善的代数运算体系。

本节内容既是对前面所学知识的深化和发展，也是今后学习二次根式、实数的预备知识，还是用直接开平方法、公式法解一元二次方程的重要依据。

因此，本节处于非常重要的地位，起着承前启后的作用。

学生分析：八年级的学生已经能从具体事例中归纳问题的本质，通过观察、类比等活动抽象出问题的规律，同时学生在前面的学习中已经熟练掌握算术平方根的知识，具备了用所学知识来分析算术平方根性质的基础。

教学目标：1. 知识与技能掌握算术平方根的概念，能通过开方运算求一个非负数算术平方根。

2. 过程与方法从现实生活中提出数学问题，在学生已有的基础上建立新旧知识的联系，让学生用自己的语言有条理地、清晰的阐述算术平方根的概念、意义及求法，提高理解能力和语言表达能力。

3 情感、态度与价值观准确理解把握概念，将对知识的理解转化为数学技能，鼓励学生积极主动地参与教与学的整个过程，激发学生求知的欲望，增加学生学习数学的兴趣与信心。

教学重、难点:本节课的重点是算术平方根的概念和性质。

正确理解这个概念是学好本章的关键之一。

本节课的难点是根据算术平方根的概念正确求出非负数的算术平方根。

说教法与学法:1 教法学生在七年级学过乘方运算，但由于间隔时间长，他们会有不同程度的遗忘，为了实现新旧教学方式和学习方式的接轨，我利用情景与问题教学激发学生的兴趣，利用对比教学让学生掌握概念的本质，完善学生的知识结构。

2 学法学生才是学习的主人，教师应该把过程还给学生，让过程与结果并重。

新课程也强调学生的学习应在教师的指导下，主动地、富有个性地学习.据此本节的学法我定为小组交流合作法和自主学习法。