青岛大学657数学分析历年考研试题

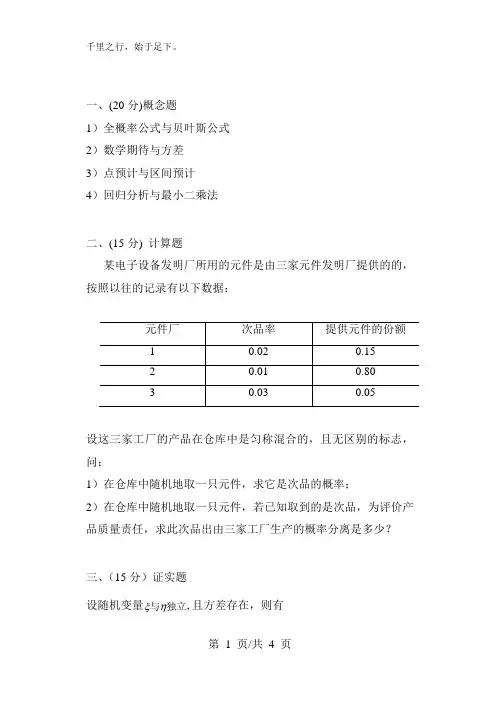
一、(20分)概念题1）全概率公式与贝叶斯公式2）数学期待与方差3）点预计与区间预计4）回归分析与最小二乘法二、(15分) 计算题某电子设备发明厂所用的元件是由三家元件发明厂提供的的，按照以往的记录有以下数据：设这三家工厂的产品在仓库中是匀称混合的，且无区别的标志，问：1）在仓库中随机地取一只元件，求它是次品的概率；2）在仓库中随机地取一只元件，若已知取到的是次品，为评价产品质量责任，求此次品出由三家工厂生产的概率分离是多少？三、（15分）证实题设随机变量独立，ξ且方差存在，则有与η22)()()(ηξηξηξξηE D D E D D D •+•+•=由此并可得ηξξηD D D •≥)(四、(15分) 计算题设二维随机变量），（ηξ的联合密度为 ⎩⎨⎧>>=--其它），（,00,0,43y x ke y x p y x问：1）求常数k;2）求相应的分布函数； 3）求），（2010<<<<ηξp 五、（15分）计算题设有A,B 两种不相关的证券，它们的收益与概率如下表：问：1）应如何投资这两种证券最佳（即要满意收益越大越好，风险越小越好）？2）若这两种证券相关，譬如相关系数5.0,-=B A ρ，结果又如何？六、 （15分）计算题假设某险种在投保时期内一共发生了N 次赔款，i ξ表示第i 次赔款额，则相应的赔款总量为：N S ξξξ+++=...21，其中N 为取非负整数值的随机变量，N ξξξ...,21，，具有相同的分布函数，且N,N ξξξ (21)，互相自立，问： 1）推导赔款总量S 的数学期待及方差公式；2）若N 顺从参数3=λ的泊松分布，第i 笔赔款额i ξ的分布列如下表：计算赔款总量S 的范围。

七、（15分）证实题设{}n ξ为自立同分布的随机变量序列，每个随机变量的期待为a ,且方差存在，证实：a k n n nk k →+∑=1)1(2ξ（依概率收敛）八、（20分）计算题设总体ξ～),(2σμN ，2,σμ为未知参数，（n ξξξ,...,,21）是来自总体ξ的一个样本，问： 1）2,σμ的矩预计； 2）2,σμ的极大似然预计；3）以上两个预计是否无偏预计？若不是如何修正？九、（20分）计算题 针对一元线性回归模型i i i i x y εεβα,++=～n i N ,...,2,1),,0(2=σ求其中参数βα，的最小二乘预计及2σ的无偏预计，其中n x x x ,...,,21不全相同。

数学类专业硕士入学考试大纲考试科目代码及名称：657数学分析一、考试要求熟练、完整掌握《数学分析》的基本概念、基础理论和重要思想方法，具备抽象思维、逻辑推理和分析运算的能力，并能灵活运用所学知识解决各种类型的问题。

二、考试内容（1）数列与函数极限、连续收敛数列的性质，数列极限存在的条件，特殊极限，函数极限存在的条件，无穷大量与无穷小量，连续函数的性质。

（2）导数和微分导数的定义、导数的几何意义，导数四则运算，反函数的导数、复合函数求导、参变量函数求导、高阶导数、微分。

（3）微分中值定理拉格朗日中值定理、柯西中值定理、不定式极限与洛必达法则，泰勒公式、函数的极值与最值。

（4）一元函数积分换元法与分部积分法、有理函数的积分、牛顿-莱布尼茨公式、可积条件、定积分的性质、定积分应用、反常积分（5）级数理论正项级数收敛性判别法、一般项级数敛散性、函数项级数的一致收敛、幂级数的收敛半径，幂级数运算、函数的幂级数展开、Fourier 级数（6）多元函数微分学二元函数的连续性、多元函数的偏导数与可微性、复合函数微分法、方向导数与梯度、泰勒公式与极值问题、隐函数求导、隐函数组、多元函数的几何应用（7）含参量积分含参量正常积分、含参量反常积分、欧拉积分（8）重积分、曲线积分与曲面积分第一和第二型曲线积分、两类曲线积分之间的联系、第一和第二型曲面积分、重积分的运算、格林公式、高斯公式、Stokes公式三、试卷结构（题型分值）1.本科目满分为150分，考试时间为180分钟。

2.题型结构（1）证明题：约占总分的80%（2）计算题: 约占总分的20%四、参考书目（1）《数学分析（第四版）》：华东师范大学数学系编，高等教育出版社，2010年（2）《数学分析新讲》张筑生, 北京大学出版社,1991年.（3）《数学分析原理》 Walter Rudin, 机械工业出版社,2004.。

目录Ⅰ历年考研真题试卷 (2)山东大学2007年招收硕士学位研究生入学考试试题 (2)山东大学2009年招收硕士学位研究生入学考试试题 (3)山东大学2010年招收硕士学位研究生入学考试试题 (5)山东大学2011年招收硕士学位研究生入学考试试题 (6)山东大学2012年招收硕士学位研究生入学考试试题 (7)山东大学2014年招收硕士学位研究生入学考试试题 (8)山东大学2015年招收硕士学位研究生入学考试试题 (10)山东大学2016年招收硕士学位研究生入学考试试题 (12)山东大学2017年招收硕士学位研究生入学考试试题 (14)Ⅱ历年考研真题试卷答案解析 (16)山东大学2007年招收硕士学位研究生入学考试试题答案解析 (16)山东大学2009年招收硕士学位研究生入学考试试题答案解析 (22)山东大学2010年招收硕士学位研究生入学考试试题答案解析 (29)山东大学2011年招收硕士学位研究生入学考试试题答案解析 (34)山东大学2012年招收硕士学位研究生入学考试试题答案解析 (39)山东大学2014年招收硕士学位研究生入学考试试题答案解析 (46)山东大学2015年招收硕士学位研究生入学考试试题答案解析 (52)山东大学2016年招收硕士学位研究生入学考试试题答案解析 (59)山东大学2017年招收硕士学位研究生入学考试试题答案解析 (68)Ⅰ历年考研真题试卷山东大学2007年招收硕士学位研究生入学考试试题科目代码：651科目名称：数学分析（答案必须写在答卷纸上，写在试卷上无效）1.求()sin 0lim cot xx x →2.求222222222222(),: 1.Vx y z x y z dxdydz V a b c a b c ++++=⎰⎰⎰3.求211.n n n x ∞-=∑()0,1x ∈4.证明：20lim sin 0.n n xdx π→∞=⎰5.()()0,()f a f b f x ''==有二阶导数，证明：存在,ξ满足24()()().()f f b f a b a ξ''≥--6.22220(,)0,0.x y f x y x y +≠=+≠⎩，证明：(,)f x y 在（0，0）连续，有有界偏导数,x y f f ''在（0，0）不可微。