目标规划例题

第三章 目标规划 第一节 目标规划的数学模型目标规划法是求一组变量的值，在一组资源约束和目标约束条件下，实现管理目标与实际目标之间的偏差最小的一种方法。

应用目标规划法解决多种目标决策问题时，首先要建立目标规划模型。

目标规划模型由变量、约束和目标函数组成。

为具体说明目标规划与线性规划在处理问题方法上的区别，先通过例子介绍目标规划的有关概念及数学模型。

一、举例例 1 某厂生产Ⅰ、Ⅱ两种产品，已知计划期有关数据如下，求获利最大的生产方案。

生产有关数据表ⅠⅡ 拥有量 原材料 （公斤） 2 1 11 设备台时（小时） 利润 （元/件） 1 82 1010用线性规划方法求解：设Ⅰ、Ⅱ两种产品产量分别为x 1，x 2⎪⎩⎪⎨⎧≥≤+≤++=0,102112108max 21212121x x x x x x x x z可得 Z=62元，X=（4，3）T但实际决策时，有可能考虑市场等其它方面因素，例如按重要性排序的下列目标：据市场信息，产品Ⅰ销售量下降，要求产品Ⅰ产量低于产品Ⅱ产量； 尽可能充分利用现有设备，但不希望加班； 达到并超过计划利润指标56元。

这样考虑生产计划问题即为多目标规划问题。

下面结合上述例题介绍有关建立目标规划数学模型的基本概念。

二、目标规划基本概念1. 设x 1，x 2为决策变量，并引入正、负偏差变量d +、d —正偏差变量d +表示决策值超过目标值的部分；负偏差变量d —表示决策值未达到目标值的部分，d +，d －≥0。

决策值不可能既超过又未达到目标值，因此恒有d +×d －＝0。

2.绝对约束和目标约束绝对约束指必须严格满足的“≤，≥，＝” 约束，称为硬约束，例如线性规划中的约束，不满足它们的约束称为非可行解；目标约束是目标规划所特有的，它把约束的右端常数项看作追求的目标值，允许出现正、负偏差，用“d +、d －”表示，称为软约束。

约束的一般形式为：i i i j iij g d d X C =-++-∑式中i g ——第i 个目标约束的目标值；ij C ——目标约束中决策变量的参数；+-i i d d 、——以目标值i g 为标准而设置的偏差变量。

第五章 目标规划§5.1重点、难点提要一、目标规划的基本概念与模型特征 （1）目标规划的基本概念。

当人们在实践中遇到一些矛盾的目标，由于资源稀缺和其它原因，这些目标可能无法同时达到，可以把任何起作用的约束都称为“目标”。

无论它们是否达到，总的目的是要给出一个最优的结果，使之尽可能接近制定的目标。

目标规划是处理多目标的一种重要方法，人们把目标按重要性分成不同的优先等级，并对同一个优先等级中的不同目标赋权，使其在许多领域都有广泛应用。

在目标规划中至少有两个不同的目标；有两类变量：决策变量和偏差变量；两类约束：资源约束（也称硬约束）和目标约束（也称软约束）。

（2）模型特征。

目标规划的一般模型：⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥=≥==-+=≤⎪⎭⎫ ⎝⎛+=+-=+-===++--∑∑∑∑.,,2,1;0,;,,2,10,,2,1,,2,1..)(min 1111K k d d n j x K k g d d x c m i b x a t s d d P Z k k j n j k k k j kj i nj j ij Lr K k k rk k rk r ωω 其中r P 为目标优先因子，+-rk rk ωω,为目标权系数，+-k k d d ,为偏差变量。

1）正、负偏差变量,i i d d +-。

正偏差变量i d +表示决策值超过目标值的部分；负偏差变量i d -表示决策值未达到目标值的部分。

因为决策值不可能既超过目标值同时又未达到目标值，所以有0i i d d +-⨯=。

2）硬约束和软约束。

硬约束是指必须严格满足的等式约束和不等式约束；软约束是目标规划特有的。

我们可以把约束右端项看成是要努力追求的目标值，但允许发生正、负偏差，通过在约束中加入正、负偏差变量来表示努力的结果与目标的差距，于是称它们为目标约束。

3）优先因子与权系数。

一个规划问题通常有若干个目标，但决策者在要求达到这些目标时，是有主次或缓急之分的。

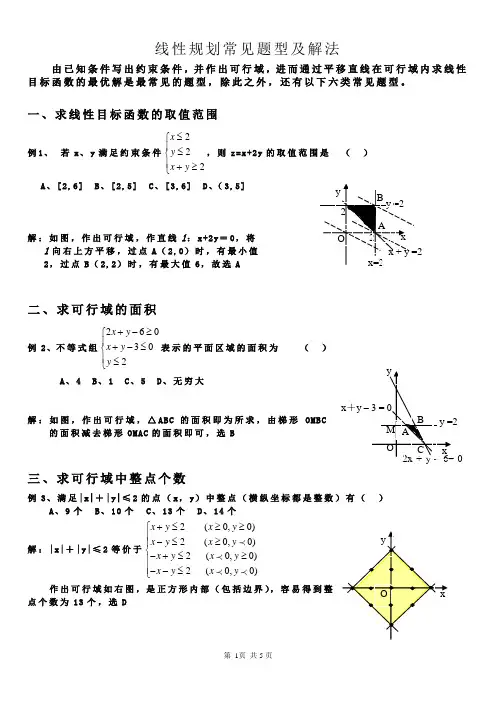
线性规划常见题型及解法由已知条件写出约束条件，并作出可行域，进而通过平移直线在可行域内求线性目标函数的最优解是最常见的题型，除此之外，还有以下六类常见题型。

一、求线性目标函数的取值范围例1、若x、y满足约束条件222xyx y≤⎧⎪≤⎨⎪+≥⎩，则z=x+2y的取值范围是（）A、[2,6]B、[2,5]C、[3,6]D、（3,5]解：如图，作出可行域，作直线l：x+2y＝0，将l向右上方平移，过点A（2,0）时，有最小值2，过点B（2,2）时，有最大值6，故选 A二、求可行域的面积例2、不等式组260302x yx yy+-≥⎧⎪+-≤⎨⎪≤⎩表示的平面区域的面积为（）A、4B、1C、5D、无穷大解：如图，作出可行域，△ABC的面积即为所求，由梯形OMBC 的面积减去梯形OMAC的面积即可，选 B三、求可行域中整点个数例3、满足|x|＋|y|≤2的点（x，y）中整点（横纵坐标都是整数）有（）A、9个B、10个C、13个D、14个解：|x|＋|y|≤2等价于2(0,0)2(0,0)2(0,0)2(0,0) x y x yx y x yx y x yx y x y+≤≥≥⎧⎪-≤≥⎪⎨-+≤≥⎪⎪--≤⎩作出可行域如右图，是正方形内部（包括边界），容易得到整点个数为13个，选 D四、求线性目标函数中参数的取值范围例4、已知x、y满足以下约束条件5503x yx yx+≥⎧⎪-+≤⎨⎪≤⎩，使z=x+ay(a>0)取得最小值的最优解有无数个，则a的值为（）A、－3B、3C、－1D、1解：如图，作出可行域，作直线l：x+ay＝0，要使目标函数z=x+ay(a>0)取得最小值的最优解有无数个，则将l向右上方平移后与直线x+y＝5重合，故a=1，选 D五、求非线性目标函数的最值例5、已知x、y满足以下约束条件220240330x yx yx y+-≥⎧⎪-+≥⎨⎪--≤⎩，则z=x2+y2的最大值和最小值分别是（）A、13，1B、13，2C、13，45D、5解：如图，作出可行域,x2+y2是点（x，y）到原点的距离的平方，故最大值为点A（2,3）到原点的距离的平方，即|AO|2=13，最小值为原点到直线2x＋y－2=0的距离的平方，即为45，选 C六、求约束条件中参数的取值范围例6、已知|2x－y＋m|＜3表示的平面区域包含点（0,0）和（－1,1），则m的取值范围是（）A、（-3,6）B、（0,6）C、（0,3）D、（-3,3）解：|2x－y＋m|＜3等价于230 230x y mx y m-++>⎧⎨-+-<⎩由右图可知3330mm+>⎧⎨-<⎩,故0＜m＜3，选 C七、比值问题当目标函数形如y az x b-=-时,可把z 看作是动点(,)P x y 与定点(,)Q b a 连线的斜率，这样目标函数的最值就转化为PQ 连线斜率的最值。

某构件公司商品混凝土车间生产能力为 20T/小时，每天工作 8 小时，现有 2 个施 工现场分别需要商品混凝土 A150T ， 商品混凝土 B100T ，两种混凝土的构成、单位利润 及企业所拥有的原料见表 10.4.2，现管理部门提出：1 、充分利用生产能力； 2、加班不超过2 小时；3 、产量尽量满足两工地需求； 4、力争实现利润 2 万元/天。

试建立目标规划模型拟定一个满意的生 产计划。

[解]1、确定变量设 X 1 、X 2 分别为两种商品混凝土 的产量2、约束条件 (1)目标约束：P 1 级： 要求生产能力充分利用， 即要求剩余工时越小越好。

x 1 + x 2 + d 一1 一 d = 160(T)其中要求d一1 →0P 2 级： 要求可以加班，但每日不 超过 2 小时，日产量不能超过 200T 。

x 1 + x 2 + d 一2一 d = 200(T)其中要求 d →0P 3 级： 两个工地需求尽量满足， 但不能超过需求。

x 1 + d 一3 = 150(T)其中要求： d 一3 →0x 2 + d 一4 = 100(T)d 一4 →0因需求量不能超过其需要，故d , d =0P 4 级：目标利润超过 2 万元。

100x 1+80x 2+ d一5一 d =20 000 (元)，其中要求 d 一5 →0(2)资源约束：ⅰ)水泥需求不超过现有资源0.35x 1+0.25x 2 ≤50ⅱ)砂需求不超过现有资源0.55x 1+0.6x 2 ≤130(3)非负约束：x 1 ≥ 0, x 2 ≥ 0, d i 一、 d i +≥ 0 (i =1,2, (5)3 、目标函数。

依目标约束中的要求， 第三层目标 中有 2 个子目标，其权数可依其利润多 少的比例确定，即 100： 80，简化为 5： 4，故 W 1=5， W 2=4 。

故目标函数为：Z min = P 1d 一1 + P 2 d + 3P (5d 一3 + 4d 一4) + P 4 d 一5整理得该问题的目标规划模型为： Z min = P 1d 一1 + P 2 d + 3P (5d 一3 + 4d 一4) + P 4 d 一5约束：x + x + d 一一 d + = 160 1 2 1 1x + x + d 一一 d + = 200 1 2 2 2x + d 一 = 150 1 3x + d 一 = 100 2 4100x 1+80x 2+ d 一5 一 d =20000 0.35x 1+0.25x 2 ≤50 0.55x 1+0.6x 2 ≤130x 1 ≥ 0, x 2 ≥ 0, d i一d i 一 ≥ 0(i=1,2,……,5水泥砂单位利润A 0.35 0.55 100B 0.25 0.65 80拥有资源 50T 130T。

目标规划图解法例题目标规划图解法是一种基于图解的方法，用于制定和实现个人或组织的目标。

下面是一个关于个人目标规划图解法的例题。

假设你是一名大学生，正在为自己的未来做规划。

你希望在未来三年内，能够顺利毕业、找到一份好工作、发展个人能力、保持健康的生活方式、建立良好的社交关系等。

首先，你需要准备一张空白的图纸，并将纵坐标分成三个部分，代表三年。

然后，将横坐标分成五个部分，分别代表毕业、工作、能力、健康、社交五个方面。

接下来，根据每个目标的优先级，将每个目标在相应的年份中进行分配。

例如，你可以在第一年将重点放在毕业和发展个人能力上，将重点放在第二年的工作和健康上，将重点放在第三年的社交上。

在每个目标的下方，你可以绘制一条水平直线，代表该目标在每年中的进展情况。

例如，如果你希望在第一年中达到一个毕业进度的目标，你可以在第一年的这条直线上标明“毕业进度70%”。

在每个目标的旁边，你可以写下具体的行动计划，包括所需要的时间、资源以及具体的行动步骤。

例如，如果你想要发展个人能力，你可以写下“每周阅读一本专业书籍，参加一个相关领域的研讨会”。

最后，在整张图上标上时间节点，以便你在未来几年中能够追踪和评估自己的目标实现情况。

例如，你可以在每个目标的左上角标明“2023年1月”等时间节点。

通过这样的目标规划图解法，你可以清晰地看到自己的目标，并有条不紊地提供行动计划，以实现每个目标。

同时，你可以通过不断更新图表，及时调整目标和行动计划，以适应不同的情况和需求。

最后，目标规划图解法是一个非常实用和灵活的方法，能够帮助你实现个人目标。

只要你认真规划、积极行动，并持续跟踪和评估自己的目标，相信你一定能够取得成功。

目标规划某企业生产甲、乙两种产品，需要用到A,B,C 三种设备，关于产品的赢利与使用设备的工时及限制如表 2 所示。

问该企业应如何安排生产，才能达到下列目标：表 2甲 乙 设备的生产能力（h ）A (h/件) 2 2 12B (h/件) 4 0 16C (h/件) 0 5 15赢利（元/件） 200 300（1）力求使利润指标不低于 1500 元；（2）考虑到市场需求，甲、乙两种产品的产量比应尽量保持 1:2；（3）设备 A 为贵重设备，严格禁止超时使用；（4）设备C 可以适当加班，但要控制；设备B 既要求充分利用，又尽可能不加班。

在重要性上，设备B 是设备C 的 3 倍。

建立相应的目标规划模型并求解。

解 设备 A 是刚性约束，其余是柔性约束。

首先，最重要的指标是企业的利润，因此，将它的优先级列为第一级；其次，甲、乙两种产品的产量保持 1:2 的比例，列为第二级；再次，设备B,C 的工作时间要有所控制，列为第三级。

在第三级中，设备B 的重要性是设备C 的三倍，因此，它们的权重不一样，设备B 前的系数是设备C 前系数的 3 倍。

设生产甲乙两种产品的件数分别为x1, x2, ，相应的目标规划模型为min z = P1d1- + P2 ( d2+ + d2- ) + P3 ( 3d3+ + 3d3- + d4+ )121211122213324412221220030015002040515,,,0(1,2,3,4...)i i x x x x d d x x d d x d d x d d x x d d i -+-+-+-+-++≤⎧⎪++-=⎪⎪-+-=⎪⎨+-=⎪⎪+-=⎪≥=⎪⎩LINGO程序编码model:sets:level/1..3/:p,z,goal;variable/1..2/:x;h_con_num/1..1/:b;s_con_num/1..4/:g,dplus,dminus;h_con(h_con_num,variable):a;s_con(s_con_num,variable):c;obj(level,s_con_num)/1 1,2 2,3 3,3 4/:wplus,wminus; endsetsdata:ctr=;goal= 0;b=12;g=1500 0 16 15;a=2 2;c=200 300 2 -1 4 0 0 5;wplus=0 1 3 1;wminus=1 1 3 0;enddatamin=@sum(level:p*z);p(ctr)=1;@for(level(i)|i#ne#ctr:p(i)=0);@for(level(i):z(i)=@sum(obj(i,j):wplus(i,j)*dplus(j)+wminus(i,j)* dminus(j)));@for(h_con_num(i):@sum(variable(j):a(i,j)*x(j))<b(i));@for(s_con_num(i):@sum(variable(j):c(i,j)*x(j))+dminus(i)-dplus(i)=g(i));@for(level(i)|i #lt# @size(level):@bnd(0,z(i),goal(i)));End程序解释当程序运行时，会出现一个对话框。

多目标规划训练例题某音像商店有5名全职熟练货员和4名兼职售货员，全职售货员每月工作160h,兼职售货员每月工作80h，根据过去的工作纪录，全职售货员每小时销售CD25张，平均每小时工资15元，加班工资每小时22.5元，兼职售货员每小时销售CD10张，平均工资每小时10元，加班工资每小时10元，现在预测下个月CD销售量为27500张，商店每周开门营业6天，所以可能要加班，每出售一张CD盈利1.5元。

商店经理认为，保持稳定的就业水平加上必要的加班，比不加班但就业水平不稳定要好，但全职售货员如果加班过多，就会因为疲劳过度而造成效益下降，因此，不允许每月加班超过100h,建立相应的目标规划模型，并应用Lingo软件求解。

解：首先建立目标约束的优先级:1P ：下月的CD 销售量达到27500张2P ：限制全职售货员加班时间不超过100h3P ：保持全体售货员充分就业，因为充分工作是良好劳资关系的重要因素，但对全职售货员要比兼职售货员加倍优先考虑4P ：尽量减少加班时间，但对两种售货员区别对待，优先权因子由他们对利润的贡献而定。

第二，建立目标约束（1）销售目标约束，设1x ：全体全职售货员下月的工作时间；2x ：全体兼职售货员下月的工作时间；-1d ：达不到销售目标的偏差；+1d ：超过销售目标的偏差；希望下月的销售超过27500张CD 片，因此销售目标为⎩⎨⎧=-+++--275001025}min{11211d d x x d （2）正常工作时间约束，设-2d ：全体全职售货员下月的停工时间； +2d ：全体全职售货员下月的加班时间； -3d ：全体兼职售货员下月的停工时间； +3d ：全体兼职售货员下月的加班时间； 由于希望保持全体售货员充分就业，同时加倍优先考虑全职售货员，因此工作目标约束为⎪⎩⎪⎨⎧=-+=-+++-+---320800}2min{33222132d d x d d x d d（3）加班时间的限制，设-4d ：全体全职售货员下月加班时间不足100h 的偏差；+4d ：全体全职售货员加班时间超过100h 的偏差；限制全职售货员加班时间不超过100h ，将加班约束看成正常班约束，不同的是右端加上100 h ，因此加班目标约束为⎩⎨⎧=-++-+900}min{4414d d x d 另外，全职售货员加班1h ，商店得到的利润为15元)155.225.125(=-⨯，兼职售货员加班1h ，商店得到的利润为5元)5105.110(=-⨯，因此加班1h 全职售货员获得的利润是兼职售货员的3倍，故权因子之比为3:1:32=++d d所以，另一个加班目标约束为⎪⎩⎪⎨⎧=-+=-+++-+-++320800}3min{33222132d d x d d x d d第三，按目标的优先级，写出相应的目标规划模型：⎪⎪⎪⎩⎪⎪⎪⎨⎧==-+=-+=-+=-+++++++=+-+-+-+-+-++--+-4,3,2,1,,,,900320800275001025..);3()2(min 2144133222111213243234211i d d x x d d x d d x d d x d d x x t s d d P d d P d P d P z i i第四，写出相应的LINGO 程序 。