任意角的三角函数的符号
- 格式:ppt
- 大小:1.79 MB
- 文档页数:32



三角函数及变形公式汇总一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=, 正弦:r y =αsin 余弦:r x =αcos 正切:x y =αtan 余切:y x =αcot 正割:x r =αsec 余割:yr =αcsc 注:我们还可以用单位圆中的有向线段表示任意角的三角函数:如图,与单位圆有关的有向..线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线。
二、同角三角函数的基本关系式倒数关系:1csc sin =⋅αα,1sec cos =⋅αα,1cot tan =⋅αα。
商数关系:αααcos sin tan =,αααsin cos cot =。
平方关系:1cos sin 22=+αα,αα22sec tan 1=+,αα22csc cot 1=+。
三、诱导公式⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
(口诀:函数名不变,符号看象限) ⑵απ+2、απ-2、απ+23、απ-23的三角函数值,等于α的异名函数值,前面加上一个把α看成..锐角时原函数值的符号。
(口诀:函数名改变,符号看象限)四、和角公式和差角公式βαβαβαsin cos cos sin )sin(⋅+⋅=+βαβαβαsin cos cos sin )sin(⋅-⋅=-βαβαβαsin sin cos cos )cos(⋅-⋅=+βαβαβαsin sin cos cos )cos(⋅+⋅=-βαβαβαtan tan 1tan tan )tan(⋅-+=+ βαβαβαtan tan 1tan tan )tan(⋅+-=- 五、二倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=…)(*ααα2tan 1tan 22tan -= 二倍角的余弦公式)(*有以下常用变形:(规律:降幂扩角,升幂缩角) αα2cos 22cos 1=+ αα2sin 22cos 1=-2)cos (sin 2sin 1ααα+=+ 2)cos (sin 2sin 1ααα-=-六、万能公式(可以理解为二倍角公式的另一种形式)ααα2tan 1tan 22sin +=,ααα22tan 1tan 12cos +-=,ααα2tan 1tan 22tan -=。

中职数学第五章三角函数知识点第五章三角函数角和任意三角函数的定义1.角:角是由两条射线共同确定的图形部分。
2.弧度制:半径长度的圆弧所对的圆心角为1弧度角。
180° = π rad180° = π rad ≈ 0. rad1 rad ≈ 57.3°3.终边相同的角的表示:β/β = k360° + α。
k∈Z} {β/β = 2kπ + α。
k∈Z}终边在坐标轴上的角的集合:x正半轴:{α/α = 2kπ。
k∈Z}y正半轴:{α/α = π + 2kπ。
k∈Z}x负半轴:{α/α = π + 2kπ。
k∈Z}y负半轴:{α/α = 3π + 2kπ。
k∈Z}x轴:{α/α = kπ。
k∈Z}y轴:{α/α = ±kπ。
k∈Z}第一象限角:0 < α < π/2第二象限角:π/2 < α < π第三象限角:π < α < 3π/2第四象限角:3π/2 < α < 2π4.任意角的三角函数:在角θ的终边上任取一点P(x。
y)。
r = √(x^2 + y^2) (r。
0)sinθ = y/rcosθ = x/rtanθ = y/x任意角三角函数符号:一全二正弦三切四余弦5.同角三角函数关系tanθ = sinθ/cosθ2sin^2θ + cos^2θ = 1sinα ± cosα)^2 = 1 ± 2sinαcosα特殊勾股数:3.4.5.6.8.10.5.12.13.8.15.17.7.24.25;诱导公式第一象限角正角α第二象限角第三象限角第四象限角2π - απ - απ + αsin(α+2kπ) = sinαcos(α+2kπ) = cosα___(α+2kπ) = tanαsin(-α) = -sinαcos(-α) = cosαtan(-α) = -tanαsin(π-α) = sinαcos(π-α) = -cosα___(π-α) = -tanαsin(π+α) = -sinαcos(π+α) = -cosαcos(π+α)=-cosα,tan(π+α)=tanα,α-πsin(2π-α)=-sinα,cos(2π-α)=cosα,tan(2π-α)=-tanα,-αsin(α-π)=-sinα,cos(α-π)=-cosα,sin(-α)=-sinα,cos(-α)=cosα,tan(-α)=-tanα,___(α-π)=tanα根据奇偶性和象限可得以上结论。



三角函数基础知识三角函数基础知识1、任意角的三角函数(1)任意角的三角函数的定义:角α的终边上任意一点p的坐标是(x,y),它与原点的距离是r(r>0),那么角α的正弦、余弦、正切、余切分别是(2)三角函数值的符号正弦值与余割值对于第一、二象限的角是正的,而对于第三、四象限的角是负的.余弦值与正割值对于第一、四象限的角是正的,而对于第二、三象限的角是负的.正切值与余切值对于第一、三象限的角是正的,而对于第二、四象限角是负的,也可以按正的在各象限的函数来记,即“一全、二正弦,三切、四余弦”(正割、余割分别与余弦、正弦符号相同)2.同角三角函数的基本关系式(1)倒数关系:sinαcsc=1 cosαsecα= tgαctgα=1(3)平方关系:sin2α+cos2α=1 1+tg2α=sec2α 1+ctg2α=csc2α3.诱导公式(1) k·360°+α(k∈Z),-α,180°±a,360°-α的三角函数值等于α的同名函数值,前面加上一个把α角看成锐角时原函数值的符号,即sin(k·360°+α)=sinα,cos(k·360°+α)=cosαtg(k·360°+α)=tgα,ct g(k·360°+α)=ctgα(k∈Z)sin(-α)=-sinα,cos(-α)=cosαtg(-α)=-tgα,ctg(-α)=-tgαsin(180°+α)=-sinα,cos(180°+α)=-cosαtg(180°+α)=tgα,ctg(180°+α)=ctgαsin(180°-α)=sinα,cos(180°-α)=-cosαtg(180°-α)=-tgα,ctg(180°-α)=-ctgαsin(360°-α)=-sinα,cos(360°-α)=cosαtg(360°-α)=-tgα,ctg(360°-α)=-ctgα(2) 90°±α,270°±α的三角函数值等于a的余名函数值,前面加上一个把α看成锐角时原函数值的符号,例如sin(90°+α)=cosα,tg(270°+α)=-ctgα综上,诱导公式可概括为k·90°±α(k∈Z)的三角函数值,等于α的同名(k为偶数时)或余名(k为奇数时)的函数值,前面加上一个把α看成锐角时原函数值的符号.简称之为“奇余偶不变,符号看象限”.4.三角函数的图象和性质(1)三角函数线以原点为圆心,以单位长为半径的圆叫做单位圆,如图2—3,设角α的终边与单位圆的交点为p ,过p作PM垂直于x轴,垂足为M,A(1,0)、B(0,1),过A、B点作单位的切线AT、BS分别与角α的终边或其反向延长线交于T、S则有向线及MP、OM、AT、BS、OT、OS分别叫作角α的正弦线、余弦线、正切线、余切线、正割线、余割线.(2)三角函数的图象正弦函数y=sinx 余弦函数y=cosx(如图2—4)正切函数y=tgx 余切函数y=ctgx (如图2—5)(3)三角函数的周期①周期函数对于函数y=f(x),如果存在着一个不为零的常数T,使得当x取定义域内的每一个值时,都成立,那么就把函数y=f(x)叫做周期函数,不为零的常数T叫做这个函数的周期.②最小正周期:对于一个周期函数来说、如果在所有的周期中存在着一个最小正数,就把这个最小的正数叫做最小正周期.教科书上所指三角函数的周期均为最小正周期.(4)三角函数的性质5、积化和差与和差化积(1)积化和差与和差化积各有四个公式,它们实质是一类公式的正用或逆用,即积化和差公式的逆用就是和差化积公式。

任意角的三角函数知识点一、终边角:与α终边相同的角表示为。
分别写出终边在下列位置时的角α的集合:1.x轴上2.y轴上3.坐标轴上4.第一象限5.第二象限6.第三象限7.第四象限 8.直线y=x上二、弧度制:1、定义:2、公式:|α|=3、换算:①度换弧度:180°=弧度; 1°=弧度②弧度换度:1弧度=度;扇形:弧长L==,面积S==三、任意角的三角函数:①定义:角α终边的终边与单位圆的交点P(x,y),则sinα= cosα= tanα=角α终边上任意一点交点P(x,y),则r= ,则sinα= cosα= tanα=②三角函数线:角的终边与单位圆交于点P,过点P作轴的垂线,垂足为M,则正弦线是余弦线是即sinα= ,cosα= .过点A(1,0)作交于点T即tonα= .③同角三角函数关系式:④三角函数的符号:(1)商数关系:(2)平方关系:⑤诱导公式:2kπ+α与απ—α与απ+α与α)(βα+C )(βα-C)(βα+S )(βα-S )(βα+T )(βα-T⑧二倍角公式: α2Sα2C α2T三角函数的图象与性质答案一、终边角:与α终边相同的角表为k ·360° + α 。
分别写出终边在下列位置时的角α的集合: 1. x 轴上 {},k k Z ααπ=∈2. y 轴上 ,2k k Z πααπ⎧⎫=+∈⎨⎬⎩⎭3. 坐标轴上,2k k Z ααπ⎧⎫=∈⎨⎬⎩⎭4. 第一象限22,2k k k Z παπαπ⎧⎫+∈⎨⎬⎩⎭5. 第二象限22,2k k k Z παπαππ⎧⎫++∈⎨⎬⎩⎭6. 第三象限322,2k k k Z παππαπ⎧⎫++∈⎨⎬⎩⎭7. 第四象限3222,2k k k Z παπαππ⎧⎫++∈⎨⎬⎩⎭8. 第一或第三象限,2k k k Z παπαπ⎧⎫+∈⎨⎬⎩⎭9. 第二或第四象限,2k k k Z παπαππ⎧⎫++∈⎨⎬⎩⎭10. 直线y =x 上,4k k Z πααπ⎧⎫=+∈⎨⎬⎩⎭11. 直线y =-x 上3,4k k Z πααπ⎧⎫=+∈⎨⎬⎩⎭二、 弧度制:1、定义:弧长等于半径的弧所对的圆心角叫一弧度的角.2、 公式:|α|=lr3、 换算:① 度换弧度:180°=π弧度;1°=180π弧度②弧度换度:1弧度=180π度;扇形: 弧长L =180n rπ= r α, 面积S =2360n r π=12lr三、 任意角的三角函数:①定义:角α终边上任意一点P(x ,y),则r =,六个三角函数的定义依次是sin y r α=、cos x r α=、tan y α=cot x α=sec r α=csc r α= ②三角函数线:角的终边与单位圆交于点P ,过点P 作x 轴的垂线,垂足为M ,则正弦线是MP 余弦线是OM即sin α=MP,cos α= OM.过点A(1,0)作 切线交 角的终边或反向延长线 于点T ,则正切线是AT 。

任意角的三角函数及基本公式三角函数是数学中的一个重要概念,它们描述了角度与三角比之间的关系。
任意角的三角函数包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。
下面将详细介绍这些函数的定义、基本公式以及它们之间的关系。
1. 正弦函数(sine function):在单位圆上,从x轴正向到射线与单位圆的交点之间的弧度即为角的弧度。
正弦函数将给定角度的正弦值映射到数轴上。
其定义如下:sin(θ) = y/r其中θ为角度,y为对边,r为斜边。
2. 余弦函数(cosine function):余弦函数表示角的余弦值在数轴上的投影长度。
其定义如下:cos(θ) = x/r其中θ为角度,x为邻边,r为斜边。
3. 正切函数(tangent function):正切函数表示角的正切值在数轴上的投影比。
其定义如下:tan(θ) = y/x其中θ为角度,y为对边,x为邻边。
4. 余切函数(cotangent function):余切函数表示角的余切值在数轴上的投影比。
其定义如下:cot(θ) = x/y其中θ为角度,y为对边,x为邻边。
5. 正割函数(secant function):正割函数表示角的正割值在数轴上的投影长度。
其定义如下:sec(θ) = r/x其中θ为角度,x为邻边,r为斜边。
6. 余割函数(cosecant function):余割函数表示角的余割值在数轴上的投影长度。
其定义如下:csc(θ) = r/y其中θ为角度,y为对边,r为斜边。
这些函数在不同的角度上有不同的值,可以通过查表或计算器得到具体数值。
同时,它们之间存在一些基本公式和关系,如下:1. 互余关系(co-function identities):sin(θ) = cos(90° - θ)cos(θ) = sin(90° - θ)tan(θ) = cot(90° - θ)cot(θ) = tan(90° - θ)sec(θ) = csc(90° - θ)csc(θ) = sec(90° - θ)2.三角函数的平方和差:sin²(θ) + cos²(θ) = 1tan²(θ) + 1 = sec²(θ)cot²(θ) + 1 = csc²(θ)3.三角函数的倒数:sec(θ) = 1/cos(θ)csc(θ) = 1/sin(θ)cot(θ) = 1/tan(θ)4.符号关系:根据角度的位置和象限,三角函数的值可能为正或负。

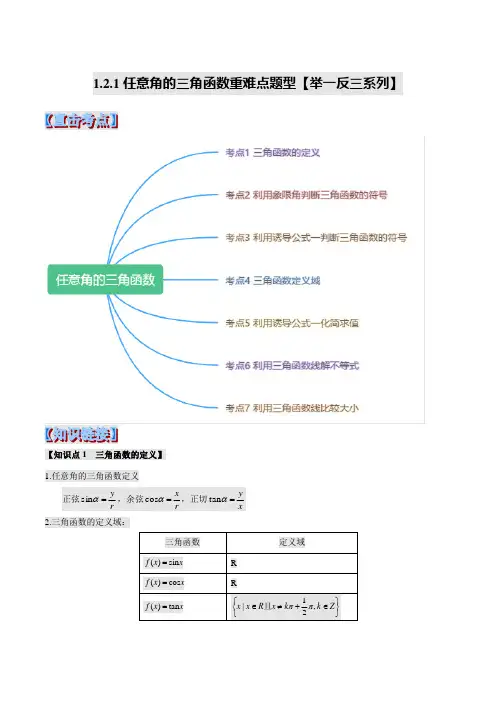
1.2.1任意角的三角函数重难点题型【举一反三系列】【知识点1 三角函数的定义】1.任意角的三角函数定义2.三角函数的定义域:【知识点2 三角函数值的符号】第一象限角的各三角函数值都为正;第二象限角的正弦值为正,其余均为负;第三象限角的正切值为正,其余均为负;第四象限角的余弦值为正,其余均为负.注:一全正,二正弦,三正切,四余弦.【知识点3 诱导公式一】由三角函数的定义,可以知道:终边相同的角的同一三角函数的值相等,由此得到诱导公式一:【知识点4 单位圆的三角函数线定义】如图(1)PM表示α角的正弦值,叫做正弦线.OM表示α角的余弦值,叫做余弦线.如图(2)AT表示α角的正切值,叫做正切线.注:线段长度表示三角函数值大小,线段方向表示三角函数值正负.【考点1 三角函数的定义】【分析】根据三角函数的定义,列方程求出m的值.【答案】解:角α的终边上一点(1,)P m,所以0m>,故选:B.【点睛】本题考查了三角函数的定义与应用问题,是基础题.A .4B .4±C .3D .3±【分析】由题意利用任意角的三角函数的定义,求得m 的值.故选:D .【点睛】本题主要考查任意角的三角函数的定义,属于基础题.)【分析】由题意利用任意角的三角函数的定义,求得tan α的值.【答案】解:角故选:C .【点睛】本题主要考查任意角的三角函数的定义,属于基础题.【变式1-3】(2019春•牡丹江期末)角α的终边上一点(P a ,2)(0)a a ≠,则2sin cos (αα-= )【分析】由题意利用任意角的三角函数的定义,分类讨论求得结果. 【答案】解:α的终边上一点(P a ,2)(0)a a ≠, 555a a =,22555a a =,555a a=-,2555a a=-故选:D .【点睛】本题主要考查任意角的三角函数的定义,属于基础题. 【考点2 利用象限角判断三角函数的符号】【例2】(2019春•湖北期中)下列命题成立的是( ) A .若θ是第二象限角,则cos tan 0θθ< B .若θ是第三象限角,则cos tan 0θθ> C .若θ是第四象限角,则sin tan 0θθ< D .若θ是第三象限角,则sin cos 0θθ>【分析】根据角所在的象限判断三角函数值的符号进行判断即可.【答案】解:若θ是第二象限角,则cos 0θ<,tan 0θ<,则cos tan 0θθ>,故A 错误, 若θ是第三象限角,则cos 0θ<,tan 0θ>,则cos tan 0θθ<,故B 错误, 若θ是第四象限角,则sin 0θ<,tan 0θ<,则sin tan 0θθ>,故C 错误, 若θ是第三象限角,则sin 0θ<,cos 0θ<,则sin cos 0θθ>,故D 正确, 故选:D .【点睛】本题主要考查三角函数值符号的判断,结合角的象限与三角函数值符号的关系是解决本题的关键. 【变式2-1】(2019春•珠海期末)已知点(sin ,tan )M θθ在第三象限,则角θ在( ) A .第一象限B .第二象限C .第三象限D .第四象限【分析】由题意可得sin 0θ<且tan 0θ<,分别求得θ的范围,取交集得答案. 【答案】解:由题意,00sin tan θθ<⎧⎨<⎩①②,由①知,θ为第三、第四或y 轴负半轴上的角; 由②知,θ为第二或第四象限角. 则角θ在第四象限. 故选:D .【点睛】本题考查三角函数的象限符号,是基础题.【变式2-2】(2019春•玉山县校级月考)若sin cos 0θθ<,则θ在( ) A .第一、二象限B .第一、三象限C .第一、四象限D .第二、四象限【分析】判断三角函数的符号,然后判断角所在象限即可.【答案】解:sin cos 0θθ<,可知sin θ与cos θ异号,说明θ在第或第四象限. 故选:D .【点睛】本题考查三角函数的符号的判断,角所在象限,是基本知识的考查. 【变式2-3】(2018秋•安庆期末)式子sin1cos2tan4的符号为( )A.正B.负C.零D.不能确定【分析】由1,2,4分别表示第一、二、三象限的角,由此可得答案.【答案】解:1,2,4分别表示第一、二、三象限的角,<,tan40>.∴>,cos20sin10故选:B.【点睛】本题考查三角函数值的符号,是基础题.【考点3 利用诱导公式一判断三角函数的符号】【例3】(2019秋•武邑县校级期中)下列三角函数值的符号判断正确的是()【分析】根据角所在的象限、诱导公式、三角函数值的符号逐项判断即可.【答案】解:A、因为156︒在第二象限,所以sin1560︒>,故A错误;︒=︒+︒=︒,且196︒在第三象限,D、因为tan556tan(360196)tan196所以tan5560︒>,故D错误;故选:C.【点睛】本题考查了三角函数的诱导公式,及三角函数在各象限的符号的应用,属于基础题.【变式3-1】(2019秋•西陵区校级期末)下列三角函数值的符号判断错误的是() A.sin1650︒<︒>D.tan3100︒>B.cos2800︒>C.tan1700【分析】直接利用诱导公式化简,判断符号即可.【答案】解:sin1650︒=︒>,正确;︒>,正确;cos280cos800tan1700︒=-︒<,正确;︒>,错误;tan310tan500故选:C.【点睛】本题考查诱导公式的应用,三角函数值的符号的判断,是基础题.【变式3-2】(2019春•武功县期中)下列值①sin(1000)-︒;④sin2是负值-︒;②cos(2200)-︒;③tan(10)的为()A.①B.②C.③D.④【分析】根据终边相同的角的三角函数值相同,利用三角函数符号判断方法,即可得出结论.【答案】解:①sin(1000)sin1000sin 2800-︒=-︒=-︒>; ②cos(2200)cos2200cos400-︒=︒=︒>; ③tan(10)tan100-︒=-︒<;综上,是负值的序号为③. 故选:C .【点睛】本题考查了终边相同的角与三角函数符号判断问题,是基础题.【变式3-3】(2019秋•夷陵区校级月考)给出下列各函数值:①sin(1- 000)︒;②cos(2- 200)︒;③tan(10)-;A .①④B .②③C .③⑤D .④⑤【分析】利用诱导公式分别对五个选项进行化简整理,进而根据三角函数的性质判断正负. 【答案】解:①,sin(1000)sin(2360280)sin 280cos100-︒=-⨯︒-︒=-︒=︒>; ②,cos(2200)cos(636040)cos400-︒=-⨯︒-︒=︒>; ③,tan(10)tan(30.58)tan(0.58)0π-=-+=-<;,πsin2cos3tan40∴<.∴其中符号为负的是:③⑤.故选:C .【点睛】本题主要考查了运用诱导公式化简求值,解题时应正确把握好函数值正负号的判定,是基础题. 【考点4 三角函数定义域】【分析】列出使函数有意义的不等式组,即由被开方数不小于零,得三角不等式组,分别利用正弦函数和余弦函数图象解三角不等式组即可【答案】解:要使函数有意义,需解得: (k ∈Z )即2k π+≤x ≤2k π+π (k ∈Z )故答案为Z )【点睛】本题考查了函数定义域的求法,三角函数的图象和性质,解简单的三角不等式的方法 可.【答案】解:函数【点睛】本题考查了函数的概念,三角函数的定义域,解三角函数的不等式,属于中档题. 【分析】由绝对值的特点得到sin α-和0的关系,由正弦曲线和角的正弦值可以得到角的范围,写出角的范围后注意加上k 的取值. 【答案】解:|sin |sin αα=-,sin 0α∴-, sin 0α∴,由正弦曲线可以得到[2k αππ∈-,2]k π,k Z ∈, 故答案为:[2k ππ-,2]k π,k Z ∈【点睛】本题主要考查三角函数不等式,解题时最关键的是要掌握三角函数的图象,通过数形结合得到要求的角的范围,这个知识点应用非常广泛,可以和其他知识结合来考查.【变式4-3】求下列函数的定义域:(2)(2sin1)=-;y lg x【分析】利用函数的定义域以及三角函数线化简求解即可.【答案】解:(1)要使y=有意义,可得cos x≥0,解得{x|﹣,k∈Z};(2)要使y=lg(2sin x﹣1)有意义,可得2sin x﹣1>0,即:sin x,解得{x|,k∈Z};(3)要使y=有意义,可得sin x≠﹣1.所以函数的定义域为:{x|x=﹣+2kπ,k∈Z}.【点睛】本题考查三角函数的定义域的求法,三角函数线的应用,考查计算能力.【考点5 利用诱导公式一化简求值】【例5】(2019春•娄星区期中)求下列各式的值:(2)sin1170cos1440tan1845︒+︒-︒【分析】(1)利用诱导公式进行恒等变形,再利用特殊角的三角函数值计算即可求出值;(1)利用诱导公式进行恒等变形,再利用特殊角的三角函数值计算即可求出值;【答案】(本题满分10分)(2)sin1170cos1440tan1845︒+︒-︒sin(336090)cos(43600)tan(536045)=⨯︒+︒+⨯︒+︒-⨯︒+︒ sin90cos0tan45=︒+︒-︒1=.【点睛】此题考查了运用诱导公式化简求值,以及特殊角的三角函数值,熟练掌握诱导公式是解本题的关键.【变式5-1】求下列各式的值(2)9cos2708cos03tan011sin180︒+︒+︒+︒.【分析】由特殊角的三角函数值即可计算得解.1(1)(1)=+-+-1=-.(2)9cos2708cos03tan011sin180︒+︒+︒+︒ 08100=+⨯++ 8=.【点睛】本题主要考查了特殊角的三角函数值在三角函数化简求值中的应用,属于基础题. 【变式5-2】(2019春•船营区校级月考)计算下列各式的值: (1)sin(1395)cos1140cos(1020)sin750-︒︒+-︒︒; tan 4ππ; 【分析】(1)原式中的角度变形后,利用诱导公式化简,再利用特殊角的三角函数值计算即可得到结果. (2)利用诱导公式即可计算得解.【答案】解:(1)原式sin(144045)cos(108060)cos(108060)sin(72030)=-︒+︒︒+︒+-︒+︒︒+︒ sin45cos60cos60sin30=︒︒+︒︒tan 4ππ )0【点睛】此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键,属于基础题. 【变式5-3】(2019春•平罗县校级期中)求下列各式的值 )cos(570)cos(1140)tan(210)sin(690)︒-︒-︒-︒-︒【分析】(1)利用诱导公式以及特殊角的三角函数化简求值即可. (2)利用诱导公式以及特殊角的三角函数化简求值即可. )cos(570)cos(1140)tan(210)sin(690)-︒-︒=-︒-︒25)sin cos tan 463πππ=+-【点睛】本题考查诱导公式的应用,三角函数化简求值,考查计算能力. 【考点6 利用三角函数线解不等式】【例6】(2019春•泗县校级月考)利用单位圆,求适合下列条件的角的集合:【分析】在单位圆中画出三角函数线. (1)由[0,2π)内,,结合正弦线得的解集;(2)由[0,2π)内,,结合余弦线得的解集.【答案】解:在单位圆内作三角函数线如图:(1)∵在[0,2π)内,,OA,OB分别为的终边,由正弦线可知,满足的角的终边在劣弧AB内,∴的解集为{α|};(2))∵在[0,2π)内,,OC,OD分别为的终边,由余弦线可知,满足的终边在劣弧CD内,∴的解集为{α|}.【点睛】本题考查了三角函数线,考查了三角不等式的解法,训练了数形结合的解题思想方法,是中低档题.【变式6-1】求下列不等式的解集:【分析】作出单元圆,利用三角函数线进行求解即可.【答案】解:(1)正弦线大于0的角为x轴的上方,对应的角为2kπ<x<2kπ+π,k∈Z,则不等式的解集为(2kπ,2kπ+π),k∈Z.(2)余弦线小于0的角为y轴的左侧,对应的角为2kπ+<x<2kπ+,k∈Z,则不等式的解集为(2kπ+,2kπ+),k∈Z.(3)sin x>对应的区域在阴影部分,对应角的范围为2kπ+<x<2kπ+,k∈Z,则不等式的解集为(2kπ+,2kπ+),k∈Z.(4)cos x≤﹣对应的区域在阴影部分,对应角的范围为2kπ+≤x≤2kπ+,k∈Z,则不等式的解集为[2kπ+,2kπ+],k∈Z.【点睛】本题主要考查三角不等式的求解,利用三角函数的三角函数线是解决本题的关键.【变式6-2】利用三角函数线,写出满足下列条件的角x的集合:(2)tan x≥﹣1.【分析】根据三角函数线分别进行求解即可.【答案】解:(1)作出y=﹣,交单位圆于B,C,则sin x>﹣对应的区域为阴影部分,作出x=,交单位圆于E,D,则cos x>对应的区域为阴影部分OD,OE之间,则sin x>﹣且cos x>对应的区域为OC到OE之间,其中OC对应的角为﹣,OE对应的角为,则阴影部分对应的范围是2kπ﹣<x<2kπ+,k∈Z,即sin x>﹣且cos x>对应的范围是{x|2kπ﹣<x<2kπ+,k∈Z}(2)作出正切函数线AT=﹣1,则tan x≥﹣1对应的区域为阴影部分,OT对应的角为﹣,则阴影部分对应的角的范围是kπ﹣≤x<kπ+,即不等式的解集为{x|kπ﹣≤x<kπ+,k∈Z}【点睛】本题主要考查三角函数对应不等式的求解,利用三角函数线是解决本题的关键.【变式6-3】利用三角函数线,写出满足下列条件的角x的集合.(3)tan x≥﹣1;【分析】作出单位圆,由三角函数值先求出角在[0,2π]内的取值范围,再由终边相同的角的概念加上周期,由此能求出满足条件的角x的集合.【答案】解:(1)由sin x,作出单位圆,如下图,∵sin x,∴,∴满足sin x≥的角x的集合为{x|2kπ+,k∈Z}.(2)由cos x≤,作出单位圆,如下图,∵cos x≤,∴,∴满足cos x≤的角x的集合为{x|2kπ+≤x≤2kπ+,k∈Z}.(3)由tan x≥﹣1,作出单位圆,如下图,∵tan x ≥﹣1,∴﹣≤x <, ∴满足tan x ≥﹣1的角x 的集合为{x |k π﹣,k ∈Z }. (4)由sin x >且cos x >,作出单位圆,如下图,∵sin x >且cos x >,∴,∴满足sin x >且cos x >x 的集合为{x |2k π+,k ∈Z }. 【点睛】本题考查角的取值范围的求法,是基础题,解题时要注意单位圆和三角函数线的合理运用.【考点7 利用三角函数线比较大小】【例7】比较下列各组数的大小:【分析】(1)根据余弦函数单调性的大小进行比较(2)利用三角函数的诱导公式以及作差法进行比较即可.704π<-cos(π∴-02πα<<则0sin(cos <cos(sin )α222ππ-<【点睛】本题主要考查三角函数值的大小比较,结合三角函数的诱导公式以及三角函数的单调性是解决本题的关键.【变式7-1】利用三角函数线比较下列各组三角函数值的大小:【分析】根据题意,依次作出各个角的三角函数值对应的三角函数线,进而比较大小即可得答案.【点睛】本题考查的知识点是三角函数线,三角函数值的大小比较,关键是掌握三角函数线的定义.【变式7-2】比较大小:可知:21AT AT >,可知:BD BC >,【点睛】本题考察了诱导公式的化简运用,正切线的画法,属于三角函数线的基础题目.【变式7-3】比较下列各组数的大小:【分析】根据三角函数线进行比较即可.)5 cos7π=在单位圆中作出对应的三角函数线如图,则余弦线为OM,正弦线为MP,(2)在单位圆中作出对应的三角函数线如图,则正切线为AT,正弦线为MP,则AT MP>,【点睛】本题主要考查三角函数值的大小比较,根据三角函数线是解决本题的关键.。
三角函数公式一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=,正弦函数:r y =αsin 余弦函数:r x =αcos 正切函数:x y=αtan 余切函数:y x =αcot 正割函数:xr=αsec 余割函数:y r =αcsc 二、同角三角函数的基本关系式六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”倒数关系:1csc sin =⋅x x ,1sec cos =⋅x x ,1cot tan =⋅x x 。
商数关系:x x x cos sin tan =,xxx sin cos cot =。
平方关系:1cos sin 22=+x x ,x x 22sec tan 1=+,x x 22csc cot 1=+。
积的关系:sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)=sinα cos (2kπ+α)=cosαtan (2kπ+α)=tanα cot (2kπ+α)=cotα (其中k ∈Z)公式二:设α为任意角,π+α的三角函数的值与α的三角函数值之间的关系: sin (π+α)=-sinα cos (π+α)=-cosα tan (π+α)=tanα cot (π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin (-α)=-sinα cos (-α)=cosα tan (-α)=-tanα cot (-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)=sinα cos (π-α)=-cosα tan (π-α)=-tanα cot (π-α)=-cotα 公式五:απ-2与α的三角函数值之间的关系:sin (απ-2)=cosα cos (απ-2)=sinα tan (απ-2)=cotα cot (απ-2)=tanα公式六:απ+2与α的三角函数值之间的关系:sin (απ+2)=cosα cos (απ+2)=-sinα tan (απ+2)=-cotα cot (απ+2)=-tanα公式七:απ-23与α的三角函数值之间的关系: sin (απ-23)=-cosα cos (απ-23)=-sinαtan (απ-23)=cotα cot (απ-23)=tanα公式八:απ+23与α的三角函数值之间的关系:sin (απ+23)=-cosα cos (απ+23)=sinαtan (απ+23)=-cotα cot (απ+23)=-tanα公式九:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)=-sinα cos (2π-α)=cosα tan (2π-α)=-tanα cot (2π-α)=-cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
第二节 任意角的三角函数知识点1.利用单位圆定义任意角的三角函数如图,在平面直角坐标系中,设α是一个任意角,它的终边与单位圆交于点P (x ,y ),那么:(1)y 叫做α的正弦,记作sin α,即sin α=y ;(2)x 叫做α的余弦,记作cos α,即cos α=x ;(3)y x 叫做α的正切,记作tan α,即tan α=y x(x ≠0). 对于确定的角α,上述三个值都是唯一确定的.故正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,统称为三角函数.2.一般地,设角α终边上任意一点的坐标为(x ,y ),它与原点的距离为r ,则sin α=y r ,cos α=x r ,tan α=y x. 2.正弦、余弦、正切函数值在各象限的符号口诀概括为:一全正、二正弦、三正切、四余弦(如图).3.三角函数的定义域4.诱导公式一终边相同的角的同一三角函数的值相等,即:sin(α+k ·2π)=sin α,cos(α+k ·2π)=cos α,tan(α+k ·2π)=tan α,其中k ∈Z .5.三角函数线如图,设单位圆与x 轴的正半轴交于点A ,与角α的终边交于P 点.过点P 作x 轴的垂线PM ,垂足为M ,过A 作单位圆的切线交OP 的延长线(或反向延长线)于T 点.单位圆中的有向线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线.记作:sin α=MP ,cos α=OM ,tan α=AT .6.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1.(2)商数关系:tan α=sin αcos α (α≠k π+π2,k ∈Z ).同角三角函数基本关系式的变形(1)sin 2α+cos 2α=1的变形公式:sin 2α=1-cos 2α;cos 2α=1-sin 2α.(2)tan α=sin αcos α的变形公式:sin α=cos αtan α;cos α=sin αtan α.题型一:三角函数的定义【例1】已知θ终边上一点P (x,3)(x ≠0),且cos θ=1010x ,求sin θ,tan θ.【例2】已知角α的终边上一点的坐标为⎝⎛⎭⎫sin 2π3,cos 2π3,则角α的最小正值为() A.5π6 B.2π3 C.5π6 D.11π6【过关练习】1.角α的终边经过点P (-b,4)且cos α=-35,则b 的值为( )A .3B .-3C .±3D .52.已知角α的终边经过点P (-4a,3a )(a ≠0),求sin α,cos α,tan α的值;3.已知角α的终边在直线y =3x 上,求sin α,cos α,tan α的值.题型二:三角函数在各象限的符号【例1】判断下列三角函数值的符号:(1)sin 3,cos 4,tan 5;(2)sin(cos θ)(θ为第二象限角).【过关练习】1.若sin θ<0且tan θ<0,则θ是第 象限的角.2.若tan x <0,且sin x -cos x <0,则角x 的终边在( )A .第一象限B .第二象限C .第三象限D .第四象限题型三:诱导公式一的应用【例1】求下列各式的值:(1)sin(-1 395°)cos 1 110°+cos(-1 020°)sin 750°;(2)sin ⎝⎛⎭⎫-11π6+cos 12π5·tan 4π.【过关练习】1.求下列各式的值:(1)cos 25π3+tan ⎝⎛⎭⎫-15π4; (2)sin 810°+tan 765°-cos 360°.2.求下列各式的值.(1)a 2sin(-1 350°)+b 2tan 405°-2ab cos(-1 080°);(2)tan 405°-sin 450°+cos 750°.题型四:三角函数线的应用【例1】在单位圆中画出满足sin α=12的角α的终边,并求角α的取值集合.【例2】利用单位圆中的三角函数线,分别确定角θ的取值范围.(1)sin θ≥32;(2)-12≤cos θ<32.【例3】求下列函数的定义域.(1)f (x )=sin x ·tan x ;(2)f (x )=lg sin x +9-x 2.【过关练习】1.根据下列三角函数值,作角α的终边,然后求角的取值集合:(1)cos α=12;(2)tan α=-1.2.如果π4<α<π2,那么下列不等式成立的是( ) A .cos α<sin α<tan αB .tan α<sin α<cos αC .sin α<cos α<tan αD .cos α<tan α<sin α3.求函数f (x )=1-2cos x +ln ⎝⎛⎭⎫sin x -22的定义域.4.设a =sin(-1),b =cos(-1),c =tan(-1),则有( )A .a <b <cB .b <a <cC .c <a <bD .a <c <b 5.若0<α<2π,且sin α<32,cos α>12,则角α的取值范围是( ) A .(-π3,π3) B .(0,π3) C .(5π3,2π) D .(0,π3)∪(5π3,2π)题型五:同角三角函数关系的应用【例1】已知cos α=-817,求sin α,tan α的值.【例2】已知tan α=2,求下列代数式的值.(1)4sin α-2cos α5cos α+3sin α; (2)14sin 2α+13sin αcos α+12cos 2α.【例3】已知sin θ+cos θ=15,θ∈(0,π),求: (1)sin θ-cos θ;(2)sin 3θ+cos 3θ.【过关练习】1.已知tan α=43,且α是第三象限角,求sin α,cos α的值.2.已知sin θ+cos θsin θ-cos θ=2,则sin θcos θ的值是( ) A.34 B .±310 C.310 D .-3103.已知sin α=55,则sin 4α-cos 4α的值为( ) A .-15 B .-35 C.15 D.354.已知tan α=3,求下列各式的值.(1)3cos α-sin α3cos α+sin α; (2)2sin 2α-3sin αcos α.5.已知sin θ、cos θ是关于x 的方程x 2-ax +a =0的两个根(a ∈R ).(1)求sin 3θ+cos 3θ的值;(2)求tan θ+1tan θ的值.题型六:三角函数化简【例1】若α是第三象限角,化简1+cos α1-cos α+1-cos α1+cos α.【例2】求证:2sin x cos x -1cos 2x -sin 2x =tan x -1tan x +1.【过关练习】1.化简:1cos 2α1+tan 2α-1+sin α1-sin α(α为第二象限角).2.证明:sin α-cos α+1sin α+cos α-1=1+sin αcos α;课后练习【补救练习】1.若sin θcos θ>0,则θ在( )A .第一、二象限B .第一、三象限C .第一、四象限D .第二、四象限2.设角α终边上一点P (-4a,3a )(a <0),则2sin α+cos α的值为() A.25 B.25或-25 C .-25 D .与a 有关3.判断下列各式的符号:(1)sin 340°cos 265°;(2)sin 4tan ⎝⎛⎭⎫-23π4;4.在[0,2π]上,满足sin x ≥12的x 的取值范围为( )A.⎣⎡⎦⎤0,π6B.⎣⎡⎦⎤π6,5π6C.⎣⎡⎦⎤π6,2π3D.⎣⎡⎦⎤5π6,π5.利用三角函数线比较下列各组数的大小(用“>”或“<”连接):(1)sin 23π________sin 45π;(2)cos 23π________cos 45π;(3)tan 23π________tan 45π.6.已知α是第四象限角,cos α=1213,则sin α等于( )A.513 B .-513 C.512 D .-512【巩固练习】1.已知角θ的终边上一点(,2)P m -,且||4OP =,则tan θ=__________。
第1课时 任意角的三角函数(一)任意角的三角函数的定义sin α,即sin α=y cos α,即cos α=x ,即tan α=yx(x ≠0) 正弦、余弦、正切都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,将它们统称为三角函数到一个比值的集合的函数.三角函数值实质是一个比值,因此分母不能为零,所以正切函数的定义域就是使分母不为零的角的集合.Z }三角函数值在各象限的符号口诀:一全正,二正弦,三正切,四余弦状元随笔 对三角函数值符号的理解三角函数值的符号是根据三角函数定义和各象限内坐标符号导出的.从原点到角的终边上任意一点的距离总是正值.根据三角函数定义知:正弦值符号取决于纵坐标y 的符号;.sin 750°=________.类型一三角函数的定义及应用1(1)若角α的终边经过点P(5,-12),则sin α=________,cos α=________,tan α=________ 2x”其他条件不变,结果又如何?的值为;(1)将本例中条件“x>0”改为“x<0”,结果如何?(2)将本例中条件“x>0”改为“x≠0”,结果又怎样?(3)将本例中“P(x,3)”改为“P(x,3x)”,且把“cos θ=10x10”去掉,结果又怎样?A.第一象限B.第二象限C.第三象限D.第四象限(2)判断下列各式的符号:①sin 145°cos(-210°);②sin 3·cos 4·tan 5.方法归纳判断三角函数值正负的两个步骤(1)定象限:确定角α所在的象限.(2)定符号:利用三角函数值的符号规律,即“一全正,二正弦,三正切,四余弦”来判断.注意:若sin α>0,则α的终边不一定落在第一象限或第二象限内,有可能终边落在y 轴的非负半轴上. 跟踪训练1 判断下列各式的符号:(1)sin 145°cos(-210°);(2)sin 3·cos 4·tan 5.2.已知角α的终边过点(3a -9,a +2)且cos α≤0,sin α>0,则实数a 的取值范围是 . 3.设角α是第三象限角,且⎪⎪⎪⎪sin α2=-sin α2,则角α2是第 象限角.(2)sin ⎝⎛⎭⎫-11π6+cos 125π·tan 4π.7.当α为第二象限角时,|sin α|sin α-cos α|cos α|的值是________.8.已知角α的终边经过点P (3,4t ),且sin(2k π+α)=-35(k ∈Z ),则t =________.三、解答题(每小题10分,共20分)9.已知角α的终边为射线y =-34x (x ≥0),求角α的正弦、余弦和正切值.10.判断下列各式的符号:(1)sin 105°·cos 230°;(2)cos 3·tan ⎝⎛⎭⎫-2π3.11.若α是第一象限角,则-α2是( )A .第一象限角B .第四象限角C .第二或第三象限角D .第二或第四象限角 12.若角α的终边与直线y =3x 重合且sin α<0,又P (m ,n )是α终边上一点,且|OP |=10,则m -n =________. 13.计算:(1)sin 390°+cos(-660°)+3tan 405°-cos 540°;(2)sin ⎝⎛⎭⎫-7π2+tan π-2cos 0+tan 9π4-sin 7π3.14.已知角α的终边过点(a,2a )(a ≠0),求角α的正弦、余弦和正切值.第2课时 任意角的三角函数(二)1.相关概念(1)单位圆:以原点O 为圆心,以单位长度为半径的圆. (2)有向线段:带有方向(规定了起点和终点)的线段.规定:方向与x 轴或y 轴的正方向一致的为正值,反之为负值. 2.三角函数线状元随笔 (1)三角函数线的方向.正弦线由垂足指向角α的终边与单位圆的交点,余弦线由原点指向垂足,正切线由切点指向切线与角α的终边或其反向延长线的交点.(2)三角函数线的正负:三条有向线段凡与x 轴或y 轴同向的,为正值,与x 轴或y 轴反向的,为负值. (1)角的三角函数线是直线.( )(2)角的三角函数值等于三角函数线的长度.( )(3)第二象限的角没有正切线.( )2.有下列四个说法:①α一定时,单位圆中的正弦线一定;②单位圆中,有相同正弦线的角相等; ③α和α+π有相同的正切线;④具有相同正切线的两个角终边相同. 不正确说法的个数是( ) A .0个 B .1个 C .2个 D .3个 3.如图所示,在单位圆中角α的正弦线、正切线完全正确的是( )A .正弦线PM ,正切线A ′T ′B .正弦线MP ,正切线A ′T ′C .正弦线MP ,正切线ATD .正弦线PM ,正切线AT 4.已知sin α>0,tan α<0,则α的( )A .余弦线方向向右,正切线方向向下B .余弦线方向向右,正切线方向向上C .余弦线方向向左,正切线方向向下D .余弦线方向向上,正切线方向向左类型一 三角函数线的作法【例1】 作出下列各角的正弦线、余弦线、正切线.(1)-π4;(2)17π6;(3)10π3.类型二 利用三角函数线比较大小【例2】 (1)已知A .若α、β是第一象限角,则sin α>sin β B .若α、β是第二象限角,则tan α>tan β C .若α、β是第三象限角,则sin α>sin β D .若α、β是第四象限角,则tan α>tan β (2)利用三角函数线比较sin2π3和sin 4π5,cos 2π3和cos 4π5,tan 2π3和tan 4π5的大小.方法归纳利用三角函数线比较大小的步骤利用三角函数线比较三角函数值的大小时,一般分三步:①角的位置要“对号入座”;②比较三角函数线的长度;③确定有向线段的正负.跟踪训练1.已知a =sin 2π7,b =cos 2π7,c =tan 2π7,则( )A .a <b <cB .a <c <bC .b <c <aD .b <a <c2 设π4<α<π2,试比较角α的正弦线、余弦线和正切线的长度.如果π2<α<3π4,上述长度关系又如何?类型三 利用三角函数线解不等式(1)cos α>-22;(2)tan α≤33;(3)|sin α|≤12.1.将本例(1)的不等式改为“cos α<22”,求α的取值范围 2.将本例(3)的不等式改为“-12≤sin θ<32”,求α的取值范围3.利用本例的方法,求函数y =2sin x -1的定义域.方法归纳利用三角函数线解三角不等式的方法利用三角函数线求解不等式,通常采用数形结合的方法,求解关键是恰当地寻求点.一般来说,对于sin x ≥b ,cos x ≥a (或sin x ≤b ,cos x ≤a ),只需作直线y =b ,x =a 与单位圆相交,连接原点和交点即得角的终边所在的位置,此时再根据方向即可确定相应的x 的范围;对于tan x ≥c (或tan x ≤c ),则取点(1,c ),连接该点和原点即得角的终边所在的位置,并反向延长,结合图象可得.跟踪训练3 在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合.(1) sin α≥32;(2)cos α≤-12.一、选择题(每小题5分,共25分)1.对三角函数线,下列说法正确的是( ) A .对任意角都能作出正弦线、余弦线和正切线 B .有的角的正弦线、余弦线和正切线都不存在C .任意角的正弦线、正切线总是存在的,但余弦线不一定存在D .任意角的正弦线、余弦线总是存在的,但正切线不一定存在2.如果MP 和OM 分别是角α=7π8的正弦线和余弦线,那么下列结论正确的是( )A .MP <OM <0B .OM >0>MPC .OM <MP <0D .MP >0>OM3.有三个命题:①π6和5π6的正弦线长度相等;②π3和4π3的正切线相同;③π4和5π4的余弦线长度相等.其中正确说法的个数为( ) A .1 B .2 C .3 D .04.使sin x ≤cos x 成立的x 的一个区间是( ) A.⎣⎡⎦⎤-3π4,π4 B.⎣⎡⎦⎤-π2,π2 C.⎣⎡⎦⎤-π4,3π4 D.[]0,π5.如果π4<θ<π2,那么下列各式中正确的是( )A .cos θ<tan θ<sin θB .sin θ<cos θ<tan θC .tan θ<sin θ<cos θD .cos θ<sin θ<tan θ二、填空题(每小题5分,共15分)6.比较大小:sin 1________sin π3(填“>”或“<”).7.不等式tan α+33>0的解集是________________________.8.用三角函数线比较sin 1与cos 1的大小,结果是________.三、解答题(每小题10分,共20分)9.做出下列各角的正弦线、余弦线、正切线.(1)5π6;(2)-2π3.10.利用三角函数线,求满足下列条件的角α的集合:(1)tan α=-1;(2)sin α≤-22.11.已知角α的正弦线和余弦线的方向相反、长度相等,则α的终边在( )A .第一象限的角平分线上B .第四象限的角平分线上C .第二、第四象限的角平分线上D .第一、第三象限的角平分线上12.若cos θ>sin 7π3,利用三角函数线得角θ的取值范围是________.13.若α∈⎝⎛⎭⎫0,π2,试利用三角函数线证明sin α+cos α>1.。