下载文档原格式
杭州电子科技大学全国硕士研究生入学考试业务课考试大纲考试科目名称：自动控制原理科目代码：861 一、自动控制的一般概念1．自动控制和自动控制系统的基本概念，负反馈控制原理。
2．控制系统的组成与分类。
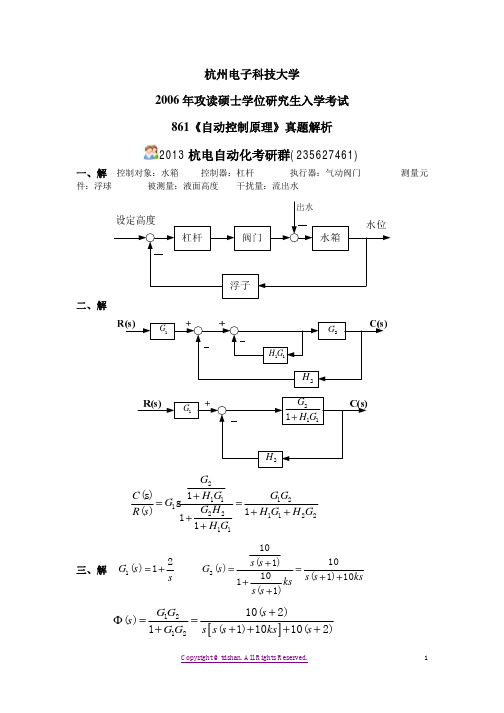
3．根据实际系统的工作原理画控制系统的方块图。
二、控制系统的数学模型1．控制系统微分方程的建立，拉氏变换求解微分方程。
2．传递函数的概念、定义和性质。
3．控制系统的结构图，结构图的等效变换。
4．控制系统的信号流图，结构图与信号流图间的关系，由梅孙公式求系统的传递函数。
三、线性系统的时域分析1．稳定性的概念，系统稳定的充要条件，劳斯稳定判据。
2．稳态性能分析（1）稳态误差的概念，根据定义求取误差传递函数，由终值定理计算稳态误差。
（2）静态误差系数，系统型别与静态误差系数，影响稳态误差的因素。
3．动态性能分析（1）一阶系统特征参数与动态性能指标间的关系。
（2）典型二阶系统的特征参数与性能指标的关系。
（3）附加闭环零极点对系统动态性能的影响。
（4）主导极点的概念，用此概念分析高阶系统。
四、线性系统的根轨迹法1．根轨迹的概念，根轨迹方程，幅值条件和相角条件。
2．绘制根轨迹的基本规则。
3．参数根轨迹的概念。
4．用根轨迹分析系统的性能。
五、线性系统的频域分析1．频率特性的定义，幅频特性与相频特性。
2．用频率特性的概念分析系统的稳态响应。
3．频率特性的几何表示方法。
（1）典型环节及开环系统幅相频率特性曲线（乃氏曲线或极坐标图）的画法。
（2）典型环节及开环系统对数频率特性曲线（伯德图）的画法。
（3）由对数幅频特性求最小相位系统的开环传递函数。
4．乃奎斯特稳定性判据。
（1）根据乃氏曲线判断系统的稳定性。
（2）由对数频率特性判断系统的稳定性。
5．稳定裕量（1）当系统稳定时，系统相对稳定性的概念。
（2）幅值裕量和相角裕量的定义及计算。
6．闭环频率特性的有关指标及近似估算。
7．频域指标与时域指标的关系。
六、系统校正1．校正的基本概念，校正的方式，常用校正装置的特性，串联超前、迟后、迟后－超前和PID校正方法。
杭电复试题目
杭电是指杭州电子科技大学，复试题目因专业而异，以下是可能出现在杭电研究生复试中的一些常见题目：
介绍一下自己的本科毕业论文或项目，并讲述你在其中的角色和贡献；
简述你的研究方向，并说明你对这个方向的兴趣和研究计划；
研究生期间你打算加入哪些实验室或课题组？请说明你的选择理由；
针对你所报考的专业，提出一些与该专业相关的问题，并请回答；
简要介绍你的个人优势和不足，并说明如何克服不足；
对于未来的发展，你有什么样的职业规划和目标？
需要注意的是，以上仅是可能出现的题目之一，具体题目还可能根据专业和个人情况而有所不同。
自动化考研面试题自动化是一门涉及控制、测量、通信和计算机科学的综合学科，广泛应用于工业生产、交通运输、能源管理等领域。
对于那些有志于深入研究自动控制理论和应用的学生来说，考取自动化专业的研究生是一个重要的里程碑。
在自动化考研面试中，面试官通常会针对学生的专业知识、研究背景和未来发展计划等方面进行提问。
下面是一些常见的自动化考研面试题，供参考。
1. 请简要介绍一下自动控制理论及其在实际应用中的作用。
自动控制理论是研究自动化系统的建模、分析和控制方法的学科。
它主要涉及系统的动力学分析、控制器设计以及反馈机制等方面。
在实际应用中，自动控制理论可以帮助提高生产过程的稳定性和效率，降低能源的消耗，并且在机器人、航空航天、智能交通等领域具有广泛应用。
2. 请谈谈您在本科期间的研究方向和成果。
在本科期间，我主要从事自动控制系统的建模与仿真研究。
我使用MATLAB等工具，对某一具体系统进行建模，并通过仿真分析系统的控制性能。
在这个过程中，我深入了解了系统的动力学特性、传感器和执行器的性能，以及控制器设计中的常见问题。
我最终完成了一篇论文，并发表在某自动化领域的国际期刊上。
3. 您对自动控制系统中的PID控制器有何了解？PID控制器是自动控制系统中最常用的控制器之一。
它通过比较被控对象的实际输出值和期望输出值，计算出一个控制信号，从而实现对被控对象的控制。
其中P代表比例控制，I代表积分控制，D代表微分控制。
PID控制器具有简单、易实现的特点，并且在许多工业应用中取得了良好的效果。
4. 在自动化系统中，您认为最重要的传感器是什么？请解释一下其重要性。
在自动化系统中，传感器是获取外部环境信息并将其转换为可用信号的设备。
在我看来，最重要的传感器是温度传感器。
温度是许多工业过程的关键参数，对于控制系统的稳定性和安全性都有重要的影响。
温度传感器的准确性和可靠性对于实时监测和控制工艺温度至关重要。
5. 请谈谈您对物联网在自动化领域中的应用前景。
