高中数学正弦三角函数的图像与性质

三角函数的图像与性质三角函数的图像与性质在数学中，三角函数是一种基本的函数类型，其中的很多图像和性质对理解数学十分重要。

它们有助于理解各种模型的表示和应用，增强数学思维的能力和加深数学知识。

本文就三角函数的图像与性质做一些简单的介绍。

I、三角函数图像1、正弦曲线：正弦曲线是由参数从0到2π（2π是将一个周期跨越两次）形成的空间曲线。

它是圆的切线，有一定的规律性，并且把圆分为一个完整的一个周期，表现的曲线是一个“s”字形，形成有节奏的变化形式。

2、余弦曲线：余弦曲线是一条由参数从0到2π（2π是将一个周期跨越两次）形成的空间曲线，它也是圆的切线，有一定的规律性，但是它把圆分为两个半周期，比较起来更加缓和，表现的曲线是一个“v”字形，形成有节奏的变化形式。

3、正切曲线：正切曲线可以由参数0到π（π是将一个周期跨越一次）形成的曲线。

它也是一个椭圆的切线，有一定的规律性，把椭圆分为一完整周期，表现的曲线是一个“z”字形，形成有节奏的变化形式。

II、三角函数的性质1、周期性：三角函数的周期性就是说其值的变化是有如左图5000式的一个循环周期，在实际应用中可以利用该性质进行参数估计。

2、增减性：三角函数具有明显的增减性，具体表现为当参数逐渐增加时，函数值会自动增大，而当参数逐渐减小时，函数值则会自动减小。

3、几何性：三角函数有一个令人惊讶的性质，即在几何上其值就等于一定参数的弧度，而且参数的变化也不会影响该弧度。

4、极限性：参数π/2处的正切函数的值无穷大，表示非常接近的范围内函数的变化是接近无穷大的，而参数为0处的余弦函数为1，表示函数在某一点的取值趋势没有了变化，变成一个规定值。

总结来说，三角函数可以说是数学之中一个基本的概念，其图形和性质极其重要，可以帮助我们更深入的理解数学，增进数学的应用能力，因此，值得我们认真好好的学习。

三角函数的图像与性质三角函数是数学中的一类重要的函数，包括正弦函数（sin）、余弦函数（cos）、正切函数（tan），以及它们的倒数函数（csc，sec，cot）。

下面是关于三角函数的一些图像与性质：1. 正弦函数（sin）的图像：正弦函数是一个周期函数，它的图像在一个周期内呈现出振荡的形式，取值范围在-1到1之间。

当自变量取0、π/2、π、3π/2等特殊值时，正弦函数的值为0、1、0、-1，分别对应于函数的最小值、最大值、0点和最大负值。

2. 余弦函数（cos）的图像：余弦函数也是一个周期函数，它的图像与正弦函数的图像非常相似，只是相位差了π/2。

余弦函数的取值范围也在-1到1之间，当自变量取0、π/2、π、3π/2等特殊值时，余弦函数的值依次为1、0、-1、0。

3. 正切函数（tan）的图像：正切函数的图像在每个周期上有无穷多个交点，它的值可以为任何实数。

正切函数与正弦函数和余弦函数之间存在着一定的关系，即tan(x) =sin(x) / cos(x)。

当自变量取π/2、3π/2、5π/2等特殊值时，正切函数的值为正无穷大；取-π/2、-3π/2、-5π/2等特殊值时，正切函数的值为负无穷大。

4. 三角函数的周期性：正弦函数、余弦函数和正切函数都是周期函数，它们的周期分别为2π、2π和π。

这意味着，当自变量增加一个周期时，函数的值将重复出现。

例如，sin(x + 2π) = sin(x)。

5. 三角函数的奇偶性：正弦函数是奇函数，余弦函数是偶函数，正切函数是奇函数。

奇函数的图像关于原点对称，即f(-x) = -f(x)；偶函数的图像关于y轴对称，即f(-x) =f(x)。

这些是关于三角函数图像与性质的一些基本信息，三角函数在数学、物理、工程等领域都有广泛的应用。

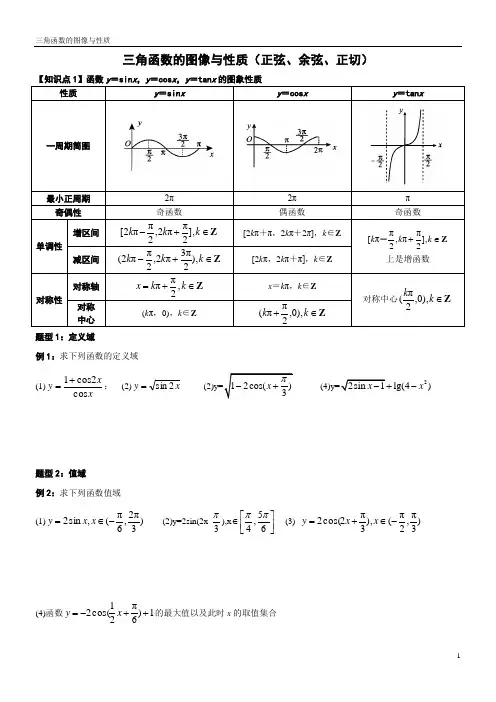
三角函数的图像与性质（正弦、余弦、正切）【知识点1】函数y ＝sin x ，y ＝cos x ，y ＝tan x 的图象性质题型1：定义域例1：求下列函数的定义域(1)xx y cos 2cos 1+=； (2)x y 2sin = 2lg(4)x -题型2：值域 例2：求下列函数值域 (1))3π2,6π(,sin 2-∈=x x y (2)y=2sin(2x-3π),x 5,46ππ⎡⎤∈⎢⎥⎣⎦(3) )3π,2π(),3π2cos(2-∈+=x x y(4)函数1)6π21cos(2++-=x y 的最大值以及此时x 的取值集合题型3：周期例3：求下列函数的周期： （1）f(x)=2sin2x (2)y=cos(123x π-) (3)y=tan(2x 4π-) （4）y=sin x 例4： 若函数()2sin(2)3f x kx π=+的最小正周期T 满足12T <<,则自然数k 的值为______.例5：若)10(sin 2)(<<=ϖϖx x f 在区间[0,]3π上的最大值是2，则ϖ=________.例6：使x y ωsin =（ω＞0）在区间[0，1]至少出现2次最大值，则ω的最小值为【 】A ．π25B ．π45C ．πD ．π23例7：设函数f(x)=2sin(25x ππ+),若对于任意的x R ∈,都有f(1x )2()()f x f x ≤≤成立，则12x x -的最小值是A.4B.2C.1D.12题型4：奇偶性 例8：函数y ＝sin （x ＋2π）（x ∈［－2π，2π］）是【 】A.增函数B.减函数C.偶函数D.奇函数例9：判断下列函数的奇偶性 (1)y=xsin(x π+) (2)y=cos 1sin x x+例10：已知函数f(x)=x 3cosx+1,若f(a)=11,则f(-a)=________ 题型5：单调性例11：函数y =21log sin(2x +4π)的单调递减区间是【 】 A.（k π－4π,k π］(k ∈Z ) B.（k π－8π,k π+8π］(k ∈Z ) C.（k π－83π,k π+8π］(k ∈ D.（k π+8π,k π+83π］(k ∈Z )例12：.求1cos()3412logx y π+=的单调区间例13：求下列函数的单调增区间(1))3π21cos(-=x y ; (2) ]0,π[),6π2sin(2-∈+=x x y ；(3))23πsin(2x y -=例14：（1）求函数y=2sin(2x-3π)的单调递减区间。

常见三角函数图像及性质三角函数在数学中具有重要的作用，主要有正弦函数、余弦函数和正切函数。

这些三角函数的图像及性质对理解三角函数在不同角度下的变化规律至关重要。

1. 正弦函数（Sine Function）正弦函数可以表示为 $y = \\sin(x)$，其中x表示自变量（角度），x表示函数值。

正弦函数的图像是一条波浪形状的曲线，在 $[-\\pi, \\pi]$ 区间内，正弦函数的图像在原点(0,0)处达到最大值1和最小值−1，且图像在x轴上对称。

正弦函数的主要性质包括：•周期性：正弦函数的周期是 $2\\pi$，即 $f(x+2\\pi) = f(x)$。

•奇函数：正弦函数是奇函数，即x(−x)=−x(x)。

•范围：正弦函数的值域为[−1,1]。

•正负性：在第一和第二象限，正弦函数为正；在第三和第四象限，正弦函数为负。

2. 余弦函数（Cosine Function）余弦函数可以表示为 $y = \\cos(x)$，余弦函数的图像是一条类似正弦函数的波浪形状曲线，不过余弦函数的图像在x轴上下移了 $\\frac{\\pi}{2}$。

余弦函数的性质包括：•周期性：余弦函数的周期也是 $2\\pi$，即$f(x+2\\pi) = f(x)$。

•偶函数：余弦函数是偶函数，即x(−x)=x(x)。

•范围：余弦函数的值域为[−1,1]。

•正负性：在第一和第四象限，余弦函数为正；在第二和第三象限，余弦函数为负。

3. 正切函数（Tangent Function）正切函数可以表示为 $y = \\tan(x)$，正切函数的图像是一条周期性的曲线，其在某些角度处会出现无穷大的值。

正切函数的图像在 $x=k\\pi + \\frac{\\pi}{2}$ 时，即 $x =\\frac{\\pi}{2}, \\frac{3\\pi}{2}, \\frac{5\\pi}{2}$ 等，会出现垂直渐近线。

正切函数的性质包括：•周期性：正切函数的周期是 $\\pi$，即 $f(x+\\pi) = f(x)$。

高中数学三角函数图像的性质及变换规律三角函数是高中数学中重要的内容之一，它们的图像性质及变换规律是我们学习和应用三角函数的基础。

在本文中，我将详细介绍正弦函数、余弦函数和正切函数的图像性质，并讨论它们的平移、伸缩和翻转变换规律。

一、正弦函数的图像性质及变换规律正弦函数的图像是一条连续的波浪线，它的周期是2π，振幅为1。

正弦函数的图像在原点处有一个特殊点，即(0, 0)，称为正弦函数的零点。

正弦函数的图像在每个周期内呈现对称性，即关于y轴对称。

下面我们来看一个具体的例子：求解方程sin(x) = 0.5在区间[0, 2π]内的解。

首先，我们可以通过观察正弦函数的图像，知道sin(x) = 0.5有两个解，一个在第一象限，一个在第二象限。

我们可以通过求解sin(x) = 0.5的解析解来验证这一点。

sin(x) = 0.5的解析解为x = π/6 + 2πn和x = 5π/6 + 2πn，其中n为整数。

在区间[0, 2π]内，满足sin(x) = 0.5的解为x = π/6和x = 5π/6。

这个例子说明了正弦函数的图像性质，以及如何通过观察图像来快速得到方程的解。

二、余弦函数的图像性质及变换规律余弦函数的图像也是一条连续的波浪线，它的周期也是2π，振幅为1。

余弦函数的图像在原点处有一个特殊点，即(0, 1)，称为余弦函数的最大值点。

余弦函数的图像在每个周期内呈现对称性，即关于y轴对称。

下面我们来看一个具体的例子：求解方程cos(x) = -0.5在区间[0, 2π]内的解。

根据余弦函数的图像性质，我们可以知道cos(x) = -0.5有两个解，一个在第二象限，一个在第三象限。

我们可以通过求解cos(x) = -0.5的解析解来验证这一点。

cos(x) = -0.5的解析解为x = 2π/3 + 2πn和x = 4π/3 + 2πn，其中n为整数。

在区间[0, 2π]内，满足cos(x) = -0.5的解为x = 2π/3和x = 4π/3。

正弦函数图像及性质
正弦函数是经典的三角函数，是一种双曲线形式的函数。

它表示某一Angle的正弦值，在数学中有很重要的地位。

在几何图表中，正
弦函数图像是一条波浪状线，也可用多边形方式表示正弦函数图像，
正弦函数图像的性质如下：
1. 正弦函数的自变量范围是从0到2π，即[0,2π]，正弦函数的值的范围是从-1到+1，即[-1,1]。

2. 正弦函数在(0,π/2)和(π,3π/2)之间单调递增，在(-
π/2,0)和(3π/2,2π)之间单调递减。

3. 正弦函数在(0,π/2)和(π,3π/2)之间为凸函数，在(-
π/2,0)和(3π/2,2π)之间为凹函数。

4. 正弦函数在(0,π/2)和(π,3π/2)之间的极值点是(π/2,1)
和(3π/2,-1)，在(-π/2,0)和(3π/2,2π)之间的极值点是(-π/2,-1)和(3π/2,1)。

5. y=sin x曲线是一个周期性的曲线，其中一个周期的长度为
2π。

正弦函数的几何图形表示的不仅是某一角度的正弦值，而且还有象征时间周期性变化的潮汐效应。

正弦函数可以解释声音波动，电磁
波动，水波动，电子信号等各种自然现象，其在数学、物理、工程等
领域有着重要作用，因此，深入理解正弦函数图像及其性质，对我们
有重要意义。

三角函数的性质和图像
三角函数的性质与其连续变化的图像形状之间息息相关，为我们解释物理世界中复杂物理关系提供了重要依据。

五个小标题，相关内容
三角函数的性质和图形
1、定义
三角函数是用变量对正n角形的三种角度和相应角的大小而表达的关系式，主要包括正弦函数sinH，余弦函数 cosH和正切函数 tanH。

2、几何性质：
三角函数在几何中有一些性质，例如正弦函数SinH，余弦函数CosH 和正切函数tanH全部符合三角形的特性，其中的SinH和CosH的图像是三角形的内切圆，而tanH的图像是三角形的外切圆。

3、参数性质：
任意线性变换，三角函数的图像也被重新变换，只要保持原来变量关
系，图像也保持类型不变。

4、增减性质：
在某种范围内，正弦函数SinH和余弦函数CosH都是增函数，正切函数TanH是减函数。

5、图像特点：
三角函数的图像大体上是正弦曲线，在Π/2位置有拐点，有半波长形状，在此基础上可以通过变换做出不同的图形。

三角函数的图像与性质详解在数学领域中，三角函数是一组常见且重要的函数。

它们不仅具有许多实际应用，同时也有着丰富的图像特性和数学性质。

本文将详细介绍三角函数的图像和性质，以帮助读者更好地理解和应用这些函数。

一、正弦函数的图像与性质正弦函数是最基本的三角函数之一，用符号sin表示。

正弦函数的图像是一个连续的波形，具有以下性质：1. 周期性：正弦函数的图像在一个周期内重复。

正弦函数的周期由2π决定。

2. 对称性：正弦函数的图像关于y轴对称，即f(x) = -f(-x)。

3. 范围：正弦函数的值在[-1, 1]的范围内变化。

二、余弦函数的图像与性质余弦函数是另一个常见的三角函数，用符号cos表示。

余弦函数的图像也是一个连续的波形，具有以下性质：1. 周期性：余弦函数的图像也在一个周期内重复。

余弦函数的周期同样由2π决定。

2. 对称性：余弦函数的图像关于y轴对称，即f(x) = f(-x)。

3. 范围：余弦函数的值同样在[-1, 1]的范围内变化。

三、正切函数的图像与性质正切函数是三角函数中的另一个重要成员，用符号tan表示。

正切函数的图像具有以下性质：1. 周期性：正切函数的图像在每个π的倍数处出现垂直渐近线。

因此，正切函数没有固定的周期。

2. 对称性：正切函数的图像关于原点对称，即f(x) = -f(-x)。

3. 范围：正切函数在定义域内可以取任何实数值。

四、其他三角函数除了正弦、余弦和正切函数之外，还有许多与三角函数相关的函数，例如反正弦、反余弦和反正切函数。

这些函数的图像和性质相对复杂，超出了本文的范围。

感兴趣的读者可以进一步学习和了解这些函数的性质。

综上所述，三角函数是数学中常见而重要的函数。

它们的图像和性质有助于我们理解和应用这些函数。

通过研究三角函数的性质，我们可以更好地解决与周期性和周期性相关的问题，例如波动、震动和周期性运动。

希望本文的内容能够对读者在学习和应用三角函数时有所帮助。

三角函数的图像与性质三角函数是数学中常见的一类函数，包括正弦函数、余弦函数、正切函数等等。

它们在数学和物理学等领域中具有重要的应用和性质。

本文将讨论三角函数的图像与性质，并通过图像展示它们的特点。

一、正弦函数（sine function）正弦函数是最基本的三角函数之一，由于其周期性的特点，在图像上呈现出波浪形状。

在单位圆上，正弦函数的图像可以用来表示角度和弧度的关系。

正弦函数的图像可以通过以下步骤绘制出来：1. 将横轴分成一定的单位，例如每个单位代表30°或π/6。

2. 在每个单位上确定正弦函数的值，即纵坐标的位置。

3. 将所有的点依次连接起来，得到正弦函数的图像。

正弦函数的图像具有以下性质：1. 周期性：正弦函数的一个周期是360°或2π。

在一个周期中，正弦函数的值从最小值到最大值再返回最小值。

2. 对称性：正弦函数是奇函数，其图像关于原点对称。

即f(x) = -f(-x)。

3. 幅值：正弦函数的幅值为1，即图像的振幅为1。

4. 位置：正弦函数的图像在(x, f(x))的点上经过零点。

二、余弦函数（cosine function）余弦函数是另一个重要的三角函数，其图像也呈现出波浪形状，但与正弦函数有一定的相位差。

余弦函数在数学中的应用广泛，例如表示交流电信号的变化。

余弦函数的图像可以通过类似于正弦函数的步骤绘制出来。

余弦函数的图像具有以下性质：1. 周期性：余弦函数的一个周期也是360°或2π。

在一个周期中，余弦函数的值从最大值到最小值再返回最大值。

2. 对称性：余弦函数是偶函数，其图像关于y轴对称。

即f(x) = f(-x)。

3. 幅值：余弦函数的幅值也为1，即图像的振幅为1。

4. 位置：余弦函数的图像在(x, f(x))的点上经过最大值。

三、正切函数（tangent function）正切函数是三角函数中最特殊的一个，其图像呈现出一系列的尖峰和波谷。

正切函数在解决直角三角形问题时经常使用，也在物理学中广泛应用。

1定义编辑数学术语正弦函数是三角函数的一种.定义与定理定义：对于任意一个实数x都对应着唯一的角（弧度制中等于这个实数），而这个角又对应着唯一确定的正弦值sin x，这样，对于任意一个实数x都有唯一确定的值sin x与它对应，按照这个对应法则所建立的函数，表示为f(x)=sin x，叫做正弦函数。

正弦函数的定理：在一个三角形中，各边和它所对角的正弦的比相等，即a/sin A=b/sin B=c/sin C 在直角三角形ABC中，∠C=90°，y为一条直角边，r为斜边，x为另一条直角边（在坐标系中，以此为底），则sin A=y/r,r=√（x^2+y^2）2性质编辑图像图像是波形图像（由单位圆投影到坐标系得出），叫做正弦曲线(sine curve)正弦函数x∈&amp定义域实数集R值域[-1，1] （正弦函数有界性的体现）最值和零点①最大值：当x=2kπ+（π/2），k∈Z时，y(max)=1②最小值：当x=2kπ+（3π/2），k∈Z时，y(min)=-1零值点：（kπ,0) ，k∈Z对称性既是轴对称图形，又是中心对称图形。

1）对称轴：关于直线x=（π/2）+kπ，k∈Z对称2）中心对称：关于点（kπ，0），k∈Z对称周期性最小正周期：y=sinx T=2π奇偶性奇函数（其图象关于原点对称）单调性在[-π/2+2kπ，π/2+2kπ]，k∈Z上是单调递增.在[π/2+2kπ，3π/2+2kπ]，k∈Z上是单调递减.3正弦型函数及其性质编辑正弦型函数解析式：y=Asin（ωx+φ）+h各常数值对函数图像的影响：φ（初相位）：决定波形与X轴位置关系或横向移动距离（左加右减）ω：决定周期（最小正周期T=2π/|ω|）A：决定峰值（即纵向拉伸压缩的倍数）h：表示波形在Y轴的位置关系或纵向移动距离（上加下减）作图方法运用“五点法”作图“五点作图法”即当ωx+φ分别取0，π/2，π，3π/2，2π时y的值.单位圆定义图像中给出了用弧度度量的某个公共角。