液面变化专题

首先出几道关于初中物理中浮力方面的液面变化类题：1、一块冰漂浮在容器的水面上，冰块中含有一块小木块，当冰完全熔化后，容器中的水面如何变化？2、一块冰漂浮在容器的水面上，冰块中含有一定质量的煤油，当冰完全熔化后容器中的液面如何变化？3、一块冰漂浮在容器的水面上，冰块中含有一定质量的盐水，当冰完全熔化后，容器中的水面如何变化？4、一块冰漂浮在容器的水面上，冰块中含有一定质量的气体（空气、氢气、二氧化碳），当冰完全熔化后，容器中的水面如何变化？对于液体中的物体由于某种变化而引起的液面升降问题，经常困惑着学生．考虑到这类问题在各种考试中多以填空、选择题的形式出现，本文介绍一种简便快捷的判断方法——“状态法”．一、什么叫状态法所谓“状态法”，就是对变化前后液体中的物体所处的状态进行比较来判断液面的升降．二、如何用“状态法”速断液面升降若变化前后液体中的物体都处于漂浮、悬浮状态，而无沉体出现，则液面不变；若液体中的物体，在变化前无沉体，而变化后有沉体出现，则液面下降；若液体中的物体，在变化前有沉体，而变化后无沉体出现，则液面升高．说明：变化前后液体中物体的总质量保持不变；容器中液体的密度不变．三、证明设液体中的物体的总重为G，变化前后在液体中所受的总浮力分别为Ｆ浮、Ｆ浮′．若变化前后均无沉体出现，由浮沉条件知Ｆ浮′＝Ｆ浮＝Ｇ，ρ液ｇＶ排′＝ρ液ｇＶ排，则Ｖ排′＝Ｖ排，液面不变．若变化前无沉体，变化后有沉体，由浮沉条件知Ｆ浮＝Ｇ，Ｆ浮′＜Ｇ，则Ｆ浮′＜Ｆ浮，即Ｖ排′＜Ｖ排，故液面下降．若变化前有沉体，变化后无沉体，由浮沉条件知Ｆ浮＜Ｇ，Ｆ浮′＝Ｇ，则Ｆ浮′＞Ｆ浮，即Ｖ排′＞Ｖ排，故液面上升．四、应用举例例1（2010.年贵阳）有三个实心小球甲、乙、丙，甲球在水中悬浮，乙球在水中下沉，丙球漂浮在水面上．现将甲、乙、丙三球同时放在一只敞口的小铁盒里，然后将小铁盒漂浮在盛水的容器中（如图1所示），下列判断正确的是（）A ． 只将小球甲从盒中取出放入水中后，容器中水面高度不变B ． 只将小球乙从盒中取出放入水中后，容器中水面高度下降C ． 只将小球丙从盒中取出放入水中后，容器中水面高度上升D ． 将甲、乙、丙三球同时放入水中后，容器中水面下降解析 原来的铁盒在水中漂浮，将小球从盒中取出放入水中后，铁盒仍漂浮，甲球悬浮，乙球下沉，丙球漂浮．显然，只要不将乙球取出放入水中，就无沉体出现，容器中的水面不变；当将乙球取出放入水中时，因有沉体出现，容器中的水面下降，故答案应选Ａ、Ｂ、Ｄ．例2（1997年北京） 如图2所示，在一较大容器的水面上放一木块，木块上面放一个体积为1分米3、重7.84牛的物体，此时木块漂浮．如果将物体从木块上拿下并放入水中，当木块和物体都静止时，容器中的水面将（ ）Ａ．上升Ｂ．下降Ｃ．不变Ｄ．无法判断 解析 将物体从木块上拿下后，木块仍漂浮在水面，容器中水面的变化取决于物体放入水中静止时所处的状态．因为ρ物＝Ｇ物／ｇＶ物＝0.8×103千克／米3＜ρ水，所以物体在水中静止呈漂浮状态，容器中水面不变．故答案应选Ｃ．例3 如图3所示，在盛水的缸底有一个实心铁球，水面上漂浮着一个脸盆．若将铁球捞出放入盆中，盆仍漂浮在水面上，则缸底所受水的压强（ ）Ａ．变大Ｂ．变小Ｃ．不变Ｄ．无法判断解析 此题虽然是液体压强大小问题，但根据液体压强公式ｐ＝ρｇｈ知，水的密度不变，压强大小取决于水的深度，即此题实质仍是判断水面变化问题． 原来水中的铁球沉底，脸盆漂浮：当将铁球捞出放入盆中后，脸盆和铁球呈漂浮状态．由“状态法”可判断缸里的水面上升，则缸底受到水的压强变大，故答案应选Ａ．甲 乙 丙图8-15。

备战2021年中考物理光、热、力学典型专题各个击破专题12 浮力中液面变化问题******************************************************************** 一．选择题（共4小题）1．如图所示，烧杯和水的总质量是1kg，烧杯与水平桌面的接触面积是200cm2，将一个质量是700g、体积是1000cm3的立方体A用细线吊着，然后将其体积的一半浸入烧杯内的水中。

下列选项正确的是（）（烧杯厚度忽略不计，杯内水没有溢出，g＝10N/kg，ρ水＝1.0×103kg/m3）A．A受到的浮力为50NB．水对A底部的压强为50PaC．烧杯对水平桌面的压强是750PaD．若剪断绳子，待A静止后，水对容器底部增大的压力为5N【解答】解：A、物体A的一半浸入水中时受到的浮力：F浮＝ρ水gV排＝1.0×103kg/m3×10N/kg××1000×10﹣6m3＝5N，故A错误；B、由V＝a3可得，物体A的边长：a＝＝＝10cm＝0.1m，A的底部到水面的高度：h＝×0.1m＝0.05m，水对A底部的压强：p＝ρ水gh＝1.0×103kg/m3×10N/kg×0.05m＝500Pa，故B错误；C、烧杯对水平桌面的压力等于烧杯和水的重力、物体A对水向下的作用力之和，即：F＝G杯和水+F浮＝1kg×10N/kg+5N＝15N，烧杯对水平桌面的压强：p＝＝＝750Pa，故C正确；D、A的重力：G A＝m A g＝700×10﹣3kg×10N/kg＝7N，物体A的全部浸入水中时受到的浮力：F浮＝ρ水gV排＝1.0×103kg/m3×10N/kg×1000×10﹣6m3＝10N ＞7N，所以A将漂浮，物体A受到浮力等于重力，即7N，则物体A受到浮力的变化量：：△F浮＝7N﹣5N＝2N，由于力作用是相互的，水对A有向上的浮力，物体A对水有向下压力，所以水对烧杯底部增大的压力：△F＝△F浮＝2N，故D错误。

精锐教育学科教师辅导讲义【模块一】考点解析知识复习：1.阿基米德原理：浸在液体中的物体受到向上的浮力，浮力的大小等于它排开的液体受到的重力。

F=G=p gV浸没时审排=守物排部分浸入时V排=V-V出2•物体的浮沉条件(1)浸没在液体中的物体(VF<G，下沉p<p)浮物液〃物F〉G,上浮p〉pJ浮物液尸物7F浮=6物'悬浮9厂p物F=G(V<V)浮物'排物(2)漂浮在液面上的物体：液面升降问题类型容器中的固态物质投入水中后判断液面升降实质是比较前后V的变化。

排实验：情景如图所示，小船和石块一起漂浮在水中，将石块(或金属块)从船中取出放入水中后，你观察到的现象是水面。

怎样用理论知识解释你看到的现象理论推导:变化：如果将沉在水底的石块放入船中使船漂浮，液面如何变化？原因是：。

进一步探讨：从船中取出怎样的固态物质放入水中，水面不变？原因是：。

类型一的结论是:此类问题判断前后液面变化，实质是比较V排的变化，因为液体密度不变，浮力跟V排有关，所以转化为判断浮力的变化。

若浮力变大，则V排变大，排排液面；若浮力变小，则V排变小，液面；若浮力不变，则V排排排不变，液面。

丛容器中往水中投放固态物质，也可以比较P物和P液的关系，若P物〉P液,则液面；若卩物W P液，则液面。

反馈练习：如图所示，一个小船中放有ABC三个小球，小船和球一起漂浮在水面上，其中A 球密度小于水，B球密度等于水，C球密度大于水，小船可以自由的漂浮在水面上。

①只将A球放入水则A球（填浮沉状液面（填“上升”或“下降”或变”）②只将B球放入水则B球（填浮沉状液面（填“上升”或“下降”或变”）③只将C球放入水则C球（填浮沉状液面（填“上升”或“下降”或④若将ABC三球同时从船中取出放入水中，则液面填“上升”或“下降”或“不变”）。

液面升降问题类型二一类型二：纯冰浸于液体，熔化后判断液面升降分析：冰块熔化后化成水，体积变小且水具有流动性。

浮力专题：浮力习题中的液面变化问题【例1】（纯冰熔于液体）容器内分别装有水和盐水，在液面上浮着一块冰，问：（1）冰在水中熔化后，水面如何变化?（2）冰在盐水中熔化后，液面如何变化?【答案】（1）不变；（2）上升【解析】液面是否变化，关键是看V排是否等于V化水。

（1）①当冰漂浮时，依漂浮条件知，F浮=G冰即ρ水ɡV排= G冰= m冰g ∴V排＝m冰/ρ水②冰化成水后，冰的质量与水的质量没有变化即m化水= m冰∴V化水＝m冰/ρ水③所以V排=V化水即冰块完全熔化后水面高度不变。

（2）同理：纯冰浮在盐水液面上，当冰熔化后液面将上升。

练习1：若一冰块在水中，冰块与容器底部相接触并相互间有压力，则当冰块完全熔化后，容器内的水面将怎样变化？【答案】上升【解析】冰块没有漂浮在水面上，冰块所受浮力小于冰块所受重力，∴熔化前F浮＜G冰，即ρ水g V排＜G冰，故得V排＜m冰/ρ水。

熔化为水的体积V化水=m水/ρ水= m冰/ρ水，∴V排＜V化水，即熔化后水面要上升。

【例2】（冰中有杂质）在盛水的烧杯中漂浮着一块冰，冰中夹着一小木块，问：（1）当冰完全熔化为水时，水面将如何变化？（2）若冰中夹杂着一小石块，冰熔化后液面如何变化？【答案】（1）不变；（2）下降【解析】方法一：比较体积变化法①冰块漂浮时：F浮=G冰+G木即ρ水gV排= G冰+G木,V前排= (m冰+m木)/ ρ水=m冰/ρ水+m木/ρ水②当冰块化成水时：m化水= m冰∴V化水＝m冰/ρ水又因为木块仍漂浮，F木浮= G木即ρ水gV木排= m木g ∴V木排=m木/ρ水V后排=V化水+V木排= m冰/ρ水+ m木/ρ水 (2)由(1)(2)得：V前排= V后排故当冰完全熔化成水时，水面不变。

方法二：比较浮力变化法熔化前冰块和木块都漂浮∴F前浮= G冰+ G木熔化后熔化成的水悬浮，木块仍漂浮∴F后浮= G化水+ G木又G化水= G冰所以F前浮＝F后浮，即熔化前后所受浮力不变，所以液面将不变。

冰融化液面变化问题
例题1：将冰块放在浓盐水中，液面位置如图所示，若冰完全熔化，杯中液面高度将（）
A．上升B．下降C．不变D．无法确定
变式1：将冰块放在水中，液面位置如图所示，若冰
完全熔化，杯中液面高度将（）
A．上升B．下降C．不变D．无法确定
解析：此类“冰融化问题”是一个重难点。

变式2：将冰块放在酒精中，液面位置如图所示，若冰
完全熔化，杯中液面高度将（）
A．上升B．下降C．不变D．无法确定
变式3：烧杯中的一大块冰内含有一定量的砂子，冰块漂浮在水面，杯中水面恰好与杯口相平，且冰块上部高出杯口．在冰块熔化的过程中（）
A．将有水从烧杯中溢出B．水面始终与杯口相平C．烧杯中水面会下降D．水面先有下降，后有水溢出
解析方法：
由于图中冰是漂浮的，
根据浮力公式g m g 冰冰排液浮===G V F ρ
冰融化成水的质量冰水冰m m =→
则：g m g 水冰排液→=V ρ ① 根据密度公式：g g m 水冰水水冰则：→→=⇒=⇒=V V m V m
ρρρ
② 公式①②连列可得：
g V g 水冰水排液→=ρρV 两边同除以g 可得
水冰水排液→=V ρρV 由此公式可以解决任何冰水融化问题
例题1：水液水浓盐水即ρρρρ〉〉
根据公式水冰水排液→=V ρρV
可得：水冰排→〈V V
冰融化得到的水的体积大于冰排开水的体积，则液面将上升 变式1、2、3都可以用此公式计算
欢迎下载，谢谢观看！资料仅供参考学习。

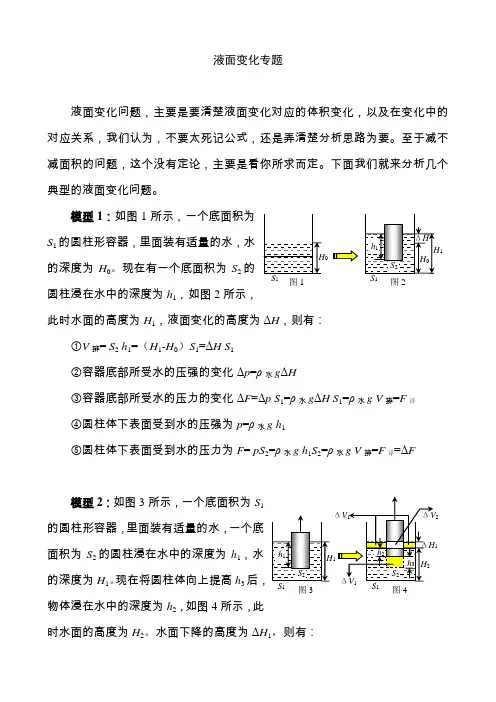
液面变化专题液面变化问题，主要是要清楚液面变化对应的体积变化，以及在变化中的对应关系，我们认为，不要太死记公式，还是弄清楚分析思路为要。

至于减不减面积的问题，这个没有定论，主要是看你所求而定。

下面我们就来分析几个典型的液面变化问题。

模型1：如图1所示，一个底面积为S 1的圆柱形容器，里面装有适量的水，水的深度为H 0。

现在有一个底面积为S 2的圆柱浸在水中的深度为h 1，如图2所示，此时水面的高度为H 1，液面变化的高度为ΔH ，则有：①V 排= S 2 h 1=（H 1-H 0）S 1=ΔH S 1②容器底部所受水的压强的变化Δp =ρ水g ΔH③容器底部所受水的压力的变化ΔF =Δp S 1=ρ水g ΔH S 1=ρ水g V 排=F 浮 ④圆柱体下表面受到水的压强为p =ρ水g h 1⑤圆柱体下表面受到水的压力为F = pS 2=ρ水g h 1S 2=ρ水g V 排=F 浮=ΔF模型2：如图3所示，一个底面积为S 1的圆柱形容器，里面装有适量的水，一个底面积为S 2的圆柱浸在水中的深度为h 1，水的深度为H 1。

现在将圆柱体向上提高h 3后，物体浸在水中的深度为h 2，如图4所示，此时水面的高度为H 2。

水面下降的高度为ΔH 1，则有：图110图211图311图41 2①圆柱体上提引起物体排开水体积的变化ΔV 1= h 3S 2=（S 1- S 2）ΔH 1 ②水面下降引起物体排开水体积的变化ΔV 2=ΔH 1S 2③圆柱体排开水的体积的变化ΔV 排=ΔV 1+ΔV 2=（S 1- S 2）ΔH 1+ΔH 1S 2=ΔH 1S 1 ④圆柱体所受浮力的变化ΔF 浮=ρ水g ΔV 排=ρ水g ΔH 1S 1 ⑤容器底部所受水的压强的变化Δp =ρ水g ΔH 1⑥容器底部所受水的压力的变化ΔF =Δp S 1=ρ水g ΔH 1 S 1=ρ水g V 排=F 浮模型3：如图5所示，一个底面积为S 1的圆柱形水槽，里面装有适量的水，一个底面积为S 2的圆柱形容器内装有一个实心金属球，容器竖直漂浮在水槽的水中，容器浸在水中的深度为h 1，水的深度为为H 0。

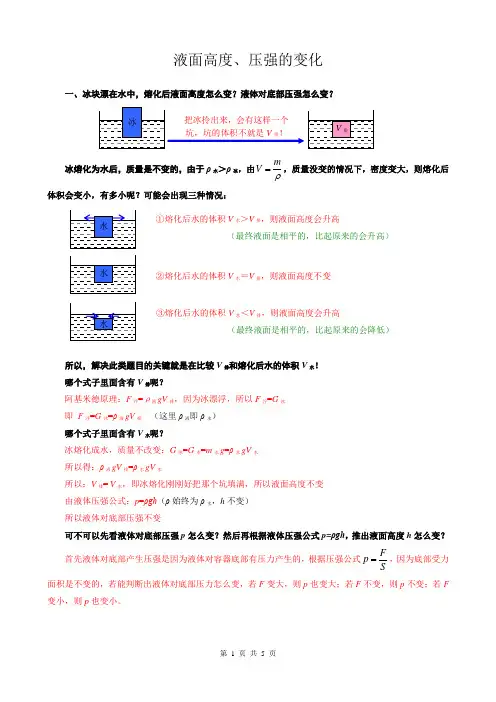
液面高度、压强的变化一、冰块漂在水中，熔化后液面高度怎么变？液体对底部压强怎么变？冰熔化为水后，质量是不变的，由于ρ水＞ρ冰，由m V ρ=，质量没变的情况下，密度变大，则熔化后体积会变小，有多小呢？可能会出现三种情况：所以，解决此类题目的关键就是在比较V 排和熔化后水的体积V 水！哪个式子里面含有V 排呢？阿基米德原理：F 浮=ρ液gV 排，因为冰漂浮，所以F 浮=G 冰即 F 浮=G 冰=ρ液gV 排 （这里ρ液即ρ水）哪个式子里面含有V 水呢？冰熔化成水，质量不改变：G 冰=G 水=m 水g =ρ水gV 水所以得：ρ液gV 排=ρ水gV 水所以：V 排= V 水，即冰熔化刚刚好把那个坑填满，所以液面高度不变由液体压强公式：p =ρgh （ρ始终为ρ水，h 不变）所以液体对底部压强不变可不可以先看液体对底部压强p 怎么变？然后再根据液体压强公式p =ρgh ，推出液面高度h 怎么变？ 首先液体对底部产生压强是因为液体对容器底部有压力产生的，根据压强公式F p S=，因为底部受力面积是不变的，若能判断出液体对底部压力怎么变，若F 变大，则p 也变大；若F 不变，则p 不变；若F 变小，则p 也变小。

把冰拎出来，会有这样一个坑，坑的体积不就是V 排！ V 排 冰 ①熔化后水的体积V 水＞V 排，则液面高度会升高 （最终液面是相平的，比起原来的会升高） 水 ②熔化后水的体积V 水＝V 排，则液面高度不变 水 ③熔化后水的体积V 水＜V 排，则液面高度会升高 （最终液面是相平的，比起原来的会降低） 水综上，得F 支=F 支′，容器底部对液体的支持力没变，故液体对容器底的压力也不变，又因为受力面积没变，所以液体对底部压强p 不变。

由液体压强公式p =ρgh ，ρ始终为ρ水，故液面高度也不变。

二、冰块漂在盐水中，熔化后液面高度怎么变？液体对底部压强怎么变？依然是比较V 排和熔化后水的体积V 水哪个式子里面含有V 排呢？阿基米德原理：F 浮=ρ液gV 排，因为冰漂浮，所以F 浮=G 冰即 F 浮=G 冰=ρ液gV 排 （这里ρ液即ρ盐水）哪个式子里面含有V 水呢？冰熔化成水，质量不改变：G 冰=G 水=m 水g =ρ水gV 水所以得：ρ盐水gV 排=ρ水gV 水即 ρ盐水V 排=ρ水V 水因为 ρ盐水＞ρ水所以：V 排＜ V 水由液体压强公式：p =ρgh （ρ始终为ρ水，h 不变）所以液体对底部压强不变冰 F 支 F 压（水对容器） 液体对容器底部的压力，容器是受力对象，以容器是受力对象不好分析，我们分析它的反作用力，即容器对液体的支持力，它们是大小相等的，所以选择液体，即水作为受力对象，分析熔化前容器底部对水的支持力F 支和熔化后容器底部对水的支持力F 支′。

专题二：液面变化问题【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 在远洋轮船的船舷上，都漆着五条“吃水线”，又称“载重线”。

如图所示，其中标有W的是北大西洋载重线，标有S的是印度洋载重线。

当船从北大西洋驶向印度洋时，轮船受到的浮力以及北大西洋与印度洋的海水密度ρ1和ρ2的关系，正确的是（）A．浮力增大，ρ1＝ρ2B．浮力减小，ρ1＝ρ2C．浮力不变，ρ1>ρ2D．浮力不变，ρ1<ρ22. 如图，小瓷碗漂浮在水面上，倾斜后能沉入水底，关于这一情景分析正确的是（）A．小瓷碗能沉入水底是因为它的重力变大了B．小瓷碗漂浮时受到的浮力大于它的重力C．小瓷碗浸没时受到的浮力比漂浮时受到的浮力大D．小瓷碗浸没后容器底受到水的压强变小了二、填空题3. 小明在水盆中洗碗，发现一个大碗正漂浮在水盆中，如图所示。

他将水盆中的一些水放入大碗中，但大碗仍然漂浮。

与原先相比，大碗所受到的浮力将（选填“变大”、“不变”或“变小”），水盆中的水面将会（选填“上升”、“不变，，或“下降，，）。

4. 如图，放有铁块的杯子漂浮在水面上，如果把铁块用细线悬挂在杯底，杯子和铁块受到的浮力将，水对容器底部的压强将。

（填增大、减小或不变）如果把细线断了，水面将。

三、选择题5. 容器内盛有水，在一试管里面放一小球后，浮在水面上。

如图所示，现将小球取下沉入水中，试管仍浮在水面上，则（）A.液面下降B.液面上升C.容器底部受到的液体的压强不变D.试管下表面受到的液体压强变小6. 如图所示，容器内有水，有一塑料试管下面挂一小铁块，浮在水面上．现将小铁块取下放入试管中，试管仍浮在水面，则（）A．液面上升B．液面下降C．容器底部受到液体的压强不变D．试管外壁上A点受到液体的压强不变7. 如图所示，四个相同的容器内水面一样高，a的容器内只有水，b容器内有木块漂浮在水面上，c容器内漂浮着一块冰块，d容器中悬浮着一个空心球，下列说法正确的一组是（）①四个容器对水平面的压力相等②四个容器中，液体对容器底的压强相同③在b容器中倒入酒精后，木块在液面下体积不变④c容器中冰块熔化后水面高度下降⑤空心球的材料密度可能等于水的密度A．①②⑤ B．①③⑤ C．②⑤ D．①②8. 容器中装有一定质量的水，先后按甲、乙两种方式使物体A和小玻璃杯漂浮在水面上（图中细线重力及体积均不计）．设甲、乙两图中物体A和小玻璃杯共同受到的浮力分别为F甲和F乙，水对容器底的压强分别为p甲和p乙，则（）A．F甲＜F乙 p甲=p乙．B．F甲＞F乙 p甲＞p乙C．F甲=F乙 p甲＜p乙．D．F甲=F乙 p甲=p乙9. （多选）如图（a），在一个较大的容器中盛有水，水中放有一个木块，木块上面放有物体A，此时木块漂浮；如果将A从木块上拿下，并放入水中，当木块和A都静止时（水未溢出），下面说法正确的是（）A．当A的密度小于水的密度时，容器中水面上升B．当A的密度大于水的密度时，容器中水面下降C．当A的密度等于水的密度时，容器中水面下降D．当A的密度大于水的密度时，将A拿下后悬挂在木块下面，如图（b），容器中水面不变10. 如图所示，一块0℃的冰放在盛有0℃水的容器中，已知冰块与容器底部相接触并相互间有压力，当冰块完全熔化为0℃的水后，则容器中水面的位置将（）A.上升B.下降C.保持不变D. 水面的升或降决定于冰和容器内水的体积11. 如图所示，在水平桌面上放置一个装有适量水的锥形瓶，瓶内漂浮着一块冰，冰融化过程中（）A．瓶内水面上升B．水对瓶底的压强减少C．桌面受到的压力增大D．桌面受到的压强不变四、填空题12. 容器内水中放有长方体木块A，木块上方压有密度为4g/cm3的金属块B，此时，木块露出水面的高度为2cm，如图甲所示；用细绳将该金属块系在木块的下方，木块露出水面的高度为3cm，如图乙所示；将细绳剪断后，如图丙所示，则木块露出水面的高度为cm。

学习好资料欢迎下载液面升降问题的分析各种情况都包含，配有详图2018年2月11日对于液体中的物体由于某种变化而引起的液面升降问题的形式出现，本文介绍一种简便快捷的判断方法——“状态法”．（一）、状态法：就是对液体变化前、后的物体所处的状态进行比较来判断液面的上升、下将、不变的方法．（二）、状态法迅速判断液面升降方法：①若变化前后液体中的物体都处于漂浮、悬浮状态，而无沉体出现，则液面不变；②若液体中的物体，在变化前无沉体，而变化后有沉体出现，则液面下降；③若液体中的物体，在变化前有沉体，而变化后无沉体出现，则液面升高;说明：变化前后液体中物体的总质量保持不变；容器中液体的密度不变．（三）、证明设液体中的物体的总重为G，变化前后在液体中所受的总浮力分别为Ｆ浮、Ｆ浮′．若变化前后均无沉体出现，由浮沉条件知①Ｆ浮′＝Ｆ浮＝Ｇ，ρ液ｇＶ排′＝ρ液ｇＶ排，则Ｖ排′＝Ｖ排，液面不变．②若变化前无沉体，变化后有沉体，由浮沉条件知Ｆ浮＝Ｇ，Ｆ浮′＜Ｇ，则Ｆ浮′＜Ｆ浮，即Ｖ排′＜Ｖ排，故液面下降．③若变化前有沉体，变化后无沉体，由浮沉条件知Ｆ浮＜Ｇ，Ｆ浮′＝Ｇ，则Ｆ浮′＞Ｆ浮，即Ｖ排′＞Ｖ排，故液面上升．一、液面升降的主要类型有：类型Ⅰ：纯冰浸于液体，熔化后判断液面升降①、纯冰在纯水中熔化；②、纯冰在盐水（或其它密度比水大的液体）中熔化；③、纯冰在密度比水小的液体中熔化；类型Ⅱ：冰块中含有其它杂质，冰块熔化后判断水面升降。

①、含有木块（或其它密度比水小的固体）的冰块在纯水中熔化；②、含有石块（或其它密度比水大的固体）的冰块在纯水中熔化；③、含有煤油（或其它密度比水小的液体）的冰块在纯水中熔化；类型Ⅲ：冰块中含有一定质量的气体，冰块熔化后判断水面升降。

类型Ⅳ：容器中的固态物质投入水中后判断液面升降①、固态物质的密度小于水的密度②、固态物质的密度等于水的密度③、固态物质的密度大于水的密度二、解题关键：无论液面上升或者下降，关键在比较的问题是什么，确立好问题就知道如何下手。

冰块熔化后液面如何变化漂浮在液面上的冰块熔化后液面如何变化？此类题因其条件的多变，而派生出多题一问的变化。

对于这类问题如果我们抓住冰块熔化前后V排的变化，就可以实现以不变应万变。

例1.漂浮在液面的上冰块（不含杂质）熔化后，液面如何变化？题析: 冰块漂浮时: V排=F浮/ρ液g=G冰/ρ液g (1)冰块熔化后: V排’ =V熔水=G熔水/ρ水g=G冰/ρ水g (2)由(1)(2)可知: ①当ρ液=ρ水时: V排=V排’故液面不变;②当ρ液>ρ水时V排〈V排’液面升高③当ρ冰<ρ液〈ρ水时V排〉V排’液面降低例2.漂浮在水面上的冰块，其中含有固体杂质，当冰块熔化后，水面如何变化？题析:冰块熔化前：V排=F浮/ρ水g=G冰/ρ水g+G物/ρ水g （3）冰块熔化后：㈠ρ物>ρ水则固体沉底V排’=V熔水+V物=G冰/ρ水g+G物/ρ物g（4）由（3）、（4）式可知 V排 >V排’故水面下降㈡ρ物≤ρ水则固体漂浮或悬浮V排’=V熔水+V物排=G冰/ρ水g+G物/ρ水g （5）由（3）（5）式可知V排=V排’故水面不变小结：（1）具备了冰块漂浮水面的条件，则冰块熔化后水面变化情况是①冰块中不含杂质，冰块熔化后水面不变②冰块中含杂质: (a)ρ物>ρ水水面下降(b)ρ物≤ρ水水面不变（2）冰块漂浮在其它液面上,冰块熔化后液面的变化情况是①冰块中不含杂质:：(a) ρ液>ρ水则冰块熔化后液面升高(b)ρ冰<ρ液<ρ水则冰块熔化后液面降低②冰块中含有杂质，同学们不妨自己讨论。

例3.漂浮在液面上的冰块，若冰块中含有气泡，（气泡质量忽略不计）则冰块熔化后，液面如何变化？题析：因气泡质量忽略不计，故。

熔化前：V排=F浮/ρ液g=(G冰+G气)/ρ液g=G冰/ρ液g熔化后：V排=V熔水=G冰/ρ水g讨论同例1例4.漂浮在水面上的冰块，若冰块中含有液体则冰块熔化后液面如何变化？题析：冰块熔化前：V排=F浮/ρ水g=G冰/ρ水g+G液/ρ水g （6）冰块熔化后：V排’=V熔水+V液=G冰/ρ水g+G液/ρ液g （7）由（6）（7）式可知：①当ρ液<ρ水V排<V液面升高排’②当ρ液=ρ水V排=V排’液面不变③当ρ液>ρ水V排>V排’液面下降思考：若含有液体的冰块漂浮在其它液面上,熔化后液面如何变化呢？练习.1试判断下列不含杂质的冰块漂浮在液面上熔化后液面升降情况。