第三章非均相物系的分离及固体流态化
- 格式：ppt
- 大小：4.02 MB
- 文档页数：1
下载文档原格式
合集下载
化工原理 第三章 非均相物系的分离和固体流态化
＜5 μm的颗粒，用袋滤器或湿法捕集； 5 200 μm的颗粒，用旋风分离器除去。
标准旋风 分离器
气体在旋风 分离器里的运动
③ 不宜处理黏性粉尘、含湿量高的粉尘 及 腐蚀性粉尘。
离心沉降23ts6udr??????????????离心力23t6udr??????????????向心力22r24ud???????????????阻力222332ttrs06624uuudddrr?????????????????????????????????????????????2str43duur??????颗粒在离心力场中的运动离心沉降速度沉降分离离心沉降????sstrt24433ugrdduu?????????????形式上相似
沉降分离－重力沉降
④ 求解 ⑴ 试差法
假设颗粒沉降的流型 根据相应的沉降公式求ut 按ut检验Ret
⑵ 摩擦数群法
ut 4 gd s 3
Ret
dut
4d s g 3ut 2 d 2ut 2 2 2 Ret 2
4d 3 s g Ret ＝ 3 2
2 3 ut 向心力= d 6 r
ur 2 2 阻力= d 2 4
2 2 2 π 3 ut π 3 ut ur π 2 s d d d 0 6 r 6 r 2 4
概念－颗粒
3. 颗粒群特性
① 粒径分布 粒径分布→不同粒径范围内所含粒子的个数或质量。 筛分分析： ⑴ 标准筛→泰勒标准筛、日本JIS标准筛和德国标准筛。 ⑵ 筛分过程→筛留物（筛余量）和筛过物（筛过量）。 ⑶ 筛分单位→目数（筛孔大小），指每英寸长度筛网 上的孔数。 比如，100目泰勒筛的筛孔宽度，网线直径为0.0042 in，
标准旋风 分离器
气体在旋风 分离器里的运动
③ 不宜处理黏性粉尘、含湿量高的粉尘 及 腐蚀性粉尘。
离心沉降23ts6udr??????????????离心力23t6udr??????????????向心力22r24ud???????????????阻力222332ttrs06624uuudddrr?????????????????????????????????????????????2str43duur??????颗粒在离心力场中的运动离心沉降速度沉降分离离心沉降????sstrt24433ugrdduu?????????????形式上相似
沉降分离－重力沉降
④ 求解 ⑴ 试差法
假设颗粒沉降的流型 根据相应的沉降公式求ut 按ut检验Ret
⑵ 摩擦数群法
ut 4 gd s 3
Ret
dut
4d s g 3ut 2 d 2ut 2 2 2 Ret 2
4d 3 s g Ret ＝ 3 2
2 3 ut 向心力= d 6 r
ur 2 2 阻力= d 2 4
2 2 2 π 3 ut π 3 ut ur π 2 s d d d 0 6 r 6 r 2 4
概念－颗粒
3. 颗粒群特性
① 粒径分布 粒径分布→不同粒径范围内所含粒子的个数或质量。 筛分分析： ⑴ 标准筛→泰勒标准筛、日本JIS标准筛和德国标准筛。 ⑵ 筛分过程→筛留物（筛余量）和筛过物（筛过量）。 ⑶ 筛分单位→目数（筛孔大小），指每英寸长度筛网 上的孔数。 比如，100目泰勒筛的筛孔宽度，网线直径为0.0042 in，
夏清主编的《化工原理》(第2版)上册-配套题库-名校考研真题-第3章 非均相物系的分离和固体流态化【
圣才电子书
十万种考研考证电子书、题库视频学习平
台
第 3 章 非均相物系的分离和固体流态化
一、填空题 1．影响颗粒沉降速度的因素如下：颗粒的因素、介质的因素、环境因素、设备因素。 就颗粒的因素而言有以下几方面： 、 、 、 等。[四川大学 2008 研] 【答案】尺寸 形状 密度 是否变形 【解析】影响颗粒沉降速度的因素包括以下几个方面：①颗粒的因素：包括尺寸、形 状、密度、是否变形等；②介质的因素：包括流体的状态（气体还是液体）、密度、粘度等； ③环境因素：包括温度（影响 、 ）、压力、颗粒的浓度（浓度达到一定程度使发生干扰 沉降等）；④设备因素：包括体现为壁效用。
答：由公式： dV KA2 dQ 2(V V )
可知增大压力，K 值增大；提高温度，K 值增大，过滤速度增大。 dV 由压力温度滤 dQ
饼的比阻，过滤饼体积比及过滤面积有关。
2．设计一实验流程（画出其实验流程示意图），并写出简要实验步骤，完成如下实验 内容：
（1）进行恒压过滤常数的测定。 （2）进行滤饼的压缩性指数 s 和物料常数 k 的测定。[天津大学 2002 研] 答：简要实验步骤如下： （1）做好准备工作，启动系统。 （2）进行过滤滤液体积和过滤时间关系曲线的测定。 （3）改变过滤压差，再进行不同压差下过滤滤液体积和过滤时间关系曲线的测定， 至少测定 3 条曲线。 （4）关闭系统，复原装置并清扫卫生。 实验流程示意图如图 3-1 所示。
十万种考研考证电子书、题库视频学习平
台
4．从地下开采出来的原油由油、水、气组成，如图 3-2 所示为一原油连续计量装置
的示意图，其原理是将原油中的油、水、气分离后用各自的流量计分别测定其流量（计量），
然后再将油、水、气汇合一起流向下游。具体工艺如下；原油首先切向进入一旋风分离器，
十万种考研考证电子书、题库视频学习平
台
第 3 章 非均相物系的分离和固体流态化
一、填空题 1．影响颗粒沉降速度的因素如下：颗粒的因素、介质的因素、环境因素、设备因素。 就颗粒的因素而言有以下几方面： 、 、 、 等。[四川大学 2008 研] 【答案】尺寸 形状 密度 是否变形 【解析】影响颗粒沉降速度的因素包括以下几个方面：①颗粒的因素：包括尺寸、形 状、密度、是否变形等；②介质的因素：包括流体的状态（气体还是液体）、密度、粘度等； ③环境因素：包括温度（影响 、 ）、压力、颗粒的浓度（浓度达到一定程度使发生干扰 沉降等）；④设备因素：包括体现为壁效用。
答：由公式： dV KA2 dQ 2(V V )
可知增大压力，K 值增大；提高温度，K 值增大，过滤速度增大。 dV 由压力温度滤 dQ
饼的比阻，过滤饼体积比及过滤面积有关。
2．设计一实验流程（画出其实验流程示意图），并写出简要实验步骤，完成如下实验 内容：
（1）进行恒压过滤常数的测定。 （2）进行滤饼的压缩性指数 s 和物料常数 k 的测定。[天津大学 2002 研] 答：简要实验步骤如下： （1）做好准备工作，启动系统。 （2）进行过滤滤液体积和过滤时间关系曲线的测定。 （3）改变过滤压差，再进行不同压差下过滤滤液体积和过滤时间关系曲线的测定， 至少测定 3 条曲线。 （4）关闭系统，复原装置并清扫卫生。 实验流程示意图如图 3-1 所示。
十万种考研考证电子书、题库视频学习平
台
4．从地下开采出来的原油由油、水、气组成，如图 3-2 所示为一原油连续计量装置
的示意图，其原理是将原油中的油、水、气分离后用各自的流量计分别测定其流量（计量），
然后再将油、水、气汇合一起流向下游。具体工艺如下；原油首先切向进入一旋风分离器，
天津大学化工原理课件第三章 非均相混合物分离及固体流态化
53
三、流体通过固体颗粒床层 （固定床）的压降
康采尼（Kozeny）方程
Reb 2
Pf L
5
(1 )2 a 2u
3
2 2
（3-55）
0.17 Reb 330
欧根（Ergun）方程
Pf
(1 ) u (1 ) u 150 3 1.75 3 2 L (s de ) (s de )
u
u ut u ut
阻力
加速度=0 加速度=0
加速度
匀速段
11
二、 球形颗粒的自由沉降
沉降速度
ut
匀速阶段中颗粒相对于流体的运动速度称为 沉降速度，由于该速度是加速段终了时颗粒相对 于流体的运动速度，故又称为“终端速度”，也 可称为自由沉降速度。
4 gd ( s ) ut 3
de Sp s 6 a s d e
2
8
二、 球形颗粒的自由沉降
图3-1 沉降颗粒的受力情况
9
二、 球形颗粒的自由沉降
颗粒受到三个力 重力 浮力 阻力
Fg
Fb
6
6
d 3 S g
d g
3
Fd A
u
2
2
阻力系数或 曳力系数
10
二、 球形颗粒的自由沉降
根据牛顿第二运动定律 3 2 u 2 3 du d ( S ) g d ( ) d S 6 4 2 6 d 分析颗粒运动情况： u0 加速度最大 加速段
床层的比表面积也可用颗粒的堆积密度估算，即
6b 6 1 ab s d d
颗粒的 真实密 度 颗粒的堆 积密度
49
第三章 非均相物系的分离和固体流态化 下
8
2.过滤介质
织物介质，如棉、麻、丝、毛、合成纤维、金属丝等编织成的滤布， 5-65m，工业应用广泛； 堆积介质，细纱、木炭、石棉、硅藻土等细小坚硬的颗粒状物质堆积 而成，多用于深床过滤。 多孔性固体介质，如多孔陶瓷，多孔塑料及多孔金属制成的板式管。 1-3m。
多孔膜：有机膜、无机膜。1 m以下
对乱堆床层，各向同性，床层自由截面积与床层截面积之比等于空 隙率ε； 受壁效应影响，壁面附近床层空隙率大于床层内部。改善壁效应的 方法通常是限制床层直径与颗粒直径之比不得小于某极限值。若床层 的直径比颗粒的直径大得多，则壁效应可忽略。
A自由 A
13
5.流体通过床层流动的压降（数学模型法）
比沉降分离更迅速更彻底，在某些场合下，过滤是沉降的后继操作 属于机械分离操作 外力可以是重力、压强差或惯性离心力
滤浆（料浆）
滤饼
过滤介质
滤液
5
3.4.1 过滤操作的基本概念
1.过滤方式
饼层过滤 >1%(v/v) 过滤方式深床过滤 <0.1%(v/v) 膜过滤
滤浆
滤饼
过滤介质为很厚的颗粒层 不形成滤饼层
22
解:（1)催化剂的当量直径de、球形度ɸs、床层孔隙率ε及比表面积ab
V
3
d 3
6
de
3
6V p
与非球形颗粒体积相等的 球形颗粒的直径。
6 2 de ( d d) 4
1.145d 1.145 3 3.435mm
S d e2 3.4352 s 0.874 2 S p 2 d 2 d 2 1.5 3 4 床层体积－颗粒体积 1－980 1760 0.4432 床层体积 1 6 ab (1 ) ab a(1 ) s d e
(完整版)新版化工原理习题答案(03)第三章非均相混合物分离及固体流态化-题解
第三章 非均相混合物分离及固体流态化1．颗粒在流体中做自由沉降，试计算（1）密度为2 650 kg/m 3，直径为0.04 mm 的球形石英颗粒在20 ℃空气中自由沉降，沉降速度是多少？（2）密度为2 650 kg/m 3，球形度6.0=φ的非球形颗粒在20 ℃清水中的沉降速度为0.1 m/ s ，颗粒的等体积当量直径是多少？（3）密度为7 900 kg/m 3，直径为6.35 mm 的钢球在密度为1 600 kg/m 3的液体中沉降150 mm 所需的时间为7.32 s ，液体的黏度是多少？解：（1）假设为滞流沉降，则：2s t ()18d u ρρμ-= 查附录20 ℃空气31.205kg/m ρ=，s Pa 1081.15⋅⨯=-μ，所以，()()()m 1276.0s m 1081.11881.9205.126501004.018523s 2t =⨯⨯⨯-⨯⨯=-=--μρρg d u 核算流型：3t 51.2050.12760.04100.3411.8110du Re ρμ--⨯⨯⨯===<⨯ 所以，原假设正确，沉降速度为0.1276 m/s 。
（2）采用摩擦数群法()()s 123t 523434 1.81102650 1.2059.81431.93 1.2050.1g Re u μρρξρ---=⨯⨯-⨯==⨯⨯ 依6.0=φ，9.431Re 1=-ξ，查出：t e t 0.3u d Re ρμ==，所以： 55e 0.3 1.8110 4.50610m 45μm 1.2050.1d --⨯⨯==⨯=⨯ （3）假设为滞流沉降，得：2s t()18d g u ρρμ-= 其中 s m 02049.0s m 32.715.0t ===θh u将已知数据代入上式得：()s Pa 757.6s Pa 02049.01881.91600790000635.02⋅=⋅⨯⨯-=μ 核算流型t 0.006350.020*******.0308116.757du Re ρμ⨯⨯===< 2．用降尘室除去气体中的固体杂质，降尘室长5 m ，宽5 m ，高4.2 m ，固体杂质为球形颗粒，密度为3000 kg/m 3。
2019年-化工原理第三章非均相物系的分离及固体流态化-PPT课件-PPT精选文档
A
r1 O
r2
r
B ur C
uT u
颗粒在旋转流场中的运动
比较：沉降速度的大小、方向
化工原理
材料与化学工程学院
非均相物系的分离和固体流态化 化学工程与工艺教研室
16
§3-2 沉降分离
Rep=dput/ 1 或 2
层流区
D
24 Re t
d 2 ad 2 2 Rd 2 u 2
化工原理
材料与化学工程学院
非均相物系的分离和固体流态化 化学工程与工艺教研室
23
§3-3 过滤
三 、滤饼的压缩性和助滤剂
◆可压缩滤饼
◆不可压缩滤饼
◆助滤剂：
要求：刚性颗粒；化学稳定性；不可压缩性
常用：不可压缩的粉状或纤维状固体如硅藻土、纤维粉末、 活性炭、石棉。
使用：可预涂，也可以混入待滤的滤浆中一起过滤。
影响因素：设备类型及尺寸、操作温度及流速、颗粒密度
化工原理
材料与化学工程学院
非均相物系的分离和固体流态化 化学工程与工艺教研室
18
§3-2 沉降分离
◆分离效率 总效率
0
c1 c2 c1
分效率（粒级效率）
i
ci1 ci2 c i1
0 xii
分割直径 d50 对标准旋风分离器
非均相物系的分离和固体流态化 化学工程与工艺教研室
13
§3-2 沉降分离
气体
气体 思考 1：要想使某一粒度的颗粒在
进口
出口 降尘室中被 100%除去，必须满足什
集灰斗 降尘室
么条件？
t
H ut
思考 2：能够被 100%除去的最小
第三章非均相物系的分离
第三章 非均相物系的分离和固 体流态化
2020年4月9日
1
3.1 概述
3.1.1 均相物系和非均相物系
均相物系：物系内部各处物料性质均匀而不存在相界面的混合物系。
非均相物系：物系内部有明显的相界面存在而界面两侧物料的性质不同的 混合物系。
3.1.2 非均相物系的分类
1.按状态分
液态非均相物系：固、液、气分散在液相中。分：
2.非球形颗粒：常用颗粒的当量直径和球形度表示其特性。 (1)体积当量直径de：与实际颗粒体积Vp相等的球形颗粒的直径 定义为非球形颗粒的当量直径。即：
de 3
6Vp
(2)表面积当量直径ds：表面积等于实际颗粒表面积Sp的球形颗 粒的直径定义为非球形颗粒的表面积当量直径。即：
ds
Sp
(3)比表面积当量直径da:比表面积等于实际颗料比表面积ap的球 形颗粒的直径定义为非球形颗粒的比表面积当量直径。即：
4.电子除尘：使含有悬浮尘粒或雾滴的气体通过金属电极间 的高压直流静电场，气体电离产生离子附着于悬浮尘粒或雾滴 上而使之荷电。荷电的尘粒、雾滴在电场力的作用下至电极后 发生中和而恢复中性从而达到分离。
3.2 颗粒及颗粒床层的特性
3.2.1 颗粒的特性(单颗粒的几何特性参数)
固体颗粒由于其形成的方法和条件不同，致使它们具有不同 的几何形状和尺寸，在工程计算中，常需要知道颗粒的几何特 性参数：即大小(尺寸)、形状和表面积(或比表面积)等。
de和s来表征。
3.颗粒群的特性
工业中碰到的颗粒大多是由大小和形状不同的若干颗粒组成 的集合体，称为颗粒群。但通常认为它们的形状一致，而只考 虑其大小分布，这样就提出了其粒度分布及其平均直径的问题。
(1) 按颗粒尺寸对颗粒群进行排列划分的结果称为粒度分布。根
2020年4月9日
1
3.1 概述
3.1.1 均相物系和非均相物系
均相物系：物系内部各处物料性质均匀而不存在相界面的混合物系。
非均相物系：物系内部有明显的相界面存在而界面两侧物料的性质不同的 混合物系。
3.1.2 非均相物系的分类
1.按状态分
液态非均相物系：固、液、气分散在液相中。分：
2.非球形颗粒：常用颗粒的当量直径和球形度表示其特性。 (1)体积当量直径de：与实际颗粒体积Vp相等的球形颗粒的直径 定义为非球形颗粒的当量直径。即：
de 3
6Vp
(2)表面积当量直径ds：表面积等于实际颗粒表面积Sp的球形颗 粒的直径定义为非球形颗粒的表面积当量直径。即：
ds
Sp
(3)比表面积当量直径da:比表面积等于实际颗料比表面积ap的球 形颗粒的直径定义为非球形颗粒的比表面积当量直径。即：
4.电子除尘：使含有悬浮尘粒或雾滴的气体通过金属电极间 的高压直流静电场，气体电离产生离子附着于悬浮尘粒或雾滴 上而使之荷电。荷电的尘粒、雾滴在电场力的作用下至电极后 发生中和而恢复中性从而达到分离。
3.2 颗粒及颗粒床层的特性
3.2.1 颗粒的特性(单颗粒的几何特性参数)
固体颗粒由于其形成的方法和条件不同，致使它们具有不同 的几何形状和尺寸，在工程计算中，常需要知道颗粒的几何特 性参数：即大小(尺寸)、形状和表面积(或比表面积)等。
de和s来表征。
3.颗粒群的特性
工业中碰到的颗粒大多是由大小和形状不同的若干颗粒组成 的集合体，称为颗粒群。但通常认为它们的形状一致，而只考 虑其大小分布，这样就提出了其粒度分布及其平均直径的问题。
(1) 按颗粒尺寸对颗粒群进行排列划分的结果称为粒度分布。根
第三章 非均相物系的分离1(09.11)
球
S V
6 d
d――球形颗粒的直径，m；
S――球形颗粒的表面积，m2；
V――球形颗粒的体积，m3；
a球――颗粒的比表面积，m2/m3
5
盐城师范学院
（二）非球形颗粒
----化工原理----
非球形颗粒
非球形颗粒必须有两个参数才能确定其特性，即球形度和当 量直径。
1．球形度φS (Degree of sphericity) 颗粒的球形度又称形状系数，它表示颗粒形状与球形的差异，
体积当量直径:与颗粒体积相等的球形颗粒的直径。
即：Vp
6
de3
de 3
6Vp
de――颗粒的等体积当量直径，m； VP――非球形颗粒的实际体积，m3。
8
盐城师范学院
颗粒的比表面积 a
----化工原理----
a
颗粒表面积 (m2 颗粒体积 (m3)
)
S V
说明：V相同时，a ↓，则颗粒越接近球形。
b
s
――颗粒的堆积密度，kg/m3； ――颗粒的真实密度，kg/m3。
b (1 )s
17
盐城师范学院
----化工原理----
３.２.３流体通过固定床流动的压力降
1．床层的简化模型
细小而密集的固体颗粒床层具有很大的比表面积，流体 通过床层的流动多为爬流，流动阻力基本上为粘性摩擦阻 力，同时使整个床层截面速度的分布均匀化。为解决流体 通过床层的压力降计算问题，在保证单位床层体积表面积 相等的前提下，将颗粒床层内实际流动过程大幅度加以简 化，以便可以用数学方程式加以描述。
根据连续相状态的不同，非均相混合物又可分为两种类型：
第三章 非均相物系的
在非均相混合物中，处于分散状态的物质（如分散于流体 中的固体颗粒液滴或气泡）称为分散相或分散物质，包 围着分散物质而处于连续状态的流体称为连续相或分散 介质。 分类：a.气态非均相混合物；b.液态非均相混合物。 悬浮在空气中的粉尘：分散相粉尘 连续相空气
• 由于分散相和连续相具有不同的物理性质（如：尺寸不 同、密度不同），可用机械方法分离。例如：气体中所 含的灰尘可以用重力、离心力或在电场中将其除去，悬 浮液可以通过过滤的方式分离成液体和滤渣两部分，大 小不等及密度不同的颗粒构成的混合物可以用分级沉降 的方法分开，大小不同的颗粒用筛子亦可分开。 均相混合物的各种方法将在下册的传质各章中介绍。
① 颗粒沉降的基本假定
② 各颗粒沉降时互不干扰（自由沉降，反之为 干扰沉降）
③ 容器壁效率忽略 ④ 分子布朗热运动对沉降无影响
mg F
重力：
6
3 d S g
② 颗粒沉降过程受力：
浮力： 阻力：
6
3 d 流 g
F阻 A Pf
2 d 4 2
u0
2
3.3.1 重力沉降分离
u
p f L
/ (1 )
3
u
2
（3-12）
3．模型参数的实验测定
• （1）康采尼（Kozeny）的实验结果
• 康采尼通过实验发现，在流速较低，床层雷诺数 Reb﹤2的滞留情况下，模型参数 可较好的符合下式：
（3-13）
• 式中 称为康采尼常数，其值可取作5.0，Reb的定义为
（3-14） （3-15）
第三章 非均相物系的分离和固体流态化
3.1 概述
化工生产中，需要将混合物加以分离的情况非常多。 原料需经过分离提纯或净化后才符合加工要求； 从反应器送出的反应产物一般都与尚未反应的原料及副 产物混在一起，也要从其中分离出纯度合格的产品及将未 反应的原料送回反应器或另行处理。 生产中的废气、废液在排放前，应将其中所含的有害物 尽量除去，以减轻环境污染，并有可能将其变为有用之物 混合物分为两类，即均相混合物（物系内部各处均匀 且无相界面，如：石油、空气）和非均相混合物。
第三章 非均相物系的分离和过滤
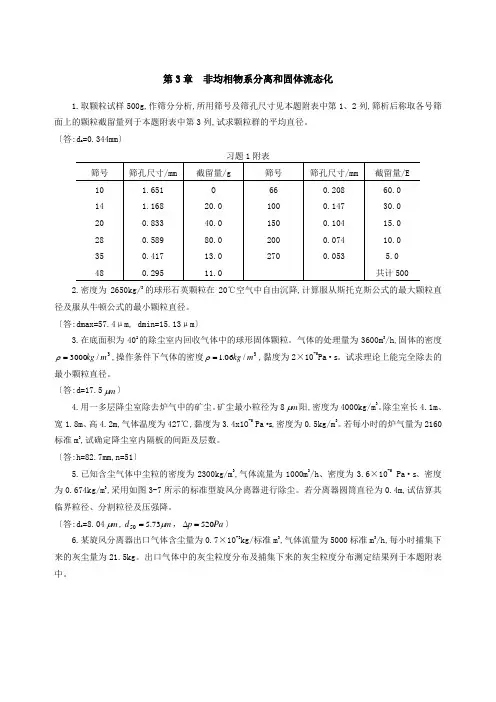
第3章 非均相物系分离和固体流态化1.取颗粒试样500g,作筛分分析,所用筛号及筛孔尺寸见本题附表中第1、2列,筛析后称取各号筛面上的颗粒截留量列于本题附表中第3列,试求颗粒群的平均直径。
〔答:d a =0.344mm 〕习题1附表2.密度为2650kg/3的球形石英颗粒在20℃空气中自由沉降,计算服从斯托克斯公式的最大颗粒直径及服从牛顿公式的最小颗粒直径。
〔答:dmax=57.4μm, dmin=15.13μm 〕3.在底面积为402的除尘室内回收气体中的球形固体颗粒。
气体的处理量为3600m 3/h,固体的密度3/3000m kg =ρ,操作条件下气体的密度3/06.1m kg =ρ,黏度为2×10-5Pa ·s 。
试求理论上能完全除去的最小颗粒直径。
〔答:d=17.5m μ〕4.用一多层降尘室除去炉气中的矿尘。
矿尘最小粒径为8m μ阳,密度为4000kg/m 3。
除尘室长4.1m 、宽1.8m 、高4.2m,气体温度为427℃,黏度为3.4x1O -5Pa ·s,密度为0.5kg/m 3。
若每小时的炉气量为2160标准m 3,试确定降尘室内隔板的间距及层数。
〔答:h=82.7mm,n=51〕5.已知含尘气体中尘粒的密度为2300kg/m 3,气体流量为1000m 3/h 、密度为3.6×10-5Pa ·s 、密度为0.674kg/m 3,采用如图3-7所示的标准型旋风分离器进行除尘。
若分离器圆筒直径为0.4m,试估算其临界粒径、分割粒径及压强降。
〔答:d c =8.04m μ,m d μ73.550=，Pa p 520=∆〕6.某旋风分离器出口气体含尘量为0.7×10-3kg/标准m 3,气体流量为5000标准m 3/h,每小时捕集下来的灰尘量为21.5kg 。
出口气体中的灰尘粒度分布及捕集下来的灰尘粒度分布测定结果列于本题附表中。
非均相物系的分离和固体流态化
第三章
非均相物系的分离和固 体流态化
3.1 概述
混合物
均相混合物
物系内部各处物料性质均匀而且不存在相界 面的混合物。
例如：互溶溶液及混合气体
物系内部有隔开两相的界面存在且界面两 非均相混合物
侧的物料性质截然不同的混合物。
固体颗粒和气体构成的含尘气体
例如
固体颗粒和液体构成的悬浮液 不互溶液体构成的乳浊液 液体颗粒和气体构成的含雾气体
在前面介绍的各种沉降速度关系式中，当颗粒的体积浓度小于0.2% 时，理论计算值的偏差在1%以内，但当颗粒浓度较高时，由于颗粒间 相互作用明显，便发生干扰沉降，自由沉降的公式不再适用。
b）器壁效应
当器壁尺寸远远大于颗粒尺寸时，（例如在100倍以上）容器效应可
忽略，否则需加以考虑。
ut '
1
ut 2.1
即表示某一粒度（粒径）或某一粒径范围的颗粒占总颗粒质量百 分数的一种函数关系。常用粒度分布曲线图表示。
4). 颗粒的平均粒径： ① 长度平均粒径（算术平均粒径）
l d m
nidi ni
② 体积平均粒径：
V 3 d m
nidi3
ni
3
1 ai di3
③ 比表面平均粒径（又称邵特Sauter平均直径）
图3-3 Ret2 Ret 及 Ret1Ret关系曲线
例：试计算直径为95μm，密度为3000kg/m3的固体颗粒分别在20℃的）在20℃水中的沉降。
用试差法计算
先假设颗粒在滞流区内沉降 ，
ut
d2s g
18
附录查得，20℃时水的密度为998.2kg/m3,μ=1.005×10-3Pa.s
6d3sg 6d3g 4d2u 2 t20
非均相物系的分离和固 体流态化
3.1 概述
混合物
均相混合物
物系内部各处物料性质均匀而且不存在相界 面的混合物。
例如：互溶溶液及混合气体
物系内部有隔开两相的界面存在且界面两 非均相混合物
侧的物料性质截然不同的混合物。
固体颗粒和气体构成的含尘气体
例如
固体颗粒和液体构成的悬浮液 不互溶液体构成的乳浊液 液体颗粒和气体构成的含雾气体
在前面介绍的各种沉降速度关系式中，当颗粒的体积浓度小于0.2% 时，理论计算值的偏差在1%以内，但当颗粒浓度较高时，由于颗粒间 相互作用明显，便发生干扰沉降，自由沉降的公式不再适用。
b）器壁效应
当器壁尺寸远远大于颗粒尺寸时，（例如在100倍以上）容器效应可
忽略，否则需加以考虑。
ut '
1
ut 2.1
即表示某一粒度（粒径）或某一粒径范围的颗粒占总颗粒质量百 分数的一种函数关系。常用粒度分布曲线图表示。
4). 颗粒的平均粒径： ① 长度平均粒径（算术平均粒径）
l d m
nidi ni
② 体积平均粒径：
V 3 d m
nidi3
ni
3
1 ai di3
③ 比表面平均粒径（又称邵特Sauter平均直径）
图3-3 Ret2 Ret 及 Ret1Ret关系曲线
例：试计算直径为95μm，密度为3000kg/m3的固体颗粒分别在20℃的）在20℃水中的沉降。
用试差法计算
先假设颗粒在滞流区内沉降 ，
ut
d2s g
18
附录查得，20℃时水的密度为998.2kg/m3,μ=1.005×10-3Pa.s
6d3sg 6d3g 4d2u 2 t20
第三章非均相物系的分离及固体流态化
3.2.1颗粒的特性
（1）球形颗粒
球形颗粒的尺寸由直径d确定，其它参数均可为直径的函数。
如：体积
V d3
6
表面积
S d 2
比表面积 S 6
Vd
2010-9-1
不同颗粒的 形状
（2）非球形颗粒
①球形度（形状系数）
定义为：与该颗粒体积相等的球体的表面积除以颗粒的表面
积的，球即体：的表面S 积S。SP 由于SP同－体颗积粒不表同面形积状，的S－颗与粒颗中粒，体球积形相颗等粒 的表面积最小，因此对非球形颗粒，总有S 1 ，颗粒的形 状越接近球形， S越接近1，对于球形颗粒 S 1。
单位重量流体所具有的动能
u2
2g
H f
u2 2g
所以：p1
p2
gH f
g u 2 ＝
2g
u 2
2
即流体绕过颗粒前后产生的压差：p＝ u 2
2
2010-9-1
流体绕过颗粒流动的曳力系数与流体流动状态有关，而流
动状态可用颗粒雷诺数Ret的大小来判断。Ret dut
均匀来流绕过球形颗粒，当流速很低时，称为爬流（又称
非均相混合物 物系内部有隔开两相的界面存在且 界面两侧的物料性质截然不同的混 合物。
固体颗粒和气体构成的含尘气体 固体颗粒和液体构成的悬浮液 例如 不互溶液体构成的乳浊液
液体颗粒和气体构成的含雾气体
非均相物系
分散相 分散物质
处于分散状态的物质 如：分散于流体中的固体颗粒、 液滴或气泡
连续相 包围着分散相物质且处于连续 分散相介质 状态的流体
。采用前述简化模型，将流体通过床层流道看作通过一组当
量直径为 deb的平行细管流动。其压力降为：Pf
第三章非均相物系的分离
K ' 0 . 0556 湍流区： Re du t 1 . 74 u t
3 2
t
( s )g
1 . 74 K ' 10
3
K ' 3027 . 6 过渡区： K' 0 . 0556 ~ 3027.6
计算步骤：
1 .计算 K' u t
3 2
( s )g d： 滞流区： d 18 u t ( s )g
湍流区：
3.摩擦数群法
• (1)已知d求ut
ut 4 d ( s )g 3 du t
2 t
4 d ( s )g 3 u t
2 2 2
Re
t
Re
2
2 t
2
d ut
2 3
2
Re
4 d ( s )g d u t 2 2 3 u t
3.1.2 颗粒床层的特性
3.1.2.1.床层空隙率ε • 床层堆积的疏密程度用空隙率表示，指单位体 积床层所具有的空隙体积(m3/m3)。即： • ε=(床层体积-颗粒体积)/床层体积 • ε的大小与颗粒的大小、形状、粒度分布、填 充方式等有关，其值由实验测定。 • [说明] • 非球形颗粒的球形度愈小，床层的空隙率愈大； • 大小愈不均匀的颗粒，空隙率愈小； • 颗粒愈光滑，空隙率愈小； • 愈靠近壁面，空隙率愈大。
0.6 t
K 2.62 ~ 69.1
过渡区：
u t 0 . 27
K 69 . 1
湍流区：
u t 1 . 74
(2)已知ut求d
令 K' u t
非均相物系的分离和固体流态化练习题
4.对板框式过滤机，洗涤面积 和过滤面积 的定量关系为，洗水走过的距离 和滤液在过滤终了时走过的距离 的定量关系为，洗涤速率（ 和终了时的过滤速率 的定量关系为。
5.对叶滤机，洗涤面积 和过滤面积 的定量关系为_______，洗水走过的距离 和滤液在过滤终了时走过的距离 的定量关系为________，洗涤速率( 与过滤终了时的过滤速率（ 的定量关系为_______。
11.评价旋风分离器分离性能指标有，和，旋风分离器性能的好坏，主要以来衡量。
12.降尘室的生产能力只与和有关。在除去某粒径的颗粒时，若降尘室的高度增加一倍，生产能力。
13.离心分离设备的分离因数定义式为Kc=。某颗粒在离心力场中做圆周运动，其旋转半径为0.2 m，切向速度为20 m/s，则分离因素为。
6.转筒真空过滤机，转速越大，则生产能力就越，每转一周所获得的滤液量就越，形成的滤饼厚度越，过滤阻力越。
7.非球形颗粒的等体积当量直径的表达式为。
8.球形度(形状系数)恒小于或等于1，此值越小，颗粒的形状离球形越远，球形度的定义式可写为。
9．在讨论旋风分离器分离性能时，临界粒径这一术语是指。
10.旋风分离器的总的分离效率是指。
（3）若滤液量不变，仅将过滤压差提高1倍，问过滤时间为多少？
（4）若过滤时间不变，仅将过滤压强提高1倍，问滤液量为多少？
2．在实验室内用一片过滤面积为0.05 m2的滤叶在36 kPa（绝）下进行吸滤（大气压为101 kPa），在300 s内共吸出0.4 L滤液，再过600 s，又吸出0.4 L滤液。求该减压过滤操作下的过滤常数K，qe及θe。
第三章 非均相物系分离习题
一、填空题
1.用板框式过滤机进行恒压过滤操作，随着过in)，转鼓表面积为A，转鼓的沉浸度为 ，则过滤周期为(s)，在一个过滤周期中过滤时间为(s)，过滤面积为。
5.对叶滤机，洗涤面积 和过滤面积 的定量关系为_______，洗水走过的距离 和滤液在过滤终了时走过的距离 的定量关系为________，洗涤速率( 与过滤终了时的过滤速率（ 的定量关系为_______。
11.评价旋风分离器分离性能指标有，和，旋风分离器性能的好坏，主要以来衡量。
12.降尘室的生产能力只与和有关。在除去某粒径的颗粒时，若降尘室的高度增加一倍，生产能力。
13.离心分离设备的分离因数定义式为Kc=。某颗粒在离心力场中做圆周运动，其旋转半径为0.2 m，切向速度为20 m/s，则分离因素为。
6.转筒真空过滤机，转速越大，则生产能力就越，每转一周所获得的滤液量就越，形成的滤饼厚度越，过滤阻力越。
7.非球形颗粒的等体积当量直径的表达式为。
8.球形度(形状系数)恒小于或等于1，此值越小，颗粒的形状离球形越远，球形度的定义式可写为。
9．在讨论旋风分离器分离性能时，临界粒径这一术语是指。
10.旋风分离器的总的分离效率是指。
（3）若滤液量不变，仅将过滤压差提高1倍，问过滤时间为多少？
（4）若过滤时间不变，仅将过滤压强提高1倍，问滤液量为多少？
2．在实验室内用一片过滤面积为0.05 m2的滤叶在36 kPa（绝）下进行吸滤（大气压为101 kPa），在300 s内共吸出0.4 L滤液，再过600 s，又吸出0.4 L滤液。求该减压过滤操作下的过滤常数K，qe及θe。
第三章 非均相物系分离习题
一、填空题
1.用板框式过滤机进行恒压过滤操作，随着过in)，转鼓表面积为A，转鼓的沉浸度为 ，则过滤周期为(s)，在一个过滤周期中过滤时间为(s)，过滤面积为。
第三章非均相物系的分离和固体流态化
xi di粒径段内颗粒的质量率分
3、堆积密度（表观密度）b：粒子体积包括
颗粒间的空
隙，则称为粒子的堆
积密度。显然， b s
三、粒子的密度
1、密度：单位体积内的粒子质量称为粒子的 密度。
2、真实密度s：粒子体积不包括颗粒间的空 隙，
则称为粒子的真实密度。
（4）基本常识：非球形 球形，均非均， 边壁中心，乱堆床层在0.47～0.70。
6R
阻力 d2 ur2
42
根据沉降速度的定义，以上三个力达到平衡时颗粒在径向上 相对于流体的速度ur便是它在此位置上的离心沉降速度，即：
6d3su R T 2 6d3u R T 2 4d22 ur 20
ur
4d(s ) uT2 3 R
若降尘室设置n层水平隔板，则多层降尘室的生产能力为：
V s (n 1 )bt l( u n 1 )A u t
V s (n 1 )bt l( u n 1 )A u t
H 降尘室的高度m，;
l 降尘室的长度，m; u气体在降将尘室通的过水速平度 m/， s;
Vs降尘室的生 含产 尘能 气力 体（ 通 体 即 过 积降 流 m 尘 3量 /s;
为避免沉降颗粒被重新卷起，通常板间距∆H≥40mm，且一 般使气流流动处于层流区。降尘室
（二）沉降槽
1、 沉降槽的构造与操作 2、 浓悬浮液的沉聚过
（三）分级器
3－2－2 离心沉降
依靠惯性离心力的作用二实现的沉降过程称为离心沉降 分类： 气固分离――旋风分离器；
气液分离――旋液分离器，沉降离心机 一、惯性离心力作用下的沉降速度
在惯性离心力的作用下，颗粒将沿切线方向甩出。 当流体带着颗粒旋转时，如果颗粒的密度大于流体密度，
3、堆积密度（表观密度）b：粒子体积包括
颗粒间的空
隙，则称为粒子的堆
积密度。显然， b s
三、粒子的密度
1、密度：单位体积内的粒子质量称为粒子的 密度。
2、真实密度s：粒子体积不包括颗粒间的空 隙，
则称为粒子的真实密度。
（4）基本常识：非球形 球形，均非均， 边壁中心，乱堆床层在0.47～0.70。
6R
阻力 d2 ur2
42
根据沉降速度的定义，以上三个力达到平衡时颗粒在径向上 相对于流体的速度ur便是它在此位置上的离心沉降速度，即：
6d3su R T 2 6d3u R T 2 4d22 ur 20
ur
4d(s ) uT2 3 R
若降尘室设置n层水平隔板，则多层降尘室的生产能力为：
V s (n 1 )bt l( u n 1 )A u t
V s (n 1 )bt l( u n 1 )A u t
H 降尘室的高度m，;
l 降尘室的长度，m; u气体在降将尘室通的过水速平度 m/， s;
Vs降尘室的生 含产 尘能 气力 体（ 通 体 即 过 积降 流 m 尘 3量 /s;
为避免沉降颗粒被重新卷起，通常板间距∆H≥40mm，且一 般使气流流动处于层流区。降尘室
（二）沉降槽
1、 沉降槽的构造与操作 2、 浓悬浮液的沉聚过
（三）分级器
3－2－2 离心沉降
依靠惯性离心力的作用二实现的沉降过程称为离心沉降 分类： 气固分离――旋风分离器；
气液分离――旋液分离器，沉降离心机 一、惯性离心力作用下的沉降速度
在惯性离心力的作用下，颗粒将沿切线方向甩出。 当流体带着颗粒旋转时，如果颗粒的密度大于流体密度，
化工原理(非均相分离)
第3章非均相物系的分离和固体流态化3．1 概述本章介绍利用流体力学原理(颗粒与流体之间相对运动)实现非均相物系的分离流态化及固体颗粒的气力输送等工业过程。
1．混合物的分类自然界的大多数物质是混合物。
若物系内部各处组成均匀且不存在相界面，则称为均相混合物或均相物系，溶液及混合气体都是均相混合物。
由具有不同物理性质(如密度差别)的分散物质和连续介质所组成的物系称为非均相混合物或非均相物系。
在非均相物系中，处于分散状态的物质，如分散于流体中的固体颗粒、液滴或气泡，称为分散物质或分散相；包围分散物质且处于连续状态的物质称为分散介质或连续相。
根据连续相的状态，非均相物系分为两种类型：①气态非均相物系，如含尘气体、含雾气体等；②液态非均相物系，如悬浮液、乳浊液及泡沫液等。
2．非均相混合物的分离方法由于非均相物系中分散相和连续相具有不同的物理性质，故工业上一般都采用机械方法将两相进行分离。
要实现这种分离，必须使分散相与连续相之间发生相对运动。
根据两相运动方式的不同，机械分离可按下面两种操作方式进行。
①颗粒相对于流体(静止或运动)运动而实现悬浮物系分离的过程称为沉降分离。
实现沉降操作的作用力可以是重力，也可以是惯性离心力，因此，沉降过程有重力沉降与离心沉降之分。
②流体相对于固体颗粒床层运动而实现固液分离的过程称为过滤。
实现过滤操作的外力可以是重力、压强差或惯性离心力。
因此，过滤操作又可分为重力过滤、加压过滤、真空过滤和离心过滤。
气态非均相混合物的分离，工业上主要采用重力沉降和离心沉降方法。
在某些场合，根据颗粒的粒径和分离程度要求，也可采用惯性分离器、袋滤器、静电除尘器或湿法除尘设备等，如表3—1所示。
┘此外，还可采用其他措施．预先增大微细粒子的有效尺寸而后加以机械分离。
例如，使含尘或含雾气体与过饱和蒸汽接触，发生以粒子为核心的冷凝；又如，将气体引入超声场内，使细粒碰撞并凝聚。
这样，可使微细颗粒附聚成较大颗粒，然后在旋风分离器中除去。
化工原理第3章课后习题参考答案
第三章非均相物系的分离和固体流态化3. 在底面积为40m²的除尘室内回收气体中的球形固体颗粒。
气体的处理量为3600m³/h，固体的密度ρs=3600kg/m³，操作条件下气体的密度ρ=1.06kg/m³，粘度为3.4×10-5Pa•s。
试求理论上完全除去的最小颗粒直径。
解：理论上完全除去的最小颗粒直径与沉降速度有关。
需根据沉降速度求。
1）沉降速度可根据生产能力计算ut = Vs/A= (3600/3600)/40 = 0.025m/s （注意单位换算）2）根据沉降速度计算理论上完全除去的最小颗粒直径。
沉降速度的计算公式与沉降雷诺数有关。
（参考教材P148）。
假设气体流处在滞流区则可以按ut = d2（ρs- ρ）g/18μ进行计算∴dmin2 = 18μ/（ρs- ρ）g ·ut可以得到dmin= 0.175×10-4 m=17.53）核算Ret = dminutρ/μ< 1 ，符合假设的滞流区∴能完全除去的颗粒的最小直径d = 0.175×10-4 m = 17.5 μm5. 含尘气体中尘粒的密度为2300kg/m³，气体流量为1000m³/h，粘度为3.6×10-5Pa•s密度为0.674kg/m³，采用如图3-8所示的标准型旋风分离器进行除尘。
若分离器圆筒直径为0.4m，试估算其临界直径，分割粒径及压强降。
解：P158图3-7可知，对标准旋风分离器有：Ne = 5 ，ξ= 8.0 B = D/4 ，h = D/2(1) 临界直径根据dc = [9μB/(πNeρsui )]1/2 计算颗粒的临界直径其中：μ=3.6×10-5Pa•s；B = D/4=0.1m；Ne = 5；ρs=2300kg/m³；将以上各参数代入，可得dc = *9μB/(πNeρsui )+1/2 = *9×3.6×10×0.25×0.4/(3.14×5×2300×13.89)+1/2= 8.04×10-6 m = 8.04 μm（2）分割粒径根据d50 = 0.27[μD/ut（ρs- ρ）]1/2 计算颗粒的分割粒径∴d50 = 0.27[3.6×10-5×0.4/(13.889×2300)]1/2= 0.00573×10-3m = 5.73μm（3）压强降根据△P = ξ·ρui2/2 计算压强降∴△P = 8.0×0.674×13.8892/2 = 520 Pa7、实验室用一片过滤面积为0.1m2的滤叶对某种颗粒在水中的悬浮液进行实验，滤叶内部真空读为500mmHg，过滤5min的滤液1L，又过滤5min的滤液0.6L，若再过滤5min得滤液多少？已知：恒压过滤，△P =500mmHg ，A=0.1m，θ1=5min时，V1=1L；θ2=5min+5min=10min 时，V2=1L+0.6L=1.6L求：△θ3=5min时，△V3=？解：分析：此题关键是要得到虚拟滤液体积，这就需要充分利用已知条件，列方程求解思路：V2 + 2VVe= KA2θ（式中V和θ是累计滤液体积和累计过滤时间），要求△V3，需求θ3=15min时的累计滤液体积V3=？则需先求Ve和K。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
☆壁面效应：ε在床层同一截面上的分布是不均匀的，在容 器壁面附近ε较大，而床层中心ε较小。器壁对ε的这种影响称 为壁面效应。壁面效应使得流体通过床层的速度不均匀，流 动阻力较小的近壁处流速较床层内部大。改善壁面效应的方 法通常是限制床层直径与颗粒直径之比不得小于某极限值。
（3）床层的比表面积 指单位体积床层中具有的b颗粒表面积（即颗粒与流体接触面 积），如果忽略颗粒间相互重叠的接触面积则 b (1 )
2010-9-1
b可用堆积密度估算： b
6b Sd
6(ቤተ መጻሕፍቲ ባይዱ d
)
,
b
(1 ) S
（4）床层的当量直径
床层简化模型：即将固定床中不规则的流道简化成一组与床 层高度相等的平行细管。细管的当量直径可用床层的空隙率 可颗粒的比表面积计算 deb 4rH 4 流通截面积 润湿周边
deb （流通截面积 流道长度）（润湿周边 流道长度）， deb 流通容积 流道表面积
考虑1平方米高度1米的固定床，床层体积＝1×1＝1m3
假设细管的全部流动空间等于床层的空隙体积，故
流道容积＝1×ε＝εm³
2010-9-1
2010-9-1
若忽略床层中因颗粒相互接触而彼此覆盖的表面积。则
流道表面积＝颗粒体积×颗粒比表面积＝1（1－ε）а m³
所以床层的当量直径为：d eb
b)堆积密度
：粒子体积包含颗粒之间的空隙。
b
3.2.2颗粒床层的特性
(1)床层的空隙率
床层体积－颗粒体积 床层体积
m3 / m3
2010-9-1
ε的大小与颗粒形状、粒度分布、颗粒直径与床层直径的 比值、床层的填充方式等因素有关。
床层的空隙率可通过实验测定：在体积V的颗粒床层中 加水直至水面达到床层表面，测定加入水的体积V水，则 床层空隙率为ε＝ V水/V。也可用称量法测定，称量体积V的 颗粒床层的质量G，若固体颗粒的密度为 ， S则空隙率为 。 (V G / S ) /V
（4）电除尘：利用高压电场的作用，使悬浮在气相中的微粒 带电并被板状或管状电极吸引而除尘。适于更细小的悬浮物 系的分离。
2010-9-1
3.2颗粒与颗粒床层的特性
流体流过颗粒或颗粒床层时，其流动特性与流体流经管 道的情况有相同之处，即都是流体相对于固体界面的流动， 但床层中颗粒任意堆积形成的流道形状多变，很不规则， 边界条件复杂，对于这种复杂流道内的流动规律的研究， 需要从组成流道的颗粒入手。
2010-9-1
②离心分离：利用微粒所受惯性离心力的作用，使其与介质 分离，适于细小微粒悬浮物系的处理。
（2）过滤
利用某种多孔物质作过滤介质，流体通过介质而固体颗粒 被截留在介质上，从而得到分离。适于较细小悬浮物系的处 理。
（3）湿法除尘：利用液体（通常是水）洗涤含尘气体，除去 其中的尘粒，适于细小颗粒。
非均相混合物 物系内部有隔开两相的界面存在且 界面两侧的物料性质截然不同的混 合物。
固体颗粒和气体构成的含尘气体 固体颗粒和液体构成的悬浮液 例如 不互溶液体构成的乳浊液
液体颗粒和气体构成的含雾气体
非均相物系
分散相 分散物质
处于分散状态的物质 如：分散于流体中的固体颗粒、 液滴或气泡
连续相 包围着分散相物质且处于连续 分散相介质 状态的流体
一般，乱堆床层ε＝0.4～0.7；均匀球体：松排列ε＝ 0.4，紧密排列ε＝0.26。
（2）床层的自由截面积
床层截面上未被颗粒占据的流体可以自由通过的面积， 称为床层的自由截面积。
2010-9-1
☆床层的各向同性：小颗粒乱堆床层可以认为是各向同性的 。各向同性床层的重要特性之一是其自由截面积与床层截面 积之比在数值上与床层的空隙率相等。同床层空隙率一样， 由于壁面效应的影响，壁面附近的自由截面积大。
如：气态非均相物系中的气体 液态非均相物系中的连续液体
连续相与分散相 分离
不同的物理性质
机械 分离
分散相和连续相 发生相对运动的方式
2010-9-1
沉降 过滤
3.1.2非均相物系分离的目的 （1）收集分散物质 例如从气流干燥器或喷雾干燥器排出的气体中回收固体产品。 （2）净化分散介质 例如：生产硫酸，二氧化硫炉气含杂质，净化。 （3）环境保护 空气中的粉尘、废水、废气治理。 3.1.3非均相物系分离常用方法 （1）沉降分离（颗粒相对流体的运动过程） ①重力沉降：微粒借助本身重力在介质中沉降而分离，适于处 理粗粒悬浮物系。
②颗粒的当量直径
颗粒的当量直径表示非球形颗粒的大小，通常有两种表示
方法： a)等体积当量直径
2010-9-1
de
3
6
VP
V
－颗粒体积m3
P
b)等比表面积当量直径
即与非球形颗粒比表面积相等的球形颗粒的直径为该颗粒的
等比表面积当量直径。即： d
6
③比表面积 S P 6 VP S de
（3）颗粒群 ①颗粒粒度分布 筛分分析：泰勒标准筛（表3－2） ②颗粒群的平均粒径
3.2.1颗粒的特性
（1）球形颗粒
球形颗粒的尺寸由直径d确定，其它参数均可为直径的函数。
如：体积
V d3
6
表面积
S d 2
比表面积 S 6
Vd
2010-9-1
不同颗粒的 形状
（2）非球形颗粒
①球形度（形状系数）
定义为：与该颗粒体积相等的球体的表面积除以颗粒的表面
积的，球即体：的表面S 积S。SP 由于SP同－体颗积粒不表同面形积状，的S－颗与粒颗中粒，体球积形相颗等粒 的表面积最小，因此对非球形颗粒，总有S 1 ，颗粒的形 状越接近球形， S越接近1，对于球形颗粒 S 1。
2010-9-1
停留在第i层筛网上的颗粒的平均直径dpi可按di-1和di的算术平
均值计算。即：d pi
di
di1 2
颗粒的平均粒径
d P
1 xi
d Pi
式中xi－粒径段内颗粒的质量分率。
di-1
di di+
1
di+
③颗粒密度（单位体积内粒子的质量）
2
a)真密度 S ：粒子体积不包含颗粒之间的空隙。
第三章 非均相物系的分离及固体流态化
3.1概述 3.2颗粒及颗粒床层的特性 3.3重力沉降 3.4离心沉降 3.5过滤 3.6固体流态化
2010-9-1
3.1概述
3.1.1混合物的分类
混合物
均相混合物 物系内部各处物料性质均匀而且不 存在相界面的混合物。
例如：互溶溶液及混合气体
2010-9-1
（3）床层的比表面积 指单位体积床层中具有的b颗粒表面积（即颗粒与流体接触面 积），如果忽略颗粒间相互重叠的接触面积则 b (1 )
2010-9-1
b可用堆积密度估算： b
6b Sd
6(ቤተ መጻሕፍቲ ባይዱ d
)
,
b
(1 ) S
（4）床层的当量直径
床层简化模型：即将固定床中不规则的流道简化成一组与床 层高度相等的平行细管。细管的当量直径可用床层的空隙率 可颗粒的比表面积计算 deb 4rH 4 流通截面积 润湿周边
deb （流通截面积 流道长度）（润湿周边 流道长度）， deb 流通容积 流道表面积
考虑1平方米高度1米的固定床，床层体积＝1×1＝1m3
假设细管的全部流动空间等于床层的空隙体积，故
流道容积＝1×ε＝εm³
2010-9-1
2010-9-1
若忽略床层中因颗粒相互接触而彼此覆盖的表面积。则
流道表面积＝颗粒体积×颗粒比表面积＝1（1－ε）а m³
所以床层的当量直径为：d eb
b)堆积密度
：粒子体积包含颗粒之间的空隙。
b
3.2.2颗粒床层的特性
(1)床层的空隙率
床层体积－颗粒体积 床层体积
m3 / m3
2010-9-1
ε的大小与颗粒形状、粒度分布、颗粒直径与床层直径的 比值、床层的填充方式等因素有关。
床层的空隙率可通过实验测定：在体积V的颗粒床层中 加水直至水面达到床层表面，测定加入水的体积V水，则 床层空隙率为ε＝ V水/V。也可用称量法测定，称量体积V的 颗粒床层的质量G，若固体颗粒的密度为 ， S则空隙率为 。 (V G / S ) /V
（4）电除尘：利用高压电场的作用，使悬浮在气相中的微粒 带电并被板状或管状电极吸引而除尘。适于更细小的悬浮物 系的分离。
2010-9-1
3.2颗粒与颗粒床层的特性
流体流过颗粒或颗粒床层时，其流动特性与流体流经管 道的情况有相同之处，即都是流体相对于固体界面的流动， 但床层中颗粒任意堆积形成的流道形状多变，很不规则， 边界条件复杂，对于这种复杂流道内的流动规律的研究， 需要从组成流道的颗粒入手。
2010-9-1
②离心分离：利用微粒所受惯性离心力的作用，使其与介质 分离，适于细小微粒悬浮物系的处理。
（2）过滤
利用某种多孔物质作过滤介质，流体通过介质而固体颗粒 被截留在介质上，从而得到分离。适于较细小悬浮物系的处 理。
（3）湿法除尘：利用液体（通常是水）洗涤含尘气体，除去 其中的尘粒，适于细小颗粒。
非均相混合物 物系内部有隔开两相的界面存在且 界面两侧的物料性质截然不同的混 合物。
固体颗粒和气体构成的含尘气体 固体颗粒和液体构成的悬浮液 例如 不互溶液体构成的乳浊液
液体颗粒和气体构成的含雾气体
非均相物系
分散相 分散物质
处于分散状态的物质 如：分散于流体中的固体颗粒、 液滴或气泡
连续相 包围着分散相物质且处于连续 分散相介质 状态的流体
一般，乱堆床层ε＝0.4～0.7；均匀球体：松排列ε＝ 0.4，紧密排列ε＝0.26。
（2）床层的自由截面积
床层截面上未被颗粒占据的流体可以自由通过的面积， 称为床层的自由截面积。
2010-9-1
☆床层的各向同性：小颗粒乱堆床层可以认为是各向同性的 。各向同性床层的重要特性之一是其自由截面积与床层截面 积之比在数值上与床层的空隙率相等。同床层空隙率一样， 由于壁面效应的影响，壁面附近的自由截面积大。
如：气态非均相物系中的气体 液态非均相物系中的连续液体
连续相与分散相 分离
不同的物理性质
机械 分离
分散相和连续相 发生相对运动的方式
2010-9-1
沉降 过滤
3.1.2非均相物系分离的目的 （1）收集分散物质 例如从气流干燥器或喷雾干燥器排出的气体中回收固体产品。 （2）净化分散介质 例如：生产硫酸，二氧化硫炉气含杂质，净化。 （3）环境保护 空气中的粉尘、废水、废气治理。 3.1.3非均相物系分离常用方法 （1）沉降分离（颗粒相对流体的运动过程） ①重力沉降：微粒借助本身重力在介质中沉降而分离，适于处 理粗粒悬浮物系。
②颗粒的当量直径
颗粒的当量直径表示非球形颗粒的大小，通常有两种表示
方法： a)等体积当量直径
2010-9-1
de
3
6
VP
V
－颗粒体积m3
P
b)等比表面积当量直径
即与非球形颗粒比表面积相等的球形颗粒的直径为该颗粒的
等比表面积当量直径。即： d
6
③比表面积 S P 6 VP S de
（3）颗粒群 ①颗粒粒度分布 筛分分析：泰勒标准筛（表3－2） ②颗粒群的平均粒径
3.2.1颗粒的特性
（1）球形颗粒
球形颗粒的尺寸由直径d确定，其它参数均可为直径的函数。
如：体积
V d3
6
表面积
S d 2
比表面积 S 6
Vd
2010-9-1
不同颗粒的 形状
（2）非球形颗粒
①球形度（形状系数）
定义为：与该颗粒体积相等的球体的表面积除以颗粒的表面
积的，球即体：的表面S 积S。SP 由于SP同－体颗积粒不表同面形积状，的S－颗与粒颗中粒，体球积形相颗等粒 的表面积最小，因此对非球形颗粒，总有S 1 ，颗粒的形 状越接近球形， S越接近1，对于球形颗粒 S 1。
2010-9-1
停留在第i层筛网上的颗粒的平均直径dpi可按di-1和di的算术平
均值计算。即：d pi
di
di1 2
颗粒的平均粒径
d P
1 xi
d Pi
式中xi－粒径段内颗粒的质量分率。
di-1
di di+
1
di+
③颗粒密度（单位体积内粒子的质量）
2
a)真密度 S ：粒子体积不包含颗粒之间的空隙。
第三章 非均相物系的分离及固体流态化
3.1概述 3.2颗粒及颗粒床层的特性 3.3重力沉降 3.4离心沉降 3.5过滤 3.6固体流态化
2010-9-1
3.1概述
3.1.1混合物的分类
混合物
均相混合物 物系内部各处物料性质均匀而且不 存在相界面的混合物。
例如：互溶溶液及混合气体
2010-9-1