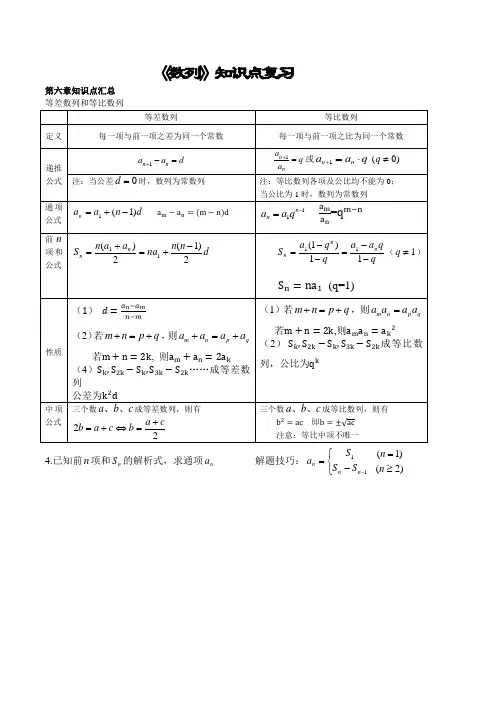
中职统计基础知识分布数列
- 格式:pdf
- 大小:9.25 MB
- 文档页数:99

中职数学数列课件一、引言数列是数学中一个重要的概念,它是按照一定顺序排列的一列数。
数列可以用于描述自然界和现实生活中的许多现象,例如人口增长、物理运动等。
因此,掌握数列的知识对于中职学生来说具有重要的意义。
二、数列的基本概念1.数列的定义:数列是由一系列按照一定顺序排列的数构成的集合。
数列中的每个数称为数列的项,通常用字母表示,如a1,a2,a3等。
2.数列的表示方法:数列可以用列举法、通项公式法、递推公式法等方式表示。
列举法是将数列的前几项直接写出来,如1,2,3,4,5;通项公式法是通过一个公式来表示数列的任意一项,如an=n^2;递推公式法是通过前一项或前几项来递推下一项,如an=an-1+2。
3.数列的项数:数列的项数可以是有限的,也可以是无限的。
有限数列的项数是有限的,如1,2,3,4,5;无限数列的项数是无限的,如1,2,3,4,5,三、等差数列1.等差数列的定义:如果一个数列从第二项起,每一项与它前一项的差都等于同一个常数,那么这个数列称为等差数列。
这个常数称为等差数列的公差。
2.等差数列的表示方法:等差数列可以用通项公式an=a1+(n-1)d表示,其中a1是首项,d是公差,n是项数。
任意两项之间的差是公差d。
数列中的任意一项都可以表示为首项和项数的函数。
数列的前n项和可以表示为Sn=n(a1+an)/2。
四、等比数列1.等比数列的定义:如果一个数列从第二项起,每一项与它前一项的比都等于同一个常数,那么这个数列称为等比数列。
这个常数称为等比数列的公比。
2.等比数列的表示方法:等比数列可以用通项公式an=a1r^(n-1)表示,其中a1是首项,r是公比,n是项数。
任意两项之间的比是公比r。
数列中的任意一项都可以表示为首项和项数的函数。
数列的前n项和可以表示为Sn=a1(1r^n)/(1r)。
五、数列的应用数列在现实生活中有着广泛的应用,例如在金融领域中的复利计算、在物理学中的运动学问题、在生物学中的人口增长问题等。

数列知识点归纳总结职高数列是数学中的一个重要概念,也是职高数学教学中的重点内容之一。
掌握数列的基本概念、性质和相关计算方法,对于学生在数学学习和解决实际问题中都具有重要的意义。
本文将对数列的知识点进行归纳总结,帮助职高学生快速理解和应用数列知识。
一、数列的定义和表示方式1. 数列的定义:数列是将一系列按照某种规律排列的数按一定次序排列成一个有序数.2. 数列的表示方式:数列可用函数、递推公式、通项公式等方式来表示,不同的表示方式适用于不同的问题和计算方法。
二、常见数列的类型及性质1. 等差数列:- 定义:等差数列是指数列中的相邻两项之差保持不变的数列。
- 性质:a. 通项公式:an = a1 + (n - 1) * d,其中a1为首项,d为公差。
b. 前n项和公式:Sn = (a1 + an) * n / 2,其中Sn为前n项和。
- 例题应用:计算等差数列的第n项、前n项和以及根据已知条件求等差数列中未知项数等。
2. 等比数列:- 定义:等比数列是指数列中的相邻两项之比保持不变的数列。
- 性质:a. 通项公式:an = a1 * q^(n - 1),其中a1为首项,q为公比。
b. 前n项和公式(当|q|<1时):Sn = a1 * (1 - q^n) / (1 - q),其中Sn为前n项和。
- 例题应用:计算等比数列的第n项、前n项和以及根据已知条件求等比数列中未知项数等。
3. 斐波那契数列:- 定义:斐波那契数列是指数列中的每一项都等于前两项之和的数列。
- 性质:a. 通项公式:an = an-1 + an-2,其中a1 = 1,a2 = 1。
- 例题应用:求解斐波那契数列的第n项、前n项和以及根据已知条件求斐波那契数列中未知项数等。
4. 等差中项数列:- 定义:等差中项数列是指等差数列中由相邻两项的中间项构成的数列。
- 性质:a. 通项公式:an = a1 + (2n - 1) * d / 2,其中a1为首项,d为公差。


中职数学数列的基本知识ppt课件目录•数列基本概念与性质•数列求和与通项公式•数列递推关系与性质•数列极限与收敛性判断•数列在实际问题中应用举例PART01数列基本概念与性质数列定义数列表示方法数列的项通常用带下标的字母来表示数列,如{an}。
数列中的每一个数都叫做数列的项。
0302 01数列定义及表示方法按照一定顺序排列的一列数。
等差数列性质任意两项之差为常数。
从第一项开始,依次成等差数列的若干个数的和等于项数乘以中间项。
中间项等于首尾两项和的一半。
等差数列定义:从第二项起,每一项与它的前一项的差等于同一个常数的一种数列。
等比数列定义:从第二项起,每一项与它的前一项的比值等于同一个常数的一种数列。
等比数列性质任意两项之比为常数。
中间项的平方等于首尾两项的乘积。
从第一项开始,依次成等比数列的若干个数的积等于首项乘以末项再乘以公比的次幂。
算术数列几何数列调和数列混合数列常见数列类型及特点01020304每一项与前一项的差为常数,如1, 3, 5, 7,...每一项与前一项的比为常数,如2, 4, 8, 16,...每一项的倒数成等差数列,如1, 1/2, 1/3, 1/4,...不具有明显规律的数列,需要通过其他方法进行分析和处理。
PART02数列求和与通项公式等差数列求和公式推导通过倒序相加法或错位相减法推导等差数列求和公式。
等差数列求和公式应用利用等差数列求和公式解决与等差数列相关的问题,如计算前n项和、求某一项的值等。
等比数列求和公式推导通过错位相减法或等比数列的性质推导等比数列求和公式。
等比数列求和公式应用利用等比数列求和公式解决与等比数列相关的问题,如计算前n 项和、求某一项的值等。
通过观察数列的前几项,找出数列的通项公式。
观察法根据已知的递推关系式,逐步推导出数列的通项公式。
递推法通过设定未知数,建立方程组,求解得到数列的通项公式。
待定系数法通项公式求解方法典型例题解析已知等差数列的前n项和为Sn,且S10=100,S20=300,求S30。



分布数列知识点总结数列是数学中的一个重要概念,它在许多领域都有着广泛的应用。
在数学分析中,有一类特殊的数列被称为分布数列,它们具有一些特殊的性质和特点,是数学研究中的重要研究对象。
本文将对分布数列的相关知识点进行总结,包括分布数列的定义、性质、定理和应用等内容,以期能帮助读者深入了解和掌握这一重要概念。
一、分布数列的定义首先,我们来看一下分布数列的定义。
分布数列是指数列中具有一定分布规律的数列,其一般表示形式为{an},其中an是数列中的元素,n表示元素的序号。
通常来讲,分布数列中的元素满足一定的分布规律,这就要求我们能够找到一种规律来描述数列中各个元素之间的关系,从而能够清楚地表达出数列的分布规律。
分布数列通常可以用一个通项公式来表示,通项公式是一种能够描述数列中元素分布规律的公式,它包含了数列中各个元素的计算方式,通过通项公式,我们可以方便地求解数列中的任意元素,同时也能够描述数列中的一些重要特性和性质。
二、分布数列的性质分布数列作为一类特殊的数列,其具有一些特殊的性质和特点,这些性质和特点也是我们在研究分布数列时需要重点关注的内容。
下面,我们将来看一下分布数列的一些重要性质。
1. 有界性:分布数列通常具有一定的有界性,即数列中的元素存在一个上确界和下确界。
这是因为分布数列所描述的分布规律通常是有一定范围和限制的,因此数列中的元素通常也是有限的,这就决定了分布数列具有有界性。
2. 单调性:分布数列通常具有一定的单调性,即数列中的元素满足一定的单调增减规律。
这是因为分布数列所描述的分布规律通常是有顺序性的,因此数列中的元素通常也会具有一定的单调性。
根据数列的单调性,我们可以更好地理解和分析数列的分布规律。
3. 收敛性:分布数列通常具有一定的收敛性,即数列中的元素存在一个极限。
这是因为分布数列所描述的分布规律通常是有稳定性的,因此数列中的元素通常也会具有一定的收敛性。
通过数列的收敛性,我们可以更好地理解和分析数列的极限性质。


中职数学对口升学复习第六部分《数列》基础知识点归纳及山西历年真题汇编第六部分数列【知识点1】数列的概念1.数列的定义数列:按一定次序排列的一列数叫做数列。
项:数列中每个数都叫做数列的项。
各项依次叫作这个数列的第1项(首项)、第2项、...第n 项。
项数:各项在数列中所处位置的编号。
2.数列的分类有穷数列:项数有限的数列. 无穷数列:项数无限的数列.3.数列的一般形式:一般形式:a 1,a 2,a 3,...,a n ,...,其中an 是数列的第n 项,叫作数列的通项,n 叫作a n 的序号整个数列记作{an }.【知识点2】数列的通项1.通项公式:a n 与n 之前的函数关系式a n =f(n).数列的通项a n 可看成是n 的函数(以正整数的子集为定义域)。
注意:①数列的通项公式可以不止一个;②数列中的数依次出现正负相间的数时,可把符合分离出来,用(-1)n 或(-1)n+1来表示;③求数列的通项公式关键是寻求各项与项数的关系并归纳其规律。
2.递推公式:给出数列第1项(或前几项)以及后一项与前1项(或前几项)的关系式【知识点3】等差数列1.定义:一个数列从第二项开始后项减前项为一个常数就是等差数列。
d a a n n =-+1(1≥n )注意:公差d 一要用后项减前项,而不能用前项减后项。
2.常数列:公差的0的数列。
例如:0,0,0,0,...3.等差通项公式①m n a d n a a m n )()1(1-+=-+=;②b kn a n +=(k=d,b=a 1-d); ()n ma a d n m-=- 4.等差中项:2后前中=a a a +5.一个数列是否为等差数列的判定:(1)定义法:看相邻两项后项与前项差是否为常数d a a n n =-+1(1)n ≥.(2)中项法:11(2)2n n n a a a n -++=≥.6. 等差数列性质:1.m n s ta a a a +=+若m+n=s+t,则2. 项数(下标)成等差数列则对应项也成等差数列【知识点4】等差数列前n 项和1.等差数列求和公式:①11()(1)2n n n a a s na n n d +==+-② Bn An s n +=22,21da B d A -== ③()n n s n n a +=为奇数时2. 若{a n }是等差数列,则nn n n n S S S S S 23,2,--成等差数列3.已知数列的前n 项和公式如何求通项公式:1111)1()2({==≥-=-n S a n S S a n n n【知识点5】等比数列1.定义:一般地,如果一个数列从第2项起,每一项与它前一项的比都等于同一个常数,那么这个数列叫作等比数列,这个常数叫做等比数列的公比,通常用字母q 表示.1,0,0n n na q a q a +=≠≠ 注意:①求公比q 一要用后项除以项,而不能用前项除以后项;②等比数列中每一项及公比q 都不为0;③不为0的常数列既是公差为0的等差数列,又是公比为1的等比数列。

中专数列知识点归纳总结数列作为高中数学中的重要概念,在中专数学学习中也占据着重要的地位。
它不仅在数学中有着广泛的应用,而且还在其他科学领域中发挥着重要的作用。
本文将对中专数列的知识点进行归纳总结,帮助读者更好地理解和掌握相关知识。
一、数列的概念和性质1. 数列的定义数列指的是按照一定规律排列的一组数,通常用字母表示,如a₁,a₂,a₃...。
数列中的每个数称为项,用a₁,a₂,a₃...表示。
2. 数列的公式表示数列可以通过递推公式或通项公式来表示。
递推公式表示每一项与前一项之间的关系;通项公式表示第n项与n的关系。
3. 数列的分类数列可以按照公式的不同形式进行分类,常见的有等差数列和等比数列。
二、等差数列1. 等差数列的定义和性质等差数列是指数列中,任意两项之间的差恒定的数列。
设等差数列的首项为a₁,公差为d,则其通项公式为an = a₁ + (n-1)d。
2. 等差数列的求和公式等差数列的前n项和可以通过求和公式来计算,公式为Sn = (a₁ + an) * n / 2。
三、等比数列1. 等比数列的定义和性质等比数列是指数列中,任意两项之比恒定的数列。
设等比数列的首项为a₁,公比为r,则其通项公式为an = a₁ * r^(n-1)。
2. 等比数列的求和公式等比数列的前n项和可以通过求和公式来计算,公式为Sn = a₁ *(r^n - 1) / (r - 1),其中r ≠ 1。
四、数列的应用1. 等差数列的应用等差数列在实际生活中有着广泛的应用,如物理学中的匀速运动、财务学中的等额增长等。
2. 等比数列的应用等比数列在实际生活中也有着重要的应用,如生物学中的细胞分裂、经济学中的复利等。
五、数列的特殊情况1. 常数列常数列是指数列中所有的项都相等的特殊情况,其递推公式和通项公式都可以简化成相同的形式。
2. 斐波那契数列斐波那契数列是指从第3项开始,每一项都是前两项之和的数列,如1, 1, 2, 3, 5, 8, 13...。
职高数列知识点归纳总结数列是高中数学中的重要概念之一,职高数列知识点的掌握对于学生在高职阶段的学习和职业发展具有重要意义。
本文将对职高数列知识点进行归纳总结,帮助学生更好地理解和应用数列概念。
一、数列的概念与表示方法1. 数列的定义:数列是由一系列按照一定顺序排列的数所组成的有限或无限序列。
2. 数列的表示方法:数列可以用各种符号来表示,常用的有通项公式、递推公式和文字描述等。
3. 等差数列与等比数列:等差数列中,任意两项之间的差值相等;等比数列中,任意两项之间的比值相等。
二、等差数列1. 等差数列的通项公式:设等差数列的首项为a₁,公差为d,第n 项为aₙ,则通项公式为aₙ = a₁ + (n-1)d。
2. 等差数列的求和公式:设等差数列的首项为a₁,末项为aₙ,项数为n,公差为d,则求和公式为Sₙ = (a₁ + aₙ) * n / 2。
3. 等差数列的性质:等差数列的任意几项的和等于这几项的平均值乘以项数。
三、等比数列1. 等比数列的通项公式:设等比数列的首项为a₁,公比为q,第n 项为aₙ,则通项公式为aₙ = a₁ * q^(n-1)。
2. 等比数列的求和公式:设等比数列的首项为a₁,末项为aₙ,项数为n,公比为q,则求和公式为:- 当q ≠ 1时,Sₙ = a₁ * (q^n - 1) / (q - 1)。
- 当q = 1时,Sₙ = a₁ * n。
3. 等比数列的性质:等比数列的任意几项的和等于首项与末项的比值乘以公比减一。
四、特殊数列1. 等差中项数列:等差中项数列是指等差数列中的每两项的中间项组成的数列。
其通项公式为aₙ = a₁ + (n-1)d/2。
2. 等差三项数列:等差三项数列是指等差数列中的每三项的中间项组成的数列。
其通项公式为aₙ = a₁ + (n-1)d/3。
3. 斐波那契数列:斐波那契数列是一个无限数列,其通项公式为fₙ = fₙ₋₁ + fₙ₋₂,其中前两项为1,1。