同济大学-高等钢结构和组合结构-塑性设计和抗震性能
- 格式:docx
- 大小:1.83 MB
- 文档页数:53

试卷一22011/20~1/8较多的地区取其中的较大值。
2屋盖横向支撑以构成几何不变体系。
3刚性45、当实腹6 23 7820mm 2201A(A) 等稳定 (B) 等刚度 (C) 等强度 (D) 计算长度相等 2 A (A) 垫板数不宜少于两个 (B) 垫板数不宜少于一个 (C) 垫板数不宜多于两个 (D) 可不设垫板3 D (A) 支座竖杆中的内力 (B) 下弦杆中的最大内力 (C) 上弦杆中的最大内力 (D) 腹杆中的最大内力4、槽钢檩条的每一端一般用下列哪一项连于预先焊在屋架上弦的B(A) 一个普通螺栓 (B) 两个普通螺栓 (C) 安装焊缝 (D) 一个高强螺栓5、如轻型钢屋架上弦杆的节间距为L(D )。
(A) L (B) 0.8L (C) 0.9L (D) 侧向支撑点间距 6 C (A) 端竖杆处 (B) 下弦中间 (C) 下弦端节间 (D) 斜腹杆处 7 A(A) 可以受压 (B) 只能受拉 (C) 可以受弯 (D) 可以受压和受弯 8、某房屋屋架间距为6m 24m 24m 。
房屋C(A) 上弦横向支撑 (B) 下弦横向支撑 (C) 纵向支撑(D) 垂直支撑9、梯形屋架的端斜杆和受较大节间荷载作用的屋架上弦杆的合理C(A) 等肢角钢相连 (B) 不等肢角钢相连(C) 不等肢角钢长肢相连 (D) 等肢角钢十字相连10 C(A)屋面活荷载 (B)雪荷载(C)屋面活荷载和雪荷载两者中的较大值 (D)屋面活荷载和雪荷载20182636试卷二220123时它0.9L 4度高的连接焊透的k型坡口焊缝5至少两块填板6上玄横向支撑下玄横向支撑下玄纵向支撑竖向支撑系杆201、门式刚架轻型房屋屋面 A区取其中的较大值。
(A) 120—18 (B) 130—18 (C) 120—1 5(D) 130—1 52 B不变体系。
(A) 屋盖纵向支撑 (B) 屋盖横向支撑 (C) 刚性系杆(D) 柔性系杆3C(A) 刚性和柔性 (B) 刚性或柔性 (C) 刚性 (D) 柔性4 AB(A) 2 (B) 3 (C) 4 (D) 55 A(A) (B)不等边角钢短边相(C) (D)等边角钢相连6、屋B(A)10mm (B)20mm (C)30mm (D)40mm7 CA(A)强度 (B)刚度 (C)整体稳定 (D)局部稳定8Q≤30t度l≤6m Al~A5 A的(A) 加强上翼缘 (B) 加强下翼缘 (C) 设制动梁(D) 设制动桁架20182、为何冷弯薄壁构件在其强度和稳定性计算公式中截面特性以63、简述D6试卷三2201件起整体作填板2整体稳定3长度Lox=0.8 L Loy= 1L L为杆件的几何长度。


钢结构塑性设计与钢材的应变硬化性能*梁远森 徐建设 王 步(同济大学建筑工程系 上海 200092)李 峰(中国通信建设第四工程局 郑州 450052)摘 要:从钢结构塑性设计基本原理入手,分析了塑性设计中引入材料理想弹塑性假定的实质。
以此为基础,首先从理论上解释了没有应变硬化性能的材料不能用于结构塑性设计的原因,然后又用试验数据说明了应变硬化性能过弱的材料也不能用于塑性设计。
提出了钢结构塑性设计的用材要求。
关键词:钢结构 塑性设计 极限分析 应变硬化性能PLASTIC DESIGN OF STEEL STRUCTURE AND STR AIN HARDENING PERFORMANC E OF STEELLi ang Yuansen Xu Jianshe Wang Bu(Department of Struc tural and Building Engineering,Tongji Universi ty Shanghai 200092)Li Feng(The Forth Engineeri ng Bureau for the Communication Construction of China Zhengzhou 450052)Abstract :On the pri mary principles of the plas tic design of a steel structure,the real purpose of adopti ng the hypothesis that the materialused in the plastic design being of ideal elastic -plastic property i s revealed in thi s paper.Furthermore,the reason that why the material without any s train hardening performance cannot be us ed in plas tic desi gn is explai ned.Then,a tes t data s hows that the material with over -weak performance on strain hardening is not fit to plas tic design,either.At las t,a way of selecting proper sorts of steel for the plastic desi gn of a s teel s tructure is suggested here.Keywords :s teel s tructure plastic desi gn ultimate -l oad s analysis s train hardening performance*郑州市科委科研攻关项目资助。

火灾后钢结构检测分析及加固处理何建红上海市消防局普陀防火监督处工程师同济大学土木工程学院在读工程硕士摘要:随着钢结构建筑近年来被建筑业的大量采用,钢结构建筑火灾也日益增多。
本文从分析火灾后钢材的表观特征、力学性能入手,探讨了火灾后钢结构建筑损伤部位及整体结构的检测分析、修复的方法,并提出了通过加强钢材内部分子结构的机械性能、耐火性能来提高钢结构建筑的抗火能力,从而减少火灾损失及修复成本的一些想法。
关键词:钢结构火灾检测分析修复加固1 前言1.1 钢结构建筑的优点钢材是一种不会燃烧的建筑材料,它具有抗震、抗弯等特性。
在实际应用中,钢材既可以相对增加建筑物的荷载能力,也可以满足建筑设计美感造型的需要,还避免了混凝土等建筑材料不能弯曲、拉伸的缺陷,因此钢材受到了建筑行业的青睐,单层、多层、摩天大楼,厂房、库房、候车室、候机厅等采用钢材都很普遍。
钢结构以自重轻、施工快、可利用空间大、平面布置灵活、建筑外观美观、经济效益高等优点被广泛应用。
尤其是一些超高层建筑,采用钢结构材料更为广泛。
大型钢结构建筑建设工期短,收益快,是建造厂房、库房、商场等首选的建筑结构形式之一。
随着城市规模的发展,钢结构在我国建筑业的应用具有非常广阔的前景。
1.2 钢结构建筑的火灾危险性钢结构本身虽然是非燃材料,但它具有耐火性能差的致命弱点。
在未进行防火处理的情况下发生火灾时,它的机械性能,如屈服强度、抗拉及弹性模量等均会因温度的升高而急剧下降。
一般结构温度达到350ºC、500ºC、600ºC时,屈服强度分别下降1/3、l/2、2/3。
据理论计算,在全负荷情况下,使钢结构失去静态平衡稳定性的临界温度为500ºC左右,而一般火场温度达到800~1000ºC,在这样高的温度下,裸露的钢结构会很快出现塑性变形,产生局部破坏,造成钢结构整体倒塌失效。
1.3 结构检测及鉴定的意义通过对火灾后结构安全检测及鉴定,掌握经高温火烧后的钢结构建筑是否需要加固,哪些部位需要加固,哪些部位需要重建,哪些部位可以继续承重,对灾后建筑的修复提供科学、合理的依据,并对修复程序、修复部位、修复方法加以明确,使建筑的修复、加固更具经济性、时效性。

这是同济大学《高等混凝土结构理论》期末考试的复习要点,希望对考博选考3007高等混凝土与钢结构这门课的同学有所帮助。
1.Stress-strain curves of concrete under monotonic, repeated and cyclic uniaxial loadings. 单轴受力时混凝土在单调、重复、反复加载时的应力应变曲线。
2.Creep of concrete (linear and nonlinear) 混凝土的徐变(线性、非线性徐变)3.Components of deformation of concrete 混凝土变形的多元组成4.Process of failure of concrete under uniaxial compression 混凝土在单向受压时破坏的过程。
5.Strength indices of concrete and the relations among them 混凝土的强度指标及其之间关系6.Features of stress-strain envelope curve of concrete under repeated compressive loading. 混凝土单向受压重复加载时的应力应变关系的包络线的特征。
7.The crack contact effect of concrete and its representation in stress-strain diagram. 混凝土的裂面效应及其在应力应变关系图上的表示。
8.The multi-level two-phase system of concrete. 混凝土的多层次二相体系。
9.The rheological model of concrete. 混凝土的流变学模型。
10.Influence of stress gradient on strength of concrete. 应力梯度对混凝土强度的影响。

高等钢结构理论-4高等结钢构理论(结钢硕构――士程课)济同大建学筑工系程1.钢构基本性能结特点及1.钢1生材对产材性影的响 .21钢加材工(施)工对件构能性的响1.3影外作界用对结钢性构的影能响2 .结钢构几个的特问殊题目录.12残余应力及其影2.2响钢构结稳定问的题2 3.结钢的构裂问断2题.4结构钢疲劳问题的第一3讲.钢结构本构件3基. 1拉杆3.轴2压心3.3杆受弯件构3.4弯构件压.4钢架框理论41 .失稳式形4 2.析分法方4 3.实际应用第二讲第三讲5.结构钢连接的5.焊1接.5螺2栓接连四第讲目录续)5.(混合3连接6 .钢结构构造设计7 .弯冷薄壁型结构的钢点8.特他其一些心关问题8的. 1塑性计设8 . 2抗钢结震8构3箱.形梁 .84受构件扭8.设计5中试的工作8.6验钢结构固设加计第讲五第六讲第七讲.5钢结构的连接.15接连形式:焊接铆、、普接通栓连螺接高、螺强连栓5.2接角缝焊连接角焊缝性的能:试验研究角缝焊的算计:计公式算有效厚和度度长理论究研缝群的计焊算5 3高强.螺栓接连抗螺栓连接剪:承受轴心剪力螺的连接:栓承受偏心剪的力栓连螺接:放孔和大加长孔剪拉合破联坏.5钢结构连的接(续).5高3螺栓连强(接)续抗螺拉栓接连高螺栓连强抗接拉能:性连接柔性的影板响螺栓和:板时计同的方算法:兼剪力承拉力和的栓连螺接承受重荷复的载栓螺连接抗剪接连:抗拉接连:54混合连.接6.钢结的构构造设计构设造计意义的处结构理的细部解:构件或决零件间的衔之问接重要题:性造构处往形成应往集中或局部力应、力时有不易精确算(数计值分、试验析究)、研避局免破坏而部影响构结性的能发挥影、施工响造(、质价等量) 构件拼接:的等截面拉、压杆变面柱截梁端板接中连的板厚度梁、梁接连:简连接支续和半连连连接续梁、柱连接. 6钢构的构造结计(设)续柔连性接半刚连性接刚性连接:柱脚柱的脚成构脚的计算柱架节桁点节的点侧刚向度节点受板力分析相关范规造构节点上偏心的抵抗疲的劳构造抵抗性断裂的脆构造连接形式焊:接现代钢结最构主的连接方要式9适用广构造简、单、省料省工、自动可、效率化。
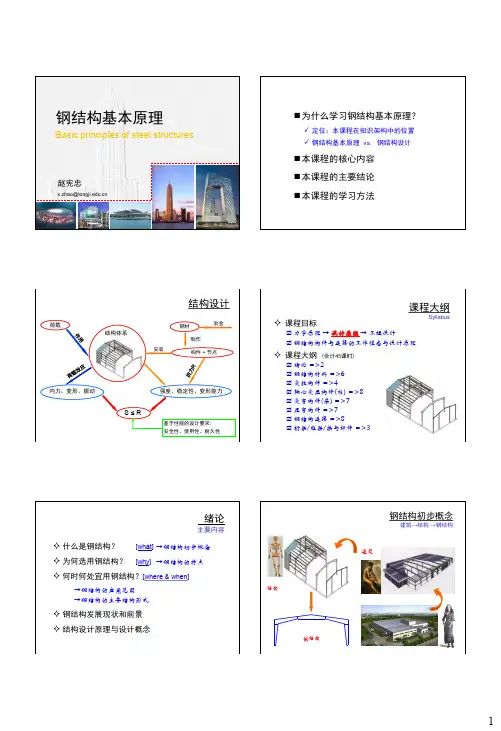

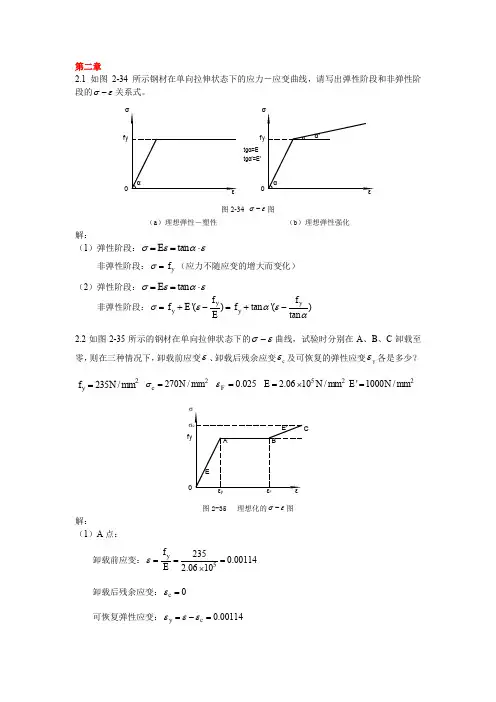
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。

浅谈钢结构建筑的抗震能力设计及建议作者:邓锋李继梅来源:《中国建筑金属结构·下半月》2013年第07期摘要:钢材具有延性好、质轻和强度高等特点,钢结构在建筑中的应用日益广泛,钢结构建筑在受到地震作用下,良好的延性即使在产生很大变形的情况下不容易倒塌,从而保证整个建筑的安全性,但是钢结构建筑如果设计和建造存在不当,在地震作用下,结构很可能发生脆性破坏,不能够充分发挥钢材的性能,造成严重的后果,因而研究钢结构建筑的抗震设计具有十分重要的意义和价值。
关键词:钢结构建筑;抗震设计;构造中图分类号:TU391 文献标识码:A 文章编号:1671-3362(2013)07-0019-011 钢结构建筑的震害特点分析1.1 节点连接破坏节点连接破坏大致分为框架梁柱节点破坏和支撑连接破坏两种情况。
引起框架梁柱节点破坏产生的原因如下:裂缝出现在节点的下翼缘是由于钢结构的梁的上翼缘焊接缝无腹板而影响焊接;梁端焊缝穿过孔边缘而出现应力集中,进而导致裂缝产生;焊缝本身存在质量缺陷;焊缝金属的冲击韧性比较低,不符合钢结构性能的要求等。
采用螺栓支撑连接的钢结构,支撑杆件螺孔之间的剪切滑移,节点板端的剪切滑移以及支撑面的断裂都会降低钢结构的稳定性,钢结构建筑的支撑结构中影响抗震性能的抗侧力部分,一旦发生地震将会首先承受地震的水平作用,如果建筑的某一个楼层的支撑发生损坏,将会削弱整个楼层抗震性能,进而会影响到整个建筑的抗震性能。
1.2 构件破坏支撑杆件的失稳和断裂破坏在框架支撑结构中比较常见,支撑杆件只要设计得当,在多遇地震作用下能够保持弹性工作状态,一般不会出现失去整体稳定,在罕遇地震作用下,支撑构件由于受到巨大的往复拉压作用,将会出现整体失稳,建筑解耦股进入塑性屈服状态,随找拉压循环次数的增加,钢结构的承载力将会衰弱,在支撑杆件的中央形成塑性铰,只有杆件形成反向塑性铰之后,支撑杆件的抗拉刚度才会逐步恢复。
分析1995年的阪神地震,钢柱的脆性断裂主要发生在14层以下的楼层中,并且都是脆性受拉断裂,出现钢柱脆性断裂的成因如下:钢柱断裂主要出现在拼接焊缝周围,这和焊接质量有很大的关系;钢柱都是暴露在室外,而地震发生的寒冬季节,温度比较低,影响钢材的抗拉伸刚度;一些钢柱的壁厚超过50mm,焊接过程中造成焊接区域过热,降低钢柱的延展性能;倾覆力矩和竖向地震在钢柱中产生很大的拉力。

同济大学研究生课程考核试卷2015-2016 学年第一学期课号:2020388 课名:高等钢结构与组合理论考试考查:考试此卷选为:期中考试( )、期终考试(√)、重考( )试卷、开卷()、闭卷(√)年级专业学号姓名命题教师:郭小农、童乐为、邓长根、孙飞飞、张其林、陈以一、蒋首超、陈世鸣考试说明:(1)本课程为闭卷考试,学生不得将教材、笔记以及作业本等与考试有关的书籍、资料带入考场。
(2)考卷装订成册,学生不得自行拆开。
试题一(钢材性能与结构体系部分,共6分)1.(3分)某简支钢梁,两端承受端弯矩,长度为6m,截面为工字形,截面高度400mm,已知钢材的弹性模量为E=200GPa,屈服强度为235MPa,屈服平台的最大流幅2.0%。
若假定钢梁在整个加载过程中一直满足平截面假定;试分别计算:(1)钢材边缘纤维刚刚屈服时,钢梁的跨中挠度;(1分)(2)边缘纤维应变达2.0%时,钢梁的跨中挠度;(1分)(3)说明屈服平台段长度对于结构承载性能的重要性。
(1分)⏹答案答:1)根据已知条件,εy=f y/E=235/2.0×105=0.1175%由材料力学可知,简支纯弯钢梁的变形曲线为圆弧;截面曲率为:ψ=2εy/0.4=2*0.1175%/0.4=0.005875 m-1因此曲率半径为:R=1/ψ=170.213m跨中挠度为:δ=R-(R2-32)0.5=1/ψ=170.213-170.186=0.027m=27mm2)根据已知条件,ε=2%截面曲率为:ψ=2ε/0.4=2*2%/0.4=0.1 m-1因此曲率半径为:R=1/ψ=10m跨中挠度为:δ=R-(R2-32)0.5=1/ψ=10-9.5394=0.4606m=460.6mm3)屈服平台段使得结构具有良好的塑性和变形能力。
2.(3分)如何理解结构形态对结构受力性能的影响?举例说明结构体系与结构形态的关系。
⏹答案(其他回答若理论上正确也可给分)(a)在相同的荷载条件下,不同的结构形态将导致不同的结构内力(弯矩或轴力),从而影响结构的受力性能。
《高等钢结构原理》第3章塑性设计第4章抗震性能作业目录1第3.1b题 (1)1.1剪力对受弯截面的极限抗弯承载力的影响 (1)1.2钢材应力-应变曲线强化对受弯截面的极限抗弯承载力的影响 (5)2第3.2c题 (7)3第3.3c题 (9)3.1各种塑性铰、塑性区方法的概念、假设和使用情况 (9)3.1.1典型弹塑性铰法 (9)3.1.2等效荷载塑性铰法 (9)3.1.3精化塑性铰法 (10)3.1.4伪塑性区法 (10)3.1.5改进塑性铰法 (11)3.1.6典型塑性铰区法 (11)3.1.7准塑性铰区法 (12)3.2各种塑性铰、塑性区方法的研究和应用进展 (12)4第3.4a题 (15)4.1模型的建模 (15)4.1.1截面选取 (15)4.1.2模型建立 (16)4.2结果与分析 (17)4.2.1应力与变形云图 (17)4.2.2无量纲位移和弯矩图 (21)4.2.3无量纲极限弯矩对比图 (21)4.3结论和收获 (22)5第3.5a题 (23)5.1模型建立 (23)5.1.1建模-2层单跨平面框架 (23)5.1.2建模-4层单跨平面框架 (24)5.2有限元计算结果 (25)5.2.1结果-2层单跨平面框架 (26)5.2.2结果-4层单跨平面框架 (28)5.2.3综合结果对比 (30)5.3分析 (31)6第4.1b题 (32)6.1滞回曲线的理解 (32)6.2算例分析 (33)7第4.2a题 (35)7.1钢支撑的滞回曲线特点 (35)7.2钢支撑的滞回曲线模拟要点 (36)7.3钢支撑滞回曲线模拟 (37)8第4.3a题 (38)8.1屈曲约束支撑的构成与原理 (38)8.2屈曲约束支撑研究与设计现状 (40)8.2.1试验与理论研究 (40)8.2.2设计现状和工程应用 (41)9第4.4b题 (43)9.1目前的抗震设计的局限性 (44)9.2基于性能的结构抗震设计的优点 (45)9.3基本思想和基本步骤 (45)9.3.1基本思想 (45)9.3.2基本步骤 (45)9.4性能目标 (45)9.4.1地震水平 (46)9.4.2性能水平 (46)9.4.3性能目标的确定 (46)9.5设计方法 (46)9.5.1承载力设计方法 (46)9.5.2基于位移的设计方法 (46)9.5.3能量设计方法 (47)9.6目前存在的困难 (47)9.7国内外研究进展 (48)10参考文献 (49)1 第3.1b 题题目:简述剪力和钢材应力-应变曲线强化对受弯截面的极限抗弯承载力的影响。
高等钢结构作业系所:专业:学号:姓名:指导教师:二零一四年十一月十一日1、焊接结构可能出现哪些类似裂纹的缺陷?答:焊接结构可能出现的类似裂纹的缺陷有:焊接裂纹、气孔、错边和错口、咬边、未焊透、焊瘤。
1)焊接裂纹裂纹是焊接结构中危害比较严重的缺陷。
她减少焊缝断面面积的同时引起应力集中,使得裂纹扩大,造成接头破坏。
它可能发生在焊缝金属中,也可能发生在母材中,可能垂直于焊缝,也可能平行于焊缝。
常见的有焊缝金属内部凝固裂纹和热影响区中的氢裂纹,前者主要取决于凝固速率,后者主要为硬显微组织和材料内氢气逸散情况决定,二者均可通过预热加以控制。
根据裂纹受力状况不同,裂纹可分为张开型、滑开型和撕开型。
张开型是受垂直于裂纹面的拉应力作用所致;滑开型是受平行于裂纹面、同时垂直于裂纹前缘的剪应力所致;撕开型是受平行于裂纹面、同时平行于裂纹前缘的剪应力所致。
裂纹形态如图1所示。
张开型滑开型撕开型图1根据裂纹发展方向,裂纹可以分为纵向裂纹和横向裂纹。
纵向裂纹在焊缝熔池的凹口内是最常见。
横向裂纹一般常见于合金钢焊接时,低碳钢在冷却过快或冷却不均匀时也可能产生横向裂纹。
裂纹形态如图2所示。
2)气孔气孔(如图3)指的是焊缝金属凝固时,金属内气体由于被截留而引起的孔穴。
通常呈球状,尺寸差别很大,很可能散及整个焊缝,也可能局部成串出现。
母材或电焊条中的高含硫量、焊条药皮中过量的水分和不稳定的保护气层都可能产生密集气孔。
气孔降低焊缝的强度的同时可能使接头处产生渗漏。
在焊缝检查时发现有均匀的、成群的链形成气孔必须将这一段焊缝铲去,重新补焊,对单个气孔需根据所在位置的重要性决定是否处理。
3)错边和错口错边(如图4)指的是焊接后两个焊件未在同一平面内,一个高,一个低。
若焊件是板材,则称错边,若焊件是管材,则称错口。
焊件检验中根据不同情况,对错边和错口量有所要求。
4)咬边咬边(如图5)是指焊趾、焊缝根部或焊道间的沟槽状缺陷。
主要是因为焊接时电流、电压过高或焊缝空间位置不合适,造成融化金属分布不均匀。
同济结构工程考研专业介绍一、简介结构工程学科是土木工程属下的二级学科,在国民经济建设中有着重要的地位,在促进城市建设、社会发展过程中做出了重大贡献。
结构工程是同济大学历史最为悠久、综合实力最强的传统强势学科,以其培养的卓越人才和丰硕的教学科研成果在国内外学术界、工程界享有重要的地位和影响。
早在1914年同济大学就已设立了结构类专业,1952年全国高等院校院系调整以及1996年上海城市建设学院、上海建筑材料学院和2000年上海铁道大学先后并入同济大学,都促进了本学科的发展。
1981年首批获得硕士和博士学位授予权,1984年首批获得博士后流动站,1987年入选为国家级重点学科,2001年又入选为上海市重点学科,2006年专业评估中继续入选国家级重点学科。
本学科在钢筋混凝土结构与砌体结构、钢结构与木结构、空间结构、结构分析、结构与生命线工程抗震防灾和控制、结构全寿命设计与维护等方向特色鲜明,有着十分强实的师资和科研力量。
现有教学、科研和试验人员167人,其中工程院院士1人、长江学者及讲座教授4人、教授39人、副教授61人、高级工程师3人、高级实验师5人。
这些师资中有许多是成就卓著、享有国际声誉的著名专家、学者,引领着国内结构工程学科的发展。
近年来本学科在人才培养、教学改革、国际合作与交流、科学研究、社会服务等各个层面取得了国内外公认的丰硕成果。
每年平均招收硕士研究生200余名、博士研究生60多名,完成了众多的教学改革项目,出版了大量的高水平教材。
已与欧洲、美国、加拿大、澳大利亚、日本、韩国等许多大学和机构建立了合作关系,经常开展师生访问、学术交流、共同研究等活动和项目,主办了多次国际学术会议。
主持完成了国家攀登B计划、国家863计划、国家自然科学基金重点项目、国家杰出青年基金项目、国家科技部、建设部、教育部、上海市科委、建委、教委等资助的大量纵向科研项目及国际合作重点项目。
负责完成了上海市及其他省市许多重大、重点工程项目关键课题的研究,获得50余项国家级、省部级的科技进步奖及国家专利。
《高等钢结构原理》第3章塑性设计第4章抗震性能作业目录1第3.1b题 (1)1.1剪力对受弯截面的极限抗弯承载力的影响 (1)1.2钢材应力-应变曲线强化对受弯截面的极限抗弯承载力的影响 (5)2第3.2c题 (7)3第3.3c题 (9)3.1各种塑性铰、塑性区方法的概念、假设和使用情况 (9)3.1.1典型弹塑性铰法 (9)3.1.2等效荷载塑性铰法 (9)3.1.3精化塑性铰法 (10)3.1.4伪塑性区法 (10)3.1.5改进塑性铰法 (11)3.1.6典型塑性铰区法 (11)3.1.7准塑性铰区法 (12)3.2各种塑性铰、塑性区方法的研究和应用进展 (12)4第3.4a题 (15)4.1模型的建模 (15)4.1.1截面选取 (15)4.1.2模型建立 (16)4.2结果与分析 (17)4.2.1应力与变形云图 (17)4.2.2无量纲位移和弯矩图 (21)4.2.3无量纲极限弯矩对比图 (21)4.3结论和收获 (22)5第3.5a题 (23)5.1模型建立 (23)5.1.1建模-2层单跨平面框架 (23)5.1.2建模-4层单跨平面框架 (24)5.2有限元计算结果 (25)5.2.1结果-2层单跨平面框架 (26)5.2.2结果-4层单跨平面框架 (28)5.2.3综合结果对比 (30)5.3分析 (31)6第4.1b题 (32)6.1滞回曲线的理解 (32)6.2算例分析 (33)7第4.2a题 (35)7.1钢支撑的滞回曲线特点 (35)7.2钢支撑的滞回曲线模拟要点 (36)7.3钢支撑滞回曲线模拟 (37)8第4.3a题 (38)8.1屈曲约束支撑的构成与原理 (38)8.2屈曲约束支撑研究与设计现状 (40)8.2.1试验与理论研究 (40)8.2.2设计现状和工程应用 (41)9第4.4b题 (43)9.1目前的抗震设计的局限性 (44)9.2基于性能的结构抗震设计的优点 (45)9.3基本思想和基本步骤 (45)9.3.1基本思想 (45)9.3.2基本步骤 (45)9.4性能目标 (45)9.4.1地震水平 (46)9.4.2性能水平 (46)9.4.3性能目标的确定 (46)9.5设计方法 (46)9.5.1承载力设计方法 (46)9.5.2基于位移的设计方法 (46)9.5.3能量设计方法 (47)9.6目前存在的困难 (47)9.7国内外研究进展 (48)10参考文献 (49)1 第3.1b 题题目:简述剪力和钢材应力-应变曲线强化对受弯截面的极限抗弯承载力的影响。
解答:1.1 剪力对受弯截面的极限抗弯承载力的影响梁截面上兼有正应力σ和剪应力τ时,屈服准则是:222233y vy f f στ+== 3.1.1因此,当截面上存在剪应力时,至少有一部分正应力还未达到y f 时就完全进入塑性。
但是梁截面完全进入塑性时,其正应力和剪应力分布的精确计算比较复杂,往往采用一些简化图式来分析。
对于工字形截面梁,常有以下几种简化计算图式:(1) 假定假定梁翼缘和腹板同样承担弯曲正应力和剪应力,即整个截面上正应力都是σ,剪应力都是τ,如下图所示:图3.1b-1完全屈服的关系式为2222()()11y vyp p f f M Q M Q στ+=⎛⎫⎛⎫+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭或3.2.2 根据剪力流的方向,腹板剪力为:0A Q dA h d ττ==⎰ 3.2.3使腹板受剪屈服的剪力则为:0p vy Q f h d = 3.2.4以上屈服的关系式比较简单,但翼缘的正应力低于y f ,偏于保守。
(2) 假设翼缘正应力为y f ,腹板正应力低于y f ,同时假设翼缘没有剪应力,而腹板应力满足公式3.2.2,如下图所示:图3.1b-2则可得:122()()1ypw p M h btf Q M Q -+= 3.2.5式中pw M 为腹板全塑性弯矩,即20/4y h df 。
这一相关公式只适用于1y M h btf >的范围。
(3) 腹板只有部分高度承受剪力,如下图所示:图3.1b-3上图显示了该种类型的两种具体正应力和剪应力分布方式。
前一种方式,正应力在梁上下边缘一定范围内为y f ,腹板中间没有正应力而承受剪应力;后一种方式,正应力在梁上下边缘一定范围内为y f ,在腹板中间一定范围内呈线性变化,而剪应力呈曲线变化。
剪应力使塑性弯矩降低的程度和梁的荷载类型以及高跨比有关。
从比较保守的式3.2.2出发,设M aQ =,可得p M M =3.2.6此式右端代表塑性弯矩降低系数,它和1/a 及/p p M Q 两个因素有关,且这两个因素愈大,降低得愈多。
其中a 和荷载情况有关,可以看成是个等效悬臂梁的长度,它的影响通常由无量纲化的0/a h 来表现;/p p M Q 则和截面尺寸有关,10/A A 愈大,/p p M Q 随之增大,其中1A 是腹板面积,0A 是翼缘面积。
以在跨度中央承受集中荷载的梁为例,如下图所示。
图3.1b-4在中央截面处//2a M Q l ==,代入可得p M M = 3.2.7当0/ 5.0a h =,10/1A A =时,得0.937p M M =当0/ 5.0a h =,10/0.5A A =时,得0.977p M M =此梁中央截面弯矩和剪力都是最大值,塑性弯矩只下降6.3%和2.3%,按公式3.2.6,比上述情况不利的是承受两个对称集中荷载的梁,如下图所示。
原因是荷载距支点近,0/a h 值小,所以算的的塑性弯矩要下降多一点。
然而,由于材料存在硬化阶段,以及剪力影响只出现在梁的很小的范围内,梁中段剪力为0,因此梁所能承受的弯矩并不会下降。
图3.1b-5从上图可以看出,达到这一弯矩后梁的承载能力并未穷竭,载还可继续增大,甚至超过p M 值。
由其他试验结果也可以得知,简支梁承受一集中荷载者,最大弯矩都超过p M ,承受两个集中荷载者大部分达到或超过p M ,但也有一部分0/1a h =的梁未达到。
多数设计规范对塑性开展的梁未对剪应力值作特殊限制,有的规范虽不对剪应力做特殊限制,却要求0/a h 不得小于一定限度,即1001.52 1.2A a h A ≥+ 3.2.8还有规范以屈服条件为准,限制弯矩最大截面的剪应力不超过0.5/vy r f γ,其中r γ是抗力分项系数。
如果超过此值,塑性弯矩应相应降低。
有推荐以下算法:当剪力00.50.5p vy Q Q h df ≤=,弯矩可达p M ;当0.5p p Q Q Q ≤≤,弯矩降为22(1)p p P Q M M M Q ω=-- 3.2.9此时当p Q Q =时,p p pf M M M M ω=-=,即翼缘全塑形弯矩,相关曲线如下图所示。
图3.1b-61.2钢材应力-应变曲线强化对受弯截面的极限抗弯承载力的影响钢结构的塑形设计法建立在充分利用钢材所具有的塑性变形能力的基础上,它使得结构发生以形成破坏机构为目标的内力重分布,可以使得设计简化分析,比较经济合理并且符合实际。
在钢结构的塑性设计中,通常假定材料为理想弹塑性材。
这样处理计算简单,且硬化阶段的强度提升可提供额外的安全储备。
但这种简化并不意味着所有材料可以不具有应变硬化性能。
恰恰相反,材料必须具有一定的应变硬化工作阶段才有可能达到形成机构的极限状态。
下面以受均布荷载q的固端梁来说明,当跨中和梁端均产生塑性铰时,该梁达到极限承载力,如下图所示:图3.1b-7表3.1b-1M梁端和跨中均产生塑性铰:阶段1,梁端弯矩2/12qL大于跨中弯矩2/24qL,处于弹性阶段;阶段2,A和B两截面先出现塑性铰,荷载继续增大时,这两个截面在保持塑性弯矩pM的同时出现转动,梁如同两端铰支杆一样继续工作;阶段3,跨中截面达到塑性弯矩。
从A、B两截面刚达到塑性弯矩到C截面达到塑形弯矩时,截面A和B需要转动角度Aθ可求得:6LpAM LM MdsEI EIθ==⎰ 3.2.10 但如果材料是理想弹塑性体,则只有曲率K为无限大时,才能出现这一转动。
这是因为曲率/K d dxθ=,当转动只在一个截面发生时,0dx=,K必然趋于无限大,事实上这是不可能的。
因此,机构也就无从实现。
图3.1b-8具有应变硬化性能的材料,截面A的弯矩不仅可以达到pM,还能超过这一值。
这样,在梁端会出现一个短的塑性区,如下图所示,即0dx≠,曲率K成为有限值,机构也就有可能实现了,梁的材料具有应变硬化性能时,最大荷载maxq不仅可以达到uq还能超过这一值,塑性设计得以实现。
钢材考虑应力-应变强化曲线后弯矩和截面曲率关系如下图所示。
图3.1b-9通过以上说明可知,应变硬化性能过弱的材料也不适用于塑性设计。
所以钢结构设计规范规定,用于钢结构塑性设计的钢材一般应满足以下三个条件:①极限强度u f 与屈服强度y f 的比值(强屈比)不应小于1.2;②单向拉伸试件的伸长率5δ不小于15%,即515%δ≥;③相应于u f 的应变u ε不小于20倍的屈服应变y ε。
2 第3.2c 题题目:试用简单塑性分析方法,求出图3.2c 所示超静定梁的极限荷载。
当0<<1时,试求最大极限荷载的作用位置和数值(用Mp 表示)。
图3.2c-1(此题题目有错,红色标识部分应该改为“最小极限荷载”,因为从下面的求解过程来看,P 在01ξ<<区间内仅存在最小值,而没有最大值)。
解答:采用极限平衡法求解。
取基本体系如图1所示:图 3.2c-2外荷载P和未知荷载V引起的弯矩分别如图2所示:图 3.2c-3对于1,2点,其叠加弯矩为:1M P l Vlξ=-+2(1)M Vlξ=-且容易判断1、2截面最终将达到塑性弯矩,使结构成为机构,故有:12(1)ppM P l Vl MM Vl Mξξ=-+=-=-=由上两式解得,极限荷载为:2(1)pMPlξξξ-=-()上式对ξ求导得:2'22(42)()(1)Pξξξξξ--+=-令'()0P ξ=解得:2ξ=2ξ=+P 在0,2⎡⎣区间递减,在2⎡⎤⎣⎦递增。
故当2ξ=min 5.828p M M P l ===3 第3.3c 题题目:综述各种塑性铰、塑性区方法的概念、假设、使用情形、研究和应用进展。
解答:3.1 各种塑性铰、塑性区方法的概念、假设和使用情况经过查阅文献和相关资料,我得知塑性铰法主要包括典型弹塑性铰法以及由它发展或改进而产生的精化塑性铰法、等效荷载塑性铰法、伪塑性区法、改进塑性铰法;塑性区法主要包括典型塑性铰区法以及由它发展得到的准塑性铰区法。
下面详细介绍这些典型钢结构塑性分析高等分析方法。
3.1.1 典型弹塑性铰法弹塑性铰法基于集中塑性的概念,它一般假定构件不发生局部屈曲,即限定构件采用紧凑型截面。