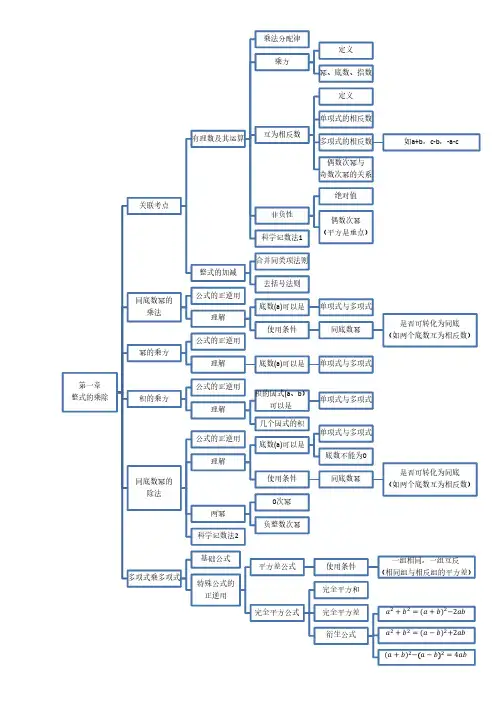
各种常用的关系图模版(思维导图可用)

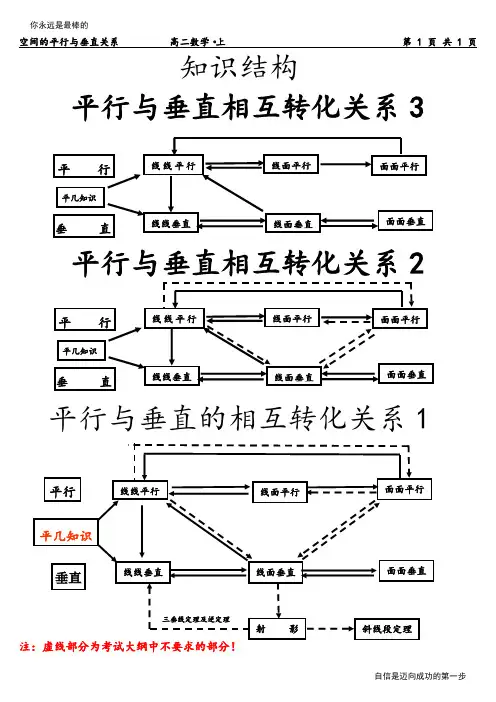
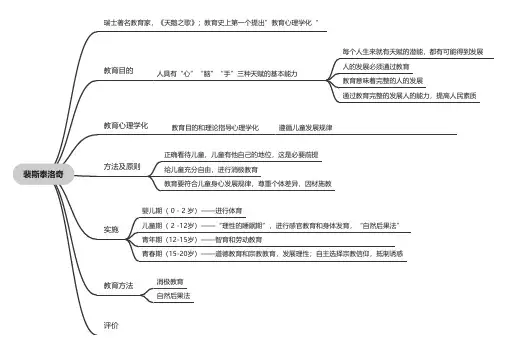
裴斯泰洛奇瑞士著名教育家，《天鹅之歌》；教育史上第一个提出”教育心理学化“
教育目的人具有“心”“脑”“手”三种天赋的基本能力
每个人生来就有天赋的潜能，都有可能得到发展
人的发展必须通过教育
教育意味着完整的人的发展
通过教育完整的发展人的能力，提高人民素质教育心理学化教育目的和理论指导心理学化遵循儿童发展规律
方法及原则
正确看待儿童，儿童有他自己的地位，这是必要前提
给儿童充分自由，进行消极教育
教育要符合儿童身心发展规律，尊重个体差异，因材施教
实施
婴儿期（ 0 - 2 岁）——进行体育
儿童期（ 2 -12岁）——“理性的睡眠期”，进行感官教育和身体发育，“自然后果法”
青年期（12-15岁）——智育和劳动教育
青春期（15-20岁）——道德教育和宗教教育，发展理性；自主选择宗教信仰，抵制诱惑
教育方法消极教育
自然后果法
评价。

用户分层，这样做才有效（思维导图）来源：运营狗Oliver老舅在城里开了家拉面馆，让我去帮忙，我很高兴地答应了。

干了几个月，小饭店来来往往的那些客人，就都很熟悉了。

张老板是我们这儿的常客，每周都要来个三四次，时不时还带一帮朋友，点菜阔绰。

我们特别感谢这位客人，人多时会多送两个小菜，结账时抹个零头，逢年过节还会准备一盒土特产让他带回去。

久而久之成了朋友，竟是谁也离不开谁了。

李哥的儿子特别喜欢吃我们家羊肉串，经常带儿子来。

但最近总是独自一人来，听他说，儿子刚升了中学，放学太晚来不了。

结账时，我就送了几串羊肉串给李哥，让他打包回去给孩子。

李哥很高兴，从这以后，每次李哥来吃饭，都会多点10串羊肉串带走。

杨小姐是附近公司的白领，年轻漂亮，北方人，喜欢吃面。

因为工作忙，每次来都急匆匆的，随便吃点就走了。

我看着心疼，就向她推荐了我们的外卖服务，她点了几次觉得不错，就推荐给了同事，给我们带来了不少生意。

……凭借着对每位客人的熟悉，我总能为不同的客人提供他们想要的服务，不知不觉生意竟火爆起来，老舅开了几家分店，生意蔓延到省城。

我从一个小二做到经理，但是问题也来了。

以前只有几十个客人，很容易区别对待，现在盘子大了，客人少说也有上万，想要认识他们尚且不可能，更不要说一对一的服务了。

百愁莫展之时，老舅家大儿子大学毕业回到家，给我提了一个建议。

脑袋记不住，为什么不用电脑来记？好主意！我立刻召集手下几十个店长，请他们整理了开业以来所有客人信息，包括多久来吃一次、几个人吃、点了什么菜、花了多少钱等等，并交代他们，以后要注意客人信息的搜集，最好能规范化。

几天后，店长们陆陆续续发来一些客人的消费数据，按照大表弟教的方法，我把这些数据分门别类，整理成不同的人群，在这些人群里，我发现了数千个张老板、李哥和白领杨小姐。

我立刻设计了一套针对不同人群标准化的服务和推销方法，印成小册子发给所有店长，让他们照着做。

果不其然，没过多久，店长们纷纷反馈业绩上涨，客人们的满意度也提高了很多。

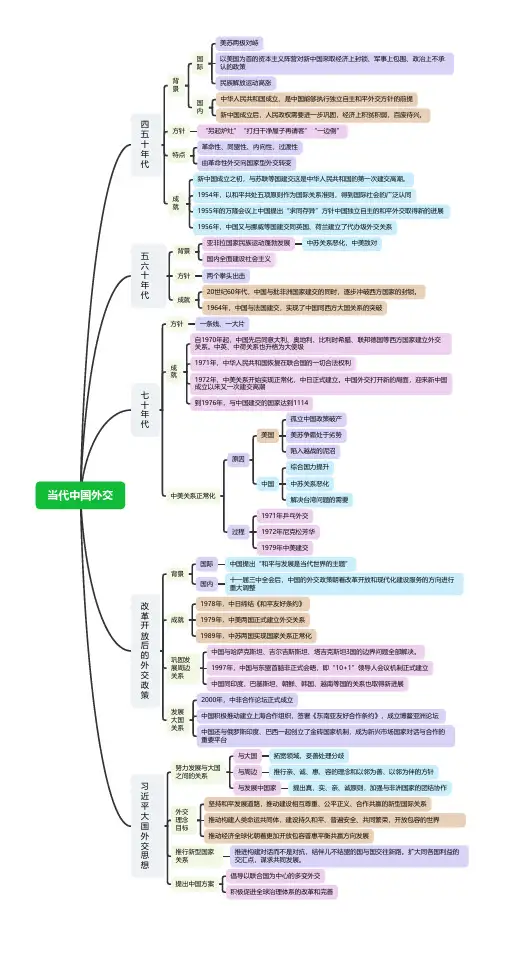
当代中国外交四五十年代背景国际美苏两极对峙以美国为首的资本主义阵营对新中国采取经济上封锁、军事上包围、政治上不承认的政策民族解放运动高涨国内中华人民共和国成立、是中国能够执行独立自主和平外交方针的前提新中国成立后，人民政权需要进一步巩固，经济上积贫积弱，百废待兴。

方针“另起炉灶”“打扫干净屋子再请客”“一边倒”特点革命性、同盟性、内向性、过渡性由革命性外交向国家型外交转变成就新中国成立之初，与苏联等国建交这是中华人民共和国的第一次建交高潮。

1954年，以和平共处五项原则作为国际关系准则，得到国际社会的广泛认同1955年的万隆会议上中国提出“求同存异”方针中国独立自主的和平外交取得新的进展1956年，中国又与挪威等国建交同英国、荷兰建立了代办级外交关系五六十年代背景亚非拉国家民族运动蓬勃发展中苏关系恶化，中美敌对国内全面建设社会主义方针两个拳头出击成就20世纪60年代，中国与批非洲国家建交的同时，逐步冲破西方国家的封锁。

1964年，中国与法国建交，实现了中国同西方大国关系的突破七十年代方针一条线、一大片成就自1970年起，中国先后同意大利、奥地利、比利时希腊、联邦德国等西方国家建立外交关系。

中英、中荷关系也升格为大使级1971年，中华人民共和国恢复在联合国的一切合法权利1972年，中美关系开始实现正常化，中日正式建立。

中国外交打开新的局面，迎来新中国成立以来又一次建交高潮到1976年，与中国建交的国家达到1114中美关系正常化原因美国孤立中国政策破产美苏争霸处于劣势陷入越战的泥沼中国综合国力提升中苏关系恶化解决台湾问题的需要过程1971年乒乓外交1972年尼克松芳华1979年中美建交改革开放后的外交政策背景国际中国提出“和平与发展是当代世界的主题”国内十一届三中全会后，中国的外交政策朝着改革开放和现代化建设服务的方向进行重大调整成就1978年，中日缔结《和平友好条约》1979年，中美两国正式建立外交关系1989年，中苏两国实现国家关系正常化巩固发展周边关系中国与哈萨克斯坦、吉尔吉斯斯坦、塔吉克斯坦3国的边界问题全部解决。

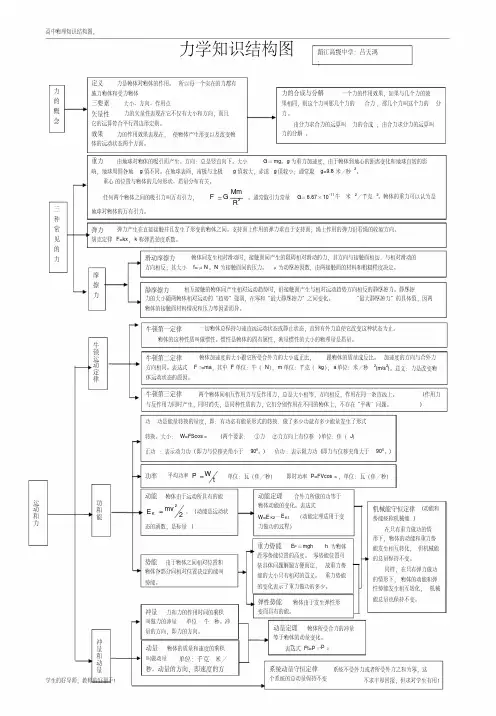
力学知识结构图力的概念定义力是物体对物体的作用。

所以每一个实在的力都有施力物体和受力物体三要素大小、方向、作用点矢量性力的矢量性表现在它不仅有大小和方向，而且它的运算符合平行四边形定则。

效果力的作用效果表现在，使物体产生形变以及改变物体的运动状态两个方面。

力的合成与分解一个力的作用效果，如果与几个力的效果相同，则这个力叫那几个力的合力，那几个力叫这个力的分力。

由分力求合力的运算叫力的合成；由合力求分力的运算叫力的分解。

重力由地球对物体的吸引而产生。

方向：总是竖直向下。

大小G ＝mg 。

g 为重力加速度，由于物体到地心的距离变化和地球自转的影响，地球周围各地g 值不同。

在地球表面，南极与北极g 值较大，赤道g 值较小；通常取g=9.8米／秒2。

重心的位置与物体的几何形状、质量分布有关。

任何两个物体之间的吸引力叫万有引力，2RMm GF 。

通常取引力常量G ＝6.67×10-11牛·米2／千克2。

物体的重力可以认为是地球对物体的万有引力。

弹力弹力产生在直接接触并且发生了形变的物体之间。

支持面上作用的弹力垂直于支持面；绳上作用的弹力沿着绳的收缩方向。

胡克定律F=kx ，k 称弹簧劲度系数。

滑动摩擦力物体间发生相对滑动时，接触面间产生的阻碍相对滑动的力，其方向与接触面相切，与相对滑动的方向相反；其大小f=μN 。

N 为接触面间的压力。

μ为动摩擦因数，由两接触面的材料和粗糙程度决定。

静摩擦力相互接触的物体间产生相对运动趋势时，沿接触面产生与相对运动趋势方向相反的静摩擦力。

静摩擦力的大小随两物体相对运动的“趋势”强弱，在零和“最大静摩擦力”之间变化。

“最大静摩擦力”的具体值，因两物体的接触面材料情况和压力等因素而异。

摩擦力三种常见的力牛顿第一定律一切物体总保持匀速直线运动状态或静止状态，直到有外力迫使它改变这种状态为止。

物体的这种性质叫做惯性。

惯性是物体的固有属性，衡量惯性的大小的物理量是质量。

2.2常见函数一、一次函数和常函数：思维导图：（一） 、一次函数 〔二〕、常函数 定义域：〔- ∞，+ ∞〕 定义域: 〔- ∞，+ ∞〕 值 域：〔- ∞，+ ∞〕 正 k=0 反 值 域：{ b }解析式：y = kx + b ( k ≠ 0 ) 解析式：y = b ( b 为常数)图 像：一条与x 轴、y 轴相交的直线 图 像：一条与x 轴平行或重合的直线b>0 b=0 b<0 K > 0 k < 0单调性： k > 0 ,在〔- ∞，+ ∞〕↑ 单调性：在〔- ∞，+ ∞〕上不单调 k < 0 ,在〔- ∞，+ ∞〕↓奇偶性：奇函数⇔=0b 奇偶性: 偶函数 非奇非偶⇔≠0b周期性: 非周期函数 周期性：周期函数，周期为任意非零实数 反函数：在〔- ∞，+ ∞〕上有反函数 反函数:在〔- ∞，+ ∞〕上没有反函数 反函数仍是一次函数例题：二、二次函数1、定义域：〔- ∞，+ ∞〕2、值 域： ),44[,02+∞-∈>ab ac y a]44,(,02ab ac y a --∞∈<3、解析式：)0(2≠++=a c bx ax y4、图 像:一条开口向上或向下的抛物线 开口向下，开口向上；正负：增大，开口缩小绝对值：随着,00<>a a a a正半轴相交与负半轴相交与y c y c c,0,0><对称轴：ab x 2-=对称轴： ；)44,2(2ab ac ab --顶点： 轴交点个数图像与x ac b →-=∆42：与x 轴交点的个数。

两个交点,0>∆一个交点,0=∆无交点,0<∆5、单调性：↑+∞-↓--∞>),2[]2,(,0ab ab a↓+∞-↑--∞<),2[]2,(,0ab ab a6、奇偶性：偶函数⇔=0b7、周期性：非周期函数8、反函数：在〔- ∞，+ ∞〕上无反函数，上及其子集上有反函数或在),2[]2,(+∞---∞ab ab例题:三、反比例函数和重要的分式函数〔一〕、反比例函数 〔二〕、分式函数bax dcx y ++= 定义域：〔- ∞，0〕∪〔0，+ ∞〕 定义域：),(),(+∞---∞aba b 值 域：〔- ∞，0〕∪〔0，+ ∞〕 值 域: ),(),(+∞-∞a c a c解析式：)0()(≠=k xk x f 解析式：)(a bx b ax d cx y -≠++=图 像：以x 轴、y 轴为渐进线的双曲线 图 像：以abx -=和a c y =为渐近线的双曲线y y0 x 0 xk > 0 k < 0单调性： k>0,〔- ∞，0〕↓,〔0，+ ∞〕↓ 单调性:在),(a b --∞和),(+∞-ab上 k<0,〔- ∞，0〕↑,〔0，+ ∞〕↑ 单调性相同 奇偶性：奇函数 奇偶性：非奇非偶 对称性：关于原点对称 对称性：关于点),(aca b -成中心对称 周期性：非周期函数 周期性：非周期函数反函数：在定义域上有反函数， 反函数：在定义域有反函数， 反函数是其本身。