2011—2018年新课标全国卷1理科数学分类汇编——12.程序框图

2011年—2018年新课标全国卷(1卷、2卷、3卷)理科数学试题分类汇编——1.集合2011年至2018年的新课标全国卷理科数学试题分类汇编中，集合与简易逻辑是一个重要的考点。

下面是一些选择题的例子：1.已知集合A={x|x^2-x-2>0}，则C∪A=（）A。

{x|-1<x<2}B。

{x|-1≤x≤2}C。

{x|x2}D。

{x|x≤-1}∪{x|x≥2}2.已知集合A={(x,y)|x^2+y^2≤3，x∈Z，y∈Z}，B={[1,2]}，则A∩B的元素个数为（）A。

9B。

8C。

5D。

43.已知集合A={x|x-1≥0}，B={[1,2]}，则A∩B=（）A。

{[ ]}B。

{[1]}C。

{[1,1,2]}D。

{[2]}4.已知集合A={x|x<1}，B={x|x^3<1}，则A∩B=（）A。

{x|x<0}B。

{x|x≤0}C。

{x|x>1}D。

∅5.已知集合A={1,2,4}，B={x|(x+1)(x-2)<0，x∈Z}，则A∩B=（）A。

{1}B。

{1,2}C。

{0,1,2,3}D。

{-1,0,1,2,3}6.已知集合S={x|(x-2)(x-3)≥0}，T={x|x>0}，则S∩T=（）A。

[2,3]B。

(-∞,2]∪[3,+∞)C。

[3,+∞)D。

(0,2]∪[3,+∞)7.命题p：∃n∈N，n>2，则¬p为（）A。

∀n∈N，n>2B。

∃n∈N，n≤2C。

∀n∈N，n≤2D。

∃n∈N，n=2以上内容由XXXXXX收集整理，欢迎研究交流）2015·新课标Ⅱ，1）已知集合A={-2，-1，2}，B={x|(x-1)(x+2)<0}，求A∩B。

解：首先求出B的解析式为B={x|-2<x<1}，然后将A和B的元素进行比较，得到A∩B={-1}，因此选项A.{-1，0}为正确答案。

2014·新课标Ⅰ，1）已知集合A={x|x22x3≥0}，B={x|x-2≤x<2}，求A∩B。

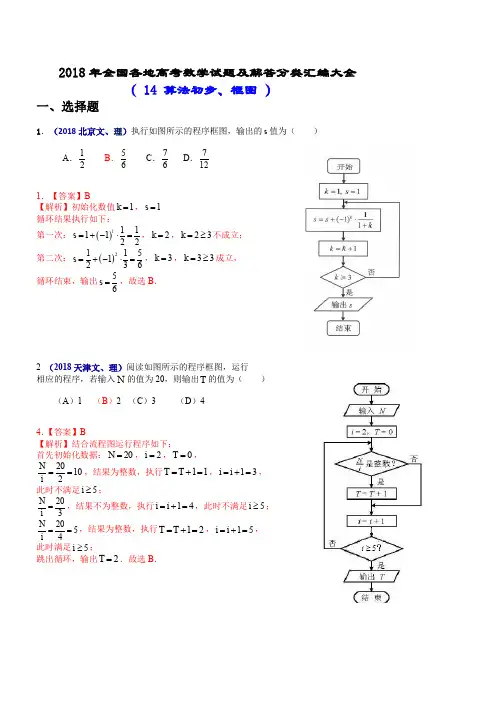
2018年全国各地高考数学试题及解答分类汇编大全（ 14 算法初步、框图 ）一、选择题1．（2018北京文、理）执行如图所示的程序框图，输出的s 值为（ ）A ．12B ．56C ．76D ．7121．【答案】B【解析】初始化数值1k =，1s = 循环结果执行如下：第一次：()1111122s =+-⋅=，2k =，23k =≥不成立；第二次：()21151236s =+-⋅=，3k =，33k =≥成立，循环结束，输出56s =，故选B ．2 （2018天津文、理）阅读如图所示的程序框图，运行相应的程序，若输入N 的值为20，则输出T 的值为（ ）（A ）1 （B ）2 （C ）3 （D ）4 4．【答案】B【解析】结合流程图运行程序如下：首先初始化数据：20N =，2i =，0T =， 20102N i ==，结果为整数，执行11T T =+=，13i i =+=， 此时不满足5i ≥； 203N i =，结果不为整数，执行14i i =+=，此时不满足5i ≥； 2054N i ==，结果为整数，执行12T T =+=，15i i =+=， 此时满足5i ≥；跳出循环，输出2T =．故选B ．3．（2018全国新课标Ⅱ文、理）为计算11111123499100S =-+-++-，设计了如图的程序框图， 则在空白框中应填入（ ）A ．1i i =+B ．2i i =+C ．3i i =+D ．4i i =+ 3．【答案】B【解析】由11111123499100S =-+-+⋯+-得程序框图先对奇数项累加，偶数项累加，最后再相减． 因此在空白框中应填入2i i =+，选B ．二、填空1．（2018江苏）一个算法的伪代码如图所示，执行此算法，最后输出的S 的值为 ▲ ．1．【答案】8【解析】由伪代码可得3I =，2S =；5I =，4S =；7I =，8S =；因为76>，所以结束循环，输出8S =．三、解答题开始0,0N T ==S N T =-S 输出1i =100i <1N N i =+11T T i =++结束是否。

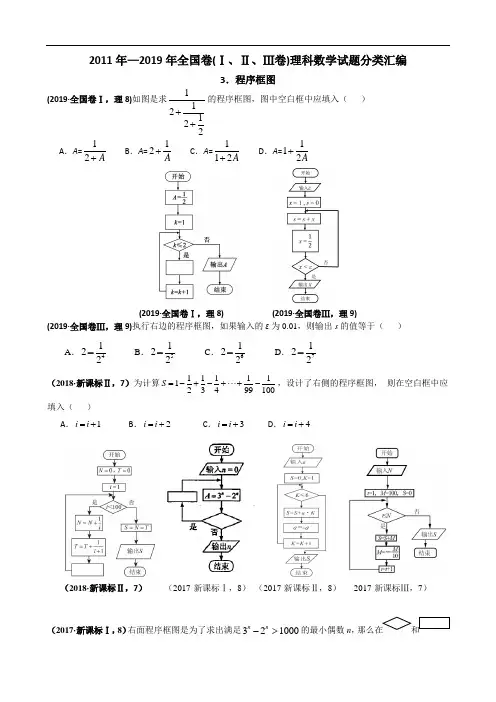
2012-2021十年全国高考数学真题分类汇编 算法与框图（原卷版）一、选择题1．(2019年高考数学课标Ⅲ卷理科)执行如图所示的程序框图，如果输入的ε为0.01，则输出s 的值等于( )．A ．4122-B ．5122-C ．6122-D ．7122- 2．(2019年高考数学课标全国Ⅰ卷理科)右图是求112122++的程序框图，图中空白框中应填入 ( )A ．12A A=+ B ．12A A=+ C ．112A A=+ D ．112A A =+ 3．(2018年高考数学课标Ⅱ卷（理）)为计算11111123499100S =-+-++-，设计了右侧的程序框图，则在空白框中应填入( ) A ．1i i =+ B ．2i i =+C ．3i i =+D ．4i i =+4．(2017年高考数学新课标Ⅰ卷理科)右面程序框图是为了求出满足]的最小偶数,那么在和两个空白框中,可以分别填入 ( )A ．和B ．和C ．和D ．和5．(2017年高考数学课标Ⅲ卷理科)执行右面的程序框图，为使输出的值小于，则输入的正整数的最小值为( ) A ． B ． C ． D ．321000n n ->n 1000A >1n n =+1000A >2n n =+1000A ≤1n n =+1000A ≤2n n =+S 91N 54326．(2017年高考数学课标Ⅱ卷理科)执行右面的程序框图，如果输入的，则输出的 ( )A ．2B ．3C ．4D ．57．(2016高考数学课标Ⅲ卷理科)执行右面的程序框图,如果输入的4a =,6b =,那么输出的n =( ) A ．3 B ．4 C ．5 D ．61a =-S=8．(2016高考数学课标Ⅱ卷理科)中国古代有计算多项式值的秦九韶算法，右图是实现该算法的程序框图．执行该程序框图，若输入的2x =，2n =，依次输入的a 为2，2，5，则输出的s = ( )输入输出停止 开始( ) A ．7 B ．12 C ．17 D ．349．(2016高考数学课标Ⅰ卷理科)执行右面的程序图，如果输入的011x y n ===，，，则输出,x y 的值满足( )( )(A )2y x =(B )3y x =(C )4y x =(D )5y x =10．(2015高考数学新课标2理科)右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入,a b 分别为14,18，则输出的a = ( )( )A ．0B ．2C ．4D ．1411．(2015高考数学新课标1理科)执行右面的程序框图，如果输入的t =0．01，则输出的n = () A ．5 B ．6 C ．7 D ．812．(2014高考数学课标2理科)执行右图程序框图，如果输入的x ,t 均为2，则输出的S = () A ．4 B ．5 C ．6 D ．7 a > b a = a - b b = b - a 输出a结 束开 始输入a ，ba ≠ b13．(2014高考数学课标1理科)执行下图的程序框图,若输入的分别为1,2,3,则输出的=( )( ) A．B．C．D．14．(2013高考数学新课标2理科)执行右面的程序框图，如果输入的10N=，那么输出的S＝( )A．11112310+++⋅⋅⋅B．11112!3!10!+++⋅⋅⋅C．11112311+++⋅⋅⋅D．11112!3!11!+++⋅⋅⋅,,a b k M20 31657215815．(2013高考数学新课标1理科)运行如下程序框图，如果输入的[1,3]t ∈-，则输出s 属于 ( )A ．[-3,4]B ．[-5,2]C ．[-4,3]D ．[-2,5] 16．(2012高考数学新课标理科)如果执行如图所示的程序框图，输入正整数(2)N N ≥和实数12,,...,N a a a ，输出,A B ，则( ) A ．A B +为12,,...,N a a a 的和B ．2A B +为12,,...,N a a a 的算术平均数 C ．A 和B 分别是12,,...,N a a a 中最大的数和最小的数D ．A 和B 分别是12,,...,N a a a 中最小的数和最大的数S = S +T否 开始k =1, S = 0,T =1T=T kk > N输出S结束 输入Nk = k +1。

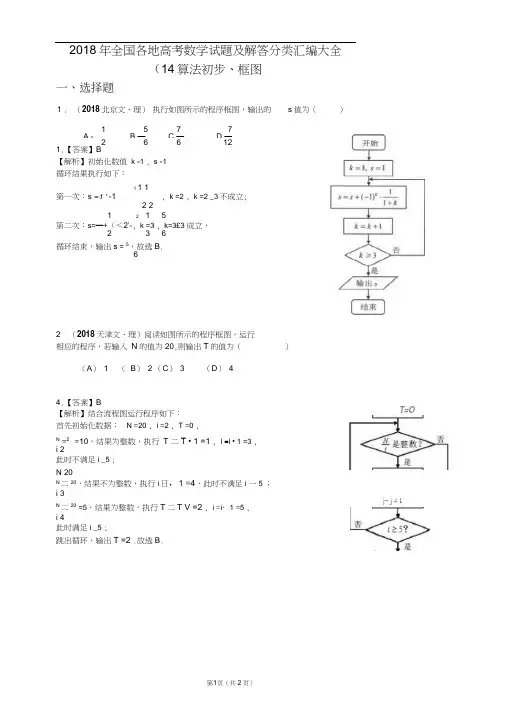
2018年全国各地高考数学试题及解答分类汇编大全（14算法初步、框图一、选择题1.【答案】B【解析】初始化数值 k =1 , s =1 循环结果执行如下：11 1第一次：s =1 ' -1, k =2 , k =2 _3不成立;2 21 2 1 5第二次：s=—+（＜2'-, k =3 , k=3£3 成立，2 3 6 循环结束，输出s = 5，故选B .62 （2018天津文、理）阅读如图所示的程序框图，运行 相应的程序，若输入 N 的值为20,则输出T 的值为（）（A ） 1（ B ） 2 （C ） 3（D ） 44.【答案】B【解析】结合流程图运行程序如下：首先初始化数据： N =20 , i =2 , T =0 ,N=2° =10，结果为整数，执行 T 二T • 1 =1 , i =i • 1 =3 , i 2此时不满足i _5 ;N 20 N二20，结果不为整数，执行i 日，1 =4，此时不满足i 一5 ； i 3N二20=5，结果为整数，执行T 二T V =2 , i =i ・1 =5 , i 4此时满足i _5 ;跳出循环，输出T =2 .故选B .1 . （2018北京文、理） 执行如图所示的程序框图，输出的s 值为（ ）15 7 7 A.-B.—C.—D.— 26 6 12T=Oj= j 4 1i则在空白框中应填入 A . i =i 1 C . i =i 33.【答案】B11 +— — +一 八+ —— 3 4 99 100先对奇数项累加，偶数项累加，最后再相减. 因此在空白框中应填入i =i ，选B .1 . （2018江苏）一个算法的伪代码如图所示，执行此算法，最后输出的 S 的值为 ▲.r----------------------------------------------- 1"I:|I門::While /<6: :I 十 2:；S —2S； :End While ；| Print S\…诵了軾…1.【答案】8【解析】由伪代码可得1=3 , S=2 ; 1=5, S=4 ; 1=7, S=8;因为7 6，所以结束循环，输出S =8 .三、解答题3. （2018全国新课标n 文、理）为计算 1 1 11 1S =1 一丄•1 一丄 1-，设计了如图的程序框图,2 3 499 100填空【解析】由S =1得程序框图。

WORD格式整理绝密★启用前2017年普通高等学校招生全国统一考试理科数学本试卷5页，23小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。

用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。

将条形码横贴在答题卡右上角“条形码粘贴处”。

2．作答选择题时，选出每小题答案后，用2B铅笔在答题卡上对应题目选项的答案信息点涂黑；如需要改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

x1．已知集合A={x|x<1}，B={x|3 1}，则A．A B{x|x0}B．A B RC．A B{x|x1}D．A B2．如图，正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是1πA．B．48C．12D．π43．设有下面四个命题p：若复数z满足11zR，则z R；p：若复数z满足22z R，则z R；p：若复数z1,z2满足z1z2R，则z1z2；3专业技术参考资料WORD 格式整理p ：若复数z R，则z R.4其中的真命题为A．p1, p3 B．p1, p4 C．p2 , p3 D．p2, p44．记S为等差数列{ a n} 的前n项和．若a4 a5 24 ，S6 48 ，则{ a n} 的公差为nA．1 B．2 C．4 D． 85．函数 f (x) 在( , ) 单调递减，且为奇函数．若 f (1) 1，则满足 1 f (x2) 1的x 的取值范围是A．[ 2,2] B．[ 1,1] C．[0,4] D．[1,3]6．16(1 )(1 x)2x展开式中 2x 的系数为A．15 B．20 C．30 D．357．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形. 该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10 B．12 C．14 D．168．右面程序框图是为了求出满足 3n- 2n>1000 的最小偶数n，那么在和两个空白框中，可以分别填入A．A>1 000 和n=n+1B．A>1 000 和n=n+2C．A 1 000 和n=n+1D．A 1 000 和n=n+29．已知曲线C1：y=cos x，C2：y=sin (2 x+ 2π) ，则下面结论正确的是3专业技术参考资料WORD 格式整理A．把C1 上各点的横坐标伸长到原来的 2 倍，纵坐标不变，再把得到的曲线向右平移π个单位长度，得6到曲线C2B．把C1 上各点的横坐标伸长到原来的 2 倍，纵坐标不变，再把得到的曲线向左平移π个单位长度，得12到曲线C2C．把C1 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π个单位长度，得6到曲线C2D．把C1 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π个单位长度，得12到曲线C210．已知 F 为抛物线C：y2=4x 的焦点，过F作两条互相垂直的直线l2=4x 的焦点，过F作两条互相垂直的直线l 1，l 2，直线l 1 与C交于A、B两点，直线l 2 与C交于D、E两点，则|AB|+| DE| 的最小值为A．16 B．14 C．12 D．10x y z11．设x yz 为正数，且 2 3 5 ，则A．2x<3y<5z B．5z<2x<3y C．3y<5z<2x D．3y<2x<5z12．几位大学生响应国家的创业号召，开发了一款应用软件. 为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，⋯，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推.求满足如下条件的最小整数N：N>100 且该数列的前N项和为 2 的整数幂.那么该款软件的激活码是A．440 B．330 C．220 D．110二、填空题：本题共 4 小题，每小题 5 分，共20 分。

12011年—2018年新课标全国卷Ⅰ理科数学分类汇编不等式选讲【2018，23】已知()|1||1|f x x ax =+--.（1）当1a =时，求不等式()1f x >的解集；（2）若(0,1)x ∈时不等式()f x x >成立，求a 的取值范围.【2017，23】已知函数()24f x x ax =-++，()11g x x x =++-．（1）当1a =时，求不等式()()f x g x ≥的解集；（2）若不等式()()f x g x ≥的解集包含[]1,1-，求a 的取值范围．【2016，23】已知函数321)(--+=x x x f ． （Ⅰ）在答题卡第（24）题图中画出)(x f y =的图像； （Ⅱ）求不等式1)(>x f 的解集．【2015，24】已知函数()12,0f x x x a a =+-->.（I ）当1a =时求不等式()1f x >的解集；（II ）若()f x 的图像与x 轴围成的三角形面积大于6，求a 的取值范围.3【2014，24）】若0,0a b >>，且11a b+=. (Ⅰ) 求33a b +的最小值；（Ⅱ）是否存在,a b ，使得236a b +=？并说明理由.【2013，24】已知函数()||1|22|f x x x a ＝－＋＋，()3g x x ＝＋. (1)当2a ＝-时，求不等式()()f x g x ＜的解集； (2)设1a ＞-，且当1,22x a ⎡⎫-⎪⎢⎣⎭∈时，()()f x g x ≤，求a 的取值范围．【2012，24】已知函数()|||2|f x x a x =++-。

（1)当3-=a 时，求不等式3)(≥x f 的解集；（2）若|4|)(-≤x x f 的解集包含[1，2]，求a 的取值范围。

【2011，24】设函数()3f x x a x =-+,其中0a >。

（Ⅰ）当1a =时，求不等式()32f x x ≥+的解集； （Ⅱ）若不等式()0f x ≤的解集为{}|1x x ≤- ，求a 的值.5【2018，23】已知()|1||1|f x x ax =+--.（1）当1a =时，求不等式()1f x >的解集；（2）若(0,1)x ∈时不等式()f x x >成立，求a 的取值范围.【解析】（1）当1a =时，()|1||1|f x x x =+--，即2,1,()2,11,2, 1.x f x x x x -≤-⎧⎪=-<<⎨⎪≥⎩故不等式()1f x >的解集为1{|}2x x >．（2）当(0,1)x ∈时|1||1|x ax x +-->成立等价于当(0,1)x ∈时|1|1ax -<成立． 若0a ≤，则当(0,1)x ∈时|1|1ax -≥； 若0a >，|1|1ax -<的解集为20x a <<，所以21a≥，故02a <≤． 综上，a 的取值范围为(0,2]．【2017，23】已知函数()24f x x ax =-++，()11g x x x =++-．（1）当1a =时，求不等式()()f x g x ≥的解集；（2）若不等式()()f x g x ≥的解集包含[]1,1-，求a 的取值范围．【解析】（1）当1a =时，()24f x x x =-++，是开口向下，对称轴12x =的二次函数． ()211121121x x g x x x x x >⎧⎪=++-=-⎨⎪-<-⎩，，≤x ≤，，当(1,)x ∈+∞时，令242x x x -++=，解得x ，()g x 在()1+∞，上单调递增，()f x 在()1+∞，上单调递减，∴此时()()f x g x ≥解集为1⎛ ⎝⎦．当[]11x ∈-，时，()2g x =，()()12f x f -=≥． 当()1x ∈-∞-，时，()g x 单调递减，()f x 单调递增，且()()112g f -=-=． 综上所述，()()f x g x ≥解集1⎡-⎢⎣⎦．（2）依题意得：242x ax -++≥在[]11-，恒成立．即220x ax --≤在[]11-，恒成立． 则只须()()2211201120a a ⎧-⋅-⎪⎨----⎪⎩≤≤，解出：11a -≤≤．故a 取值范围是[]11-，． 【2016，23】已知函数321)(--+=x x x f ．（Ⅰ）在答题卡第（24）题图中画出)(x f y =的图像； （Ⅱ）求不等式1)(>x f 的解集．【解析】：⑴ 如图所示：⑵ ()4133212342x x f x x x x x ⎧⎪--⎪⎪=--<<⎨⎪⎪-⎪⎩，≤，，≥ ,()1f x >,①1x -≤，41x ->，解得5x >或3x <,1x -∴≤ ②312x -<<，321x ->，解得1x >或13x <，113x -<<∴或312x << ③32x ≥，41x ->，解得5x >或3x <，332x <∴≤或5x >综上，13x <或13x <<或5x > ()1f x >∴，解集为()()11353⎛⎫-∞+∞ ⎪⎝⎭，，，7【2015，24】已知函数()12,0f x x x a a =+-->.（I ）当1a =时求不等式()1f x >的解集；（II ）若()f x 的图像与x 轴围成的三角形面积大于6，求a 的取值范围.解析：（I ）（方法一）当1a =时，不等式()1f x >可化为1211x x +-->，等价于11221x x x ≤-⎧⎨--+->⎩或111221x x x -<<⎧⎨++->⎩或11221x x x ≥⎧⎨+-+>⎩，解得223x <<. （方法二）当1a =时，不等式()1f x >可化为1211x x +-->，结合绝对值的几何意义，不等式的含义为：数轴上一点x 到点1-的距离与它到1的距离的2倍之差大于1.设点x 到1-的距离为1d ，到1的距离为2d ，结合数轴可知：若x 在[1,1]-内，则有1212221d d d d +=⎧⎨->⎩解得213d <；故2(,1]3x ∈. 若x 在(1,)+∞内，则有1212221d d d d -=⎧⎨->⎩解得21d <；故(1,2)x ∈.综上可得223x <<. （Ⅱ）由题设可得，12,1()312,112,x a x f x x a x a x a x a --<-⎧⎪=+--≤≤⎨⎪-++>⎩， 所以函数()f x 的图像与x 轴围成的三角形的三个顶点分别为21(,0)3a A -，(21,0)B a +，(,+1)C a a ，所以△ABC 的面积为22(1)3a +.由题设得22(1)3a +＞6，解得2a >.所以a 的取值范围为（2，+∞）.【2014，24）】若0,0a b >>，且11a b+=. (Ⅰ) 求33a b +的最小值；（Ⅱ）是否存在,a b ，使得236a b +=？并说明理由. 【解析】：(Ⅰ) 11a b =+≥，得2ab ≥，且当a b ==-1 1x -1 1x故3342a b+≥=，且当a b ==∴33a b +的最小值为……5分（Ⅱ）由623a b =+≥32ab ≤，又由(Ⅰ)知2ab ≥，二者矛盾， 所以不存在,a b ，使得236a b +=成立. ……………10分【2013，24】已知函数f (x )＝|2x －1|＋|2x ＋a |，g (x )＝x ＋3.(1)当a ＝－2时，求不等式f (x )＜g (x )的解集；(2)设a ＞－1，且当x ∈1,22a ⎡⎫-⎪⎢⎣⎭时，f (x )≤g (x )，求a 的取值范围． 解：(1)当a ＝－2时，不等式f (x )＜g (x )化为|2x －1|＋|2x －2|－x －3＜0.设函数y ＝|2x －1|＋|2x －2|－x －3，则y ＝15,,212,1,236, 1.x x x x x x ⎧-<⎪⎪⎪--≤≤⎨⎪->⎪⎪⎩其图像如图所示．从图像可知，当且仅当x ∈(0,2)时，y ＜0. 所以原不等式的解集是{x |0＜x ＜2}．(2)当x ∈1,22a ⎡⎫-⎪⎢⎣⎭时，f (x )＝1＋a . 不等式f (x )≤g (x )化为1＋a ≤x ＋3.所以x ≥a －2对x ∈1,22a ⎡⎫-⎪⎢⎣⎭都成立． 故2a-≥a －2，即43a ≤.从而a 的取值范围是41,3⎛⎤- ⎥⎝⎦.【2012，24】已知函数()|||2|f x x a x =++-。

2011年—2018年新课标全国卷理科数学试题分类汇编（逐题解析）11．立体几何一、选择题(2018·新课标Ⅰ，理7) 某圆柱的高为2，底面周长为16，其三视图如右图所示，圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为（ ）A ．B ．C ．3D ．2(2018·新课标Ⅰ，理12) 已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为（ ）A B C D（2018·新课标Ⅱ，9）在长方体1111ABCD A B C D -中，1AB BC ==，1AA =1AD 与1DB 所成角的余弦值为（ ）A ．15B C D （2018·新课标Ⅲ，理3）中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫棒头，凹进部分叫卯眼，图中木构件右边的小长方体是棒头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（ ）（2018·新课标Ⅲ，理10）设A B C D ，，，是同一个半径为4的球的球面上四点，ABC ∆为等边三角形且其面积为D ABC -体积的最大值为（ ）A ．B ．C ．D ．（2017·新课标Ⅰ，7）某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（ ）A ．10B ．12C ．14D ．16（2017·新课标Ⅱ，4）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为（ ）A ．90πB ．63πC ．42πD ．36π（2017·新课标Ⅰ，7） （2017·新课标Ⅱ，4） （2016·新课标Ⅰ，6）（2017·新课标Ⅱ，10）已知直三棱柱111C C AB -A B 中，C 120∠AB =，2AB =，1C CC 1B ==，则异面直线1AB 与1C B 所成角的余弦值为（ ）A B C D （2017·新课标Ⅲ，8）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（ ）A ．πB ．3π4C ．π2D ．π4（2016·新课标Ⅰ，6）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是283π，则它的表面积是（ ） （A ）π17 （B ）π18 （C ）π20 （D ）π28（2016·新课标Ⅰ，11）平面α过正方体1111D C B A ABCD -的顶点A ，//α平面11D CB ，αI 平面ABCD m =， α平面n A ABB =11，则n m ,所成角的正弦值为（ ）（A （B （C （D ）13（2016·新课标Ⅱ，6积为（ ） A ．20πB ．24πC ．28πD ．32π（2016·新课标Ⅲ，9）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为（ ）A. 18+B. 54+C. 90D. 81（2016·新课标Ⅲ，10）在封闭的直三棱柱ABC －A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ，AB =6，BC =8，AA 1=3，则V 的最大值是（ ）A. 4πB.9π2C. 6πD. 32π3（2015·新课标Ⅰ，6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺.问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有（ ）（A ）14斛 （B ）22斛 （C ）36斛 （D ）66斛 （2015·新课标Ⅰ，11）圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图所示. 若该几何体的表面积为1620π+，则r =（ ）（A ）1 （B ）2 （C ）4 （D ）8（2015·新课标Ⅱ，6）一个正方体被一个平面截去一部分后，剩余部分的三视图如图，则截去部分体积与剩余部分体积的比值为（ ） A ．81B ．71 C ．61 D ．51（2015·新课标Ⅱ，6） （2014·新课标Ⅰ，12）（2015·新课标Ⅱ，9）已知A ，B 是球O 的球面上两点，∠AOB =90º，C 为该球面上的动点，若三棱锥O -ABC 体积的最大值为36，则球O 的表面积为（ ） A ．36πB ．64πC ．144πD ．256π（2014·新课标Ⅰ，12）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为( )A .B .C .6D .4（2014·新课标Ⅱ，6）如图，网格纸上正方形小格的边长为1（表示1cm ），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ） A ．1727B ．59C ．1027D ．13（2014·新课标Ⅱ，6） （2013·新课标Ⅰ，6） （2013·新课标Ⅰ，8）（2014·新课标Ⅱ，11）直三棱柱ABC -A 1B 1C 1中，∠BCA =90º，M ，N 分别是A 1B 1，A 1C 1的中点，BC =CA =CC 1，则BM 与AN 所成的角的余弦值为（ ） A ．110B ．25CD（2013·新课标Ⅰ，6）如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器的厚度，则球的体积为( )．A ．500π3cm 3 B ．866π3cm 3 C ．1372π3cm 3 D ．2048π3cm 3（2013·新课标Ⅰ，8）某几何体的三视图如图所示，则该几何体的体积为( )． A ．16＋8π B ．8＋8π C ．16＋16π D ．8＋16π（2013·新课标Ⅱ，4）已知,m n 为异面直线，m ⊥平面α，n ⊥平面β.直线l 满足l m ⊥，l n ⊥，l α⊄，l β⊄，则（ ）A.α // β且l // αB.αβ⊥且l β⊥C.α与β相交，且交线垂直于lD.α与β相交，且交线平行于l（2013·新课标Ⅱ，7）一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1)，(1,1,0)，(0,1,1)，(0,0,0)，画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到正视图可以为（ ）（2012·新课标Ⅰ，7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）A ．6B ．9C ．12D ．15（2012·新课标Ⅰ，11）已知三棱锥S －ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形，SC 为球O 的直径，且SC =2，则此棱锥的体积为（ ） A．6B．6C．3D．2（2011·新课标Ⅰ，6）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（ ）二、填空题（2018·新课标Ⅱ，理16）已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成B. C. D.角为45︒．若SAB △的面积为_________．（2017·新课标Ⅲ，16）a ，b 为空间中两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以直线AC 为旋转轴旋转，有下列结论：①当直线AB 与a 成60角时，AB 与b 成30角；②当直线AB 与a 成60角时，AB 与b 成60角； ③直线AB 与a 所称角的最小值为45；④直线AB 与a 所称角的最小值为60；其中正确的是________.（填写所有正确结论的编号）（2016·新课标Ⅱ，14）α、β是两个平面，m 、n 是两条直线，有下列四个命题： （1）如果m ⊥n ，m ⊥α，n ∥β，那么α⊥β. （2）如果m ⊥α，n ∥α，那么m ⊥n . （3）如果α∥β，m ⊂α，那么m ∥β.（4）如果m ∥n ，α∥β，那么m 与α所成的角和n 与β所成的角相等. 其中正确的命题有 . (填写所有正确命题的编号.)（2011·新课标Ⅰ，15）已知矩形ABCD 的顶点都在半径为4的球O 的球面上，且6,AB BC ==则棱锥O ABCD -的体积为 ． 三、解答题（2018·新课标I ，理18）如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥．（1）证明：平面PEF ⊥平面ABFD ； （2）求DP 与平面ABFD 所成角的正弦值．（2018·新课标Ⅱ，20）如图，在三棱锥P ABC -中，AB BC ==4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且二面角M PA C --为30︒，求PC 与平面PAM 所成角的正弦值．（2018·新课标Ⅲ，理19）如图，边长为2的正方形ABCD 所在平面与半圆弧CD 所在平面垂直，M 是CD上异于C ，D 的点．⑴证明：平面AMD ⊥平面BMC ；⑵当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．（2017·新课标Ⅰ，18）如图，在四棱锥P-ABCD 中，AB//CD ，且90BAP CDP ∠=∠=（1）证明：平面P AB ⊥平面P AD ；（2）若P A =PD =AB =DC ,90APD ∠=,求二面角A -PB -C 的余弦值．（2017·新课标Ⅱ，19）如图，四棱锥P -ABCD 中，侧面P AD 为等比三角形且垂直于底面ABCD ，12AB BC AD ==，o 90BAD ABC ∠=∠=， E 是PD 的中点. （1）证明：直线//CE 平面P AB ；（2）点M 在棱PC 上，且直线BM 与底面ABCD 所成锐角为o 45 ，求二面角M -AB -D 的余弦值（2017·新课标Ⅲ，19）如图所示，四面体ABCD 中，ABC △是正三角形，ACD △是直角三角形，ABD CBD ∠=∠，AB BD =．（1）证明：平面ACD ⊥平面ABC ；（2）过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角––D AE C 的余弦值．（2016·新课标Ⅰ，18）如图，在以F E D C B A ,,,,,为顶点的五面体中，面ABEF 为正方形，︒=∠=90,2AFD FD AF ，且二面角E AF D --与二面角F BE C --都是︒60．（Ⅰ）证明：平面⊥ABEF 平面EFDC ； （Ⅱ）求二面角A BC E --的余弦值．ABCDE（2016·新课标Ⅱ，19）如图，菱形ABCD 的对角线AC 与BD 交于点O ，AB =5，AC =6，点E ，F 分别在AD ，CD 上，AE =CF =54，EF 交BD 于点H . 将△DEF 沿EF 折到△D ´EF的位置，OD '=（Ⅰ）证明：D H '⊥平面ABCD ；（Ⅱ）求二面角B D A C '--的正弦值.（2016·新课标Ⅲ，19）如图，四棱锥P -ABCD 中，P A ⊥底面ABCD ，AD ∥BC ，AB =AD =AC =3，P A =BC =4，M 为线段AD 上一点，AM =2MD ，N 为PC 的中点.(1)证明MN ∥平面P AB ；(2)求直线AN 与平面PMN 所成角的正弦值.OBACFDHED '（2015·新课标Ⅰ，18）如图，四边形ABCD 为菱形，120ABC ∠=，,E F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，2BE DF =，AE EC ⊥.（I ）证明：平面AEC ⊥平面AFC ； （II ）求直线AE 与直线CF 所成角的余弦值.（2015·新课标Ⅱ，19）如图，长方体ABCD -A 1B 1C 1D 1中AB =16，BC =10，AA 1=8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E =D 1F =4，过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形.（Ⅰ）在图中画出这个正方形（不必说出画法和理由）； （Ⅱ）求直线AF 与平面α所成角的正弦值.（2014·新课标Ⅰ，19）如图三棱柱111ABC A B C -中，侧面11BB C C 为菱形，1AB B C ⊥.（Ⅰ） 证明：1AC AB =；（Ⅱ）若1AC AB ⊥，o160CBB ∠=，AB=BC 求二面角111A A B C --的余弦值.（2014·新课标Ⅱ，18）如图，四棱锥P -ABCD 中，底面ABCD 为矩形，P A ⊥平面ABCD ，E 为PD 的中点. （Ⅰ）证明：PB // 平面AEC ；（Ⅱ）设二面角D -AE -C 为60º，AP =1，ADE -ACD 的体积.（2013·新课标Ⅰ，18）如图，三棱柱ABC－A1B1C1中，CA＝CB，AB＝AA1，∠BAA1＝60°.(1)证明：AB⊥A1C；(2)若平面ABC⊥平面AA1B1B，AB＝CB，求直线A1C与平面BB1C1C所成角的正弦值．1AD1B1CA CEB（2012·新课标Ⅰ、Ⅱ，19）如图，直三棱柱ABC －A 1B 1C 1中，AC=BC=21AA 1，D 是棱AA 1的中点， DC 1⊥BD ．（1）证明：DC 1⊥BC ；（2）求二面角A 1－BD －C 1的大小．（2011·新课标Ⅰ、Ⅱ，18）如图，四棱锥P-ABCD 中，底面ABCD 为平行四边形，∠DAB=60°,AB=2AD ,PD ⊥底面ABCD .(Ⅰ)证明：P A ⊥BD ；(Ⅱ)若PD =AD ，求二面角A-PB-C 的余弦值．A 1C2011年—2018年新课标全国卷理科数学试题分类汇编11．立体几何（解析版）一、选择题(2018·新课标全国Ⅰ卷理7) 某圆柱的高为2，底面周长为16，其三视图如右图所示，圆柱表面上的点M在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为（ ）A ．B ．C ．3D ．2【答案】B 解析：当路径为线段MN(2018·新课标Ⅰ，理12)已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为（ ）A B C D 【答案】A 解析：（直接法）平面11A C B 符合题意，如图（1）所示，例题中的平面α可得面11A C B 平移平移后的图象如图（1）所示，六边形EFGHMN 为该截面设1A N x =，则有,)EN MN x ==-根据对称性可知),EF x FG =-=，延长,EN HM 相交于点P延长,EF HG 相交于点Q ，易证60HEF EHG ∠=∠= 所以EHQ ∆为等边三角形，同理EHP ∠为等边三角形， 所以maxEHG EPG PMN FGQEFGHMNS S S S S ∆∆∆∆=+--六边形2222)))4444x =+---2(221)2x x =-+当12x =时，max 4EFGHMN S =六边形．【解法2】（特殊位置法）由题可知，截面α应与正方体体对角线垂直，当平面平移至截面为六边形时，此时六边形的周长恒定不变，所以当截面为正六边形时，面积最大max26(2EFGHMN S ==六边形．（2018·新课标Ⅱ，9）在长方体1111ABCD A B C D -中，1AB BC ==，1AA =1AD 与1DB 所成角的余弦值为（ ）A ．15B C D ．2【答案】C 解析：法一：由几何关系可知：112EF B D ==，AE ，1AF =，由余弦定理可知：cos θ解法二：坐标法：由几何关系可知：(1B D =，点A 的坐标为(，点1D 的坐标为()1,1,0(10,1,AD = ，cos θ==解法三：补型法（以右补为例）：由几何关系可知：BD ，2DG =，1B G =cos θ=.（2018·新课标Ⅲ，理3）中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫棒头，凹进部分叫卯眼，图中木构件右边的小长方体是棒头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（ ）【答案】A 解析：根据题意，A 选项符号题意.（2018·新课标Ⅲ，理10）设A B C D ，，，是同一个半径为4的球的球面上四点，ABC ∆为等边三角形且其面积为D ABC -体积的最大值为（ ）A ．B ．C ．D ．【答案】B 解析：如图，ABC ∆为等边三角形，点O 为A ，B ，C ，D 外接球的球心，G 为ABC ∆的重心，由ABC S ∆=，得6AB =，取BC 的中点H ，∴sin 60AH AB =⋅︒=，∴23AG AH ==O 到面ABC 的距离为2d ==，∴三棱锥D ABC -体积最大值1(24)3D ABC V -=⨯+=（2017·新课标Ⅰ，7）某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（ ）A ．10B ．12C ．14D ．16【答案】 B 解析：由三视图可画出立体图，该立体图平面内只有两个相同的梯形的面，()24226S =+⨯÷=梯，6212S =⨯=全梯，故选B ；（2017·新课标Ⅱ，4）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为（ ）A ．90πB ．63πC ．42πD ．36π【答案】 B 解析：从三视图可知：一个圆柱被一截面截取一部分而剩余的部分，剩下的体积分上下两部分阴影的体积，下面阴影的体积为V Sh =，3r =，4h =，∴ 136V π=；上面阴影的体积2V 是上面部分体积3V 的一半，即2312V V =，3V 与1V 的比为高的比（同底），即3132V V =，213274V V π==，故总体积02163V V V π=+=.方法2：354V Sh π==，其余同上，故总体积02163V V V π=+=.（2017·新课标Ⅱ，10）已知直三棱柱111C C AB -A B 中，C 120∠AB =，2AB =，1C CC 1B ==，则异面直线1AB 与1C B 所成角的余弦值为（ ）ABCD【答案】 B 解析：解法一：在边1BB ﹑11B C ﹑11A B ﹑AB 上分别取中点E ﹑F ﹑G ﹑H ，并相互连接. 由三角形中位线定理和平行线平移功能，异面直线1AB 和1BC 所成的夹角为FEG ∠或其补角，通过几何关系求得EF =FG =FH =，利用余弦定理可求得异面直线 1AB 和1BC.解法二：补形通过补形之后可知：1BC D ∠或其补角为异面直线1AB 和1BC 所成的角，通过几何关系可知：1BC =1C D =，BD 1AB 和1BC. 解法三：建系建立如左图的空间直角坐标系，()0,2,1A ，()10,0,0B ，()0,0,1B，11,02C ⎫-⎪⎪⎝⎭，∴ 131,12BC ⎛⎫=-- ⎪⎪⎝⎭，()10,2,1B A =，∴1111cos 5B A BC B A BC θ⋅===⋅ （2017·新课标Ⅲ，8）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（ ） A ．πB ．3π4C ．π2D ．π4【答案】 B 解析：由题可知球心在圆柱体中心，圆柱体上下底面圆半径r =则圆柱体体积23ππ4V r h ==.故选B.（2016·新课标Ⅰ，6）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是328π，则它的表面积是（ ） （A ）π17 （B ）π18 （C ）π20 （D ）π28【答案】 A 解析：原立体图如图所示：是一个球被切掉左上角的18表面积是78的球面面积和三个扇形面积之和2271=42+32=1784S ⨯⨯⨯⨯πππ，故选A ．（2016·新课标Ⅰ，11）平面α过正方体1111D C B A ABCD -的顶点A ，//α平面11D CB ，αI 平面ABCD m =， α平面n A ABB =11，则n m ,所成角的正弦值为（ ）（A ）23 （B ）22 （C ）33（D ）31【答案】 A 解析：如图所示：111∵11CB D α∥平面，∴若设平面11CB D 平面1ABCD m =，则1m m ∥又∵平面ABCD ∥平面1111A B C D ，结合平面11B D C 平面111111A B C D B D =∴111B D m ∥，故11B D m ∥，同理可得：1CD n ∥故m 、n 的所成角的大小与11B D 、1CD 所成角的大小相等，即11CD B ∠的大小． 而1111B C B D CD ==（均为面对交线），因此113CD B π∠=，即11sin CD B ∠=． 故选A ．（2016·新课标Ⅱ，6）右图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（ ）A ．20πB ．24πC ．28πD ．32π【答案】 C 解析：几何体是圆锥与圆柱的组合体，设圆柱底面圆半径为r ，周长为c ，圆锥母线长为l ，圆柱高为h ．由图得2r =， 2π4πc r ==，由勾股定理得：4l ==，21π4π16π8π28π2S r ch cl =++=++=表，故选C ．（2016·新课标Ⅲ，9）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为A. 18+B. 54+C. 90D. 81【答案】 B 解析：由三视图可知该几何体是一个平行六面体，上下底面为俯视图的一半，各个侧面平行四边形，故表面积为2332362354⨯⨯+⨯⨯+⨯=+（2016·新课标Ⅲ，10）在封闭的直三棱柱ABC －A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ，AB =6，BC =8，AA 1=3，则V 的最大值是A. 4πB.9π2C. 6πD. 32π3【答案】 B 解析：由题意知，当球为直三棱柱的内接球时，体积最大，选取过球心且平行于直三棱柱底面的截面，如图所示，则由切线长定理可知，内接圆的半径为2， 又1322AA =<⨯，所以内接球的半径为32，即V 的最大值为34932R ππ=2016，62015，62014，686（2015·新课标Ⅰ，6）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺.问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有（A ）14斛 （B ）22斛 （C ）36斛 （D ）66斛 【答案】 B 解析：284R π=，圆锥底面半径16R π=，米堆体积21320123V R h ππ==，堆放的米约有221.62V≈，选（B ）.（2015·新课标Ⅰ，11）圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图所示. 若该几何体的表面积为1620π+，则r =（ ）（A ）1（B ）2（C ）4（D ）8【答案】 B 解析：由正视图和俯视图知，该几何体是半球和半个圆柱的组合体，圆柱的半径与球的半径都r ，圆柱的高为2r ，其表面积为2222142225416202r r r r r r r r πππππ⨯+⨯++⨯=+=-，解得2r =，故选（B ）.（2015·新课标Ⅱ，6）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（ ） A ．81 B ．71 C ．61 D ．51（2015·6）D 解析：由三视图得，在正方体ABCD-A 1B 1C 1D 1中，截去四面体A-A 1B 1D 1，如图所示，设正方体棱长为a ，则11133111326A AB D V a a -=⨯=，故剩余几何体体积为3331566a a a -=，所以截去部分体积与剩余部分体积的比值为，故选D.1（2015·新课标Ⅱ，9）已知A ，B 是球O 的球面上两点，∠AOB =90º，C 为该球面上的动点，若三棱锥O -ABC 体积的最大值为36，则球O 的表面积为（ ） A ．36πB ．64πC ．144πD ．256π【答案】 C 解析：如图所示，当点C 位于垂直于面AOB 的直径端点时，三棱锥O ABC -的体积最大，设球O 的半径为R ，此时2311136326O ABC C AOB V V R R R --==⨯⨯==，故R=6，则球O 的表面积为24144S R ππ==，故选C ．（2014·新课标Ⅰ，12）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为A. B. C .6 D .4D ABC -，【答案】 C 解析：（解析）：如图所示，原几何体为三棱锥其中4,AB BC AC DB DC =====6DA ==，故最长的棱的长度为6DA =，选C（2014·新课标Ⅱ，6）如图，网格纸上正方形小格的边长为1（表示1cm ），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ） A ．1727B ．59C ．1027D ．13【答案】 C 解析：原来毛坯体积为π·32·6=54π (cm 2)，由三视图得，该零件由左侧底面半径为2cm ，高为4cm 的圆柱和右侧底面半径为3cm ，高为2cm 的圆柱构成，所以该零件的体积为：π·32·2+π·22·4=34π (cm 2)，则切削掉部分的体积为54π-34π =20π(cm 2)，所以切削掉部分的体积与原来毛坯体积的比值为20105427ππ=.（2014·新课标Ⅱ，11）直三棱柱ABC-A1B1C1中，∠BCA=90º，M，N分别是A1B1，A1C1的中点，BC=CA=CC1，则BM与AN所成的角的余弦值为（）A．110B．25CD【答案】C 解析：取BC的中点P，连结NP、AP，∵M，N分别是A1B1，A1C1的中点，∴四边形NMBP为平行四边形，∴BM//PN，∴所求角的余弦值等于∠ANP的余弦值，不妨令BC=CA=CC1=2，则AN=APNP=，∴222||||||cos2||||AN NP APANPAN NP+-∠=⨯⋅=.【另解】如图建立坐标系，令AC=BC=C1C=2，则A(0, 2, 2)，B(2, 0, 2)，M(1, 1, 0)，N(0, 1, 0)，(1,1,2)(0,1,2),BM AN∴=--=--，cos||||BM ANθBM AN⋅===⋅（2013·新课标Ⅰ，6）如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器的厚度，则球的体积为()．A．500π3cm3B．866π3cm3 C．1372π3cm3D．2048π3cm3【答案】 A 解析：设球半径为R，由题可知R，R－2，正方体棱长一半可构成直角三角形，即△OBA为直角三角形，如图．BC＝2，BA＝4，OB＝R－2，OA＝R，由R2＝(R－2)2＋42，得R＝5，所以球的体积为34500π5π33=(cm3)，故选A.AC B1A1C1BNMP（2013·新课标Ⅰ，8）某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π【答案】 A 解析：由三视图可知该几何体为半圆柱上放一个长方体，由图中数据可知圆柱底面半径r ＝2，长为4，在长方体中，长为4，宽为2，高为2，所以几何体的体积为πr 2×4×12＋4×2×2＝8π＋16.故选A.（2013·新课标Ⅱ，4）已知,m n 为异面直线，m ⊥平面α，n ⊥平面β.直线l 满足l m ⊥，l n ⊥，l α⊄，l β⊄，则（ ）A.α // β且l // αB.αβ⊥且l β⊥C.α与β相交，且交线垂直于lD.α与β相交，且交线平行于l【答案】 D 解析：因为m ⊥α，l ⊥m ，l ⊄α，所以l ∥α. 同理可得l ∥β. 又因为m ，n 为异面直线，所以α与β相交，且l 平行于它们的交线．故选D.（2013·新课标Ⅱ，7）一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1)，(1,1,0)，(0,1,1)，(0,0,0)，画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到正视图可以为（ ）【答案】A 解析：如图所示，该四面体在空间直角坐标系O －xyz 的图像为右图，则它在平面zOx 上的投影即正视图为右图，故选A.（2012·新课标Ⅰ，7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）B.C. D.A．6 B．9 C．12 D．15 【答案】 B 解析：由三视图可知，该几何体为三棱锥A-BCD，底面△BCD为底边为6，高为3的等腰三角形，侧面ABD⊥底面BCD，AO⊥底面BCD，因此此几何体的体积为11(63)3932V=⨯⨯⨯⨯=，故选择B．（2012·新课标Ⅰ，11）已知三棱锥S－ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC=2，则此棱锥的体积为（）A．6B C．3D．2【答案】A 解析：如图所示，根据球的性质，知⊥1OO平面ABC，则COOO11⊥．在直角COO1∆中，1=OC，331=CO，所以36)33(122121=-=-=COOCOO．因此三棱锥S－ABC的体积6236433122=⨯⨯⨯==-ABCOVV，故选择A（2011·新课标Ⅰ，6）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（）【答案】D 解析：条件对应的几何体是由底面棱长为r的正四棱锥沿底面对角线截出的部分与底面为半径为r的圆锥沿对称轴截出的部分构成的．故选D二、填空题（2018·新课标Ⅱ，理16）已知圆锥的顶点为S，母线SA，SB所成角的余弦值为78，SA与圆锥底面所成角为45︒．若SAB△的面积为_________．【答案】解析：由面积的关系可知：SA SB==由几何关系可知：SO AO==侧面积S SA l =⋅，2l OA π==，侧面积S SA l =⋅=（2017·新课标Ⅲ，）16.a ，b 为空间中两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以直线AC 为旋转轴旋转，有下列结论：①当直线AB 与a 成60角时，AB 与b 成30角； ②当直线AB 与a 成60角时，AB 与b 成60角； ③直线AB 与a 所称角的最小值为45； ④直线AB 与a 所称角的最小值为60；其中正确的是________.（填写所有正确结论的编号）【答案】② ③ 解析：由题意知，a ，b ，AC 三条直线两两相互垂直，画出图形如图．不妨设图中所示正方体边长为1，故1AC =，AB =边AB 以直线AC 为旋转轴旋转，则A 点保持不变，B 点的运动轨迹是以C 为圆心，1为半径的圆．以C 为坐标原点，以CD 为x 轴正方向，CB 为y 轴正方向，CA 为z 轴正方向建立空间直角坐标系．则(1,0,0)D ，(0,0,1)A ，直线a 的方向单位向量(0,1,0)=a ，1=a ．B 点起始坐标为(0,1,0)，直线b 的方向单位向量(1,0,0)=b ，1=b ．设B 点在运动过程中的坐标()cos ,sin ,0B θθ'， 其中θ为B C '与CD 的夹角，[0,2π)θ∈．那么'AB 在运动过程中的向量(cos ,sin ,1)AB θθ'=--，2AB '=设AB '与a 所成夹角为π0,2α⎡⎤∈⎢⎥⎣⎦，则(cos ,sin ,1)(0,1,0)cos AB θθαθ⎡--⋅==∈⎢'⎣⎦a ．故ππ,42α⎡⎤∈⎢⎥⎣⎦，所以③正确，④错误．设AB '与b 所成夹角为π[0,]2β∈，(cos ,sin ,1)(1,0,0)cos AB AB AB θθβθ'⋅-⋅===''b b b . 当AB '与a 夹角为60︒时，即π3α=，sin 32πθα===．因为22cos sin 1θθ+=，所以cos θ1cos 2βθ=． 因为π0,2β⎡⎤∈⎢⎥⎣⎦．所以π=3β，此时AB '与b 夹角为60︒．所以②正确，①错误．故填② ③.（2016·新课标Ⅱ，14）α、β是两个平面，m 、n 是两条直线，有下列四个命题： （1）如果m ⊥n ，m ⊥α，n ∥β，那么α⊥β. （2）如果m ⊥α，n ∥α，那么m ⊥n . （3）如果α∥β，m ⊂α，那么m ∥β.（4）如果m ∥n ，α∥β，那么m 与α所成的角和n 与β所成的角相等. 其中正确的命题有 . (填写所有正确命题的编号.) 【答案】②③④ 解析：略.（2011·新课标Ⅰ，15）已知矩形ABCD 的顶点都在半径为4的球O 的球面上，且6,AB BC ==则棱锥O ABCD -的体积为 ．【答案】解析：设ABCD 所在的截面圆的圆心为M,则=,22=，1623O ABCD V -=⨯⨯=三、解答题（2018·新课标I ，理18）如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥．（1）证明：平面PEF ⊥平面ABFD ； （2）求DP 与平面ABFD 所成角的正弦值．解析：（1）由已知可得，BF ⊥PF ，BF ⊥EF ，所以BF ⊥平面PEF 由BF ⊂平面ABFD ，所以平面PEF ⊥平面ABFD（2）【解法1】作PH ⊥EF ，垂足为H ，由（1）得，PH ⊥平面ABFD ，以H 为坐标原点，HF 的方向为y 轴正方向，BF 为单位长，建立如图所示的空间直角坐标系H xyz -由（1）可得DE ⊥PE ，又DP=2，DE=1，所以PE ，又PF=1，EF=2，故PE ⊥PF ，可得32PH EH ==，则333(0,0,0),(1,,0),(1,,),22H P D DP HP --== 为平面ABFD 的法向量，设DP 与平面ABFD 所成的角θ，则3sin HP DP HP DPθ⋅==⋅.所以DP 与平面ABFD 。

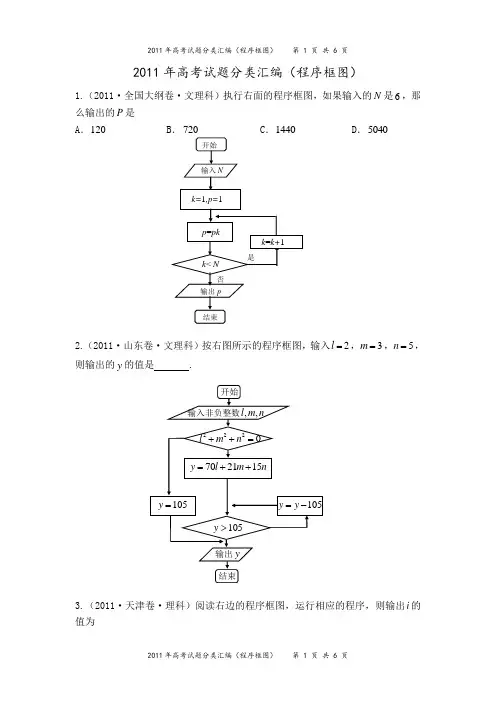
2011年高考试题分类汇编（程序框图）1.（2011·全国大纲卷·文理科）执行右面的程序框图，如果输入的N 是6，那么输出的P 是A ．120B ．720C ．1440D ．50402.（2011·山东卷·文理科）按右图所示的程序框图，输入2l =，3m =，5n =，则输出的y 的值是 .3.（2011·天津卷·理科）阅读右边的程序框图，运行相应的程序，则输出i 的值为A．3 B．4 C．5 D．64.（2011x的值为4-，则输出y的值为A．0.5 B．．45.（2011·浙江卷·文理科）若某程序框图如图所示，则该程序运行后输出的k 值为 .6.（2011·辽宁卷·文理科）执行右面的程序框图，如果输入的n 是4，则输出的p 是A ．8B ．5C ．3D ．2 7.（2011·福建卷·文科）阅读右图所示的程序框图，运行相应的程序，输出的结果是A ．3B ．11．1238.（2011·安徽卷·文理科）如图所示，程序框图（算法流程图）的输出结果是 .9.（2011·北京卷·理科）执行如图所示的程序框图，输出的s 值为A ．3-B ．1- C ．1D ．210.（2011·北京卷·文科）执行如图所示的程序框图，若输入A 的值为2，则输出的P 值为A ．2B ．3C ．4D ．511．（2011·湖南卷·文科）若执行如图2所示的框图，输入11x =，22x =，34x =，48x =，则输出的数等于 ．12．（2011·陕西卷·理科）图中，1x ，2x ，3x 为某次考试三个评阅人对同一道题的独立评分，p 为该题的最终得分.当16x =，29x =，8.5p =时，3x 等于 A ．11 B ．10 C ．8 D ．713．（2011·陕西卷·文科）如右框图，16x=，29x=，8.5p=时，3x等于A．7 B．8 C．10 D．11。