开普勒的三大定律典型例题

（1）第一定律：太阳系中各行星是以椭圆轨道运行的，太阳处在这些椭圆的一个焦点上。

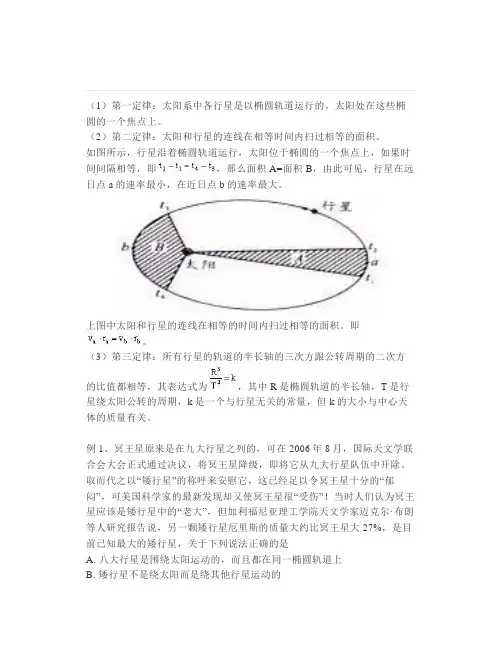
（2）第二定律：太阳和行星的连线在相等时间内扫过相等的面积。

如图所示，行星沿着椭圆轨道运行，太阳位于椭圆的一个焦点上，如果时间间隔相等，即，那么面积A=面积B，由此可见，行星在远日点a的速率最小，在近日点b的速率最大。

上图中太阳和行星的连线在相等的时间内扫过相等的面积。

即。

（3）第三定律：所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等，其表达式为，其中R是椭圆轨道的半长轴，T是行星绕太阳公转的周期，k是一个与行星无关的常量，但k的大小与中心天体的质量有关。

例1、冥王星原来是在九大行星之列的，可在2006年8月，国际天文学联合会大会正式通过决议，将冥王星降级，即将它从九大行星队伍中开除。

取而代之以“矮行星”的称呼来安慰它，这已经足以令冥王星十分的“郁闷”，可美国科学家的最新发现却又使冥王星很“受伤”！当时人们认为冥王星应该是矮行星中的“老大”，但加利福尼亚理工学院天文学家迈克尔·布朗等人研究报告说，另一颗矮行星厄里斯的质量大约比冥王星大27%，是目前已知最大的矮行星，关于下列说法正确的是A. 八大行星是围绕太阳运动的，而且都在同一椭圆轨道上B. 矮行星不是绕太阳而是绕其他行星运动的C. 冥王星被降级以后其轨道也发生了相应的变化D. 冥王星与厄里斯有着一个共同的轨道焦点答案：D例2、飞船沿半径为R的圆周绕地球运动，其周期为T，如果飞船要返回地面，可在轨道上的某一点A处，将速率降低到适当数值，从而使飞船沿着以地心为焦点的椭圆轨道运动，椭圆和地球表面在B点相切，如图所示，如果地球半径为，求飞船由A点到B点所需要的时间。

解析：开普勒第三定律虽然是根据行星绕太阳的运动总结出来的，但也适用于卫星、飞船绕行星的运动。

因此，飞船绕地球做圆周（半长轴和半短轴相等的特殊椭圆）运动时其轨道半径的三次方跟周期平方的比值等于飞船绕地球沿椭圆轨道运行时其半长轴的三次方跟周期平方的比值。

应用一：开普勒三定律的应用开普勒行星运动三大定律基本内容： 1、开普勒第一定律(轨道定律)：所有的行星围绕太阳运动的轨道都是椭圆，太阳处在所有椭圆的一个焦点上。

阳处在所有椭圆的一个焦点上。

2、开普勒第二定律(面积定律): 对于每一个行星而言，太阳和行星的联线在相等的时间内扫过相等的面积。

等的时间内扫过相等的面积。

3、开普勒第三定律(周期定律): 所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。

的二次方的比值都相等。

实际应用：1、如图所示是行星m 绕恒星M 运动的情况示意图，则下面的说法正确的是 A 、速度最大的点是B 点 B 、速度最小的点是C 点 C 、m 从A 到B 做减速运动做减速运动 D 、m 从B 到A 做减速运动做减速运动2、 哈雷彗星最近出现的时间是1986年，天文学家哈雷预言，这颗彗星将每隔一定时间就会出现，请预算下一次飞近地球是哪一年？提供数据：（1）地球公转接近圆，地球公转接近圆，彗星的运动轨道则是一个非常扁彗星的运动轨道则是一个非常扁的椭圆；（2）彗星轨道的半长轴R 1约等于地球轨道半长轴R 2的18倍。

倍。

3、神舟七号沿半径为R 的圆周绕地球运动，其周期为T ，如果飞船要返回地面，可在轨道上的某一点A 处，将速率降低到适当数值，从而使飞船沿着以地心为焦点的特殊椭圆轨道运动，椭圆和地球表面在B 点相切，如图所示，如果地球半径为R0，求飞船由A 点返回到地面B 点所需的时间。

点所需的时间。

4、两颗行星的质量分别为m 1和m 2，它们绕太阳运动的轨道半径分别为R 1和R 2，若m 1 = 2m 2 、R 1 = 4R 2，则它们的周期之比T 1：T 2是多少？是多少？5、2007年10月26日33分，嫦娥一号实施了第一次近地点火变轨控制，卫星进入了24小时周期椭圆轨道运动，此时卫星的近地点约为200km ，则卫星的远地点大约为（已知地球的半径为6.4×6.4×10103km ，近地环绕卫星周期约为1.5h ）：A. 4.8×105km B . 3.6×104km 104km C. 7.0×104km D.1.2×D.1.2×105km 105km 8．太阳系八大行星公转轨道可近似看作圆轨道，“行星公转周期的平方”与“行星与太阳的平均距离的三次方”成正比。

典型例题关于开普勒的三大定律例1 月球环绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天。

应用开普勒定律计算：在赤道平面内离地面多少高度，人造地球卫星可以随地球一起转动，就像停留在无空中不动一样．分析：月球和人造地球卫星都在环绕地球运动，根据开普勒第三定律，它们运行轨道的半径的三次方跟圆周运动周期的二次方的比值都是相等的．解：设人造地球卫星运行半径为R，周期为T，根据开普勒第三定律有：同理设月球轨道半径为，周期为，也有：由以上两式可得：在赤道平面内离地面高度：km点评：随地球一起转动，就好像停留在天空中的卫星，通常称之为定点卫星．它们离地面的高度是一个确定的值，不能随意变动。

利用月相求解月球公转周期例2 若近似认为月球绕地球公转与地球绕日公转的轨道在同一平面内，且都为正圆.又知这两种转动同向，如图所示，月相变化的周期为29.5天（图是相继两次满月，月、地、日相对位置示意图）．解：月球公转（2π+）用了29.5天．故转过2π只用天．由地球公转知．所以=27.3天．例3如图所示，A、B、C是在地球大气层外的圆形轨道上运行的三颗人造地球卫星，下列说法中正确的是哪个？（）A．B、C的线速度相等，且大于A的线速度B．B、C的周期相等，且大于A的周期C．B、C的向心加速度相等，且大于A的向心加速度D．若C的速率增大可追上同一轨道上的B分析：由卫星线速度公式可以判断出，因而选项A是错误的．由卫星运行周期公式，可以判断出，故选项B是正确的．卫星的向心加速度是万有引力作用于卫星上产生的，由，可知，因而选项C是错误的．若使卫星C速率增大，则必然会导致卫星C偏离原轨道，它不可能追上卫星B，故D也是错误的．解：本题正确选项为B。

点评：由于人造地球卫星在轨道上运行时，所需要的向心力是由万有引力提供的，若由于某种原因，使卫星的速度增大。

则所需要的向心力也必然会增加，而万有引力在轨道不变的时候，是不可能增加的，这样卫星由于所需要的向心力大于外界所提供的向心力而会作离心运动。

万有引力及天体运动一．开普勒行星运动三大定律 1、开普勒第一定律(轨道定律):所有的行星围绕太阳运动的轨道都是椭圆，太阳处在所有椭圆的一个焦点上。

2、开普勒第二定律(面积定律):对于每一个行星而言，太阳和行星的联线在相等的时间内扫过相等的面积。

3、开普勒第三定律(周期定律):所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。

1、如图所示是行星m 绕恒星M 运动的情况示意图，则下面的说法正确的是： A 、速度最大的点是B 点 B 、速度最小的点是C 点C 、m 从A 到B 做减速运动D 、m 从B 到A 做减速运动 二、万有引力定律1、万有引力定律的建立①太阳与行星间引力公式 ②月—地检验③卡文迪许的扭秤实验——测定引力常量G 2、万有引力定律①内容：自然界中任何两个物体都相互吸引，引力的大小与物体的质量1m 和2m 的乘积成正比，与它们之间的距离r的二次方成反比。

即： ②适用条件（Ⅰ）可看成质点的两物体间，r 为两个物体质心间的距离。

（Ⅱ）质量分布均匀的两球体间，r 为两个球体球心间的距离。

③运用地上：忽略地球自转可得： 2）计算重力加速度地球上空距离地心r=R+h 处 方法：在质量为M ’，半径为R ’的任意天体表面的重力加速度''g方法：（3）计算天体的质量和密度利用自身表面的重力加速度：天上：利用环绕天体的公转： 等等（注：结合 得到中心天体的密度）（4）双星：两者质量分别为m 1、m 2，两者相距L特点：距离不变，向心力相等，角速度相等，周期相等。

双星轨道半径之比：双星的线速度之比：三、宇宙航行1、人造卫星的运行规律2Mm F G r =11226.6710/G N m kg -=⨯⋅122m mF G r =2R Mm Gmg =2''''''R m M G mg =mg R MmG =2r T m r m r v m r Mm G 222224πω===334R M πρ⋅=2')(h R Mm G mg +=122121m m v v R R ==22(1) :M m GM v G m v r r r==卫地地卫由得rTm r m r v m r Mm G 222224πω===332T=2.GM GM GM r M v a G r r rωπ=== ， ， ，例.两颗人造卫星A 、B 绕地球作圆周运动，周期之比为T A ：T B =1：8，则轨道半径之比和运动速率之比分别为（ ） 2、宇宙速度第一宇宙速度：V 1=7.9km/s 第二宇宙速度：V 2=11.2km/s 脱离速度 第三宇宙速度：V 3=16.7km/s 逃逸速度注：（1）宇宙速度均指发射速度（2）第一宇宙速度为在地面发射卫星的最小速度，也是环绕地球运行的最大速度（环绕速度） 3、地球同步卫星（通讯卫星）（1）运动周期与地球自转周期相同，且T=24h ；（2）运转角速度等于地球自转的角速度，周期等于地球自转的周期； （3）同步卫星高度不变，运行速率不变（因为T 不变）； （4）同步卫星的轨道平面必须与赤道平面平行，在赤道正上方。

关于开普勒的三大定律例1 月球环绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天。

应用开普勒定律计算：在赤道平面内离地面多少高度，人造地球卫星可以随地球一起转动，就像停留在无空中不动一样．分析：月球和人造地球卫星都在环绕地球运动，根据开普勒第三定律，它们运行轨道的半径的三次方跟圆周运动周期的二次方的比值都是相等的．解：设人造地球卫星运行半径为R，周期为T，根据开普勒第三定律有：同理设月球轨道半径为，周期为，也有：由以上两式可得：在赤道平面内离地面高度：km点评：随地球一起转动，就好像停留在天空中的卫星，通常称之为定点卫星．它们离地面的高度是一个确定的值，不能随意变动。

利用月相求解月球公转周期例2 若近似认为月球绕地球公转与地球绕日公转的轨道在同一平面内，且都为正圆.又知这两种转动同向，如图所示，月相变化的周期为29.5天（图是相继两次满月，月、地、日相对位置示意图）．解：月球公转（2π+）用了29.5天．故转过2π只用天．由地球公转知．所以=27.3天．例3如图所示，A、B、C是在地球大气层外的圆形轨道上运行的三颗人造地球卫星，下列说法中正确的是哪个？（）A．B、C的线速度相等，且大于A的线速度B．B、C的周期相等，且大于A的周期C．B、C的向心加速度相等，且大于A的向心加速度D．若C的速率增大可追上同一轨道上的B分析：由卫星线速度公式可以判断出，因而选项A是错误的．由卫星运行周期公式，可以判断出，故选项B是正确的．卫星的向心加速度是万有引力作用于卫星上产生的，由，可知，因而选项C是错误的．若使卫星C速率增大，则必然会导致卫星C偏离原轨道，它不可能追上卫星B，故D也是错误的．解：本题正确选项为B。

点评：由于人造地球卫星在轨道上运行时，所需要的向心力是由万有引力提供的，若由于某种原因，使卫星的速度增大。

则所需要的向心力也必然会增加，而万有引力在轨道不变的时候，是不可能增加的，这样卫星由于所需要的向心力大于外界所提供的向心力而会作离心运动。

天体运动问题：1，开普勒第三定律：=k例：月球环绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天，应用开普勒第三定律计算：在赤道平面离地多高时，人造卫星随地球一起转动，就像是停留在天空中不动一样。

规律总结：若将天体的运动看成圆周运动，则=k,解题时常用两星体比较，此时有=因此利用开普勒第三定律可以求解运动时间，轨道半径，绕行速度的比值问题。

注意点：公式中的k是一个与行星无关的常量，但不是恒量，在不同的星系中，k的值不同，k的值与中心天体有关。

练习：对于开普勒第三定律的表达式=k的理解，正确的是（）A.k与成正比B.k与成反比C,k的值是与a和T无关的量D,k值与行星自身无关2，太阳对行星引力规律的推导基本思想：引力作为合外力提供向心力。

（合外力提供向心力是解决天体运动问题的核心思想）结论：F正比于例1：地球质量约为月球质量的81倍，宇宙飞船从地球飞往月球，当飞至某一位置时，宇宙飞船所受到的合力为零，问：此时飞船在空间的什么位置？（已知地球与月球之间的距离是3.84x km）例2：已知太阳光从太阳射到地球需要500s，地球绕太阳的公转周期约为3.2x s，地球的、质量约为6x kg，求太阳对地球的引力为多少?练习：把火星和地球绕太阳运行的轨道视为圆周，有火星和地球绕太阳运动的周期之比可以求得（）A,火星和地球的质量之比B,火星和太阳的质量之比C.火星和地球到太阳的距离之比D.火星和地球绕太阳运行速度大小之比3,万有引力定律注意点：1，万有引力定律公式适用的条件；1：万有引力公式适用于质点间的引力大小计算2：对于可视为质点的物体间的引力求解也可以利用万有引力公式，如两物体间的距离远小于物体本身的大小时，物体可以视为质点：均匀球体可以视为质量集中于球心的质点3：当物体不能看成是质点时，可以把物体假想分割成无数个质点，理论上讲，求出两个物体上每个质点与另一个物体上所有质点的万有引力，然后求合力在通常情况下，万有引力非常小，只有在质量巨大的星球之间或天体与天体附近的物体间，它的存在才有实际意义，故在分析地球表面上物体间的受力时，不考虑物体间的万有引力，只考虑地球对物体的引力。

典型例题关于开普勒的三大定律例1 月球环绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天。

应用开普勒定律计算：在赤道平面内离地面多少高度，人造地球卫星可以随地球一起转动，就像停留在无空中不动一样．分析：月球和人造地球卫星都在环绕地球运动，根据开普勒第三定律，它们运行轨道的半径的三次方跟圆周运动周期的二次方的比值都是相等的．解：设人造地球卫星运行半径为R，周期为T，根据开普勒第三定律有：同理设月球轨道半径为，周期为，也有：由以上两式可得：在赤道平面内离地面高度：km点评：随地球一起转动，就好像停留在天空中的卫星，通常称之为定点卫星．它们离地面的高度是一个确定的值，不能随意变动。

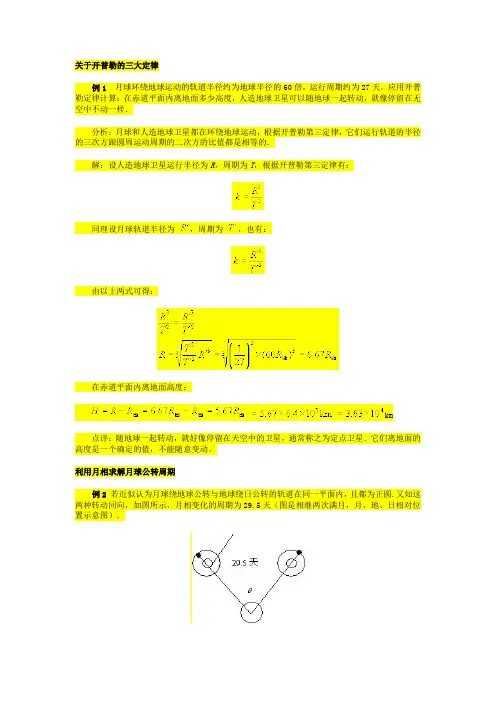
利用月相求解月球公转周期例2 若近似认为月球绕地球公转与地球绕日公转的轨道在同一平面内，且都为正圆.又知这两种转动同向，如图所示，月相变化的周期为29.5天（图是相继两次满月，月、地、日相对位置示意图）．解：月球公转（2π+）用了29.5天．故转过2π只用天．由地球公转知．所以=27.3天．例3如图所示，A、B、C是在地球大气层外的圆形轨道上运行的三颗人造地球卫星，下列说法中正确的是哪个？（）A．B、C的线速度相等，且大于A的线速度B．B、C的周期相等，且大于A的周期C．B、C的向心加速度相等，且大于A的向心加速度D．若C的速率增大可追上同一轨道上的B分析：由卫星线速度公式可以判断出，因而选项A是错误的．由卫星运行周期公式，可以判断出，故选项B是正确的．卫星的向心加速度是万有引力作用于卫星上产生的，由，可知，因而选项C是错误的．若使卫星C速率增大，则必然会导致卫星C偏离原轨道，它不可能追上卫星B，故D也是错误的．解：本题正确选项为B。

点评：由于人造地球卫星在轨道上运行时，所需要的向心力是由万有引力提供的，若由于某种原因，使卫星的速度增大。

则所需要的向心力也必然会增加，而万有引力在轨道不变的时候，是不可能增加的，这样卫星由于所需要的向心力大于外界所提供的向心力而会作离心运动。

万 有 引 力一．开普勒三定律1.开普勒第一定律:所有行星绕太阳运行的轨道都是_______,太阳处在所有椭圆的_______上.2.开普勒第二定律:对于每一个行星,太阳和行星的连线在相等的时间内扫过的_______相等.如图1所示:设行星在A 处的速度为V A ,距太阳的距离为r A ,在B 处的速度为V B ,距太阳的距离为r B ,则由____________________得_________。

3.开普勒第三定律:所有行星的半长轴的_____次方跟公转周期的______的比值都相等。

即_____________.注意:对同一星系中的所有行星,k 值____等;对不同星系间的两颗行星,k 值____等.比如: 对太阳系中的所有行星,有:R 地3 / T 地2 = R 金3 / T 金2 = R 木3 / T 木2 = R 水3 / T 水2 =……= k 1;对地球系中的所有行星,有:R 月3 / T 月2 = R 人造卫星3 / T 人造卫星2 = ……= k 2；注意这里k 1_____k 2.例1:已知某地球卫星的运行轨道为椭圆,近地点与远地点的距离之比为1:9,则对应的速度之比为______.例2:把火星和地球绕太阳运行的轨道视为圆周。

由火星和地球绕太阳的周期之比可求得( )A ．火星和地球的质量之比 B.火星和太阳的质量之比C. 火星和地球到太阳的距离之比D.火星和地球绕太阳运行速度大小之比二.万有引力定律及应用1.万有引力定律: 表达式:F 引=_________,其中引力常量G =_____________.由英国物理学家________测出,适用条件:两物体的大小与两者之间的距离相比可以忽略不计.常见规律:当两物间的距离增大为原来的2倍时,其作用力将变为原来的_____倍;当两物间的作用力变为原来的2倍时,其距离应变为原来的______倍.2.万有引力定律在地(星)球表面的应用:对地球表面上静止的物体m: 由mg = ________,有:(1)地(星)球表面物体的重力加速度:g = __ _;(2)地(星)球的质量:M =___________;据此人们称卡文迪许为“ 能称出地球质量的人”.(3)一个重要的关系式:GM = gR 2.3.重力的产生:考虑到地球的自转影响,地球表面物体的重力实际上并不等于万有引力,而只是万有引力的一个分力(另一个分力为物体绕地球转动所需的向心力),如图2-1所示,由此可见:同一物体在赤道处所受的重力____(大、小)于在两极处所受的重力.例1:地球表面的重力加速度为g ，地球半径为R ，若高空中某处的重力加速度为g/2，则该 处 距地球表面的高度为________.例2:A 、B 两颗行星,质量之比为M A :M B =p,半径之比R A :R B =q,则两行星表面的重力加速度之比为______.例3: 2007年10月29日18时01分，嫦娥一号卫星成功实施入轨后的第 三 次变轨。

开普勒三大定律考题
开普勒三大定律是描述行星运动的基本规律，下面我将从多个角度全面回答与开普勒三大定律相关的考题。

1. 第一定律（椭圆轨道定律）：
开普勒第一定律指出，行星绕太阳运动的轨道是一个椭圆，其中太阳位于椭圆的一个焦点上。

这一定律的数学表达式是，行星轨道的形状可以用椭圆的离心率来描述，离心率越接近于0，轨道越接近于圆形；离心率越接近于1，轨道越扁平。

此外，行星在轨道上的运动速度是不均匀的，它在离太阳较远的位置运动较慢，在离太阳较近的位置运动较快。

2. 第二定律（面积速度定律）：
开普勒第二定律又称为面积速度定律，它描述了行星在轨道上的运动速度与它与太阳连线所扫过的面积之间的关系。

具体来说，行星在相同时间内扫过的面积是相等的。

这意味着当行星离太阳较远时，它的线速度较慢，但它在单位时间内扫过的面积较大；而当行星离太阳较近时，它的线速度较快，但它在单位时间内扫过的面
积较小。

3. 第三定律（调和定律）：
开普勒第三定律是描述行星运动周期与轨道半长轴之间的关系。

根据这一定律，行星绕太阳运动的周期的平方与它的轨道半长轴的
立方成正比。

换句话说，行星绕太阳公转的周期越短，它的轨道半
长轴就越小；反之，行星绕太阳公转的周期越长，它的轨道半长轴
就越大。

总结起来，开普勒三大定律提供了描述行星运动的基本规律。

第一定律说明了行星轨道的形状和行星在轨道上的运动速度的不均
匀性；第二定律描述了行星在轨道上扫过的面积相等的规律；第三
定律则揭示了行星运动周期与轨道半长轴之间的关系。

这些定律的
发现对于后来的天体力学和宇宙学的发展起到了重要的推动作用。

（答题时间：15分钟）1. （重庆模拟）火星和木星沿各自的椭圆轨道绕太阳运行，根据开普勒行星运动定律可2. （浙江二模）假设有一载人宇宙飞船在距地面高度为4200km 的赤道上空绕地球做匀速圆周运动，地球半径约为6400km，地球同步卫星距地面高度为36000km，宇宙飞船和地球同步卫星绕地球同向运动，每当二者相距最近时，宇宙飞船就向同步卫星发射信号，然后再由同步卫星将信号发送到地面接收站，某时刻二者相距最远，从此刻开始，在一昼夜的时3. （浙江高考）长期以来“卡戎星（Charon）”被认为是冥王星唯一的卫星，它的公转轨道半径r1=19600km，公转周期T1=6.39天。

2006年3月，天文学家发现两颗冥王星的小卫星，4. （朝阳区一模）1980年10月14日，中国科学院紫金山天文台发现了一颗绕太阳运行的小行星，2001年12月21日，经国际小行星中心和国际小行星命名委员会批准，将这颗小行星命名为“钱学森星”，以表彰这位“两弹一星”的功臣对我国科技事业做出的卓越贡献。

若将地球和“钱学森星”绕太阳的运动看作匀速圆周运动，它们的运行轨道如图所示。

已知“钱学森星”绕太阳运行一周的时间约为3.4年，设地球绕太阳运行的轨道半径为R，则“钱学森星”绕太阳运行的轨道半径约为（）5. （辽宁模拟）月球绕地球运转的周期为T1，半径为R1；地球绕太阳运转的周期为T2，6. 16世纪，哥白尼根据天文观测的大量资料，经过40多年的天文观测和潜心研究，提出“日心说”的如下四个基本论点，这四个论点目前看存在缺陷的是（ ）A. 宇宙的中心是太阳，所有行星都绕太阳做匀速圆周运动B. 地球是绕太阳做匀速圆周运动的行星，月球是绕地球做匀速圆周运动的卫星，它绕地球运转的同时，还跟地球一起绕太阳运动C. 天空不转动，因为地球每天自西向东转一周，造成太阳每天东升西落的现象D. 与日地距离相比，恒星离地球都十分遥远，比日地间的距离大得多7. 太阳系八大行星公转轨道可近似看作圆轨道，“行星公转周期的平方”与“行星与太阳的平均距离的三次方”成正比。

开普勒的三大定律典型例题(总3页) -本页仅作为预览文档封面，使用时请删除本页-典型例题关于开普勒的三大定律例1月球环绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天。

应用开普勒定律计算：在赤道平面内离地面多少高度，人造地球卫星可以随地球一起转动，就像停留在无空中不动一样．分析：月球和人造地球卫星都在环绕地球运动，根据开普勒第三定律，它们运行轨道的半径的三次方跟圆周运动周期的二次方的比值都是相等的．解：设人造地球卫星运行半径为R，周期为T，根据开普勒第三定律有：同理设月球轨道半径为，周期为，也有：由以上两式可得：在赤道平面内离地面高度：km点评：随地球一起转动，就好像停留在天空中的卫星，通常称之为定点卫星．它们离地面的高度是一个确定的值，不能随意变动。

利用月相求解月球公转周期例2 若近似认为月球绕地球公转与地球绕日公转的轨道在同一平面内，且都为正圆.又知这两种转动同向，如图所示，月相变化的周期为天（图是相继两次满月，月、地、日相对位置示意图）．解：月球公转（2π+）用了天．故转过2π只用天．由地球公转知．所以=天．例3如图所示，A、B、C是在地球大气层外的圆形轨道上运行的三颗人造地球卫星，下列说法中正确的是哪个（）A．B、C的线速度相等，且大于A的线速度B．B、C的周期相等，且大于A的周期C．B、C的向心加速度相等，且大于A的向心加速度D．若C的速率增大可追上同一轨道上的B分析：由卫星线速度公式可以判断出，因而选项A是错误的．由卫星运行周期公式，可以判断出，故选项B是正确的．卫星的向心加速度是万有引力作用于卫星上产生的，由，可知，因而选项C是错误的．若使卫星C速率增大，则必然会导致卫星C偏离原轨道，它不可能追上卫星B，故D也是错误的．解：本题正确选项为B。

点评：由于人造地球卫星在轨道上运行时，所需要的向心力是由万有引力提供的，若由于某种原因，使卫星的速度增大。

则所需要的向心力也必然会增加，而万有引力在轨道不变的时候，是不可能增加的，这样卫星由于所需要的向心力大于外界所提供的向心力而会作离心运动。

典型例题关于开普勒的三大定律例1 月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天.应用开普勒定律计算：在赤道平面内离地面多少高度，人造地球卫星可以随地球一起转动，就像停留在无空中不动一样．分析：月球和人造地球卫星都在环绕地球运动,根据开普勒第三定律，它们运行轨道的半径的三次方跟圆周运动周期的二次方的比值都是相等的．解：设人造地球卫星运行半径为R，周期为T，根据开普勒第三定律有：同理设月球轨道半径为,周期为，也有：由以上两式可得：在赤道平面内离地面高度：km点评：随地球一起转动，就好像停留在天空中的卫星，通常称之为定点卫星．它们离地面的高度是一个确定的值，不能随意变动。

利用月相求解月球公转周期例2 若近似认为月球绕地球公转与地球绕日公转的轨道在同一平面内,且都为正圆。

又知这两种转动同向,如图所示，月相变化的周期为29.5天(图是相继两次满月,月、地、日相对位置示意图)．解：月球公转(2π+）用了29。

5天．故转过2π只用天．由地球公转知．所以=27。

3天．例3如图所示，A、B、C是在地球大气层外的圆形轨道上运行的三颗人造地球卫星，下列说法中正确的是哪个？( ）A．B、C的线速度相等，且大于A的线速度B．B、C的周期相等，且大于A的周期C．B、C的向心加速度相等，且大于A的向心加速度D．若C的速率增大可追上同一轨道上的B分析：由卫星线速度公式可以判断出,因而选项A是错误的．由卫星运行周期公式,可以判断出，故选项B是正确的．卫星的向心加速度是万有引力作用于卫星上产生的，由，可知,因而选项C是错误的．若使卫星C速率增大，则必然会导致卫星C偏离原轨道，它不可能追上卫星B，故D也是错误的．解：本题正确选项为B。

点评：由于人造地球卫星在轨道上运行时，所需要的向心力是由万有引力提供的，若由于某种原因，使卫星的速度增大.则所需要的向心力也必然会增加,而万有引力在轨道不变的时候,是不可能增加的,这样卫星由于所需要的向心力大于外界所提供的向心力而会作离心运动。

典型例题关于开普勒的三大定律例1 月球环绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天。

应用开普勒定律计算：在赤道平面内离地面多少高度，人造地球卫星可以随地球一起转动，就像停留在无空中不动一样．分析：月球和人造地球卫星都在环绕地球运动，根据开普勒第三定律，它们运行轨道的半径的三次方跟圆周运动周期的二次方的比值都是相等的．解：设人造地球卫星运行半径为R，周期为T，根据开普勒第三定律有：同理设月球轨道半径为，周期为，也有：由以上两式可得：在赤道平面内离地面高度：km点评：随地球一起转动，就好像停留在天空中的卫星，通常称之为定点卫星．它们离地面的高度是一个确定的值，不能随意变动。

利用月相求解月球公转周期例2 若近似认为月球绕地球公转与地球绕日公转的轨道在同一平面内，且都为正圆.又知这两种转动同向，如图所示，月相变化的周期为29.5天（图是相继两次满月，月、地、日相对位置示意图）．解：月球公转（2π+）用了29.5天．故转过2π只用天．由地球公转知．所以=27.3天．例3如图所示，A、B、C是在地球大气层外的圆形轨道上运行的三颗人造地球卫星，下列说法中正确的是哪个？（）A．B、C的线速度相等，且大于A的线速度B．B、C的周期相等，且大于A的周期C．B、C的向心加速度相等，且大于A的向心加速度D．若C的速率增大可追上同一轨道上的B分析：由卫星线速度公式可以判断出，因而选项A是错误的．由卫星运行周期公式，可以判断出，故选项B是正确的．卫星的向心加速度是万有引力作用于卫星上产生的，由，可知，因而选项C是错误的．若使卫星C速率增大，则必然会导致卫星C偏离原轨道，它不可能追上卫星B，故D也是错误的．解：本题正确选项为B。

点评：由于人造地球卫星在轨道上运行时，所需要的向心力是由万有引力提供的，若由于某种原因，使卫星的速度增大。

则所需要的向心力也必然会增加，而万有引力在轨道不变的时候，是不可能增加的，这样卫星由于所需要的向心力大于外界所提供的向心力而会作离心运动。