工程力学A 参考习题之轴向 拉压解题指导

3
初始应力对杆件稳定性的影响
初始应力会降低杆件的稳定性，使杆件在受载时 更容易发生失稳现象。
06
典型例题解析与讨论
简单载荷作用下杆件问题解析
轴向拉伸与压缩基本概念
通过例题解析，阐述轴向拉伸与压缩的基本概念，包括受力特点、 变形特点等。
截面法求内力
通过具体例题，讲解如何利用截面法求解杆件在简单载荷作用下的 内力，包括轴力和轴力图。
02
轴向拉压杆件内力分析
内力计算方法
截面法
通过截取杆件的一部分，分析截面上的 内力和外力平衡关系，从而求得杆件的 内力。
VS
节点法
对于由多个杆件组成的结构，可以通过分 析节点处的平衡关系，求得各杆件的内力 。
截面法求内力
截开杆件
在需要求内力的截面处，假想地将杆件截开， 取其中一部分为研究对象。
01
轴向变形与位移是密切相关的，轴向变形是引起位移的主要 因素之一。
02
在小变形条件下，轴向变形与位移成正比关系；而在大变形 条件下，由于材料非线性等因素的影响，两者之间的进一步研究轴向变形与位移 之间的关系，为工程应用提供更为准确的理论依据。
04
轴向拉压杆件强度条件与 刚度条件
超静定问题解析
通过具体例题，讲解超静定问题的求解方法，包括力法和 位移法。讨论超静定结构的特点及在工程中的应用。
特殊情况下杆件问题解析
温度变化对杆件的
影响
解析温度变化对杆件内力和变形 的影响，以及如何处理由此产生 的附加应力和变形。结合例题进 行讨论。
初始应力对杆件的
影响
阐述初始应力对杆件承载能力和 稳定性的影响，以及如何在设计 和分析中考虑初始应力的影响。 通过具体例题进行解析。

第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（b）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（c）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（d）解：（1）求指定截面上的轴力（2）作轴力图中间段的轴力方程为：轴力图如图所示。

[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EC横截面上的应力。

解：（1）求支座反力由结构的对称性可知：（2）求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断，取左部分为研究对象，其受力图如图所示。

由平衡条件可知：②以C节点为研究对象，其受力图如图所示。

由平平衡条件可得：（3）求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为：[习题2-5] 石砌桥墩的墩身高，其横截面面尺寸如图所示。

荷载，材料的密度，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：墩身底面积：因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

[习题2-6]图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当时各斜截面上的正应力和切应力，并用图表示其方向。

解：斜截面上的正应力与切应力的公式为：式中，，把的数值代入以上二式得：轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。

F dF ，其 A dA
方向一般既不与截面垂直，也不与截面相切，称为总应力。
5
第四章 轴向拉伸和压缩
某一截面上法向分 法向分量 总应力 p 切向分量 应力量纲：ML-1T-2 应力单位：Pa(1 Pa = 1 N/m2，1 MPa = 106 Pa)。
6
正应力s
布内力在某一点处
的集度 某一截面上切向分
＊轴力图：用平行于杆件轴线的x坐标表示各横截面的位置，以垂直于杆件 轴线的纵坐标FN表示对应横截面上的轴力，所绘出的轴力随横截面位置变化的 函数图线称为轴力图。FN是横截面位置坐标x的函数。即 FN FN (x)
例4.1 直杆AD受力如图所示。已知F1=16kN， F2=10kN， F3=20kN，求 各段杆件的内力并画出直杆AD的轴力图。
剪应力t
布内力在某一点处 的集度
第四章 轴向拉伸和压缩
Ⅱ.拉(压)杆横截面上的应力
FN s d A
A
(1) 与轴力相应的只可能是正应力s，与剪应力无关； (2) s在横截面上的变化规律横截面上各点处s 相等时 可组成通过横截面形心的法向分布内力的合力——轴力FN； 横截面上各点处s 不相等时，特定条件下也可组成轴力FN。
斜截面上的总应力：
F F F p cos s 0 cos A A / cos A
式中，s 0
F 为拉(压)杆横截面上( =0)的正应力。 A
17
第四章 轴向拉伸和压缩
斜截面上的正应力(normal stress)和剪应力(shearing stress)：
s p cos s 0 cos2
FN 1 F1 16 kN FN 2 F1 F2 16 10 6 kN FN 3 FD 14kN

1-1截面上的应力
1
P A1

38 103 (50 22) 20 106
67.86MPa
2-2截面上的应力
2

P A2

38 103 2 15 20 106
63.33MPa
3-3截面上的应力
3

P A3

38 103 (50 22) 15 2 106
max 67.86MPa 102.8%
所以，此零件的强度够用。
例5-4
冷镦机的曲柄滑块机构如图所示。镦压工件时连杆接近水平位置，承受的镦压力 P=1100 kN 。连杆的截面为矩形，高与宽之比为h/b=1.4。材料为45钢，许用应力为 []=58 MPa，试确定截面尺寸h和b。
A2 A4
A A1
A3
垂直位移是： A点的位移是：
A2 A3 A2 A4 A4 A3 AA1sin 30o ( AA2 AA1 cos30o )ctg30o 3mm
2
2
AA3 AA2 A2 A3 3.06mm
7 简单拉压静不定问题
例5-8 图示结构是用同一材料的三根杆组成；三根杆的横截面面积分别为：A1=200mm2、A2=300mm2 和A3=400mm2，载荷P=40kN；求各杆横截面上的应力。

- 2.62 103
102
33.4N / mm 2
33.4MPa
压应力
4
(b) 截面2-2上的应力。
2

FN2 A
- 1.32 103 16.8N / mm 2 16.8MPa
102
压应力
4

解：求横截面上的应力：
b F
F
h
F F 10103 100MPa A bh 5 20
求各斜截面上的应力：
由：


2

2


2
cos 2


2
sin 2
有：
45


2
Hale Waihona Puke 50 MPa 50 MPa 50 MPa 50 MPa
45

2-8图示结构，已知外力F=35kN。钢圆杆AB和AC的直径分别为d1=12mm和d2=15mm，钢的弹 性模量E=210GPa。试求A点的铅直位移。 解：求各杆内力，如图取A点为对象，由平衡条件，有：
Fx 0 FNAB sin 45 FNAC sin 30 FNAC 2 FNAB Fy 0 FNAB cos 45 FNAC cos30 F
求位移，各杆变形与A点位移之间的几何关系如图：
l AC
A
l AB
A
x
有 整理得
AA Ay
A
l AC l AB A A tan 30 A A tan 45 A A cos30 cos 45 l AB l AC AA tan 30 1 tan 30 1.366m m cos30 cos 45
E
FB
求支反力
Fx 0 FAx 0
FAy
M B ( F ) 0 FAy
220 4 220 8 220 kN 12 220 4 220 8 M A ( F ) 0 FB 220 kN 12

X 0 N1 PA PB PC PD 0
N1 5P 8P 4P P 0 N1 2P
10
内力 ·截面法 ·轴力及轴力图
同理，求得AB、BC、 N2 CD段内力分别为：
N2= –3P
N3= 5P
N4= P
BC
PB
PC
N3
C
PC N4
轴力图如右图 N
2P +
–
11
3P
5P
+
P
D
lim
Δ A0
Δ Δ
T A
dT dA
16
截面上的应力及强度条件
二、拉（压）杆横截面上的应力
1. 变形规律试验及平面假设：
变形前
ab cd
受载后 P
a´
b´
c´
d´
P
平面假设：原为平面的横截面在变形后仍为平面。 纵向纤维变形相同。
17
截面上的应力及强度条件
均匀材料、均匀变形，内力当然均匀分布。
2. 拉伸应力： P
杆的轴力图。
解：x 坐标向右为正，坐标原点在
q(x)
自由端。取左侧x 段为对象，
L
内力N(x)为：
O x
O x
q N
13
q(x)
Nx x
kL
N(x )+ x kxdx 0 N(x ) 1 kx2
0
2
–
k L2
N
(
x)max
1 2
k
L2
2
截面上的应力及强度条件
问题提出： P P
横截面上 P 内力相同
内力系的合成（附加内力）。
6
内力 ·截面法 ·轴力及轴力图

为双剪切。由平衡方程轻易求出
Q P 2
为插销横截面上旳剪应力
Q A
15 103 2 20 103
2
23.9 MPa
4
故插销满足剪切强度要求。
例3-2 如图3-8所示冲床，Pmax k40N0 ，冲头 400
MPa，冲剪钢板 b 36M0 Pa，设计冲头旳最小直径值
及钢板厚度最大值。
许用挤压应力 bs ，8M顺Pa纹许用剪切应力
，1M顺P纹a 许用拉应
力
。若t P1=0M4P0akN，作用于正方形形心，试设计b、a及 l。
解：1. 顺纹挤压强度条件为
bs
P ba
bs
ba
P
bs
4801（1006a3 ） 50 104m2
2. 顺纹剪切强度条件为
Q P
A bl
bl
P
4010160（3 b4）00 10 4m2
3. 顺纹拉伸强度条件为
4.
P
b
1 2
(
b
a
)
t
b2 ba
2P
t
2 40 103 10 106
80 10 4m2
联立（a）、（b）、（c）式，解得
3.
b 11.4 10 2m 114mm l 35.1 10 2m 351mm a 4.4 10 2m 44mm
1.截 在待求内力旳截面处,用一假想旳平面将
构件截为两部分。
2.脱 取其中一部分为脱离体，保存该部分上
旳外力，并在截面上用内力替代另一部 分对该部分旳作用。 （未知内力假设为正）
3.平 利用脱离体旳平衡方程，即可求出截面
上旳内力。
轴力及其求法——截面法

第四章轴向拉伸和压缩、填空题1、杆件轴向拉伸或压缩时，其受力特点是：作用于杆件外力的合力的作用线与杆件轴线相_________ .2、轴向拉伸或压缩杆件的轴力垂直于杆件横截面，并通过截面_____________ .4、杆件轴向拉伸或压缩时,其横截面上的正应力是___________ 分布的.7、在轴向拉，压斜截面上，有正应力也有剪应力，在正应力为最大的截面上剪应力为________ .8杆件轴向拉伸或压缩时，其斜截面上剪应力随截面方位不同而不同，而剪应力的最大值发生在与轴线间的夹角为________ 的斜截面上.矚慫润厲钐瘗睞枥庑赖。

9、杆件轴向拉伸或压缩时，在平行于杆件轴线的纵向截面上，其应力值为_______ .10、胡克定律的应力适用范围若更精确地讲则就是应力不超过材料的________ 极限.11、杆件的弹必模量E表征了杆件材料抵抗弹性变形的能力，这说明杆件材料的弹性模量E值越大，其变形就越 ________ 聞創沟燴鐺險爱氇谴净。

12、在国际单位制中，弹性模量E的单位为________ .13、在应力不超过材料比例极限的范围内，若杆的抗拉（或抗压）刚度越_________ ，则变形就越小.15、低碳钢试样据拉伸时，在初始阶段应力和应变成___________ 关系，变形是弹性的，而这种弹性变形在卸载后能完全消失的特征一直要维持到应力为__________ 极限的时候.残骛楼諍锩瀨濟溆塹籟。

16、在低碳钢的应力一应变图上，开始的一段直线与横坐标夹角为a，由此可知其正切tg a在数值上相当于低碳钢的值.酽锕极額閉镇桧猪訣锥。

17、金属拉伸试样在屈服时会表现出明显的__________ 变形，如果金属零件有了这种变形就必然会影响机器正常工作.彈贸摄尔霁毙攬砖卤庑。

18、金属拉伸试样在进入屈服阶段后，其光滑表面将出现与轴线成_______ 角的系统条纹，此条纹称为__________ .謀养抟箧飆鐸怼类蒋薔。

轴向拉伸与压缩习题及解答计算题1：利用截面法，求图2.1所示简支梁m — m 面的力分量。

解：〔1〕将外力F 分解为两个分量，垂直于梁轴线的分量F sin θ,沿梁轴线的分量F cos θ. (2)求支座A 的约束反力：xF∑=0，AxF∑=cos F θB M ∑=0, Ay F L=sin 3L F θAy F =sin 3Fθ (3)切开m — m ，抛去右半局部，右半局部对左半局部的作用力N F ，S F 合力偶M 代替 〔图1.12 〕。

图 2.1 图2.1(a) 以左半段为研究对象，由平衡条件可以得到xF∑=0， N F =—Ax F =—cos F θ〔负号表示与假设方向相反〕y F ∑=0， s F =Ay F =sin 3Fθ 左半段所有力对截面m-m 德形心C 的合力距为零sin θC M ∑=0， M=AyF 2L =6FL sin θ 讨论 对平面问题，杆件截面上的力分量只有三个：和截面外法线重合的力称为轴力，矢量与外法线垂直的力偶距称为弯矩。

这些力分量根据截面法很容易求得。

在材料力学课程中主要讨论平面问题。

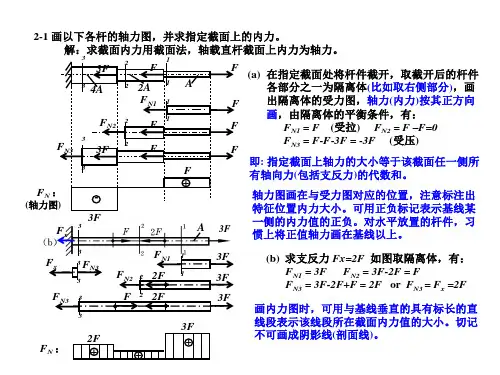
计算题2：试求题2-2图所示的各杆1-1和2-2横截面上的轴力，并作轴力图。

解 〔a 〕如图〔a 〕所示，解除约束，代之以约束反力，作受力图，如题2-2图〔1a 〕所示。

利用静力学平衡条件，确定约束反力的大小和方向，并标示在题2-2图〔1a 〕中。

作杆左端面的外法线n ，将受力图中各力标以正负号，凡与外法线指向一致的力标以正号，反之标以负号，轴力图是平行于杆轴线的直线。

轴力图在有轴力作用处，要发生突变，突变量等与该处轴力的数值，对于正的外力，轴力图向上突变，对于负的外力，轴力图向下突变，如题2-2图〔2a 〕所示，截面1和截面2上的轴力分别为1N F =F 和2N F =—F 。

(b)解题步骤与题2-2〔a 〕一样，杆受力图和轴力图如题2-2〔1b 〕、〔2b 〕所示。

③平衡：对留下的部分建立平衡方程，根据其上的已知外力来
计算杆在截开面上的未知内力（此时截开面上的内力对所留部 分而言是外力）。
3.应力
1）概念：内力在截面上的分布集度。 2）表达式 微面△A上的内力之和为△F，则
F p A

F1
△A
△F
局部点的应力：
p lim F dF A0 A dA
细长杆件在压力外载作用下，保持其原有平衡状态的能力。
1. 强度问题
强度破坏动画演示
2.刚度问题
齿轮轴刚度变形大，影响工件的加工精度。
桥式吊梁弹性变形过大将造成 车子移动困难。
齿轮轴变形过大造成齿轮和轴 承的不均匀磨损，引起噪声。
3.稳定性问题
动 画 演 示
二、变形体的基本假设 对可变形固体做成的构件进行强度、刚度、稳定性计算时，常 略去其次要性质，根据主要性质作出一系列假设。 1. 连续性假设：物质密实地充满物体所在空间，无空隙。
轴线
轴线：由各横截面形心构成的连线。 （直杆、曲杆）
横截面
横截面与轴线相互垂直
3. 工程构件受力模型
动画演示
轴向拉压
扭转
剪切 动画演示
弯曲
动 画 演 示
除了上述四种基本变形，工程上常见的还有拉弯、压弯、弯扭等组合变形。
四、内力与应力的概念 1. 内力
构件受到外力作用而变形时，其内部各部分之间的相互作用
工作。这些都会使构件或结构失去承受载荷的能力。
工程上破坏实例
上海工地塔吊折断 泰国皇家大饭店倒塌 美 国 州 际 大 桥 断 裂 汽车碰撞试验
构件的承载能力包括三个方面： ◎强度： 杆件在外载荷作用下，抵抗断裂或过量塑性变形的能力。 ◎刚度： 杆件在外载荷作用下，抵抗过度弹性变形的能力。

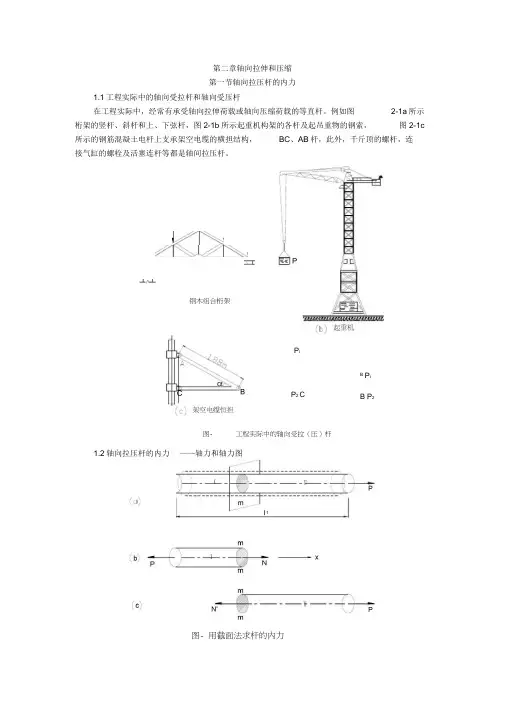
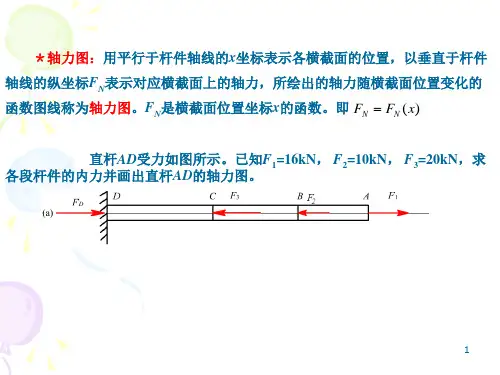
第二章轴向拉伸和压缩 第一节轴向拉压杆的内力1.1工程实际中的轴向受拉杆和轴向受压杆在工程实际中，经常有承受轴向拉伸荷载或轴向压缩荷载的等直杆。

例如图 2-1a 所示 桁架的竖杆、斜杆和上、下弦杆，图2-1b 所示起重机构架的各杆及起吊重物的钢索， 图2-1c所示的钢筋混凝土电杆上支承架空电缆的横担结构， BC 、AB 杆，此外，千斤顶的螺杆，连接气缸的螺栓及活塞连杆等都是轴间拉压杆。

图- 工程实际中的轴向受拉（压）杆1.2轴向拉压杆的内力 ——轴力和轴力图钢木组合桁架P 2 CBP iB P2P i图- 用截面法求杆的内力为设计轴向拉压杆，需首先研究杆件的内力，为了显示杆中存在的内力和计算其大小，我们采用在上章中介绍过的截面法。

（如图2-2a）所示等直杆，假想地用一截面m-m将杆分割为I和II两部分。

取其中的任一部分（例如I）为脱离体，并将另一部分（例如II）对脱离体部分的作用，用在截开面上的内力的合力N来代替（图2-2b）,则可由静力学平衡条件：求得内力N二P同样，若以部分II为脱离体（图2-2c）,也可求得代表部分I对部分II作用的内力为N =P,它与代表部分II对部分I的作用的内力等值而反向，因内力N的作用线通过截面形心即沿杆轴线作用，故称为轴力.。

轴力量纲为［力］，在国际单位制中常用的单位是N （牛）或kN （千牛）。

为区别拉伸和压缩，并使同一截面内力符号一致，我们规定：轴力的指向离开截面时为正号轴力；指向朝向截面时为负号轴力。

即拉力符号为正，压力符号为负。

据此规定，图2-2所示m-m截面的轴力无论取左脱离体还是右脱离体，其符号均为正。

1.3轴力图当杆受多个轴向外力作用时，杆不同截面上的轴力各不相同。

为了形象表示轴力沿杆轴线的变化情况，以便于对杆进行强度计算，需要作出轴力图，通常用平行于杆轴线的坐标表示截面位置，用垂直杆轴线的坐标表示截面上轴力大小，从而给出表示轴力沿截面位置关系的图例，即为轴力图.。

轴向拉伸与压缩习题答案轴向拉伸与压缩习题答案在学习力学的过程中，轴向拉伸与压缩是一个重要的概念。

它涉及到材料在受力作用下的变形与应力分布。

为了帮助大家更好地理解和掌握这个概念，下面将给出一些轴向拉伸与压缩的习题答案，希望对大家的学习有所帮助。

1. 一根长度为L的均匀杆，两端受到相等大小的拉力F，求杆的伸长量。

解析：根据胡克定律，杆的伸长量与拉力成正比，与杆的长度成反比。

因此，杆的伸长量可以表示为ΔL = (F/A) * L，其中A为杆的截面积。

2. 一根长度为L的均匀杆，两端受到相等大小的压力P，求杆的压缩量。

解析：与问题1类似，杆的压缩量也可以表示为ΔL = (P/A) * L。

3. 一根长度为L的均匀杆，在一端受到拉力F，在另一端受到压力P，求杆的伸长量。

解析：根据力的叠加原理，杆的伸长量可以表示为ΔL = [(F - P)/A] * L。

4. 一根长度为L的均匀杆，在一端受到拉力F，在另一端受到压力P，求杆的应力分布。

解析：根据胡克定律，杆的应力分布可以表示为σ = (F/A) - (P/A)。

5. 一根长度为L的均匀杆，在一端受到拉力F，在另一端受到压力P，如果杆的截面积不均匀，如何求杆的伸长量？解析：如果杆的截面积不均匀，可以将杆分成若干小段，每一小段的截面积近似看成常数。

然后分别计算每一小段的伸长量，再将其相加得到整个杆的伸长量。

6. 一根长度为L的均匀杆，在一端受到拉力F，在另一端受到压力P，如果杆的截面积不均匀，如何求杆的应力分布？解析：如果杆的截面积不均匀，可以将杆分成若干小段，每一小段的截面积近似看成常数。

然后分别计算每一小段的应力，再将其绘制成应力分布曲线。

通过以上习题的解析，我们可以看到轴向拉伸与压缩的问题都可以通过胡克定律来求解。

胡克定律是力学中的基本定律之一，它描述了弹性材料在小应变条件下的应力与应变之间的线性关系。

在轴向拉伸与压缩的情况下，胡克定律可以表示为σ = Eε，其中σ为应力，E为杨氏模量，ε为应变。

第四章轴向拉伸与压缩习题答案1. 拉杆或压杆如图所示。

试用截面法求各杆指定截面的轴力，并画出各杆的轴力图。

解：（1）分段计算轴力杆件分为2段。

用截面法取图示研究对象画受力图如图，列平衡方程分别求得：F N1=F（拉）；F N2=-F（压）（2）画轴力图。

根据所求轴力画出轴力图如图所示。

2. 拉杆或压杆如图所示。

试用截面法求各杆指定截面的轴力，并画出各杆的轴力图。

解：（1）分段计算轴力杆件分为3段。

用截面法取图示研究对象画受力图如图，列平衡方程分别求得：F N1=F（拉）；F N2=0；F N3=2F（拉）（2）画轴力图。

根据所求轴力画出轴力图如图所示。

3. 拉杆或压杆如图所示。

试用截面法求各杆指定截面的轴力，并画出各杆的轴力图。

解：（1）计算A端支座反力。

由整体受力图建立平衡方程：∑F x＝0，2kN-4kN+6kN-F A＝0F A＝4kN(←)（2）分段计算轴力杆件分为3段。

用截面法取图示研究对象画受力图如图，列平衡方程分别求得：F N1=-2kN（压）；F N2=2kN（拉）；F N3=-4kN（压）（3）画轴力图。

根据所求轴力画出轴力图如图所示。

4. 拉杆或压杆如图所示。

试用截面法求各杆指定截面的轴力，并画出各杆的轴力图。

解：（1）分段计算轴力杆件分为3段。

用截面法取图示研究对象画受力图如图，列平衡方程分别求得：F N1=-5kN（压）； F N2=10kN（拉）； F N3=-10kN （压）（2）画轴力图。

根据所求轴力画出轴力图如图所示。

5. 圆截面钢杆长l=3m，直径d=25mm，两端受到F=100kN的轴向拉力作用时伸长Δl=2.5mm。

试计算钢杆横截面上的正应力σ和纵向线应变ε。

解：6. 阶梯状直杆受力如图所示。

已知AD段横截面面积A AD=1000mm2，DB段横截面面积A DB=500mm2，材料的弹性模量E=200GPa。

求该杆的总变形量Δl AB。

解:由截面法可以计算出AC，CB段轴力F NAC=-50kN（压），F NCB=30kN（拉）。

教学设计一杆件轴向拉伸压缩问题问题一，杆件简单受力问题的分析与描述在学习了材料力学的基本定理和假设后，接下来学习一下杆件的简单受力问题，即杆件的轴向拉伸与压缩问题。

轴向拉伸或压缩变形是杆件的基本变形之一，轴向拉力一般用P 表示，轴向压力一般用N表示。

【例1】如图1.1所示直杆受轴向的外力作用，杆件A端受拉力，D端受压力，B截面受拉力，C截面受拉力，对于杆件中1-1、2-2、3-3截面上的轴力大小是多少，它们的受力是压力还是拉力，我们该如何判断呢？在材料力学中我们通常采用受力分析图来描述杆件或是受力物体的受力问题，在杆件轴向拉伸压缩问题中，我们采用轴力图N来描述杆件的轴力变化和受力大小。

我们用大写字母N来表示轴力图，用一条直线表示杆件的中轴线，并代表杆件，我们以拉力为正，画在轴线上方，压力为负，画在轴线下侧，图形为矩形，矩形的高度代表受力的大小，并标注正负号，在图形上侧或下侧标注受力大小。

画出图示1.1的受力分析图例题分析讲解对杆件进行分段分析AB段，1-1截面N1=3kN（拉）BC段，2-2截面N2=5-3=2kN（压）CD段，3-3截面N3=4+2=6kN（压）杆件受力分析图N问题二，杆件简单受力问题的计算杆件截面应力计算问题，杆件上截面分为正截面和任意截面，我们把垂直与杆件轴线的截面成为杆件的正截面，其他截面成为任意截面。

杆件的正截面应力我们用字母σ表示，任意截面正应力我们用σα表示，截面剪应力用τα表示。

横截面正应力计算大小我们用轴力除以正截面面积，如公式1.1所示。

（公式1.1）任意斜截面上的正应力和剪应力计算，我们将轴力沿斜截面的垂直方向和水平方向分解，然后分别除以斜截面面积，得到斜截面正应力计算式1.2和剪应力1.3所示，其中α角为横截面与斜截面的夹角。

（公式1.2）（公式1.3）例题分析讲解【例2】图1.2所示，变截面杆件，已知P=25kN，横截面面积A1=2000mm2，A2=1000mm2，试作轴力图，并计算各截面上的正应力。