反比例函数图象与图形面积

一、反比例函数的定义与特点反比例函数是一种特殊的函数关系，其定义形式为y=k/x，其中k为非零常数。

在反比例函数中，x和y之间的关系是倒数关系，即x越大，y越小；x越小，y越大。

反比例函数的图像通常呈现出由一条横轴和一条纵轴围成的超出范围的特殊形状。

二、反比例函数的图像及性质对于反比例函数y=k/x而言，其图像通常为从第一象限一直延伸到第四象限的一条曲线，图像特点为：1. 与坐标轴交点- 当x=0时，y=无穷大，即反比例函数图像与y轴有一个渐近线；- 当y=0时，x=无穷大，即反比例函数图像与x轴有一个渐近线。

2. 对称性反比例函数的图像具有关于原点对称的特点，即对于图像上的任意一点P(x,y)，其关于原点O的对称点P'(-x,-y)也在图像上。

3. 导数的性质反比例函数y=k/x的导数为y'=-k/x^2，即导数的绝对值随着x的增大而减小，因此反比例函数的导数曲线呈现出逐渐下降的趋势。

三、坐标轴围成的面积对于反比例函数y=k/x而言，当x轴、y轴和反比例函数围成一个封闭的区域时，我们可以计算这一区域的面积。

这个面积的计算可以分别计算x轴、y轴和反比例函数所围成的三个三角形的面积，然后相加。

具体而言，设反比例函数y=k/x与x轴和y轴所围成的区域为A，则区域A的面积可以表示为：A = 2∫[a, b] k/x dx其中，[a, b]为反比例函数y=k/x在定义域内的区间，∫表示定积分。

根据定积分的性质，我们可以对反比例函数进行积分计算，从而求得区域A的面积。

四、实例分析举例来说，我们考虑反比例函数y=2/x在区间[1, 3]内的图像与x轴、y轴所围成的区域。

首先对反比例函数进行积分计算：∫[1, 3] 2/x d x = 2ln|x| |[1, 3] = 2(ln|3| - ln|1|) = 2ln(3)反比例函数y=2/x在区间[1, 3]内与x轴、y轴所围成的面积为2ln(3)。

反比函数图像上的四种三角形的面积函数是解决实际生活问题的重要模型，在近几年各省市的考题中，对于函数的考查比例占有相当重的份量，绝大部分是考查考生对其基本概念、图象性质的理解和应用，甚至成为中考压轴题的大类。

反比例函数的图像经常与三角形的面积联系在一起，下面就举例说明。

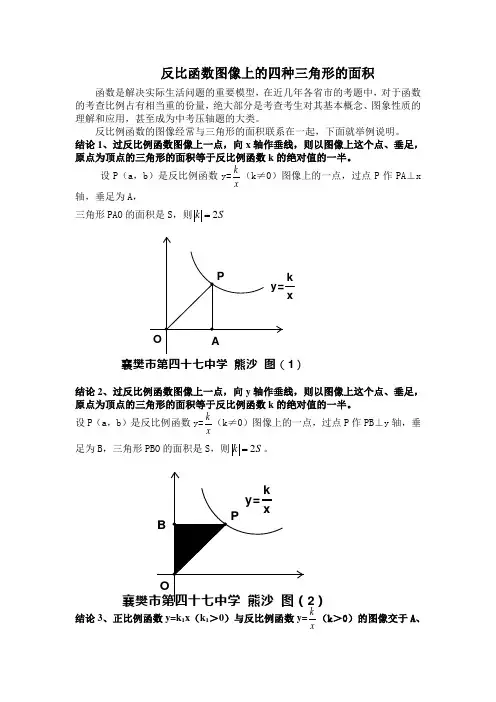
结论1、过反比例函数图像上一点，向x 轴作垂线，则以图像上这个点、垂足，原点为顶点的三角形的面积等于反比例函数k 的绝对值的一半。

设P （a ，b ）是反比例函数y=xk（k ≠0）图像上的一点，过点P 作PA ⊥x轴，垂足为A ，三角形PAO 的面积是S ，则S k 2=结论2、过反比例函数图像上一点，向y 轴作垂线，则以图像上这个点、垂足，原点为顶点的三角形的面积等于反比例函数k 的绝对值的一半。

设P （a ，b ）是反比例函数y=x k（k ≠0）图像上的一点，过点P 作PB ⊥y 轴，垂足为B ，三角形PBO 的面积是S ，则S k 2=。

结论3、正比例函数y=k 1x （k 1＞0）与反比例函数y=xk（k ＞0）的图像交于A 、kx 襄樊市第四十七中学 熊沙 图（1）2）B 两点，过A 点作AC ⊥x 轴，垂足是C ，三角形ABC 的面积设为S ，则S=|k|，与正比例函数的比例系数k 1无关。

证明：I因为，正比例函数y=k 1x （k 1＞0）与反比例函数y=x k（k ＞0）的图像交于A 、B 两点，所以，x k xk1=，所以，x=±111k kk k k =， 当x=11k kk 时，y= k 1x=1kk ，所以，点A 的坐标是（11k kk ，1kk ），当x =-11k kk 时，y= k 1x =-1kk ，所以，点B 的坐标是（-11k kk ，-1kk ），所以，OC 的长度是11k kk ，三角形ABC 的面积=三角形AOC 的面积+三角形BOC 的面积=21×OC ×AC+21×OC ×BD =21×11k kk ×1kk +21×11k kk ×|-1kk | =21k+21k=k 。

反比例函数图象与几何图形的面积 签名_______一. 反比例函数与矩形面积 1. 如图，P 是反比例函数y kxk =≠()0的图象上一点，过P 点分别向x 轴、y 轴作垂线，所得到的图中阴影部分的面积为6，求这个反比例函数的解析式。

二. 反比例函数与三角形面积 2．如图，点A 在反比例函数y kxk =≠()0的图象上，AB 垂直于x 轴，若S AOB ∆=4，那么这个反比例函数的解析式为_____________。

评析：如图，若A 点是反比例函数y k xk =≠()0图象上的任意一点，且AB 垂直于x 轴，垂足为B ，AC 的垂直于y 轴，垂足为C ，则矩形面积=ABOC S ；三角形AOB 的面积=∆AOB S _____,常做的辅助线是过图像上的点做X 轴或者Y 轴的垂线构建矩形或者直角三角形。

1．如图，正比例函数y kx k =>()0与反比例函数y x=1的图象相交于A 、C 两点，过A 点作x 轴的垂线交x 轴于B ，连结BC ，若∆ABC 面积为S ，则________.练习：1. （2010湖北孝感）如图，点A 在双曲线1y x =上，点B 在双曲线3y x=上， 且AB ∥x 轴，C 、D 在x 轴上，若四边形ABCD 为矩形，则它的面积为 . 2. 如图，A 、B 是函数y x=1的图象上关于原点O 对称的任意两点，AC 平行于y 轴，BC 平行于x 轴，∆ABC 的面积为S ，则（ ） A. S ＝1 B. 12<<SC. S ＝2D. S >23、 如图，正比例函数y kx k =>()0与反比例函数y x=2的图象相交于A 、C 两点，过A 点作x 轴的垂线，交x 轴于B ，过C 作x 轴的垂线，交x 轴于D ，则四边形ABCD 的面积为____________。

4、如图，反比例函数y=xk(x>0)与矩形OABC 的边AB 、BC 交于F 、E 两点，且BE=CE ，四边形OEBF 的面积为2 ；求三角形OAF 的面积和k5、如图，双曲线)0(2>=x xy 经过四边形OABC 的顶点A 、C ，∠ABC ＝90°，OC 平分OA 与x 轴正半轴的夹角，AB ∥x 轴，将△ABC 沿AC 翻折后得到△AB ＇C ，B ＇点落在OA 上，则四边形OABC 的面积是 .x。

反比例函数的面积问题的解题技巧
反比例函数是指一种具有如下形式的函数：y=k/x，其中k是常数。

在解决反比例函数的面积问题时，有以下几种解题技巧：
1. 确定函数图像：反比例函数的图像通常是一条双曲线。

确定函数图像可以帮助我们更好地理解函数的性质和规律，从而更好地解决面积问题。

2. 确定积分区间：反比例函数的积分区间通常是有限的，因为函数在x = 0处不存在。

在解决面积问题时，需要确定积分区间以便进行积分计算。

3. 利用对称性：反比例函数具有对称性，即在y轴和x轴上对称。

在解决面积问题时，可以利用对称性简化计算。

4. 利用换元法：在进行积分计算时，可以利用换元法将反比例函数变形成容易积分的形式，从而简化计算。

5. 利用图形面积计算公式：反比例函数的面积可以用图形面积计算公式求解。

这种方法适用于简单的反比例函数图形，但对于复杂的反比例函数图形不太实用。

总之，在解决反比例函数的面积问题时，需要充分理解函数性质和规律，灵活运用解题技巧，才能得到准确的答案。

- 1 -。

例谈与反比例函数有关的图形面积计算反比例函数y＝(k≠0)的图象是双曲线，双曲线上任一点的横坐标与纵坐标的乘积是一定值k，所以过双曲线上任意一点向x轴（或y轴）引垂线，由该点、垂足和坐标原点所构成的三角形的面积都相等，等于│k│。

类似地，过双曲线上任一点分别向x轴和y轴引垂线，由垂线与两坐标轴所围成的矩形的面积为定值│k│。

反之，已知上述三角形或矩形的面积，求反比例函数的解析式，则应注意图象所在的象限；对于k值进行恰当的取舍，或应注意多解。

1题:如图1所示，在反比例函数y＝（x＞0）的图象上有三点a、b、c，经过此三点分别向x轴引垂线，交x轴于d、e、f三点，连接oa、ob、oc，记△oad、△obe、△ocf的面积分别为s1、s2、s3，则有（）图1a、s1＜s2＜s3b、s1＞s2＞s3c、s1＝s2＝s3d、s3＜s1＜s2分析：∵s△oad＝od·ad＝xa·ya＝1同理s△obe＝s△ocf＝s△oad＝1答案：c2题:如图2，在反比例函数y＝－(x＜0)的图象上任取一点p。

过p分别作x轴、y轴的垂线，垂足分别为n、m，则四边形onpm的面积为___________。

图2分析：s矩形pnom＝pn·on＝│xp│·│yp│＝│xp· yp│＝6答案：63题．如图3所示，a、b是反比例函数y＝的图象上关于原点o 对称的任意两点。

ac平行于y轴交x轴于d点，bc平行于x轴。

求：△abc的面积、△abd的面积、△bod的面积。

分析：由题意知，△abc是直角三角形，s△abc＝bc·ac，因为a、b两点关于原点对称，所以，设a的坐标为（xa、ya）且（xa＞0，ya＞0）则b的坐标为（－xa、－ya）、c点坐标为（xa、－ya）线段ac＝2ya bc＝2xa因为点a、b在在反比例函数y＝上；xa·ya＝1所以，s△abc＝bc·ac＝·2xa·2ya＝2xaya＝2s△abd＝s△abc－s△bcd＝s△abc－·2 xa·ya＝2－1＝1或s△abd＝s△aod＋s△bod＝×od·ad＋×od·│yb│＝│xa· ya│＋│xa ·ya│＝＋＝1s△bod＝s△abd－s△aod＝1－＝或s△bod＝×od·│yb│＝│xa· ya│＝解略拓展：若a、b是反比例函数y＝(k≠0)的图象上关于原点对称的任意两点。

反比例函数面积问题
反比例函数面积问题通常是指与反比例函数相关的图形面积的计算
问题。

例如，给定反比例函数y=k/x的图像与坐标轴所围成的区域，要求该区域的面积。

解决这类问题通常需要应用积分学知识，因为反比例函数的图像通常是一个双曲线，与坐标轴围成的区域是一个不规则图形。

通过积分，我们可以求出这个不规则图形的面积。

具体地，如果要求反比例函数y=k/x在第一象限内与x轴、y轴所围成的区域面积，可以先求出该函数在第一象限内的图像与x轴之间的面积，然后再乘以2（因为反比例函数在第一、三象限内是对称的）。

这个面积可以通过定积分来计算，积分区间是从0到正无穷大，被积函数是y=k/x。

需要注意的是，由于反比例函数的图像在x轴和y轴上都趋于无穷大，
因此所求得的面积也是无穷大的。

但是，在某些特定情况下，例如给定一个特定的矩形区域，我们可以通过计算该矩形区域内反比例函数图像的面积来得到一个有限的数值。

总之，反比例函数面积问题需要根据具体情况进行具体分析，通常需要应用积分学知识和几何知识来解决。

以上是对于反比例函数面积问题5的回答，希望对你有所帮助。