2018版高中数学人教B版必修一学案：第二单元 2.2.1 一次函数的性质与图象 Word版含答案

高中数学学习材料（灿若寒星精心整理制作）第二章第二单元一次函数和二次函数1．一次函数（1）一次函数的概念函数叫做一次函数，它的定义域是R，值域为R.一次函数的图象是，其中k叫做该直线的，b叫做该直线在y轴上的．一次函数又叫．（2）一次函数的性质①函数的改变量Δy＝与自变量改变量Δx＝的比值等于，k的大小表示直线与x轴的．②当k>0时，一次函数是；当k<0时，一次函数是．③当b＝0时，一次函数为，是；当b≠0时，它．④直线y＝kx＋b与x轴的交点为，与y轴的交点为。

2．二次函数（1）函数y＝ax2＋bx＋c(a≠0)叫做，它的定义域为R.（2）二次函数的性质与图象图象函数性质a＞0 a＜0 定义域x∈R值域a>0 a<024[,)4ac bya-∈+∞24(,]4ac bya-∈-∞奇偶性b=0时为偶函数，b≠0时既非奇函数也非偶函数单调性a>0 a<0(,],2bxa∈-∞-时递增[,)2bxa∈-+∞时递减(,],2bxa∈-∞-时递减[,)2bxa∈-+∞时递增图象特点()()241:;2:(,)224b b ac b x a a a-=--对称轴顶点 最值抛物线有最低点， 当2bx a=-时，y 有最小值2min44ac b y a-=抛物线有最高点， 当2bx a=-时，y 有最大值2max44ac b y a-=(3) 配方法将二次函数y ＝ax 2＋bx ＋c 配成顶点式y ＝x (a(－)h)2＋k 来求抛物线的顶点和函数y 的最值问题．配方法是研究二次函数的主要方法，熟练地掌握配方法是掌握二次函数性质的关键，对一个具体的二次函数，通过配方就能知道这个二次函数的主要性质．（4）二次函数解析式的三种形式 ①一般式：f （x ）= ax 2+bx+c(a ≠0) .②顶点式：f(x)= f(x)=a(x-h)2+k (a ≠0) ，(k ，h)为顶点坐标． ③两根式：f(x)=a(x-x 1)(x-x 2)(a ≠0) ， x 1、x 2为两实根． 3．待定系数法一般地，在求一个函数时，如果知道这个函数的一般形式，可先把所求函数写为一般形式，其中系数待定，然后再根据题设条件求出这些待定系数. 这种通过求待定系数来确定变量之间关系式的方法叫做待定系数法。

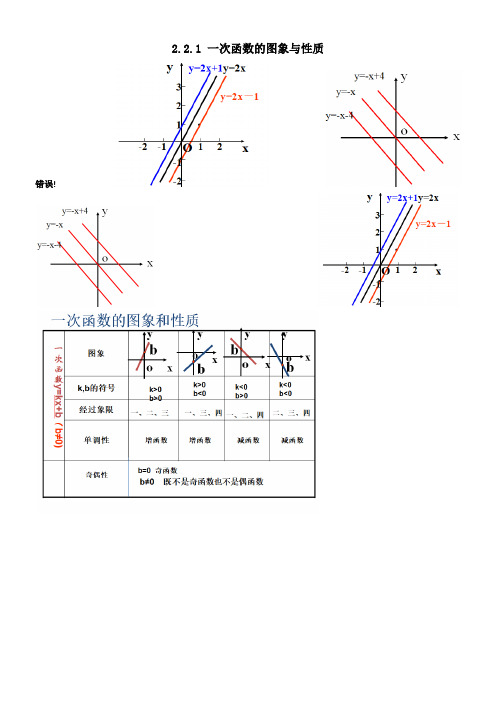
2.2.1 一次函数的图象与性质错误!
-m-2,若它的图象经过原点，则m= ; 若点（0 ，3 在它的图象上，则m = ;若它的图象经过一、二、四象限，则m
大显身手
1、已知一次函数=1-2mm-1 , 求满足下列条件的m的值：
（1）函数值随的增大而增大；
（2）函数图象与轴的负半轴相交；
（3）函数的图象过第二、三、四象限；
（4）函数的图象过原点。

2 对于一次函数= 3, 当1≤≤4时, 的取值范围是___________
六、课堂小结
1会画一次函数的图象
2一次函数的图象与性质，常数，b的意义和作用
3数形结合的思想与方法
4进一步体验研究函数的一般思路与方法
七作业：课后练习A。

示范教案整体设计教学分析一次函数是全面介绍函数的开始．由于学生对一次函数已经有了认识基础，学起来会比较顺利．因此，在实际教学中可以适度综合和抽象，提出一些带有思考性质的综合性问题．三维目标1．理解掌握一次函数的概念、图象和性质，提高学生分析问题的能力，培养数形结合的思想．2．能够解决与一次函数有关的问题，提高学生解决问题的能力．重点难点教学重点：一次函数的性质与图象．教学难点：一次函数的性质的应用．课时安排1课时教学过程导入新课思路1.观察下列函数有什么共同特点：①y＝2x－1；②y＝3x＋6；③y＝x；④y＝－25x＋1.学生回答后，教师指出本节课题．思路2.前面我们已经学习了函数的性质：定义域、解析式、值域、单调性、奇偶性等．从本节开始，我们讨论具体的函数，首先讨论的是一次函数．推进新课新知探究提出问题①回顾一次函数的定义.②一次函数的图象是什么形状？③一次函数解析式y＝kx＋b k≠0 中字母k和b具有什么意义？④如下图所示，直线y＝kx＋b上有两点P x1，y1 、Q x2，y2 .试写出自变量的改变量Δx和函数值的改变量Δy.⑤试探讨k，Δx，Δy的关系.讨论结果：①形如函数y＝kx＋b(k≠0)叫做一次函数．它的定义域为R，值域为R.②一次函数的图象是直线，以后简写为直线y＝kx＋b.因此一次函数又称为线性函数．③k叫做直线y＝kx＋b的斜率，b叫做直线y＝kx＋b在y轴上的截距．④Δx＝x2－x1，Δy＝y2－y1.⑤由于点P(x1，y1)、Q(x2，y2)在直线y＝kx＋b上，则y1＝kx1＋b，y2＝kx2＋b，两式相减，得y2－y1＝k(x2－x1)，Δy Δx＝y2－y1x2－x1＝k或Δy＝kΔx(x2≠x1)．这就是说它的平均变化率为常数k，即对任意点x1，相应函数值的改变量与自变量的改变量成正比．提出问题①在同一坐标系中，画出下列一次函数的图象：ⅰ y＝x； ⅱ y＝3x＋3； ⅲ y＝2x－1.②这三个一次函数的图象有什么共同点？③这三个一次函数解析式中的k有什么共同点？④由此可以归纳出什么结论？并加以证明.⑤按同样的方法可以得到，当k满足什么条件时，一次函数y＝kx＋b是减函数？并加以证明.讨论结果：①如下图所示．②都是上升的．③k＞0.④当k＞0时，一次函数y＝kx＋b在R上是增函数．证明如下：设x1＜x2，则f(x1)－f(x2)＝(kx1＋b)－(kx2＋b)＝kx1－kx2＝k(x1－x2)，∵x1＜x2，k＞0，∴k(x1－x2)＜0.∴f(x1)＜f(x2)．∴当k＞0时，一次函数y＝kx＋b在R上是增函数．⑤当k＜0时，一次函数y＝kx＋b在R上是减函数．证明如下：设x1＜x2，则f(x1)－f(x2)＝(kx1＋b)－(kx2＋b)＝kx1－kx2＝k(x1－x2)，∵x1＜x2，k＜0，∴k(x1－x2)＞0.∴f(x1)＞f(x2)．∴当k＜0时，一次函数y＝kx＋b在R上是减函数．提出问题①归纳一次函数的奇偶性.②写出一次函数y＝kx＋b与两坐标轴的交点的坐标.③试归纳一次函数的性质.讨论结果：①当b ＝0时，一次函数y ＝kx ＋b 的图象关于原点对称；当b≠0时，一次函数y ＝kx ＋b 的图象关于原点和y 轴均不对称．因此得：当b ＝0时，一次函数变为正比例函数，是奇函数； 当b≠0时，它既不是奇函数，也不是偶函数．②直线y ＝kx ＋b 与x 轴的交点为(－bk ，0)，与y 轴的交点为(0，b)．③一次函数y ＝kx ＋b ， 定义域：R . 值域：R .单调性：当k ＞0时，一次函数y ＝kx ＋b 在R 上是增函数； 当k ＜0时，一次函数y ＝kx ＋b 在R 上是减函数．奇偶性：当b ＝0时，一次函数变为正比例函数，是奇函数； 当b≠0时，它既不是奇函数，也不是偶函数．图象：形状是直线，与x 轴的交点为(－bk，0)，与y 轴的交点为(0，b)．应用示例思路1例1指出下列函数中的一次函数：(1)y ＝－x ；(2)y ＝2x；(3)y ＝9x －2；(4)y ＝x 2＋1.解：根据一次函数的定义可知仅有(1)和(3)是一次函数．才是一次函数.例2求函数y ＝－5x －1，x ∈[1,4]的最小值．解：∵k ＝－5＜0，∴函数y ＝－5x －1在R 上是减函数． ∴函数y ＝－5x －1，x ∈[1,4]的最小值是f(4)＝－21. 点评：通常利用单调性求一次函数的最值.例1如下图所示，已知三个一次函数y ＝k 1x ＋b 1，y ＝k 2x ＋b 2，y ＝k 3x ＋b 3的图象，试分别按从小到大的顺序排列：(1)k 1，k 2，k 3；(2)b 1，b 2，b 3.解：(1)k 1，k 2，k 3分别是三条直线的斜率，由于直线y ＝k 2x ＋b 2和y ＝k 3x ＋b 3是上升的，则0＜k 3＜k 2，由于直线y ＝k 1x ＋b 1是下降的，则k 1＜0，所以k 1＜k 3＜k 2.(2)b 1，b 2，b 3分别是三条直线在y 轴上的截距， 观察图可得b 3＜b 1＜b 2.点评：本题主要考查一次函数解析式y ＝kx ＋b(k≠0)中k 和b 的几何意义，k 是直线的答案：D．若a ＞0且b ＞0，则函数y ＝ax ＋b 的图象不经过( )．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 例2对于每个实数x ，设f(x)是y ＝2x ＋1，y ＝x ＋2和y ＝－2x 三个函数中的最大值，则f(x)的最小值是________．解：在同一坐标系中画出这三个函数的图象，如下图所示，则f(x)＝⎩⎪⎨⎪⎧－2x ，x≤－23，x ＋2，－23<x<1，2x ＋1，x≥1.则函数f(x)图象如下图所示，则f(x)的最小值是f(－23)＝43.点评：本题主要考查分段函数及其性质．讨论分段函数的最值时，通常利用数形结合来解决.知能训练1．下列说法错误的是( ) A ．y ＝ax ＋b 叫做一次函数 B ．y ＝ax ＋b 的图象是一条直线C ．当a ＞0时，函数y ＝ax ＋b 在R 上递增D ．一次函数的平均变化率就是其对应直线的斜率 答案：A2．已知一次函数过点(12，0)且在y 轴上的截距为4，则其表达式为( )A ．y ＝－4x ＋8B ．y ＝－8x －4C ．y ＝－4x －8D ．y ＝－8x ＋4 答案：D3．已知点(3,5)和(a,7)在直线y ＝2x ＋b 上，则a ，b 的值分别为( ) A ．－4,1 B ．－4，－2 C ．4，－1 D ．－4，－1 答案：C4．直线y ＝x ＋3与y ＝－2x 的交点坐标为( )A ．(－1,2)B ．(1，－2)C ．(1,2)D ．(－1，－2) 答案：A5．函数y ＝2与y ＝|x|围成的封闭图形的面积是________．解析：围成的封闭图形是等腰三角形，底边长4，底边上的高为2，面积为4. 答案：46．若f[g(x)]＝6x ＋3，且g(x)＝2x ＋1，则f(x)等于________． 答案：3x7．若直线y ＝x ＋b 与直线y ＝－2x ＋4的交点在第一象限内，则实数b 的取值范围是________．答案：(－2,4) 拓展提升1．设集合A ＝{(x ，y)|y －3x －1＝2，x ，y ∈R }，B ＝{(x ，y)|－4x ＋y ＋1＝0，x ，y ∈R }，则A∩B 等于( )A ．{1,3}B ．{(1,3)}C ．D ． {(3,10)} 答案：C2．某商人购货，进货已按原价a 扣去25%，他希望对货物订一新价，以便按新价让利20%，销售后仍可获得售价25%的纯利，求此商人经营这种货物的件数x 与按新价让利总额y 之间的函数关系式．解：设新价为b ，则售价为b(1－20%)，因原价为a ，所以进价为a(1－25%)， 根据题意得b(1－20%)－a(1－25%)＝b(1－20%)×25%，化简得b ＝54a.所以y ＝b·20%·x ， 即y ＝14ax(x ∈N *)．课堂小结本节学习了一次函数的性质与图象． 作业课本本节练习B 1、2.设计感想本节在设计过程中，以学生熟悉的实例引入，体现了由特殊到一般和由易到难的认知规律，有关一次函数的图象问题，有条件的学校应该充分发挥信息技术的威力．备课资料 用一次函数的性质解题某些数学问题，通过构造一次函数，将问题转化为判断一次函数f(x)在区间[a ，b]上函数值的符号问题，从而使问题获得解决．1对于满足0≤p≤4的一切实数，不等式x 2＋px ＞4x ＋p －3恒成立，试求x 的取值范围． 解：令f(p)＝(x －1)p ＋(x 2－4x ＋3)， 当x ＝1时，f(p)＝0，不满足f(p)＞0.所以函数f(p)的图象是一条线段，要使f(p)＞0恒成立，当且仅当f(0)＞0，且f(4)＞0.解不等式组得x ∈(－∞，－1)∪(3，＋∞)．2设a ，b ，c 为绝对值小于1的实数，求证：ab ＋bc ＋ca ＋1＞0.证明：因为ab ＋bc ＋ca ＋1＝(b ＋c)a ＋bc ＋1且|a|＜1，|b|＜1，|c|＜1， 所以当b ＋c ＝0时，有ab ＋bc ＋ca ＋1＝1－c 2＞0. 当b ＋c≠0时，构造函数f(x)＝(b ＋c)x ＋bc ＋1，由f(1)＝b＋c＋bc＋1＝(b＋1)(c＋1)＞0，f(－1)＝－b－c＋bc＋1＝(1－b)(1－c)＞0，知对－1＜x＜1，都有f(x)＞0成立，所以f(a)＞0，即ab＋bc＋ca＋1＞0.(设计者：张新军)。

2.1.1函数的概念和图象（二）教学目标：使学生掌握函数图像的画法. 教学重点：函数图像的画法. 教学难点：函数图像的画法. 教学过程： 一、复习回顾上节课，我们学习了函数的概念，请同学们回忆一下，函数的定义是怎样的？它有几个要素？分别是什么？设A 、B 是非空的数集，如果按照某个确定的对应关系f ，使对于集合A 中的任意一个数x ，在集合B 中都有惟一确定的数f(x)和它对应，那么就称f ︰A →B 为从集合A 到集合B 的一个函数.函数有三要素：定义域、值域、对应关系.练习：下列函数中，哪个函数与函数y ＝x 是同一个函数？ ()()()()()xx y 4x y 3x y 2x y 122332====两个只有当它们的三要素完全相同时才为同一个函数.二、学生活动在初中，我们已学过函数的图象，并能作出函数y ＝2x －1，y ＝1x（x ≠0）以及y ＝x2的图象.社会生活中还有许多函数图象的例子，如心电图、示波图等.回想一下，在初中我们是采用什么方法来画出函数的图象？ 描点法描点法作图的步骤有哪些？ 列表、描点、连线练习（P25例4）试画出下列函数的图象： ⑴f(x)＝x ＋1⑵f(x)＝(x －1)2＋1,x ∈[1,3)三、建构数学将自变量的一个值x 0作为横坐标，相应的函数值f(x 0)作为纵坐标，就得到坐标平面上的一个点(x 0,f(x 0)).当自变量取遍函数定义域A 中的每一个值时，就得到一系列这样的点.所有这些点组成的集合（点集）为{(x,f(x))｜x ∈A}，即{(x,f(x))｜y ＝f(x),x ∈A}， 所有这些点组成的图形就是函数y ＝f(x)的图象. 四、数学运用例5 估计人口数量变化趋势是我们制定一系列相关政策的依据.从人口统计年鉴中可以查得我国从1949年至1999年人口数据资料如表所示，你能根据这个表说出我国人口变化情况解：由上表的数据，画出的函数图象是11个点.补：一物体从静止开始下落，下落的距离y(m)与下落时间x(s)之间近似地满足关系式y ＝4.9x 2.若一物体下落2s ，你能求出它下落的距离吗？并画出它的图象.思考：设函数y ＝f(x)的定义域为A ，则集合P ＝{(x,y)｜y ＝f(x),x ∈A}与集合Q ＝{y ｜y ＝f(x),x ∈A}相等吗？请说明理由.解析：P ≠Q ，因为P 、Q 的代表元素不一样，P 是点集，Q 是值域.问题：直线x ＝1和函数y ＝x 2＋1的图象的公共点可能几个？ 解析：根据图象知有且仅有一个公共点.变：⑴（P29习题6）直线x ＝a 和函数y ＝x 2＋1几个？解析：根据图象知有且仅有一个公共点.⑵直线x ＝－1和函数y ＝x 2＋1，x ∈[0.＋∞）的图象的公共点可能几个？ 解析：根据图象知没有公共点.⑶直线x ＝a 和函数y ＝x 2＋1，x ∈A 的图象的公共点可能几个？解析：当a ∈A ，则根据图象知有且仅有一个公共点；当a ∉A 时，没有公共点.例6 试画出函数f(x)＝x 2＋1的图象，并根据图象回答下列问题： ⑴比较f(－2),f(1),f(3)的大小；⑵若0＜x 1＜x 2,试比较f(x 1)与f(x 2)的大小.解：函数的图象如下 ⑴根据图象知f(3)＞f(－2)＞f(1),⑵根据图象知，当0＜x 1＜x 2f(x 1)＜f(x 2).思考：在上例⑵中，⑴如果把“0＜x 1＜x 2”改为 “x 1＜x 2＜0”，那么f(x 1)与f(x 2) 哪个大？⑵如果把“0＜x 1＜x 2”改为 “|x 1|＜|x 2|”，那么f(x 1)与f(x 2)哪个大？解析：仍然根据函数的图象，有 ⑴f(x 1)＞f(x 2).⑵∵f(x)的图象关于y 轴对称，∴当|x 1|＜|x 2|时有f(x 1)＜f(x 2). 学生练习P28练习1,2,3 五、回顾反思能用描点法画出常见函数的图象，并能根据函数的图象解决有关问题 六、作业P20习题2.1⑴7,8,9。

2.2 一次函数和二次函数自主整理(1)定义:函数y=kx+b(k≠0)叫做一次函数,又叫线性函数;它定义域为R ,值域为R .(2)性质:①函数改变量y 2-y 1与自变量改变量x 2-x 1比值等于常数k;k 大小表示直线与x 轴倾斜程度; ②当k>0时,一次函数为增函数,当k<0时,一次函数为减函数;③当b=0时,一次函数为正比例函数,是奇函数;当b≠0时,一次函数既不是奇函数也不是偶函数;④直线y=kx+b(k≠0)与x 轴交点为(kb -,0),与y 轴交点为(0,b).(1)定义:函数y=ax 2+bx+c(a≠0)叫做二次函数,它定义域为R .(2)性质:①函数图象是一条抛物线,它顶点坐标为(a b 2-,),它对称轴为x=ab 2-. ②当a>0时,抛物线开口向上,函数在x=a b 2-处取得最小值,在区间(-∞,a b 2-］上是减函数,在区间［ab 2-,+∞)上是增函数. ③当a<0时,抛物线开口向下,函数在x=a b 2-处取得最大值,在区间［a b 2-,+∞)上是减函数,在区间(-∞,ab 2-］上是增函数. ④当二次函数图象对称轴与y 轴重合即b=0时二次函数为偶函数,否那么既不是奇函数也不是偶函数.⑤在y=ax 2(a≠0)中,假设a>0,a 越大,抛物线开口越小,a 越小,抛物线开口越大;反之,假设a<0,a 越大,抛物线开口越大,a 越小,抛物线开口越小.总之,y=ax 2(a≠0)中,假设|a|越大,抛物线开口越小,|a|越小,抛物线开口越大.(3)三种形式:①一般式:f(x)=ax 2+bx+c(a≠0),其中a 是开口方向与大小,c 是y 轴上截距,而a b 2-是对称轴.②顶点式(配方式):f(x)=a(x-h)2+k(a≠0),其中(h,k)是抛物线顶点坐标.h=ab 2 ,k=. ③两根式(因式分解):f(x)=a(x-x 1)(x-x 2)(a≠0),其中x 1、x 2是抛物线与x 轴两个交点横坐标.如果知道一个函数一般形式,可先把所求函数写为一般形式,其中系数待定,然后再根据题设条件求出这些待定系数,这种通过求待定系数来确定变量之间关系式方法称为待定系数法. 高手笔记1.常数函数是较为特殊函数,原因在于在函数解析式y=b 中没有出现自变量x.其实常数函数就是一个多对一映射.注意:当a=0时,函数y=ax 2=0是一个常数函数,其图象即为x 轴.2.式子x=a(a 是一固定常数)虽然含有x,但不能称其为函数,原因在于一个x 对应无穷多个y,不符合函数定义,应将其与y=b 区别开来.3.二次函数是重要根底函数,必须作为重点内容来掌握.应从解析式、定义域、值域、图象、单调性、奇偶性几个方面内容进展把握.4.解决二次函数问题一定要牢牢树立数形结合思想,通过对函数图象分析寻找解决问题思路和分类讨论依据.名师解惑1.如何认识与理解常数函数？剖析:要全面认识一个函数,主要从解析式、定义域、值域、单调性、奇偶性等五个方面来认识,对于常数函数:解析式:当k=0时,y=kx+b 就变成了y=b,这就是常数函数解析式,其中b 是某一固定常数.这个解析式特点在于没有出现自变量x,这也是许多同学对常数函数感到难于理解原因.定义域:自变量x 可以取任意实数.解析式中没有出现x,说明解析式对x 没有要求,可以取任意实数.值域:常数函数值域为{b}.常数函数只有一个函数值b,就是说不管自变量怎么取值,都对应同一个函数值b.图象:因为不管自变量x 取什么值都对应一个函数值b,所以函数图象是平行于x 轴水平直线(特殊情况是x 轴).单调性:因为函数值是固定常数b,没有增减变化,函数图象也是一条水平直线,没有起伏变化,所以常数函数在定义域上没有单调性.奇偶性:定义域为R ,并且f(-x)=f(x)=b,所以一定是偶函数.如果b=0那么既是奇函数又是偶函数.2.如何由函数y=x 2图象变化得到函数y=a·x 2(a≠0)图象？又如何由函数y=ax 2(a≠0)图象变化得到y=a(x+h)2+k(a≠0)图象？再如何由函数y=ax 2(a≠0)图象得到函数y=ax 2+bx+c(a≠0)图象？剖析:(1)二次函数y=a·x 2(a≠0)图象可由y=x 2图象各点纵坐标变为原来a 倍得到,而横坐标保持不变.(2)二次函数y=a(x+h)2+k(a≠0)可由y=ax 2(a≠0)图象向左(或向右)平移|h|个单位,再向上(或下)平移|k|个单位得到.(3)要得到二次函数y=ax 2+bx+c(a≠0)图象,先将其化为y=a(x+h)2+k(a≠0)形式,再通过y=ax 2(a≠0)图象上下左右平移得到.3.二次函数性质常见有哪些综合应用？剖析:(1)关于对称轴问题:假设二次函数f(x)满足f(t+x)=f(t-x),那么f(x)关于直线x=t对称,这一性质对于一般函数也适用.(2)关于二次函数在闭区间上最值问题:当a>0时,f(x)在区间［p,q ］上最大值为M,最小值为m,令x 0=21(p+q). 假设a b 2-<p,那么f(p)=m,f(q)=M; 假设p≤a b 2-<x 0,那么f(ab 2-)=m,f(q)=M; 假设x 0≤a b 2-<q,那么f(p)=M,f(ab 2-)=m; 假设a b 2-≥q,那么f(p)=M,f(q)=m. (3)关于二次方程f(x)=ax 2+bx+c=0实根分布问题:①方程f(x)=0两根中一根比r 大,另一根比r 小a·f(r)<0.②二次方程f(x)=0两根都大于r ⇔③二次方程f(x)=0在区间(p,q)内有两根⇔讲练互动【例题1】方程ax-by+c=0(ab≠0)所对应一次函数,当a 、b 满足什么条件时函数为减函数 分析：首先将直线方程化为一次函数y=kx+b 形式,然后根据k>0时函数为增函数,k<0时函数为减函数,进而求得a 、b 所满足条件,即ab<0. 解：把ax-by+c=0整理,得y=b a x+bc , 要使得一次函数为减函数,那么b a <0,即只要a 、b 异号就可以了. 绿色通道处理一次函数问题常把解析式整理成标准形式,然后再求解.变式训练1.直线mx+(m-2)y=3(m≠2,m≠0)所对应一次函数,当函数为增函数时m 满足条件是( )A.0<mB.m<2C.0<m<2解析：把mx+(m-2)y=3整理,得y=x+,要使得一次函数为增函数,那么>0,即只要-m 、m-2同号就可以了,所以易得0<m<2. 答案：C【例题2】二次函数f(x)=ax 2+(2a-1)x+1在区间［23-,2］上最大值为3,求实数a 值. 分析：这是一个逆向最值问题,假设从求最值入手,需分a>0与a<0两大类五种情形讨论,过程烦琐不堪.假设注意到f(x)最值总是在闭区间端点或抛物线顶点处取到,因此先计算这些点函数值,再检验其真假,过程简明.解：(1)令f()=3,得a=21-. 此时抛物线开口向下,对称轴为x=-2,且-2［23-,2］,故a=21-不合题意. (2)令f(2)=3,得a=21,此时抛物线开口向上,对称轴为x=0,闭区间右端点2距离对称轴远些,故a=21符合题意. (3)假设f(23-)=3,得a=32-,此时抛物线开口向下,对称轴为x=47-,闭区间为单调减区间,所以a=-32符合题意. 综上,a=21或a=32-. 绿色通道此题利用特殊值检验法,先计算特殊点(闭区间端点、抛物线顶点)函数值,再检验其真假,思路明了、过程简洁,是解决逆向型闭区间二次函数最值问题一种有效方法.变式训练2.二次函数y=x 2+2ax-3,x∈［1,2］,试求函数最小值.分析：首先观察到函数图象过(0,-3),再考虑对称轴位置,由于对称轴在不同位置会出现不同结果,所以需要分三种情况讨论.解：y=x 2+2ax-3=(x+a)2-a 2-3,当-a∈(2,+∞),即a<-2时,此时函数在［1,2］上为减函数,故此时最小值为f(2)=4a+1; 当-a∈(-∞,1),即a>-1时,函数最小值为f(1)=2a-2;当-a∈［1,2］,即-2≤a≤-1时,函数最小值为f(-a)=-a 2-3.【例题3】二次函数图象过(0,1)、(2,4)、(3,10)三点,求这个二次函数解析式.分析：是二次函数,且知三个点坐标,所以可以先设出二次函数解析式,用待定系数法求得.解：根据题意设这个二次函数解析式为y=ax 2+bx+c(a≠0),然后将图象所经过三个点坐标分别带入方程,联立三个方程,得解得故f(x)=23x 223-x+1. 绿色通道使用待定系数法解题根本步骤是第一步,设出含有待定系数解析式;第二步,根据恒等条件,列出含待定系数方程或方程组;第三步,解方程或方程组解出待定系数,使问题得到解决.变式训练3.假设f(x)为一次函数,且满足f ［f(x)］=1+2x,那么f(x)解析式为______.解析：f(x)为一次函数,可以使用待定系数法.设f(x)=kx+b,那么f ［f(x)］=f(kx+b)=k(kx+b)+b=k 2x+kb+b,利用对应系数相等即可求得k=2-,b=2--1或k=2,b=2-1.答案：f(x)=2-x 2--1或f(x)=2x+2-14.〔2007黄冈第一次高三诊断试卷,17〕二次函数f(x)满足条件f(0)=1,及f(x+1)-f(x)=2x.(1)求f(x)解析式;(2)求f(x)在[-1,1]上最值.分析：此题求函数解析式根本方法仍然是待定系数法,但确定待定系数方法是根据代数式恒等对应项系数相等来确定.求函数在给定区间上最值时,要注意对称轴位置.解：(1)由f(0)=1,可设f(x)=ax 2+bx+1.那么由f(x+1)-f(x)=2x,可得2ax+a+b=2x.∴a=1,a+b=0,即b=-1.∴f(x)=x 2-x+1.(2)∵f(x)=x 2-x+1=(x 21-)2+43, 又x∈［-1,1］,∴当x=21时有最小值43,x=-1时有最大值3. 【例题4】二次函数f(x)=ax 2+bx+c,a∈N *,c≥1,a+b+c≥1,方程ax 2+bx+c=0有两个小于1不等正根,那么a 最小值为( )B.3C.4解析：由题意有由于方程有两个小于1不等正根,画图可知0<a b 2-<1,即b 2<4a 2. ∴4ac<b 2<4a 2,即a(a-c)>0.又a∈N *,且c≥1,∴a 最小值为2.答案：A绿色通道一般地,一元二次方程根分布情况问题往往从三个角度加以考虑:Δ符号,对称轴是否在区间内,端点函数值正负.变式训练2+2mx+2m+1=0.假设方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m 范围. 分析：二次方程根问题实质上是讨论二次函数图象与x 轴交点与坐标原点位置关系问题,因此,理解交点及二次函数系数(a ——开口方向,a 、b ——对称轴,c ——图象与y 轴交点)几何意义,掌握二次函数图象特点,是解决此类问题关键.解：条件说明抛物线f(x)=x 2+2mx+2m+1与x 轴交点分别在区间(-1,0)和(1,2)内,画出示意图,得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧->-<∈-<⇒⎪⎪⎩⎪⎪⎨⎧>+=<+=>=-<+=.65,21,,21056)2(024)1(02)1(012)0(m m R m m m f m f f m f ∴65-<m<21-. 教材链接1.［探索与研究］设一次函数y=5x-3,取一系列x值,使得每一个x值总是比前一个大2,然后计算对应y值,这一系列函数值之间有什么关系？对任意一个一次函数都有类似性质吗？答:对于一次函数y=5x-3,取一系列x值总是比前一个大2时,那么有与之对应每一个y值总是比前一个大10;对任意一个一次函数y=kx+b(k>0),假设取一系列x值总是比前一个大m 时(m为正整数),那么有与之对应每一个y值总是比前一个大mk.2.［探索与研究］结合课件1207,对一次函数性质进展探索.答:注意强调一次函数定义中一次项系数k≠0这一条件,当k=0时,函数为y=b,它不再是一次函数,它图象是一条与x轴平行直线,通常称为常值函数.函数值改变量y2-y1与自变量改变量x2-x1比值,称作函数x1到x2之间平均变化率,对一次函数来说它是一个常数,等于这条直线斜率.一次函数y=kx+b(k≠0)单调性与一次项系数正负有关,当k>0时,函数为增函数,当k<0时,函数为减函数.理由如下:设x1、x2是任意两个不相等实数,且x1<x2,那么Δx=x2-x1>0,所以Δy=f(x2)-f(x1)=(kx2+b)-(kx1+b)=k(x2-x1)=kΔx.当k>0时,kΔx>0,所以Δy>0,所以f(x)在R上是增函数;当k<0时,同理可证f(x)在R上是减函数.要准确地作出一次函数图象,只要找准图象上两个点即可,这两个点通常是找图象与坐标轴交点.3.［探索与研究］在同一坐标系中,作函数y=x2,y=(x+1)2,y=(x-1)2,y=x2+1,y=x2-1图象,研究它们图象之间关系.答:列表:x …-3 -2 -1 0 1 2 3 …y=x2…9 4 1 0 1 4 9 …y=(x+1)2… 4 1 0 1 4 9 16 …y=(x-1)2…16 9 4 1 0 1 4 …y=x2+1 …10 5 2 1 2 5 10 …y=x2-1 …8 3 0 -1 0 3 8 …在同一坐标系中画出这五个图,如图2-2-1所示:图2-2-1通过图象,可知后四个图象都可以由y=x2通过左右上下平移得到,y=(x+1)2由y=x2向左平移一个单位得到;y=(x-1)2由y=x2向右平移一个单位得到,y=x2+1由y=x2向上平移一个单位得到,y=x 2-1由y=x 2向下平移一个单位得到.4.［探索与研究］二次函数y=ax 2+bx+c=a(x+a b 2)2+中a 、b 、c 对函数性质与图象各有哪些影响？ 答:二次函数y=ax 2+bx+c(a≠0)中系数a 、b 、c 决定着函数图象和性质.(1)二次项系数a 决定了函数图象开口方向、开口大小和单调性,当a>0时,开口向上,a 越大,开口越小,函数在对称轴两侧先减后增.当a<0时,开口向下,a 绝对值越大开口越小,函数在对称轴两侧先增后减.(2)b 是否为零决定着函数奇偶性.当b=0时,函数为偶函数;当b≠0且c≠0时,函数既不是奇函数也不是偶函数.(3)c 是否为零决定着函数图象是否经过原点.另外,a 和b 共同决定着函数对称轴,a 、b 和c 三者共同决定着函数顶点位置.5.［探索与研究］请同学们自己探索研究一下,给定哪些条件,才能求出一个具体二次函数.答:运用待定系数法求二次函数解析式时,一般可设出二次函数一般形式y=ax 2+bx+c(a≠0),但如果函数对称轴或顶点坐标或最值,那么解析式可设为y=a(x-h)2+k 会使求解比拟方便.具体来说:(1)顶点坐标为(m,n),可设为y=a(x-m)2+n,再利用一个独立条件求a;(2)对称轴方程x=m,可设为y=a(x-m)2+k,再利用两个独立条件求a 与k;(3)最大值或最小值为n,可设为y=a(x+h)2+n,再利用两个独立条件求a 与h;(4)二次函数图象与x 轴只有一个交点时,可设为y=a(x+h)2,再利用两个独立条件求a 与h.。

§2.2.1一次函数的性质与图象一、新知导学（课前预习案）1、一次函数的概念：函数 叫做一次函数，它的定义域为R ，值域为 。

2、一次函数(0)y kx b k =+≠的图像是 ，简写为 ，其中k 叫做该直线的 。

b 叫做该直线在y 轴上的 。

一次函数又叫做 。

3、一次函数的性质（1）函数值的改变量 与自变量的改变量12x x x -=∆的比值等于常数 。

（2）当k >0时，一次函数是增函数；当k <0时，一次函数是 。

（3）当 时，一次函数变为正比例函数，是奇函数；当 时，它既不是奇函数也不是偶函数。

（4）直线y kx b =+与x 轴的交点为 ，与y 轴的交点为 。

二、课前自测1.函数y=(2k-1)x+b(k ≠12)在（-∞，+∞）上平均变化率小于零，则k 的取值范围是（ ） A.（-12，12） B.（-∞，-12） C.（-∞，12） D.（12，+∞） 典例分析（课内探究案）例1.已知函数y=(2m-1)x+1-3m ，为何值时，（1）这个函数为正比例函数； （2）这个函数为一次函数；（3）这个函数是减函数； （4）这个函数的图象与直线y=x+1的交点在x 轴上。

例2、如果0,0ab bc ><，那么一次函数0ax by c ++=的图象可能是图中的（ ）A B C D跟进练习： 作函数3y x =-的图象，求：（1）该图象与两条坐标轴交点的坐标；（2）不等式30x ->的解集当堂检测1、一次函数y=mx-2m+3在(0,)+∞上为增函数，且在y 轴上的截距大于0，则m 的取值范围是 。

2、已知函数()f x 是一次函数，且(())98f f x x =+，()f x = 。

3、已知一次函数的图象经过点(3,4),(1,2)A B --。

（1）求这个一次函数的解析式，并画出图象。

（2）求AOB ∆面积课后拓展案：课本P 56练习B.2中国书法艺术说课教案今天我要说课的题目是中国书法艺术，下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。