四川省仁寿一中北校区2021届高三数学9月月考试题理【含答案】

14．现代科学的发展极大地促进了人们对原子、原子核的认识，下列有关原子、原子核的叙述正确的是()A．卢瑟福α粒子散射实验说明原子核内部具有复杂的结构B．轻核聚变反应方程有：21H＋31H→42He＋10nC．天然放射现象表明原子核内部有电子D．氢原子从n＝3能级跃迁到n＝1能级和从n＝2能级跃迁到n＝1能级，前者跃迁辐射出的光子波长比后者的长15．如图所示，质量为m的长木板放在水平地面上，站在木板上的人用斜向右下方的力F推箱子，三者都保持静止．人和箱子的质量也均为m，重力加速度为g.下列说法正确的是()A．人对长木板的压力大小为mgB．长木板对地面的压力大于3mgC．箱子受到的摩擦力的方向水平向左D．地面对长木板的摩擦力的方向水平向左16．在2018年5月5日世乒赛上，中国队再次夺冠，马龙实现男单七连冠．假设马龙发球过程为：他首先竖直向上抛出乒乓球，然后让乒乓球落回抛出位置时，再用球拍击打；若选向上为正方向，空气阻力大小不变，则乒乓球在空中运动的v－t图像正确的是()17．用传感器研究质量为2kg的物体由静止开始做直线运动的规律时，在计算机上得到0～6s内物体的加速度随时间变化的关系如图所示．下列说法正确的是()A．0～6s内物体先向正方向运动，后向负方向运动B．0～6s内物体在4s时的速度最大C．物体在2～4s时的速度不变D．0～4s内合力对物体做的功等于0～6s内合力对物体做的功18．如图所示，一可视为质点的物体以某一速度冲上一光滑斜面，前4s的位移为16m，随后4s的位移为零，已知斜面足够长，关于物体的运动，下列说法正确的是()A．物体在后4s保持静止B．物体一直做匀减速直线运动C．物体的加速度大小为a＝1m/s2D．斜面倾角为30°19．下列四幅图的说法中，正确的是()甲乙0246510v /ms -1t /sA ．图a 所示，α粒子散射实验证实了汤姆孙原子枣糕模型的正确性B ．图b 可知，在光颜色保持不变的情况下，入射光越强，饱和光电流越大C ．图c 所示，放射线丙由α粒子组成，每个粒子带电荷量为＋2eD ．图d 所示，该链式反应属于原子核的聚变反应20．甲、乙两个物体从同一地点沿同一方向做直线运动的v －t 图象如图所示，则()A ．t ＝2s 时两物体相距最远B ．t ＝4s 时甲在乙的前面C ．两个物体两次相遇的时刻是2s 末和6s 末D ．t ＝2s 之前甲在前面，2s<t<6s 乙在前面21．如图所示，水平细杆上套一细环A ，环A 与球B 间用一轻质绳相连，质量分别为m A 、m B ，由于B 球受到水平恒力F 的作用，A 环与B 球一起向右匀速运动，绳与竖直方向的夹角为θ.则下列说法正确的是（）A ．B 球受到的恒力F 大小为m A g tan θB ．A 环与杆的动摩擦因数为θtan BA B m m m +C ．力F 逐渐增大，杆对A 环的弹力保持不变D ．力F 逐渐增大，绳对B 球的拉力保持不变第Ⅱ卷（非选择题共174分）三、非选择题：本卷包括必考题和选考题两部分。

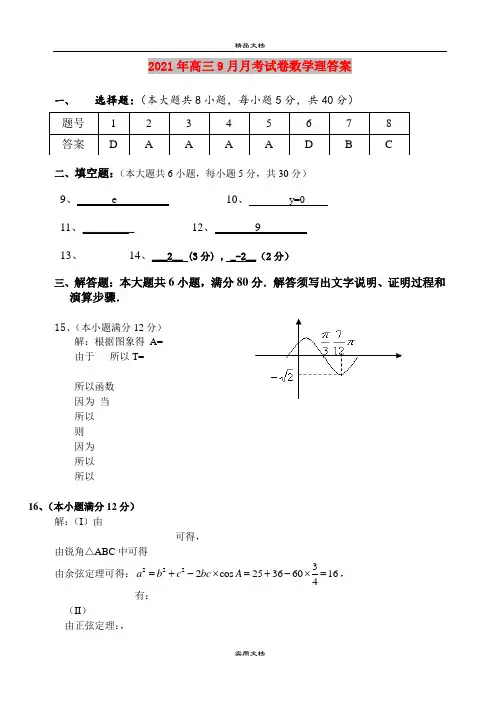
2021年高三9月月考试卷数学理答案一、选择题：（本大题共8小题，每小题5分，共40分）二、填空题：（本大题共6小题，每小题5分，共30分）9、 e 10、 y=011、_________ 12、 913、 14、___2__ (3分) , _-2__（2分）三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 15、（本小题满分12分）解：根据图象得 A=由于 所以T=所以函数 因为 当 所以 则 因为 所以 所以16、（本小题满分12分）解：（I ）由可得，由锐角△ABC 中可得由余弦定理可得：22232cos 253660164a b c bc A =+-⨯=+-⨯=， 有：（II ）由正弦定理：，题号 1 2 3 4 5 6 7 8 答案DAAAADBC即17、 （本小题满分14分） (1)（2）因为 所以的最小正周期为 (3）因为 于是，当时，取得最大值2； 当取得最小值—1.18、（本小题满分14分）解：（I ）因为x=5时，y=11，所以（II ）由（I ）可知，该商品每日的销售量 所以商场每日销售该商品所获得的利润222()(3)[10(6)]210(3)(6),363f x x x x x x x =-+-=+--<<- 从而，2'()10[(6)2(3)(6)]30(4)(6)f x x x x x x =-+--=--所以，当x=4时，函数取得最大值，且最大值等于42。

答：当销售价格为4元/千克时，商场每日销售该商品所获得的利润最大。

19、(本小题满分14分)【解】（Ⅰ）当时，，．，．所以曲线在点（2，3）处的切线方程为，即． （Ⅱ）．令，解得或．针对区间，需分两种情况讨论： (1) 若．则,所以在区间上的最小值在区间的端点得到．因此在区间上，恒成立，等价于10,210,2f f ⎧⎛⎫-> ⎪⎪⎪⎝⎭⎨⎛⎫⎪> ⎪⎪⎝⎭⎩ 即解得，又因为，所以． (2) 若 ．则 当变化时，的变化情况如下表：所以在区间上的最小值在区间的左端点或处得到．因此在区间上，恒成立，等价于 10,210,f f a ⎧⎛⎫-> ⎪⎪⎪⎝⎭⎨⎛⎫⎪> ⎪⎪⎝⎭⎩ 即解得或，又因为，所以．综上所述：20、(本小题满分14分)解：（1）当221,()(1),'()()x x a x x x e x e x x --=Φ=++Φ=-+时.∴的单调递增区间为（0，1），单调递减区间为：，.（2）切线的斜率为，∴ 切线方程为. （图略） 所求封闭图形面积为1121000111[(1)](1)()|22x x x S e x dx e x dx e x x e---=--+=+-=-+-=-⎰⎰.（3）22'()(2)()[(2)]x x x x x a e e x ax a e x a x ---Φ=+-++=-+-， 令.设，∴上是增函数∴ ，即，∴不存在实数a ，使极大值为3.综上所述：不存在实数a ，使极大值为3.35036 88DC 補21556 5434 吴N-39863 9BB7 鮷1j)23789 5CED 峭33335 8237 舷j25298 62D2拒 23874 5D42 嵂。

四川省仁寿一中北校区2021届高三理综9月月考试题第Ⅰ卷（选择题共126分）可能用到的相对原子质量：H-1 C-12 O-16 Ni-59 Cu-64 Zn-65一、选择题：本题共13小题，每小题6分，共78分．在每小题给出的四个选项中，只有一项符合题目要求．1.下列关于人类性别决定与伴性遗传的叙述，正确的是（）A. 性染色体上的基因都与性别决定有关B. 性染色体上的基因都伴随性染色体遗传C. 生殖细胞中只表达性染色体上的基因D. 初级精母细胞和次级精母细胞中都含Y 染色体2.如图表示人体唾液腺细胞中的某生理过程，下列有关说法错误．．的是（）A．图中的②与⑥是同种物质B．若②中A+U占36％，则①对应片段中G占32％C．图中的⑤可能对淀粉水解起催化作用D．图中④携带的氨基酸对应的密码子为UCA3.玉米(2n=20)花药离体培养的单倍体幼苗，经秋水仙素处理后形成二倍体植株。

下图是该诱导过程某时段细胞中核DNA含量变化示意图，相关叙述错误．．的是( )A．c-d过程中细胞内发生了染色体数目加倍B．a-b过程中细胞不会发生基因重组C．c点后细胞内各染色体组的基因组成相同D．f-g过程中同源染色体分离，细胞内染色体数目减半4.下图中a、b、c表示一条染色体的一个DNA分子上相邻的3个基因，m、n为不具有遗传效应的DNA 片段。

下列相关叙述错误．．的是（）A. 基因a、b、c中若发生碱基对的增添、缺失、替换，必然导致a、b、c基因分子结构改变B. m、n片段中发生碱基对的增添、缺失、替换不属于基因突变C. 基因a、b、c均可能发生基因突变，体现了基因突变具有普遍性D. 在生物个体发育的不同时期，基因a、b、c不一定都能表达5.盐酸吗啉胍(又名病毒灵，英文缩写ABOB)能抑制病毒的DNA和RNA聚合酶的活性，从而抑制病毒增殖。

下列叙述正确的是（）A. DNA病毒增殖时，DNA中碱基之间的氢键会发生断裂B. 在RNA聚合酶的作用下，脱氧核糖核苷酸依次连接形成RNAC. 可通过向普通培养基中添加适量的ABOB试剂培养病毒，进而研究ABOB对病毒增殖的抑制作用D. ABOB作用于基因表达的翻译阶段，从而抑制病毒的增殖6.右图为某种动物性染色体结构简图，要判断某伴性遗传基因位于片段Ⅰ上还是片段Ⅱ-2.现用一只隐性雌性个体与一只显性雄性个体杂交，不考虑突变。

2024~2025学年高三第一次联考（月考）试卷数学考生注意：1.本试卷分选择题和非选择题两部分.满分150分，考试时间120分钟.2.答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.3.考生作答时，请将答案答在答题卡上.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷､草稿纸上作答无效.4.本卷命题范围：集合､常用逻辑用语､不等式､函数､导数及其应用.一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合，，则集合的真子集的个数为（）{}4,3,2,0,2,3,4A =---{}2290B x x =-≤A B ⋂A.7B.8C.31D.322.已知，，则“，”是“”的（ ）0x >0y >4x ≥6y ≥24xy ≥A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件3.国家速滑馆又称“冰丝带”，是北京冬奥会的标志性场馆，拥有亚洲最大的全冰面设计，但整个系统的碳排放接近于零，做到了真正的智慧场馆､绿色场馆，并且为了倡导绿色可循环的理念，场馆还配备了先进的污水､雨水过滤系统，已知过滤过程中废水的污染物数量与时间（小时）的关系为()mg /L N t （为最初污染物数量，且）.如果前4个小时消除了的污染物，那么污染物消0e kt N N -=0N 00N >20%除至最初的还需要（ ）64%A.3.8小时 B.4小时C.4.4小时D.5小时4.若函数的值域为，则的取值范围是（）()()2ln 22f x x mx m =-++R m A.B.()1,2-[]1,2-C.D.()(),12,-∞-⋃+∞(][),12,-∞-⋃+∞5.已知点在幂函数的图象上，设，(),27m ()()2n f x m x =-(4log a f =，，则，，的大小关系为（ ）()ln 3b f =123c f -⎛⎫= ⎪⎝⎭a b c A.B.c a b <<b a c<<C. D.a c b <<a b c<<6.已知函数若关于的不等式的解集为，则的()()2e ,0,44,0,x ax xf x x a x a x ⎧->⎪=⎨-+-+≤⎪⎩x ()0f x ≥[)4,-+∞a 取值范围为（ ）A.B. C. D.(2,e ⎤-∞⎦(],e -∞20,e ⎡⎤⎣⎦[]0,e 7.已知函数，的零点分别为，，则（ ）()41log 4xf x x ⎛⎫=- ⎪⎝⎭()141log 4xg x x ⎛⎫=- ⎪⎝⎭a b A. B.01ab <<1ab =C.D.12ab <<2ab ≥8.已知，，，且，则的最小值为（ ）0a >0b >0c >30a b c +-≥6b a a b c ++A. B. C. D.29495989二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.下列说法正确的是（ ）A.函数是相同的函数()f x =()g x =B.函数6()f x =C.若函数在定义域上为奇函数，则()313xx k f x k -=+⋅1k =D.已知函数的定义域为，则函数的定义域为()21f x +[]1,1-()f x []1,3-10.若，且，则下列说法正确的是（）0a b <<0a b +>A. B.1a b >-110a b+>C. D.22a b <()()110a b --<11.已知函数，则下列说法正确的是（ ）()()3233f x x x a x b=-+--A.若在上单调递增，则的取值范围是()f x ()0,+∞a (),0-∞B.点为曲线的对称中心()()1,1f ()y f x =C.若过点可作出曲线的三条切线，则的取值范围是()2,m ()()3y f x a x b =+-+m ()5,4--D.若存在极值点，且，其中，则()f x 0x ()()01f x f x =01x x ≠1023x x +=三､填空题：本题共3小题，每小题5分，共15分.12.__________.22lg 2lg3381527log 5log 210--+⋅+=13.已知函数称为高斯函数，表示不超过的最大整数，如，，则不等式[]y x =x []3.43=[]1.62-=-的解集为__________；当时，的最大值为__________.[][]06x x <-0x >[][]29x x +14.设函数，若，则的最小值为__________.()()()ln ln f x x a x b =++()0f x ≥ab 四､解答题：本题共5小题､共77分.解答应写出文字说明､证明过程或演算步骤.15.（本小题满分13分）已知全集，集合，.U =R {}231030A x x x =-+≤{}220B x xa =+<（1）若，求和；8a =-A B ⋂A B ⋃（2）若，求的取值范围.()UA B B ⋂= a 16.（本小题满分15分）已知关于的不等式的解集为.x 2280ax x --<{}2x x b-<<（1）求，的值；a b （2）若，，且，求的最小值.0x >2y >-42a bx y +=+2x y +17.（本小题满分15分）已知函数.()()()211e 2x f x x ax a =--∈R （1）讨论的单调性；()f x （2）若对任意的恒成立，求的取值范围.()e x f x x ≥-[)0,x ∈+∞a 18.（本小题满分17分）已知函数是定义在上的奇函数.()22x xf x a -=⋅-R（1）求的值，并证明：在上单调递增；a ()f x R （2）求不等式的解集；()()23540f x x f x -+->（3）若在区间上的最小值为，求的值.()()442x x g x mf x -=+-[)1,-+∞2-m 19.（本小题满分17分）已知函数.()()214ln 32f x x a x x a =---∈R （1）若，求的图像在处的切线方程；1a =()f x 1x =（2）若恰有两个极值点，.()f x 1x ()212x x x <（i ）求的取值范围；a （ii ）证明：.()()124ln f x f x a+<-数学一参考答案､提示及评分细则1.A 由题意知，又，所以{}2290B x x ⎡=-=⎢⎣∣ {}4,3,2,0,2,3,4A =---，所以的元素个数为3，真子集的个数为.故选.{}2,0,2A B ⋂=-A B ⋂3217-=A 2.A 若，则，所以“”是“”的充分条件；若，满足4,6x y 24xy 4,6x y 24xy 1,25x y ==，但是，所以“”不是“”的必要条件，所以“”是24xy 4x <4,6x y 24xy 4,6x y “”的充分不必要条件.故选A.24xy 3.B 由题意可得，解得，令，可得4004e 5N N -=44e 5k -=20004e 0.645t N N N -⎛⎫== ⎪⎝⎭，解得，所以污染物消除至最初的还需要4小时.故选B.()248e e ek kk---==8t =64%4.D 依题意，函数的值域为，所以，解得()()2ln 22f x x mx m =-++R ()2Δ(2)420m m =--+ 或，即的取值范围是.故选D.2m 1m - m ][(),12,∞∞--⋃+5.C 因为是軍函数，所以，解得，又点在函数的图()()2nf x m x =-21m -=3m =()3,27()n f x x =象上，所以，解得，所以，易得函数在上单调递增，又273n=3n =()3f x x =()f x (),∞∞-+，所以.故选C.1241ln3lne 133log 2log 2->==>=>=>a c b <<6.D 由题意知，当时，；当时，；当时，(),4x ∞∈--()0f x <[]4,0x ∈-()0f x ()0,x ∞∈+.当时，，结合图象知；当时，，当()0f x 0x ()()()4f x x x a =-+-0a 0x >()e 0x f x ax =- 时，显然成立；当时，，令，所以，令，解0a =0a >1e x x a (),0e x x g x x =>()1e xxg x -='()0g x '>得，令0，解得，所以在上单调递增，在上单调递减，所以01x <<()g x '<1x >()g x ()0,1()1,∞+，所以，解得综上，的取值范围为.故选D.()max 1()1e g x g ==11e a0e a < a []0,e 7.A 依题意得，即两式相减得4141log ,41log ,4a b a b ⎧⎛⎫=⎪ ⎪⎝⎭⎪⎨⎛⎫⎪= ⎪⎪⎝⎭⎩441log ,41log ,4a ba b ⎧⎛⎫=⎪ ⎪⎪⎝⎭⎨⎛⎫⎪-= ⎪⎪⎝⎭⎩.在同一直角坐标系中作出的图()44411log log log 44a ba b ab ⎛⎫⎛⎫+==- ⎪ ⎪⎝⎭⎝⎭4141log ,log ,4xy x y x y ⎛⎫=== ⎪⎝⎭象，如图所示：由图象可知，所以，即，所以.故选A.a b >1144ab⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭()4log 0ab <01ab <<8.C 因为，所以，所以30a b c +- 30a b c +> 11911121519966399939911b a b a b b b b a b c a b a b a a a a ⎛⎫++=+=++--=-= ⎪+++⎝⎭++ ，当且仅当，即时等号成立，所以的最小值为.故选C.1911991b b a a ⎛⎫+= ⎪⎝⎭+29b a =6b aa b c ++599.AD 由解得，所以，由，解得10,10x x +⎧⎨-⎩ 11x - ()f x =[]1,1-210x -，所以的定义域为，又，故函数11x - ()g x =[]1,1-()()f x g x ===与是相同的函数，故A 正确；，()f x ()g x ()6f x ==当且仅当方程无解，等号不成立，故B 错误；函数=2169x +=在定义域上为奇函数，则，即，即()313x x k f x k -=+⋅()()f x f x -=-331313x xx x k k k k ----=-+⋅+⋅，即，整理得，即，()()33313313x x xxxxk k k k ----=-+⋅+⋅313313x x x x k kk k ⋅--=++⋅22919x x k k ⋅-=-()()21910x k -+=所以，解得.当时，，该函数定义域为，满足，210k -=1k =±1k =()1313xx f x -=+R ()()f x f x -=-符合题意；当时，，由可得，此时函数定义域为1k =-()13311331x x xxf x --+==--310x -≠0x ≠，满足，符合题意.综上，，故C 错误；由，得{}0x x ≠∣()()f x f x -=-1k =±[]1,1x ∈-，所以的定义域为，故D 正确.故选AD.[]211,3x +∈-()f x []1,3-10.AC 因为，且，所以，所以，即，故A 正确；0a b <<0a b +>0b a >->01a b <-<10ab -<<因为，所以，故В错误；因为，所以，0,0b a a b >->+>110a ba b ab ++=<0a b <<,a a b b =-=由可得，所以，故C 正确；因为当，此时，故0a b +>b a >22a b <11,32a b =-=()()110a b -->D 错误.故选AC.11.BCD 若在上单调递增，则在上佰成立，所以()f x ()0,∞+()23630f x x x a '=-+- ()0,x ∞∈+，解得，即的取值范围是，故A 错误；因为()min ()13630f x f a '==--'+ 0a a (],0∞-，所以，又()()32333(1)1f x x x a x b x ax b =-+--=---+()11f a b =--+，所以点()()()332(21)21(1)1222f x f x x a x b x ax b a b -+=-----++---+=--+为曲线的对称中心，故B 正确；由题意知，所以()()1,1f ()y f x =()()3233y f x a x b xx =+-+=-，设切点为，所以切线的斜率，所以切线的方程为236y x x =-'()32000,3x x x -20036k x x =-，所以，整理得()()()3220000336y x x x x x x --=--()()()322000003362m xx x x x --=--.记，所以3200029120x x x m -++=()322912h x x x x m =-++()26h x x '=-，令，解得或，当时，取得极大值，当时，1812x +()0h x '=1x =2x =1x =()h x ()15h m =+2x =取得极小值，因为过点可作出曲线的三条切线，所以()h x ()24h m=+()2,m ()()3y f x a x b =+-+解得，即的取值范围是，故C 正确；由题意知()()150,240,h m h m ⎧=+>⎪⎨=+<⎪⎩54m -<<-m ()5,4--，当在上单调递增，不符合题意；当，()223633(1)f x x x a x a =-+-=--'()0,a f x (),∞∞-+0a >令，解得，令，解得在()0f x '>1x <-1x >+()0f x '<11x -<<+()f x 上单调递增，在上单调递堿，在上单调递增，因为,1∞⎛- ⎝1⎛+ ⎝1∞⎛⎫+ ⎪ ⎪⎝⎭存在极值点，所以.由，得，令，所以，()f x 0x 0a >()00f x '=()2031x a-=102x x t+=102x t x =-又，所以，又，()()01f x f x =()()002f x f t x =-()()32333(1)1f x x x a x b x ax b =-+--=---+所以，又，所以()()()330000112121x ax b t x a t x b ---+=-----+()2031x a-=，化简得()()()()()()()322320000000013112121312x x x b x x b t x x t x b----=----=------，又，所以，故D 正确.故选BCD.()()20330t x t --=010,30x x x t ≠-≠103,23t x x =+=12. 由题意知10932232862log 184163381255127log 5log 210log 5log 121027---⎛⎫+⋅+=+⋅-+ ⎪⎝⎭62511411410log 5log 2109339339=-⋅+=-+=13.（2分）（3分） 因为，所以，解得，又函数[)1,616[][]06x x <-[][]()60x x -<[]06x <<称为高斯函数，表示不超过的最大整数，所以，即不等式的解集为.当[]y x =x 16x < [][]06x x <-[)1,6时，，此时；当时，，此时01x <<[]0x =[]2[]9x x =+1x []1x ，当且仅当3时等号成立.综上可得，当时，的[][][]2119[]96x x x x ==++[]x =0x >[]2[]9x x +最大值为.1614. 由题意可知：的定义域为，令，解得令，解21e -()f x (),b ∞-+ln 0x a +=ln ;x a =-()ln 0x b +=得.若，当时，可知，此时，不合题1x b =-ln a b -- (),1x b b ∈--()ln 0,ln 0x a x b +>+<()0f x <意；若，当时，可知，此时，不合ln 1b a b -<-<-()ln ,1x a b ∈--()ln 0,ln 0x a x b +>+<()0f x <题意；若，当时，可知，此时；当ln 1a b -=-(),1x b b ∈--()ln 0,ln 0x a x b +<+<()0f x >时，可知，此时，可知若，符合题意；若[)1,x b ∞∈-+()ln 0,ln 0x a x b ++ ()0f x ln 1a b -=-，当时，可知，此时，不合题意.综上所ln 1a b ->-()1,ln x b a ∈--()ln 0,ln 0x a x b +<+>()0f x <述：，即.所以，令，所以ln 1a b -=-ln 1b a =+()ln 1ab a a =+()()ln 1h x x x =+，令，然得，令，解得，所以在()ln 11ln 2h x x x '=++=+()0h x '<210e x <<()0h x '>21e x >()h x 上单调递堿，在上单调递增，所以，所以的最小值为.210,e ⎛⎫ ⎪⎝⎭21,e ∞⎛⎫+ ⎪⎝⎭min 2211()e e h x h ⎛⎫==- ⎪⎝⎭ab 21e -15.解：（1）由题意知，{}2131030,33A x x x ⎡⎤=-+=⎢⎥⎣⎦∣ 若，则，8a =-{}()22802,2B x x =-<=-∣所以.(]1,2,2,33A B A B ⎡⎫⋂=⋃=-⎪⎢⎣⎭（2）因为，所以，()UA B B ⋂= ()UB A ⊆ 当时，此时，符合题意；B =∅0a 当时，此时，所以，B ≠∅0a <{}220Bx x a ⎛=+<= ⎝∣又，U A ()1,3,3∞∞⎛⎫=-⋃+ ⎪⎝⎭13解得.209a -< 综上，的取值范围是.a 2,9∞⎡⎫-+⎪⎢⎣⎭16.解：（1）因为关于的不等式的解集为，x 2280ax x --<{2}xx b -<<∣所以和是关于的方程的两个实数根，且，所以2-b x 2280ax x --=0a >22,82,b a b a⎧=-⎪⎪⎨⎪-=-⎪⎩解得.1,4a b ==（2）由（1）知，所以1442x y +=+()()()221141422242241844242y xx y x y x y x y y x ⎡⎤+⎛⎫⎡⎤+=++-=+++-=+++-⎢⎥ ⎪⎣⎦++⎝⎭⎣⎦，179444⎡⎢+-=⎢⎣ 当且仅当，即时等号成立，所以.()2242y x y x +=+x y ==2x y +74-17.解：（1）由题意知，()()e e x x f x x ax x a=-=-'若，令.解得，令，解得，所以在上单调递琙，在0a ()0f x '<0x <()0f x '>0x >()f x (),0∞-上单调递增.()0,∞+若，当，即时，，所以在上单调递增；0a >ln 0a =1a =()0f x ' ()f x (),∞∞-+当，即时，令，解得或，令，解得，ln 0a >1a >()0f x '>0x <ln x a >()0f x '<0ln x a <<所以在上单调递增，在上单调递减，在上单调递增；()f x (),0∞-()0,ln a ()ln ,a ∞+当，即时，令，解得或，令，解得，ln 0a <01a <<()0f x '>ln x a <0x >()0f x '<ln 0a x <<所以在上单调递增，在上单调递减，在上单调递增.()f x (),ln a ∞-()ln ,0a ()0,∞+综上，当时，在上单调递减，在上单调递增；当时，在0a ()f x (),0∞-()0,∞+01a <<()f x 上单调递增，在上单调递减，在上单调递增当时，在上(,ln )a ∞-()ln ,0a ()0,∞+1a =()f x (),∞∞-+单调递增；当时，在上单调递增，在上单调递减，在上单调递增.1a >()f x (),0∞-()0,ln a ()ln ,a ∞+（2）若对任意的恒成立，即对任意的恒成立，()e xf x x - [)0,x ∞∈+21e 02xx ax x -- [)0,x ∞∈+即对任意的恒成立.1e 102x ax -- [)0,x ∞∈+令，所以，所以在上单调递增，当()1e 12x g x ax =--()1e 2x g x a=-'()g x '[)0,∞+，即时，，所以在上单调递增，所以()10102g a =-' 2a ()()00g x g '' ()g x [)0,∞+，符合题意；()()00g x g = 当，即时，令，解得，令，解得，所()10102g a =-<'2a >()0g x '>ln 2a x >()0g x '<0ln 2a x < 以在上单调递减，()g x 0,ln 2a ⎡⎫⎪⎢⎣⎭所以当时，，不符合题意.0,ln 2a x ⎛⎫∈ ⎪⎝⎭()()00g x g <=综上，的取值范围是.a (],2∞-18.（1）证明：因为是定义在上的奇函数，所以，()f x R ()010f a =-=解得，所以，1a =()22x xf x -=-此时，满足题意，所以.()()22x x f x f x --=-=-1a =任取，所以12x x <，()()()()211122121211122222122222222122x x x x x x x x x x x x f x f x x x --⎛⎫--=---=--=-+ ⎪++⎝⎭又，所以，即，又，12x x <1222x x <12220x x -<121102x x ++>所以，即，所以在上单调递增.()()120f x f x -<()()12f x f x <()f x R （2）解：因为，所以，()()23540f x x f x -+->()()2354f x x f x ->--又是定义在上的奇函数，所以，()f x R ()()2354f x x f x ->-+又在上单调递增，所以，()f x R 2354x x x ->-+解得或，即不等式的解集为.2x >23x <-()()23540f x x f x -+->()2,2,3∞∞⎛⎫--⋃+ ⎪⎝⎭（3）解：由题意知，令，()()()44244222xxxxxxg x mf x m ---=+-=+--322,,2x x t t ∞-⎡⎫=-∈-+⎪⎢⎣⎭所以，所以.()2222442x xxxt --=-=+-()2322,,2y g x t mt t ∞⎡⎫==-+∈-+⎪⎢⎣⎭当时，在上单调递增，所以32m -222y t mt =-+3,2∞⎡⎫-+⎪⎢⎣⎭，解得，符合题意；2min317()323224g x m m ⎛⎫=-++=+=- ⎪⎝⎭2512m =-当时，在上单调递减，在上单调递增，32m >-222y t mt =-+3,2m ⎛⎫- ⎪⎝⎭(),m ∞+所以，解得或（舍）.222min ()2222g x m m m =-+=-=-2m =2m =-综上，的值为或2.m 2512-19.（1）解：若，则，所以，1a =()214ln 32f x x x x =---()14f x x x =--'所以，又，()14112f =--='()1114322f =--=所以的图象在处的切线方程为，即.()f x 1x =()1212y x -=-4230x y --=（2）（i ）解：由题意知，()22444a x a x x x af x x x x x '---+=--==-又函数恰有两个极值点，所以在上有两个不等实根，()f x ()1212,x x x x <240x x a -+=()0,∞+令，所以()24h x x x a =-+()()00,240,h a h a ⎧=>⎪⎨=-<⎪⎩解得，即的取值范围是.04a <<a ()0,4（ii ）证明：由（i ）知，，且，12124,x x x x a +==04a <<所以()()2212111222114ln 34ln 322f x f x x a x x x a x x ⎛⎫⎛⎫+=---+--- ⎪ ⎪⎝⎭⎝⎭()()()2212121214ln ln 62x x a x x x x =+-+-+-，()()()21212121214ln 262x x a x x x x x x ⎡⎤=+--+--⎣⎦()116ln 1626ln 22a a a a a a =----=-+要证，即证，只需证.()()124ln f x f x a+<-ln 24ln a a a a -+<-()1ln 20a a a -+-<令，所以，()()()1ln 2,0,4m a a a a a =-+-∈()11ln 1ln a m a a a a a -=-++=-'令，所以，所以即在上单调递减，()()h a m a ='()2110h a a a =--<'()h a ()m a '()0,4又，所以，使得，即，()()1110,2ln202m m '-'=>=<()01,2a ∃∈()00m a '=001ln a a =所以当时，，当时，，所以在上单调递增，在()00,a a ∈()0m a '>()0,4a a ∈()0m a '<()m a ()00,a 上单调递减，所以.()0,4a ()()()max 00000000011()1ln 2123m a m a a a a a a a a a ==-+-=-+-=+-令，所以，所以在上单调递增，所以()()13,1,2u x x x x =+-∈()2110u x x =->'()u x ()1,2，所以，即，得证.()000111323022u a a a =+-<+-=-<()0m a <()()124ln f x f x a +<-。

卜人入州八九几市潮王学校仁寿一中等西南四八校2021届高三数学9月份联考试题理〔含解析〕一、选择题：在每一小题给出的四个选项里面，只有一项为哪一项哪一项符合题目要求的。

{}24A x x =<，{}2,1,0,1B =--，那么AB =〔〕A.{}0,1B.{}1,0,1-C.{}2,1,0--D.{}2,1,0,1--【答案】B 【解析】 【分析】先计算得到集合A ，再计算A B 得到答案.【详解】{}{}24=-22A x x x x =<<<故答案选B【点睛】此题考察了集合的交集，属于根底题型. 2.()()131i i +-=〔〕A.42i +B.24i +C.22i -+D.22i -【答案】A 【解析】 【分析】把复数乘积展开，化简为a +bi 〔a 、b ∈R 〕的形式，可以判断选项． 【详解】∵〔1+3i 〕〔1-i 〕＝1+3+3i-i ＝4+2i 应选：A ．【点睛】此题考察复数代数形式的运算，是根底题．x ∈R ，那么“21x <〞是“31x <〞的〔〕A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】 【分析】求出不等式的等价形式，结合充分条件和必要条件的定义进展判断即可． 【详解】由2x<1得x<0，由“x 3<1〞得x ＜1，x<0是x ＜1的充分不必要条件 那么“2x<1〞是“x 3<1〞的充分不必要条件， 应选：A ．【点睛】此题主要考察充分条件和必要条件的判断，结合不等式的关系是解决此题的关键．p ：0x ∀>，lg 0x >，那么p ⌝是〔〕A.0x ∀>，lg 0x ≤B.00x ∃>，0lg 0x < C.0x ∀>，lg 0x < D.00x ∃>，0lg 0x ≤【答案】D 【解析】 【分析】p ：∀x ＞0，总有lgx ＞0， p 为：∃x 0＞0，使得lg x 0≤0，应选：D ．{}n a 中，242a a +=，53a =，那么{}n a 的前6项和为〔〕A.6B.9C.10D.11【答案】B 【解析】 【分析】利用等差数列{a n }通项公式列方程组求出a 1，d ，由此能求出{a n }的前6项和． 【详解】∵在等差数列{a n }中，a 53=，a 2+a 4＝2，∴1111433242a d a d a d a d +=⎧⎨+++=+=⎩，解得a 11=-，d 1=， ∴{a n }的前6项和S 6的值：616562S a d ⨯=+=61⨯-+（）15×19=． 应选B ．【点睛】此题考察等差数列的前n 项和的公式，考察等差数列的通项公式的应用，考察运算求解才能，是根底题．()()506f x x πωω⎛⎫=+> ⎪⎝⎭的局部图像，假设AB 4=，那么()1f -=〔〕A.-1B.1C.32-D.32【答案】D 【解析】 【分析】 由图可设A 〔a，那么B 〔a 2T +，AB =〔2T，，利用向量模的坐标运算，求得T 2πω==4，从而可得ω的值，代入x=-1计算可得结果．【详解】设A 〔a，函数f 〔x〕=〔ωx +56π〕的周期为T ，那么B 〔a 2T+，，∴AB =〔2T ，224T =+12=16， ∴T 2＝16， ∴T 2πω==4，解得：ω2π=．∴f 〔x 〕=〔2πx +56π〕，∴f 〔-1〕32=， 应选：D ．【点睛】此题考察函数y ＝A sin 〔ωx +φ〕的图象解析式确实定及应用，涉及向量模的坐标运算及其应用，属于中档题．7.()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.假设(1)2f =，那么(1)(2)(3)(50)f f f f ++++=〔〕A.50-B.0C.2D.50【答案】C 【解析】分析：先根据奇函数性质以及对称性确定函数周期，再根据周期以及对应函数值求结果. 详解：因为()f x 是定义域为(,)-∞+∞的奇函数，且(1)(1)f x f x -=+，所以(1)(1)(3)(1)(1)4f x f x f x f x f x T +=--∴+=-+=-∴=, 因此(1)(2)(3)(50)12[(1)(2)(3)(4)](1)(2)f f f f f f f f f f ++++=+++++，因为(3)(1)(4)(2)f f f f =-=-，，所以(1)(2)(3)(4)0f f f f +++=，(2)(2)(2)(2)0f f f f =-=-∴=，从而(1)(2)(3)(50)(1)2f f f f f ++++==，选C.点睛：函数的奇偶性与周期性相结合的问题多考察求值问题，常利用奇偶性及周期性进展变换，将所求函数值的自变量转化到解析式的函数定义域内求解．8.522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为A.10B.20C.40D.80【答案】C 【解析】分析：写出103152r rr r T C x -+=，然后可得结果详解：由题可得()5210315522rrrr r rr T Cx C x x --+⎛⎫== ⎪⎝⎭令103r 4-=,那么r 2=所以22552240rr C C =⨯=应选C.点睛：此题主要考察二项式定理，属于根底题。

高三9月月考（数学）（考试总分：150 分）一、 单选题 （本题共计12小题，总分60分）1.（5分）1．已知集合A ＝{x |log 2(x －1)＜0}，B ＝{x |x ≤3}，则∁R A ∩B ＝( )A ．(－∞，1)B ．(2，3)C ．(2，3]D ．(－∞，1]∪[2，3]2.（5分）2．已知i 为虚数单位，且复数z 满足z －2i ＝11－i ，则复数z 在复平面内的点到原点的距离为( )A.132B.262C.102 D.523.（5分）3．已知x 、y 取值如下表：x 0 1 4 5 6 8 y1.3m5.66.17.49.3 从所得的散点图分析可知：y 与x 线性相关，且y ＝0.95x ＋1.45，则m ＝( ) A ．1.5 B ．1.55 C ．1.8 D ．3.54.（5分）4已知cos ⎝ ⎛⎭⎪⎫α＋π2＝35，－π2<α<π2，则sin 2α的值等于( )A.1225 B ．－1225 C ．－2425 D .24255.（5分） 5．已知互不重合的直线a ，b ，互不重合的平面α，β，给出下列四个命题，错误的命题是( )A ．若a ∥α，a ∥β，α∩β＝b ，则a ∥bB ．若α⊥β，a ⊥α，b ⊥β则a ⊥bC ．若α⊥β，α⊥γ，β∩γ＝a ，则a ⊥αD ．若α∥β，a ∥α，则a ∥β 6.（5分）6．“a ≤－2”是“函数f (x )＝|x －a |在[－1，＋∞)上单调递增”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件7.（5分）7．已知O 为△ABC 内一点，且AO →＝12(OB →＋OC →)，AD →＝tAC →，若B ，O ，D 三点共线，则t 的值为( )A.14B.13C.12D.238.（5分）8．执行如图所示的程序框图，若输出的S 值为－2，则①中应填( )A ．n <98?B ．n <99?C ．n <100?D ．n <101?9.（5分）9．已知点F 1、F 2是双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左、右焦点，若双曲线左支上存在点P 与点F 2关于直线y ＝bax 对称，则该双曲线的离心率为( )A.2B.52 C ．2 D.5 10.（5分）10．若实数x 、y 满足xy >0，则x x ＋y ＋2y x ＋2y的最大值为( ) A ．2－2 B ．2＋2 C ．4－22 D ．4＋22 11.（5分）11．曲线y ＝ln x 上的点到直线2x －y ＋3＝0的最短距离是( ) A.4－ln 25 B.4＋ln 25 C.4－ln 25D.4＋ln 2512.（5分）12．已知三棱锥P ­ABC 的棱AP 、AB 、AC 两两垂直，且长度都为3，以顶点P 为球心，以2为半径作一个球，则球面与三棱锥的表面相交所得到的四段弧长之和等于( ) A ．3π B.3π2 C.4π3 D.5π6 二、 填空题 （本题共计4小题，总分20分）13.（5分）13．已知等比数列{a n }的前n 项和为S n ，前n 项积为T n ，若S 3＝a 2＋4a 1，T 5＝243，则a 1的值为____________．14.（5分）14．已知点Q 在圆C ：x 2＋y 2＋2x －8y ＋13＝0上，抛物线y 2＝8x 上任意一点P 到直线l ：x ＝－2的距离为d ，则d ＋|PQ |的最小值等于________． 15.（5分）15．“克拉茨猜想”又称“3n ＋1猜想”，是德国数学家洛萨·克拉茨在1950年世界数学家大会上公布的一个猜想：任给一个正整数n ，如果n 是偶数，就将它减半；如果n 为奇数就将它乘3加1，不断重复这样的运算，经过有限步后，最终都能够得到1.己知正整数m 经过6次运算后得到1，则m 的值为________． 16.（5分）16．已知偶函数f (x )满足f (x －1)＝f (x ＋1)，且当x ∈[0，1]时，f (x )＝x 2，若关于x 的方程f (x )＝|log a |x ||(a >0，a ≠1)在[－2，3]上有5个根，则a 的取值范围是________．三、 解答题 （本题共计6小题，总分70分）17.（10分）17．(本小题满分10分)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，设m ＝⎝ ⎛⎭⎪⎫2cos ⎝ ⎛⎭⎪⎫π6＋A ，cos 2A －cos 2B ，n ＝⎝ ⎛⎭⎪⎫1，cos ⎝ ⎛⎭⎪⎫π6－A ，且m ∥n .(1)求角B 的值；(2)若△ABC 为锐角三角形，且A ＝π4，外接圆半径R ＝2，求△ABC 的周长． 18.（12分）18.(本小题满分12分)甲、乙两俱乐部举行乒乓球团体对抗赛．双方约定：①比赛采取五场三胜制(先赢三场的队伍获得胜利，比赛结束)；②双方各派出三名队员，前三场每位队员各比赛一场．已知甲俱乐部派出队员A 1、A 2、A 3，其中A 3只参加第三场比赛，另外两名队员A 1、A 2比赛场次未定；乙俱乐部派出队员B 1、B 2、B 3，其中B 1参加第一场与第五场比赛，B 2参加第二场与第四场比赛，B 3只参加第三场比赛．根据以往的比赛情况，甲俱乐部三名队员对阵乙俱乐部三名队员获胜的概率如下表：(1)12得取胜的概率最大？(2)若A 1参加第一场与第四场比赛，A 2参加第二场与第五场比赛，各队员每场比赛的结果互不影响，设本次团体对抗赛比赛的场数为随机变量X ，求X 的分布列及数学期望E (X )．19.（12分）19．(本小题满分12分)如图，在四棱锥P ­ABCD 中，底面四边形ABCD 内接于圆O ，AC 是圆O 的一条直径，P A ⊥平面ABCD ，P A ＝AC ＝2，E 是PC 的中点，∠DAC ＝∠AOB .(1)求证：BE ∥平面P AD ；(2)若二面角P ­CD ­A 的正切值为2，求直线PB 与平面PCD 所成角的正弦值． 20.（12分）20．(本小题满分12分)已知圆E ：x 2＋⎝⎛⎭⎫y －122＝94经过椭圆C ：x 2a 2＋y2b 2＝1(a >b >0)的左、右焦点F 1，F 2且与椭圆C 在第一象限的交点为A ，且F 1，E ，A 三点共线．直线l 交椭圆C 于M ，N 两点，且MN →＝λOA →(λ≠0)．(1)求椭圆C 的方程；(2)当△AMN 的面积取到最大值时，求直线l 的方程．21．21.（12分）(本小题满分12分)已知椭圆C 1：x 26＋y 2b 2＝1(b >0)的左、右焦点分别为F 1、F 2，点F 2也为抛物线C 2：y 2＝8x 的焦点，过点F 2的直线l 交抛物线C 2于A ，B 两点． (1)若点P (8，0)满足|P A |＝|PB |，求直线l 的方程；(2)T 为直线x ＝－3上任意一点，过点F 1作TF 1的垂线交椭圆C 1于M ，N 两点，求|TF 1||MN |的最小值．22.（12分）已知函数f (x )＝ax －12x 2－b ln(x ＋1)(a >0)，g (x )＝e x －x －1，曲线y ＝f (x )与y ＝g (x )在原点处有公共的切线．(1)若x ＝0为函数f (x )的极大值点，求f (x )的单调区间(用a 表示)； (2)若∀x ≥0，g (x )≥f (x )＋12x 2，求a 的取值范围．答案一、 单选题 （本题共计12小题，总分60分）1.（5分）1．解析：选D.由集合A ＝{x |log 2(x －1)＜0}＝{x |1＜x ＜2}，则∁R A ＝{x |x ≤1或x ≥2}，又B ＝{x |x ≤3}，所以∁R A ∩B ＝(－∞，1]∪[2，3]．2.（5分）2．解析：选B.由z －2i ＝11－i ，得z ＝2i ＋11－i ＝2i ＋1＋i （1－i ）（1＋i ）＝12＋52i ，所以复数z 在复平面内的点的坐标为⎝⎛⎭⎫12，52，到原点的距离为14＋254＝262.故选B.3.（5分）3．解析：选 C.由题意知x －＝0＋1＋4＋5＋6＋86＝4，y －＝1.3＋m ＋5.6＋6.1＋7.4＋9.36＝29.7＋m6，将⎝⎛⎭⎪⎫4，29.7＋m 6代入y ^＝0.95x ＋1.45中，得29.7＋m 6＝0.95×4＋1.45，解得m ＝1.8. 4.（5分）4．解析：选C.因为cos ⎝ ⎛⎭⎪⎫α＋π2＝35，所以sin α＝－35，又－π2<α<π2，所以cos α＝45，所以sin 2α＝2sin αcos α＝2×⎝⎛⎭⎫－35×45＝－2425，5.（5分）5．解析：选D. A 中，由线面平行的判定和性质得满足条件的直线a ，b 平行，故正确．B 中，满足条件的直线a ，b 垂直，故正确．C 中，由面面垂直的性质可得，交线a 与α垂直，故正确．D 中，直线a 与β可能平行，也可能在β内，故不正确．综上D 不正确．答案D. 6.（5分）解析：选A.结合图象可知函数f (x )＝|x －a |在[a ，＋∞)上单调递增，易知当a ≤－2时，函数f (x )＝|x －a |在[－1，＋∞)上单调递增，但反之不一定成立，故选A.7.（5分）7．解析：选B.设线段BC 的中点为M ，则OB →＋OC →＝2OM →，因为2AO →＝OB →＋OC →，所以AO →＝OM →，则AO →＝12AM →＝14(AB →＋AC →)＝14(AB →＋1t AD →)＝14AB →＋14t AD →，由B ，O ，D 三点共线，得14＋14t ＝1，解得t ＝13.故选B.8.（5分）8．解析：选B.由题意知，该程序框图的功能是计算S ＝lg 12＋lg 23＋…＋lgnn ＋1＝－lg(n ＋1)，当n ＝98时，S ＝－lg 99>－2；当n ＝99时，S ＝－lg 100＝－2，跳出循环，故①中应填n <99?故选B.9.（5分）解析：选D.如图所示，点P 与点F 2关于直线y ＝ba x 对称，所以|OP |＝|OF 2|＝|OF 1|＝c ，所以PF 1⊥PF 2，tan ∠PF 1F 2＝ba ，又|F 1F 2|＝2c ，所以|PF 2|＝2b ，|PF 1|＝2a ，又因为点P 在双曲线上，所以|PF 2|－|PF 1|＝2a ，即2b －2a ＝2a ，b ＝2a ，故e ＝ca＝ 5.10.（5分）10．解析：选C. x x ＋y ＋2yx ＋2y ＝x （x ＋2y ）＋2y （x ＋y ）（x ＋y ）（x ＋2y ）＝x 2＋4xy ＋2y 2x 2＋3xy ＋2y 2＝1＋xyx 2＋3xy ＋2y 2＝1＋1x y ＋3＋2y x ≤1＋13＋22＝4－22，当且仅当x y ＝2y x ，即x 2＝2y 2时取等号． 11.（5分）11．解析：选D.因为直线2x －y ＋3＝0的斜率为2，所以令y ′＝1x ＝2，解得x ＝12，把x ＝12代入曲线方程得y ＝－ln 2，即曲线在点⎝⎛⎭⎫12，－ln 2处的切线斜率为2，⎝⎛⎭⎫12，－ln 2到直线2x －y ＋3＝0的距离d ＝|1＋ln 2＋3|22＋（－1）2＝4＋ln 25，故曲线y ＝ln x 上的点到直线2x －y ＋3＝0的最短距离是4＋ln 25.12.（5分）12．解析：选B.如图所示，Rt △P AC ，Rt △P AB 为等腰直角三角形，且AP ＝AB ＝AC ＝ 3.以顶点P 为球心，以2为半径作一个球与Rt △P AC 的PC ，AC 分别交于点M ，N ，得cos ∠APN ＝32，所以∠APN ＝π6，所以∠NPM ＝π12，所以MN ︵＝π12×2＝π6，同理GH ︵＝π6，HN ︵＝π2×1＝π2，又GM ︵是以顶点P 为圆心，以2为半径的圆的周长的16，所以GM ︵＝2π×26＝2π3， 所以球面与三棱锥的表面相交所得到的四段孤长之和等于π6＋π6＋π2＋2π3＝9π6＝3π2.故选B.二、 填空题 （本题共计4小题，总分20分）13.（5分）解析：由已知，S 3＝a 1＋a 2＋a 3＝a 2＋4a 1，则a 3＝3a 1，所以q 2＝3.又T 5＝a 1a 2a 3a 4a 5＝a 53＝243，所以a 3＝a 1q 2＝3，a 1＝1.故答案为1.14.（5分）解析：抛物线y 2＝8x 的焦点为F (2，0)，故直线l ：x ＝－2为抛物线的准线，由抛物线的定义可知，d ＝|PF |.圆C 的方程可变形为(x ＋1)2＋(y －4)2＝4，圆心为C (－1，4)，半径r ＝2.如图所示，d ＋|PQ |＝|PF |＋|PQ |.显然，|PF |＋|PQ |≥|FQ |(当且仅当F ，P ，Q 三点共线，且点P 在点F ，Q 之间时取等号)．而|FQ |为圆C 上的动点Q 到定点F 的距离，显然当Q 处在Q ′的位置，P 处在P ′的位置时，|FQ |取得最小值，且最小值为|CF |－r ＝（－1－2）2＋（4－0）2－2＝ 5－2＝3.答案：315.（5分）15．解析：如果正整数m 按照上述规则经过6次运算得到1，则经过5次运算后得到的一定是2；经过4次运算后得到的一定是4；经过3次运算后得到的为8或1；经过2次运算后得到的是16；经过1次运算后得到的是5或32；所以开始时的数为10或64.所以正整数m 的值为10或64.故答案为1,8,10或64.16.（5分）解析：由f (x －1)＝f (x ＋1)得函数f (x )的最小正周期T ＝2，根据函数的奇偶性、周期性画出函数f (x )在[－2，3]上的图象，然后再画函数g (x )＝|log a |x ||的图象，如图所示，使它们有5个交点即可，当a >1时，只要保证log a 3≤1即可，解得a ≥3，当0<a <1时，只要保证－log a 3≤1即可，即log a 3≥－1，解得0<a ≤13， 综上a ∈⎝⎛⎦⎤0，13∪[)3，＋∞.三、 解答题 （本题共计6小题，总分70分）17.（10分）17．解：(1)由m ∥n ，得cos 2A －cos 2B ＝2cos ⎝ ⎛⎭⎪⎫π6＋A cos ⎝ ⎛⎭⎪⎫π6－A ，即2sin 2B －2sin 2A ＝2⎝⎛⎭⎫34cos 2A －14sin 2A ，化简得sin B ＝32，故B ＝π3或2π3.(2) 易知B ＝π3，则由A ＝π4，得C ＝π－(A ＋B )＝5π12.由正弦定理a sin A ＝bsin B ＝csin C ＝2R ， 得a ＝4sin π4＝22，b ＝4sin π3＝23，c ＝4sin 5π12＝4sin ⎝ ⎛⎭⎪⎫π4＋π6＝4×⎝⎛⎭⎪⎫22×32＋12×22＝6＋2， 所以△ABC 的周长为6＋23＋3 2.18.（12分）18.解：(1)设A 1、A 2分别参加第一场、第二场，则P 1＝56×23×23＝1027，设A 2、A 1分别参加第一场、第二场，则P 2＝34×23×23＝13，所以P 1>P 2， 所以甲俱乐部安排A 1参加第一场，A 2参加第二场，则甲俱乐部以3∶0取胜的概率最大．(2)比赛场数X 的所有可能取值为3、4、5， P (X ＝3)＝56×23×23＋16×13×13＝718，P (X ＝4)＝56C 12×23×13×23＋16×⎝⎛⎭⎫233＋16C 12×13×23×13＋56×⎝⎛⎭⎫133＝1954，P (X ＝5)＝1－P (X ＝3)－P (X ＝4)＝727， 所以X 的分布列为X 3 4 5 P7181954727所以E (X )＝3×718＋4×1954＋5×727＝20954.19.（12分）19．解：(1)证明：因为∠DAC ＝∠AOB ，所以AD ∥OB .因为E 为PC 的中点，O 为圆心，连接OE ，所以OE ∥P A ，又OB ∩OE ＝O ，P A ∩AD ＝A ，所以平面P AD ∥平面EOB ， 因为BE ⊂平面EOB ，所以BE ∥平面P AD .(2)因为四边形ABCD 内接于圆O 且AC 为直径，所以AD ⊥CD ，又P A ⊥平面ABCD ，所以P A ⊥CD ，又P A ∩AD ＝A ，所以CD ⊥平面P AD ，所以CD ⊥PD ，所以∠PDA 是二面角P ­CD ­A 的平面角，因为tan ∠PDA ＝2，P A ＝2，所以AD ＝1， 如图，以D 为坐标原点，DA 所在的直线为x 轴，DC 所在的直线为y 轴，过点D 且垂直于平面ABCD 的直线为z 轴建立空间直角坐标系D ­xyz .P A ＝AC ＝2，AD ＝1，延长BO 交CD 于点F ，因为BO ∥AD ，所以BF ⊥CD ，又因为BF ＝BO ＋OF ，所以BF ＝1＋12＝32，又CD ＝3，所以DF ＝32，所以P (1，0，2)，B ⎝ ⎛⎭⎪⎫32，32，0， C (0，3，0)，设平面PCD 的法向量n ＝(x ，y ，z )，因为⎩⎪⎨⎪⎧n ·CP →＝0，n ·DC →＝0.所以⎩⎨⎧（x ，y ，z ）·（1，－3，2）＝0，（x ，y ，z ）·（0，3，0）＝0，即⎩⎨⎧x －3y ＋2z ＝0，3y ＝0.令z ＝1，则x ＝－2，y ＝0.所以n ＝(－2，0，1)是平面PCD 的一个法向量，又PB →＝⎝ ⎛⎭⎪⎫12，32，－2，所以|cos 〈PB →，n 〉|＝⎪⎪⎪⎪⎪⎪⎪⎪PB →·n |PB →||n |＝⎪⎪⎪⎪⎪⎪－1＋0－25×5＝35， 所以直线PB 与平面PCD 所成角的正弦值为35.20.（12分）20．解：(1)因为F 1，E ，A 三点共线，所以F 1A 为圆E 的直径，所以AF 2⊥F 1F 2.由x 2＋⎝⎛⎭⎫0－122＝94，得x ＝±2，所以c ＝2，|AF 2|2＝|AF 1|2－|F 1F 2|2＝9－8＝1，2a ＝|AF 1|＋|AF 2|＝4，所以a ＝2.因为a 2＝b 2＋c 2，所以b ＝2，所以椭圆C 的方程为x 24＋y 22＝1.(2)由题知，点A 的坐标为(2，1)，因为MN →＝λOA →(λ≠0)，所以直线的斜率为22， 故设直线l 的方程为y ＝22x ＋m ，联立⎩⎪⎨⎪⎧y ＝22x ＋m x 24＋y22＝1得，x 2＋2mx ＋m 2－2＝0，设M (x 1，y 1)，N (x 2，y 2)，所以x 1＋x 2＝－2m ，x 1x 2＝m 2－2，Δ＝2m 2－4m 2＋8>0，所以－2<m <2.又|MN |＝1＋k 2|x 2－x 1|＝1＋12（x 1＋x 2）2－4x 1x 2＝12－3m 2，点A 到直线l的距离d ＝6|m |3， 所以S △AMN ＝12 |MN |·d ＝1212－3m 2×63 |m |＝22（4－m 2）m 2≤22×4－m 2＋m 22＝2，当且仅当4－m 2＝m 2，即m ＝±2时等号成立，此时直线l 的方程为y ＝22x ± 2. 21.（12分）21．解：(1)由抛物线C 2：y 2＝8x 得F 2(2，0)，当直线l 的斜率不存在，即l ：x ＝2时，满足题意．当直线l 的斜率存在时，设l ：y ＝k (x －2)(k ≠0)，A (x 1，y 1)，B (x 2，y 2)，由⎩⎨⎧y 2＝8x ，y ＝k （x －2）得k 2x 2－(4k 2＋8)x ＋4k 2＝0，所以x 1＋x 2＝4k 2＋8k 2，y 1＋y 2＝k (x 1＋x 2)－4k ＝8k .设AB 的中点为G ，则G ⎝ ⎛⎭⎪⎫2k 2＋4k2，4k ，因为|P A |＝|PB |，所以PG ⊥l ，k PG ·k ＝－1，所以4k －02k 2＋4k 2－8·k ＝－1， 解得k ＝±2，则y ＝±2(x －2)，所以直线l 的方程为y ＝±2(x －2)或x ＝2.(2)因为F 2(2，0)，所以F 1(－2，0)，b 2＝6－4＝2，所以椭圆C 1：x 26＋y 22＝1.设点T 的坐标为(－3，m )，则直线TF 1的斜率kTF 1＝m －0－3＋2＝－m ，当m ≠0时，直线MN 的斜率k MN ＝1m ， 直线MN 的方程是x ＝my －2，当m ＝0时，直线MN 的方程是x ＝－2，也符合x ＝my －2的形式，所以直线MN 的方程是x ＝my －2.设M (x 3，y 3)，N (x 4，y 4)，则联立⎩⎪⎨⎪⎧x 26＋y 22＝1x ＝my －2，得(m 2＋3)y 2－4my －2＝0，所以y 3＋y 4＝4m m 2＋3，y 3y 4＝－2m 2＋3 .|TF 1|＝m 2＋1，|MN |＝（x 3－x 4）2＋（y 3－y 4）2 ＝（m 2＋1）[（y 3＋y 4）2－4y 3y 4]＝24（m 2＋1）m 2＋3 .所以|TF 1||MN |＝124×（m 2＋3）2m 2＋1＝124⎝ ⎛⎭⎪⎫m 2＋1＋4m 2＋1＋4≥33，当且仅当m 2＋1＝4m 2＋1，即m ＝±1时，等号成立，此时|TF 1||MN |取得最小值33.22.（12分）22.解：(1)由题意知，f (x )的定义域为x ∈(－1，＋∞)，且f ′(x )＝a －x －b x ＋1，g ′(x )＝e x －1， 因为曲线y ＝f (x )与y ＝g (x )在原点处有公共的切线，故f ′(0)＝g ′(0)，解得a ＝b ，所以f (x )＝ax －12 x 2－a ln(x ＋1)，f ′(x )＝a －x －a x ＋1＝－x 2＋（a －1）x x ＋1＝－x [x －（a －1）]x ＋1， 当a ＝1时，f ′(x )≤0，函数f (x )在定义域上是减函数，故不满足题意；当a ≠1时，因为x ＝0为函数f (x )的极大值点，故由y ＝－x 2＋(a －1)x 的图象可知a －1<0，由f ′(x )<0得x ∈(－1，a －1)∪(0，＋∞)，由f ′(x )>0得x ∈(a －1，0)，所以函数f (x )的单调递增区间为(a －1，0)，单调递减区间为(－1，a －1)，(0，＋∞)．(2)因为g ′(x )＝e x －1，且当－1<x <0时，g ′(x )<0，当x >0时，g ′(x )>0，故当x ＝0时，g (x )取得最小值0，所以g (x )≥0，即e x ≥x ＋1，从而x ≥ln(x ＋1)．设F (x )＝g (x )－f (x )－12x 2＝e x ＋a ln(x＋1)－(a ＋1)x －1，则F ′(x )＝e x ＋a x ＋1－(a ＋1)， ①当a ＝1时，因为x ≥0，所以F ′(x )≥x ＋1＋a x ＋1－(a ＋1)＝x ＋1＋1x ＋1－2≥0，所以F (x )在[0，＋∞)上单调递增，从而F (x )≥F (0)＝0，即e x ＋ln(x ＋1)－2x －1≥0，所以g (x )≥f (x )＋12x 2.②当0<a <1时，由①知e x ＋ln(x ＋1)－2x －1≥0，所以g (x )＝e x －x －1≥x －ln(x ＋1)≥a [x －ln(x ＋1)]，故F (x )≥0，即g (x )≥f (x )＋12x 2.③当a >1时，令h (x )＝e x ＋a x ＋1－(a ＋1)，则h ′(x )＝e x －a （x ＋1）2. 显然h ′(x )在[0，＋∞)上单调递增，又h ′(0)＝1－a <0，h ′(a －1)＝e a －1－1>0，所以h ′(x )在(0，a －1)上存在唯一零点x 0，当x ∈(0，x 0)时，h ′(x )<0，所以h (x )在(0，x 0)上单调递减，从而h (x )<h (0)＝0，即F ′(x )<0，所以F (x )在(0，x 0)上单调递减，从而当x ∈(0，x 0)时，F (x )<F (0)＝0，即g (x )<f (x )＋12x 2，不符合题意．综上，实数a 的取值范围为(0，1]．。

2021年高三上学期9月月考数学理试卷 Word 版含答案一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．已知集合，集合B ＝{－2，－1，0，1，2}，则（∁R A)∩B=（ ）A ．{0,1,2}B ．{-2,-1}C ．{0}D ．{-2,-1,0}2．已知命题:,,那么命题为（ ） A ． B ． C ．D ．3．下列函数中，既是奇函数，又是在区间（0，1）上单调递增的函数是（ ） A ．B ．C ．D ．4．已知，则的值等于 A ．B ．C ．D ．5．“龟兔赛跑”讲述了这样的故事：领先的兔子看着慢慢爬行的乌龟，骄傲起来，睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点.用S 1、S 2分别表示乌龟和兔子所行的路程，t 为时间，则下图与故事情节相吻合的是（ ）6．已知函数为定义在R 上的奇函数，当时，为常数），则的值是( ) A ． B ． C ． D ． 7．若)0)(sin(3)(:;,22:≠+=∈+=ωϕωππϕx x f q Z k k p 是偶函数，则p 是q 的（ ）A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件8．设函数f (x )＝g (x )＋x 2，曲线y ＝g (x )在点(1，g (1))处的切线方程为y ＝3x -2，则曲线y ＝f (x )在点(1，f (1))处切线的斜率为()B.A ．－12B ．1C ．4D ．59．在△ABC 中，若2cos B ·sin A =sin C ，则△ABC 的形状一定是 A ．等腰直角三角形 B ．直角三角形 C ．等腰三角形 D ．等边三角形 10．若,则值为（ ） A ．3 B ． C ． D ． 11．已知为R 上的可导函数，当时，，则关于x 的函数的零点个数为（ ） A ．0 B ．1 C ．2 D ．0或 2 12．定义在上的函数，当时，．若，，，则a ，b ，c 的大小关系为（ ） A ．a ＞b ＞c B ．a ＞c ＞b C ．b ＞c ＞a D ．c ＞b ＞a第II 卷（非选择题）二、填空题（本大题共4小题，每小题5分 ，共20分，把答案填在答题卡中对应题号后的横线上．）13．设函数 则的单调减区间为___________． 14．函数,（均为常数）,且,则 ．15．定义在R 上的偶函数在[0，)上是增函数，则方程的所有实数根的和为 ． 16．给出下列命题：①若是锐角的内角,则；②存在实数,使；③直线是函数图象的一条对称轴；④函数的图象向右平移个单位,得到的图象．其中正确的命题是 ． 三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（本小题满分10分）已知函数()⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛++⎪⎭⎫⎝⎛-=x x x x f 4sin 4sin 223cos πππ， （I ）求函数的最小正周期；（II ）求函数在区间上的最值及相应的x 的值．18．（本小题满分12分）设命题p ：函数f (x )＝lg(ax 2－12x ＋116a )的定义域为R ；命题q ：不等式(12)x +1－a <0对均成立．(I)如果p 是真命题，求实数a 的取值范围；(II)如果命题“p 或q ”为真命题，且“p 且q ”为假命题，求实数a 的取值范围．19．（本小题满分12分）在中，内角对边的边长分别是，已知．(I)若的面积等于，求；(II)若，求的面积．20．（本小题满分12分）某大桥长3150米，通过大桥的车速不能超过30米/秒，一个由10辆同一车型组成的车队匀速通过该大桥．设车队的速度为x米/秒，根据安全的需要，相邻两车至少保持米的距离，其中为常数且．从第一辆车上桥到最后一辆车下桥（不记车长）所用时间为y（秒）．（I）若大桥限制最低速度为20米/秒，则两车之间的最低安全距离为多少？（II）求车队通过大桥所用时间取最小值时，车队的速度．21．（本小题满分12分）设点、是函数的图象上的任意两点，且角的终边经过点P．当时，的最小值为．（I）求函数的解析式；（II）当时，不等式恒成立，求实数的取值范围．22．（本小题满分12分）已知f(x)＝ln(x＋1)，g(x)＝ax2＋12bx(a，b∈R)．(I) 若b＝6且h(x)＝f(x－1)－g(x)存在单调递减区间，求实数a的取值范围；(II)若a＝0，b＝2，求证：当x∈(－1，＋∞)时，f(x)－g(x)≤0恒成立；(III)利用(II)的结论证明：若x>0，y>0，x≠y，则x ln x＋y ln y>(x＋y)ln x＋y 2.郴州市二中xx届高三9月月考答卷数学（理科）二、填空题（本大题共4小题，每小题5分，共20分，）13.______________________; 14.___________________________;15.______________________; 16.___________________________.三、解答题（本大题共6小题，共70分．）17.（本小题满分10分）19.（本小题满分12分）21.（本小题满分12分）郴州市二中xx 届高三9月月考试卷数学（理科）参考答案二、填空题（本大题共4小题，每小题5分 ，共20分，）13. ; 14. 2; 15.4; 16. ①③.三、解答题（本大题共6小题，共70分．）17．解：(I)()⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛++⎪⎭⎫⎝⎛-=x x x x f 4sin 4sin 223cos πππ ()()x x x x x x sin cos sin cos 2sin 232cos 21-+++=⎪⎭⎫ ⎝⎛+=++=32sin 32cos 2sin 232cos 21πx x x x ． ． …………………………………………………………5分(II) ,． 所以，，此时，即；，此时，即．…………………………………………………………10分18．解：(I)若命题p 为真，即ax 2－12x ＋116a >0对任意x 恒成立．(ⅰ)当a ＝0时，不合题意；(ⅱ)当a ≠0时，可得⎩⎪⎨⎪⎧a >0，Δ<0，即⎩⎪⎨⎪⎧a >0，14－14a 2<0，解得a >1.所以实数a 的取值范围是(1，＋∞)．……………………………………………6分 (II) 命题q ：不等式(12)x +1－a <0对均成立．即(12)x < a －1，所以 a －1>[(12)x ]max =2， 因此，若命题q 为真，则a >3.由命题“p 或q ”为真且“p 且q ”为假，得命题p 、q 一真一假．所以实数a 的取值范围是(1,3]． ……………………………………………12分 19．解：(I )由余弦定理及已知条件得，又因为的面积等于，所以，得．联立方程组解得．……………………………………………………………5分(II )由题意得B A B A B A B A B B sin cos cos sin sin cos cos sin cos sin 4+=+-， 即， ……………………………………………7分 当时，，当时，得，由正弦定理得，联立方程组解得．………………10分所以,不论如何，的面积．…………………12分20.解：（I ）两车之间的安全距离：2211()50()5024g x ax x a x a a=++=++-，时，是增函数．（米） …………………………………5分 （II ）车队通过大桥所用时间：29(50)3150360099(030)ax x y ax x x x+++==++<≤ ……………8分当时，22236009(400)(0,30],'90ax x y a x x-∈∴=-=< 时， ………………………………10分当时，360099y ax x =++≥=当且仅当时，取得最小值． ……………………………12分21.解：(I)角ϕ的终边经过点P(，-1)，∵，∴ϕ=. 由于=，且的最小值为， 所以T=，即，∴ω=3，∴ ………………………………5分 (II) 当时，，，…………………7分 ①当时，因为，所以，可化为所以，由，可知；…………………9分 ②当时，因为，可化为所以，由，可知．……………11分因此，实数的取值范围是或． …………………………12分22.解：(I)当b ＝6时，h (x )＝ln x －ax 2－3x∴h ′(x )＝1x －2ax －3.∵h (x )有单调减区间，∴h ′(x )<0有解，即1－2ax 2－3xx <0 ∵x >0，∴2ax 2＋3x －1>0有解． (ⅰ)当a ≥0时符合题意；精品文档实用文档 (ⅱ)当a <0时，Δ＝9＋8a >0，即a >－98，所以，－98<a <0. 综上所述，a 的取值范围是(－98，＋∞)． …………………………………………4分(II)当a ＝0，b ＝2时，设φ(x )＝f (x )－g (x )＝ln(x ＋1)－x ，∴φ′(x )＝1x ＋1－1＝－x x ＋1. ∵x >－1，讨论φ′(x )的正负得下表： ↗ ↘ ∴当x ＝0∴当x ∈(－1，＋∞)时，f (x )－g (x )≤0恒成立．…………………………………8分 (III)证明：∵x >0，y >0，∴x ln x ＋y ln y －(x ＋y )ln x ＋y 2＝x ⎝⎛⎭⎫ln x －ln x ＋y 2＋y ⎝⎛⎭⎫ln y －ln x ＋y 2 ＝x ln 2x x ＋y ＋y ln 2y x ＋y＝－x ln x ＋y 2x －y ln x ＋y 2y ＝－x ln ⎝⎛⎭⎫1＋y －x 2x －y ln ⎝⎛⎭⎫1＋x －y 2y . ∵x >0，y >0，x ≠y ，∴y －x 2x +1=y +x 2x >0, y －x 2x >－1,且y －x 2x ≠0，由(2)有ln ⎝⎛⎭⎫1＋y －x 2x <y －x 2x 同理ln ⎝⎛⎭⎫1＋x －y 2y <x －y 2y . ∴ －x ln ⎝⎛⎭⎫1＋y －x 2x －y ln ⎝⎛⎭⎫1＋x －y 2y >－x ·y －x 2x －y ·x －y 2y ＝0 ∴ x ln x ＋y ln y >(x ＋y )lnx ＋y 2. …………………………………………12分 20933 51C5 凅27630 6BEE 毮30756 7824 砤HIEk21379 5383 厃31649 7BA1 管|0(W21741 54ED 哭。

2021届四川省仁寿一中等西南四省八校高三9月联考数学（文）试题一、单选题1．设集合{}0,1A =，{}1,0B =-，则A B =（）A ．{}0,1B ．{}1,0,1-C ．{}0D ．{}1,0-【答案】B【解析】根据并集的定义写出A ∪B ． 【详解】 集合A ＝{0，1}，B ＝{﹣1，0}，则A ∪B ＝{﹣1，0，1}． 故选：B ． 【点睛】本题考查了并集的概念及列举法表示集合的形式，是基础题． 2．()()131i i +-=（） A ．42i + B ．24i + C ．22i -+ D ．22i -【答案】A【解析】把复数乘积展开，化简为a +bi （a 、b ∈R ）的形式，可以判断选项． 【详解】∵（1+3i ）（1-i ）＝1+3+3i-i ＝4+2i 故选：A ． 【点睛】本题考查复数代数形式的运算，是基础题． 3．设x ∈R ，则“21x <”是“31x <”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】求出不等式的等价形式，结合充分条件和必要条件的定义进行判断即可．由2x<1得x<0，由“x 3<1”得x ＜1，x<0是x ＜1的充分不必要条件 则“2x<1”是“x 3<1”的充分不必要条件， 故选：A ． 【点睛】本题主要考查充分条件和必要条件的判断，结合不等式的关系是解决本题的关键． 4．已知命题p ：0x ∀>，lg 0x >，则p ⌝是（） A ．0x ∀>，lg 0x ≤ B ．00x ∃>，0lg 0x <C ．0x ∀>，lg 0x <D ．00x ∃>，0lg 0x ≤【答案】D【解析】根据全称命题的否定方法，结合已知中的原命题，可得答案． 【详解】∵命题p ：∀x ＞0，总有lgx ＞0， ∴命题¬p 为：∃x 0＞0，使得lg x 0≤0， 故选：D ． 【点睛】本题考查了命题的否定，考查了推理能力，属于基础题．5．在等差数列{}n a 中，242a a +=，53a =，则{}n a 的前6项和为（） A ．6 B ．9C ．10D ．11【答案】B【解析】利用等差数列{a n }通项公式列方程组求出a 1，d ，由此能求出{a n }的前6项和． 【详解】∵在等差数列{a n }中，a 53=，a 2+a 4＝2， ∴1111433242a d a d a d a d +=⎧⎨+++=+=⎩，解得a 11=-，d 1=， ∴{a n }的前6项和S 6的值：616562S a d ⨯=+=61⨯-+（）15×19=．【点睛】本题考查等差数列的前n 项和的公式，考查等差数列的通项公式的应用，考查运算求解能力，是基础题． 6．若0a >，0b >，2ab =，则2+a b 的最小值为（） A ．22 B ．4C ．42D ．6【答案】B【解析】由a +2b ≥22ab ，可得a +2b 的最小值． 【详解】∵a ＞0，b ＞0，ab ＝2， ∴a +2b ≥224ab =， 当且仅当a ＝2b ＝2时取等号， ∴a +2b 的最小值为4． 故选：B ． 【点睛】本题考查了基本不等式的应用，关键是等号成立的条件，属基础题． 7．如图是函数()()53sin 06f x x πωω⎛⎫=+> ⎪⎝⎭的部分图像，若AB 4=，则()1f -=（）A ．-1B ．1C ．32-D ．32【答案】D【解析】由图可设A （a 3，则B （a 2T +，3-，可得AB =（2T，3，利用向量模的坐标运算，求得T 2πω==4，从而可得ω的值，代入x=-1计算可得结果．【详解】设A （a ），函数f （x ）=（ωx +56π）的周期为T ，则B （a 2T +，，∴AB =（2T，，∵|AB|224T =+12=16，∴T 2＝16， ∴T 2πω==4，解得：ω2π=．∴f （x ）=（2πx +56π），∴f （-1）32=，故选：D ． 【点睛】本题考查函数y ＝A sin （ωx +φ）的图象解析式的确定及应用，涉及向量模的坐标运算及其应用，属于中档题．8．在区间[]6,9-内任取一个实数m ，设()2f x x mx m =-++，则函数()f x 的图像与x 轴有公共点的概率等于（） A ．815B ．35C ．23D ．1115【答案】D【解析】利用f （x ）＝﹣x 2+mx +m 的图象与x 轴有公共点，可得m ≤﹣4或m ≥0，根据在[﹣6，9]内任取一个实数m ，以长度为测度，可求概率． 【详解】∵f （x ）＝﹣x 2+mx +m 的图象与x 轴有公共点， ∴△＝m 2+4m ≥0， ∴m ≤﹣4或m ≥0，∴在[﹣6，9]内任取一个实数m ，函数f （x ）的图象与x 轴有公共点的概率等于4690119615-++-=+． 故选：D ． 【点睛】本题考查概率的计算，确定以长度为测度是关键，是基础题． 9．已知()f x 是定义在R 上的奇函数，且在(),-∞+∞上是减函数，12f ，则满足()232f x -<的实数x 的取值范围是（）A ．()1,1-B ．()2,0-C ．()2,2-D ．()0,2【答案】C【解析】根据题意，由函数奇偶性的性质可得f （﹣1）的值，结合函数的单调性分析可得231x ->-，解可得x 的取值范围． 【详解】根据题意，函数f （x ）是R 上的奇函数，若f （1）＝﹣2，则f （﹣1）＝﹣f （1）＝2，则()232(1)f x f -<=-，又由函数在(),-∞+∞上为减函数， 则有231x ->-， 解可得：24x <，即x 的取值范围是（-2，2）； 故选：C ． 【点睛】本题考查函数的奇偶性与单调性的综合应用，得出f （﹣1）=2是关键．10．直线20x y ++=分别与x 轴，y 轴交于A ，B 两点，点P 在圆()2222x y -+=上，则ABP △面积的取值范围是A ．[]26，B ．[]48，C ．D ．⎡⎣【答案】A【解析】分析：先求出A ，B 两点坐标得到AB ，再计算圆心到直线距离，得到点P 到直线距离范围，由面积公式计算即可详解： 直线x y 20++=分别与x 轴，y 轴交于A ，B 两点()()A 2,0,B 0,2∴--,则AB =点P 在圆22x 22y -+=（）上∴圆心为（2，0），则圆心到直线距离1d ==故点P 到直线x y 20++=的距离2d 的范围为则[]2212,62ABPSAB d ==∈ 故答案选A.点睛：本题主要考查直线与圆，考查了点到直线的距离公式，三角形的面积公式，属于中档题。

卜人入州八九几市潮王学校仁寿县铧强2021届高三数学9月月考试题文一、单项选择题1．设集合2{|log ,04}A y y x x ==<≤，集合{|1}x B x e =>，那么A B 等于()A ．(0,2)B ．(0,2]C ．(,2]-∞D ．R2．集合2{|230},A x x x B N =-->=，那么集合()R C A B 中元素的个数为()A ．2B ．3C ．4D ．53．函数31()22log x f x x =-+的定义域为〔〕 4．()sin tan f x x x =-00:(0,)()02p x f x π∃∈<，那么 A ．p :(0,)()02p x f x π⌝∀∈≥ B ．p 00:(0,)()02p x f x π⌝∃∈≥ C ．p :(0,)()02p x f x π⌝∀∈≥ D ．p 00:(0,)()02p x f x π⌝∃∈≥ 5．||cos x x x x y e e -=+的局部图像大致为 6．如图，在ABC ∆中，BE 是边AC 的中线，O 是BE 边的中点，假设,AB a AC b ==,那么AO =A ．1122a b +B ．1124a b + C ．1142a b +D ．1144a b + 7:p 假设α为第一象限角，那么sin αα<;:q 函数2()2x f x x =-有两个零点，那么〔〕A ．p q ∧B ．p q ∨C ．p q ⌝∨⌝D ．p q ⌝∧ 8．定义在R 上的函数()f x 满足(1)(1)f x f x +=-且在[1,)+∞上是增函数，不等式(2)(1)f ax f x +≤-对任意1[,1]2x ∈恒成立，那么实数a 的取值范围是() A ．[3,1]--B ．[2,0]-C ．[5,1]--D ．[2,1]-9．函数1,2()2log ,2a x x f x x x -≤⎧=⎨+>⎩〔0a >且1a ≠〕的最大值为1,那么a 的取值范围是〔〕 A ．1[,1)2B ．(0,1)C ．1(0,]2D ．(1,)+∞ 10．假设(1)()(4)2(1)2x a x f x a x x ⎧>⎪=⎨-+≤⎪⎩是R 上的单调递增函数,那么实数a 的取值范围为〔〕 A ．(1,+∞)B．(4,8)C ．[4,8)D ．(1,8)11．函数()x e f x ax x =-，(0,)x ∈+∞，当21x x >时，不等式1221()()0f x f x x x -<恒成立，那么实数a 的取值范围为A ．(,]e -∞B ．(,)e -∞C ．(,)2e -∞D ．(,]2e -∞ 12．假设(,0)F c 是双曲线22221(0)x y a b a b-=>>的右焦点，过F 作该双曲线一条渐近线的垂线与两条渐近线交于,A B 两点，O 为坐标原点，OAB ∆的面积为2127a ，那么该双曲线的离心率e =〔〕 A ．53B ．43C ．54D ．85二、填空题13．函数2,0(),2(2),0x x f x f x x +≤⎧=⎨->⎩那么(3)f =__________．14．函数()f x 是(,)-∞+∞上的奇函数，当[0,2)x ∈时，2()f x x =，假设对于任意x R ∈，都有(4)()f x f x +=，那么(2)(3)f f -的值是__________．15．函数2ln ,0(),0x x f x ax x x >⎧=⎨+<⎩，其中0a >，假设函数()y f x =的图象上恰好有两对关于y 轴对称的点，那么实数a 的取值范围为____．16．函数()ln .x f x e a x =+ ①当1a =时，()f x 有最大值；②对于任意的0a >，函数()f x 是(0,)+∞上的增函数；③对于任意的0a<，函数()f x 一定存在最小值；④对于任意的0a >，都有()0f x >． 其中正确结论的序号是_________．〔写出所有正确结论的序号〕三、解答题17．等差数列{}n a 满足153,15a a ==,数列{}n b 满足154,31b b ==,设正项等比数列{}n c 满足n n n c b a =-.(1)求数列{}n a 和{}n c 的通项公式;(2)求数列{}n b 的前n 项和.18．中国海HY ，正在以不可阻挡的气魄向深蓝进HY 。

仁寿一中北校区高三上学期九月月考理科综合能力测试注意事项：1．答题前，考生务必将自己的姓名、准考证号填写，将条形码准确粘贴在条形码区域内。

2．选择题必须使用2B铅笔填涂；非选择题必须用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

可能用到的相对原子质量：H-1C-12O-16Ni-59As-75第Ⅰ卷选择题（共126分）一、选择题：本题共13小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项符合题目要求。

1．红细胞中含有大量血红蛋白，我们可以选用猪、牛、羊或其他脊椎动物的血液进行实验来提取和分离血红蛋白。

下列对血红蛋白提取和分离的叙述，正确的是（）A．红细胞洗涤时需要高速长时间离心以便彻底分离白细胞和红细胞B．电泳过程中，蛋白质分子的移动速度与其所带电荷量有关，与分子形状大小无关C．利用凝胶色谱法分离蛋白质时，相对分子质量小的蛋白质先洗脱出来D．用磷酸缓冲液进行透析时可除去样品中小分子杂质2．用3H标记蚕豆根尖分生区细胞的DNA双链，再将这些细胞转入不含3H、但含有秋水仙素的培养液中培养。

若秋水仙素对细胞连续发挥作用，则下列相关叙述错误的是（）A．通过计数分裂后期细胞被3H标记的染色体数目可推测复制次数B．检测DNA双链上3H标记情况可判断DNA复制的方式C．秋水仙素通过抑制纺锤体的形成来抑制着丝粒的分裂D．细胞完成第二次DNA复制时有一半的染色单体被标记3．如图表示生物新物种形成的基本环节，对图示分析正确的是（）A．a表示基因重组，为生物进化提供原材料B．b表示生殖隔离，生殖隔离是生物进化的标志C．c表示新物种形成，新物种与生活环境协同进化D．d表示地理隔离，新物种形成一定需要地理隔离4．近日，武汉某高校出现了一例霍乱病例，引起了人们的广泛关注。