杆件的内力分析
- 格式：ppt
- 大小：7.07 MB
- 文档页数：54
下载文档原格式
合集下载
专升本工程力学第6章 杆件的内力分析.
29
机电工程学院
2018/12/8
6.3.2 剪力和弯矩
【例6.3】求简支梁横截面1-1、2-2、3-3上的剪力和弯矩。
30
机电工程学院
2018/12/8
6.3.2 剪力和弯矩
解 （1）求支座反力。由梁的平衡方程，求得支座反力为
FA=FB=10kN
（2）求横截面1-1上的剪力和弯矩。假想地沿横截面1-1把梁
2018/12/8
6.3 杆件弯曲时的内力分析
6.3.1 平面弯曲的概念 6.3.2 剪力和弯矩
6.3.3 剪力图和弯矩图
26
机电工程学院
2018/12/8
6.3.2 剪力和弯矩
以悬臂梁为例，其上作用有载荷F，由平衡方程可求出固定端
B处的支座反力为FB=F，MB=Fl。
27
机电工程学院
2018/12/8
（3）求横截面2-2上的剪力和弯矩。假想地沿横截面2-2把梁截
成两段，取左段为研究对象，列出平衡方程
F
y
0, FA F1 FS2 0
FS2 FA F1 0
D
M
0, M2 FA (4m) F1 (2m) 0
M 2 FA (4m) F1 (2m) 20kN m
16
机电工程学院
2018/12/8
6.2.2 扭矩与扭矩图
解 （1）计算外力偶矩。作用于各轮上的外力偶矩分别为
PA M eA 9549 4.46kN m n PB M eB 9549 1.91kN m n PC M eC M eD 9549 1.27kN m n
T2 M eA M eB 2.55kN m T3 M eD 1.27kN m
杆件的内力分析与内力图
F M
y
0 0
C
F l a FS FA l F l a M FA x x l
由其右边分离体的平衡条件同样可得 a FA m F 0
F
y
FB B
FS F FB 0 F l a FS F FB l
A y FA
x
m
m M 切向应力的合力， C A 称为剪力 x m FS x FS m MC 0 M C m M F a x FB l x 0
1 1 FN1
60kN
2
A
30kN
B
x
FN2
2
C
60kN
解：1、计算杆件各段的轴力。 AB 段
X 0
BC 段
FN1 30 0
FN1=30kN
1 30kN
2
X 0
FN2 60 0
FN2= 60kN
+
FN图
2、绘制轴力图。
60kN
| FN |max=60 kN
第三节 扭转和扭矩图
x
Fab l
由剪力、弯矩图知： 在集中力作用点，弯 矩图发生转折，剪力 图发生突变，其突变 值等于集中力的大小， 从左向右作图，突变 方向沿集中力作用的 方向。
Fa l
x
M
三. 弯矩、剪力与分布荷载集度之间的关系及其应用
y O m m x q(x) n n dx F Me x M ( x) m FS(x) m n M(x)+dM(x) C n FS(x)+dFS(x)
1分钟me作功
W ' M e M e (2n 1) 2nMe
杆件受力分析杆件的内力计算和受力平衡
杆件受力分析杆件的内力计算和受力平衡杆件受力分析是工程力学中一个重要的内容，能够帮助我们了解和计算杆件内力以及保证杆件的受力平衡。
本文将介绍杆件受力分析的基本概念和计算方法，并根据实际例子进行说明和分析。
一、杆件受力分析概述杆件，指的是工程结构中的长条形构件，常用于支撑和传递力量。
在实际应用中，杆件往往会受到多方向的力的作用，因此需要进行受力分析，计算出杆件内部的力，以保证其受力平衡。
在进行杆件受力分析时，我们需要明确以下几个概念：1. 受力点：指的是外力作用到杆件上的点，也是进行受力分析的起点。
2. 内力：指的是杆件内部存在的力，可以是拉力或压力。
3. 受力平衡：指的是杆件上所有受力的合力和合力矩为零的状态，保证了杆件受力的平衡。
二、杆件内力计算方法1. 自由体图法：自由体图法是杆件受力分析的基本方法，通过将杆件与外界切割开来，分析切割面上的受力情况，进而计算出杆件内力。
过程：选择合适的切割面，画出自由体图，分析受力平衡条件，解方程计算内力。
2. 杆件法：杆件法是将整个杆件视为一个整体，通过利用杆件的几何关系和受力条件进行计算。
过程：根据杆件的几何形状和受力情况，建立方程组求解。
三、杆件受力分析实例为了更好地理解和应用杆件受力分析的方法，下面以一个实际例子进行说明：假设有一根长度为L的杆件，一端固定在墙上，另一端悬挂一个质量为m的物体。
我们需要计算杆件的内力以及保证受力平衡。
首先，我们选择杆件的中点作为切割面，并画出自由体图。
根据受力平衡条件，我们可以得出以下方程：∑Fx = 0: T - F = 0 （水平方向受力平衡）∑Fy = 0: N - mg = 0 （竖直方向受力平衡）其中，T代表杆件的张力，F代表杆件所受悬挂物体的重力，N代表杆件与墙壁接触点的支撑力，g代表重力加速度。
通过解以上方程组，我们可以计算出T和N的数值，进而得到杆件内部的力。
根据实际情况，可以通过杆件截面积和材料的力学性质，计算出杆件的应力和变形情况。
杆件内力分析
M
max
FS Pcos FN Psin
M PR 2
FN P 2
FS
FN
max
max
FS 0 FS P
内力图
PR
-
R
M图
P
M PRsin （ ）
qa
B D C
qa2 2
x1
a
x2
q
RC
qa 2
qa2
x3
A RAx qa a 3qa RAy 2
M图
qa 2
a
qa
qa
FN图
3qa 2
Fs图
作图示刚架的内力图
C
D
a
A
q
qa2
B
a
解：求约束反力
C
D
a
q
A
3qa 2
qa
qa2
B
a
3qa 2
分析各段内力
内力方程:
D
BD:
FN ( x1 )
杆件的内力分析
杆件内力的一般分类 杆件在外力作用下，内部的相互作用称为内力。 对于一个在外力和约束力作用下处于平衡状态的杆件，将其 在所要求内力的截面假想地截开（一般按横截面截开）考虑部分 平衡。与刚体的不同是杆件的内力在截面上为一分布力系。将其 向截面形心简化，如图所示
Y
FSY FN X Z
FSZ Y
FN 30 5 x( kN )
(4m x 6m)
轴力图
FA=10kN 2m
20kN 2m
5kN/m 2m
FN
kN
10
第3章 杆件的内力分析
50
基本概念：
外力、内力、内力分量、轴力、剪力、 弯矩、扭矩、内力函数、内力图、 轴力、 扭转、平面弯曲。
内力图的作法及特点：
(1)直杆受轴向拉伸或压缩时的内力图--轴力图
剪力 Fy 0 RA Q 0
Fb Q RA l
弯矩
对截面m-m上的形心O取矩，得：
Mo 0
M RA x 0
Fb M RA x x l
40
按照同样方法，在2-2处将梁截开为左右两部分， 仍取左段为分离体，就可求出2-2截面上的内力及 内力矩。
41
③ 剪力和弯矩的符号 截面上的剪力对梁上任意 一点的矩为顺时针转向时， 剪力为正；反之为负。
点击图标播放
24
(3)力偶矩的计算及横截面上的内力
1)外力偶矩
直接计算:
25
按输入功率和转速计算
P Fv
v R P F R T
2n 2n Tn P T T ＝T ＝ 60 60 9.55
2n n 60 30
30 P P T 9.55 n n
PC 15 TC 9.55 9.55 0.478 n 300
kN· m
PD 25 m TD 9.55 9.55 0.796 kN· n 300
(3)求出各段的扭矩 BC段：Tn1-TB=0， Tn1=TB=0.318 kN· m； CA段：Tn2-TB-TC=0，Tn2=TB+TC=0.796 kN· m； AD段：Tn3+TD=0， Tn3=-TD=-0.796 kN· m。
第3章 杆件的内力分析
外力与内力的平衡 内力分量 内力分析与内力图
杆件的内力分析--材料力学
取3-3截面右侧分析 列方程
M
x
0
M x 3 TD 0
M x 3 TD 2859 N m
由上述计算得到扭矩 值
M x1 4300 N m M x 2 6690 N m M x 3 2859 N m
画扭矩图
课堂练习（时间 3分钟） 试画出下面轴的扭矩图
力矩矢方向
力矩旋转方向
根据平衡，截面上有内力矩Mx—扭矩 由此确定扭矩及外力矩的力矩矢方向
扭矩的正负号规定 按照右手螺旋法则， 扭矩矢量的指向与截 面外法线方向一致为 正，反之为负。
力矩矢方向
扭矩矢量 Mx n
力矩旋转方向
截面
截面外法线
1、计算各外力矩的大小（已知功率和转速）； 2、将各外力矩采用右手螺旋定则绘出外力矩矢； 3、取各控制截面，预设扭矩矢（内力矩矢）为正 方向，列平衡方程，计算扭矩矢的大小； 4、以轴线方向为横坐标，扭矩大小为纵坐标绘出 扭矩图。
将外力矩转换为力矩 矢量
取1-1截面左侧分析 将截面上的扭矩设为 正 列方程
M
x
0
TB M x1 0
M x1 TB 4300 N m
取2-2截面左侧分析 列方程
M
x
0
TB TC M x 2 0
M x 2 TB TC 6690 N m
• 2-2直杆轴向拉伸（压缩）时的内力及内力 图
工程中经常遇到承受轴向拉伸或压缩的直杆，例如：
一些机器和结构中所 用的各种紧固螺栓，在紧 固时，要对螺栓施加预紧 力，螺栓承受轴向拉力， 将发生伸长变形。
这些杆件所受的外力特征可以描述为： 作用在杆上的外力的合力作用线与杆的轴线重合
工程力学杆件的内力分析和内力图
工程力学
第五章 杆件的内力分析与内力图
2. 截面法旳基本环节：
例3： 截面法求内力
F
截开：
替代： 平衡：
F F
FS
F 0
上刀刃 n
n 下刀刃
F Fs 0 Fs F
工程力学
第五章 杆件的内力分析与内力图
2. 截面法旳基本环节总结：
① 截开：在所求内力旳截面处，假想地用截面将杆件一分为二。
②替代：任取一部分为研究对象，将弃去部分对留下部分旳作用， 作用在截开面上相应旳内力（力或力偶）替代。
写剪力方程和弯矩方程旳措施和前面简介旳求内力分量旳措施 和过程相同，所不同旳，目前旳指定横截面是坐标为x旳任意 横截面。x是变量，FS（x）、M(x)是函数。
2. 剪力图和弯矩图：
剪力图
Fs Fs(x) 旳图线表达 例题5-4
弯矩图
M M (x) 旳图线表达 例题5-5
工程力学
第五章 杆件的内力分析与内力图
工程力学 5.2.2 扭矩和扭矩图
第五章 杆件的内力分析与内力图
工程力学
第五章 杆件的内力分析与内力图
5.2.2 扭矩和扭矩图
扭转变形是指杆件受到大小相等，方向相反且作用平面垂直于
杆件轴线旳力偶作用，使杆件旳横截面绕轴线产生转动。
A
B O
一、传动轴旳外力偶矩
A
BO
m
m
1.由定义直接计算
外力偶矩： Me＝Fd
L CB段
Fs( x)
RA
P
a L
P(a
x
L)
x M (x) Pa b Px(a x L) L
③根据方程画内力图
工程力学
第五章 杆件的内力分析与内力图
第五章-杆件的内力分析
2、只适用于离杆件受力区域稍远处的横截面。
例题：图示结构，试求杆件AB、CB的应力。已知 P=20kN；斜杆AB为直径20mm的圆截面杆，水平杆 CB为15×15的方截面杆。 解：1、计算各杆件的轴力。（设斜杆AB为1杆， 水平杆BC为2杆）用截面法取节点B为研究对象
A
Fx 0 Fy 0
依方程画出剪力图和弯矩图。
目录
42
3.
梁弯曲时的应力
概述 • 纯弯曲(Pure Bending):某段梁的内力只有弯矩没有剪力时，该段梁的变形称
为纯弯曲。
P a A
Q
P a B
x
x M
§7－2 平面弯曲时梁横截面上的正应力 一、 纯弯曲时梁横截面上的 正应力 中性轴 中性面 （一）变形几何规律：
1. 横截面上的正应力
2. 斜截面上的应力
（1）轴向拉压杆横截面上的正应力 研究方法：
实验观察 作出假设 理论分析 实验验证
N A
F
结论：横截面上应力为均匀分布，以表示。
F
F
即
正负号规定：拉应力为正，压应力为负。
FN A
的适用条件:
1、只适用于轴向拉伸与压缩杆件，即杆端处力的合 力作用线与杆件的轴线重合。
N 2 20 103 2 2 6 A2 15 10 89 106 P a 89MP a
45° B
C
N1
N2
45°
y
B
P
P
x
§4-1
概述
起重机大梁
1
目录
20
§4-1
概述
镗刀杆
目录
21
第二章 杆件的内力与内力图
第二章 杆件的内力与内力图§2-1 杆件内力的概念与杆件变形的基本形式一、杆件的内力与内力分量内力是工程力学中一个非常重要的概念。
内力从广义上讲，是指杆件内部各粒子之间的相互作用力。
显然，无荷载作用时，这种相互作用力也是存在的。
在荷载作用下，杆件内部粒子的排列发生了改变，这时粒子间相互的作用力也发生了改变。
这种由于荷载作用而产生的粒子间相互作用力的改变量，称为附加内力，简称内力。
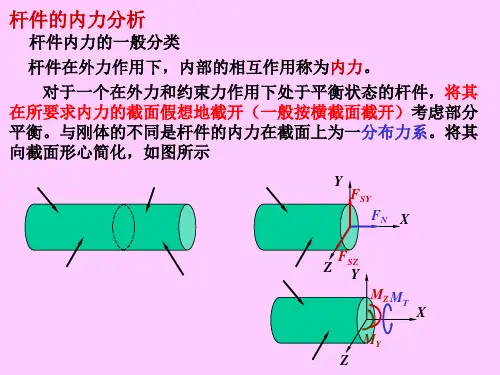
需要指出的是：受力杆件某横截面上的内力实际上是分布在截面上的各点的分布力系，而工程力学分析杆件某截面上的内力时，一般将分布内力先表示成分布内力向截面的形心简化所得的主矢分量和主矩分量进行求解，而内力的具体分布规律放在下一步（属于本书第二篇中的内容）考虑。
受力杆件横截面上可能存在的内力分量最多有四类六个：轴力N F 、剪力y Q F )(和z Q F )(、扭矩x M 、弯矩y M 和z M 。
轴力N F 是沿杆件轴线方向（与横截面垂直）的内力分量。
剪力y Q F )(和z Q F )(是垂直于杆件轴线方向（与横截面相切）的内力分量。
扭矩xM 是力矩矢量沿杆件轴线方向的内力矩分量。
弯矩y M 和z M 是力矩矢量与杆件轴线方向垂直的内力矩分量。
二、杆件变形的基本形式实际的构件受力后将发生形状、尺寸的改变，构件这种形状、尺寸的改变称为变形。
杆件受力变形的基本形式有四种：轴向拉伸和压缩、扭转、剪切、弯曲。
1、轴向拉伸和压缩变形轴向拉伸和压缩简称为轴向拉压。
其受力特点是：外力沿杆件的轴线方向。
其变形特点是：拉伸——沿轴线方向伸长而横向尺寸缩小，压缩——沿轴线方向缩短而横向尺寸增大，如图4-1所示。
轴向受拉的杆件称为拉杆，轴向受压的杆件压杆。
图2-1 图2-2 土木工程结构中的桁架，由大量的拉压杆组成，如图2-2所示。
内燃机中的连杆、压缩机中的活塞杆等均属此类。
它们都可以简化成图2-1所示的计算简图。
2、剪切变形工程中的拉压杆件有时是由几部分联接而成的。
第二章 杆件的内力分析
第二章杆件的内力分析要想对杆件进行强度、刚度和稳定性方面的分析计算，首先必须知道杆件横截面上的内力，因此，本章主要对此作分析讨论。
首先引入了内力的基本概念和求内力的基本方法——截面法，然后讨论了各种变形情况下截面上的内力及求解和内力图的绘制，这是材料力学最基本的知识。
第一节内力与截面法杆件因受到外力的作用而变形，其内部各部分之间的相互作用力也发生改变。
这种由于外力作用而引起的杆件内部各部分之间的相互作用力的改变量，称为附加内力，简称内力。
内力的大小随外力的改变而变化，它的大小及其在杆件内部的分布方式与杆件的强度、刚度和稳定性密切相关。
为了研究杆件在外力作用下任一截面m-m上的内力，可用一平面假想地把杆件分成两部分，如图2-1a。
取其中任一部分为研究对象，弃去另一部分。
由于杆件原来处于平衡状态，截开后各部分仍应保持平衡，弃去部分必然有力作用于研究对象的m-m截面上。
由连续性假设，在m-m截面上各处都有内力，所以内力实际上是分布于截面上的一个分布力系（图2-1b）。
把该分布内力系向截面上某一点简化后得到内力的主矢和主矩，以后就称之为该截面上的内力。
但在工程实际中更有意义的是主矢和主矩在确定的坐标方向上的分量，如图2-1c，这六个内力分量分别对应着四种基本变形形式，依其所对应的基本变形，把这六个内力分量分别称为轴力、剪力、扭矩和弯矩。
（1）轴力。
沿杆件轴线方向（x轴方向）的内力分量FN，它垂直于杆件的横截面，使杆件产生轴向变形（伸长或缩短）。
（2）剪力。
与截面相切（沿y轴和z轴方向）的内力分量FQy、FQz ，使杆件产生剪切变形。
（3）扭矩。
绕x轴的主矩分量Mx，它是一个力偶，使杆件产生绕轴线转动的扭转变形。
（4）弯矩。
绕y轴和z轴的主矩分量My、Mz，它们也是力偶，使杆件产生弯曲变形。
为了求出这些内力分量，只需对所研究部分列出平衡方程就可。
这种计算截面上内力的方法通常称为截面法。
其步骤可归纳为：(1) 沿需要计算内力的截面假想地把构件分成两部分，取其中的任一部分作为研究对象, 弃去另一部分。
河海大学 材料力学 第二章杆件的内力分析第一节
zM z x
Mx
FN (轴力normal force): 沿x 轴(轴线)的内力分量。 FQy、FQz (剪力shearing force)：与横截面相切的内力分量。 Mx (扭矩torsion moment): 沿x 轴(轴线)的主矩分量。 My、Mz (弯矩) :(bending moment)：绕y(z) 轴的主矩分量。
(矢量位于横截面内)
y
My
y
C
x
=
z
My
C x
z
截面法求内力的步骤：
F1
y
My
Hale Waihona Puke FQy FQz C FN F2
zM z
x
1、截成两半 2、取其之一 3、代以内力 4、平衡求解
Mx ∑Fx = 0, ∑Fy = 0, ∑Fz = 0, ∑Mx = 0, ∑My = 0, ∑Mz = 0,
例1 已知F ，沿杆轴线，不计杆重。求杆件内力 。
第二章 杆件的内力分析
§2-1 内力与截面法
一、内力(internal force) 由于外力作用，杆件内部相连两部分之间的相互 作用力。 F1 F2
F3
Fn
二、截面法(method of sections) 将杆件假想地切开以显示内力，并由平衡条件建立
内力与外力间关系或由外力确定内力的方法，称为
C y
F My
F
解： 研究任一截面的 以左部分杆件， ∑Fx = 0, FN – F= 0 FN = F；
FQy F
FQz C FN
zM z x
Mx
FQy=FQz =0 Mx =My=Mz =0
如研究右半部分， ∑Fx = 0, F –FN= 0 FN = F；
Mx
FN (轴力normal force): 沿x 轴(轴线)的内力分量。 FQy、FQz (剪力shearing force)：与横截面相切的内力分量。 Mx (扭矩torsion moment): 沿x 轴(轴线)的主矩分量。 My、Mz (弯矩) :(bending moment)：绕y(z) 轴的主矩分量。
(矢量位于横截面内)
y
My
y
C
x
=
z
My
C x
z
截面法求内力的步骤：
F1
y
My
Hale Waihona Puke FQy FQz C FN F2
zM z
x
1、截成两半 2、取其之一 3、代以内力 4、平衡求解
Mx ∑Fx = 0, ∑Fy = 0, ∑Fz = 0, ∑Mx = 0, ∑My = 0, ∑Mz = 0,
例1 已知F ，沿杆轴线，不计杆重。求杆件内力 。
第二章 杆件的内力分析
§2-1 内力与截面法
一、内力(internal force) 由于外力作用，杆件内部相连两部分之间的相互 作用力。 F1 F2
F3
Fn
二、截面法(method of sections) 将杆件假想地切开以显示内力，并由平衡条件建立
内力与外力间关系或由外力确定内力的方法，称为
C y
F My
F
解： 研究任一截面的 以左部分杆件， ∑Fx = 0, FN – F= 0 FN = F；
FQy F
FQz C FN
zM z x
Mx
FQy=FQz =0 Mx =My=Mz =0
如研究右半部分， ∑Fx = 0, F –FN= 0 FN = F；
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
故：
W W'
(c)
将(a)、(b)两式代入上式，于是求得：
Me
9549
P n
（N·m）
如果功率P以马力为单位，代入〈c〉式则可得：
Me
7024
N n
（N·m）
例1、 传动轴如图所示，主动轮A输入功率PA=50kW，从动轮 B、C、D输出功率分别为PB=PC=15kW，PD=20kW，轴的转速 n=300r/min，计算各轮上所受的外力偶矩。
x
T3
3
D
Mx 0 MD T3 0 T3 MD＝ 637N m
横截面3-3处的扭矩T3也可以利用3—3截面左边的受力平 衡来解决。
1
MB
MC
2 MA
3
1
B
2
C
3
A
M x 0 M B M C M A T3 0
T3
M
B
MC
M
＝
A
637
N
m
4、扭矩图：用来表示受扭杆件横截面上扭矩随轴线位置变化
A B
已知：电动机通过皮带轮输给AB轴的功率为P千瓦。AB轴 的转速n转/分。
则： 电动机每秒钟所作的功为：
W P1000N m
（a）
设电动机通过皮带轮作用于AB轴上的外力偶矩为Me
则：Me在每秒内完成的功为：
W
2
n 60
M
e
（N
m）
(b)
由于Me所作的功也就是电动机通过皮带轮给AB轴输入的功
N
单位：KN
F
N
正
20kN
10kN
30kN
10kN
30kN
20kN
20kN
20kN
30kN
10kN
轴力图
40kN
45kN 35kN 30kN 10kN
10kN 30kN 35kN 45kN 40kN
思考题
在画轴力图之前，能否使用静力学中学过的 力的平移原理将力平移后再作轴力图？
F
F
F
F
§ 轴向扭转时横截面上 的内力和内力图
955N m
x 0
637N m
目录
T T T=T
M A 1592N m,M B MC 477.5N m,M D 637N m
MB
MC
MA
MD
B MB
C MC
A MA
D MD
B
C
A
D
M A 1592N m,M B MC 477.5N m,M D 637N m
MB
MC
2、变形特点：轴向伸长或缩短
二、举例说明：
二力直杆
A
计算简图
P1
拉杆
P1
B P2
压杆
P2
C
F
目录
F
F
F
F
一.轴力及轴力图 1.轴力的概念
（1）举例
1
F
F
1
用截面法将杆件分成左右两部分，取左边为研究
对象
1
F
F
1
F
N
1
利用 x 轴方向的平衡可得 ：
X 0NF 0N F
1
F
F
1
结论 因F力的作用线与杆件的轴线重合，故，由 杆件处于平衡状态可知，内力合力的作用线也必 然与杆件的轴线相重合。
应用截面法将横截面1-1处假想的截开为二，如图，并保留 左半部分为研究对象
1
MB
T1
x
1
Mx 0 MB T1 0 T1 MB＝477.5N m
1
MB
MC
2 T2 x
B1
C2
Mx 0 MB MC T2 0 T2 MB MC＝477.52 955N m
3 MD
1、扭矩：横截面上的内力： (T)
T T T=T
T T
T=T
2、扭转正、负号的规定：
（1）联系扭转变形来规定扭矩符号：杆因扭转使某一段内的纵 向母线有变成右手螺旋的趋势时，则该截面上的扭矩为正，反 之为负。 （2）右手螺旋法则：若按右手螺旋法则把Mn表示为矢量，当矢 量方向与截面的外法线方向一致时，为正，反之为负。
25kN A
15kN B
10kN C
15kN A
15kN B
10kN 10kN
C
用 截 面 法 求 出 各 段 轴 力
4
P4
N4
③根据轴力图的作法即可画出轴力图
N
0
选一个坐标系，用其横坐标 表示横截面的位置，纵坐标 表示相应截面上的轴力。
单位：KN
x
拉力绘在x轴的上侧， 压力绘在x轴的下侧。
简易法作轴力图
的坐标图（与轴力图作法完全相同）。
扭矩图的作法同轴力图的作法完全一样。如图所示：以x 轴表示杆件各横截面的位置，以垂直向上的纵轴表示Mn的大 小。
MB
T1 477 .5N m T2 955 N m B
1 MC
1
C
2 MA 2
3 MD
3
A
D
T3 637 N m
Tn (M n ) 477.5N m
§ 轴向拉压时横截面上 的内力和内力图
工程实例
工程实例
大仓货架
埃菲尔铁塔
斜拉桥
§1-1轴向拉伸和压缩的概念
一、基本概念：
所谓的轴向拉伸和压缩是指作用于杆件上的 外力合力的作用线与杆件的轴线重合时，杆件沿 着轴线方向发生的伸长或缩短。
F
拉杆
FF
F
压杆
1、受力特点：外力或外力合力的作用线与杆轴线重合
F
F
1
F
N
1
N
F
1
3.轴力图
（1）作法： A、用截面法求出各段轴力的大小；
B、选一个坐标系，用其横坐标表示横截面的位置，纵 坐标表示相应截面上的轴力；
C、拉力绘在 x 轴的上侧，压力绘在 x 轴的下侧。
（2）举例：
5kN A
5kN B
10kN C
黑板讲
轴力
5kN
5kN
轴力图
X轴
优点：当保证轴向长度一致时，可 以方便读出任意截面处轴力值。
Me
Me
受力特征：杆受一对大小相等、方向相反的力偶，力偶作用面 垂直于轴线。
变形特征：横截面绕轴线转动。
§2-2 外力偶矩的计算 扭矩和扭矩图
一、外力偶矩的计算
在工程实践中，外力偶矩往往不是直接给出的。而直接给出的 往往都是轴所传递的功率和轴的转速。例如：下图中，外力偶矩没 有给出，给出的仅仅是电动机的转速和输出的功率。如果我们要分 析传动轴中某点处的应力情况，首先必须知道A端皮带轮上的外力 偶矩，下面我们来看看如何根据电动机的转速和输出功率来求解外 力偶矩 Me的大小。
3、扭矩的计算
例2、 传动轴如图所示，主动轮A输入功率PA=50kW，从动轮 B、C、D输出功率分别为PB=PC=15kW，PD=20kW，轴的转速 n=300r/min，计算各段轴上所受的扭矩。
1
MB
MC
2 MA
3 MD
1
B
2
C
3
A
D
解： 根据例1的计算结果可知各轮上的外力偶矩分别为：
M A 1592N m M B M C 477.5N m M D 637N m
（2）定义：上述内力的合力N就称为轴力 。 （其作用线因与杆件的轴线重合而得名）ຫໍສະໝຸດ 取右边为研究对象1
F
F
1
N
F
1
利用 x 轴方向的平衡可得 ：
X 0NF 0N F
1
F
F
1
F
N
1
N
F
1
2.轴力正负号规定：
①规定引起杆件拉伸时的轴力为正，即拉力为正； ②压缩时的轴力为负，即压力为负。
F
NF
N
正
负
1
连接汽车方向盘的轴
扭转测仪 G 仪
主动轮
Me 从动轮
n
主轴
叶片
§ 2.2 扭转的概念
一、引例 F
F
M
主要研究对象:以圆截面(实心圆截面或空心圆截面)杆。 此外，所研究的问题限于杆在线弹性范围内工作的情况。
目录
二、概念
作用于杆件上的外力，为两个大小相等、方向相反、且作 用平面垂直于杆件轴线的力偶时，杆件中任意两个横截面即会 发生绕杆件轴线相对转动，这种形式的变形就称为扭转变形。
25kN.m A
15kN.m B
10kN.m C
151k5NkN.m A
15kN.m B
10kN.m 10kN.m
C
MA
MD
B
C
Tn (M n )
477.5N m
A
955N m
0
D
x
637N m
20kN.m 10kN.m
30kN.m
10kN.m 30kN.m
20kN.m
20kN.m
20kN.m 30kN.m
10kN.m
扭矩图
5kN.m A
5kN.m B
10kN.m C
扭矩
5kN.m
10kN.m
扭矩图
X轴
MB
MC
MA
MD
B
C
A
D
解：计算外力偶矩
MA
9549 PA n
1592N m
MB
MC
9549 PB n
477.5N m
MD
9549 PD n
637N m
二、外力偶矩转向的确定：
主动轮上外力偶矩的转向与轴的转动方向相同，