3假设检验

《数理统计》试题库假设检验1设2521,,,ξξξ 取自正态母体)9,(μN 其中μ为未知参数,ξ为子样均值，对检验问题0100:,:μμμμ≠=H H 取检验的拒绝域:{}c x x x C ≥-=0251:)(μ , 试决定常数c 使检验的显著性水平为0.05.解:因为），，（9N ~μξ所以），（259N ~μξ 在0H 成立下, ,05.03512C 3553P C P 000=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛Φ-=⎪⎪⎪⎭⎫⎝⎛≥-=≥-C μξμξ）（ 96.135,975.035==⎪⎭⎫⎝⎛ΦC C , 所以 C=1.176. 2．设子样),,(1n ξξ 取自正态母体2020),,(σσμN 已知，对检验假设0100:,:μμμμ>=H H 的问题，取临界域{}01:)(c x x x C n ≥= .（i ）求此检验犯第一类错误的概率α,犯第二类错误的概率β,并讨论它们之间的关系.（ii ）设9,05.0,04.0,5.0200====n ασμ,求65.0=μ时不犯第二类错误的概率.解: (i).在0H 成立下, ），（nN ~200σμξ()⎪⎪⎭⎫⎝⎛-≥-=≥=n C n P C P 0000000σμσμξξα, 0100100μμσμσμαα+=∴=-∴--nC n C其中αμ-1是N （0，1）分布的α-1分位点。

在H 1成立下,），（nN ~20σμξ,()⎪⎪⎭⎫⎝⎛-<-=<=n C n P C P 00011σμσμξξβ =⎪⎪⎭⎫⎝⎛--Φ=⎪⎪⎪⎪⎭⎫⎝⎛-+Φ=⎪⎪⎭⎫ ⎝⎛-Φ--n n n n C 001001000σμμμσμμμσσμαα 当α增加时，αμ-1减少，从而β减少；反之当α减少时，将导致β增加。

（ii ）不犯第二类错误的概率为1-β。

⎪⎭⎫ ⎝⎛⨯--Φ-=⎪⎪⎭⎫ ⎝⎛--Φ-=--32.05.065.011105.0001μσμμμβαn =()()().7274.0605.0605.0125.2645.11=Φ=-Φ-=-Φ-3．设一个单一观测的子样ξ取自密度函数为f(x)的母体，对f(x)考虑统计假设：⎩⎨⎧≤≤=≤≤⎩⎨⎧=其它）（：其它10021001)(:1100x x x f H x x f H 试求一个检验函数使犯第一，二类错误的概率满足min 2=+βα，并求其最小值。

实验报告课程名称试验设计与数据分析姓名邵建智学号3110100122专业生物系统工程实验名称假设检验浙江大学生物系统工程与食品科学学院二O一三年八月制实验三：假设检验实验类型：上机操作实验地点：农生环D-414指导老师：傅霞萍实验日期：2013 年10 月8 日一、实验目的和要求（1）熟练使用SPSS进行假设检验（工具/Analyze/Compare means）二、实验内容和原理2.1实验原理假设检验是一种由样本的差异去推断样本所在总体是否存在差异的统计方法。

常用于解决两种工艺方法的比较、一种新添加剂与对照两处理的比较、两种食品内含物测定方法的比较、检验某产品是否达到某项质量标准、检验某项有害物指标是否超标等问题。

根据涉及的统计量不同，选择进行u检验、t检验、F检验等显著性检验。

2.2 实验内容（显著性水平α＝5%）（1）单样本t检验问题1：某公司经理宣称他的雇员英语水平很高，如果按照英语六级考试，一般平均得分为75分，现从雇员中随机选出11人参加考试，得分如下：80，81，72，60，78，65，56，79，77，87，76问：该经理的宣称是否可信？（2）两独立样本t检验问题2：分别在10个食品厂各自测定了大米饴糖和玉米饴糖的还原糖含量，结果见下表，试比较两种饴糖的还原糖含量有无显著差异？（3）成对样本（两配对样本）t检验目的：利用来自两个总体的配对样本数据，推断两个总体的均值是否存在显著差异。

问题3：以下是对促销人员进行培训前后的促销数据，试问该培训是否产生了显著效果。

三、主要仪器设备/实验环境（使用的软件等）IBM SPSS 19.0等四、操作方法与实验步骤（必填，上机操作过程，可以插图）a)提出原假设H0b)选择检验统计量c)计算检验统计量观测值和概率P值d)给定显著性水平α并作出决策（1）单样本t检验选择“分析”-“比较均值”-“单样本T检验”检验变量选择“成绩”，检验值设为75，单击“确定”（2）两独立样本t检验选择“分析”-“比较均值”-“独立样本T检验”使用指定值，组1为：1，组2为：2，单击“继续”检验变量选择“含糖量”，分组变量选择“品种”，单击“确定”（3）成对样本（两配对样本）t检验选择“分析”-“比较均值”-“配对样本T检验”成对变量选择“培训前”和“培训后”为一对，单击“确定”五、实验数据记录和处理（必填，图表数据、计算结果、对图表的处理）（1）单样本t检验（3）成对样本（两配对样本）t检验六、实验结果与分析（必填）（1）单样本t检验1）11个样本的均值，标准差，均值的标准误分别为73.73,9,51,2,880。

统计学三大检验方法引言统计学三大检验方法是指假设检验、置信区间估计和方差分析。

这三种方法是统计学中非常重要的工具，用来对样本数据进行分析和推断。

本文将详细介绍这三种方法的原理、应用和步骤。

一、假设检验假设检验是一种基于样本数据对总体参数进行推断的方法。

它的目的是判断样本数据对某一假设的支持程度。

假设检验的步骤可以分为以下几个部分：1.明确研究问题和假设。

首先确定研究的目的和问题，然后提出关于总体参数的假设，包括原假设和备择假设。

2.选择合适的检验统计量。

根据问题和数据的特点，选择适合的检验统计量，如均值差检验的t统计量、比例差检验的z统计量等。

3.设定显著性水平。

显著性水平是在假设检验中用来判断是否拒绝原假设的标准，通常取0.05或0.01。

4.计算检验统计量的观察值。

根据样本数据计算出具体的检验统计量的观察值。

5.给出结论。

通过计算观察值与临界值的比较，得出对原假设的结论，并解释结果的意义。

二、置信区间估计置信区间估计是一种用来对总体参数进行估计的方法。

它通过样本数据计算出的区间，给出了总体参数的一个估计范围。

1.确定置信水平。

置信水平是在置信区间估计中用来描述区间的可靠程度，通常取0.95。

2.选择适合的估计方法。

根据总体参数的类型和样本数据的特点，选择适合的估计方法，如均值估计的t分布、比例估计的正态分布等。

3.计算置信区间。

根据样本数据和所选的估计方法，计算出具体的置信区间，通常采用公式：估计值±临界值×标准差/√n。

4.解释结果。

解释置信区间的意义，并进行合理的解释和讨论。

三、方差分析方差分析是一种用于比较两个或多个组之间差异的方法。

它是通过分解总体方差，分析组内与组间的差异，来判断组间的差异是否显著。

1.确定研究问题。

确定需要比较的组，并明确研究的目的和问题。

2.设定假设。

设定组间差异的原假设和备择假设。

3.计算方差。

计算组内方差和组间方差。

4.计算F统计量。

根据方差计算出F统计量。

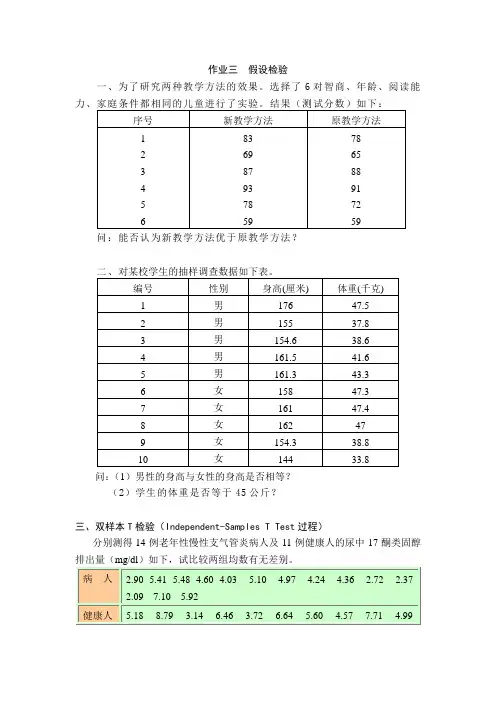
作业三假设检验一、为了研究两种教学方法的效果。

选择了6对智商、年龄、阅读能问：能否认为新教学方法优于原教学方法？问：（1）男性的身高与女性的身高是否相等？（2）学生的体重是否等于45公斤？三、双样本T检验（Independent-Samples T Test过程）分别测得14例老年性慢性支气管炎病人及11例健康人的尿中17酮类固醇实验步骤：1．建立数据文件。

定义变量名：把实际观察值定义为x，再定义一个变量group来区分病人与健康人。

输入原始数据，在变量group中，病人输入1，健康人输入2。

2. 选择菜单“Analyz e→Compare Means→Independent-samples T Test”项，弹出“Independent- samples T Test”对话框。

从对话框左侧的变量列表中选x，进入“Test Variable(s)”框，选择变量“group”，进入“Grouping Variable”框，点击“Define Groups”钮弹出“Define Groups”定义框，在Group 1中输入1，在Group 2中输入2。

3．单击“OK”按钮，得到输出结果。

四.成对样本T检验（Paired-Samples T Test过程）某单位研究饲料中缺乏维生素E与肝中维生素A含量的关系，将大白鼠按性别、体重等配为8对，每对中两只大白鼠分别喂给正常饲料和维生素E缺乏饲料，一段时期后将之宰杀，测定其肝中维生素A含量（μmol/L）如下，问饲料中缺乏维生素E对鼠肝中维生素A含量有无影响？实验步骤：1．建立数据文件。

定义变量名：正常饲料组测定值为x1，维生素E缺乏饲料组测定值为x2，输入原始数据。

2．选择菜单“Analyz e→Compare Means→Paired-samples T Test”项，弹出“Paired - samples T Test”对话框。

从对话框左侧的变量列表中选择变量x1、x2进入Variables框。

概率论与数理统计实验实验3 参数估计假设检验实验目的实验内容直观了解统计描述的基本内容。

2、假设检验1、参数估计3、实例4、作业一、参数估计参数估计问题的一般提法X1, X2,…, Xn要依据该样本对参数作出估计，或估计的某个已知函数.现从该总体抽样，得样本设有一个统计总体，总体的分布函数向量). 为F(x, )，其中为未知参数( 可以是参数估计点估计区间估计点估计——估计未知参数的值区间估计——根据样本构造出适当的区间，使他以一定的概率包含未知参数或未知参数的已知函数的真?（一）、点估计的求法1、矩估计法基本思想是用样本矩估计总体矩.令设总体分布含有个m未知参数??1 ，…，??m解此方程组得其根为分别估计参数??i ，i=1,...,m，并称其为??i 的矩估计。

2、最大似然估计法（二）、区间估计的求法反复抽取容量为n的样本,都可得到一个区间,这个区间可能包含未知参数的真值,也可能不包含未知参数的真值,包含真值的区间占置信区间的意义1、数学期望的置信区间设样本来自正态母体X(1) 方差?? 2已知, ?? 的置信区间(2) 方差?? 2 未知, ?? 的置信区间2、方差的区间估计未知时, 方差?? 2 的置信区间为（三）参数估计的命令1、正态总体的参数估计设总体服从正态分布，则其点估计和区间估计可同时由以下命令获得：[muhat,sigmahat,muci,sigmaci] = normfit(X,alpha)此命令以alpha 为显著性水平，在数据X下，对参数进行估计。

（alpha缺省时设定为0.05），返回值muhat是X的均值的点估计值，sigmahat是标准差的点估计值, muci是均值的区间估计,sigmaci是标准差的区间估计.例1、给出两列参数?? =10, ??=2正态分布随机数，并以此为样本值，给出?? 和?? 的点估计和区间估计命令:r=normrnd(10,2,100,2);[mu,sigm,muci,sigmci]=normfit(r);[mu1,sigm1,muci1,si gmci1]=normfit(r,0.01);mu=9.8437 9.9803sigm=1.91381.9955muci=9.4639 9.584310.2234 10.3762sigmci=1.68031.75202.2232 2.3181mu1=9.8437 9.9803sigm1=1.91381.9955muci1=9.3410 9.456210.3463 10.5043sigmci1=1.6152 1.68412.3349 2.4346例2、产生正态分布随机数作为样本值，计算区间估计的覆盖率。

第三章 假设检验课后作业参考答案3.1 某电器元件平均电阻值一直保持2.64Ω，今测得采用新工艺生产36个元件的平均电阻值为2.61Ω。

假设在正常条件下，电阻值服从正态分布，而且新工艺不改变电阻值的标准偏差。

已知改变工艺前的标准差为0.06Ω，问新工艺对产品的电阻值是否有显著影响？(01.0=α)解：(1)提出假设64.2:64.2:10≠=μμH H ， (2)构造统计量36/06.064.261.2/u 00-=-=-=nX σμ(3)否定域⎭⎬⎫⎩⎨⎧>=⎭⎬⎫⎩⎨⎧>⋃⎭⎬⎫⎩⎨⎧<=--21212αααu u uu u u V (4)给定显著性水平01.0=α时，临界值575.2575.2212=-=-ααuu ，(5) 2αu u <，落入否定域，故拒绝原假设，认为新工艺对电阻值有显著性影响。

3.2 一种元件,要求其使用寿命不低于1000（小时）,现在从一批这种元件中随机抽取25件,测得其寿命平均值为950（小时）。

已知这种元件寿命服从标准差100σ=（小时）的正态分布，试在显著水平0.05下确定这批元件是否合格。

解：{}01001:1000, H :1000X 950 100 n=25 10002.5V=u 0.05H x u αμμσμα-≥<====->=提出假设：构造统计量：此问题情形属于u 检验，故用统计量：此题中：代入上式得：拒绝域：本题中：0.950.950u 1.64u 0.0u H =>∴即，拒绝原假设认为在置信水平5下这批元件不合格。

3.3某厂生产的某种钢索的断裂强度服从正态分布()2,σμN ，其中()2/40cm kg =σ。

现从一批这种钢索的容量为9的一个子样测得断裂强度平均值为X ，与以往正常生产时的μ相比，X 较μ大20(2/cm kg )。

设总体方差不变，问在01.0=α下能否认为这批钢索质量显著提高？ 解：(1)提出假设0100::μμμμ>=H H ， (2)构造统计量5.13/4020/u 00==-=nX σμ (3)否定域{}α->=1u u V(4)给定显著性水平01.0=α时，临界值33.21=-αu(5) α-<1u u ，在否定域之外，故接受原假设，认为这批钢索质量没有显著提高。