规则与不规则图形的计算公式

不规则立体图形的分类和计算一、不规则立体图形的定义及特点不规则立体图形是指那些没有规则几何形状的立体图形，它们由不规则的多边形组成。

不规则立体图形在生活中广泛存在，如天然石块、树枝、果实的形状等。

不规则立体图形的特点是形状复杂、无规律，但可以通过数学方法进行分类和计算。

二、不规则立体图形的分类1.根据组成元素分类：（1）单体不规则立体图形：由一个不规则的多边形组成，如天然石块、树枝等。

（2）组合不规则立体图形：由多个不规则多边形组成，如拼图、建筑物的外观等。

2.根据空间结构分类：（1）一维不规则立体图形：如线段、曲线等。

（2）二维不规则立体图形：如平面上的不规则多边形等。

（3）三维不规则立体图形：如立体拼图、建筑物等。

三、不规则立体图形的计算方法1.单体不规则立体图形的计算：（1）体积计算：通过排水法、溢水法等实验方法测量不规则立体图形的体积。

（2）表面积计算：将不规则立体图形切割成多个规则几何图形，计算每个规则图形的面积，再求和。

2.组合不规则立体图形的计算：（1）体积计算：分别计算每个单体不规则立体图形的体积，再求和。

（2）表面积计算：分别计算每个单体不规则立体图形的表面积，再求和。

四、不规则立体图形的实际应用1.建筑设计：建筑师利用不规则立体图形设计独特的建筑物，提高建筑物的美观性和实用性。

2.工业制造：在不规则立体图形的基础上，设计生产各种形状的零件、产品，满足工业生产的需求。

3.艺术创作：艺术家利用不规则立体图形进行绘画、雕塑等艺术创作，展现个性和创意。

4.自然科学研究：科学家通过研究不规则立体图形，探索自然界中的规律和奥秘。

总结：不规则立体图形的分类和计算是中学数学的重要内容，通过对不规则立体图形的认识和计算，可以提高学生的空间想象能力、创新思维能力和实际应用能力。

习题及方法：1.习题一：计算下列不规则立体图形的体积。

一个天然石块，测量其排水体积为200cm³。

答案：200cm³解题思路：根据题目所给的排水体积，直接得出天然石块的体积。

图形面积体积公式大全一、平面图形的面积公式。

1. 正方形的面积公式。

正方形的面积公式为，A = a²，其中a为正方形的边长。

2. 长方形的面积公式。

长方形的面积公式为，A = l w，其中l为长方形的长度，w为长方形的宽度。

3. 圆的面积公式。

圆的面积公式为，A = πr²，其中π为圆周率（取3.14），r为圆的半径。

4. 三角形的面积公式。

三角形的面积公式为，A = 0.5 b h，其中b为三角形的底边长，h为三角形的高。

5. 梯形的面积公式。

梯形的面积公式为，A = 0.5 (a + b) h，其中a、b分别为梯形的上底和下底长，h为梯形的高。

6. 正多边形的面积公式。

正n边形的面积公式为，A = 0.25 n a² / tan(π/n)，其中n为边数，a为边长。

二、立体图形的体积公式。

1. 正方体的体积公式。

正方体的体积公式为，V = a³，其中a为正方体的边长。

2. 长方体的体积公式。

长方体的体积公式为，V = l w h，其中l为长方体的长度，w为长方体的宽度，h为长方体的高度。

3. 圆柱体的体积公式。

圆柱体的体积公式为，V = πr²h，其中r为圆柱的底面半径，h为圆柱的高。

4. 圆锥体的体积公式。

圆锥体的体积公式为，V = 0.33 πr²h，其中r为圆锥的底面半径，h为圆锥的高。

5. 球体的体积公式。

球体的体积公式为，V = 4/3 πr³，其中r为球的半径。

6. 锥体的体积公式。

锥体的体积公式为，V = 0.33 πr²h，其中r为锥的底面半径，h为锥的高。

三、不规则图形的面积公式。

1. 长方形的面积公式。

不规则图形的面积可以通过分割成多个规则图形来计算，然后相加得到总面积。

2. 圆形的面积公式。

对于不规则的圆形，可以通过近似法来计算其面积，将其分割成多个小扇形，然后相加得到总面积。

3. 其他不规则图形的面积公式。

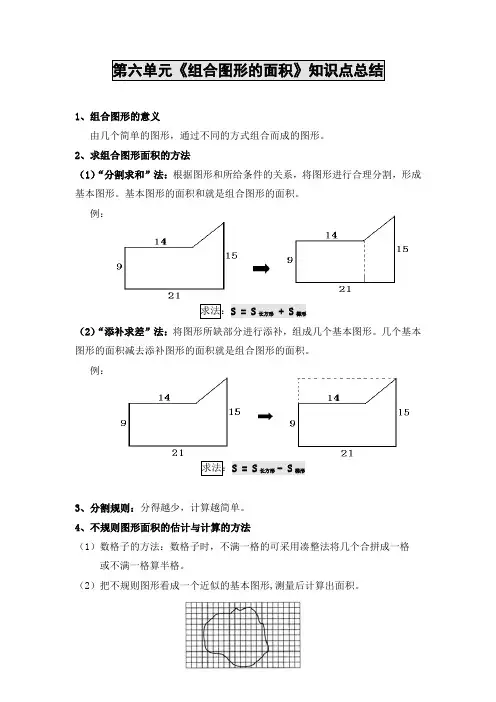
第六单元《组合图形的面积》知识点总结1、组合图形的意义由几个简单的图形，通过不同的方式组合而成的图形。

2、求组合图形面积的方法（1）“分割求和”法：根据图形和所给条件的关系，将图形进行合理分割，形成基本图形。

基本图形的面积和就是组合图形的面积。

例：求法：S = S长方形 + S梯形（2）“添补求差”法：将图形所缺部分进行添补，组成几个基本图形。

几个基本图形的面积减去添补图形的面积就是组合图形的面积。

例：求法：S = S长方形- S梯形3、分割规则：分得越少，计算越简单。

4、不规则图形面积的估计与计算的方法（1）数格子的方法：数格子时，不满一格的可采用凑整法将几个合拼成一格或不满一格算半格。

（2）把不规则图形看成一个近似的基本图形,测量后计算出面积。

5、常见基本图形的面积（1）长方形：周长＝(长+宽)×2字母公式：C=(a+b)×2面积＝长×宽字母公式：S＝ab（2）正方形：周长＝边长×4字母公式：C=4a面积＝边长×边长字母公式：S＝a2（3）平行四边形的面积＝底×高字母公式：S＝ah底=面积÷高；高=面积÷底（4）三角形的面积＝底×高÷2 字母公式：S＝ah÷2 底=面积×2÷高；高=面积×2÷底（5）梯形的面积＝(上底＋下底)×高÷2 字母公式：S＝(a＋b)×h÷2 上底=面积×2÷高－下底；下底=面积×2÷高－上底；高=面积×2÷（上底+下底）6、常用的单位间的进率（1）长度单位：千米（km）米（m）分米（dm）厘米（cm）毫米（mm）1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米（2）面积单位：平方千米（km2）公顷平方米（m2）平方分米（dm2）平方厘米（cm2）1平方千米=100公顷=1000000平方米 1公顷=10000平方米1平方米=100平方分米=10000平方厘米 1平方分米=100平方厘米（3）质量单位：吨（t）千克（kg）克（g）1吨=1000千克 1千克=1000克【注】单位换算的方法：大化小，乘进率；小化大，除以进率。

不规则面积计算公式和方法以下是 8 条关于不规则面积计算公式和方法的内容：1. 嘿，你知道吗？不规则图形的面积计算也有妙招呢！就像要给一块奇形怪状的拼图算面积。

比如说，咱可以把它分割成几个熟悉的图形，然后分别算出它们的面积，最后加起来不就得了嘛！就像那形状怪怪的花园，分成小块来算面积就轻松多了。

2. 哇塞，不规则面积的计算方法可多啦！其中有一种叫填补法，这就好比给不完整的东西补上缺失的那一块。

比如有个形状不规则的空洞，我们用一些规则的东西把它填满，填满部分的面积加上原来规则部分的面积，不就能算出整体面积了吗！多有意思呀！3. 嘿呀，要算不规则面积，还可以用称重法呢！这就好像通过称东西的重量来了解它的价值一样新奇。

像有块形状很怪的布料，我们可以通过称它和同样材质已知面积的布料的重量比例来算出它的面积，神奇吧！4. 哎呀呀，不规则面积还有这种计算方法咧！叫什么网格法哟。

就好像在一张大网上去数格子一样。

比如看那歪歪扭扭的池塘，我们在上面铺上网格，数数有多少个完整的和部分的格子，不就能大概知道它的面积了嘛，超好玩的！5. 哈哈，你晓得不，还有个估算不规则面积的办法呢！这就如同我们估算事情的难易程度一样。

好比有个不规则的岛屿，我们可以大致和一些熟悉的形状比较，给出个大概的面积范围哟，是不是挺简单粗暴但有用呀！6. 哇哦，对于一些不规则图形的面积计算，我们可以用相似图形法呀！就跟找相似的人一样。

比如说，有个不太规则的场地和另一个已知面积的相似场地，通过对比它们的相似之处就能算出我们要的面积啦，很妙吧！7. 咳咳，不规则面积的计算还有个投影法呢！这就好比把东西的影子投出来算大小。

像那个奇形怪状的雕塑，把它的投影画出来算面积，再根据角度推算真实面积，神奇不神奇？8. 哎哟喂，可别忘了还有蒙特卡罗法来算不规则面积哦！这就像是不断地尝试和猜测。

比如说在一个不规则的图形区域里随机扔很多点，统计在图形内的点的比例，就能算出面积啦，多酷啊！总之，计算不规则面积的方法多种多样，只要我们开动脑筋，总能找到合适的办法来搞定它们！。

五年级不规则图形面积计算我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表：实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

一、例题与方法指导例1 如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米.求阴影部分的面积。

思路导航：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

例2 如右图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求三角形AEF的面积.思路导航：∵△ABE 、△ADF 与四边形AECF 的面积彼此相等，∴四边形 AECF 的面积与△ABE 、△ADF 的面积都等于正方形ABCD 的13。

在△ABE 中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=2， ∴△ECF 的面积为2×2÷2=2。

所以S △AEF=S 四边形AECF-S △ECF=12-2=10（平方厘米）。

例3 两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

思路导航：在等腰直角三角形ABC 中∵AB=10∵EF=BF=AB-AF=10-6=4，∴阴影部分面积=S △ABG-S △BEF=25-8=17（平方厘米）。

例4 如右图，A 为△CDE 的DE 边上中点，BC=CD ，若△ABC （阴影部分）面积为5平方厘米.求△ABD 及△ACE 的面积.B C思路导航：取BD中点F，连结AF.因为△ADF、△ABF和△ABC等底、等高，所以它们的面积相等，都等于5平方厘米.∴△ACD的面积等于15平方厘米，△ABD的面积等于10平方厘米。

不规则图形计算的方法总结总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决.常用的基本方法有：一、相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如，右图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了.二、相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如，右图，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可.三、直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形面积.如下页右上图，欲求阴影部分的面积，通过分四、重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可.例如，欲求右图中阴影部分面积，可以把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了.五、辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可.如右图，求两个正方形中阴影部分的面积.此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便.六、割补法：这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决.例如，如右图，欲求阴影部分的面积，只需把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半.七、平移法：这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图形，便于求出面积.例如，如上页最后一图，欲求阴影部分面积，可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。

八、旋转法：这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积.例如，欲求上图（1）中阴影部分的面积，可将左半图形绕B点逆时针方向旋转180°，使A与C重合，从而构成如右图（2）的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法：这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如，欲求右图中阴影部分的面积，沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。

不规则图形面积的求法求不规则图形面积的基本思路是通过分割、重叠、等积替换等方法把不规则图形转化为规则图形或规则图形面积的和差。

一、等积替换（1）三角形等积替换依据：等底等高的三角形面积相等或全等的三角形面积相等。

例1、如图1所示，半圆O 中,直径AB 长为4,C 、D 为半圆O 的三等分点.,求阴影部分的面积.解：连结OC 、OD ， 由C 、D 为半圆O 的三等分点知：∠COD=60°，且∠ADC=∠DAB=30°， ∴CD ∥AB ，所以ODC ADC S S ∆∆=（同底等高的三角形面积相等）∴＝＝扇形阴影O CD S S ππ323602602=⨯⨯例2、如图2所示，在矩形ABCD 中,AB=1,以AD 为直径的半圆与BC 切于M 点,求阴影部分面积.解：由AB ＝1，半圆与BC 相切，得AD ＝2 取AD 的中点O ，则OD ＝BM ＝1。

连结OM 交 BD 于E; 则△OED ≌△MEB∴MEB OED S S ∆∆= （全等三角形面积相等）∴＝＝扇形阴影O M D S S 43601902ππ=⨯⨯ (２）弓形等积替换依据：等弧所对的弓形面积相等。

例3、 在RT △ABC 中,∠B=90°,AB=BC=4,AB 为直径的⊙O 交AC 于点D, 求图中两个阴影部分的面积之和.解：连结BD ，由AB 为⊙O 的直径得∠ADB ＝90°， RT △ABC 中∠B ＝90°AB ＝BC ＝4，得∠A ＝45°且AC＝AD ＝BD ＝CD＝∴A D BnD S S 弓形m 弓形＝∴CDB 11S CD BD 422S ∆⨯⨯⨯阴影＝＝＝例4、点Ａ、Ｂ、Ｃ、Ｄ是圆周上四点，且 AB ＋ CD＝ AC ＋ BD ， 弦ＡＢ＝８，ＣＤ＝４，求两个阴影部分的面积之和。

解：作⊙ O 的直径BE 连结AE ，则∠BAE ＝90°，AB AE =＋半圆；A图2图4又∵ AB ＋ CD＝ AC ＋ BD ＝ 1AB CD AC BD 2（＋＋＋）＝半圆， ∴ AE ＝ CD ，所以A E C DS m n S 弓形弓形＝，AE=CD=4。

不规求不规则图形面积的基本思路是通过分割、重叠、等积替换等方法把不规则图形转化为规则图形或规则图形面积的和差。

一、等积替换（1）三角形等积替换依据：等底等高的三角形面积相等或全等的三角形面积相等。

例1、如图1所示，半圆O 中,直径AB 长为4,C 、D 为半圆O 的三等分点.,求阴影部分的面积.解：连结OC 、OD ， 由C 、D 为半圆O 的三等分点知：∠COD=60°，且∠ADC=∠DAB=30°， ∴CD ∥AB ，所以ODC ADC S S ∆∆=（同底等高的三角形面积相等） ∴＝＝扇形阴影OCD S S ππ323602602=⨯⨯例2、如图2所示，在矩形ABCD 中,AB=1,以AD 为直径的 半圆与BC 切于M 点,求阴影部分面积.解：由AB ＝1，半圆与BC 相切，得AD ＝2 取AD 的中点O ，则OD ＝BM ＝1。

连结OM 交 BD 于E; 则△OED ≌△MEB∴MEB OED S S ∆∆= （全等三角形面积相等） ∴＝＝扇形阴影OMD S S 43601902ππ=⨯⨯(２）弓形等积替换依据：等弧所对的弓形面积相等。

例3、 在RT △ABC 中,∠B=90°,AB=BC=4,AB 为直径的⊙O 交AC 于点D, 求图中两个阴影部分的面积之和.解：连结BD ，由AB 为⊙O 的直径得∠ADB ＝90°， RT △ABC 中∠B ＝90°AB ＝BC ＝4，得∠A ＝45°且AC＝，AD ＝BD ＝CD＝∴A D BnD S S 弓形m 弓形＝∴C D B 11S C D B D 422S ∆⨯⨯⨯阴影＝＝＝例4、点Ａ、Ｂ、Ｃ、Ｄ是圆周上四点，且 AB ＋ CD ＝ A C ＋ BD ， 弦ＡＢ＝８，ＣＤ＝４，求两个阴影部分的面积之和。

解：作⊙ O 的直径BE 连结AE ，则∠BAE ＝90°，A B A E =＋半圆；A图2图4又∵ AB ＋ CD ＝ A C ＋ BD ＝ 1A B C D A C B D 2（＋＋＋）＝半圆， ∴ AE ＝ C D ，所以A E C DS m n S 弓形弓形＝，AE=CD=4。

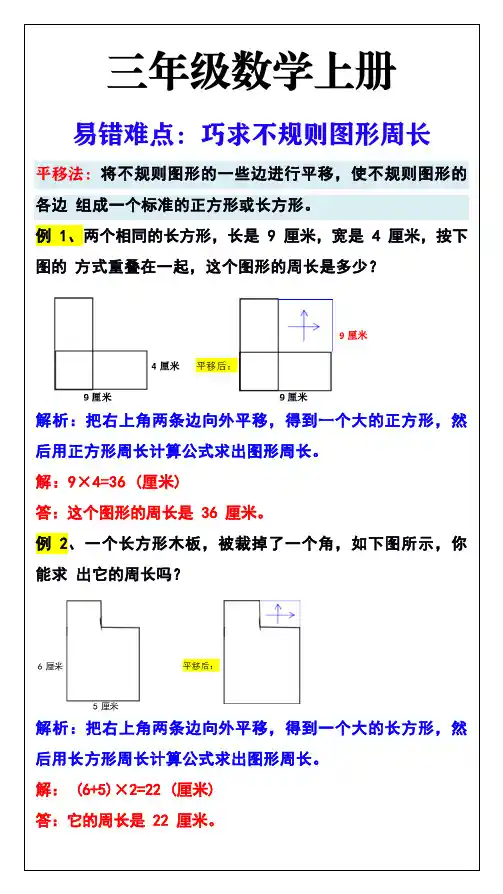
不规则三角形面积计算公式咱们在数学的世界里溜达，经常会碰到各种各样的图形，三角形就是其中一个常客。

不过呢，三角形也有“守规矩”和“不守规矩”的，咱们今天就专门来聊聊这“不守规矩”的不规则三角形，说说它面积的计算方法。

先来说说啥是不规则三角形。

其实很简单，就是那些三条边长度都不一样，三个角大小也没啥规律的三角形。

比如说，你在路上看到一个三角形的花坛，边边弯弯扭扭的，那很可能就是个不规则三角形。

那怎么算它的面积呢？这就得请出咱们的“大救星”——海伦公式。

这个公式看起来有点复杂，但是别怕，咱们一点点来。

海伦公式是这样的：假设三角形的三条边分别是 a、b、c，那先算出半周长 p，p = （a + b + c）÷ 2，然后三角形的面积 S 就等于√[p×(p - a)×(p - b)×(p - c)] 。

听起来是不是有点晕？咱们来举个例子。

有个三角形，三条边分别是 3 厘米、4 厘米、5 厘米。

那咱们先算半周长 p ，就是（3 + 4 + 5）÷ 2 = 6 厘米。

然后呢，面积S = √[6×(6 - 3)×(6 - 4)×(6 - 5)] = √[6×3×2×1] = √36 = 6 平方厘米。

再给您说个我遇到的事儿。

有一次我去朋友家，他家小孩正在为一道不规则三角形面积的数学题发愁。

我一看，嘿，这不是刚好用上海伦公式嘛！我就耐心地给他讲，一步一步带着他算。

刚开始这孩子还一脸懵，觉得这公式太复杂。

我就跟他说：“你别把它想得那么可怕，就把它当成一个解谜的游戏，每一步都是找到答案的线索。

”慢慢地，他跟着我的思路走，算出了答案，那高兴劲儿，眼睛都放光了！从那以后，这孩子对数学的兴趣都浓了不少。

咱们再回到这个公式。

其实海伦公式用起来还是挺方便的，只要知道了三角形三条边的长度，就能算出面积。

但是呢，有时候题目给的条件不是三条边的长度，而是其他的，比如一个角和两条边，那这时候就得用另外的方法了。

《不规则图形的计算方法》
1.学校园里有一块草坪(如下图)，它的面积是多少平方米？
方法一：分成一个长方形和一个梯形
12X4+(12+15) X6÷2
=129(m²)
答:这块草坪的面积是129m²。

方法二：分成一个三角形和一个梯
形
15X6÷2+ (4+10)X12÷2
=129(m²)
答:这块草坪的面积是129m²。

方法三：分成一个三角形和一个长方形。

3X6÷2+12X10
=129(m²)
答:这块草坪的面积是129m²。

方法四：添补成一个长方形。

15X10-(4+10)X3÷2
=129(m²)
答:这块草坪的面积是129m²。

《不规则图形的计算方法》2.求阴影部分的面积
正方形面积: 5X5=25 (cm²)
三角形面积: 8X5÷2=20 (cm²)
阴影面积: 25+20=45 (cm²)
3.求下面图形的面积
长方形面积:10X8=80 (cm²)
梯形面积:(10+6)X2÷2=16 (cm²)
组合图形面积: 80-16=64 (cm²)
4.计算下面图形的面积。

14×4÷2+14×6÷2=70（cm²)。

不规则圆弧面积计算公式摘要：一、不规则圆弧面积计算公式简介1.不规则圆弧的定义2.计算不规则圆弧面积的重要性二、不规则圆弧面积计算公式推导1.圆弧面积公式2.拆分不规则圆弧为多个规则圆弧3.计算每个规则圆弧的面积4.求和得到不规则圆弧的总面积三、计算实例与技巧1.计算单个不规则圆弧面积2.计算多个不规则圆弧重叠部分的面积3.使用计算机辅助计算四、总结1.不规则圆弧面积计算公式的应用范围2.提高计算效率的方法正文：一、不规则圆弧面积计算公式简介不规则圆弧是指在平面内，由两条射线和一条弧线组成的闭合图形。

在工业生产、建筑设计、科研等领域，经常需要计算不规则圆弧的面积。

为了方便计算，数学家们推导出了不规则圆弧面积计算公式。

1.不规则圆弧的定义不规则圆弧是由一条射线R 和一条射线R"以及它们之间的弧线组成的闭合图形。

其中，射线R 和射线R"的端点重合，弧线与射线R 和射线R"均相交。

2.计算不规则圆弧面积的重要性在实际应用中，不规则圆弧的面积是一个重要的参数。

例如，在机械加工中，需要知道工件的形状以确定刀具的尺寸；在建筑设计中，需要计算楼板的面积以确定结构荷载；在科研领域，需要对实验数据进行处理以得出结论。

因此，掌握不规则圆弧面积计算公式具有实际意义。

二、不规则圆弧面积计算公式推导1.圆弧面积公式对于一个规则圆弧，其面积计算公式为：S = 1/2 × r × r × θ，其中r 为圆弧半径，θ为圆心角的弧度制表示。

2.拆分不规则圆弧为多个规则圆弧将不规则圆弧分割成多个规则圆弧，每个规则圆弧可以单独计算面积。

为了实现这一步操作，需要找到不规则圆弧的圆心角。

通过测量或计算，可以得到圆心角的度数或弧度制表示。

然后，将圆心角分解为多个规则圆弧的圆心角之和。

3.计算每个规则圆弧的面积利用圆弧面积公式，可以计算出每个规则圆弧的面积。

需要注意的是，对于每个规则圆弧，半径可能不同。

求不规则三角形面积公式三角形是几何学中最基本的形状之一，它有着丰富的性质和应用。

我们通常所熟知的三角形是指具有三条边和三个角的图形。

而在数学中，三角形还可以根据边长和角度的关系进一步分类，其中之一就是不规则三角形。

不规则三角形是指边长和角度均不相等的三角形，它的形状和大小都是独特的。

要计算不规则三角形的面积，我们可以利用海伦公式或分解为两个直角三角形来求解。

海伦公式是由古希腊数学家海伦提出的，它适用于任意三角形，包括不规则三角形。

海伦公式的表达式如下：面积 = √(s(s-a)(s-b)(s-c))其中，s是三角形的半周长，a、b、c分别是三角形的三条边的长度。

通过计算半周长和三边的长度，就可以得到不规则三角形的面积。

除了海伦公式，我们还可以将不规则三角形分解为两个直角三角形来计算面积。

不规则三角形可以通过任意一条边的高度分成两个直角三角形，然后分别计算两个直角三角形的面积，最后将两个面积相加即可得到不规则三角形的面积。

不规则三角形面积公式的应用非常广泛。

在建筑设计、地理测量、物理学等领域，经常需要计算不规则三角形的面积。

例如，在建筑设计中，计算房间的面积就需要使用不规则三角形面积公式。

在地理测量中，计算地块的面积也需要使用不规则三角形面积公式。

在物理学中，计算物体的质量分布中心也可以通过不规则三角形面积公式来求解。

不规则三角形面积公式的推导过程较为复杂，涉及到大量的数学运算和几何性质的推导。

在本文中，我们主要介绍了不规则三角形面积公式的应用和计算方法，以及它在实际生活中的重要性。

总结起来，不规则三角形面积公式是计算不规则三角形面积的基本工具之一。

无论是在学术研究还是实际应用中，都离不开这个公式的帮助。

通过掌握和应用不规则三角形面积公式，我们可以更好地理解和应用三角形的性质，从而解决实际问题。

希望本文对读者能够有所启发和帮助。