2006年高考文科数学试题及答案(湖南卷)

2006年高考试题文科数学试题（全国II 卷）一．选择题（1）已知向量a =（4，2），向量b =（x ，3），且a ∥b ，则x=（A ）9 （B ）6 （C ）5 （D ）3 （2）已知集合{}2{|3},|log 1M x x N x x =<=>，则M N = （A ）∅ （B ）{}|03x x <<（C ）{}|13x x << （D ）{}|23x x <<（3）函数sin 2cos 2y x x =的最小正周期是（A ）2π （B ）4π （C ）4π （D ）2π（4）如果函数()y f x =的图像与函数y=3-2x 的图像关于原点对称，则y=()f x 的表达式为（A ） y=2x-3 （B ）y=2x+3（C ） y=-2x+3 （D ）y=-2x-3（5）已知ABC ∆的顶点B 、C 在椭圆2213x y +=上，顶点A 是椭圆的一个焦点，且椭圆另外一个焦点在BC 边上，则ABC ∆的周长是（A） （B ）6 （C） （D ）12（6）已知等差数列{}n a 中，a 2=7,a 4=15,则前10项和S 10=（A ）100 （B ）210 （C ）380 （D ）400 （7）如图，平面α⊥平面β，,,A B AB αβ∈∈与两平面α、β所成的角分别为4π和6π。

过A 、B 分别作两平面交线的垂线，垂足为'A 、',B 若AB=12，则'A 'B = （A ）4 （B ）6 （C ）8 （D ）9（8）函数ln 1(0)y x x =+>的反函数为 （A ）1()x y e x R +=∈ （B ）1()x y e x R -=∈（C ）1(1)x y ex +=> （D ）1(1)x y e x -=>（9）已知双曲线22221x y a b-=的一条渐近线方程为43y x =，则双曲线的离心率为（A ）53 （B ）43 （C ）54 （D ）32（10）若(sin )3cos2,f x x =-则(cos )f x =（A ）3cos 2x - （B ）3sin 2x -（C ）3cos 2x + （D ）3sin 2x +（11）过点（-1，0）作抛物线y=x 2+x+1的切线，其中一条切线为（A ）2x+y+2=0 （B ）3x-y+3=0 （C ）x+y+1=0 （D ）x-y+1=0（12）5名志愿者分到3所学校支教，要求每所学校至少有1名志愿者，则不同的分法共有A'B'A B βα（A ）150种 （B ）180种 （C ）200种 （D ）280种 二．填空题：（13）在4101()x x+的展开式中常数项是＿＿＿＿＿。

2006年普通高等学校招生全国统一考试文科数学本试卷分第I 卷（选择题）第II 卷（非选择题）两部分。

第I 卷1至2页。

第II 卷3 至4页。

考试结束后，将本试卷和答题卡一并交回。

第I 卷注意事项： 1．答题前，考生在答题卡上务必用黑色签字笔将自己的姓名、 准考证号填写清楚，并贴好条形码。

请认真核准条形码上的准考证号、姓名和科目。

2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效。

3．本卷共12小题，每小题5分， 共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

参考公式：如果事件A 、B 互斥，那么 球的表面积公式 P （A +B ）=P （A ）+P （B ） S =4πR 2如果事件A 、B 相互独立，那么其中R 表示球的半径 P （A ·B ）=P （A ）· P （B ）球的体积公式如果事件A 在一次试验中发生的概率是P ，那么334R V π=n 次独立重复试验中恰好发生k 次的概率其中R 表示球的半径k n k k n n P P C k P --=)1()(一．选择题（1）已知向量a 、b 满足| a |=1，| b |=4，且a ·b =2，则a 与b 的夹角为（A ）6π （B ）4π （C ）3π （D ）2π （2）设集合}2|||{},0|{2<=<-=x x N x x x M ，则 （A ）=N M ∅ （B ）M N M =（C ）M N M =（D ）=N M R（3）已知函数xe y =的图像与函数)(xf y =的图像关于直线x y =对称，则 （A ）∈=x e x f x()2(2R ） （B ）2ln )2(=x f ·x ln （0>x ）（C ）∈=x e x f x (2)2(R ）（D ）+=x x f ln )2(2ln （0>x ）（4）双曲线122=+y mx 的虚轴长是实轴长的2倍，则m =（A ）41-（B ）－4（C ）4 （D ）41（5）设n S 是等差数列}{n a 的前n 项和，若S 7=35，则a 4=（A ）8（B ）7（C ）6（D ）5（6）函数)4tan()(π+=x x f 的单调增区间为（A ）∈+-k k k ),2,2(ππππZ（B ）∈+k k k ),)1(,(ππZ（C ）∈+-k k k ),4,43(ππππZ（D ）∈+-k k k ),43,4(ππππZ （7）从圆012222=+-+-y y x x 外一点P （3，2）向这个圆作两条切线，则两切线夹角的余弦值为（A ）21 （B ）53 （C ）23 （D ）0（8）△ABC 的内角A 、B 、C 的对边分别为a 、b 、c . 若a 、b 、c 成等比数列，且==B a c cos ,2则（A ）41（B ）43 （C ）42 （D ）32 （9）已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是（A ）16π（B ）20π（C ）24π（D ）32π（10）在10)21(xx -的展开式中，4x 的系数为（A ）－120 （B ）120（C ）－15 （D ）15（11）抛物线2x y -=上的点到直线0834=-+y x 距离的最小值是（A ）34 （B ）57 （C ）58 （D ）3（12）用长度分别为2、3、4、5、6（单位：cm ）的5根细木棒围成一个三角形（允许连接，但不允许折断），能够得到的三角形的最大面积为 （A ）58cm 2 （B ）106cm 2（C ）553cm 2（D ）20cm 22006年普通高等学校招生全国统一考试文科数学第Ⅱ卷注意事项： 1．答题前，考生先在答题卡上用黑色签字笔将自己的姓名、准考证号填写清楚，然后贴好条形码。

2006年高考湖南卷文科综合试题及参考答案本试卷分第I卷（选择题）和第II卷（非选择题）两部分。

第I卷1至8页，第II卷9至12页。

全卷共300分。

考试用时150分钟。

第I卷注意事项：1.答题前，考生务必将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2.每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

答在试题卷上无效。

3.考试结束，监考人员将本试题卷和答题卡一并收回。

4.第I卷共35小题，每小题4分，共140分。

在每题给出的四个选项中，只有一项是最符合题目要求的。

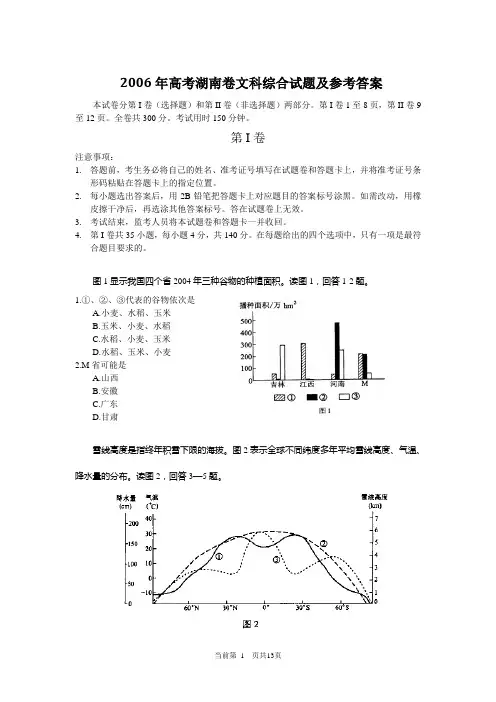
图1显示我国四个省2004年三种谷物的种植面积。

读图1，回答1-2题。

1.①、②、③代表的谷物依次是A.小麦、水稻、玉米B.玉米、小麦、水稻C.水稻、小麦、玉米D.水稻、玉米、小麦2.M省可能是A.山西B.安徽C.广东D.甘肃雪线高度是指终年积雪下限的海拔。

图2表示全球不同纬度多年平均雪线高度、气温、降水量的分布。

读图2，回答3—5题。

3. 表示多年平均雪线高度、气温、降水量的曲线依次是A.①②③B.①③②C.③②①D.③①②4. 多年平均雪线高度A. 随纬度增高而降低B. 在副热带地区最高C. 在降水量大的地区较高D. 在南半球低纬度地区最低5. 依图示资料可知A. 北半球高纬地区多年平均气温与降水量变化趋势基本一致B. 南半球中纬地区多年平均雪线高度与降水量变化趋势基本一致C. 多年平均雪线高度与气温变化趋势一致D. 北半球高纬地区陆地比重小于南半球表1为四个国家1998年能源消费情况。

读表1，回答6—8题。

6. 表1数据表明A. ①国以煤为主，且核电消费量最大B. ②国光矿物源消费构成较均衡，且石油消费量最大C. ③国以石油为主，且石油消费量在四国中居首位D. ④国以天然气为主，且天然气消费量在四国中居首位7.①～④所代表的国家依次是A.俄罗斯、美国、日本、中国B.中国、美国、日本、俄罗斯C.美国、中国、日本、俄罗斯D.中国、美国、俄罗斯、日本8.人均能源消费量较为相近的一组是A.①②B.②③C.③④D.①④据报道，哈尔滨地区2004年10月14日出现的日偏食开始于9时20分，结束于10时57分。

美好的友谊东升小学5.4班王馨叶在我不长的人生经历中有着一段纯洁、美好的友情—那就是和郑璐瑶的友谊。

认识她还是在幼儿园里。

一开始我和她并不认识，还是在游戏的时候，偶然相遇。

我们先做简单的自我介绍，不久便开始玩起来了。

后来，我们才知道我俩是同一个班的，便把对方都列为最好的朋友。

三年后，我们一起上了同一个学校，在同一个班里。

上学后不久，我们因为性格不合常常无端争吵起来。

一次，我一气之下竟提出了“绝交”，但提出后，我马上后悔了。

她听了之后，十分伤心，没有说什么，一个人默默离开了。

那天晚上，我想了好久，终于想通了在第二天要对她说：对不起，那些都是气话不是真的。

因为第二天要向她道歉，所以我早早的来到了学校。

一开始，我一直在等她，后来因为我要收作业就忘了这件事。

当我猛地想起这件事，准备起身去她的座位时，偶然发现她已经站在我的座位前了。

“昨天的事，是我不对，对不起。

”她说道。

“不，昨天提出‘绝交’的是我，所以该我说对不起。

”在几声对不起中，原本已走到尽头的友情又回来了三年级，她奉父母之命转学了。

当我知道这个消息时异常伤心，因为做了这么长时间的朋友居然就这么散了。

当她回学校交作业的时候，我和她聊了好久。

我俩都好伤心，但我和她的友情却更加坚定了，那是用我们的心在慢慢交织着。

转眼又过去两年多了，我们并没有因为不在一起而疏远，因为我们的心是彼此相通的。

和朋友的友谊不需要像彩虹那样绚烂多彩和华丽无比，只要向陈酿的古酒那么醇香便足够了。

更像西伯利亚的蝶那样，经过了一次次寒流的侵袭，依然那么顽强、美丽。

评语：文章详细具体地记叙了自己和好朋友之间由和到不和，再到和的经过，抓住了人物的语言和心理描写，刻画的细腻逼真，真实地反映了同学之间珍贵的友谊，希望你们的友谊地久天长！赠人玫瑰手留余香东升小学5.4班郝佳欣下课了，同学们像一群快乐的小鸟飞奔出教室，只有几人坐在教室看书、做作业。

崔永康正在埋头做一道语文题。

突然，他手中的笔停了下来，原来“拦路虎”出现了，崔永康紧皱着眉，一会儿搔搔头皮，一会儿用手托着下巴，绞劲脑汁地想，可怎么也想不出来，他的脸涨得像一个红透了的苹果。

绝密★启用前2006年高考文科数学试卷（湖南卷）本试题卷他选择题和非选择题（包括填空题和解读回答题）两部分. 选择题部分1至2页. 非选择题部分3至5页. 时量120分钟. 满分150分. 参阅公式: 如果事件A 、B 互斥，那么()()()P A B P A P B +=+ 如果事件A 、B 相互独立，那么)()()(B P A P AB P ⋅=如果事件A 在一次试验中发生的概率乃是P ，那么n 次独立重复试验中恰好发生k 次的概率乃是()(1)k k n kn n P k C P P -=- 球的体积公式 343V R π=,球的表面积公式24S R π=，其中R 表示球的半径一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，惟有一项乃是符合题目要求的. 1．函数x y 2log =的定义域乃是A ．(0,1］ B. (0,+∞) C. (1,+∞) D. ［1,+∞)2．已知向量),2,1(),,2(==b t a若1t t =时，a ∥b ；2t t =时，b a ⊥，则A ．1,421-=-=t t B. 1,421=-=t t C. 1,421-==t t D. 1,421==t t 3. 若5)1(-ax 的展开式中3x 的系数乃是80，则实数a 的值乃是 A ．-2 B. 22 C. 34 D. 24．过半径为12的球O 表面上一点A 作球O 的截面，若OA 与该截面所成的角乃是60°则该截面的面积乃是A ．π B. 2π C. 3π D. π32 5．“a =1”乃是“函数a x x f -=)(在区间［1，＋∞）上为增函数”的A ．充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件6．在数字1,2，3与符号＋，－五个元素的所有全排列中，任意两个数字都不相邻的全排列个数乃是A ．6 B. 12 C. 18 D. 24 7．圆0104422=---+y x y x 上的点到直线014=-+y x 的最大距离与最小距离的差乃是A ．36 B. 18 C. 26 D. 25 8．设点P 乃是函数x x f ωsin )(=的图象C 的一个对称中心，若点P 到图象C 的对称轴上的距离的最小值4π，则)(x f 的最小正周期乃是 A ．2π B. π C. 2π D. 4π 9．过双曲线M ：1222=-hy x 的左顶点A 作斜率为1的直线l ,若l 与双曲线M 的两条渐近线分别相交于点B 、C ，且BC AB =，则双曲线M 的离心率乃是A ．25B. 310C. 5D. 1010. 如图1：OM ∥AB ，点P 由射线OM 、线段OB 及AB的延长线围成的阴影区域内（不含边界）.且OB y OA x OP +=，则实数对（x ,y ）能够乃是A ．)43,41( B. )32,32(-C. )43,41(-D. )57,51(-二．填空题：本大题共5小题，每小题４分，共20分，把答案填在答题上部 对应题号的横上.11. 若数列{}n a 满足：1.2,111===+n a a a n n ，2，3….则=+++n a a a 21 . 12. 某高校有甲、乙两个数学建模兴趣班. 其中甲班有40人，乙班50人. 现分析两个班的一次考试成绩，算得甲班的平均成绩乃是90分，乙班的平均成绩乃是81分，则该校数学建模兴趣班的平均成绩乃是 分.13. 已知⎪⎩⎪⎨⎧≤--≤+-≥022011y x y x x 则22y x +的最小值乃是 .14. 过三棱柱 ABC －A 1B 1C 1 的任意两条棱的中点作直线，其中与平面ABB 1A 1平行的直线共有 条.15. 若)4sin(3)4sin()(ππ-++=x x a x f 乃是偶函数，则a = .A图1三．解读回答题：本大题共６小题，共80分. 解读回答应写出文字说明，证明过程或演算步骤.16.（本小题满分１２分）已知),,0(,1cos )cos()22sin(sin 3πθθθπθπθ∈=⋅+--求θ的值.17.（本小题满分１２分）某安全生产监督部门对5家小型煤矿进行安全稽查(简称安检). 若安检不合格，则必须整改. 若整改后经复查仍不合格，则强制关闭. 设每家煤矿安检乃是否合格乃是相互独立的，且每家煤矿整改前安检合格的概率乃是0.5，整改后安检合格的概率乃是0.8，计算(结果精确到0.01)：(Ⅰ)恰好有两家煤矿必须整改的概率； (Ⅱ)某煤矿不被关闭的概率； (Ⅲ)至少关闭一家煤矿的概率.18.（本小题满分１4分）如图2，已知两个正四棱锥P -ABCD 与Q -ABCD 的高都乃是2，AB =4. (Ⅰ)证明PQ ⊥平面ABCD ；(Ⅱ)求异面直线AQ 与PB 所成的角； (Ⅲ)求点P 到平面QAD 的距离.19.（本小题满分14分）QBCP A D图2已知函数ax ax x f 313)(23-+-=. （Ｉ）讨论函数)(x f 的单调性；（Ⅱ）若曲线)(x f y =上两点A 、B 处的切线都与y 轴垂直，且线段AB 与x 轴有公共点，求实数a 的取值范围.20.（本小题满分14分）在m （m ≥2）个不同数的排列P 1P 2…P n 中，若1≤i ＜j ≤m 时P i ＞P j （即前面某数大于后面某数），则称P i 与P j 构成一个逆序. 一个排列的全部逆序的总数称为该排列的逆序数. 记排列321)1()1( -+n n n 的逆序数为a n ，如排列21的逆序数11=a ，排列321的逆序数63=a . （Ⅰ）求a 4、a 5，并写出a n 的表达式； （Ⅱ）令nn n n n a aa ab 11+++=，证明32221+<++<n b b b n n ，n =1,2,….21.（本小题满分14分）已知椭圆C 1：13422=+y x ，抛物线C 2：)0(2)(2>=-p px m y ，且C 1、C 2的公共弦AB 过椭圆C 1的右焦点.（Ⅰ）当x AB ⊥轴时，求p 、m 的值，并判断抛物线C 2的焦点乃是否在直线AB 上；（Ⅱ）若34=p 且抛物线C 2的焦点在直线AB 上，求m 的值及直线AB 的方程.2006年高考文科数学参阅答案（湖南卷）1－10：DCDAABCBCDC11.12-n , 12. 85, 13. 5 ,14. 6 ,15. -3 . 16. 解 由已知条件得1cos cos 2cos sin 3=⋅--θθθθ. 即0sin 2sin 32=-θθ. 解得0sin 23sin ==θθ或. 由0＜θ＜π知23sin =θ，从而323πθπθ==或.17. 解 （Ⅰ）每家煤矿必须整改的概率乃是1－0.5，且每家煤矿乃是否整改乃是相互独立的. 所以恰好有两家煤矿必须整改的概率乃是31.01655.0)5.01(32251==⨯-⨯=C P .（Ⅱ）解法一 某煤矿被关闭，即该煤矿第一次安检不合格，整改后经复查仍不合格，所以该煤矿被关闭的概率乃是1.0)8.01()5.01(2=-⨯-=P ，从而煤矿不被关闭的概率乃是0.90.解法二 某煤矿不被关闭包括两种情况：（i ）该煤矿第一次安检合格；（ii ）该煤矿第一次安检不合格，但整改后合格.所以该煤矿不被关闭的概率乃是90.08.0)5.01(5.02=⨯-+=P .(Ⅲ)由题设（Ⅱ）可知，每家煤矿不被关闭的概率乃是0.9，且每家煤矿乃是否被关闭乃是相互独立的，所以到少关闭一家煤矿的概率乃是41.09.0153=-=P . 18. 解法一 （Ⅰ）连结AC 、BD ，设O BD AC = .由P －ABCD 与Q －ABCD 都乃是正四棱锥，所以PO ⊥平面ABCD ，QO ⊥平面ABCD . 从而P 、O 、Q 三点在一条直线上，所以PQ ⊥平面ABCD . （Ⅱ）由题设知，ABCD 乃是正方形，所以AC ⊥BD .由（Ⅰ），QO ⊥平面ABCD . 故可分别以直线CA 、DB 、QP 为x 轴、y 轴、z 轴建立空间直角坐标系（如图），由题条件，相关各点的坐标分别乃是P （0，0，2），A （22，0，0），Q （0，0，－2），B （0，22，0）.所以)2,0,22(--=AQ )2,22,0(-=PB于乃是3132324,cos =⨯=<. 从而异面直线AQ 与PB 所成的角乃是31arccos .(Ⅲ)由（Ⅱ），点D 的坐标乃是（0，－22，0），)0,22,22(--=，)4,0,0(-=，设),,(z y x =乃是平面QAD 的一个法向量，由⎪⎩⎪⎨⎧=⋅=⋅00AD n 得⎪⎩⎪⎨⎧=+=+002y x z x . 取x =1，得)2,1,1(--=.所以点P 到平面QAD的距离22==d . 解法二 （Ⅰ）取AD 的中点，连结PM ，QM .因为P －ABCD 与Q －ABCD 都乃是正四棱锥， 所以AD ⊥PM ，AD ⊥QM . 从而AD ⊥平面PQM . 又⊂PQ 平面PQM ，所以PQ ⊥AD .同理PQ ⊥AB ，所以PQ ⊥平面ABCD .（Ⅱ）连结AC 、BD 设O BD AC = ，由PQ ⊥平面ABCD 及正四棱锥的性质可知O 在PQ 上，从而P 、A 、Q 、C 四点共面.因为OA ＝OC ，OP ＝OQ ，所以PAQC 为平行四边形，AQ ∥PC .从而∠BPC （或其补角）乃是异面直线AQ 与PB 所成的角.因为322)22(2222=+=+==OP OC PC PB ，所以31323221612122cos 222=⨯⨯-+=⋅-∠PC PB BC PC PB BPC ＋＝. 从而异面直线AQ 与PB 所成的角乃是31arccos .(Ⅲ)连结OM ，则PQ AB OM 21221===. 所以∠PMQ ＝90°，即PM ⊥MQ .由（Ⅰ）知AD ⊥PM ，所以PM ⊥平面QAD . 从而PM 的长乃是点P 到平面QAD 的距离. 在直角△PMO 中，22222222=+=+=OM PO PM . 即点P 到平面QAD 的距离乃是22.BCPAD OM19. 解 （Ⅰ）由题设知)2(363)(,02ax ax x ax x f a -=-='≠.令ax x x f 2,00)(21==='得. 当（i ）a >0时，若)0,(-∞∈x ，则0)(>'x f ，所以)(x f 在区间)2,(a -∞上乃是增函数；若)2,0(a x ∈，则0)(<'x f ，所以)(x f 在区间)2,0(a 上乃是减函数；若),2(+∞∈a x ，则0)(>'x f ，所以)(x f 在区间),2(+∞a上乃是增函数；（i i ）当a ＜0时，若)2,(a x -∞∈，则0)(<'x f ，所以)(x f 在区间)2,(a -∞上乃是减函数；若)2,0(a x ∈，则0)(<'x f ，所以)(x f 在区间)2,0(a上乃是减函数；若)0,2(a x ∈，则0)(>'x f ，所以)(x f 在区间)0,2(a上乃是增函数；若),0(+∞∈x ，则0)(<'x f ，所以)(x f 在区间),0(+∞上乃是减函数.（Ⅱ）由（Ⅰ）的讨论及题设知，曲线)(x f y =上的两点A 、B 的纵坐标为函数的极值，且函数)(x f y =在a x x 2,0==处分别乃是取得极值a f 31)0(-=，134)2(2+--=a aa f . 因为线段AB 与x 轴有公共点，所以0)2()0(≤⋅af f .即0)31)(134(2≤-+--a a a .所以0)4)(3)(1(2≤--+aa a a . 故0,0)4)(3)(1(≠≤--+a a a a 且.解得 －1≤a ＜0或3≤a ≤4.即所求实数a 的取值范围乃是[-1，0)∪[3，4]. 20. 解 （Ⅰ）由已知得15,1054==a a ， 2)1(12)1(+=+++-+=n n n n a n . （Ⅱ）因为 ,2,1,22222211==+⋅+>+++=+=++n nn n n n n n n a a a a b n n n n n ， 所以n b b b n 221>+++ . 又因为 ,2,1,222222=+-+=+++=n n n n n n n b n ， 所以)]211()4121()3111[(2221+-++-+-+=+++n n n b b b n=32221232+<+-+-+n n n n .综上， ,2,1,32221=+<++<n n b b b n n .21. 解 （Ⅰ）当AB ⊥x 轴时，点A 、B 关于x 轴对称，所以m ＝0，直线AB 的方程为 x =1，从而点A 的坐标为（1，23）或（1，－23）. 因为点A 在抛物线上，所以p 249=，即89=p . 此时C 2的焦点坐标为（169，0），该焦点不在直线AB 上. （Ⅱ）解法一 当C 2的焦点在AB 时，由（Ⅰ）知直线AB 的斜率存在，设直线AB 的方程为)1(-=x k y .由⎪⎩⎪⎨⎧=+-=134)1(22y x x k y 消去y 得01248)43(2222=-+-+k x k x k . ……①设A 、B 的坐标分别为（x 1,y 1）, （x 2,y 2）, 则x 1,x 2乃是方程①的两根，x 1＋x 2＝22438k k +.因为AB 既乃是过C 1的右焦点的弦，又乃是过C 2所以)(214)212()212(2121x x x x AB +-=-+-=，且 34)2()2(212121++=++=+++=x x p x x p x p x AB .从而)(214342121x x x x +-=++. 所以91621=+x x ，即91643822=+kk . 解得6,62±==k k 即.因为C 2的焦点),32(m F '在直线)1(-=x k y 上，所以k m 31-=.即3636-==m m 或. 当36=m 时，直线AB 的方程为)1(6--=x y ； 当36-=m 时，直线AB 的方程为)1(6-=x y . 解法二 当C 2的焦点在AB 时，由（Ⅰ）知直线AB 的斜率存在，设直线AB 的方程为)1(-=x k y . 由⎪⎩⎪⎨⎧-==-)1(38)(2x k y x m y 消去y 得x m k kx 38)(2=--. ……①因为C 2的焦点),32(m F '在直线)1(-=x k y 上，所以)132(-=k m ，即k m 31-=.代入①有x k kx 38)32(2=-.即094)2(342222=++-k x k x k . ……② 设A 、B 的坐标分别为（x 1,y 1）, （x 2,y 2）, 则x 1,x 2乃是方程②的两根，x 1＋x 2＝223)2(4kk +.由⎪⎩⎪⎨⎧=+-=134)1(22y x x k y 消去y 得01248)43(2222=-+-+k x k x k . ……③由于x 1,x 2也乃是方程③的两根，所以x 1＋x 2＝22438kk +.从而223)2(4k k +＝22438k k +. 解得6,62±==k k 即.因为C 2的焦点),32(m F '在直线)1(-=x k y 上，所以k m 31-=.即3636-==m m 或. 当36=m 时，直线AB 的方程为)1(6--=x y ； 当36-=m 时，直线AB 的方程为)1(6-=x y . 解法三 设A 、B 的坐标分别为（x 1,y 1）, （x 2,y 2）, 因为AB 既过C 1的右焦点)0,1(F ，又乃是过C 2的焦点),32(m F '，所以)212()212()2()2(212121x x p x x p x p x AB -+-=++=+++=.即916)4(3221=-=+p x x . ……① 由（Ⅰ）知21x x ≠，于乃是直线AB 的斜率m m x x y y k 313201212=--=--=， ……② 且直线AB 的方程乃是)1(3--=x m y , 所以32)2(32121mx x m y y =-+-=+. ……③ 又因为⎪⎩⎪⎨⎧=+=+1243124322222121y x y x ，所以0)(4)(312122121=--⋅+++x x y y y y x x . ……④ 将①、②、③代入④得322=m ，即3636-==m m 或.当36=m 时，直线AB 的方程为)1(6--=x y ； 当36-=m 时，直线AB 的方程为)1(6-=x y .。

2006年全国统一高考数学试卷（文科）（全国卷Ⅱ）一、选择题（共12小题，每小题5分，满分60分）1．（5分）已知向量=（4，2），向量=（x，3），且∥，则x=（）A．9 B．6 C．5 D．32．（5分）已知集合M={x|x＜3}，N={x|log2x＞1}，则M∩N=（）A．∅B．{x|0＜x＜3}C．{x|1＜x＜3}D．{x|2＜x＜3}3．（5分）函数y=sin2x•cos2x的最小正周期是（）A．2πB．4πC．D．4．（5分）如果函数y=f（x）的图象与函数y′=3﹣2x的图象关于坐标原点对称，则y=f（x）的表达式为（）A．y=2x﹣3 B．y=2x+3 C．y=﹣2x+3 D．y=﹣2x﹣35．（5分）已知△ABC的顶点B，C在椭圆+y2=1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是（）A．B．6 C．D．126．（5分）已知等差数列{a n}中，a2=7，a4=15，则前10项的和S10=（）A．100 B．210 C．380 D．4007．（5分）如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和．过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB：A′B′=（）A．2：1 B．3：1 C．3：2 D．4：38．（5分）已知函数f（x）=lnx+1（x＞0），则f（x）的反函数为（）A．y=e x+1（x∈R）B．y=e x﹣1（x∈R）C．y=e x+1（x＞1）D．y=e x﹣1（x＞1）9．（5分）已知双曲线=1（a＞0，b＞0）的一条渐近线方程为y=x，则双曲线的离心率为（）A．B．C．D．10．（5分）若f（sinx）=2﹣cos2x，则f（cosx）等于（）A．2﹣sin2x B．2+sin2x C．2﹣cos2x D．2+cos2x11．（5分）过点（﹣1，0）作抛物线y=x2+x+1的切线，则其中一条切线为（）A．2x+y+2=0 B．3x﹣y+3=0 C．x+y+1=0 D．x﹣y+1=012．（5分）5名志愿者分到3所学校支教，每个学校至少去一名志愿者，则不同的分派方法共有（）A．150种B．180种C．200种D．280种二、填空题（共4小题，每小题4分，满分16分）13．（4分）在的展开式中常数项为（用数字作答）．14．（4分）圆O1是以R为半径的球O的小圆，若圆心O1到球心O的距离与球半径面积S1和球O的表面积S的比为S1：S=2：9，则圆心O1到球心O的距离与球半径的比OO1：R=．15．（4分）过点的直线l将圆（x﹣2）2+y2=8分成两段弧，当劣弧所对的圆心角最小时，直线l的斜率k=．16．（4分）一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如图）．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在[2500，3000）（元）月收入段应抽出人．三、解答题（共6小题，满分74分）17．（12分）在△ABC中，∠B=45°，AC=，cosC=，（1）求BC的长；（2）若点D是AB的中点，求中线CD的长度．18．（12分）设等比数列{a n}的前n项和为S n，S4=1，S8=17，求通项公式a n．19．（12分）某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意出取2件产品进行检验．设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品．（1）用ξ表示抽检的6件产品中二等品的件数，求ξ的分布列及ξ的数学期望；（2）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品被用户拒绝的概率．20．（12分）如图，在直三棱柱ABC﹣A1B1C1中，AB=BC，D、E分别为BB1、AC1的中点．（I）证明：ED为异面直线BB1与AC1的公垂线；（II）设，求二面角A 1﹣AD﹣C1的大小．21．（14分）设a∈R，二次函数f（x）=ax2﹣2x﹣2a．若f（x）＞0的解集为A，B={x|1＜x＜3}，A∩B≠∅，求实数a的取值范围．22．（12分）已知抛物线x2=4y的焦点为F，A、B是抛物线上的两动点，且．过A、B两点分别作抛物线的切线，设其交点为M．（Ⅰ）证明为定值；（Ⅱ）设△ABM的面积为S，写出S=f（λ）的表达式，并求S的最小值．2006年全国统一高考数学试卷（文科）（全国卷Ⅱ）参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．（5分）已知向量=（4，2），向量=（x，3），且∥，则x=（）A．9 B．6 C．5 D．3【分析】本题考查向量共线的充要条件，坐标形式的充要条件容易代错字母的位置，只要细心，这是一道送分的题目，但一些考试中会考到．【解答】解：∥，∴4×3﹣2x=0，∴x=6，故选：B．【点评】向量平行、垂直是经常考到的问题，掌握两个向量共线、垂直的几何判断，会证明两向量垂直，以及能解决一些简单问题．2．（5分）已知集合M={x|x＜3}，N={x|log2x＞1}，则M∩N=（）A．∅B．{x|0＜x＜3}C．{x|1＜x＜3}D．{x|2＜x＜3}【分析】解出集合N，结合数轴求交集．【解答】解：N={x|log2x＞1}={x|x＞2}，用数轴表示可得答案D故选：D．【点评】考查知识点有对数函数的单调性，集合的交集，本题比较容易3．（5分）函数y=sin2x•cos2x的最小正周期是（）A．2πB．4πC．D．【分析】将函数化简为：y=Asin（ωx+φ）的形式即可得到答案．【解答】解：所以最小正周期为，故选：D．【点评】考查知识点有二倍角公式，最小正周期公式本题比较容易4．（5分）如果函数y=f（x）的图象与函数y′=3﹣2x的图象关于坐标原点对称，则y=f（x）的表达式为（）A．y=2x﹣3 B．y=2x+3 C．y=﹣2x+3 D．y=﹣2x﹣3【分析】先假设函数f（x）上的点（x，y），∵（x，y）关于原点对称的点为（﹣x，﹣y）在函数y′=3﹣2x上代入即可得到答案．【解答】解：设（x，y）为函数f（x）上的点，∵（x，y）关于原点对称的点为（﹣x，﹣y）在函数y′=3﹣2x上∴以﹣y，﹣x代替函数y'=3﹣2x中的y′，x，得y=f（x）的表达式为y=﹣2x﹣3故选：D．【点评】本题主要考查根据函数对称性求函数解析式的问题．根据求谁设谁的原则，先假设函数f（x）上的点，根据对称性找关系式即可得到答案．5．（5分）已知△ABC的顶点B，C在椭圆+y2=1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是（）A．B．6 C．D．12【分析】由椭圆的定义：椭圆上一点到两焦点的距离之和等于长轴长2a，可得△ABC的周长．【解答】解：由椭圆的定义：椭圆上一点到两焦点的距离之和等于长轴长2a，可得△ABC的周长为4a=，故选：C．【点评】本题主要考查数形结合的思想和椭圆的基本性质，难度中等6．（5分）已知等差数列{a n}中，a2=7，a4=15，则前10项的和S10=（）A．100 B．210 C．380 D．400【分析】由第二项和第四项的值可以求出首项和公差，写出等差数列前n项和公式，代入n=10得出结果．【解答】解：d=，a1=3，∴S10==210，故选：B．【点评】若已知等差数列的两项，则等差数列的所有量都可以求出，只要简单数字运算时不出错，问题可解．7．（5分）如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和．过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB：A′B′=（）A．2：1 B．3：1 C．3：2 D．4：3【分析】设AB的长度为a用a表示出A'B'的长度，即可得到两线段的比值．【解答】解：连接AB'和A'B，设AB=a，可得AB与平面α所成的角为，在Rt△BAB'中有AB'=，同理可得AB与平面β所成的角为，所以，因此在Rt△AA'B'中A'B'=，所以AB：A'B'=，故选：A．【点评】本题主要考查直线与平面所成的角以及线面的垂直关系，要用到勾股定理及直角三角形中的边角关系．有一定的难度8．（5分）已知函数f（x）=lnx+1（x＞0），则f（x）的反函数为（）A．y=e x+1（x∈R）B．y=e x﹣1（x∈R）C．y=e x+1（x＞1）D．y=e x﹣1（x＞1）【分析】本题考查反函数的概念、求反函数的方法、指数式与对数式的互化，求函数的值域；将y=lnx+1看做方程解出x，然后由原函数的值域确定反函数的定义域即可．【解答】解：由y=lnx+1解得x=e y﹣1，即：y=e x﹣1∵x＞0，∴y∈R所以函数f（x）=lnx+1（x＞0）反函数为y=e x﹣1（x∈R）故选：B．【点评】由于是基本题目，解题思路清晰，求解过程简捷，所以容易解答；解答时注意函数f（x）=lnx+1（x＞0）值域的确定，这里利用对数函数的值域推得．9．（5分）已知双曲线=1（a＞0，b＞0）的一条渐近线方程为y=x，则双曲线的离心率为（）A．B．C．D．【分析】由题意设出双曲线的方程，得到它的一条渐近线方程y=x即y=x，由此可得b：a=4：3，结合双曲线的平方关系可得c与a的比值，求出该双曲线的离心率．【解答】解：∵双曲线的中心在原点，焦点在x轴上，∴设双曲线的方程为，（a＞0，b＞0）由此可得双曲线的渐近线方程为y=±x，结合题意一条渐近线方程为y=x，得=，设b=4t，a=3t，则c==5t（t＞0）∴该双曲线的离心率是e==．故选：A．【点评】本题给出双曲线的一条渐近线方程，求双曲线的离心率，着重考查了双曲线的标准方程、基本概念和简单几何性质等知识，属于基础题．10．（5分）若f（sinx）=2﹣cos2x，则f（cosx）等于（）A．2﹣sin2x B．2+sin2x C．2﹣cos2x D．2+cos2x【分析】本题考查的知识点是函数解析式的求法，根据已知中f（sinx）=2﹣cos2x，结合倍角公式对解析式进行凑配，不难得到函数f（x）的解析式，然后将cosx 代入，并化简即可得到答案．【解答】解：∵f（sinx）=2﹣（1﹣2sin2x）=1+2sin2x，∴f（x）=1+2x2，（﹣1≤x≤1）∴f（cosx）=1+2cos2x=2+cos2x．故选：D．【点评】求解析式的几种常见方法：①代入法：即已知f（x），g（x），求f（g （x））用代入法，只需将g（x）替换f（x）中的x即得；②换元法：已知f（g （x）），g（x），求f（x）用换元法，令g（x）=t，解得x=g﹣1（t），然后代入f （g（x））中即得f（t），从而求得f（x）．当f（g（x））的表达式较简单时，可用“配凑法”；③待定系数法：当函数f（x）类型确定时，可用待定系数法．④方程组法：方程组法求解析式的实质是用了对称的思想．一般来说，当自变量互为相反数、互为倒数或是函数具有奇偶性时，均可用此法．在解关于f（x）的方程时，可作恰当的变量代换，列出f（x）的方程组，求得f（x）．11．（5分）过点（﹣1，0）作抛物线y=x2+x+1的切线，则其中一条切线为（）A．2x+y+2=0 B．3x﹣y+3=0 C．x+y+1=0 D．x﹣y+1=0【分析】这类题首先判断某点是否在曲线上，（1）若在，直接利用导数的几何意义，求函数在此点处的斜率，利用点斜式求出直线方程（2）若不在，应首先利用曲线与切线的关系求出切点坐标，进而求出切线方程．此题属于第二种．【解答】解：y'=2x+1，设切点坐标为（x0，y0），则切线的斜率为2x0+1，且y0=x02+x0+1于是切线方程为y﹣x02﹣x0﹣1=（2x0+1）（x﹣x0），因为点（﹣1，0）在切线上，可解得x0=0或﹣2，当x0=0时，y0=1；x0=﹣2时，y0=3，这时可以得到两条直线方程，验正D正确．故选：D．【点评】函数y=f（x）在x=x0处的导数的几何意义，就是曲线y=f（x）在点P（x0，y0）处的切线的斜率，过点P的切线方程为：y﹣y0=f′（x0）（x﹣x0）12．（5分）5名志愿者分到3所学校支教，每个学校至少去一名志愿者，则不同的分派方法共有（）A．150种B．180种C．200种D．280种【分析】根据题意，分析可得人数分配上有两种方式即1，2，2与1，1，3；分别计算两种情况下的情况数目，相加可得答案．【解答】解：人数分配上有两种方式即1，2，2与1，1，3若是1，1，3，则有=60种，若是1，2，2，则有=90种所以共有150种，故选：A．【点评】本题考查组合的运用，难点在于分组的情况的确定．二、填空题（共4小题，每小题4分，满分16分）13．（4分）在的展开式中常数项为45（用数字作答）．【分析】利用二项式的通项公式（让次数为0，求出r）就可求出答案．【解答】解：要求常数项，即40﹣5r=0，可得r=8代入通项公式可得T r=C108=C102=45+1故答案为：45．【点评】二项展开式的通项公式是解决二项展开式的特定项问题的工具．14．（4分）圆O1是以R为半径的球O的小圆，若圆心O1到球心O的距离与球半径面积S1和球O的表面积S的比为S1：S=2：9，则圆心O1到球心O的距离与球半径的比OO1：R=1：3．【分析】利用两个圆的面积之比，推出半径比，结合圆心O1到球心O的距离与球半径、圆心O1的半径满足勾股定理，即可求出结果．【解答】解：设圆O1的半径为r，则S1=πr2，S=4πR2，由S1：S=2：9得r：R=：3又r2+OO12=R2，可得OO1：R=1：3故答案为：1：3【点评】本题考查球的表面积，球的截面知识，考查计算能力，是基础题．15．（4分）过点的直线l将圆（x﹣2）2+y2=8分成两段弧，当劣弧所对的圆心角最小时，直线l的斜率k=．【分析】由劣弧所对的圆心角最小弦长最短，及过圆内一点最短的弦与过该点的直径垂直，易得到解题思路．【解答】解：由题意，点P（1，）在圆（x﹣2）2+y2=8的内部，圆心为C（2，0），要使得劣弧所对的圆心角最小，只能是直线l⊥CP，所以k=﹣=，故答案为．【点评】垂径定理及其推论是解决直线与圆关系时常用的定理，要求大家熟练掌握，垂径定理：垂直于弦的直径平分这条弦，并且平分这条弦所对的两条弧．相关推论，过圆内一点垂直于该点直径的弦最短，且弦所在的劣弧最短，优弧最长，弦所对的圆心角、圆周角最小．16．（4分）一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如图）．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在[2500，3000）（元）月收入段应抽出25人．【分析】直方图中小矩形的面积表示频率，先计算出[2500，3000）内的频率，再计算所需抽取人数即可．【解答】解：由直方图可得[2500，3000）（元）月收入段共有10000×0.0005×500=2500人按分层抽样应抽出人故答案为：25【点评】本题主要考查直方图和分层抽样，难度不大．三、解答题（共6小题，满分74分）17．（12分）在△ABC中，∠B=45°，AC=，cosC=，（1）求BC的长；（2）若点D是AB的中点，求中线CD的长度．【分析】（1）先由cosC求得sinC，进而根据sinA=sin（180°﹣45°﹣C）求得sinA，再由正弦定理知求得BC．（2）先由正弦定理知求得AB，进而可得BD，再在△ACD中由余弦定理求得CD．【解答】解：（1）由由正弦定理知（2）由余弦定理知=【点评】本题主要考查正弦定理和余弦定理在解三角形中的应用．属基础题．18．（12分）设等比数列{a n}的前n项和为S n，S4=1，S8=17，求通项公式a n．【分析】设出数列的公比，由题意知公比不为0，根据题目所给的两个前几项的和，列出方程求出公比有两个值，对于这两种情况分别写出数列的通项公式．【解答】解：设{a n}的公比为q，由S4=1，S8=17知q≠1，∴得①②由①和②式整理得解得q4=16所以q=2或q=﹣2将q=2代入①式得，∴将q=﹣2代入①式得，∴，综上所述或【点评】本题是一个等比数列的基本量的运算，这种问题是数列中最容易出的一种小型题目，多出在选择和填空中，是考查数列的基础知识的一道送分的题目，只要解题认真就可以得分．19．（12分）某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意出取2件产品进行检验．设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品．（1）用ξ表示抽检的6件产品中二等品的件数，求ξ的分布列及ξ的数学期望；（2）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品被用户拒绝的概率．【分析】（1）由取出的第一、二、三箱中分别有0件、1件、2件二等品可知变量ξ的取值，结合变量对应的事件做出这四个事件发生的概率，写出分布列和期望．（2）由上一问做出的分布列可以知道，P（ξ=2）=，P（ξ=3）=，这两个事件是互斥的，根据互斥事件的概率公式得到结果．【解答】解（1）由题意知抽检的6件产品中二等品的件数ξ=0，1，2，3==，∴ξ的分布列为∴ξ的数学期望E（ξ）=（2）∵P（ξ=2）=，P（ξ=3）=，这两个事件是互斥的∴P（ξ≥2）=【点评】本题主要考查分布列的求法以及利用分布列求期望和概率，求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题，题目做起来不难，运算量也不大．20．（12分）如图，在直三棱柱ABC﹣A1B1C1中，AB=BC，D、E分别为BB1、AC1的中点．（I）证明：ED为异面直线BB1与AC1的公垂线；（II）设，求二面角A 1﹣AD﹣C1的大小．【分析】（Ⅰ）设O为AC中点，连接EO，BO，欲证ED为异面直线AC1与BB1的公垂线，只需证明ED与直线AC1与BB1都垂直且相交，根据线面垂直的性质可知ED⊥CC1，而ED⊥BB1，即可证得；（Ⅱ）连接A1E，作EF⊥AD，垂足为F，连接A1F，根据二面角的平面角定义可知∠A1FE为二面角A1﹣AD﹣C1的平面角，在三角形A1FE中求出此角即可．【解答】解：（Ⅰ）设O为AC中点，连接EO，BO，则EO C1C，又C1C B1B，所以EO DB，EOBD为平行四边形，ED∥OB．（2分）∵AB=BC，∴BO⊥AC，又平面ABC⊥平面ACC1A1，BOÌ面ABC，故BO⊥平面ACC1A1，∴ED⊥平面ACC1A1，ED⊥AC1，ED⊥CC1，∴ED⊥BB1，ED为异面直线AC1与BB1的公垂线．（6分）（Ⅱ）连接A1E，由AA1=AC=AB可知，A1ACC1为正方形，∴A1E⊥AC1，又由ED⊥平面ACC1A1和EDÌ平面ADC1知平面ADC1⊥平面A1ACC1，∴A1E⊥平面ADC1．作EF⊥AD，垂足为F，连接A1F，则A1F⊥AD，∠A1FE为二面角A1﹣AD﹣C1的平面角．不妨设AA1=2，则AC=2，AB=，ED=OB=1，EF==，tan∠A1FE=，∴∠A1FE=60°．所以二面角A1﹣AD﹣C1为60°．（12分）【点评】本题主要考查了异面直线公垂线的证明，二面角的度量，以及空间想象能力和推理能力，属于基础题．21．（14分）设a∈R，二次函数f（x）=ax2﹣2x﹣2a．若f（x）＞0的解集为A，B={x|1＜x＜3}，A∩B≠∅，求实数a的取值范围．【分析】解：注意到△=4+8a2＞0，则函数有两个零点，由a的正负，确定不等式解集的形式．结合着数轴分类讨论．【解答】解：由题意可知二次函数a≠0，令f（x）=0解得其两根为由此可知x1＜0，x2＞0（i）当a＞0时，A={x|x＜x1}∪{x|x＞x2}，则A∩B≠ϕ的充要条件是x2＜3，即解得（ii）当a＜0时，A={x|x1＜x＜x2}A∩B≠ϕ的充要条件是x2＞1，即解得a＜﹣2综上，使A∩B≠ϕ成立的a的取值范围为【点评】在对集合的相关问题进行求解时，分类讨论时经常考查到的思想方法，另外对于一元二次不等式的解法也是一个基本的知识点，要熟练掌握．22．（12分）已知抛物线x2=4y的焦点为F，A、B是抛物线上的两动点，且．过A、B两点分别作抛物线的切线，设其交点为M．（Ⅰ）证明为定值；（Ⅱ）设△ABM的面积为S，写出S=f（λ）的表达式，并求S的最小值．【分析】（1）设A（x1，y1），B（x2，y2），M（x o，y o），根据抛物线方程可得焦点坐标和准线方程，设直线方程与抛物线方程联立消去y，根据判别式大于0求得x1+x2和x1x2，根据曲线4y=x2上任意一点斜率为y′=，可得切线AM和BM的方程，联立方程求得交点坐标，求得和，进而可求得•的结果为0，进而判断出AB⊥FM．（2）利用（1）的结论，根据x1+x2的关系式求得k和λ的关系式，进而求得弦长AB，可表示出△ABM面积．最后根据均值不等式求得S的范围，得到最小值．【解答】解：（1）设A（x1，y1），B（x2，y2），M（x o，y o），焦点F（0，1），准线方程为y=﹣1，显然AB斜率存在且过F（0，1）设其直线方程为y=kx+1，联立4y=x2消去y得：x2﹣4kx﹣4=0，判别式△=16（k2+1）＞0．x1+x2=4k，x1x2=﹣4于是曲线4y=x2上任意一点斜率为y′=，则易得切线AM，BM方程分别为y=（）x1（x﹣x1）+y1，y=（）x2（x﹣x2）+y2，其中4y1=x12，4y2=x22，联立方程易解得交点M坐标，x o==2k，y o==﹣1，即M（，﹣1）从而，=（，﹣2），（x2﹣x1，y2﹣y1）•=（x1+x2）（x2﹣x1）﹣2（y2﹣y1）=（x22﹣x12）﹣2[（x22﹣x12）]=0，（定值）命题得证．这就说明AB⊥FM．（Ⅱ）由（Ⅰ）知在△ABM中，FM⊥AB，因而S=|AB||FM|．∵，∴（﹣x1，1﹣y1）=λ（x2，y2﹣1），即，而4y1=x12，4y2=x22，则x22=，x12=4λ，|FM|====．因为|AF|、|BF|分别等于A、B到抛物线准线y=﹣1的距离，所以|AB|=|AF|+|BF|=y1+y2+2=+2=λ++2=（）2．于是S=|AB||FM|=（）3，由≥2知S≥4，且当λ=1时，S取得最小值4．【点评】本题主要考查了抛物线的应用．抛物线与直线的关系和抛物线的性质等都是近几年高考的热点，故应重点掌握．。

2006年普通高等学校招生全国统一考试文科数学一、选择题⑴、已知向量a b 、满足1,4,a b ==,且2a b =，则a 与b 的夹角为A ．6πB ．4πC ．3πD ．2π ⑵、设集合{}20M x x x =-<，{}2N x x =<，则 A ．M N =∅ B ．M N M =C ．M N M =D ．M N R =⑶、已知函数x y e =的图象与函数()y f x =的图象关于直线y x =对称,则A ．()22()x f x e x R =∈B ．()2ln 2ln (0)f x x x =>C ．()22()x f x e x R =∈D ．()2ln ln 2(0)f x x x =+>⑷、双曲线221mx y +=的虚轴长是实轴长的2倍，则m =A ．14-B ．4-C ．4D ．14⑸、设n S 是等差数列{}n a 的前n 项和，若735S =，则4a =A ．8B ．7C ．6D ．5⑹、函数()tan 4f x x π⎛⎫=+ ⎪⎝⎭的单调增区间为 A ．,,22k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭ B ．()(),1,k k k Z ππ+∈ C ．3,,44k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭ D ．3,,44k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭ ⑺、从圆222210x x y y -+-+=外一点()3,2P 向这个圆作两条切线,则两切线夹角的余弦值为A ．12B ．35C ．0 ⑻、ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ，若a 、b 、c 成等比数列，且2c a =，则cos B =A ．14B ．34C ．4D ．3 ⑼、已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是A ．16πB ．20πC ．24πD ．32π抛物线2y x =-上的点到直线4380x y +-=距离的最小值是A ．43B ．75C ．85D ．3 ⑽、在1012x x ⎛⎫- ⎪⎝⎭的展开式中，4x 的系数为 A ．120- B ．120 C ．15- D ．15⑾、抛物线2y x =-上的点到直线4380x y +-=距离的最小值是A ．43B ．75C ．85D ．3 ⑿、用长度分别为2、3、4、5、6（单位:cm )的5根细木棒围成一个三角形（允许连接，但不允许折断)，能够得到的三角形的最大面积为A ．285cmB ．2610cmC ．2355cmD ．220cm二、填空题：本大题共4小题，每小题4分,共16分，把答案填在横线上.⒀、已知函数()1,1x f x a z =-+，若()f x 为奇函数，则a =________. ⒁、已知正四棱锥的体积为12,底面对角线的长为26，则侧面与底面所成的二面角等于_______________.⒂、设2z y x =-，式中变量x y 、满足下列条件21x y -≥- 3223x y +≤1y ≥则z 的最大值为_____________.⒃、安排7位工作人员在5月1日到5月7日值班，每人值班一天，其中甲、乙二人都不能安排在5月1日和2日，不同的安排方法共有__________种。

财务管理课程实验实习小结本次维持一周的财务管理课程实验在小组成员共同的努力和相互的配合下完成了，这其中我们也遇到了很多的问题，经过多方面的搜集资料，对解决和发现这些问题提供了很好的帮助。

各小组成员积极的配合，并确定了一致的目标，使本次实习也很好的体现了团队合作的精神。

在课程实验开始，辅导老师给我们讲解了有关做财务分析报告的具体要求,包括课程实验的目的，课程实验设计的组织形式，课程实验设计的内容，其中内容这一部分强调了重点，要求我们对以财务报告分析为主线，设计上市公司三年的财务指标分析，会计政策分析，筹资投资政策的分析，股利分配政策分析，内部控制分析，股权结构分析等一系列内容，是一次综合性极强的实验设计课程。

我们小组在完成这一部分的时候投入了最多的时间和精力，这一部分在整个课程实验阶段也最为重要，通过对网上信息的浏览，我们首先确定了几家比较适合的上市公司进行初步的了解和查询，了解它近三年的业绩，以及各项发展指标，经过小组成员的讨论和最后的表决，选出一个或两个的备选方案，在经过深入的研究，通过对其财务政策的初步了解，选择出近期财务政策有利于企业发展的项目，并最终予以确定，在确定投资的上市公司后，就要对其三年财务报告进行系统的分析，对已搜集好的三年财务报告进行整理，并列出所选上市公司财务相关问题，并进行讨论分析。

问题提出后，就要考虑到小组成员如何安排的问题，按照小组成员自己对各个问题的兴趣度，让小组成员自己发挥出自己对处理和分析哪个板块的能力，小组长统筹后，安排人员调度，让其中一名组员参与对偿债能力分析，营运能力分析，营利能力分析，发展能力分析，后一位小组成员在前一名组员分析的基础上，指出公司可能存在的问题，并提出相应的改进措施，并同时对现金流量表中相关现金流量的数据分析公司偿债能力，收益能力，以及收益质量。

在这一部分进行的同时，负责第三名组员对公司的财务的政策进行分析，包括三件筹资，投资，分配政策的变化及其存在的问题。

2006年全国统一高考数学试卷（文科）（全国卷Ⅰ）一、选择题（共12小题，每小题5分，满分60分）1．（5分）已知向量、满足||=1，||=4，且•=2，则与夹角为（）A．B．C．D．2．（5分）设集合M={x|x2﹣x＜0}，N={x||x|＜2}，则（）A．M∩N=∅ B．M∩N=M C．M∪N=M D．M∪N=R3．（5分）已知函数y=e x的图象与函数y=f（x）的图象关于直线y=x对称，则（）A．f（2x）=e2x（x∈R）B．f（2x）=ln2•lnx（x＞0）C．f（2x）=2e x（x∈R）D．f（2x）=lnx+ln2（x＞0）4．（5分）双曲线mx2+y2=1的虚轴长是实轴长的2倍，则m=（）A．B．﹣4 C．4 D．5．（5分）设S n是等差数列{a n}的前n项和，若S7=35，则a4=（）A．8 B．7 C．6 D．56．（5分）函数的单调增区间为（）A．B．（kπ，（k+1）π），k∈ZC．D．7．（5分）从圆x2﹣2x+y2﹣2y+1=0外一点P（3，2）向这个圆作两条切线，则两切线夹角的余弦值为（）A．B．C．D．08．（5分）△ABC的内角A、B、C的对边分别为a、b、c，若a、b、c成等比数列，且c=2a，则cosB=（）A．B．C．D．9．（5分）已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是（）A．16πB．20πC．24πD．32π10．（5分）在的展开式中，x4的系数为（）A．﹣120 B．120 C．﹣15 D．1511．（5分）抛物线y=﹣x2上的点到直线4x+3y﹣8=0距离的最小值是（）A．B．C．D．312．（5分）用长度分别为2、3、4、5、6（单位：cm）的5根细木棒围成一个三角形（允许连接，但不允许折断），能够得到的三角形的最大面积为（）A．B．C．D．20cm2二、填空题（共4小题，每小题4分，满分16分）13．（4分）已知函数f（x）=a﹣，若f（x）为奇函数，则a=．14．（4分）已知正四棱锥的体积为12，底面对角线长为，则侧面与底面所成的二面角等于°．15．（4分）设z=2y﹣x，式中变量x、y满足下列条件：，则z的最大值为．16．（4分）安排7位工作人员在5月1日至5月7日值班，每人值班一天，其中甲、乙二人都不安排在5月1日和2日．不同的安排方法共有种（用数字作答）．三、解答题（共6小题，满分74分）17．（12分）已知{a n}为等比数列，，求{a n}的通项公式．18．（12分）ABC的三个内角为A、B、C，求当A为何值时，取得最大值，并求出这个最大值．19．（12分）A、B是治疗同一种疾病的两种药，用若干试验组进行对比试验．每个试验组由4只小白鼠组成，其中2只服用A，另2只服用B，然后观察疗效．若在一个试验组中，服用A有效的小白鼠的只数比服用B有效的多，就称该试验组为甲类组．设每只小白鼠服用A有效的概率为，服用B有效的概率为．（Ⅰ）求一个试验组为甲类组的概率；（Ⅱ）观察3个试验组，用ξ表示这3个试验组中甲类组的个数，求ξ的分布列和数学期望．20．（12分）如图，l1、l2是互相垂直的异面直线，MN是它们的公垂线段．点A、B在l1上，C在l2上，AM=MB=MN．（Ⅰ）证明AC⊥NB；（Ⅱ）若∠ACB=60°，求NB与平面ABC所成角的余弦值．21．（12分）设P是椭圆=1（a＞1）短轴的一个端点，Q为椭圆上一个动点，求|PQ|的最大值．22．（14分）设a为实数，函数f（x）=x3﹣ax2+（a2﹣1）x在（﹣∞，0）和（1，+∞）都是增函数，求a的取值范围．2006年全国统一高考数学试卷（文科）（全国卷Ⅰ）参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．（5分）（2006•全国卷Ⅰ）已知向量、满足||=1，||=4，且•=2，则与夹角为（）A．B．C．D．【分析】本题是对向量数量积的考查，根据两个向量的夹角和模之间的关系，用数量积列出等式，变化出夹角的余弦表示式，代入给出的数值，求出余弦值，注意向量夹角的范围，求出适合的角．【解答】解：∵向量a、b满足，且，设与的夹角为θ，则cosθ==，∵θ∈【0π】，∴θ=，故选C．2．（5分）（2006•全国卷Ⅰ）设集合M={x|x2﹣x＜0}，N={x||x|＜2}，则（）A．M∩N=∅ B．M∩N=M C．M∪N=M D．M∪N=R【分析】M、N分别是二次不等式和绝对值不等式的解集，分别解出再求交集合并集．【解答】解：集合M={x|x2﹣x＜0}={x|0＜x＜1}，N={x||x|＜2}={x|﹣2＜x＜2}，∴M∩N=M，故选：B．3．（5分）（2006•全国卷Ⅰ）已知函数y=e x的图象与函数y=f（x）的图象关于直线y=x对称，则（）A．f（2x）=e2x（x∈R）B．f（2x）=ln2•lnx（x＞0）C．f（2x）=2e x（x∈R）D．f（2x）=lnx+ln2（x＞0）【分析】本题考查反函数的概念、互为反函数的函数图象的关系、求反函数的方法等相关知识和方法．根据函数y=e x的图象与函数y=f（x）的图象关于直线y=x对称可知f（x）是y=e x 的反函数，由此可得f（x）的解析式，进而获得f（2x）．【解答】解：函数y=e x的图象与函数y=f（x）的图象关于直线y=x对称，所以f（x）是y=e x的反函数，即f（x）=lnx，∴f（2x）=ln2x=lnx+ln2（x＞0），选D．4．（5分）（2006•全国卷Ⅰ）双曲线mx2+y2=1的虚轴长是实轴长的2倍，则m=（）A．B．﹣4 C．4 D．【分析】由双曲线mx2+y2=1的虚轴长是实轴长的2倍，可求出该双曲线的方程，从而求出m的值．【解答】解：双曲线mx2+y2=1的虚轴长是实轴长的2倍，∴m＜0，且双曲线方程为，∴m=，故选：A．5．（5分）（2006•全国卷Ⅰ）设S n是等差数列{a n}的前n项和，若S7=35，则a4=（）A．8 B．7 C．6 D．5【分析】充分运用等差数列前n项和与某些特殊项之间的关系解题．【解答】解：S n是等差数列{a n}的前n项和，若S7=×7=7a4=35，∴a4=5，故选D．6．（5分）（2006•全国卷Ⅰ）函数的单调增区间为（）A．B．（kπ，（k+1）π），k∈ZC．D．【分析】先利用正切函数的单调性求出函数单调增时x+的范围i，进而求得x 的范围．【解答】解：函数的单调增区间满足，∴单调增区间为，故选C7．（5分）（2006•全国卷Ⅰ）从圆x2﹣2x+y2﹣2y+1=0外一点P（3，2）向这个圆作两条切线，则两切线夹角的余弦值为（）A．B．C．D．0【分析】先求圆心到P的距离，再求两切线夹角一半的三角函数值，然后求出结果．【解答】解：圆x2﹣2x+y2﹣2y+1=0的圆心为M（1，1），半径为1，从外一点P （3，2）向这个圆作两条切线，则点P到圆心M的距离等于，每条切线与PM的夹角的正切值等于，所以两切线夹角的正切值为，该角的余弦值等于，故选B．8．（5分）（2006•全国卷Ⅰ）△ABC的内角A、B、C的对边分别为a、b、c，若a、b、c成等比数列，且c=2a，则cosB=（）A．B．C．D．【分析】根据等比数列的性质，可得b=a，将c、b与a的关系结合余弦定理分析可得答案．【解答】解：△ABC中，a、b、c成等比数列，则b2=ac，由c=2a，则b=a，=，故选B．9．（5分）（2006•全国卷Ⅰ）已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是（）A．16πB．20πC．24πD．32π【分析】先求正四棱柱的底面边长，然后求其对角线，就是球的直径，再求其表面积．【解答】解：正四棱柱高为4，体积为16，底面积为4，正方形边长为2，正四棱柱的对角线长即球的直径为2，∴球的半径为，球的表面积是24π，故选C．10．（5分）（2006•全国卷Ⅰ）在的展开式中，x4的系数为（）A．﹣120 B．120 C．﹣15 D．15【分析】利用二项展开式的通项公式求出第r+1项，令x的指数为4求出x4的系数【解答】解：在的展开式中x4项是=﹣15x4，故选项为C．11．（5分）（2006•全国卷Ⅰ）抛物线y=﹣x2上的点到直线4x+3y﹣8=0距离的最小值是（）A．B．C．D．3【分析】设抛物线y=﹣x2上一点为（m，﹣m2），该点到直线4x+3y﹣8=0的距离为，由此能够得到所求距离的最小值．【解答】解：设抛物线y=﹣x2上一点为（m，﹣m2），该点到直线4x+3y﹣8=0的距离为，分析可得，当m=时，取得最小值为，故选B．12．（5分）（2006•全国卷Ⅰ）用长度分别为2、3、4、5、6（单位：cm）的5根细木棒围成一个三角形（允许连接，但不允许折断），能够得到的三角形的最大面积为（）A．B．C．D．20cm2【分析】设三角形的三边分别为a，b，c，令p=，则p=10．海伦公式S=≤=故排除C，D，由于等号成立的条件为10﹣a=10﹣b=10﹣c，故“=”不成立，推测当三边长相等时面积最大，故考虑当a，b，c三边长最接近时面积最大，进而得到答案．【解答】解：设三角形的三边分别为a，b，c，令p=，则p=10．由海伦公式S=知S=≤=＜20＜3由于等号成立的条件为10﹣a=10﹣b=10﹣c，故“=”不成立，∴S＜20＜3．排除C，D．由以上不等式推测，当三边长相等时面积最大，故考虑当a，b，c三边长最接近时面积最大，此时三边长为7，7，6，用2、5连接，3、4连接各为一边，第三边长为7组成三角形，此三角形面积最大，面积为，故选B．二、填空题（共4小题，每小题4分，满分16分）13．（4分）（2006•全国卷Ⅰ）已知函数f（x）=a﹣，若f（x）为奇函数，则a=．【分析】因为f（x）为奇函数，而在x=0时，f（x）有意义，利用f（0）=0建立方程，求出参数a的值．【解答】解：函数．若f（x）为奇函数，则f（0）=0，即，a=．故答案为14．（4分）（2006•全国卷Ⅰ）已知正四棱锥的体积为12，底面对角线长为，则侧面与底面所成的二面角等于60°．【分析】先根据底面对角线长求出边长，从而求出底面积，再由体积求出正四棱锥的高，求出侧面与底面所成的二面角的平面角的正切值即可．【解答】解：正四棱锥的体积为12，底面对角线的长为，底面边长为2，底面积为12，所以正四棱锥的高为3，则侧面与底面所成的二面角的正切tanα=，∴二面角等于60°，故答案为60°15．（4分）（2006•全国卷Ⅰ）设z=2y﹣x，式中变量x、y满足下列条件：，则z的最大值为11．【分析】先根据约束条件画出可行域，再利用几何意义求最值，z=2y﹣x表示直线在y轴上的截距，只需求出可行域直线在y轴上的截距最大值即可．【解答】解：，在坐标系中画出图象，三条线的交点分别是A（0，1），B（7，1），C（3，7），在△ABC中满足z=2y﹣x的最大值是点C，代入得最大值等于11．故填：11．16．（4分）（2006•全国卷Ⅰ）安排7位工作人员在5月1日至5月7日值班，每人值班一天，其中甲、乙二人都不安排在5月1日和2日．不同的安排方法共有2400种（用数字作答）．【分析】本题是一个分步计数问题，先安排甲、乙两人在假期的后5天值班，有A52种排法，其余5人再进行排列，有A55种排法，根据分步计数原理得到结果．【解答】解：由题意知本题是一个分步计数问题，首先安排甲、乙两人在假期的后5天值班，有A52=20种排法，其余5人再进行排列，有A55=120种排法，∴根据分步计数原理知共有20×120=2400种安排方法．故答案为：2400三、解答题（共6小题，满分74分）17．（12分）（2006•全国卷Ⅰ）已知{a n}为等比数列，，求{a n}的通项公式．【分析】首先设出等比数列的公比为q，表示出a2，a4，利用两者之和为，求出公比q的两个值，利用其两个值分别求出对应的首项a1，最后利用等比数列的通项公式得到即可．【解答】解：设等比数列{a n}的公比为q，则q≠0，a2==，a4=a3q=2q所以+2q=，解得q1=，q2=3，当q1=，a1=18．所以a n=18×（）n﹣1==2×33﹣n．当q=3时，a1=，所以a n=×3n﹣1=2×3n﹣3．18．（12分）（2006•全国卷Ⅰ）ABC的三个内角为A、B、C，求当A为何值时，取得最大值，并求出这个最大值．【分析】利用三角形中内角和为π，将三角函数变成只含角A，再利用三角函数的二倍角公式将函数化为只含角，利用二次函数的最值求出最大值【解答】解：由A+B+C=π，得=﹣，所以有cos=sin．cosA+2cos=cosA+2sin=1﹣2sin2+2sin=﹣2（sin﹣）2+当sin=，即A=时，cosA+2cos取得最大值为故最大值为19．（12分）（2006•全国卷Ⅰ）A、B是治疗同一种疾病的两种药，用若干试验组进行对比试验．每个试验组由4只小白鼠组成，其中2只服用A，另2只服用B，然后观察疗效．若在一个试验组中，服用A有效的小白鼠的只数比服用B有效的多，就称该试验组为甲类组．设每只小白鼠服用A有效的概率为，服用B 有效的概率为．（Ⅰ）求一个试验组为甲类组的概率；（Ⅱ）观察3个试验组，用ξ表示这3个试验组中甲类组的个数，求ξ的分布列和数学期望．【分析】（1）由题意知本题是一个独立重复试验，根据所给的两种药物对小白鼠有效的概率，计算出小白鼠有效的只数的概率，对两种药物有效的小白鼠进行比较，得到甲类组的概率．（2）由题意知本试验是一个甲类组的概率不变，实验的条件不变，可以看做是一个独立重复试验，所以变量服从二项分布，根据二项分布的性质写出分布列和期望．【解答】解：（1）设A i表示事件“一个试验组中，服用A有效的小鼠有i只“，i=0，1，2，B i表示事件“一个试验组中，服用B有效的小鼠有i只“，i=0，1，2，依题意有：P（A1）=2××=，P（A2）=×=．P（B0）=×=，P（B1）=2××=，所求概率为：P=P（B0•A1）+P（B0•A2）+P（B1•A2）=×+×+×=（Ⅱ）ξ的可能值为0，1，2，3且ξ～B（3，）．P（ξ=0）=（）3=，P（ξ=1）=C31××（）2=，P（ξ=2）=C32×（）2×=，P（ξ=3）=（）3=∴ξ的分布列为：ξ0123P∴数学期望Eξ=3×=．20．（12分）（2006•全国卷Ⅰ）如图，l1、l2是互相垂直的异面直线，MN是它们的公垂线段．点A、B在l1上，C在l2上，AM=MB=MN．（Ⅰ）证明AC⊥NB；（Ⅱ）若∠ACB=60°，求NB与平面ABC所成角的余弦值．【分析】（1）欲证AC⊥NB，可先证BN⊥面ACN，根据线面垂直的判定定理只需证AN⊥BN，CN⊥BN即可；（2）易证N在平面ABC内的射影H是正三角形ABC的中心，连接BH，∠NBH 为NB与平面ABC所成的角，在Rt△NHB中求出此角即可．【解答】解：（Ⅰ）由已知l2⊥MN，l2⊥l1，MN∩l1=M，可得l2⊥平面ABN．由已知MN⊥l1，AM=MB=MN，可知AN=NB且AN⊥NB．又AN为AC在平面ABN内的射影．∴AC⊥NB（Ⅱ）∵AM=MB=MN，MN是它们的公垂线段，由中垂线的性质可得AN=BN，∴Rt△CAN≌Rt△CNB，∴AC=BC，又已知∠ACB=60°，因此△ABC为正三角形．∵Rt△ANB≌Rt△CNB，∴NC=NA=NB，因此N在平面ABC内的射影H是正三角形ABC的中心，连接BH，∠NBH为NB与平面ABC所成的角．在Rt△NHB中，cos∠NBH===．21．（12分）（2006•全国卷Ⅰ）设P是椭圆=1（a＞1）短轴的一个端点，Q为椭圆上一个动点，求|PQ|的最大值．【分析】依题意可知|PQ|=，因为Q在椭圆上，所以x2=a2（1﹣y2），|PQ|2=a2（1﹣y2）+y2﹣2y+1=（1﹣a2）y2﹣2y+1+a2=（1﹣a2）（y﹣）2﹣+1+a2．由此分类讨论进行求解．【解答】解：由已知得到P（0，1）或P（0，﹣1）由于对称性，不妨取P（0，1）设Q（x，y）是椭圆上的任一点，则|PQ|=，①又因为Q在椭圆上，所以，x2=a2（1﹣y2），|PQ|2=a2（1﹣y2）+y2﹣2y+1=（1﹣a2）y2﹣2y+1+a2=（1﹣a2）（y﹣）2﹣+1+a2．②因为|y|≤1，a＞1，若a≥，则||≤1，所以如果它包括对称轴的x的取值，那么就是顶点上取得最大值，即当﹣1≤＜0时，在y=时，|PQ|取最大值；如果对称轴不在y的取值范围内的话，那么根据图象给出的单调性来求解．即当＜﹣1时，则当y=﹣1时，|PQ|取最大值2．22．（14分）（2006•全国卷Ⅰ）设a为实数，函数f（x）=x3﹣ax2+（a2﹣1）x在（﹣∞，0）和（1，+∞）都是增函数，求a的取值范围．【分析】先对函数f（x）进行求导得到一个二次函数，根据二次函数的图象和性质令f'（x）≥0在（﹣∞，0）和（1，+∞）成立，解出a的值．【解答】解：f'（x）=3x2﹣2ax+（a2﹣1），其判别式△=4a2﹣12a2+12=12﹣8a2．（ⅰ）若△=12﹣8a2=0，即a=±，当x∈（﹣∞，），或x∈（，+∞）时，f'（x）＞0，f（x）在（﹣∞，+∞）为增函数．所以a=±．（ⅱ）若△=12﹣8a2＜0，恒有f'（x）＞0，f（x）在（﹣∞，+∞）为增函数，所以a2＞，即a∈（﹣∞，﹣）∪（，+∞）（ⅲ）若△12﹣8a2＞0，即﹣＜a＜，令f'（x）=0，解得x1=，x2=．当x∈（﹣∞，x1），或x∈（x2，+∞）时，f'（x）＞0，f（x）为增函数；当x∈（x1，x2）时，f'（x）＜0，f（x）为减函数．依题意x1≥0且x2≤1．由x1≥0得a≥，解得1≤a＜由x2≤1得≤3﹣a，解得﹣＜a＜，从而a∈[1，）综上，a的取值范围为（﹣∞，﹣]∪[，+∞）∪[1，），即a∈（﹣∞，﹣]∪[1，+∞）．。

2006年湖南省高考数学试卷（文科）一、选择题（共10小题，每小题5分，满分50分） 1. 函数y =√2x 的定义域是（ ） A.(0, 1]B.(0, +∞)C.[1, +∞)D.(1, +∞)2. 已知向量a →=(2,t)，b →=(1,2)，若t =t 1时，a → // b →；t =t 2时，a →⊥b →，则（ ） A.t 1=−4，t 2=−1 B.t 1=−4，t 2=1 C.t 1=4，t 2=−1D.t 1=4，t 2=13. 若(ax −1)5的展开式中x 3的系数是80，则实数a 的值是（ ） A.−2B.2√2C.√43D.24. 过半径为2的球O 表面上一点A 作球O 的截面，若OA 与该截面所成的角是60∘则该截面的面积是（ ） A.πB.2πC.2√3πD.3π5. “a ＝1”是“函数f(x)＝|x −a|在区间[1, +∞)上为增函数”的（ ） A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件6. 在数字1，2，3与符号+，-五个元素的所有全排列中，任意两个数字都不相邻的全排列个数是（ ） A.6B.12C.24D.187. 圆x 2+y 2−4x −4y −10=0上的点到直线x +y −14=0的最大距离与最小距离的差是( ) A.36B.18C.5√2D.6√28. 设点P 是函数f(x)=sin ωx 的图象C 的一个对称中心，若点P 到图象C 的对称轴上的距离的最小值π4，则f(x)的最小正周期是（ ） A.2πB.πC.π4D.π29. 过双曲线M:x 2−y 2b 2=1的左顶点A 作斜率为1的直线l ，若l 与双曲线M 的两条渐近线分别相交于点B ，C ，且|AB|=|BC|，则双曲线M 的离心率是（ ） A.√10B.√5C.√103D.√5210. 如图，OM // AB ，点P 由射线OM 、线段OB 及AB 的延长线围成的阴影区域内（不含边界）．且OP →=xOA →+yOB →，则实数对(x, y)可以是（ ）A.(14，34)B.(−23，23)C.(−14，34)D.(−15，75)二、填空题（共5小题，每小题4分，满分20分）11. 若数列{a n }满足：a 1=1，a n+1=2a n ．n =1，2，3…．则a 1+a 2+...+a n =________．12. 某高校有甲、乙两个数学建模兴趣班．其中甲班有40人，乙班50人．现分析两个班的一次考试成绩，算得甲班的平均成绩是90分，乙班的平均成绩是81分，则该校数学建模兴趣班的平均成绩是________分．13. 已知{x ≥1x −y +1≤02x −y −2≤0，则x 2+y 2的最小值是________．14. 过三棱柱ABC −A 1B 1C 1的任意两条棱的中点作直线，其中与平面ABB 1A 1平行的直线共有________条．15. 若f(x)=a sin (x +π4)+3sin (x −π4)是偶函数，则a =________． 三、解答题（共6小题，满分80分） 16. 已知√3sin θ−sin (π2−2θ)cos (π+θ)⋅cos θ=1，θ∈(0, π)，求θ的值．17. 某安全生产监督部门对5家小型煤矿进行安全检查（简称安检）．若安检不合格，则必须进行整改．若整改后经复查仍不合格，则强行关闭．设每家煤矿安检是否合格是相互独立的，且每家煤矿整改前安检合格的概率是0.5，整改后安检合格的概率是0.8，计算（结果精确到0.01）：（1）恰好有两家煤矿必须整改的概率；（2）平均有多少家煤矿必须整改；（3）至少关闭一家煤矿的概率．18. 如图，已知两个正四棱锥P−ABCD与Q−ABCD的高分别为1和2，AB=4．（1）证明PQ⊥平面ABCD；（2）求异面直线AQ与PB所成的角；（3）求点P到平面QAD的距离．19. 已知函数f(x)=ax3−3x2+1−3a．（1）讨论函数f(x)的单调性；（2）若曲线y=f(x)上两点A、B处的切线都与y轴垂直，且线段AB与x轴有公共点，求实数a的取值范围．。