全等三角形模型之手拉手模型

完整版)全等三角形之手拉手模型
本文将介绍手拉手模型中的全等三角形。

所谓手拉手模型，是指有公共顶点的两个等腰三角形，顶角相等。

因为顶点相连的四条边，形象的可以看作两双手，所以通常称为手拉手模型。

基本模型如下：已知，△ABB'和△ACC'都是等腰三角形，AB=AB'，AC=AC'，且∠BAB'=∠CAC'。

可以得出三个结论：结论1：△ABC≌△AB'C'(SAS)，BC=B'C'；结论2：
∠BOB'=∠BAB'；结论3：AO平分∠BOC'。

在共顶点的等腰直角三角形中，也可以应用手拉手模型。

例如，如下图所示，△ABC和△ADE是等腰直角三角形，且
∠BAC=∠DAE=90°。

可以证明：⑴BD=CE⑵BD⊥CE。

另外，在共顶点的等边三角形中，也可以使用手拉手模型。

如下图，点A为线段BD上一点，△ABC和△ADE均是等边
三角形。

可以求出：（1）CD=BE；（2）∠DAE＋
∠BFD=180°；（3）∠BFA=∠DFA=60°。

总之，手拉手模型在全等三角形的证明中是一个非常有用的工具，能够帮助我们更好地理解和应用三角形的性质。

长线交 CE 于 F 点.
证明重要结论：
C
① △ABD≌△ACE；
FD
② BD = CE；
③ BD 的延长线 BF⊥CE；
EA
B
解：∵△ABC、△ADE 都是等腰直角三角形， ∴ AB = AC，AD = AE. 在△ABD 和△ACE 中，
∴ △ABD≌△ACE(SAS). ∴ BD = CE. ∴ ∠ABD = ∠ACE. ∵ ∠BDC = ∠ABD + ∠BAC
E
① △ABD≌△ACE
② BD = CE
③ ∠BFC = ∠BAC = ∠DAE B
F D G
C
解：∵△ABC、△ADE 都是等腰三角形，
∴ AB = AC，AD = AE.
又∵∠BAC = ∠DAE，
A
∴∠BAC + ∠CAD =∠DAE +∠CAD，
即∠BAD = ∠CAE.
在△ABD 和△ACE 中
BE 交于点 O，AD 与 BC 交于点 P，BE 与 CD 交于点
Q，连接 PQ，则有以下五个结论： B ① AD = BE； ② PQ∥AE；
③ AP = BQ； ④ DE = DP；
⑤∠AOB = 60°．
P
OD Q
其中正确的结论有__①__②__③__⑤___.
A
C
E
=∠ACE + ∠BFC， ∴ ∠BFC = ∠BAC = 90°. ∴ BF⊥CE.
C FD
EA
B
练一练
2. 如图，△ABC、△ADE 都是等腰直角三角形，
∠BAC = ∠DAE = 90°，连接 BD、CE 交于点 F.
(1) 求证：BD = CE； (2) 求证：BD⊥CE. C

《三角形证明》题型解读12 全等典型模型：“手拉手”模型【知识梳理】（一）“手拉手模型”的基本图形题型特征：△ABC 与△BDE 是等边三角形，A 、B 、D 三点在同一直线上。

解题方法：一定有以下六个结论（三组全等、一个60°、一个等边△、一组平行线） ①△ABE ≌△CBD证明过程：∵△ABC 与△BDE 是等边三角形，∴∠1=∠2=∠3=60°，∴∠ABE=∠CBD=120°，∵AB=BC ，BE=BD ， ∴△ABE ≌△CBD （SAS ） ②△ABH ≌△CBF证明过程：∵△ABE ≌△CBD ，∴∠4=∠5，∵AB=BC ，∠1=∠2，∴△ABH ≌△CBF （SAS ） ③△BHE ≌△BFD证明过程：∵△ABE ≌△CBD ，∴∠6=∠7，∵BE=BD ，∠2=∠3，∴△BHE ≌△BFD （SAS ） ④∠AGC=60°证明过程：∵△ABE ≌△CBD ，∴∠6=∠7，在△GFE 和△BFD 中（“8”字模型），∠3=180°-∠BFD-∠7，∠EGF=180°-∠GFE-∠6，∵∠6=∠7，∠GFE=∠BFD ，∴∠3=∠EGF ，∵∠AGC=∠EGF ，∠3=60°，∴∠AGC=∠3=60° ⑤△BHF 是等边三角形证明过程：∵△BHE ≌△BFD （SAS ），∴BH=BF ，∵∠2=60°，∴△BHF 是等边三角形（有一个角是60°的等腰三角形是等边三角形） ⑥HF//AD证明过程：∵△BHF 是等边三角形，∴∠8=60°，∵∠3=60°，∴∠8=∠3，∴HF//AD （二）“手拉手模型”的变化图形题型特征：△ABC 与△BDE 是等边三角形，A 、B 、D 三点不在同一直线上。

图2M N 765431H GFEDCBA765431HG F ED CBA解题方法：一定有以下三个结论（一组全等，一个60°、一个角平分线） ①△ABE ≌△CBD证明过程：∵△ABC 与△BDE 是等边三角形，∴∠1=∠3=60°，∴∠ABE=∠CBD （共角模型），∵AB=BC ，BE=BD ， ∴△ABE ≌△CBD （SAS ） ②∠AGC=60°证明过程：∵△ABE ≌△CBD ，∴∠6=∠7，在△GFE 和△BFD 中（“8”字模型），∠3=180°-∠BFD-∠7，∠EGF=180°-∠GFE-∠6，∵∠6=∠7，∠GFE=∠BFD ，∴∠3=∠EGF ，∵∠AGC=∠EGF ，∠3=60°，∴∠AGC=∠3=60° ③BG 平分∠HBF证明过程：作BM ⊥AE 于点M ，BN ⊥GD 于点N ，如图2，∵△ABE ≌△CBD ，∴∠4=∠5，∵AB=BC ，∠AMB=∠CNB=90°，∴△ABM ≌△CBN （AAS ），∴BM=BN ，∴BG 平分∠HBF （到角两边的距离相等的点，在这个角的角平分线上） （三）常见“手拉手”变化图形【典型例题】例1.如图，C 为线段AE 上一动点（不与A 、E 重合），在AE 同侧分别作等边△ABC 和等 边△CDE ，AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连接PQ ，以下五个结论： ①AD ＝BE ；②PQ ∥AE ；③CP ＝CQ ；④BO ＝OE ；⑤∠AOB ＝60°，恒成立的结论有（ ）。

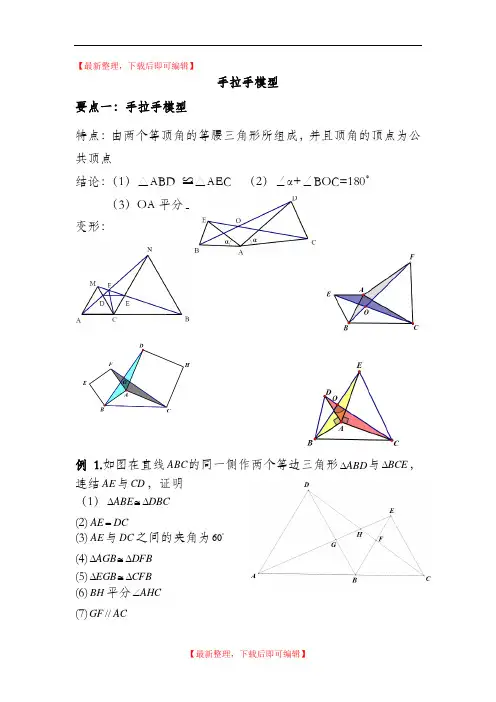
【最新整理，下载后即可编辑】手拉手模型要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°（3）OA平分∠BOC变形：例1.如图在直线ABC的同一侧作两个等边三角形ABD∆，∆与BCE 连结AE与CD，证明（1）DBC∆ABE∆≅(2)DCAE=(3)AE与DC之间的夹角为︒60(4)DFB≅∆AGB∆(5)CFB≅∆EGB∆(6)BH平分AHC∠(7)ACGF//变式精练1：如图两个等边三角形ABD∆与∆，连结AE与CD，BCE证明（1）DBC∆≅ABE∆（2）DCAE=（3）AE与DC之间的夹角为︒60（4）AE与DC的交点设为H,BH平分AHC∠变式精练2：如图两个等边三角形ABD∆与∆，连结AE与CD，BCE证明（1）DBC∆≅ABE∆(2）DCAE=(3）AE与DC之间的夹角为︒60(4）AE与DC的交点设为H,BH平分AHC∠例2：如图，两个正方形ABCD与DEFG,连结CEAG,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例4：两个等腰三角形ABD ∆与BCE ∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ， 问：（1）DBC ABE ∆≅∆是否成立？（2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？（4）HB 是否平分AHC ∠？。

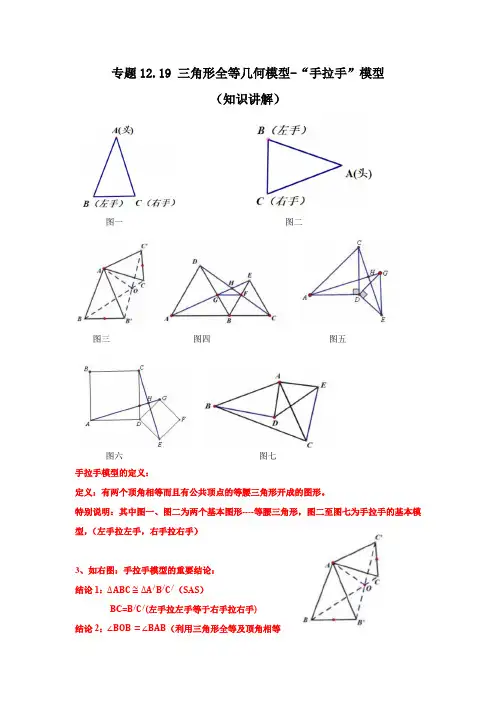
专题12.19 三角形全等几何模型-“手拉手”模型（知识讲解）图一图二图三图四图五图六图七手拉手模型的定义：定义：有两个顶角相等而且有公共顶点的等腰三角形开成的图形。

特别说明：其中图一、图二为两个基本图形----等腰三角形，图二至图七为手拉手的基本模型，（左手拉左手，右手拉右手）3、如右图：手拉手模型的重要结论：结论1：∆ABC≅∆A/B/C/（SAS）BC=B/C/(左手拉左手等于右手拉右手)结论2：∠BOB=∠BAB（利用三角形全等及顶角相等的等腰三角形底角相等）结论3：AO平分∠B O C/（利用三角形全等面积相等，再利用角平分线性质定理证明）典型例题讲练：在学习全等三角形知识时、教学兴趣小组发现这样一个模型：它是由两个共顶点且顶角相等的等腰三角形构成．在相对位置变化的同时，始终存在一对全等三角形．通过资料查询，他们得知这种模型称为“手拉手模型” 兴趣小组进行了如下操究：（1）如图1、两个等腰三角形△ABC和△ADE中，AB=AC，AE=AD，△BAC=△DAE，连接BD、CE、如果把小等腰三角形的腰长看作小手，大等腰三角形的腰长看作大手，两个等腰三角形有公共顶点，类似大手拉着小手，这个就是“手拉手模型”，在这个模型中，和△ADB 全等的三角形是，此线BD和CE的数量关系是（2）如图2、两个等腰直角三角形△ABC和△ADE中，AB=AC，AE=AD，△BAC=△DAE=90°，连接BD，CE，两线交于点P，请判断线段BD和CE的数量关系和位置关系，并说明理由：（3）如图3，已知△ABC、请完成作图：以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE（等边三角形三条边相等，三个角都等于60°），连接BE，CD，两线交于点P，并直接写出线段BE和CD的数量关系及△PBC+△PCB的度数、【答案】（1）△AEC，BD=CE；（2）BD=CE且BD△CE，理由见解析；（3）作图见解析，BE=CD，△PBC+△PCB=60°．【分析】（1）根据SAS证明两个三角形全等即可证明；（2）通过条件证明△DAB△△EAC（SAS），得到△DBC+△ECB=90°，即可证明BD△CE，从而得到结果；≅即可得到证明；（3）根据已知条件证明DAC BAE解：（1）△AB=AC，AE=AD，△BAC=△DAE，∠+∠=∠+∠，△DAE EAB BAC EAB即DAB EAC ∠=∠，△()△△ADB AEC SAS ≅，△BD=CE ；（2）BD=CE 且BD△CE ；理由如下：因为△DAE=△BAC=90°，如图2．所以△DAE+△BAE=△BAC+△BAE ．所以△DAB=△EAC ．在△DAB 和△EAC 中，,,.AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩所以△DAB△△EAC （SAS ）．所以BD=CE ，△DBA=△ECA ．因为△ECA+△ECB+△ABC=90°，所以△DBA+△ECB+△ABC=90°．即△DBC+△ECB=90°．所以△BPC=180°-（△DBC+△ECB ）=90°．所以BD△CE ．综上所述：BD=CE 且BD△CE ．（3）如图3所示，BE=CD ，△PBC+△PCB=60°．由图可知60DAB EAC ∠=∠=︒，AD=AB ，AE=AC ，△+DAB BAC EAC BAC ∠∠=∠+∠，即DAC BAE ∠=∠，△()△DAE △BAE SAS ≅，△BE=CD ，ABE ADC ∠=∠，又△60BDA ∠=︒，△60ADC BDC ABE BDC ∠+∠=∠+∠=︒，△120BPC ABP BDC BDA ∠=∠+∠+∠=︒，△△PBC+△PCB=60°．【点拨】本题主要考查了全等三角形的知识点应用，准确分析图形是解题的关键． 举一反三变式1：如图，AC △BC ，DC △EC ，AC ＝BC ，DC ＝EC ，AE 与BD 交于点F ．（1）求证：AE ＝BD ；（2）求△AFD 的度数．【答案】（1）详情见解析；（2）90AFD ∠=︒【分析】（1）利用角的等量代换求出ACE BCD ∠=∠，再判断ACE ≌BCD △即可求解； （2）利用全等三角形的性质得到E D ∠=∠，再通过角的等量代换求解即可．解：（1）△AC BC ⊥，DC EC ⊥△90ACB ECD ∠=∠=︒△ACB BCE ECD BCE ∠+∠=∠+∠△ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD DC EC =⎧⎪∠=∠⎨⎪=⎩△ACE ≌BCD △(SAS)△AE BD =（2）设BD 与CE 的交点为G ，如图所示：△ACE ≌BCD △△E D ∠=∠△180EFG FGE E ++=︒∠∠∠，180GCD CGD D ++=︒∠∠∠，且BGE CGD ∠=∠△90EFG GCD ==︒∠∠△90AFD ∠=︒【点拨】本题主要考查了全等三角形的性质和判定，灵活运用角的等量代换是解题的关键．例题2．已如：如图1，B ，C ，D 三点在一条直线上，△ABC 和△ECD 均为等边三角形，连接BE ，AD 交于点F ，BE 交AC 于点M ，AD 交CE 于点N ．（1）以下结论正确的有 ；△AD =BE △△EFD =60° △MC =NC △△AMB =△END（2）探究：将图1中的△ECD 绕点C 顺时针旋转一个角度（旋转角小于60°），如图2所示． △问：（1）中的正确结论哪些还成立？若成立，请说明理由；△连接FC ，如图3所示，求证：FC 平分△BFD【答案】（1）△△△；（2）△ △△；△见解析．【分析】（1）△根据等边三角形的性质得CA =CB ，CD =CE ，△ACB =60°，△DCE =60°，则△ACE =60°，利用“SAS ”可判断△ACD △△BCE ，则AD =BE ；△根据三角形外角关系得△EFD =△EBC +△ADC =△DAC +△ADC =△ACB =60°,从而可得结论； △连接MN ，证明△MCN 是等边三角形即可得出结论；△60,60AMB EBC END NDC ∠=︒+∠∠=︒+∠，而AC ≠CD 得CAD CDA ∠≠∠，从而可得出结论；（2）△方法同（1），逐个结论进行证明即可；△作,CG BE CH AD ⊥⊥于点G ，H ，证明△BGC △△AHC ，△CGF △△CHF 可得△CFG CFH =∠，从而可得结论．解：（1）△△ABC ，△ECD 是等边三角形，△AC=BC ，CE=CD ，△ACB=△ECD=60°△△ACD=△BCE=△120°△△ACD△△BCE△AD=BE ，故△正确；△△FEN=△NDC又△△ENF=△CND△△EFD=△ECD=60°，故△正确；又△△ACE=△NCD=60°△MEC=△NDCEC=CD△△EMC△△DNC△MC=NC ，故△正确；又△△AMB=△ACB+△ECB=60°+△ECB ，△END=△ECD+△NDC=60°+△NDC而AC CD ≠△CAD CDA ∠≠∠△MBC NDC ∠≠∠△MBC END ∠≠∠，故△错误；故答案为：△△△；（2）△△ACB=△ECD=60°△△BCE=△ACD又AC=BC ，CE=CD△△ACD△△BCE△AD=BE,故△正确；△△ADC=△BEC又△ENF=△CND△△EFD=△ECD=60°，故△正确△△ACE≠60°=△ECD△△EMC 不全等于△DNC ，△MC≠NC ，故△错误（3）,CG BE CH AD ⊥⊥于点G ，H ，如图，由(2)△知，△CBG=△CAHAC=BC△BGC=△AHC=90°△△BGC△△AHC△CG=CH又CF=CF ，△CGF=△CHF=90°△△CGF△△CHF△△CFG=△CFH△FC 平分△BFD【点拨】本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”；全等三角形的对应边相等．也考查了等边三角形的判定与性质．举一反三变式：如图，在ABC∆中，分别以AC，BC为边作等边三角形ACD和等边三角形BCE，连接AE，BD交于点O，则AOB∠的度数为（）A．100︒B．120︒C．130︒D．150︒【答案】B【分析】先证明△DCB△△ACE，求出△CAE＝△CDB，再利用“8字型”证明△AOH＝△DCH ＝60°即可解决问题．解：如图：AC与BD交于点H，△△ACD，△BCE都是等边三角形，△CD＝CA，CB＝CE，△ACD＝△BCE＝60°，△△DCB＝△ACE，在△DCB和△ACE中，CD CADCB ACECB CE⎧⎪∠∠⎨⎪⎩＝＝＝，△△DCB△△ACE，△△CAE＝△CDB，△△DCH＋△CHD＋△BDC＝180°，△AOH＋△AHO＋△CAE＝180°，△DHC＝△OHA，△△AOH＝△DCH＝60°，△△AOB＝180°−△AOH＝120°．故选：B.【点拨】本题考查全等三角形的判定和性质、等边三角形的性质等知识，解题的关键是正确寻找全等三角形，学会利用“8字型”证明角相等，属于中考常考题型．例题3．（阅读材料）小明同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的项角的顶点，并把它们的底角顶点连接起来则形成一组全等的三角形，小明把具有这个规律的图形称为“手拉手”图形．如图1，在“手拉手”图形中，小明发现若△BAC=△DAE，AB=AC，AD=AE，则△ABD△△ACE．（材料理解）（1）在图1中证明小明的发现．（深入探究）（2）如图2，△ABC和△AED是等边三角形，连接BD，EC交于点O，连接AO，下列结论：△BD=EC；△△BOC=60°；△△AOE=60°；△EO=CO，其中正确的有．(将所有正确的序号填在横线上)．（延伸应用）（3）如图3，AB=BC，△ABC=△BDC=60°，试探究△A与△C的数量关系．【答案】（1）证明见解析；（2）△△△；（3）△A+△C=180°．【分析】（1）利用等式的性质得出△BAD=△CAE，即可得出结论；（2）同（1）的方法判断出△ABD△△ACE，得出BD=CE，再利用对顶角和三角形的内角和定理判断出△BOC=60°，再判断出△BCF△△ACO，得出△AOC=120°，进而得出△AOE=60°，再判断出BF＜CF，进而判断出△OBC＞30°，即可得出结论；（3）先判断出△BDP是等边三角形，得出BD=BP，△DBP=60°，进而判断出△ABD△△CBP（SAS ），即可得出结论．（1）证明：△△BAC=△DAE ，△△BAC+△CAD=△DAE+△CAD ， △△BAD=△CAE ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝ ，△△ABD△△ACE ；（2）如图2，△△ABC 和△ADE 是等边三角形， △AB=AC ，AD=AE ，△BAC=△DAE=60°， △△BAD=△CAE ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩＝＝＝ ，△△ABD△△ACE ，△BD=CE ，△正确，△ADB=△AEC ， 记AD 与CE 的交点为G ，△△AGE=△DGO ，△180°-△ADB -△DGO=180°-△AEC -△AGE ， △△DOE=△DAE=60°，△△BOC=60°，△正确，在OB上取一点F，使OF=OC，△△OCF是等边三角形，△CF=OC，△OFC=△OCF=60°=△ACB，△△BCF=△ACO，△AB=AC，△△BCF△△ACO（SAS），△△AOC=△BFC=180°-△OFC=120°，△△AOE=180°-△AOC=60°，△正确，连接AF，要使OC=OE，则有OC=12 CE，△BD=CE，△CF=OF=12 BD，△OF=BF+OD，△BF＜CF，△△OBC＞△BCF，△△OBC+△BCF=△OFC=60°，△△OBC＞30°，而没办法判断△OBC大于30度，所以，△不一定正确，即：正确的有△△△，故答案为△△△；（3）如图3，延长DC至P，使DP=DB，△△BDC=60°，△△BDP 是等边三角形，△BD=BP ，△DBP=60°，△△BAC=60°=△DBP ，△△ABD=△CBP ，△AB=CB ，△△ABD△△CBP （SAS ），△△BCP=△A ，△△BCD+△BCP=180°，△△A+△BCD=180°．【点拨】此题考查三角形综合题，等腰三角形的性质，等边三角形的性质，全等三角形的判定和性质，构造等边三角形是解题的关键．举一反三变式：如图，C 为线段AE 上一动点(不与点,A E 重合)，在AE 同侧分别作等边三角形ABC 和等边三角形,CDE AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连结PQ ．以下结论：①AD BE =；①//PQ AE ；①60AOB ∠=︒；①CPQ 是等边三角形，恒成立的是______．【答案】△△△△【分析】△由△ABC 和△CDE 都是等边三角形，可知AC=BC ，CD=CE ，△ACB=△DCE=60°，所以△ACD=△BCE=120°，所以△ACD△△BCE （SAS ），从而AD=BE ，故△正确；△△由△ACD△△BCE 得△CBE=△DAC ，加之AC=BC ，易得△ACB=△BCQ=60°，可证△CQB△△CPA （ASA ），从而CP=CQ ，再加之△PCQ=60°，可推出△PCQ 为等边三角形，易得△PQC=60°=△DCE ，根据内错角相等，两直线平行，可知△△正确；△结合△ACD△△BCE 和三角形的外角的性质，可得△AOB=60°，故△正确．解：△△等边△ABC 和等边△CDE ，△AC=BC ，CD=CE ，△ACB=△DCE=60°，△△ACB+△BCD=△DCE+△BCD ，即△ACD=△BCE ，△在△ACD 与△BCE 中，AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩＝＝＝△△ACD△△BCE （SAS ），△AD=BE ，故△正确；△△△△ACD△△BCE ，△△CBE=△DAC ，△由△ACB=△DCE=60°得△BCD=60°，△△ACP=△BCQ ，又△AC=BC ，△△CQB△△CPA （ASA ），△CP=CQ ，又△△PCQ=60°△△PCQ 为等边三角形，△△PQC=60°，△△PQC=60°=△DCE△PQ△AE故△△正确；△△△ACD△△BCE （SAS ），△△CAD=△CBE ，△△AOB=△CAD+△CEB=△CBE+△CEB ，又△△ACB=△CBE+△CEB=60°，△△AOB=△ACB=60°，故△正确.故答案为：△△△△.【点拨】本题考查了等边三角形的性质、全等三角形的判定与性质、三角形外角的性质，熟练应用三角形全等的判定是解题的关键．。

专题12全等三角形模型之手拉手模型全攻略【模型说明】【例题精讲】例1（等边三角形）如图，已知B C E、、三点共线，分别以BC CE、为边作等边ABC∆和等边CDE∆，连接BD AE、分别与AC CD、交于,M N AE、与BD的交点为F．（1）求证：BD AE=；（2）求AFB∠的度数；（3）连接MN，求证：//BCMN【答案】（1）证明见解析（2）60AFB∠=︒（3）证明见解析【分析】（1）根据等边三角形的性质去证明BCD ACE≌，即可得证BD AE=；（2）根据等边三角形的性质得60ABC BAC∠=∠=︒，再根据（1）中BCD ACE≌可得CAE DBE=∠∠，再根据三角形的外角的性质即可求出AFB∠的度数；（3）根据等边三角形的性质去证明BCM ACN△≌△，可得CM CN=，从而求得60CMN ACB==︒∠∠即可得证//MN BC．【详解】（1）∵ABC∆和CDE∆是等边三角形∴,,60AC BC CD CE ACB DCE====︒∠∠∴,BCD ACB ACD ACE DCE ACD=+=+∠∠∠∠∠∠∴BCD ACE∠=∠在△BCD和△ACE中AC BCBCD ACECE BD=⎧⎪∠=∠⎨⎪=⎩∴BCD ACE≌拓展研究：（2）如图③，△ACB 和△DCE 均为等腰直角三角形，∠ACB=∠DCE=90°，点A 、D 、E 在同一条直线上，CF 为△DCE 中DE 边上的高，连接BE ．请求∠AEB 的度数及线段CF 、AE 、BE 之间的数量关系，并说明理由．【答案】（1）证明见解析；∠AEB=60︒；（2）∠AEB=90︒；2AE BE CF =+；理由见解析．【分析】（1）小雪的题目：先利用SAS 证明ADC BEC ≅ ，再利用全等三角形的性质、三角形外角的性质及等量代换即可得证；小华的题目：先利用SAS 证明ADC BEC ≅ ，再利用全等三角形的性质得出ADC BEC ∠∠=，然后根据等边三角形的性质求出60CDE CED ∠=∠=︒，最后根据邻补角的概念和角的和与差即可得出答案；（2）根据题意易证ADC BEC ≅ ，再根据全等三角形的性质及邻补角的概念即可求得∠AEB 的度数；然后根据三线合一即可得出CF DF EF ==，最后根据线段的和与差及等量代换即可得出答案．【详解】（1）小雪的题目：证明：ACB DCE∠=∠ ACD BCE∠∠∴=在ADC △和DCE △中，CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△CAD CBE∴∠=∠又ACD BCE ∠=∠ ,CDE CAD ACD∠=∠+∠CDE CBE BCE ∴∠=∠+∠；小华的题目：解：ACB DCE∠=∠ ACD BCE∠∠∴=在ADC △和DCE △中，CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△ADC BEC∠∠∴=CDE 为等边三角形60CDE CED ∴∠=∠=︒又 点A 、D 、E 在同一条直线上120ADC BEC ∴∠=∠=︒60AEB BEC CED ∴∠=∠-∠=︒（2）∠AEB=90︒；2AE BE CF =+；理由如下：△ACB 和△DCE 均为等腰直角三角形，,,9045AC BC CD CE ACB DCE CDE CED ∴==∠=∠=︒∠=∠=︒，,ACB DCB DCE DCB∴∠-∠=∠-∠即ACD BCE∠=∠在ADC △和DCE △中，CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩()ADC BEC SAS ∴≅△△,BE AD BEC ADC ∴=∠=∠,点A 、D 、E 在同一直线上18045135ADC ∴∠=︒-︒=︒135BEC ∴∠=︒1354590AEB BEC CED ∴∠=∠-∠=︒-︒=︒90,DCE CD CE CF DE∠=︒=⊥ ，CF DF EF∴==2DE DF EF CF∴=+=2AE AD DE BE CF ∴=+=+．【点睛】本题考查了全等三角形的判定及性质、等腰三角形的性质、等边三角形的性质，熟练掌握性质定理是解题的关键．例4．（拓展）如图，在ABC 中，90C ∠=︒，AC BC =，点O 是AB 中点，90MON ∠=︒，将MON ∠绕点O 旋转，MON ∠的两边分别与射线AC 、CB 交于点D 、E ．(1)当MON ∠转动至如图一所示的位置时，连接CO ，求证：COD BOE ≅ ；(2)当MON ∠转动至如图二所示的位置时，线段CD 、CE 、AC 之间有怎样的数量关系？请说明理由．【答案】(1)见解析(2)CE ﹣CD ＝AC ．理由见解析【分析】（1）结论：CD CE AC +=．连接OC ．证明()ASA COD BOE ≅ ；（2）结论：CE CD AC -=，证明方法类似（1）．【详解】（1）证明：∵AC BC =，90C ∠=︒，AO OB =，∴OC AB ⊥，OC AO OB ==，∴45OCD B ∠=∠=︒，∵90MON COB ∠=∠=︒，∴DOC EOB ∠=∠，在COD △和BOE △中，OCD B OC OB OCD BOE ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ASA COD BOE ≅ ．（2）解：CE CD AC -=．理由：连接OC ．∵AC BC =，90C ∠=︒，AO OB =，∴OC AB ⊥，OC AO OB ==，∴45OCD B ∠=∠=︒，∴135DOC CBE ∠=∠=︒，∵90MON COB ∠=∠=︒，∴DOC EOB ∠=∠，在COD △和BOE △中，OCD B OC OB OCD BOE ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ASA COD BOE ≅ ，∴CD BE =，∴CE CD CE BE BC AC -=-==．【点睛】本题考查等腰直角三角形的性质，全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题．例5．（培优综合）已知，在ABC ∆中，90BAC ︒∠=，45ABC ︒∠=，点D 为直线BC 上一动点（点D 不与点B C ，重合），以AD 为边作正方形ADEF ，连接CF ．（1）如图①，当点D 在线段BC 上时，求证CF CD BC +=．（2）如图②，当点D 在线段BC 的延长线上时，其他条件不变，请直接写出CF BC CD ，，三条线段之间的关系．（3）如图③，当点D 在线段BC 的反向延长线上，且点A ，F 分别在直线BC 的两侧时，其他条件不变，请直接写出CF BC CD ，，三条线段之间的关系．【答案】（1）见解析；（2）CF CD BC -=，见解析；（3）CD CF BC -=，见解析.【分析】（1）△ABC 是等腰直角三角形，利用SAS 即可证明△BAD ≌△CAF ，从而证得CF=BD ，据此即可证得；（2）同（1）相同，利用SAS 即可证得△BAD ≌△CAF ，从而证得BD=CF ，即可得到CF-CD=BC ；（3）同理，证明△BAD ≌△CAF 即可得出结论.【详解】（1）证明：如图1，∵∠BAC=90°，∠ABC=45°，∴∠ACB=∠ABC=45°，∴AB=AC ，∵四边形ADEF 是正方形，∴AD=AF ，∠DAF=90°，∵∠BAD=90°-∠DAC ，∠CAF=90°-∠DAC ，∴∠BAD=∠CAF ，在△BAD 和△CAF 中，AB AC BAD CAF AD AF ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△BAD ≌△CAF （SAS ），∴BD=CF ，∵BD+CD=BC ，∴CF+CD=BC ；（2）解：CF-CD=BC ．理由如下：如图2，∵∠BAD=90°+∠CAD ，∠CAF=90°+∠CAD ，∴∠BAD=∠CAF ，在△BAD 和△CAF 中，AB AC BAD CAF AD AF ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△BAD ≌△CAF （SAS ），∴BD=CF ，∵BD=BC+CD ，∴CF-CD=BC ．【答案】65°【分析】先判断出ACD BCE∆，再判断出≅∆(1)①如图1，求证：ABD ACE ≌△△；②当点D 在BC 边上时，请直接写出ABC ，ACD 所满足的关系；(2)当点D 在BC 的延长线上时，试探究ABC ，ACD ，ACE △的面积（ABC S ，ACD S ，ACE S ）所满足的关系，并说明理由．【答案】(1)①证明见解析；②AC ABC C D A E S S S =+ ，理由见解析(2)ACE ABC ACD S S S =+△△△，理由见解析【分析】（1）①先证明BAD CAE ∠=∠，再利用SAS 证ABD ACE ≌△△即可；②利用全等三角形的性质得到ABD ACE S S = ，再由ABC ACD ABD S S S =+△△△即可得到结论；（2）由已知条件可得证出，ABD ACE ≌△△，推出ABD ACE S S = ，再由ABD ABC ACD S S S =+△△△，即可得到ACE ABC ACD S S S =+△△△．【详解】（1）证明：①∵BAC DAE ∠=∠，∴BAC CAD DAE CAD ∠-∠=∠-∠，即BAD CAE ∠=∠．在ABD △和ACE △中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩。

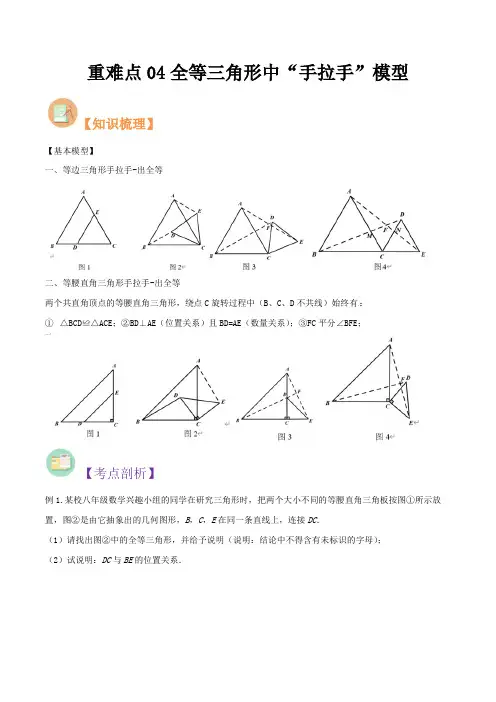
全等三角形——手拉手模型-CAL-FENGHAI.-(YICAI)-Company One1手拉手模型要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180°（3）OA平分∠BOC变形：例1.如图在直线ABC的同一侧作两个等边三角形ABD∆，连结AE与∆与BCECD，证明（1）DBC∆≅ABE∆(2)DCAE=(3)AE与DC之间的夹角为︒60(4)DFB≅∆AGB∆(5)CFB≅∆EGB∆(6)BH平分AHC∠(7)ACGF//变式精练1：如图两个等边三角形ABD∆，连结AE与CD，∆与BCE证明（1）DBC∆≅ABE∆（2）DCAE=（3）AE与DC之间的夹角为︒60（4）AE与DC的交点设为H,BH平分AHC∠变式精练2：如图两个等边三角形ABD∆，∆与BCE连结AE与CD，证明（1）DBCABE∆∆≅(2）DCAE=(3）AE与DC之间的夹角为︒60(4）AE与DC的交点设为H,BH平分AHC∠例2：如图，两个正方形ABCD与DEFG,连结AG,,二者相交于点HCE问：（1）CDEADG∆∆是否成立≅（2）AG是否与CE相等（3）AG与CE之间的夹角为多少度（4）HD是否平分AHE∠例3：如图两个等腰直角三角形ADC与AG,,二者相交于点HEDG，连结CE问：（1）CDE∆是否成立ADG∆≅（2）AG是否与CE相等（3）AG与CE之间的夹角为多少度（4）HD是否平分AHE∠例4：两个等腰三角形ABD ∆与BCE ∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ， 问：（1）DBC ABE ∆≅∆是否成立（2）AE 是否与CD 相等（3）AE 与CD 之间的夹角为多少度（4）HB 是否平分AHC ∠。

重难点04全等三角形中“手拉手”模型【知识梳理】【基本模型】一、等边三角形手拉手-出全等二、等腰直角三角形手拉手-出全等两个共直角顶点的等腰直角三角形，绕点C旋转过程中（B、C、D不共线）始终有：①△BCD≌△ACE；②BD⊥AE（位置关系）且BD=AE（数量关系）；③FC平分∠BFE；【考点剖析】例1.某校八年级数学兴趣小组的同学在研究三角形时，把两个大小不同的等腰直角三角板按图①所示放置，图②是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC．（1）请找出图②中的全等三角形，并给予说明（说明：结论中不得含有未标识的字母）；（2）试说明：DC与BE的位置关系．【变式1】已知：△ACB和△DCE都是等腰直角三角形，∠ACB=∠DCE=90°，连结AE,BD交于点O,AE与DC 交于点0，AE与DC交于点M,BD与AC交于点N.【变式2】如图，在△AOB和△COD中，OA＝OB，OC＝OD，若∠AOB＝∠COD＝60°．（1）求证：AC＝BD．（2）求∠APB的度数．【变式3】已知，在△ABC中，AB＝AC，点P平面内一点，将AP绕A顺时针旋转至AQ，使∠QAP＝∠BAC，连接BQ、CP，⑴若点P在△ABC内部，求证BQ＝CP；⑵若点P在△ABC外部，以上结论还成立吗？【变式4】（2023•定西模拟）（1）问题发现如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．填空：①∠AEB的度数为；②线段AD，BE之间的数量关系为．（2）拓展探究如图2，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A，D，E在同一直线上，CM 为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．【变式5】阅读与理解：如图1，等边△BDE按如图所示方式设置．操作与证明：（1）操作：固定等边△ABC，将△BDE绕点B按逆时针方向旋转120°，连接AD，CE，如图2；在图2中，请直接写出线段CE与AD之间具有怎样的大小关系．（2）操作：若将图1中的△BDE，绕点B按逆时针方向旋转任意一个角度α（60°＜α＜180°），连接AD，CE，AD与CE相交于点M，连BM，如图3；在图3中线段CE与AD之间具有怎样的大小关系？∠EMD的度数是多少？证明你的结论．猜想与发现：（3）根据上面的操作过程，请你猜想在旋转过程中，∠DMB的度数大小是否会随着变化而变化？请证明你的结论．【过关检测】一．选择题（共1小题）1．（2021秋•普陀区期末）如图，AB＝3，AC＝，连结BC，分别以AC、BC为直角边作等腰Rt△ACD 和等腰Rt△BCE，连结AE、BD，当AE最长时，BC的长为（）A．2B．3C．D．二．填空题（共3小题）2．（2022秋•椒江区校级月考）如图，△ADB≌△ECB，且点A的对应点是点E，点D的对应点是点C，若∠CBD＝40°，BD⊥EC，则∠D的度数为．3．（2022秋•上城区校级期中）如图，AD⊥BC于点D，BE⊥AC于点E，AD与BE交于点O，连接CO并延长交AB于点F，延长AD至点G，若GE平分∠DGC，CE平分∠DCH，则下列结论：①∠ABE＝∠ACF；②∠GEB＝45°；③EO＝EC；④AE﹣CE＝BF；⑤AG﹣CG＝BC，其中正确的结论有（写序号）．4．（2020秋•金东区校级月考）等边三角形ABC和等边三角形ADE的位置如图所示，若∠1＝25°，则∠2的度数为．三．解答题（共13小题）5．（2021秋•临海市月考）如图，点E在CD上，BC与AE交于点F，AB＝CB，BE＝BD，∠1＝∠2．（1）求证：AE＝CD；（2）证明：∠1＝∠3．6．如图1，△ABC、△DCE均为等边三角形，当B、C、E三点在同一条直线上时，连接BD、AE交于点F，易证：△ACE≌△BCD．聪明的小明将△DCE绕点C旋转的过程中发现了一些不变的结论，让我们一起开启小明的探索之旅！（探究一）如图2，当B、C、E三点不在同一条直线上时，小明发现∠BFE的大小没有发生变化，请你帮他求出∠BFE的度数．（探究二）阅读材料：在平时的练习中，我们曾探究得到这样一个正确的结论：两个全等三角形的对应边上的高相等．例如：如图3，如果△ABC≌△A′B′C′，AD、A′D′分别是△ABC、△A′B′C′的边BC、B′C′上的高，那么容易证明AD＝A′D′．小明带着这样的思考又有了新的发现：如图4，若连接CF，则CF平分∠BFE，请你帮他说明理由．（探究三）在探究二的基础上，小明又进一步研究发现，线段AF、BF、CF之间还存在一定的数量关系，请你写出它们之间的关系，并说明理由．7．（2021秋•北仑区期末）如图，已知AB∥EF，∠A＝∠E，BD＝CF，试证明：AC∥DE．8．（2021秋•鹿城区校级期中）已知：如图，点B，E，F，C在同一条直线上，AB＝DC，∠B＝∠C，BE＝CF．（1）求证：△ABF≌△DCE．（2）若∠AGE＝70°，求∠AFE的度数．9．（2020秋•开化县期末）如图，△ABC和△ADE是正三角形，点D在BC边上，连结CE．（1）证明：△BAD≌△CAE；（2）当AB＝4，BD：CD＝3：1时，求CE的长．10．（2021秋•余杭区月考）在△ABC中，AB＝AC，D是射线BC上一点，点E在AD的右侧，线段AE＝AD，且∠DAE＝∠BAC，连结CE．（1）如图1，点D在线段BC上，求证：∠BAC+∠DCE＝180°．（2）如图2，点D在线段BC延长线上，判断∠BAC与∠DCE的数量关系并说明理由．11．如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．（1）求证：AD＝BE；（2）求∠AEB的度数；（3）如图2，△ACB和△DCE均为等腰三角形，且∠ACB＝∠DCE＝90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．12．（2020秋•萧山区期末）如图，在△AOB和△COD中，OA＝OB，OC＝OD，若∠AOB＝∠COD＝60°．（1）求证：AC＝BD．（2）求∠APB的度数．13．（2021秋•东阳市期末）以△ABC的AB，AC为边作△ABD和△ACE，且AD＝AB，AE＝AC，∠DAB＝∠CAE＝α．CD与BE相交于O，连结AO，如图①所示．（1）求证：BE＝CD；（2）判断∠AOD与∠AOE的大小，并说明理由．（3）在EB上取点F，使EF＝OC，如图②，请直接写出∠AFO与α的数量关系．14．（2021秋•武义县期末）如图1，在△ABC中，AB＝AC，点D为直线BC上一动点（不与点B，C重合），在AD的左侧作△ADE，使得AE＝AD，∠DAE＝∠BAC，连接BE．（1）当点D在线段BC上时，求证：△ABE≌△ACD．（2）如图2，若BE∥AC，BC＝2．①求△ABC的面积．②在点D在运动过程中，若△ABE的最小角为25°，求∠EAC的度数．15．（2021秋•定海区期末）（1）如图1，在Rt△ABC中，AB＝AC，D是直线BC上的一点，将线段AD绕点A逆时针旋转90°至AE，连接CE，求证：△ABD≌△ACE；（2）如图2，A是△BDC内一点，∠ABC＝∠ADB＝45°，∠BAC＝90°，BD＝6，线段AD绕点A逆时针旋转90°至AE，点D、E、B恰好共线，求△BDC的面积；（3）如图3，在图1的条件下，延长DE，AC交于点G，BF⊥AB交DE于点F，求证：FG＝AE．16．（2022秋•义乌市校级月考）在△ABC中，AB＝AC，点，D是直线BC上一点（不与B、C重合），以AD 为一边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连接CE．（1）如图1，当点D在线段BC上，如果∠BAC＝90°，则∠BCE＝度；（2）设∠BAC＝α，∠BCE＝β．①找出图2中的一对全等三角形：，并写出其全等的依据：；②如图2，当点D在线段BC上移动，请直接写出α，β之间的数量关系；②当点D在线段BC或CB的延长线上时，请直接写出α，β之间的数量关系．17．已知△ABC和△DEC都是等腰直角三角形，且∠ACB＝∠DCE＝90°．（1）如图1，点D在△ABC内，求证：AD⊥BE；（2）如图2，A，D，E三点在同一条直线上，若AB＝13，DE＝10，求△ACD的面积；（3）如图3，若AB＝9，点D在边AB上运动，求△BDE周长的最小值．。

全等三角形之手拉手模型倍长中线截长补短法手拉手模型要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：△ ≌△ ∠α+∠=° OA平分∠ 变形：例1如图在直线的同一侧作两个等边三角形与，连结AE与CD，证明(2)AE DC(3)AE与DC之间的夹角为60 (4) (5) (6)BH平分 (7)GF//AC 1变式精练1：如图两个等边三角形与，连结AE与CD，证明 AE DCAE与DC之间的夹角为60AE与DC的交点设为HBH平分变式精练2：如图两个等边三角形与，连结AE与CD，证明 (2）AE DC(3）AE与DC之间的夹角为60(4）AE与DC的交点设为HBH平分例2：如图，两个正方形与连结AGCE二者相交于点H问：是否成立？ AG是否与CE相等？AG与CE之间的夹角为多少度？ HD是否平分？例3：如图两个等腰直角三角形与，连结AGCE二者相交于点H问：是否成立？ AG是否与CE相等？AG与CE之间的夹角为多少度？ HD是否平分？2例4：两个等腰三角形与，其中AB BDCB EB连结AE与CD，问：是否成立？ AE是否与CD相等？AE与CD之间的夹角为多少度？ HB是否平分？倍长与中点有关的线段倍长中线类☞考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的1已知：中，是中线．求证：(AB AC)．2ABMC在△中，AB5，AC9，则BC边上的中线AD的长的取值范围是什么？如图所示，在的AB边上取两点E、F，使AE BF，连接CE、CF，求证：AC BC EC FC．如图，已知在中，AD是BC边上的中线，E是AD上一点，延长交AC于F，AF EF，求证：AC．3AFEBD如图，已知在中，AD是BC边上的中线，E是AD上一点，且AC，延长交AC于F，求证：AF EFCDEABCF如图，在中，AD交BC于点D，点E是BC中点，EF∥AD交CA的延长线于点F，交AB 于点G，若BG CF，求证：AD为的角平分线．CDAGBE如图所示，已知中，AD平分，E、F分别在BD、AD上．DE CD，EF AC．求证：EF∥ABAF已知为的中线，，的平分线分别交AB于E、交AC于F．求证：CF EF．CFMAEB在Rt中，F是斜边AB的中点，D、E分别在边CA、CB上，满足90．若AD3，4，则线段DE的长度为_________．4ADFCEB在中，点D为BC的中点，点M、N分别为AB、AC上的点，且MD ND．若A90，以线段BM、MN、CN为边能否构成一个三角形？若能，该三角形是锐角三角形、直角三角形或钝角三角形？1如果BM2CN2DM2DN2，求证AD2AB2AC2．4AMBNDC如图所示，在中，AB AC，延长AB到D，使BD AB，E为AB的中点，连接CE、CD，求证CD2EC．AEBCD已知中，AB AC，BD为AB的延长线，且BD AB，CE为的AB边上的中线．求证：CD2CECAEBD★全等之截长补短：人教八年级上册课本中，在全等三角形部分介绍了角的平分线的性质，这一性质在许多问题里都有着广泛的应用而“截长补短法”又是解决这一类问题的一种特殊方1 如图所示，中，C90B45，AD平分交BC于D求证：AB=AC+CD5ACDB如图所示，在中，B60，的角平分线AD、CE相交于点O求证：AE+CD=ACAEOBDC2 如图所示，已知12，P为BN上一点，且PD BC于D，AB+BC=2BD，求证：MAB12PNCDC3 如图所示，在Rt中，AB=AC，90，，CE垂直于BD的延长线于E求证：BD=2CE5如图所示，在中，90，AD为的平分线，C=30，AD于E点，求证：AC-AB=26AEDCBAEBD。

AB =
∵ቐ∠ABE = ∠EBC
= BC
∴△ABE≌△DBC(SAS)
过B点分别向AE和DC作垂线，垂足为点M，N
∵BM，BN分别为△ABE和△DBC对应边上的高
∴BM=BN
在Rt△BMF和Rt△BNF中
BF =
∵ቊ
BM =
∴Rt△BMF≌Rt△BNF(HL）
手拉手模型-等边三角形
为右手顶点。
B(左手）
(头 ）
(头）
B(左手
）
C(右手 ）
C(右手）
手拉手模型基于
“ASA全等判定”
2、手拉手模型-模型分析
二、“手拉手模型”的基本构图：
常见变形：
手拉手模型-等边三角形
例1、如图在直线ABC的同一侧作两个等边三角形△ABD与△BCE，连结AE与CD.
证明：（1）△ ≌△ （2） = （3）与之间的夹角为60°（4）△ ≌△ （5）△ ≌△ （6）


∴AE=DC



（3）延长AE分别交BD于点N，CD于H
由（1）可知，∠BDC=∠BAE
又∵∠ANB=∠HND（对顶角相等）
∴180°-（ ∠BDC + ∠HND ）=
180°-(∠BAE + ∠ANB )
即∠DHN=∠ABD=60°
∴ 与的夹角为60°
（4）过点B分别向AE和DC所在直
变式1-4.
D
如果两个等边三角形△ABD和△BCE，连接AE与CD，证明：
1. △ABE≌△DBC
2. AE=DC
3. AE与DC的夹角为60°
4. AE与DC的交点设为H,BH平分∠AHC
【解析】①利用角度的和差关系证明∠ABE=∠DBC，且AB=DB，BC=BE

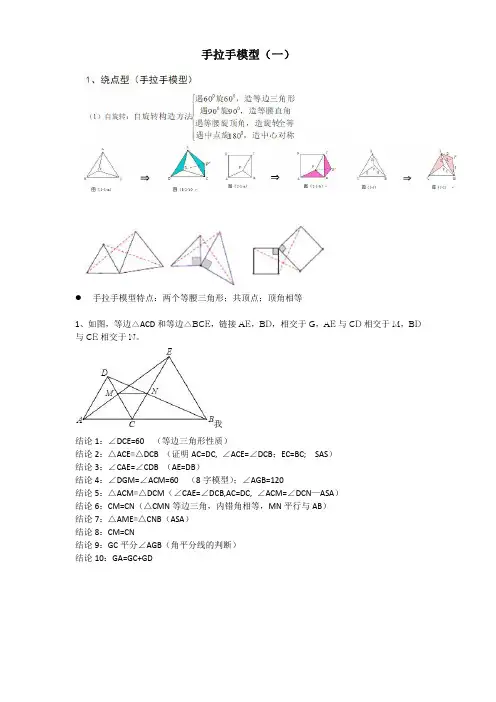
手拉手模型（一）l手拉手模型特点：两个等腰三角形；共顶点；顶角相等1、如图，等边△ACD和等边△BCE，链接AE，BD，相交于G，AE与CD相交于M，BD 与CE相交于N。

我结论1：∠DCE=60°（等边三角形性质）结论2：△ACE≅△DCB （证明AC=DC, ∠ACE=∠DCB；EC=BC; SAS）结论3：∠CAE=∠CDB （AE=DB）结论4：∠DGM=∠ACM=60°（8字模型）；∠AGB=120°结论5：△ACM≅△DCM（∠CAE=∠DCB,AC=DC, ∠ACM=∠DCN—ASA）结论6：CM=CN（△CMN等边三角，内错角相等，MN平行与AB）结论7：△AME≅△CNB（ASA）结论8：CM=CN结论9：GC平分∠AGB（角平分线的判断）结论10：GA=GC+GD拓展1△ABE 和△ACF 均为等边三角形 结论1：△ABF ≅△AEC结论2：∠BOE=∠BAE=60°结论3：OA 平分∠EOF （四点共圆证明）拓展2△ABD 和△ACE 均为等腰直角三角形 结论1：BE=CD结论2：BE 垂直于CD拓展3四边形ABEF 和四边形ACHD 均为正方形 结论1：BD=CF结论2：BD 垂直于CF例题：已知：如图,点C 是线段AB 上的动点(C 点于A. B 不重合)，分别以AC 、BC 为边在直线AB 的同侧作等边三角形ACD 和等边三角形BCE ，AE 于CD 相交于点M ，BD 与CE 相交于点N.①△≌△ACE DCB;②∥MN AB;③△CMN 是等边三角形;④若AB 的长为10cm,当点C 在线段AB 上移动时,则线段MN 的最大长度为2.5cm;⑤MN2=EN⋅DM ； 其中结论正确的为：例题：(1) 如图1，点C是线段AB上一点，分别以AC，BC为边在AB的同侧作等边△ACM 和△CBN，连接AN，BM.分别取BM，AN的中点E，F，连接CE，CF，EF.观察并猜想△CEF的形状，并说明理由。

全等三角形专题复习
---初识手拉手
一、知识准备
已知： ∵∠BAC=∠B’AC’（已知） ∴∠BAC-∠CAB’=∠B’AC’即∠BAB’=
（等式的性质）
二、互动探究
（一）由倒下的直角板想到
Байду номын сангаас
二、互动探究
（二）常见“手拉手”模型的构成及证明
1.共顶点的两个等腰直角三角形构成的手拉手模型
二、互动探究
思考：手拉手模型中的变与不变，及两个三角形 全等的证明
（1）不论三角形旋转到什么位置，哪两对线段始终是相 等的？ （2）哪一对角在旋转过程中，大小在变化，但始终是相 等的？
二、互动探究
例1.已知，如图，在∆ABC和∆A’B’C’中， A’C=B’C,AC=BC,∠ACB=∠A’CB’=90〫. 求证：∆ACA’ ∆BCB’
三、小结反思
三个常见手拉手模型共同特征是：
四、直击期末
如图，∠BAD=∠CAE=90〫,AB=AD,AE=AC,AF⊥CB,垂足为F。 求证：（1）∆ABC ∆ADE （2）求∠FAE的度数 （3）延长CF到G点，使BF=GF，连接AG。求证：CD=CG；并 猜想CD与2BF+DE的关系
回顾上面的问题及证明过程，你了解到手拉手模型 有哪些特征？
二、互动探究
2.共顶点的两个等边三角形构成的手拉手模型 例2.如图，已知∆ABC和∆AED是等边三角形。 求证：BD=CE
二、互动探究
3.共顶点的两个正方形构成的手拉手模型
例3.如图，四边形ABCD和四边形DEFG都是 正方形。 求证：（1）∆EDC ≌ ∆GDA （2）AG⊥CE

第九讲初识手拉手全等（一）知识体系：定义：所谓手拉手全等，即有公共顶角顶点的两个等腰三角形，顶角相等，顺次连接两底角顶点所形成的两个三角形全等.基本图形：如下图，△ABC和△ADE有公共顶点，AB=AC，AD=AE，∠BAC=∠DAE，连接BD、CE，则△ABD≌△ACE.图形变式：如图1、2，等腰直角△AB C和等腰直角△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°，则△ABD≌△ACE.如图3、4，等边△AB C和等边△ADE，AB=AC，AD=AE，∠BAC=∠DAE=60°，则△ABD≌△ACE.进阶探究：如图，△ABC和△ADE有公共顶点，AB=AC，AD=AE，∠BAC=∠DAE，连接BD、CE交于点O，连接AO.则：①∠BOC=∠DOE=∠BAC；②AO平分∠BOE.思考：在上图1、2、3、4中，上述结论还成立吗？（二）典例精讲例1.在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=30°，CD、BE交于点O，连接OA （1）如图1，求证：△ABE≌△ACD；（2）如图1，求∠AOE的大小；（3）当绕点A旋转至如图2所示位置时，若∠BAC=∠DAE=α，∠AOE=_________.练：如图，A在DE上，F在AB上，且AC=CE，∠1=∠2=∠3=α求∠BAC.（用α表示）例2：如图，△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，连接BD、CE交于点P.（1）求证：△ABD≌△ACE；（2）判断BD、CE的关系并证明；（3）连接PA，求∠APB的度数.练：在例2的条件下，将△ADE旋转至如图所示的位置时，BD与CE的关系还成立吗？请说明理由.例3：如图，分别以△ABC的边AB、AC向外作等边△ABD和等边△ACE，连接BE、CD交于点P，连接AP.（1）求证：BE=CD；（2）求∠BPD的度数；（3）求证：PA平分∠DPE.变式：在例3的条件下，若点F为CD上一点，且∠DBF=∠ADC，试判断△BFP的形状并证明.练：已知，Rt△ABC中，∠ACB＝90°，∠CAB＝30°．分别以AB、AC为边，向三角形外作等边△ABD和等边△ACE.（1）如图1，连接线段BE、CD，求证：BE＝CD；（2）如图2，连接DE交AB于点F，求证：F为DE中点.例4：如图，△ADC和△CBE均为等边三角形，连接AE、AB、BD，∠ABD=80°，求∠EAB的度数.练1.如图，△ABC 和△CDE 都是等边三角形，∠EBD =78°，则∠AEB =_________度.练2.已知AC=BC ，DC=EC ，∠ACB =∠ECD =90°，且∠EBD =42°，则∠AEB =.例5.如图，ΔAOB 是等边三角形，以直线OA 为x 轴建立平面直角坐标系，B （a ，b ）且a ，b 满足2(0b -=，D 为y 轴上一动点，以AD 为边作等边ΔADC ，直线CB 交y 轴于点E .（1）如图1，求A 点坐标；（2）如图2，D 在y 轴正半轴上，C 在第二象限，CE 的延长线交x 轴于点M ，当D 点在y 轴正半轴上运动时，M 点的坐标是否发生变化，若不变，求M 点的坐标，若变化，说明理由.练1.如图，已知直线AB 交x 轴于点A （a ，0），交y 轴于点B （0，b ），且a ，b 满足2(4)0a b a +++=，若点C 在第一象限，且BE ⊥AC 于点E ，延长BE 至点D ，使BD=AC ，连接OC 、OD 、CD ，试判断ΔCOD 的形状，并说明理由.练2.如图，ΔAOB和ΔACD是等边三角形，其中AB⊥x轴于E点.（1）如图，若OC=5，求BD的长；（2）设BD交x轴于点F，求证：∠OFA=∠DFA.例6.如图，已知△ABC是等边三角形，点E在线段AB上，点D在射线CB上，且DE=CE，以CE为边作等边三角形CEF，连接EF.（1）求证：BE=AF；（2）试猜想线段AB、DB、AF之间的数量关系，并证明你的猜想.练1.如图，ΔBAC为等腰直角三角形，其中AB=AC，∠BAC=90°，点A、D在BC的异侧且∠BDC=90°，连接AD，过点A作AE⊥AD交DB的延长线于点E，求∠E的度数.。

手拉手全等模型特点:由两个顶角相等的等腰三角形所组成，并且顶角顶点为公共顶点．（是左手拉左手，右手拉右手如果拉错了手，则为婆罗摩笈多模型。

）判断左右:将等腰三角形顶角顶点朝上，正对读者，读者左边为左手顶点，右边为右手顶点。

顶角相等的两任意等腰三角形：两个等边三角形：CDEAB图①CDEAB图②CDEAB图③两个等腰直角三角形：【例题】如图，已知△ABD 和△BCE 为等边三角形，连接AE 交BD 于点G ，连接CD 交BE 于点F ，AE 与CD 交点为M ，A 、B 、C 三点共线。

请求证以下内容： （1）△ABE ≌ △DBC （2）AE ＝DQ （3）∠DHA ＝60°（4）连接MB ，MB 平分∠AMC （5）△AGB ≌ △DFB （6）△EGB ≌ △CFB（7）连接GF ，△BGF 为等边三角形 【简证】（1）∵△ABD 和△BCE 为等边三角形∴∠ABD=∠CBE=60°∴∠ABD+∠DBE=∠CBE+∠DBE 即∠ABE=∠DBC 在△ABE 和△DBC 中 BA BD ABE DBC BE BC =⎧⎪∠=∠⎨⎪=⎩﹐﹐﹐∴△ABE ≌ △DBC(SAS)（经典全等） （2）∵△ABE ≌ △DBC∴AE ＝DC ．（经典拉手线）PCABDECEF A BMCDE FG AB51234（3）∵△ABE ≌△DBC∴∠1＝∠2∴∠DGM＝∠AGB∴∠DMA＝∠4＝60°（拉手线夹角找8字）（4）过点B作BQ⊥DC于Q，过点B作BN⊥AE于点N ∵△ABE ≌△DBC∴S△ABE＝S△DBC∴½×AE×BN＝½×CD×BQ∵AE＝CD∴BN＝BQ∴点B在∠AMC的平分线上∴MB平分∠AMC（拉手线交点与顶点连线平分角）(5)∵∠5＝180°－∠4－∠CBE＝60°∴∠4＝∠5∵△ABE≌△DBC∴∠1＝∠2又∵AB＝DB∴△AGB ≌△DFB（ASA）（6）同（5）可证△EGB ≌△CFB（ASA）（7）连接GF，由（5）得△AGB ≌△DFB∴BG＝BF又∵∠5＝60°∴△BGF是等边三角形（1）如图①中，C 点为线段AB 上一点，△ACM，△CBN 是等边三角形，AN 与BM 相等吗？说明理由；（2）如图②中，C 点为线段AB 上一点，等边三角形ACM 和等边三角形CBN 在AB 的异侧，此时AN 与BM 相等吗？说明理由；（3）如图③中，C 点为线段AB 外一点，△ACM，△CBN 是等边三角形，AN 与BM相等吗？说明理由．解析：题中三问均是对等边三角形性质的考查以及全等三角形的证明，由已知条件，利用等边三角形的性质可找出对应边及夹角相等，证明全等，即可得到线段相等．（1）如图①，点C 是线段AB 上一点，分别以AC，BC 为边在AB 的同侧作等边△ACM 和△CBN，连接AN，BM．分别取BM，AN 的中点E，F，连接CE，CF，EF．观察并猜想△CEF 的形状，并说明理由．（2）若将（1）中的“以AC、BC 为边作等边△ACM 和△CBN”改为“以AC，BC 为腰在AB 的同侧作等腰△ACM 和△CBN”，如图2，其他条件不变，那么（1）中的结论还成立吗？若成立，加以证明；若不成立，请说明理由．图②图①解析：此题综合考查等边三角形的性质与判定，三角形全等的判定与性质，等腰三角形的性质等知识点．（1）先求证△ACN≌△MCB，得出AN=BM ，∠ANC=∠MBA，再证△NFC≌△BEC，得出CE=CF，∠BCE=∠NCF，得出∠ECF=60°，证得结论成立；（2）证明过程如上（1）中的结论只有CE=CF，而∠ECF等于等腰三角形的顶角≠60°，得出结论不成立．（1）发现：如图①，点A为线段BC外一动点，且BC=a，AB=b．当点A位于时，线段AC的长取得最大值，且最大值为（用含a，b的式子表示）（2）应用：点A为线段BC外一动点，且BC=3，AB=1，如图②所示，分别以AB、AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．①请找出图中与BE相等的线段，并说明理由；②直接写出线段BE长的最大值．解析：本题主要考察等边三角形的性质以及SAS定理的应用。

专题12全等三角形中的手拉手模型【模型1】等腰三角形中的手拉手全等模型如图，△ABC 与△ADE 均为等腰三角形，且∠BAC ＝∠DAE ，连接BD 、CE ，则△ABD ≌△ACE。

【证明】∠BAC ＝∠DAECAEBAD ∠=∠∴又△ABC 与△ADE 均为等腰三角形∴在ABD ∆和ACE ∆中⎪⎩⎪⎨⎧=∠=∠=AE AD CAE BAD AC AB ∴△ABD ≌△ACE【模型2】等边三角形中的手拉手全等模型如图，△ABC 与△CDE 均为等边三角形，点B 、C 、E 三点共线，连接AE 、BD ，则△BCD≌△ACE。

【模型3】一般三角形中的手拉手全等模型如图，在任意△ABC 中，以AB 为边作等边△ADB ，以AC 为边作等边△ACE ，连接DC 、BE ，则△ADC ≌△ACE .【模型4】正方形中的手拉手全等模型如图，在任意△ABC中，以AB为边作正方形ABDE，以AC为边作正方形ACFG，连接EC、BG，则△AEC≌△ABG.【例1】如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边三角形ABC和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ．以下结论错误的是（）A．∠AOB=60°B．AP=BQC．PQ∥AE D．DE=DP【答案】D【分析】利用等边三角形的性质，BC∥DE，再根据平行线的性质得到∠CBE=∠DEO，于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°，得出A正确；根据△CQB≌△CPA （ASA），得出B正确；由△ACD≌△BCE得∠CBE=∠DAC，加之∠ACB=∠DCE=60°，AC=BC，得到△CQB≌△CPA（ASA），再根据∠PCQ=60°推出△PCQ为等边三角形，又由∠PQC=∠DCE，根据内错角相等，两直线平行，得出C正确；根据∠CDE=60°，∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ，可知∠DQE ≠∠CDE ，得出D 错误．【解析】解：∵等边△ABC 和等边△CDE ，∴AC =BC ，CD =CE ，∠ACB =∠DCE =60°，∴∠ACB +∠BCD =∠DCE +∠BCD ，即∠ACD =∠BCE ，在△ACD 与△BCE 中，AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△BCE （SAS ），∴∠CBE =∠DAC ，又∵∠ACB =∠DCE =60°，∴∠BCD =60°，即∠ACP =∠BCQ ，又∵AC =BC ，在△CQB 与△CPA 中，ACP BCQ AC BC PAC CBQ ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△CQB ≌△CPA （ASA ），∴CP =CQ ，又∵∠PCQ =60°可知△PCQ 为等边三角形，∴∠PQC =∠DCE =60°，∴PQ ∥AE ，故C 正确，∵△CQB ≌△CPA ，∴AP =BQ ，故B 正确，∵AD =BE ，AP =BQ ，∴AD -AP =BE -BQ ，即DP =QE ，∵∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ，∠CDE =60°，∴∠DQE ≠∠CDE ，故D 错误；∵∠ACB =∠DCE =60°，∴∠BCD =60°，∵等边△DCE ，∠EDC =60°=∠BCD ，∴BC ∥DE ，∴∠CBE =∠DEO ，∴∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°，故A 正确．故选：D ．【例2】如图，ABC 是边长为5的等边三角形，BD CD =，120BDC ∠=︒．E 、F 分别在AB 、AC 上，且60EDF ∠=︒，则三角形AEF 的周长为______．【答案】10【分析】延长AB 到N ，使BN =CF ，连接DN ，求出∠FCD =∠EBD =∠NBD =90°，根据SAS 证△NBD ≌△FCD ，推出DN =DF ，∠NDB =∠FDC ，求出∠EDF =∠EDN ，根据SAS 证△EDF ≌△EDN ，推出EF =EN ，易得△AEF 的周长等于AB +AC ．【解析】解：延长AB 到N ，使BN =CF ，连接DN，∵△ABC 是等边三角形，∴∠ABC =∠ACB =60°，∵BD =CD ，∠BDC =120°，∴∠DBC =∠DCB =30°，∴∠ACD =∠ABD =30°+60°=90°=∠NBD ，∵在△NBD 和△FCD 中，BD DC NBD FCD BN CF =⎧⎪∠=∠⎨⎪=⎩，∴△NBD ≌△FCD （SAS ），∴DN =DF ，∠NDB =∠FDC ，∵∠BDC =120°，∠EDF =60°，∴∠EDB +∠FDC =60°，∴∠EDB +∠BDN =60°，即∠EDF =∠EDN ，在△EDN 和△EDF 中，DE DE EDF EDN DN DF =⎧⎪∠=∠⎨⎪=⎩，∴△EDN ≌△EDF （SAS ），∴EF =EN =BE +BN =BE +CF ，即BE +CF =EF ．∵△ABC 是边长为5的等边三角形，∴AB =AC =5，∵BE +CF =EF ，∴△AEF 的周长为：AE +EF +AF =AE +EB +FC +AF =AB +AC =10，故答案为：10．【例3】如图1，B 、C 、D 三点在一条直线上，AD 与BE 交于点O ，△ABC 和△ECD 是等边三角形．(1)求证：△ACD ≌△BCE ；(2)求∠BOD 的度数；(3)如图2，若B 、C 、D 三点不在一条直线上，∠BOD 的度数是否发生改变？（填“改变”或“不改变”）【答案】(1)证明见解析(2)∠BOD ＝120°(3)不改变，理由见解析【分析】（1）根据“SAS ”证明△ACD ≌△BCE 即可；（2）由全等三角形的性质得∠ADC ＝∠BEC ，再由三角形的外角性质得∠AOB ＝60°，即可求解；（3）同（1）得：△ACD ≌△BCE ，得出∠DAC ＝∠EBC ，根据三角形外角求出∠AOE =120°，即可得出答案．【解析】（1）证明：∵△ABC 和△ECD 是等边三角形，∴∠ACB ＝∠ECD ＝60°，BC ＝AC ，EC ＝CD ，∴∠ACB +∠ACE ＝∠ECD +∠ACE ，∴∠BCE ＝∠ACD ，在△BCE 和△ACD 中∵BC AC BCE ACD CE CD =⎧⎪∠=∠⎨⎪=⎩，∴△BCE ≌△ACD （SAS ）．（2）解：∵△BCE ≌△ACD ，∴∠ADC ＝∠BEC ，∵∠AOB ＝∠EBC +∠ADC ，∴∠AOB ＝∠EBC +∠BEC ＝∠DCE ＝60°，∵∠AOB +∠BOD ＝180°，∴∠BOD ＝120°．（3）解：不改变，理由如下：同（1）得：△ACD ≌△BCE （SAS ），∴∠DAC ＝∠EBC ，∵∠AOE ＝∠ABO +∠OAB＝∠ABO +∠DAC +∠BAC＝∠ABO +∠EBC +∠BAC＝∠ABC +∠BAC＝120°∴∠BOD ＝∠AOE ＝120°，即∠BOD 的度数不改变．故答案为：不改变．一、单选题1．如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，连接CE交AD于点F，连接BD交CE于点G，连接BE．下列结论中，正确的结论有（）①CE＝BD；②△ADC是等腰直角三角形；③∠ADB＝∠AEB；④S四边形BCDE ＝12BD•CE；⑤BC2+DE2＝BE2+CD2．A．1个B．2个C．3个D．4个【答案】C【分析】根据等腰直角三角形的性质可得AB=AC，AD=AE，然后求出∠BAD=∠CAE，再利用“边角边”证明△ABD和△ACE全等，根据全等三角形对应边相等可得CE=BD，判断①正确；根据全等三角形对应角相等可得∠ABD=∠ACE，从而求出∠BCG+∠CBG=∠ACB+∠ABC=90°，再求出∠BGC=90°，从而得到BD⊥CE，根据四边形的面积等于两个三角形的面积之和可判断出④正确；根据勾股定理表示出BC2+DE2，BE2+CD2，得到⑤正确；再求出AE CD∥时，∠ADC=90°，判断出②错误；∠AEC与∠BAE 不一定相等判断出③错误．【解析】解：∵，△ABC和△ADE都是等腰直角三角形，∴AB=AC，AD=AE，∵∠BAD=∠BAC+∠CAD=90°+∠CAD，∠CAE=∠DAE+∠CAD=90°+∠CAD，∴∠BAD=∠CAE，∴△ABD≌△ACE（SAS），∴CE=BD，∠ABD=∠ACE，故①正确；∴∠BCG+∠CBG=∠ACB+∠ABC=90°，在△BCG中，∠BGC=180°-（∠BCG+∠CBG）=180°-90°=90°，∴BD⊥CE，∴S四边形BCDE =11··22BCE DCES S CE BG CE DG+=+=12BD•CE，故④正确；由勾股定理，在Rt△BCG中，BC2=BG2+CG2，在Rt△DEG中，DE2=DG2+EG2，∴BC2+DE2=BG2+CG2+DG2+EG2，在Rt△BGE中，BE2=BG2+EG2，在Rt△CDG中，CD2=CG2+DG2，∴BE 2+CD 2=BG 2+CG 2+DG 2+EG 2，∴BC 2+DE 2=BE 2+CD 2，故⑤正确；从题干信息没有给出,AC AD =所以只有AE CD ∥时，DAE ADC ∠=∠=90°，无法说明AE CD ∥，更不能说明,CD AD =故②错误；∵△ABD ≌△ACE ，∴∠ADB =∠AEC ，条件不足以证明,CAE BAE ≌∴∠AEC 与∠AEB 相等无法证明，∴∠ADB =∠AEB 不一定成立，故③错误；综上所述，正确的结论有①④⑤共3个．故选：C ．2．如图，正ABC 和正CDE △中，B 、C 、D 共线，且3BC CD =，连接AD 和BE 相交于点F ，以下结论中正确的有（）个①60AFB ∠=︒②连接FC ，则CF 平分BFD ∠③3BF DF =④BF AF FC=+A ．4B ．3C ．2D ．1【答案】A【分析】根据“手拉手”模型证明BCE ACD ≌，从而得到CBE CAD ∠=∠，再结合三角形的外角性质即可求解60AFB ACB ∠=∠=︒，即可证明①；作CM BE ⊥于M 点，CN AD ⊥于N 点，证明CEM CDN ≌，结合角平分线的判定定理即可证明②；利用面积法表示BCF △和DCF 的面积，然后利用比值即可证明③；利用“截长补短”的思想，在AD 上取点Q ，使得FC FQ =，首先判断出FCQ 为等边三角形，再结合“手拉手”模型推出BCF ACQ ≌即可证明④．【解析】解：①∵ABC 和CDE △均为等边三角形，∴60ACB ECD ∠=∠=︒，AC BC =，EC DC =，∴ACB ACE ECD ACE ∠+∠=∠+∠，∴BCE ACD ∠=∠，在BCE 和ACD △中，BC AC BCE ACD EC DC =⎧⎪∠=∠⎨⎪=⎩∴()BCE ACD SAS ≌，∴CBE CAD ∠=∠，∵AFB CBE CDA ∠=∠+∠，ACB CDA CAD ∠=∠+∠，∴60AFB ACB ∠=∠=︒，故①正确；②如图所示，作CM BE ⊥于M 点，CN AD ⊥于N 点，则90CME CND ∠=∠=︒，∵BCE ACD ≌，∴CEM CDN ∠=∠，在CEM 和CDN △中，CME CND CEM CDN CE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CEM CDN AAS ≌，∴CM CN =，∴CF 平分BFD ∠，故②正确；③如图所示，作FP BD ⊥于P 点，∵1122BCF SBF CM BC FP ==，1122DCF S DF CN CD FP ==，∴11221122BCFDCF BF CM BC FP SS DF CN CD FP ==，∵CM CN =，∴整理得：BF BC DF CD =，∵3BC CD =，∴33BF CD DF CD==，∴3BF DF =，故③正确；④如图所示，在AD 上取点Q ，使得FC FQ =，∵60AFB ACB ∠=∠=︒，CF 平分BFD ∠，∴120BFD ∠=︒，1602CFD BFD ∠=∠=︒，∴FCQ 为等边三角形，∴60FCQ ∠=︒，CF CQ =，∵60ACB ∠=︒，∴ACB ACF FCQ ACF ∠+∠=∠+∠，∴BCF ACQ ∠=∠，在BCF △和ACQ 中，BC AC BCF ACQ CF CQ =⎧⎪∠=∠⎨⎪=⎩∴()BCF ACQ SAS ≌，∴BF AQ =，∵AQ AF FQ =+，FQ FC =，∴BF AF FC =+，故④正确；综上，①②③④均正确；故选：A．3．如图，在直线AC 的同一侧作两个等边三角形△ABD 和△BCE ，连接AE 与CD 交于点H ，AE 与DB 交于点G ，BE 与CD 交于点F ，下列结论：①AE ＝CD ；②∠AHD ＝60°；③△AGB ≌△DFB ；④BH 平分∠GBF ；⑤GF ∥AC ；⑥点H 是线段DC 的中点．正确的有（）A ．6个B ．5个C ．4个D ．3个【答案】C 【分析】连接GF ，过点B 作BM ⊥AE 于M ，BN ⊥CD 于N ；结合题意，利用等边三角形、全等三角形的性质，推导得AE ＝CD ，∠AHD ＝∠ABG ＝60°；再根据等边三角形、角平分线的性质分析，即可得到答案．【解析】连接GF ，过点B 作BM ⊥AE 于M ，BN ⊥CD 于N∵△ABD ，△BCE 都是等边三角形，∴∠ABD ＝∠EBC ＝60°，BA ＝BE ，BE ＝BC ，∴∠ABE ＝∠DBC ，在△ABE 和△DBC 中，BA BD ABE DBC BE BC =⎧⎪∠∠⎨⎪=⎩＝∴△ABE ≌△DBC （SAS ），∴AE ＝CD ，故①正确；∵△ABE ≌△DBC ，∴∠BAE ＝∠BDC ，∵∠AGB ＝∠DGH ，∴∠AHD ＝∠ABG ＝60°，故②正确；在△AGB 和△DFB 中，60BAG BDF AB DB ABG DBF ∠=∠⎧⎪=⎨⎪∠∠︒⎩＝＝∴△AGB ≌△DFB （ASA ），故③正确；∵△AGB ≌△DFB ，∴BG ＝BF ，∵∠GBF ＝60°，∴△BGF 是等边三角形，∴∠FGB ＝∠ABD ＝60°，∴FG ∥AC ，故⑤正确；∵△ABE ≌△DBC ，BM ⊥AE ，BN ⊥CD ，∴BM＝BN，∴BH平分∠AHC，但不一定平分∠GBF，故④错误；根据题意，无法判断DH＝CH，故⑥错误．故选：C．4．如图，点C是线段AE上一动点（不与A，E重合），在AE同侧分别作等边三角形ABC 和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，有以下5个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°．其中一定成立的结论有（）个A．1B．2C．3D．4【答案】D【分析】①由于△ABC和△CDE是等边三角形，可知AC=BC，CD=CE，∠ACB=∠DCE=60°，从而证出△ACD≌△BCE，可推知AD=BE；③由△ACD≌△BCE得∠CBE=∠DAC，加之∠ACB=∠DCE=60°，AC=BC，得到△ACP≌△BCQ（ASA），所以AP=BQ；故③正确；②根据②△CQB≌△CPA（ASA），再根据∠PCQ=60°推出△PCQ为等边三角形，又由∠PQC=∠DCE，根据内错角相等，两直线平行，可知②正确；④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ，∠CDE=60°，可知∠DQE≠∠CDE，可知④错误；⑤利用等边三角形的性质，BC∥DE，再根据平行线的性质得到∠CBE=∠DEO，于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°，可知⑤正确．【解析】①∵等边△ABC和等边△DCE，∴BC=AC,DE=DC=CE，∠DEC=∠BCA=∠DCE=60∘，∴∠ACD=∠BCE，在△ACD和△BCE中，AC=BC，∠ACD=∠BCE，DC=CE，∴△ACD≌△BCE(SAS)，∴AD=BE；故①正确；③∵△ACD≌△BCE(已证)，∴∠CAD=∠CBE，∵∠ACB=∠ECD=60°(已证)，∴∠BCQ=180°-60°×2=60°，∴∠ACB=∠BCQ=60°，在△ACP与△BCQ中，∠CAD=∠CBE，AC=BC，∠ACB=∠BCQ=60°，∴△ACP≌△BCQ(ASA)，∴AP=BQ；故③正确；②∵△ACP≌△BCQ，∴PC=QC，∴△PCQ是等边三角形，∴∠CPQ=60∘，∴∠ACB=∠CPQ，∴PQ∥AE；故②正确；④∵AD=BE，AP=BQ，∴AD−AP=BE−BQ，即DP=QE，∠DQE=∠ECQ+∠CEQ=60°+∠CEQ，∠CDE=60°，∴∠DQE≠∠CDE，∴DE≠QE，则DP≠DE，故④错误；⑤∵∠ACB=∠DCE=60°，∴∠BCD=60°，∵等边△DCE，∠EDC=60°=∠BCD，∴BC∥DE，∴∠CBE=∠DEO，∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°.故⑤正确；综上所述，正确的结论有：①②③⑤，错误的结论只有④，故选D．5．如图，在ABC 中，AB AC =，点D 、F 是射线BC 上两点，且AD AF ⊥，若AE AD =，15BAD CAF ∠=∠=︒；则下列结论中正确的有（）①CE BF ⊥；②ABD ACE △≌△；③ABC ADCE S S =四边形△；④122BC EF AD CF -=-A ．1个B ．2个C ．3个D ．4个【答案】D 【分析】由AD ⊥AF ，∠BAD=∠CAF ，得出∠BAC=90°，由等腰直角三角形的性质得出∠B=∠ACB=45°，由SAS 证得△ABD ≌△ACE （SAS ），得出BD=CE ，∠B=∠ACE=45°，S △ABC =S 四边形ADCE ，则∠ECB=90°，即EC ⊥BF ，易证∠ADF=60°，∠F=30°，由含30°直角三角形的性质得出EF=2CE=2BD ，DF=2AD ，则BD=12EF ，由BC-BD=DF-CF ，得出BC-12EF=2AD-CF ，即可得出结果．【解析】∵AD ⊥AF ，∠BAD=∠CAF ，∴∠BAC=90°，∵AB=AC ，∴∠B=∠ACB=45°，在△ABD 和△ACE 中，AB AC BAD CAE AD AE =∠=∠=⎧⎪⎨⎪⎩，∴△ABD ≌△ACE （SAS ），∴BD=CE ，∠B=∠ACE=45°，S △ABC =S 四边形ADCE ，∴∠ECB=90°，∴EC ⊥BF ，∵∠B=45°，∠BAD=15°，∴∠ADF=60°，∴∠F=30°，∴EF=2CE=2BD ，DF=2AD ，∴BD=12EF ，∵BC-BD=DF-CF ，∴BC-12EF=2AD-CF，∴①、②、③、④正确．故选：D．6．如图，在△OAB和△OCD中，OA=OB，OC=OD，OA＞OC，∠AOB=∠COD=40°，连接AC，BD交于点M，连接OM，下列结论：①△AOC≌△BOD；②AC=BD；③∠AMB=40°；④MO平分∠BMC．其中正确的个数为（）A．4B．3C．2D．1【答案】A【分析】由题意易得∠AOC=∠BOD，然后根据三角形全等的性质及角平分线的判定定理可进行求解．【解析】解：∵∠AOB=∠COD=40°，∠AOD是公共角，∴∠COD+∠AOD=∠BOA+∠AOD，即∠AOC=∠BOD，∵OA=OB，OC=OD，∴△AOC≌△BOD（SAS），∴AC=BD，∠OAC=∠OBD，∠ODB=∠OCA，故①②正确；过点O作OE⊥AC于点E，OF⊥BD于点F，BD与OA相交于点H，如图所示：∵∠AHM=∠OHB，∠AMB=180°-∠AHM-∠OAC，∠BOA=180°-∠OHB-∠OBD，∴∠AMB=∠BOA=40°，∴∠OEC=∠OFD=90°，∵OC=OD，∠OCA=∠ODB，∴△OEC≌△OFD（AAS），∴OE=OF，∴OM平分∠BMC，故③④正确；所以正确的个数有4个；故选A ．二、填空题7．如图，在正方形ABCD 中，E 是对角线BD 上一点()BE DE <，将线段CE 绕点C 按顺时针方向旋转90︒得到线段CE '，连接AE ，DE '，EE '．下列结论：①若20BAE ∠=︒，则70DE E ∠='︒；②2222BE DE AE +=；③若30BAE ∠=︒，则DE；④若BC =，10EC =，则9sin 10DEC ∠=．其中正确的结论有___________（填正确的序号）【答案】①②④【分析】证明△BCE ≌△E CD '，可得AE CE =，BE DE '=，==45CDE EBC '∠∠，根据三角形内角和定理可判断①正确；在Rt △E CE '中，2222=2E E CE CE CE ''+=，即2222BE DE AE +=，从而判断②正确；③证明DE '，故可判断③错误；连接AC 与BD 交于点O ，计算可得CO ＝9，根据正弦定理可判断④正确．【解析】解：∵四边形ABCD 是正方形，∴BC ＝CD ，∠BCD ＝90°，∵线段CE 绕点C 按顺时针方向旋转90︒得到线段CE '，∴CE CE '=，=90ECE '∠，∴△ECE '是等腰直角三角形，∴==45EE C E EC ''∠∠，∴=BCD ECD ECE ECD '--∠∠∠∠，即=BCE E CD '∠∠，在△BCE 和△E CD '中，=BC CD BCE E CD CE CE =⎧'∠'⎪∠⎨⎪=⎩∴△BCE ≌△DCE '（SAS ），∴==45CDE EBC '∠∠，=BE E D '，∴=454590EDE '+=∠，即△EDE '是直角三角形，∵四边形ABCD 是正方形，E 在对角线BD 上，∴=BCE BAE ∠∠，∴=DEC DEE E EC EBC BCE ''+=+∠∠∠∠∠，==45E EC EBC '∠∠，∴DEE BCE BAE '==∠∠∠，∵=20BAE ∠，∴9070DE E DEE ''==∠-∠，故①正确；在Rt △E CE '中，2222=2E E CE CE CE ''+=，在Rt △E DE '中，22222=E E DE DE BE DE ''+=+，∴2222BE DE AE +=，故②正确；若=30BAE ∠，则=30DEE BCE BAE '==∠∠∠，在在Rt △E DE '中，DE '，∵BE DE '=，DE ，故③错误；连接AC 与BD 交于点O ，如图，∵四边形ABCD 是正方形，∴∠EOC ＝90°，且BOC 是等腰直角三角形，∵BC =∴CO ＝22922BC ⨯==，∵10EC =，∴sin ∠DEC ＝9=10CO BC ，故④正确．故答案为：①②④．8．如图，O 是正ABC 内一点，3,4,5OA OB OC ===，将线段BO 以点B 为旋转中心逆时针旋转60︒得到线段BO '，下列结论：①点O 与O '的距离为4；②150AOB ∠=︒；③6ABC AOC S S -=；④64AOC AOB S S +=+△△其中正确的结论是____________．（只填序号）【答案】①②④【分析】由题意可得△BOC ≌△BAO '，△BOO '是等边三角形，可得AO '=CO =5，OO '=4，可判断△AOO '是直角三角形．可判断①②③，由S 四边形AOBO ′=S △AOO '+S △OO 'B =S △BOC +S △AOC ，可判定③④．【解析】解；连接OO '，如图1，BO BO '=，60OBO '∠=︒，BOO '∴∆是等边三角形，4OO BO '∴==，故①正确；60OBO ABC '∠=∠=︒，ABO ABC '∴∠=∠且OB OB '=，AB AC =，()ABO BOC SAS '∴∆≅∆，5AO CO '∴==，225O A '=，2225AO O O '+=，222O A AO O O ''∴=+，90AOO '∴∠=︒，150AOB ∴∠=︒，故②正确；△OO B '是等边三角形，3AO =，4OO '=，3BOO S '∆∴=，6AOO S '∆=，=+=643ABC AOC ABC ABO AOBO S S S S S '∴-=+四边形如图2，AOC ∆绕A 点顺时针旋转60︒到ABO '∆位置，同理可得9364AOC AOB S S ∆∆+=+，故④正确；故答案为：①②④．9．在ABC 中，90ACB ∠=︒，60B ∠=︒，4AB =，点D 是直线BC 上一动点，连接AD ，在直线AD 的右恻作等边ADE ，连接CE ，当线段CE 的长度最小时，则线段CD 的长度为__________．【答案】3【分析】以AC 为边向左作等边三角形ACF ，连接DF ，先根据直角三角形中30°所对的直角边是斜边的一半求出BC 的长，再由勾股定理求出AC 的长，根据作的辅助线证明()ACE AFD SAS ≅，则CE DF =，当DF BC ⊥时，DF 的长是最小的，即CE 的长最小，求出此时CD '的长即可．【解析】解：如图，以AC 为边向左作等边三角形ACF ，连接DF ，∵90ACB ∠=︒，60B ∠=︒，∴30BAC ∠=︒，∵4AB =，∴122BC AB ==，∴2223AC AB BC =-=∵ACF 是等边三角形，∴CF AC AF ===60FAC ∠=︒，∵ADE 是等边三角形，∴AD AE =，60DAE ∠=︒，∵FAC DAC DAE DAC ∠-∠=∠-∠，∴CAE FAD ∠=∠，在ACE 和AFD V 中，AC AF CAE FAD AE AD =⎧⎪∠=∠⎨⎪=⎩，∴()ACE AFD SAS ≅，∴CE DF =，当DF BC ⊥时，DF 的长是最小的，即CE 的长最小，∵906030FCD '∠=︒-︒=︒，Rt CFD '，∴12D F CF '==3CD '==，∴当线段CE 的长度最小时，则线段CD 的长度为3．故答案是：3．10．如图，在ABC 中，45ABC ︒∠=，3AB =，AD BC ⊥于点D ，BE AC ⊥于点F ．1AE =，连接DE ，将AED 沿直线AE 翻折至ABC 所在的平面，得AEF ，连接DF ．过点D 作DG DE ⊥交BE 于点G ，则四边形DFEG 的周长为________．【答案】2+【分析】先证BDG DE ∆≅∆，得出1AE BG ==，再证DGE ∆与EDF ∆是等腰直角三角形，在直角AEB ∆中利用勾股定理求出BE 的长，进一步求出GE 的长，可通过解直角三角形分别求出GD ，DE ，EF ，DF 的长，即可求出四边形DFEG 的周长．【解析】∵45ABC ︒∠=，AD BC ⊥于点D ，∴9045BAD ABC ︒︒∠=-∠=，∴ABD ∆是等腰直角三角形，∴AD BD =，∵BE AC ⊥，∴90GBD C ︒∠+∠=，∵90EAD C ︒∠+∠=，∴GBD EAD ∠=∠，∵90ADB EDG ︒∠=∠=，∴ADB ADG EDG ADG ∠-∠=∠-∠，即BDG ADE ∠=∠，∴()BDG ADE ASA ∆≅∆，∴1BG AE ==，DG DE =，∵90EDG ︒∠=，∴EDG ∆为等腰直角三角形，∴9045135AED AEB DEG ︒︒︒∠=∠+∠=+=，∵AED ∆沿直线AE 翻折得AEF ∆，∴AED AEF ∆≅∆，∴135AED AEF ︒∠=∠=，ED EF =，∴36090DEF AED AEF ︒︒∠=-∠-∠=，∴DEF ∆为等腰直角三角形，∴EF DE DG ==，在Rt AEB ∆中，BE ===∴1GE BE BG =-=，在Rt DGE ∆中，22222DG GE ==，∴222EF DE ==-，在Rt DEF ∆中，1DF ==-，∴四边形DFEG 的周长为：GD EF GE DF+++221)2⎛=-+ ⎝⎭2=+，故答案为：2+．11．如图ABD △和ACE 是ABC 外两个等腰直角三角形，90BAD CAE ∠∠==，下列说法正确的是：________．①CD BE =，且DC BE ⊥；②22222DE BC BD EC +=+；③FA 平分DFE ∠；④取BC 的中点M ，连MA ，则MA DE ⊥．【答案】①③④【分析】①由ABD △与ACE 是等腰直角三角形，AD AB =，AC AE =，DAB EAC ∠=∠可证(SAS)ADC ABE △≌△，CD BE =，AEB ACD ∠=∠且ARE FRC ∠∠=，90EAR ∠=︒AER ARE FCR FRC ∠∠∠∠+=+，即可退出；②由DC BE ⊥，由勾股定理222DF EF DE +=，222+=BF CF BC ，()()22222222=DE BC DF BF CF EF BD EC ++++=+，即可；③过点A 作AS DC ⊥，AG BE ⊥，可证(AAS)ADS ABG ≌，由性质得AS AG =，结合AS DC ⊥，AG BE ⊥，即可；④取BC 中点M ，使得AM MN =，易证(SAS)BMN CMA ≌，推出BN AC =，再证(SAS)DAE ABN ≌，推出BAN ADH ∠∠=，由90DAH BAN ∠∠+=︒，推出90DAH ADH ∠+∠=︒即可．【解析】ABD 与ACE 是等腰直角三角形，AD AB ∴=，AC AE =，DAB EAC ∠=∠，DAC EAB ∴∠=∠，∴在ADC 与ABE △中，AD AB DAC EAB AC AE =⎧⎪∠=∠⎨⎪=⎩，(SAS)ADC ABE ∴≌，CD BE ∴=，设BE 交AC 于点R ，由①可知AEB ACD ∠=∠且ARE FRC ∠∠=，AER ARE FCR FRC ∠∠∠∠∴+=+，90EFC EAR ∠∠∴==︒，即DC BE ⊥，故①符合题意．②DC BE ⊥，222DF EF DE ∴+=，222+=BF CF BC ，222222DF EF BF CF DE BC ∴+++=+，且222DF BF BD +=，222CF EF CE +=，2222DE BC BD CE ∴+=+．故②不符合题意．③证明，过点A 作AS DC ⊥，AG BE ⊥，由①可知ADS ABG ∠∠=，且AD AB =，ASD AGB ∠∠=，∴在ADS △与ABG 中，ADS ABG ASD AGB AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩，(AAS)ADS ABG ∴≌，AS AG ∴=，且AS DC ⊥，AG BE ⊥，FA ∴平分DFE ∠，故③符合题意．④作BC 中点M ，倍长AM ，使得AM MN =，∴在BMN △与CMA 中，BM MC BMN CMA MN AM =⎧⎪∠=∠⎨⎪=⎩，(SAS)BMN CMA ∴≌，则BN AC =，AC AE =，BN AE ∴=，180BAC DAE ∠∠︒+=，180BAC ABN ∠∠+=︒，DAE ABN ∠∠∴=，∴在DAE △与ABN 中，AD AB DAE ABN AE BN =⎧⎪∠=∠⎨⎪=⎩，(SAS)DAE ABN ∴≌，BAN ADH ∠∠∴=，90DAH BAN ∠∠︒+=，90DAH ADH ∠∠∴+=︒，∠90AHD ∴=︒，即AM DE ⊥，故④符合题意．故答案为：①③④．12．（1）如图（1），在四边形ABCD 中，AB AD =,180B D ︒∠+∠=，E ，F 分别是,BC CD 上的动点，且12EAF BAD ∠=∠，求证：EF BE DF =+．（2）如图（2），在（1）的条件下，当点E ，F 分别运动到,BC CD 的延长线上时，,,EF BE DF 之间的数量关系是______．【答案】（1）详见解析；（2）EF BE DF=-【分析】（1）延长FD 到点G ，使DG BE =，连接AG ，先证明()ABE ADG SAS ∆∆≌，得到AE AG BAE DAG =∠=∠，，然后证明AEF AGF ∆∆≌，得到EF FG =，根据FG DG DF BE DF =+=+，可得EF BE DF =+；（2）在BC 上截取BG DF =，连接AG ，先证明△ABG ≌△ADF （SAS ），得到AG=AF ，∠BAG=∠DAF ，再证明△EAG ≌△EAF （SAS ），得到EG=EF ，根据BG=DF ，即可得EF=BE-BG=BE-DF ．【解析】（1）如图，延长FD 到点G ，使DG BE =，连接AG．180B ADF ADG ADF ︒∠+∠=∠+∠=，B ADG ∴∠=∠，又AB AD =，BE DG =，∴()ABE ADG SAS ∆∆≌，,AE AG BAE DAG ∴=∠=∠，12EAF BAD ∠=∠，GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠．,,AE AG EAF GAF AF AF =∠=∠=，∴AEF AGF ∆∆≌，EF FG ∴=．FG DG DF BE DF =+=+，EF BE DF ∴=+；（2）EF BE DF =-．如图，在BC 上截取BG DF =，连接AG，180B ADC ADC ADF ︒∠+∠=∠+∠=，B ADF ∴∠=∠，在△ABG 和△ADF 中AB AD B ADF BG DF ⎧⎩=⎪==⎪⎨∠∠，∴△ABG ≌△ADF （SAS ），∴AG=AF ，∠BAG=∠DAF ，∠BAD=2∠EAF ，∴∠BAG+∠GAE+∠EAD=∠EAD+∠DAF+∠EAD+∠DAF ，∴∠GAE=∠EAF ，在△EAG 和△EAF 中AG AF EAG EAF AE AE ===⎧⎪⎨⎪⎩∠∠，∴△EAG ≌△EAF （SAS ），∴EG=EF ，∵BG=DF ，∴EF=BE-BG=BE-DF ．三、解答题13．如图，若ABD △和ACE 都是等边三角形，求BOC ∠的度数．【答案】120°．【分析】利用等边三角形的性质可得AD ＝AB ，AC ＝AE ，∠DAB ＝∠CAE ＝60°，利用SAS 即可证明△DAC ≌△BAE ，从而得出∠ABE ＝∠ADC ，设AB 与CD 交于点F ，根据三角形内角和定理和等量代换即可求出∠BOF ，利用平角的定义即可求出结论．【解析】证明：∵△ABD 、△AEC 都是等边三角形，∴AD ＝AB ，AC ＝AE ，∠DAB ＝∠CAE ＝60°，∵∠DAC ＝∠BAC ＋60°，∠BAE ＝∠BAC ＋60°，∴∠DAC ＝∠BAE ，在△DAC 和△BAE 中，AD AB DAC BAE AC AE ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△DAC ≌△BAE （SAS ），∴∠ABE ＝∠ADC设AB 与CD 交于点F ，∵∠BFO=∠DFA∴∠BOF=180°－∠ABE －∠BFO=180°－∠ADC －∠DFA=∠DAB=60°∴∠BOC=180°－∠BOF=120°．14．如图，ACB △和ECD 都是等腰直角三角形，,,CA CB CD CE ACB ==△的顶点A 在ECD 的斜边DE 上，连接BD．（1）求证：BD AE =．（2）若3cm,6cm AE AD ==，求AC 的长．【答案】（1）证明见解析；（2）310cm 2AC =．【分析】（1）根据同角的余角相等得出∠BCD=∠ACE ，然后根据SAS 定理证明△BCD ≌△ACE ，从而得出结论；（2）根据全等三角形的性质得出∠BDC=∠AEC ，然后结合等腰直角三角形的性质求得∠BDA 是直角三角形，从而利用勾股定理求解．【解析】（1）∵ACB △和ECD 都是等腰直角三角形，∴90ACB ECD ∠=∠=︒，∴90,90ACD BCD ACD ACE ∠+∠=︒∠+∠=︒，∴BCD ACE ∠=∠，在BCD △和ACB △中，CB CA BCD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩∴()BCD ACE SAS V V ≌，∴BD AE =．（2）∵BCD ACE ≌，∴BDC AEC ∠=∠，又∵ECD 是等腰直角三角形，∴45CDE CED ∠=∠=︒，∴45BDC ∠=︒，∴90BDC CDE ∠+∠=︒，∴BDA ∠是直角三角形，∴22222223645AB BD AD AE AD =+=+=+=，在等腰直角三角形ACB 中，22222AB AC BC AC =+=，∴2AC =．15．如图，△ACB 和△DCE 均为等腰三角形，∠ACB=∠DCE=90°，点A ，D ，E 在同一条直线上，连接BE ．（1）求证：AD=BE ；（2）若∠CAE=15°，AD=4，求AB的长．【答案】（1）见解析；（2）8【分析】（1）直接证明≌ACD BCE V V ，即可得出结论；（2）由（1）可进一步推出AEB △为直角三角形，且30EAB ∠=︒，从而由2AB BE =求解即可．【解析】（1）△ACB 和△DCE 均为等腰三角形，∠ACB=∠DCE=90°，ADC BCE ∴∠=∠,在ACD △与BCE 中，AC BC ACD BCE DC EC =⎧⎪∠=∠⎨⎪=⎩()ACD BCE SAS ∴≌，AD BE ∴=；（2）ABC 是等腰直角三角形，45ABC ∴∠=︒，由（1）可知，15CAE CBE ∠=∠=︒，4BE AD ==,451560ABE ABC CBE ∴∠=∠+∠=︒+︒=︒，90ABE ACB ∴∠=∠=︒，则在Rt AEB 中，30EAB ∠=︒，28AB BE ∴==．16．如图，在△ABC 中，AB ＝BC ，∠ABC ＝120°，点D 在边AC 上，且线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合，点F 是ED 与AB 的交点．（1）求证：AE ＝CD ；（2）若∠DBC ＝45°，求∠BFE 的度数．【答案】（1）证明见解析；（2）∠BFE ＝105°．【分析】（1）根据旋转的性质证明△ABE ≌△CBD （SAS ），进而得证；（2）由（1）得出∠DBC=∠ABE=45°，BD=BE ，∠EBD=120°，最后根据三角形内角和定理进行求解即可．【解析】（1）证明：∵线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合，∴BD ＝BE ，∠EBD ＝120°，∵AB ＝BC ，∠ABC ＝120°，∴∠ABD+∠DBC ＝∠ABD+∠ABE ＝120°，∴∠DBC ＝∠ABE ，∴△ABE ≌△CBD （SAS ），∴AE ＝CD ；（2）解：由（1）知∠DBC ＝∠ABE ＝45°，BD ＝BE ，∠EBD ＝120°，∴∠BED ＝∠BDE ＝12（180°﹣120°）＝30°，∴∠BFE ＝180°﹣∠BED ﹣∠ABE＝180°﹣30°﹣45°＝105°．17．ABC 和ADE 如图所示，其中,,ABC ACB ADE AED BAC DAE ∠=∠∠=∠∠=∠．(1)如图①，连接BE CD 、，求证：BE CD =；(2)如图②，连接BE CD BD 、、，若60BAC DAE ∠=∠=︒，CD AE ⊥，3AD =，5CD =，求BD 的长．【答案】(1)见解析；34【分析】（1）只需证ABE ACD ∆∆≌，即可得到结论；（2）先证明BED ∆是直角三角形，再用勾股定理求BD ．【解析】（1）证明：ABC ACB ∠=∠，ADE AED ∠=∠，AB AC ∴=，AE AD =，，BAC DAE ∠=∠，BAE CAD ∴∠=∠，()ABE ACD SAS ∴∆∆≌，BE CD ∴=．（2）解：ADE AED ∠=∠，AE AD ∴=，60DAE ∠=︒，DAE ∴∆是等边三角形，3AD ED ∴==，60AED ADE ∠=∠=︒，CD AE ⊥，160302ADC ∴∠=⨯︒=︒，由（1）知：ABE ACD ∆∆≌，5BE CD ∴==，30AEB ADC ∠=∠=︒，90BED ∴∠=︒，2234BD BE ED ∴+18．问题：如图1，在等边三角形ABC 内，点P 到顶点A 、B 、C 的距离分别是3，4，5，求∠APB 的度数？探究：由于PA 、PB 、PC 不在同一个三角形中，为了解决本题，我们可以将△ABP 绕点A 逆时针旋转60°到△ACP ′处，连结P P ′，这样就将三条线段转化到一个三角形中，从而利用全等的知识，求出∠APB 的度数．请你写出解答过程：应用：请你利用上面的方法解答：如图2，△ABC 中，∠CAB =90°，AB =AC ，E 、F 为BC 上的点，且∠EAF =45°，求证：222BE FC EF +=【答案】探究：∠APB =150°，应用：见解析【分析】探究：运用旋转的性质，以及全等三角形的性质得对应角相等，对应边相等，得出∠PAP ′＝60°，再利用等边三角形的判定得出△APP ′为等边三角形，即可得出∠APP ′的度数，即可得出答案；应用：利用已知首先得出△AEG ≌△AFE ，即可把EF ，BE ，FC 放到一个直角三角形中，从而根据勾股定理即可证明．【解析】探究：解：将△ABP 绕顶点A 旋转到△ACP ′处，∴△BAP ≌△CAP ′，∴AB ＝AC ，AP ＝AP ′，∠BAP ＝∠CAP ′，∴∠BAC ＝∠PAP ′＝60°，∴△APP ′是等边三角形，∴∠APP ′＝60°，因为BPP ′不一定在一条直线上，∴P ′C ＝PB ＝4，PP ′＝PA ＝3，P ′C ＝PC ＝5，∴∠PP ′C ＝90°，∴△PP ′C 是直角三角形，∴∠APB ＝∠AP ′C ＝∠APP ′+∠P ′PC ＝60°+90°＝150°，∴∠BPA ＝150°；应用：证明：把△ACF 绕点A 顺时针旋转90°，得到△ABG ．连接EG ．则△ACF ≌△ABG ．∴AG ＝AF ，BG ＝CF ，∠ABG ＝∠ACF ＝45°．∵∠BAC ＝90°，∠GAF ＝90°．∴∠GAE ＝∠EAF ＝45°，在△AEG 和△AFE 中，AG AF GAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩，∴△AEG ≌△AFE （SAS ）．∴EF ＝EG ，又∵∠GBE ＝90°，∴BE 2+BG 2＝EG 2，即BE 2+CF 2＝EF 2．19．【探究发现】（1）如图1，在四边形ABCD 中，对角线AC BD ⊥，垂足是O ，求证：2222AB CD AD BC +=+．【拓展迁移】（2）如图2．以三角形ABC 的边AB 、AC 为边向外作正方形ABDE 和正方形ACFG ，求证：CE BG ⊥．（3）如图3，在（2）小题条件不变的情况下，连接GE ，若90EGA ∠=︒，6GE =，8AG =，则BC 的长_____________．（直接填写答案）【答案】（1）见解析；（2）见解析；（3）【分析】（1）根据AC BD ⊥，利用勾股定理分别求出22AB CD +和22AD BC +即可证明结论；（2）利用正方形的性质证明△CAE ≌△GAB （SAS ），可得∠CEA ＝∠GBA ，根据∠GBA ＋∠ANB ＝90°等量代换求出∠EMN ＝90°即可；（3）利用勾股定理分别求出AE 、CG 和BE ，然后利用（1）中结论求出BC 即可．【解析】解：（1）∵AC BD ⊥，∴∠AOD ＝∠AOB ＝∠COD ＝∠BOC ＝90°，由勾股定理得：222222AB CD OA OB OD OC +=+++，222222AD BC OA OD OB OC +=+++，∴2222AB CD AD BC +=+；（2）∵在正方形ABDE 和正方形ACFG 中，AC ＝AG ，AE ＝AB ，∠CAG ＝∠EAB ＝90°，∴∠CAG ＋∠GAE ＝∠EAB ＋∠GAE ，即∠CAE ＝∠GAB ，∴△CAE ≌△GAB （SAS ），∴∠CEA ＝∠GBA ，∵∠GBA ＋∠ANB ＝90°，∠ANB ＝∠MNE ，∴∠CEA ＋∠MNE ＝90°，∴∠EMN ＝90°，∴CE BG ⊥；（3）如图3，连接CG ，BE ，∵90EGA ∠=︒，6GE =，8AG =，∴AC ＝8，AE 10=，∴AB ＝10，∴CG =BE =，∵CE BG ⊥，∴由（1）可知：2222GE BC CG BE +=+，即236128200BC +=+，∵BC ＞0，∴BC =故答案为：20．△ACB 和△DCE 是共顶点C 的两个大小不一样的等边三角形．(1)问题发现：如图1，若点A，D，E在同一直线上，连接AE，BE．①求证：△ACD≌△BCE；②求∠AEB的度数．(2)类比探究：如图2，点B、D、E在同一直线上，连接AE，AD，BE，CM为△DCE中DE 边上的高，请求∠ADB的度数及线段DB，AD，DM之间的数量关系，并说明理由．(3)拓展延伸：如图3，若设AD（或其延长线）与BE的所夹锐角为α，则你认为α为多少度，并证明．【答案】(1)①见解析；②∠AEB=60°；(2)∠ADB=60°，2DM+BD=AD，理由见解析；(3)α=60°，证明见解析【分析】（1）①由△ACB和△DCE是等边三角形知AC=BC，CD=CE，∠ACD=60°-∠DCB=∠BCE，据此即可得证；②由△ACD≌△BCE知∠ADC=∠BEC=120°，结合∠CED=60°可得∠AEB=60°；（2）证△ACD≌△BCE得∠CDA=∠CED=60°，由∠ADB+∠CDA=∠DCE+∠CED知∠ADB=60°，根据CM⊥BE，且△CDE为等边三角形可得DE=2DM，DE+BD=BE=AD；（3）同理知△ACD≌△BCE，据此得∠BEC=∠ADC，继而知∠CDF+∠CEF=180°，即∠ECD+∠DFE=180°，从而得出答案．【解析】（1）①证明：∵△ACB和△DCE是等边三角形，∴AC=BC，CD=CE，∠ACB=∠DCE=60°，∴∠ACD=60°-∠DCB=∠BCE，∴△ACD≌△BCE（SAS）；②∵△ACD≌△BCE，∴∠ADC=∠BEC=180°-∠CDE=120°，又∵∠CED=60°，∴∠AEB=60°；（2）解：∠ADB=60°，2DM+BD=AD，理由如下；∵AC =BC ，CD =CE ，∠ACD =60°+∠DCB =∠BCE ，∴△ACD ≌△BCE （SAS ），∴∠CDA =∠CED =60°；∵∠ADB +∠CDA =∠DCE +∠CED ，∴∠ADB =60°；又∵CM ⊥BE ，且△CDE 为等边三角形，∴DE =2DM ，∴2DM +BD =BE =AD ；（3）解：α=60°，理由如下：同理可证△ACD ≌△BCE ，∴∠BEC =∠ADC ，∴∠CDF +∠CEF =180°，∴∠ECD +∠DFE =180°，而α+∠DFE =180°，∴α=∠ECD =60°．21．定义：我们把两条对角线互相垂直的四边形称为“垂美四边形”．(1)特例感知：如图1，四边形ABCD 是“垂美四边形”，如果13OA OD OB ==，2OB =，60OBC ∠=︒，则22AD BC +=______，22AB CD +=______．(2)猜想论证：如图1，如果四边形ABCD 是“垂美四边形”，猜想它的两组对边AB ，CD 与BC ，AD 之间的数量关系并给予证明．(3)拓展应用：如图2，分别以Rt ACB △的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ，连接CE ，BG ，GE ，已知4AC =，60BAC ∠=︒，求GE 长．【答案】(1)1529，1529(2)2222AB CD AD BC +=+，证明见解析(3)EG =【分析】（1）利用含30°角的直角三角形的性质得4BC =，OC =可得出答案；（2）由“垂美四边形”得90AOD BOC ∠=∠=︒，再根据勾股定理得22222222AB CD OA OB OD OC AD BC +=+++=+；（3）连接CG ，BE ，首先利用SAS 证明GAB CAE ∆≅∆，得GAB ACE ∠=∠，说明BG CE ⊥，从而得出2222BC GE CG BE +=+，进而解决问题．【解析】（1）解：13OA OD OB ==，2OB =，23OA OD ∴==，四边形ABCD 是“垂美四边形”，90AOD BOC ∴∠=∠=︒，60OBC ∠=︒，30BCO ∴∠=︒，4BC ∴=，OC =22222222152(2439AD BC OA OD BC ∴+=++=⨯+=，222222221529AB CD OA OB OD OC AD BC +=+++=+=，故答案为：1529，1529；（2）结论：2222AB CD AD BC +=+，证明：∵AC BD ⊥于点O ，∴90AOD ∠=︒，∴222AD OA OD =+.同理可得222AB OA OB =+，222BC OB OC =+，222CD OC OD =+∴2222AB CD AD BC +=+（3）解：如图：连接CG 、BE ，∵90GAC BAE ∠=∠=°，∴GAC CAB BAE CAB ∠+∠=∠+∠，∴GAB CAE ∠=∠，在GAB △和CAE V 中，AG AC GAB CAE AB AE =⎧⎪∠=∠⎨⎪=⎩，∴GAB CAE V V ≌，∴AGB ACE ∠=∠，∵90AGB AMG ∠+∠=°，AMG BMC ∠=∠，∴90ACE CMB ∠+∠=°，∴BG CE ⊥，∴四边形GCBE 为垂美四边形，由（2）中结论可知2222EG BC CG BE +=+，∵4AC =，60BAC ∠=︒，∴30ABC ∠=︒，∴8AB =，B C =，∴22232CG AC ==，222128BE AB ==，∴24832128EG +=+，∴2112EG =，根据线段为正数可知EG =22．在ABC 中，90BAC ∠=︒，AB AC =，点D 是射线CB 上的动点（点D 不与点B 、C 重合），连接AD ，AE AD ⊥，且AE AD =，连接DE ，过点D 作DF BC ⊥，且DF BD =，连接CF．(1)如图1，当点D 是BC 中点时，DE 与CF 的数量关系是，位置关系是；(2)如图2，当点D 是线段BC 上任意一点时，（1）中的两个结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由；(3)若722AB =，3BD =时，请直接写出线段DE 的长．【答案】(1)DE CF =；DE CF∥(2)成立，证明见解析(3)5【分析】（1）由等腰直角三角形的性质得出AD ＝BD ＝CD ，证出CF ，DE ，∠ADE ＝45°，则可得出结论；（2）证明△ABD ≌△ACE （SAS ），由全等三角形的性质得出BD ＝CE ，∠ABD ＝∠ACE ，由直角三角形的性质及平行线的判定可证出结论；（3）分类讨论，当D 在线段BC 上时，当D 在CB 的延长线上时，由勾股定理可求出答案．【解析】（1）解：数量关系：DE CF =；位置关系：DE CF ∥；∵∠BAC ＝90°，AB ＝AC ，D 为BC 的中点，∴AD ＝BD ＝CD ，∵DF ⊥BD ，DF ＝BD ，∴∠FDC ＝90°，DF ＝CD ，∴CF CD ，∵EA ⊥AD ，AE ＝AD ，∴DE AD ，∠ADE ＝45°，∴CF ＝DE ，∵CD ＝DF ，∠CDF ＝90°，∴∠F ＝45°，∴∠ADE ＝∠F ，∴DE ∥CF ．故答案为：DE ＝CF ，DE ∥CF ；（2）成立证明：如图2，连接CE ．∵90BAC ∠=︒，AE AD ⊥，∴90BAD DAC CAE DAC ∠+∠=∠+∠=︒，∴BAD CAE ∠=∠，又∵AB AC =，AE AD =，∴()SAS ABD ACE △≌△，∴BD CE =，ABD ACE ∠=∠，∵90BAC ∠=︒，AB AC =，∴45ABC ACB ∠=∠=︒，∴45ACE ∠=︒，∴454590BCE ACB ACE ∠=∠+∠=︒+︒=︒，∴BC CE ⊥，∵DF BC ⊥，DF BD =，∴DF CE =，DE CF ∥，∴四边形DECF 是平行四边形，∴DE CF =，DE CF ∥；（3）∵AB ＝AC ＝22，∠BAC ＝90°，∴BC 27222＝7，如图2，当D 在线段BC 上时，∵BD ＝DF ＝3，DF ⊥BC ，∴DC ＝BC ﹣BD ＝7﹣3＝4，∴CF 5，由（2）可知，DE ＝CF ＝5．如图3，当D 在CB 的延长线上时，同理BC ＝7，DB ＝DF ＝3，∴DC ＝BC +DB ＝10，∴CF 连接CE ，同理可证四边形DCEF 为平行四边形，∵∠FDC ＝90°，∴四边形DCEF 为矩形，∴DE ＝CF综上所述，DE 5．23．如图1，90ACD ∠=︒，AC DC =，MN 是过点A 的直线，过点D 作DB MN ⊥于点B ，连接CB ；过点C 作CE CB ⊥，与MN 交于点E ．(1)连接AD ，AD 是AC 的______倍；(2)直线MN 在图1所示位置时，可以得到线段BD 和AE 的数量关系是______，BD BA -与BC 之间的数量关系是______，请证明你的结论；(3)直线MN 绕点A 旋转到图2的位置，若2BD =，BCAB 的长为______（直接写结果）；(4)直线MN 绕点A 旋转到图3的位置时，直接写出线段BA ，BC ，BD 之间的数量关系______．【答案】(2)AE ＝BD ，BD ﹣ABBC ；(3)4；(4)BA +BD BC【分析】（1）由90ACD ∠=︒，AC DC =，根据勾股定理可直接得出答案；（2）先证明△ACE ≌△DCB ，确定△ECB 为等腰直角三角形，即可得出答案；（3）先证明△ACE ≌△DCB ，CE ＝BC ，得到△BCE 为等腰直角三角形，得到AB ＝BD ，即可得出答案；（4）先证明△ACE ≌△DCB ，确定△ECB 为等腰直角三角形即可得出答案．【解析】（1）解：连接AD ，设AC ＝a ，则DC ＝a ，∴AD ＝==，即AD 是AC ．（2）如图1，设AC 与BD 交于O ，由题可知，∠BCE ＝90°＝∠ACD ，∴∠ACE ＝∠BCD ，∵BD ⊥MN ，∴∠ABD ＝90°＝∠ACD ，∵∠AOB ＝∠DOC ，∴∠BAC ＝∠CDB ，∵AC ＝DC ，∴△ACE ≌△DCB （ASA ），∴CE ＝BC ，AE ＝BD ，∵∠BCE ＝90°，∴△ECB 为等腰直角三角形，∴BE BC ，∵BE ＝AE ﹣AB ＝BD ﹣AB ，∴BD ﹣AB BC ；故答案为：AE ＝BD ；BD ﹣AB ；（3）解：如图2，设CD 与MN 交于O ，由题可知，∠BCE ＝90°＝∠ACD ，∴∠ACE ＝∠BCD ，∵BD ⊥MN ，∴∠ABD ＝90°＝∠ACD ，∵∠AOC ＝∠DOB ，∴∠BAC ＝∠CDB ，∵AC ＝DC ，∴△ACE ≌△DCB （ASA ），∴CE ＝BC ，AE ＝BD ，∵∠BCE＝90°，∴BE BC ，∵BE ＝AB ﹣AE ＝AB ﹣BD ，∴AB =BD ，∵BD ＝2，BC ，∴AB ＝BD＝4，故答案为：4．（4）∴∠BCE ＝90°＝∠ACD ，∴∠ACE ＝∠DCB ，∠CEB +∠CBE ＝90°，∵BD ⊥MN ，∴∠ABD ＝90°，∴∠CBE +∠CBD ＝90°，∴∠CEB ＝∠CBD ，∵AC ＝DC ，∴△ACE ≌△DCB （AAS ），∴CE ＝BC ，AE ＝BD ，∵∠BCE ＝90°，∴BEBC ，∵BE ＝AE +BA ＝BD +BA ，∴BA +BD，故答案为：BA +BDBC ．24．两个顶角相等的等腰三角形，如果具有公共的顶角顶点，并将它们的底角顶点分别对应连接起来得到两个全等三角形，我们把这样的图形称为“手拉手”图形．如图1，在“手拉手”图形中，AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE ，连接BD ，CE ，则△ABD ≌△ACE．(1)请证明图1的结论成立；(2)如图2，△ABC 和△AED 是等边三角形，连接BD ，EC 交于点O ，求∠BOC 的度数；(3)如图3，AB ＝BC ，∠ABC ＝∠BDC ＝60°，试探究∠A 与∠C 的数量关系．【答案】(1)见解析(2)60°(3)∠A +∠BCD =180°，理由见解析【分析】（1）利用等式的性质得出∠BAD =∠CAE ，即可得出结论；（2）同（1）的方法判断出△ABD ≌△ACE ，得出∠ADB =∠AEC ，再利用对顶角和三角形的内角和定理判断出∠BOC =60°，即可得出答案；（3）先判断出△BDP 是等边三角形，得出BD =BP ，∠DBP =60°，进而判断出△ABD ≌△CBP （SAS ），即可得出结论．【解析】（1）解：证明：∵∠BAC =∠DAE ，∴∠BAC +∠CAD =∠DAE +∠CAD ，∴∠BAD =∠CAE ，在△ABD 和△ACE 中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ACE （SAS ）；。

第四章三角形-三角形全等几何模型-手拉手型（教案）
一、教学内容
本节课选自教材第四章“三角形”中的“三角形全等几何模型-手拉手型”。教学内容主要包括：
1.掌握手拉手型全等三角形的定义及性质。
2.学会运用SSS（边边边）和SAS（边角边）判定全等三角形。
3.熟悉手拉手型全等三角形在实际问题中的应用。
二、核心素养目标
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了手拉手型全等三角形的基本概念、判定方法以及在实际中的应用。同时，我们也通过实践活动和小组讨论加深了对这些知识点的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
-掌握手拉手型全等三角形在实际问题中的应用，如解决土地测量、建筑绘图等问题。
2.教学难点
-难点一：理解手拉手型全等三角形的“手拉手”概念。学生可能难以形象化理解两个全等三角形如何通过一条线段（手拉手）连接，形成特定的几何关系。教师需要通过动态图示或实物模型，帮助学生形成直观的认识。
-难点二：判定全等三角形的条件选择。学生在面对具体问题时，可能难以判断应该使用SSS还是SAS判定全等。教师应提供多个案例，让学生比较不同情况下的判定条件，明确何时使用SSS，何时使用SAS。
3.重点难点解析：在讲授过程中，我会特别强调SSS和SAS这两个判定全等三角形的重点。对于难点部分，如手拉手型全等三角形的构造和实际应用，我会通过举例和比较来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与手拉手型全等三角形相关的实际问题。

全等三角形-----------手拉手模型一、手拉手模型基本含义定义：所谓手拉手模型，是指有公共顶点的两个等腰三角形，顶角相等。

因为顶点相连的四条边，形象的可以看作两双手，所以通常称为手拉手模型。

二、基本图形：△ABC和△ADE均是等腰三角形，其中AC=AB,AD=AE,且∠BAC=∠DAE手拉手左手拉左手、右手拉右手基本特征：① ；② ；③ ；基本三、典例精析：➢类型一：共顶点的等边三角形中手拉手例1：在直线ABC的同一侧作两个等边三角形△ABD和△BCE，连接AE与CD，(1)证明：△ABE≌△DBC;（2）证明：AE=DC;（3）求线段AE和线段DC所夹∠AFD的度数.变式练习1：在例1的基础上，将△BEC绕点B逆时针旋转一定角度，连接AE，CD，如图.(1)证明：AE=DC;（2）求线段AE所在直线和线段DC所在直线之间的夹角.➢共顶点的等腰直角三角形的手拉手例2：如图，ACB∆均为等腰直角三角形，且90∆和DCEACB DCE∠=∠=︒，连接AD,BE.判断线段AD与线段BE之间的关系，请说明理由变式练习2：如图1，已知正方形ABCD的边CD在正方形DEFG的边DE上，连接AE、GC.(1)试猜想AE与GC有怎样的数量位置关系，并证明你的结论；(2)将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和GC. 你认为(1)中的结论是否还成立?若成立，给出证明；若不成立，请说明理由.总结归纳：如下图△ABC和△ADE均是等腰三角形，其中AC=AB,AD=AE,且∠BAC=∠DAE=α，则∠BEC 的大小是多少？GEFDABCOE DA BCA B CD E 321AB DE全等三角形-----------手拉手模型课后练习1.如图，AB=AC ，AD=AE ，∠BAC=∠DAE ，∠1=25°，∠2=30°，则∠3=__________．2.如图，△ABD ，△AEC 都是等边三角形，BE 交CD 于点O ，求△DOE 的度数.3．如图，四边形ABCD ，BEFG 均为正方形，连接AG ，CE.（1）求证：AG=CE ；（2）求证：AG△CE.4.如图，AC=BC ，DC=EC ，∠ACB=∠ECD=90°，且∠EBD=42°，求∠AEB 的度数.。