工业机器人静力及动力学分析
- 格式:doc
- 大小:384.00 KB
- 文档页数:15

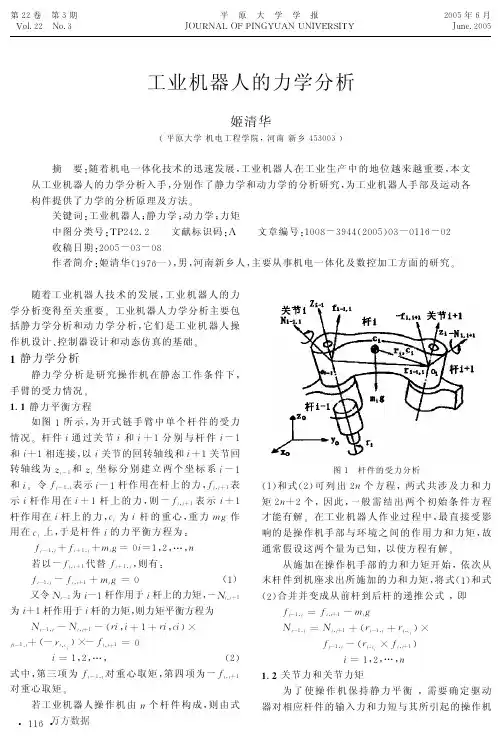
第!!卷!第"期#$%&!!!’$&"!!!!!平!原!大!学!学!报()*+’,-)./0’12*,’*’0#3+4052!!!!!667年8月!(9:;&!667工业机器人的力学分析姬清华!平原大学机电工程学院"河南新乡<7"66"#!!摘!要!随着机电一体化技术的迅速发展!工业机器人在工业生产中的地位越来越重要!本文从工业机器人的力学分析入手!分别作了静力学和动力学的分析研究!为工业机器人手部及运动各构件提供了力学的分析原理及方法"关键词!工业机器人#静力学#动力学#力矩中图分类号!5/!<!W !!!文献标识码!,!!文章编号!=66>?"@<<!!667#6"?6==8?6!!!收稿日期!!667?6"?6>作者简介!姬清华$=@A 8%&!男!河南新乡人!主要从事机电一体化及数控加工方面的研究"!!随着工业机器人技术的发展"工业机器人的力学分析变得至关重要$工业机器人力学分析主要包括静力学分析和动力学分析"它们是工业机器人操作机设计%控制器设计和动态仿真的基础$P 静力学分析静力学分析是研究操作机在静态工作条件下"手臂的受力情况$P &P 静力平衡方程如图=所示"为开式链手臂中单个杆件的受力情况$杆件)通过关节)和)N =分别与杆件)U =和)N =相连接"以)关节的回转轴线和)N =关节回转轴线为2)U =和2)坐标分别建立两个坐标系)U =和)$令5)U =")表示)U =杆作用在杆上的力"5)")N =表示)杆作用在)N =杆上的力"则U 5)")N =表示)N =杆作用在)杆上的力"*)为)杆的重心"重力<1作用在*)上"于是杆件)的力平衡方程为&5)U =")N 5)N =")N <)1K 6)K ="!"’"#若以5)")N =代替5)N =")"则有&5)U =")U 5)")N=N <)1K 6!=#!!又令;)U =为)U =杆作用于)杆上的力矩"U ;)")N =为)N =杆作用于)杆的力矩"则力矩平衡方程为;)U =")U ;)")N=U !&)")N =N &)"*)#V 5)U =")N !U &)"*)#V U 5)")N =K 6!!)K ="!"’"!!#式中"第三项为5)U =")对重心取矩"第四项为U 5)")N =对重心取矩$若工业机器人操作机由#个杆件构成"则由式图=!杆件的受力分析!=#和式!!#可列出!#个方程"两式共涉及力和力矩!#g !个"因此"一般需结出两个初始条件方程才能有解$在工业机器人作业过程中"最直接受影响的是操作机手部与环境之间的作用力和力矩"故通常假设这两个量为已知"以使方程有解$从施加在操作机手部的力和力矩开始"依次从末杆件到机座求出所施加的力和力矩"将式!=#和式!!#合并并变成从前杆到后杆的递推公式"即5)U =")K 5)")N=U <)1;)U =")K ;)")N =N !&)U =")N &)"*)#V 5)U =")U !&)"*)V 5)")N =#!!)K ="!"’"#P &N 关节力和关节力矩为了使操作机保持静力平衡"需要确定驱动器对相应杆件的输入力和力短与其所引起的操作机(8==( 万方数据手部力和力矩之间的关系!令*)为驱动元件)的第)个驱动器的驱动力或驱动力矩"并假设关节处无摩擦"则有当关节是移动副时"如图!所示"*)应与该关节的作用力5)U =")在2)U =上的分量平衡"即*)K -O)U =5)U=")式中-)U =为)U =关节轴的单位向量!上式表明驱动器的输入力只与5)U =")在2)U =轴上的分量平衡"其他方向的分量由约束力平衡"约束力不作功!当关节是转动副时"*)表示驱动力距"它与作用力矩;)U =")在2)U =轴上的分量相平衡"即*)K -O)U =;)U=")图!!移动关节上的关节力N 动力学分析动力学分析是研究操作机各主动关节驱动力与手臂运动的关系"从而得出工业机器人动力学方程!目前已提出了多种动力学分析方法"这里仅就用牛顿欧拉方程建立工业机器人动力学方程作简要介绍!图"!杆件动力学方程的建立!!动力学方程可以用两个方程表达#一个用以描述质心的移动"另一个描述质心的转动!前者称为牛顿运动方程"后者称为欧拉运动方程!取工业机器人手臂的单个杆件作为自由体"其受力分析如图"所示!图中(*)为杆件)相对于固定坐标系的质心速度"+)为杆件)的转动角速度!因为固定坐标系是惯性参考系"所以将杆件)的惯性力加入到静力学方程式$=%中"于是有牛顿运动方程#5)U =")U 5)")N=N <)1U <)W (*)K 6)K ="!"&"#$"%作用在杆件)上的惯性矩是该杆件的瞬时角动量对时间的变化率!令+)为角速度向量"B )为杆件)质心处的惯量"于是角动量为B )+)!因为惯量随杆件方位的变化而变化"所以角动量对时间的导数不仅包含B )W +)"而且包含因B )的变化而引起的变化+)V B )+)"即陀螺力矩"上述两项加到静力学力矩平衡式$!%中"得;)U =")U ;)")N =N &)"*)V 5)")N =U &)U ="*)V 5)U =")U B W +)U +)V B )+)K 6)K ="!"&"#$<%公式$"%和$<%是单个杆件的动力学特性关系式"若将工业机器人的:个杆件均列出相应的上述两个方程"即得到工业机器人完整的动力学方程组的基本形式#牛顿’欧拉方程!!!参考文献!!="徐元昌#陶学恒&工业机器人!["&北京$中国轻工业出版社#=@@@&!!"陈小川#刘晓冰&虚拟制造体系及其关键技术!("&计算机辅助设计与制造#=@@@#%=6&&!""盛晓敏#邓朝晖&先进制造技术!["&北京$机械工业出版社#!66<&!<"邱士安&机电一体化技术!["&西安$西安电子科技出版社#!66<&【责任编校!李东风】@"@"’-.()(45B %*$’")*(!"U 474#_K +)"2?$,’$C "*0$#)*$+$#DX +"*8&)*$+X #1)""&)#1H "I $&8<"#8’5%)#1.3$#6#)("&7)8."9)#:)$#1"!"#$#<7"66"40)#$%@7(#1’*##_C G BG B ;F E J C II ;T ;%$J M ;:G$O [;H B E G F E :C H D "G B ;F $K $GE J J %C ;IC :C :I 9D G F L BE T ;K ;H $M ;M $F ;E :IM $F ;C M J $FG E :G &5B C D E F G CH %;E :E %L c ;D O F $M M ;H B E :C H D "I C D H 9D D ;D O F $MG B ;D G E G C H D E :II L :E M C H D D ;J E F E G ;%L E :I$O O ;F D G B ;G B ;$F C ;D $O E :E %L c C :Q E F M M $T ;M ;:G E :I H $M J$:;:G $O F $K $G D &A %.:41/(#F $K $G (D G E G C H D (I L :E M C H D (M $T ;M ;:G )A ==) 万方数据工业机器人的力学分析作者:姬清华, JI Qing-hua作者单位:平原大学,机电工程学院,河南,新乡,453003刊名:平原大学学报英文刊名:JOURNAL OF PINGYUAN UNIVERSITY年,卷(期):2005,22(3)被引用次数:2次1.邱士安机电一体化技术 20042.盛晓敏;邓朝晖先进制造技术 20043.陈小川;刘晓冰虚拟制造体系及其关键技术 1999(10)4.徐元昌;陶学恒工业机器人 19991.陈登瑞六自由度机械手本体结构关键技术研究[学位论文]硕士 20062.张烈霞工业机器人运动及仿真研究[学位论文]硕士 2006本文链接:/Periodical_pydxxb200503036.aspx。









注:1)2008年春季讲课用;2)带下划线的黑体字为板书内容;3)公式及带波浪线的部分为必讲内容第3章工业机器人静力学及动力学分析3.1 引言在第2章中,我们只讨论了工业机器人的位移关系,还未涉及到力、速度、加速度。
由理论力学的知识我们知道,动力学研究的是物体的运动和受力之间的关系。
要对工业机器人进行合理的设计与性能分析,在使用中实现动态性能良好的实时控制,就需要对工业机器人的动力学进行分析。
在本章中,我们将介绍工业机器人在实际作业中遇到的静力学和动力学问题,为以后“工业机器人控制”等章的学习打下一个基础。
在后面的叙述中,我们所说的力或力矩都是“广义的”,包括力和力矩。
工业机器人作业时,在工业机器人与环境之间存在着相互作用力。
外界对手部(或末端操作器)的作用力将导致各关节产生相应的作用力。
假定工业机器人各关节“锁住”,关节的“锁定用”力与外界环境施加给手部的作用力取得静力学平衡。
工业机器人静力学就是分析手部上的作用力与各关节“锁定用”力之间的平衡关系,从而根据外界环境在手部上的作用力求出各关节的“锁定用”力,或者根据已知的关节驱动力求解出手部的输出力。
关节的驱动力与手部施加的力之间的关系是工业机器人操作臂力控制的基础,也是利用达朗贝尔原理解决工业机器人动力学问题的基础。
工业机器人动力学问题有两类:(1)动力学正问题——已知关节的驱动力,求工业机器人系统相应的运动参数,包括关节位移、速度和加速度。
(2)动力学逆问题——已知运动轨迹点上的关节位移、速度和加速度,求出相应的关节力矩。
研究工业机器人动力学的目的是多方面的。
动力学正问题对工业机器人运动仿真是非常有用的。
动力学逆问题对实现工业机器人实时控制是相当有用的。
利用动力学模型,实现最优控制,以期达到良好的动态性能和最优指标。
工业机器人动力学模型主要用于工业机器人的设计和离线编程。
在设计中需根据连杆质量、运动学和动力学参数,传动机构特征和负载大小进行动态仿真,对其性能进行分析,从而决定工业机器人的结构参数和传动方案,验算设计方案的合理性和可行性。
在离线编程时,为了估计工业机器人高速运动引起的动载荷和路径偏差,要进行路径控制仿真和动态模型的仿真。
这些都必须以工业机器人动力学模型为基础。
工业机器人是一个非线性的复杂的动力学系统。
动力学问题的求解比较困难,而且需要较长的运算时间。
因此,简化求解过程,最大限度地减少工业机器人动力学在线计算的时间是一个受到关注的研究课题。
在这一章里,我们将首先讨论与工业机器人速度和静力学有关的雅可比矩阵,然后介绍工业机器人的静力学问题和动力学问题。
3.2 工业机器人速度雅可比与速度分析3.2.1 工业机器人速度雅可比数学上雅可比矩阵(Jacobian matrix)是一个多元函数的偏导矩阵。
假设有六个函数,每个函数有六个变量,即:⎪⎪⎩⎪⎪⎨⎧===),,,,,(),,,,,(),,,,,(654321666543212265432111x x x x x x f y x x x x x x f y x x x x x x f y M(3-1) 可写成:Y =F (X )将其微分,得:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∂∂++∂∂+∂∂=∂∂++∂∂+∂∂=∂∂++∂∂+∂∂=666226116666222211226612211111d d d d d d d d d d d d x x f x x f x x f y x x f x x f x x f y x x f x x f x x f y ΛM ΛΛ (3-2) 也可简写成:X X F Y d d ∂∂= (3-3)式(3-3)中的(6×6)矩阵XF ∂∂叫做雅可比矩阵。
在工业机器人速度分析和以后的静力学分析中都将遇到类似的矩阵,我们称之为工业机器人雅可比矩阵,或简称雅可比。
一般用符号J 表示。
图3-1为二自由度平面关节型工业机器人(2R 工业机器人),其端点位置x ,y 与关节变量θ1、θ2的关系为:⎩⎨⎧++=++=)in(sin )cos(cos 2121121211θθθθθθs l l y l l x (3-4) 即:⎩⎨⎧==),(),(2121θθθθy y x x (3-5) 将其微分,得: ⎪⎪⎩⎪⎪⎨⎧∂∂+∂∂=∂∂+∂∂=22112211d d d d d d θθθθθθθθy y y x x x 将其写成矩阵形式为:(x ,y )T 图3-1 二自由度平面关节工业机器人⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=⎥⎦⎤⎢⎣⎡212121d d d d θθθθθθy y x xy x (3-6) 令: ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=2121θθθθy y x x J (3-7)式(3-6)可简写为:d X =J d θ (3-8)式中:⎥⎦⎤⎢⎣⎡=y x X d d d ;⎥⎦⎤⎢⎣⎡=21d d d θθθ 我们将J 称为图3-1所示二自由度平面关节型工业机器人的速度雅可比,它反映了关节空间微小运动d θ与手部作业空间微小位移d X 之间的关系。
注意:d X 此时表示微小线位移。
若对式(3-7)进行运算,则2R 工业机器人的雅可比写为:⎥⎦⎤⎢⎣⎡++++-+--=)cos()cos(cos )sin()sin(sin 2122121121221211θθθθθθθθθθl l l l l l J (3-9) 从J 中元素的组成可见,J 阵的值是θ1及θ2的函数。
对于n 个自由度的工业机器人,其关节变量可以用广义关节变量q 表示,q =[q 1 q 2 … q n ]T ,当关节为转动关节时,q i =θi ,当关节为移动关节时,q i =d i d q =[d q 1 d q 2 … d q n ]T 反映了关节空间的微小运动。
工业机器人手部在操作空间的运动参数用X 表示,它是关节变量的函数,即X =X (q ),并且是一个6维列矢量(因为表达空间刚体的运动需要6个参数,即三个沿坐标轴的独立移动和三个绕坐标轴的独立转动)。
因此,d X =[d x d y d z δφx δφy δφz ]T 反映了操作空间的微小运动,它由工业机器人手部微小线位移和微小角位移(微小转动)组成,d 和δ没差别,因为在数学上,d x =δx 。
于是,参照(3-8)式可写出类似的方程式,即:d X =J (q )d q (3-10)式中J (q )是6×n 的偏导数矩阵,称为n 自由度工业机器人速度雅可比矩阵。
它反映了关节空间微小运动d q 与手部作业空间微小运动d X 之间的关系。
它的第i 行第j 列元素为:qjq x q J i ij ∂∂=)()(, i =1,2,…,6;j =1,2,…,n (3-11) 3.2.2 工业机器人速度分析对式(3-10)左、右两边各除以d t ,得:tt d d )(d d q q J X = (3-12) 即q q J V &)(= (3-13)式中: V ——工业机器人手部在操作空间中的广义速度,V =X&; q &——工业机器人关节在关节空间中的关节速度;J (q )——确定关节空间速度q &与操作空间速度V 之间关系的雅可比矩阵。
对于图3-1所示2R 工业机器人来说,J (q )是式(3-9)所示的2×2矩阵。
若令J 1、J 2分别为式(3-9)所示雅可比的第一列矢量和第二列矢量,则式(3-13)可写成:2211θθ&&J J V +=式中右边第一项表示仅由第一个关节运动引起的端点速度;右边第二项表示仅由第二个关节运动引起的端点速度;总的端点速度为这两个速度矢量的合成。
因此,工业机器人速度雅可比的每一列表示其它关节不动而某一关节运动产生的端点速度。
图3-1所示二自由度平面关节型工业机器人手部的速度为:[][]⎥⎦⎤⎢⎣⎡+++++-++-=⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡++++-+--=⎥⎦⎤⎢⎣⎡=22121212112212121211212122121121221211)cos()c(cos )sin()sin(sin )cos()c(cos )sin()sin(sin θθθθθθθθθθθθθθθθθθθθθθθθθθ&&&&&&l l l l l l l l l l l l v v y x V 假如θ1及θ2是时间的函数,θ1=f 1(t ),θ2=f 2(t ),则可求出该工业机器人手部在某一时刻的速度V =f (t ),即手部瞬时速度。
反之,假如给定工业机器人手部速度,可由式(3-13)解出相应的关节速度,即:V J q 1-=& (3-14)式中:J -1称为工业机器人逆速度雅可比。
式(3-14)是一个很重要的关系式。
例如,我们希望工业机器人手部在空间按规定的速度进行作业,那么用式(3-14)可以计算出沿路径上每一瞬时相应的关节速度。
但是,一般来说,求逆速度雅可比J -1是比较困难的,有时还会出现奇异解,就无法解算关节速度。
通常我们可以看到工业机器人逆速度雅可比J -1出现奇异解的情况有下面两种:(1) 工作域边界上奇异。
当工业机器人臂全部伸展开或全部折回而使手部处于工业机器人工作域的边界上或边界附近时,出现逆雅可比奇异,这时工业机器人相应的形位叫做奇异形位。
(2) 工作域内部奇异。
奇异并不一定发生在工作域边界上,也可以是由两个或更多个关节轴线重合所引起的。
当工业机器人处在奇异形位时,就会产生退化现象,丧失一个或更多自由度。
这意味着在空间某个方向(或子域)上,不管工业机器人关节速度怎样选择手部也不可能实现移动。
[例3-1] 如图3-2所示二自由度平面关节型机械手。
手部某瞬沿固定坐标系X 0轴正向以1.0m/s 速度移动,杆长为l 1=l 2=0.5m 。
假设该瞬时θ1=30︒,θ1=-60︒。
求相应瞬时的关节速度。
解 由式(3-9)知,二自由度机械手的速度雅可比为:⎥⎦⎤⎢⎣⎡++++-+--=)cos()cos(cos )sin()sin(sin 2122121121221211θθθθθθθθθθl l l l l l J 因此,逆速度雅可比为:⎥⎦⎤⎢⎣⎡+--+--++=-)sin(sin )cos(cos )sin()cos(sin 121211212112122122211θθθθθθθθθθθl l l l l l l l J (3-15)图3-2 二自由度机械手手爪沿X 0方向运动⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=01y x v v V ,因此,由式(3-14)可得:⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+--+--++==⎥⎥⎦⎤⎢⎢⎣⎡=-01)sin(sin )cos(cos )sin()cos(sin 12121121211212212221121θθθθθθθθθθθθθθl l l l l l l l V J &&& 因此rad/s)(2235.023)(-60 sin 5.0)60-03( cos sin )( cos 21211-=⨯-=︒⨯︒︒=+=θθθθl & rad/s 4235.0232)(-60 sin 5.0)60-03( cos )(-60 sin 5.003 cos sin )( cos sin cos 21212212=⨯=︒⨯︒︒-︒⨯︒-=+--=θθθθθθl l & 从以上可知,在该瞬时两关节的位置和速度分别为θ1=30︒,θ2=-60︒,1θ&=-2rad/s ,2θ&=4rad/s ,手部瞬时速度为1m/s 。