关于“百化分”在估算法中的运用

2020国考行测资料分析常用公式—百化分国考行测资料分析题目中很多题目都要用到公式解答，我们做题，除了要记住公式，更重要的是要学会选择合适的公式。

题目不会没关系，会用公式是关键，今天华图教育集团阿信老师就给大家分享资料分析中常用的百化分相关公式。

百化分相关公式1/3=33.3% 1/4=25% 1/5=20%1/6=16.7% 1/7=14.3% 1/8=12.5%1/9=11.1% 1/11=9.1% 1/12=8.3%1/13=7.7% 1/14=7.1% 1/15=6.7%1/16=6.3% 1/17=5.9% 1/18=5.6% 1/19=5.3%这些常见的百化分结论用于快捷计算增长量。

当增长率为时，;当增长率为-时，。

我们要做的就是把百分数增长率变成形式的分数，方便计算。

我们来通过真题练习一下运用。

2017年，我国电信业务收入12620亿元，比上年增长6.4%，增速同比提高1个百分点。

(材料节选)【例1】2017年我国电信业务收入同比增长了大约( )亿元。

A. 681B. 759C. 808D. 818【解析】第一步，判断本题考查增长量计算。

第二步，在文字材料中找到2017年全国电信业务收入为12620亿元，比上年增长6.4%。

1/15=6.7% ，1/16=6.3% 可以把6.4%看成1/16更接近，12620/(1+16)=742第三步，根据百化分法，，由百化分结论可得1/15=6.7% 、1/16=6.3% ，所以可以把6.4%近似看成1/15.5。

增长量=，首位商7，观察选项B符合，因此，选择B选项。

2016年6月份，我国社会消费品零售总额26857亿元，同比增长10.6%，环比增长0.92%。

其中，限额以上单位消费品零售额13006亿元，同比增长8.1%。

2016年1~6月份，我国社会消费品零售总额156138亿元，同比增长10.3%。

其中，限额以上单位消费品零售额71075亿元，同比增长7.5%。

资料分析掌握技巧总结(通用3篇)资料分析掌握技巧总结第1篇分析技巧是利用新思维快速解决问题的方法，而不是直除硬算。

已知现期量和增长率，求增长量或基期量的题目，当增长率可以用百化分的方式转换成分数后，我们就可以利用份数法来进行计算。

如果增长率R可表示为a/b的分数形式，则基期量为分母b份，增长量为分子a 份，现期量为b±a份（R为负数时减）参考答案：C解题步骤：第一步：增长率R=，可看成1/6第二步：基期量6份，增长量1份，则现期量7份第三步：现期量29144对应7份，则1份=29144/7约等于4200当无法应用份数法（增长率R不能化成熟悉的分数），或选项离得近，份数法误差大时，可利用假设法求增量。

第一步：假设增长量，主要依据四个选项答案并结合着材料中已知的现期量和增长率进行假设第二步：真实的现期量-假设的增长量=假的基期量第三步：假的前期量×增长率＝增长量（答案）材料：参考答案：B解题步骤：第一步：假设增长量=第二步：第三步：50000×8%=40001、原理以盐水为例两个一模一样的杯子，里边分别装满浓度为30%和浓度为50%的盐水，然后将两杯盐水倒到一起，问倒到一起后的盐水浓度?一大一小两个的杯子，大的里边装满浓度为30%的盐水，小的里边装满浓度为50%的盐水，问混合到一起后的盐水浓度?很显然，杯子一模一样，则混合后为平均浓度40%，杯子一大一小，则混合后一定在30%-40%之间。

结论：混合溶液浓度一定在两个溶液浓度之间，且靠近于质量大的溶液浓度2、如何鉴别类浓度资料分析中不会给大家一杯溶液去分析，都是类浓度题。

类浓度题存在两个特征：一是比值，二是总分关系。

例如，增长率R，平均值等参考答案：错误分析过程：增长率R是比值，并且存在总分关系，全国是总，手机移动设备和非手机移动设备是分，根据混合溶液思想，全国的R一定在他们两者之间，即非手机R＜＜，因此非手机移动设备上网的流量同比增长R＜，没超过2倍对于除法计算，选项设置为区间范围的题目，可以将区间断点的数值与分母相乘再与分子比较，判断大小关系，进而实现快速秒杀的方法参考答案：B解题过程：根据题意，计算就能得到答案，由于选项都是区间形式，我们可以把区间断点带入验证，例如带入50，用50×发现略小于，说明应该比50略大，因此选B资料分析掌握技巧总结第2篇加减乘除的应试技巧既简单又实用，是提升资料分析计算环节速度的基础。

数资中的“百化分”你用对了吗？一、“百化分”简述“百化分”是数量关系和资料分析中的好帮手，在大家做题中会经常用到，它能够在保证准确率的前提下，精简计算，加快做题速度。

所谓“百化分”，是指将百分数转化为分数形式，比较常用是化为1n，随后代入到公式中，将复杂的数据进行简化。

那么我们来看一些比较常用的“百化分”。

【百化分表】请熟记此表，熟练百化分的换算。

分数 1/2 1/3 1/4 1/5 1/6 1/7 1/8 1/9 1/10 小数 0.5 0.333 0.25 0.2 0.167 0.143 0.125 0.111 0.1 百分数50%33.3%25%20%16.7%14.3%12.5%11.1%10%二、典型例题【例1】（2013-陕西-83）将700克14.3%的盐水与900克11.1%的盐水混合后，再加入200克盐，蒸发掉300克水后，该盐水的浓度为（ ）。

A. 22.2%B. 24.3%C. 26.7%D. 28.6%【点拨】这道题属于数量关系中的溶液问题。

欲求出盐水浓度，则需要计算出溶液中所含溶质的量。

根据⨯溶质=浓度溶液，可得70014.3%+90011.1%⨯⨯，一般情况下我们都会相乘硬算，计算量比较大，那么我们运用“百化分”，可以这样算。

→1170090010010020079⨯+⨯=+=。

那么最后混合的盐水浓度为20020040026.7%700+900+2003001500+==≈-溶质浓度=溶液，选择C 选项。

【例2】2011年，我国规模以上电子信息制造业主营业务成本占主营业务收入的比重达到88.7%，比2010年提高0.6个百分点。

行业中亏损企业2497个，同比增长36.7%，企业亏损面达16.6%；亏损企业亏损额同比增长52.9%。

2011年，我国规模以上电子信息制造企业数量约为多少万家（ ）A. 1B. 1.5C. 2D. 2.5【点拨】这道题属于资料分析中的比重问题。

百化分使用技巧百化分（Polya's Four-Step Problem Solving Process）是由数学教育家乔治·波利亚（George Polya）所提出的问题解决方法。

这种方法旨在帮助学生正确有效地解决问题。

以下是百化分方法的使用技巧：第一步：理解问题（Understand the problem）在解决问题之前，首先需要完全理解问题的要求和信息。

读懂问题之后，可以尝试回答以下问题：问题在问什么？我需要找什么？我有什么信息？我需要做什么才能解决问题？第二步：制定计划（Devise a plan）在理解问题之后，接下来需要制定一个解决问题的计划。

可以考虑以下方法：1. 寻找类似的问题或模式：回顾过去遇到的类似问题，看看是否有相似的解决方法可以借鉴。

2. 分解问题：将整个问题分解成更小的部分或子问题，再逐个解决。

3. 假设和预测：尝试根据已有信息和经验提出一些假设和预测，然后测试它们是否正确。

根据具体问题的特点，选择最适合的解决方法。

第三步：执行计划（Carry out the plan）在实施计划之前，需要整理好所有所需的信息、工具和公式等。

然后逐步执行计划，按照制定的方法去解决问题。

在执行过程中要保持思路的清晰和逻辑的严密。

第四步：检查结果（Look back）解决问题后，需要检查结果的准确性和合理性。

可以尝试通过以下方式进行检查：1. 反思解题过程：回顾解题过程，检查每个步骤的正确性和有效性。

2. 使用不同的方法验证结果：尝试使用其他方法或公式验证解答是否正确。

3. 直觉判断：根据经验和直觉来判断结果是否合理。

如果发现问题或错误，应该返回前一步重新检查和修正。

总之，百化分方法是一种灵活、有条理的解题方法，可以帮助学生有效地解决问题。

通过理解问题、制定计划、执行计划和检查结果等步骤，可以帮助学生培养问题解决的思维能力和方法。

在实践中，灵活运用这一方法，能够更好地解决各种问题。

2016公务员考试行测资料分析之估算法赣州华图在国家公务员考试中，行测是考生答题时间非常紧张的一个科目，很多考生不会合理分配时间就导致考试题目做不完，行测中的资料分析模块是考试科目中分数提高最快的，掌握一定的解题技巧就能提升分数，下面分享资料分析的解题技巧中常用的估算法，希望能对考生有一定的帮助，希望能对参加2016国家公务员的考生有所帮助。

那么在什么时候我们会用到估算法呢？如果选项相差比较大，而且所列式子中的数据比较复杂，这时我们自然会想到用估算法来解。

根据资料分析的特征可知，出现上面两种情况的时候特别多，所以估算法经常会用到。

常用估算：（1）凑整思想 （2）百化分思想比如说：（1）28/125=28*8/125*=224/1000=0.224,这个过程就是个凑整过程，也就是把分母凑成“整数”，那之后就可以移动小数点就可以搞定了。

（2）28/0.167=28/1/6=28*6=168,这个过程就是百化分思想，也就是把一些特殊的小数化成分数，那么问题就变的很简单了，所以需要大家对一些常见的特殊分数要记住，一般要求识记1/2=0.5;······;1/11=0.91。

为了减少我们在估算过程的误差：（1）除法同大同小（2）乘法一大一小（3）等比例变大或变小。

下面我们看看实际的例题如何来估算：【例1】706.38÷24.75= ( )A.20.5B.24.5C.28.5D.32.5 解析：4.28100284042547102571075.2438.706==⨯⨯=≈，所以答案选C. 【例2】10.203×5.837=( )A.55.49B.59.55C.63.28D.66.58解析：60610837.5203.10=⨯=⨯，所以选择最接近的选项B.【例3】2010年，某省广电实际总收入为145.83亿元，同比增长32.07%。

关于“百化分”在估算法中的运用华图教育 胡伟玲资料分析是公务员行测考试的一个非常重要的模块，不管是国家还是地方性的行测考试，资料分析都是必考的一个模块。

虽然其考察的基本知识点少，容易学习和把握已经是考生的通识，然而大部分考生依然望而生畏，原因是资料分析在处理数据时大部分时候都涉及到复杂数据的除法乃至复合运算，相当耗时间。

公考培训业者在早期的考试研究专家的带领下，建立了资料分析的各种速算方法，比如行测数量第一人李委明老师在其资料分析中总结了十大速算技巧。

然而问题是很多的考生在复习时依然倍感困惑，拿到具体的数据不知如何下手。

本文拟从“百化分”的技巧切入做一探讨，希望各位考生能有所收获。

为了能够对复杂的数据进行计算，我们选择速算。

其目的是为了通过速算的各种技巧，快速得出答案，然而要快速得出答案，不等于我们可以不用计算。

如果说速算法的最终目的是快速锁定答案，那么资料分析之速算法的直接目的应该是把复杂的数据变成简单的整数运算。

如果我们能够极大的简化数据，同时又能保证计算的精度，那么我们就能够掌控数据处理的进程而不是简单的知道有多少速算方法。

要记住，考场最需要的是实战的能力。

所谓“百化分”，即是将复杂的百分数变为简单的分数进行运算的能力。

比如看到增长率为24.9%，我们应该马上想到写成41来进行计算；看到22.5%，我们可以写成5141或，但更为精确的表达应该是%2.2292 ，这样计算的精度更有保证。

下边以2011年及2012年部分国考真题为例，向考生做一说明。

一、“百化分”能够将复杂的百分数变成简单的分数进行运算，比起直除法，其心理压力更小，因为我们擅长小的整数运算。

【材料1】2010年，我国进出口贸易总额为29727.6亿美元，同比增长34.7%。

【题】2012国考——117.2009年我国进出口贸易总额约为多少万亿美元?A.1.6B.2.2C.2.6D.3.0【解析】答案B 。

根据题意可知此题为根据现期求基期。

2020国考行测资料分析常用公式—百化分.doc2020国考行测资料分析常用公式—百化分国考行测资料分析题目中很多题目都要用到公式解答，我们做题，除了要记住公式，更重要的是要学会选择合适的公式。

题目不会没关系，会用公式是关键，今天华图教育集团阿信老师就给大家分享资料分析中常用的百化分相关公式。

百化分相关公式1/3=33.3% 1/4=25% 1/5=20%1/6=16.7% 1/7=14.3% 1/8=12.5%1/9=11.1% 1/11=9.1% 1/12=8.3%1/13=7.7% 1/14=7.1% 1/15=6.7%1/16=6.3% 1/17=5.9% 1/18=5.6% 1/19=5.3%这些常见的百化分结论用于快捷计算增长量。

当增长率为时，;当增长率为-时，。

我们要做的就是把百分数增长率变成形式的分数，方便计算。

我们来通过真题练习一下运用。

2017年，我国电信业务收入12620亿元，比上年增长6.4%，增速同比提高1个百分点。

(材料节选)【例1】2017年我国电信业务收入同比增长了大约( )亿元。

A. 681B. 759C. 808D. 818【解析】第一步，判断本题考查增长量计算。

第二步，在文字材料中找到2017年全国电信业务收入为12620亿元，比上年增长6.4%。

1/15=6.7% ，1/16=6.3% 可以把6.4%看成1/16更接近，12620/(1+16)=742第三步，根据百化分法，，由百化分结论可得1/15=6.7% 、1/16=6.3% ，所以可以把6.4%近似看成1/15.5。

增长量=，首位商7，观察选项B符合，因此，选择B选项。

2016年6月份，我国社会消费品零售总额26857亿元，同比增长10.6%，环比增长0.92%。

其中，限额以上单位消费品零售额13006亿元，同比增长8.1%。

2016年1~6月份，我国社会消费品零售总额156138亿元，同比增长10.3%。

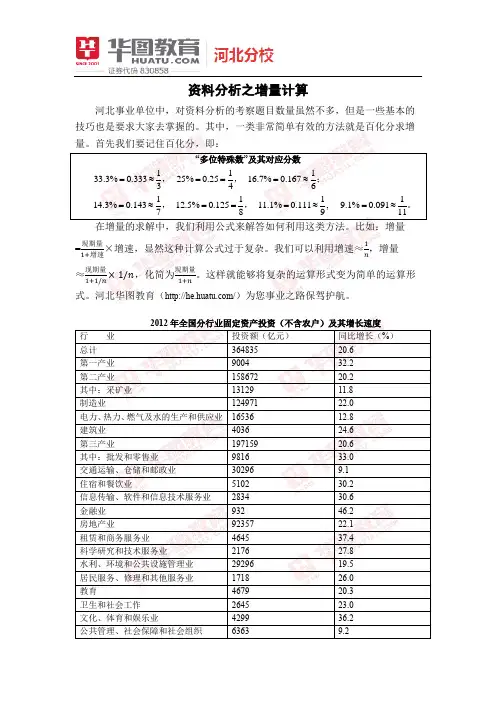
资料分析之增量计算河北事业单位中，对资料分析的考察题目数量虽然不多，但是一些基本的技巧也是要求大家去掌握的。

其中，一类非常简单有效的方法就是百化分求增量。

首先我们要记住百化分，即：在增量的求解中，我们利用公式来解答如何利用这类方法。

比如：增量=现期量1+增速×增速，显然这种计算公式过于复杂。

我们可以利用增速≈1n ，增量≈现期量1+1/n×1/n，化简为现期量1+n。

这样就能够将复杂的运算形式变为简单的运算形式。

河北华图教育（/）为您事业之路保驾护航。

2012年全国固定资产投资额约比上年同期增长多少万亿元？（）A．4 B．5C．6 D．7华图专家解析：题目问增长了多少，在问增长量是多少？显然利用百化分这个知识点比较快速。

直接带入增长量计算的公式，则有6%6.20%6.201364835≈⨯+万亿元，因此，本题正确答案为C。

2012年，某省规模以上工业增加值10875亿元，比上年增长7.1%，月度增速从1-2月的2.9%回升到10-12月的10%以上。

大型、中型和小微型企业增加值分别为3074、3217和4584亿元，比上年分别增长8.2%、6.8%和6.7%。

2012年，该省规模以上工业企业主营业务收入56730亿元，比上年增长3.5%，增速比全国低7.5个百分点；利润总额2900亿元，比上年下降6.1%。

2012年某省规模以上工业增加值同比增速情况与2011年相比，2012年该省规模以上工业增加值约增加了多少亿元？A.600B.720C.840D.960华图专家解析：计算规模以上工业增加值的增长量：10875÷（1+7.1%）×7.1%，用1/14化简，直除首位商7。

因此，答案选择B选项。

增量计算其实在考试都会出现，而百化分该知识点基本都是需要前期努力识，同学在备考这类题目的时候一定要勤奋努力。

2015河南公务员备考:资料分析中估算的应用估算在资料分析的速算中起着举足轻重的作用，关于估算有很多种应用方式，今天我们介绍一种利用简单误差分析来进行估算的方法，如果掌握了这种方法，在计算时可以大大节省我们的计算时间，接下来我们就通过一些相应的题目来深入的了解一下这种方法。

【例1】【2012年北京】2009年世界液化天然气贸易量为2427.5亿立方米，天然气贸易量为8768.5亿立方米。

则世界液化天然气贸易量占天然气贸易总量的比重为( )。

A.17.5%B.22.2%C.27.7%D.38.3%【解析】根据题目，我们可以直接列式为，结合选项我们会发现，可以利用直除法结合插值法来做，可以快速的得到答案为C选项，这里不再赘述，我们主要讲解一下如何利用结合误差分析的估算来做，我们会发现分母8768.5过于复杂，如果可以变成10000就比较简单了，如果分母变大，为了使整体的结果偏差不大，应该使分子也要变大一点，但显然不能变大相同的数，往往我们使分子分母都按照比例进行变化，比如对于，我们如果把分子分母都变大a%，即，显然两者是相等的，我们没有必要严格的按照该比例进行估算，因为那样需要大家有较强的口算能力，我们只需要大概进行一下估算就可以了，比如我们把分母8768.5看成了10000，大概增加了1230左右，而8768.5大致是分子2427.5的三倍多，所以分子只需要增加1230的三分之一不到就可以了，即大致300多点，350左右就差不多了，这样该式就变成了的样子，所以答案应该在27.7%左右，所以答案选择C选项。

国家公务员| 事业单位| 村官| 选调生| 教师招聘| 银行招聘| 信用社| 乡镇公务员| 各省公务员|国家公务员| 事业单位 | 村官 | 选调生 | 教师招聘 | 银行招聘 | 信用社 | 乡镇公务员| 各省公务员|可能有些同学对上面的这种算法并不是特别理解，这很正常，因为这种估算方法需要大家有较强的口算能力和对数字比较敏感，但是大家一旦掌握了这种方法，便可以大大提高我们的解题速度，接下来再给大家演绎一道题目，以期加深大家对该方法的理解。

关于“百化分”在估算法中的运用华图教育 胡伟玲资料分析是公务员行测考试的一个非常重要的模块，不管是国家还是地方性的行测考试，资料分析都是必考的一个模块。

虽然其考察的基本知识点少，容易学习和把握已经是考生的通识，然而大部分考生依然望而生畏，原因是资料分析在处理数据时大部分时候都涉及到复杂数据的除法乃至复合运算，相当耗时间。

公考培训业者在早期的考试研究专家的带领下，建立了资料分析的各种速算方法，比如行测数量第一人李委明老师在其资料分析中总结了十大速算技巧。

然而问题是很多的考生在复习时依然倍感困惑，拿到具体的数据不知如何下手。

本文拟从“百化分”的技巧切入做一探讨，希望各位考生能有所收获。

为了能够对复杂的数据进行计算，我们选择速算。

其目的是为了通过速算的各种技巧，快速得出答案，然而要快速得出答案，不等于我们可以不用计算。

如果说速算法的最终目的是快速锁定答案，那么资料分析之速算法的直接目的应该是把复杂的数据变成简单的整数运算。

如果我们能够极大的简化数据，同时又能保证计算的精度，那么我们就能够掌控数据处理的进程而不是简单的知道有多少速算方法。

要记住，考场最需要的是实战的能力。

所谓“百化分”，即是将复杂的百分数变为简单的分数进行运算的能力。

比如看到增长率为24.9%，我们应该马上想到写成41来进行计算；看到22.5%，我们可以写成5141或，但更为精确的表达应该是%2.2292 ，这样计算的精度更有保证。

下边以2011年及2012年部分国考真题为例，向考生做一说明。

一、“百化分”能够将复杂的百分数变成简单的分数进行运算，比起直除法，其心理压力更小，因为我们擅长小的整数运算。

【材料1】2010年，我国进出口贸易总额为29727.6亿美元，同比增长34.7%。

【题】2012国考——117.2009年我国进出口贸易总额约为多少万亿美元? A.1.6B.2.2C.2.6D.3.0【解析】答案B 。

根据题意可知此题为根据现期求基期。

博大弘仕公务员考试行测技巧：估算诀窍作者：博大弘仕杨金珏资料来源：估算法是资料分析的核心方法，但是把估算法用好还有许多窍门。

在估算过程中如何进行四舍五入？近似值保留到什么样的程度？这些都是困扰不少考生的问题。

博大弘仕杨金珏老师将介绍估算法的实用技巧，帮助大家又快又准确地计算出结果。

在估算过程中要用到四舍五入，对于1、2或者8、9这样靠近两端的数字很容易取舍，但如果遇到如3、4、5、6、7这些靠中间的数字时，我们应该如何取舍呢？特别是在选项比较接近的情况下，如果估算尺度大，有可能造成大的偏差。

如果进行精确计算，考试时间又不允许。

如何有效地四舍五入是成为了一个关键问题。

首先我们来看两道例题，按照我们常规四舍五入方法进行估算：【例1】19758÷39435=（）A．49.22% B．50.10% C．51.29% D．53.19%【博大弘仕解析】计算器计算结果：50.10%保留两位有效数字：19758÷39435≈20000÷39000≈51.28%在这样的题目中，如果进行常规的估算，结果偏差较大，很容易误选。

但是如果精确计算，此时花费时间较多。

【例2】29.342×56.363%=（）A．16.02% B．16.25% C．16.55% D．16.98%【博大弘仕解析】计算器计算结果：16.54保留两位有效数字：29.342×56.363%≈29×56%≈16.24同样，在这样的题目中，如果进行常规的估算，容易选错答案。

但是如果精确计算，用的时间会很多。

在四舍五入时，如何不增加计算量而提高结果的精度？这里博大弘仕杨金珏老师教给大家一首估算诗，可以有效提高结果的准确度。

估算诀窍一二八九两头靠，三七范围口诀套：一升一降是乘法，同升同降是除法。

升降首选小数字，结果方向有玄妙。

具体意思是：在估算四舍五入时，如果要保留数字后面是1、2或者8、9，此时就按照常规方法进行“舍”和“入”；如果要保留数字后面是3、4、5、6、7、8这样中间的数字，我们就套用口诀：在乘法中，一个乘数增大，另一个乘数减小；在除法中，分子分母同时增大或减小。

2020国考资料分析常见的百化分结论资料分析是行测中一个重要的部分，知识点虽然多，但多数都不难，容易理解，题目难度也不大，短时间内容易提高。

有些同学有这样的共性问题，在计算增长量时列式计算太复杂，浪费时间且容易出错，使用速算方法时面对一个不熟悉的增长率百分数，很难转化成分子为1的分数，深受困扰。

华图教育集团阿信老师将用五次专题文章给同学们介绍资料分析中的常见问题和解决对策，本期我们就来解决快速求得增长量的问题。

求增长量的基本公式,套入数据计算起来确实比较麻烦。

我们先来聊一聊上文提到的速算方法。

即当增长率r 1/n时增长量公式可以变为：增长量=现期量/(n+1)，下降量=现期量/(n-1)，明显能感受到这比原始公式增长量在计算量上减轻了许多。

但是考场上面对一个不熟悉的增长率百分数，比如5.6%，怎么知道它等于几分之一呢?别无他法，就是要记一些增长率百分数化分数的结论。

在记忆一些结论的基础上我们还可以大胆估算，比如若已知1/18 5.6%，1/19 5.3%，那考场上遇到5.4%我们可以大胆估算为1/18.5。

这里同学们记忆以下百化分结论，做题时直接拿来用即可。

1/2=50% 1/3 33.3% 1/4=25% 1/5=20% 1/6 16.7%1/7 14.3% 1/8=12.5% 1/9 11.1% 1/10 10% 1/11 9.1%1/12 8.3% 1/13 7.7% 1/14 7.1% 1/15 6.7% 1/16 6.3%1/17 5.9% 1/18 5.6% 1/19 5.3% 1/20 5% 1/30 3.3%同学们可以截屏设为手机壁纸，通过碎片时间观看加深记忆。

下面我们通过真题加深理解。

2017年，我国电信业务收入12620亿元，比上年增长6.4%，增速同比提高1个百分点。

其中，2017年全年固定通信业务收入完成3549亿元，比上年增长8.4%，在电信业务收入中占比为28.1%，2017年，在固定通信业务中固定数据及互联网业务收入达到1971亿元，比上年增长9.5%，拉动电信业务收入增长1.4个百分点，对全行业业务收入增长贡献率达21.9%。

资料分析百化分百度百化分是一种基于大数据技术的资料分析工具，它能够对海量的信息进行提取、整理和分析，帮助用户更好地了解和解读数据。

本文将介绍百化分的基本原理、应用场景以及一些使用注意事项。

百度百化分的基本原理是通过深度学习、自然语言处理和图像识别等技术来实现对数据的挖掘和分析。

首先，百度百化分会对数据进行预处理，包括去除噪声、清洗数据等操作，以提高数据质量。

然后，通过机器学习算法，百化分能够对数据进行分类、聚类、预测等操作，从而得出有价值的信息和结论。

最后，百化分会将分析结果呈现给用户，以帮助用户更好地理解和应用数据。

百度百化分具有广泛的应用场景。

首先，在商业领域，百度百化分可以帮助企业进行市场调研、竞争分析、产品定价等工作，从而提升市场竞争力。

其次，在金融领域，百度百化分可以帮助银行和保险公司进行风险评估、信用评分等工作，提高金融机构的风控能力。

此外，百度百化分还可以帮助政府部门进行社会热点分析、舆情监测等工作，为政策制定提供决策支持。

总之，百度百化分可以应用于各个领域，为用户提供快速、准确的数据分析服务。

然而，使用百度百化分也需要注意一些事项。

首先，由于百度百化分是基于大数据技术的，所以在使用过程中需要保护用户的隐私和数据安全。

其次，百度百化分只是一种工具，分析结果仅供参考，用户在查看和应用结果时应保持理性，不盲目追求结果。

最后，百度百化分需要大量的计算资源和数据支持，所以用户在使用时需要确保拥有足够的计算能力和数据资源。

综上所述，百度百化分是一种通过大数据技术实现资料分析的工具。

它能够对数据进行提取、整理和分析，帮助用户更好地了解和解读数据。

在商业、金融和政府等领域都有广泛的应用。

但在使用过程中需要保护数据安全、理性对待分析结果，并确保拥有足够的计算资源和数据支持。

通过正确使用百度百化分，用户可以更好地挖掘和应用数据，提升工作效率和决策能力。

百分数的化简与约分在数学中，百分数是一种常见的表示方法，它可以将一个数表示为百分之几的形式。

在实际应用中，我们经常需要对百分数进行化简和约分，以便更方便地进行计算和比较。

本文将介绍百分数的化简与约分的方法和步骤。

一、百分数的化简百分数的化简是指将一个百分数转化为最简形式的操作。

化简后的百分数更简洁明了，方便进行计算和应用。

下面是百分数化简的具体步骤：步骤一：将百分数转化为分数形式。

例如，将40%转化为分数，可以写成40/100。

步骤二：化简分数。

将分子和分母同时除以最大公约数，使分数变为最简形式。

例如，40/100可以化简为2/5，因为40和100的最大公约数是20，同时除以20得到2和5。

步骤三：将最简形式的分数转化为百分数形式。

即将分子除以分母，然后乘以100。

例如，2/5可以转化为(2/5) × 100 = 40%。

因此，化简百分数的步骤可以总结为：将百分数转化为分数形式，将分数化简，再将最简形式的分数转化为百分数形式。

二、百分数的约分百分数的约分是指对一个百分数进行简化，使其分子和分母没有公因数。

这样可以得到更简洁的表示形式，并且方便比较和计算。

以下是百分数约分的方法和步骤：步骤一：将百分数转化为分数形式。

步骤二：分别对分子和分母进行约分。

找出它们的所有公因数，然后同时除以最大公因数，使分数变为最简形式。

步骤三：将最简形式的分数转化为百分数形式。

与百分数的化简类似，百分数的约分也需要先将百分数转化为分数形式，然后对分数进行约分，最后将最简形式的分数转化为百分数形式。

三、示例为了更好地理解百分数的化简与约分，以下是一些具体的示例：示例一：将75%化简为最简分数形式。

步骤一：将百分数75%转化为分数，可表示为75/100。

步骤二：将分数75/100化简，最大公约数为25。

分子和分母同时除以25，得到3/4。

步骤三：将最简形式的分数3/4转化为百分数，即(3/4) × 100 = 75%。

百化分技巧
百化分技巧是指在求解问题时，将问题进行拆解、分析和处理的一种方法。

以下是一些常用的百化分技巧：
1. 分类：将问题中的元素或情况进行分类，找出相同或相似的部分，以便更好地理解和处理问题。

2. 比较：将问题中的元素进行比较，找出它们之间的差异和相似之处，从而找到解决问题的线索。

3. 组合：将问题中的元素进行组合，以便形成更复杂的结构或模型，从而更灵活地探索和解决问题。

4. 抽象：将问题中的具体情况或对象进行抽象，提取出它们的本质特点，以便更好地理解和处理问题。

5. 分解：将复杂的问题分解为更简单、更易处理的子问题，逐步解决每个子问题，最后得到整体的解决方案。

6. 排序：将问题中的元素或情况进行排序，以便更好地分析和处理，找出规律和关联。

7. 反证：通过假设问题的反面情况，推导出矛盾或不可能的结果，从而排除这种情况，进而找到问题的解决方案。

8. 归纳与演绎：通过观察和总结已有的具体情况，归纳出普遍规律，然后利用演绎思维方法将这些规律应用到求解问题中。

9. 迭代与递归：通过重复执行某一操作或逐步递归地进行处理，从而逐渐向问题的解决方向逼近。

10. 创新与联想：通过运用创造性思维和联想思维，将不同领域或不同问题中的思路和方法进行结合，以寻找新的解决方案。

以上是一些常用的百化分技巧，根据具体问题的情况，可以选择合适的技巧来辅助分析和解决问题。

百化分公式
百化分公式是一个概率论中的重要公式，它是用来计算真实的概率的一个广义
公式。

它的正确的使用能够提高彩票预测的准确度以及让我们更容易得到最优的解决方案。

首先，让我们来介绍一下这个百化分的公式。

公式的本质是Sum(Xi/N)*100，
其中X代表Xi的值，N代表数量，i代表位置。

这个公式意思就是将Xi值除以N
值之后再乘以100，这样得到的就是要求的百分比。

也就是说，对于一个被观察到
的结果，百化分公式可以用来计算这个结果发生的概率。

比如彩票预测结果，可以使用此百化分公式来计算每个结果发生的几率，从而
决定哪一个预测结果可能性最高，从而可以从中挑选出最可能的结果，进行彩票的投注，从而最大程度的提高彩票中奖的几率。

此外，百化分公式也可以应用在比如实验分析结果，调查问卷结果等方面，从
而得出大致的结论，更加准确的评估一个事物发生的概率。

总的来说，百化分公式是一个概率论中重要的公式，能够更加准确的计算概率，从而让我们更容易得到最优的解决方案，并且应用范围也相当广泛，因此一直深受广大从业者的青睐。

百化分通用法《话说百化分通用法》嘿，朋友们！今天咱来唠唠百化分通用法这个有意思的玩意儿。

百化分通用法啊，那可真是咱学习、考试、算数据时候的一个好帮手。

就好像是一把神奇的钥匙，能把那些复杂的百分数问题一下子就给解开咯！你想啊，遇到那些让人头疼的百分数和分数转换的时候，咱有了百化分通用法，就像有了一双火眼金睛，一下子就能识破它们的真面目。

不用再去苦哈哈地硬算，直接就能找到最简洁的转换方式，多爽呀！说起来，我第一次接触百化分通用法的时候，觉得它就像个神秘的密码。

刚开始还有点摸不着头脑呢，但慢慢理解了之后，就觉得“哇塞，原来这么好用！”就好像发现了一个大宝贝。

比如说，看到一个百分数，咱就能迅速反应过来，哦，这个百分数可以化成几分之一或者零点几。

然后在计算的时候，简直就是信手拈来，那速度，那效率，蹭蹭往上涨。

而且百化分通用法还有个特别妙的地方，它能把一些看似不可能的计算变得简单易行。

有时候看着那一大串数字和百分数就犯愁，但是用了百化分通用法，嘿，难题瞬间就变成了小菜一碟。

我记得有一次考试，有一道题特别复杂，里面全是百分数。

我当时心里一紧，想着这可咋办呀。

但突然灵机一动，想到了百化分通用法，就试着去用了一下。

哈哈，还真就轻松把那道题给搞定了，感觉自己像个数学小天才一样。

总之，百化分通用法就是那种你一用就会爱上的好东西。

它就像我们的好伙伴，在学习和生活中默默地帮我们排忧解难。

让那些让人头疼的百分数变得亲切可爱起来。

所以哇，朋友们，如果你们还没掌握百化分通用法，那可得赶紧去学学。

一旦学会了，那可是如虎添翼呀。

相信我，用了它，你会觉得数学原来也可以这么有趣，这么轻松愉快！好了，今天就先唠到这儿啦，大家赶紧和百化分通用法这个好伙伴交上朋友吧！。