(完整)2019-2020年高考数学大题专题练习——立体几何(二)

2019-2020年高考数学大题专题练习——立体几何（三）53.如图，在四棱锥E ﹣ABCD 中，平面CDE ⊥平面ABCD ，∠DAB =∠ABC =90°，AB =BC =1，AD =ED =3，EC =2．（1）证明：AB ⊥平面BCE ；（2）求直线AE 与平面CDE 所成角的正弦值．54.如图1，2，已知ABCD 是矩形，M ，N 分别为边AD ，BC 的中点，MN 与AC 交于点O ，沿MN 将矩形MNCD 折起，设AB =2，BC =4，二面角B ﹣MN ﹣C 的大小为θ． （1）当θ=90°时，求cos ∠AOC 的值；（2）点θ=60°时，点P 是线段MD 上一点，直线AP 与平面AOC 所成角为α．若sin α=714，求线段MP 的长．55.在四棱锥P ﹣ABCD 中，P A ⊥平面ABCD ，底面ABCD 为直角梯形，∠CDA =∠BAD =90°，AD =DC =2，AB =P A =22，且E 为线段PB 上的一动点． （1）若E 为线段PB 的中点，求证：CE ∥平面P AD ；（2）当直线CE 与平面P AC 所成角小于3π，求PE 长度的取值范围．56.如图，在几何体111ABC A B C -中，平面11A ACC ⊥底面ABC ，四边形11A ACC 是正方形，11B C BC ∥，Q 是1A B 的中点，且112AC BC B C ==，2π3ACB ∠=． (Ⅰ) 证明：1B Q ∥平面11A ACC ；(Ⅱ) 求直线AB 与平面11A BB 所成角的正弦值．57.如图，已知ABC V 和BCD V 所在平面互相垂直，且090BAC BCD ∠=∠=，,AB AC =CB CD =，点,E F 分别在线段,BD CD 上，沿直线EF 将EFD V 向上翻折使得D 与A 重合（Ⅰ）求证：AB CF ⊥；（Ⅱ）求直线AE 与平面ABC 所成角。

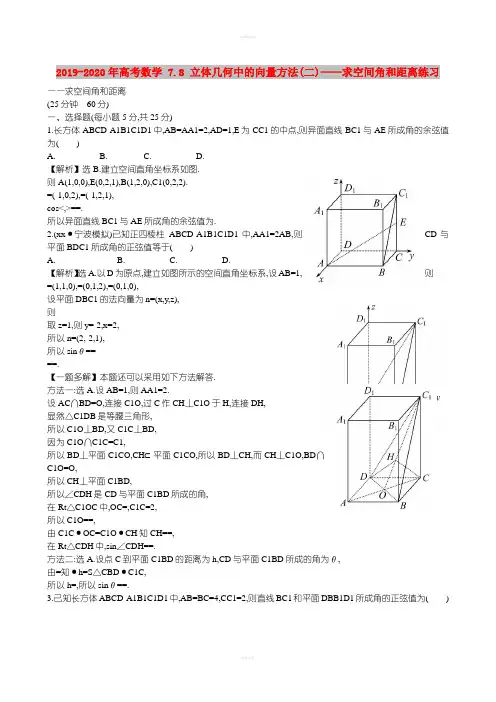
2019-2020年高考数学 7.8 立体几何中的向量方法(二)——求空间角和距离练习——求空间角和距离(25分钟60分)一、选择题(每小题5分,共25分)1.长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为()A. B. C. D.【解析】选B.建立空间直角坐标系如图.则A(1,0,0),E(0,2,1),B(1,2,0),C1(0,2,2).=(-1,0,2),=(-1,2,1),cos<,>==.所以异面直线BC1与AE所成角的余弦值为.2.(xx·宁波模拟)已知正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于()A. B. C. D.【解析】选A.以D为原点,建立如图所示的空间直角坐标系,设AB=1,则=(1,1,0),=(0,1,2),=(0,1,0),设平面DBC1的法向量为n=(x,y,z),则取z=1,则y=-2,x=2,所以n=(2,-2,1),所以sinθ====.【一题多解】本题还可以采用如下方法解答.方法一:选A.设AB=1,则AA1=2.设AC∩BD=O,连接C1O,过C作CH⊥C1O于H,连接DH,显然△C1DB是等腰三角形,所以C1O⊥BD,又C1C⊥BD,因为C1O∩C1C=C1,所以BD⊥平面C1CO,CH⊂平面C1CO,所以BD⊥CH,而CH⊥C1O,BD∩C1O=O,所以CH⊥平面C1BD,所以∠CDH是CD与平面C1BD所成的角,在Rt△C1OC中,OC=,C1C=2,所以C1O==,由C1C·OC=C1O·CH知CH==,在Rt△CDH中,sin∠CDH==.方法二:选A.设点C到平面C1BD的距离为h,CD与平面C1BD所成的角为θ,由=知·h=S△CBD·C1C,所以h=,所以sinθ==.3.已知长方体ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线BC1和平面DBB1D1所成角的正弦值为()A. B.C. D.【解题提示】以A为原点建立空间直角坐标系,分别求出直线BC1的方向向量与平面DBB1D1的法向量,用空间向量的直线与平面所成角的夹角公式计算得解.【解析】选C.如图建立空间直角坐标系,则B(4,0,0),C(4,4,0),C1(4,4,2),显然AC⊥平面BB1D1D,所以=(4,4,0)为平面BB1D1D的一个法向量.又=(0,4,2).所以cos<,>===.即直线BC1和平面DBB1D1所成角的正弦值为.4.(xx·厦门模拟)二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2,则该二面角的大小为()A.150°B.45°C.60°D.120°【解析】选C.由条件知·=0,·=0,因为=++.所以||2=||2+||2+||2+2·+2·+2·=62+42+82+2×6×8cos<,>=(2)2.所以cos<,>=-,则<,>=120°,即<,>=60°.所以二面角的大小为60°.5.(xx·北京模拟)在四面体P-ABC中,PA,PB,PC两两垂直,设PA=PB=PC=a,则点P到平面ABC的距离为()A. B.a C. D.a【解题提示】以P为原点建立空间直角坐标系,利用空间向量法求解.【解析】选B.根据题意,可建立如图所示的空间直角坐标系Pxyz,则P(0,0,0),A(a,0,0),B(0,a,0),C(0,0,a).所以=(-a,a,0),=(-a,0,a),=(a,0,0).设平面ABC的法向量为n=(x,y,z).由得得令x=1,所以n=(1,1,1),所以P到平面ABC的距离d===a.二、填空题(每小题5分,共15分)6.如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1=,M为A1B1的中点,则AM与平面AA1C1C所成角的正切值为.【解析】以C1为原点,C1A1,C1B1,C1C所在直线分别为x,y,z轴建立空间直角坐标系,则平面AA1C1C的法向量为n=(0,1,0),AM=-(1,0,)=,则直线AM与平面AA1C1C所成角θ的正弦值为sinθ=|cos<,n>|==,所以tanθ=.答案:7.已知点E,F分别在正方体ABCD -A1B1C1D1的棱BB1,CC1上,且B1E=2EB,CF=2FC1,则面AEF与面ABC 所成的二面角的正切值为.【解析】如图,建立空间直角坐标系Dxyz,设DA=1,由已知条件得A(1,0,0),E,F,=,=,设平面AEF的法向量为n=(x,y,z),面AEF与面ABC所成的二面角为θ,由图知θ为锐角,由得令y=1,z=-3,x=-1,则n=(-1,1,-3),平面ABC的法向量为m=(0,0,-1),cosθ=|cos<n,m>|=,tanθ=.答案:8.(xx·石家庄模拟)如图所示,正方体ABCD-A1B1C1D1的棱长为1,E是A1B1上的点,则点E到平面ABC1D1的距离是.【解析】以点D为坐标原点,DA,DC,DD1所在直线为x,y,z轴,建立如图所示空间直角坐标系,设点E(1,a,1)(0≤a≤1),连接D1E,则=(1,a,0).连接A1D,易知A1D⊥平面ABC1D1,则=(1,0,1)为平面ABC1D1的一个法向量.所以点E到平面ABC1D1的距离是d==.答案:三、解答题(每小题10分,共20分)9.(xx·湖南高考)如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.(1)证明:O1O⊥底面ABCD.(2)若∠CBA=60°,求二面角C1-OB1-D的余弦值.【解题提示】(1)利用矩形的邻边垂直,及线线平行证明OO1⊥AC,OO1⊥BD.(2)由二面角的定义或者向量法求二面角的余弦值.【解析】(1)因为四边形ACC1A1和四边形BDD1B1均为矩形,所以CC1⊥AC,DD1⊥BD,又CC1∥DD1∥OO1,所以OO1⊥AC,OO1⊥BD,因为AC∩BD=O,所以O1O⊥底面ABCD.(2)方法一:如图,过O1作O1H⊥B1O,垂足为H,连接C1H,由(1)可得OO1⊥A1C1,由于A1B1C1D1是菱形,所以B1D1⊥A1C1,所以A1C1⊥平面B1D1DB,所以由三垂线定理得HC1⊥B1O,所以∠O1HC1就是二面角C1-OB1-D的平面角.设棱柱的棱长为2,因为∠CBA=60°,所以OB=,OC=1,OB1=,在直角三角形O1OB1中,O1H==,因为O1C1=1,所以C1H===,所以cos∠C1HO1==,即二面角C1-OB1-D的余弦值为.方法二:因为四棱柱的所有棱长都相等,所以四边形ABCD为菱形,AC⊥BD,又O1O⊥底面ABCD,所以OB,OC,OO1两两垂直.如图,以O为原点,OB,OC,OO1所在直线分别为x,y,z轴,建立空间直角坐标系.设棱长为2,因为∠CBA=60°,所以OB=,OC=1,所以O,B1,C1,平面BDD1B1的一个法向量为n=,设平面OC1B1的法向量为m=,则由m⊥,m⊥,所以x+2z=0,y+2z=0,取z=-,则x=2,y=2,所以m=,所以cos<m,n>===.由图形可知二面角C1-OB1-D为锐二面角,所以二面角C1-OB1-D的余弦值为.10.(xx·杭州模拟)如图,将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a,(1)若a=2,求证:AB∥平面CDE.(2)求实数a的值,使得二面角A-EC-D的大小为60°.【解析】(1)如图建立空间直角坐标系,则A(0,0,0),B(2,0,0),C(1,1,),D(0,2,0),E(0,0,2),=(2,0,0),=(0,-2,2),=(1,-1,),设平面CDE的一个法向量为n1=(x,y,z),则有-2y+2z=0,x-y+z=0,取z=时,n1=(0,2,),所以·n1=0,又AB不在平面CDE内,所以AB∥平面CDE.(2)如图建立空间直角坐标系,则A(0,0,0),B(2,0,0),C(1,1,),D(0,2,0),E(0,0,a),=(0,-2,a),=(1,-1,),设平面CDE的一个法向量为n2=(x,y,z),则有-2y+az=0,x-y+z=0,取z=2时,n2=(a-2,a,2),又平面AEC的一个法向量为n3=(-1,1,0),因为二面角A-EC-D的大小为60°,所以=,即a2-2a-2=0, 解得a=±2.(20分钟40分)1.(5分)如图,在四面体ABCD中,AB=1,AD=2,BC=3,CD=2,∠ABC=∠DCB=,则二面角A-BC-D的大小为()A. B.C. D.【解析】选 B.二面角A-BC-D的大小等于AB与CD所成角的大小.=++.而=+++2||||·cos<,>,即12=1+9+4+2×1×2cos<,>,所以cos<,>=-,所以AB与CD所成角为,即二面角A-BC-D的大小为.2.(5分)(xx·北京模拟)已知在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到平面AB1D1的距离是.【解析】如图所示建立空间直角坐标系Dxyz,则A1(2,0,4),A(2,0,0),B1(2,2,4),D1(0,0,4),=(-2,0,4),=(0,2,4),=(0,0,4),设平面AB1D1的法向量为n=(x,y,z),则即解得x=2z且y=-2z,不妨设n=(2,-2,1),设点A1到平面AB1D1的距离为d,则d==.答案:3.(5分)(xx·郑州模拟)正四棱锥S -ABCD中,O为顶点在底面上的射影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC的夹角的大小为.【解析】如图所示,以O为原点建立空间直角坐标系Oxyz.设OD=SO=OA=OB=OC=a,则A(a,0,0),B(0,a,0),C(-a,0,0),P.则=(2a,0,0),=,=(a,a,0).设平面PAC的法向量为n,可求得n=(0,1,1),则cos<,n>===.所以<,n>=60°,所以直线BC与平面PAC的夹角为90°-60°=30°.答案:30°4.(12分)(能力挑战题)如图,在平行四边形ABCD中,AB=2BC=2,∠ABC=120°,M,N分别为线段AB,CD的中点,连接AN,DM交于点O,将△ADM沿直线DM翻折成△A′DM.使平面A′DM⊥平面BCD,F为线段A′C的中点.(1)求证:ON⊥平面A′DM.(2)求证:BF∥平面A′DM.(3)求直线FO与平面A′DM所成的角.【解析】(1)连接MN,由平面几何知四边形AMND是菱形.所以AN⊥DM.因为平面A′DM⊥平面ABCD,DM是交线,AN⊂平面ABCD,所以AN⊥平面A′DM,即ON⊥平面A′DM.(2)取A′D的中点E,连接EF,EM,因为F是A′C中点,所以EFCD.又M是AB中点,所以在平行四边形ABCD中,BMCD,所以EF BM,所以四边形EFBM是平行四边形.所以BF∥EM,因为EM⊂平面A′DM,BF⊄平面A′DM,所以BF∥平面A′DM.(3)因为AB=2BC=2,M是AB中点,所以A′D=A′M=1.因为菱形ADNM中O是DM中点,所以A′O⊥DM,因为平面A′DM⊥平面ABCD,所以A′O⊥平面ABCD.以ON为x轴,OM为y轴,OA′为z轴建立空间直角坐标系,∠ADN=∠ABC=120°,在△ADN中,AD=DN=1,所以AN==.同理求得DM=AD=AM=1,所以N,D,A′,因为N是CD的中点,所以C.因为F是A′C的中点,所以F.因为NO⊥平面A′DM,所以平面A′DM的一个法向量=.因为=,所以||==1.设OF与平面A′DM所成的角为θ,0<θ<,则sinθ=|cos<,>|===,所以θ=.所以直线FO与平面A′DM所成的角为.5.(13分)(xx·江西高考)如图,四棱锥P-ABCD中,ABCD为矩形,平面PAD⊥平面ABCD.(1)求证:AB⊥PD.(2)若∠BPC=90°,PB=,PC=2,问AB为何值时,四棱锥P-ABCD的体积最大?并求此时平面PBC与平面DPC 夹角的余弦值.【解题提示】(1)利用面面垂直的性质定理证明AB⊥平面PAD即可.(2)借助两平面垂直的性质,作PO⊥AD,即四棱锥的高找到,过点O作OM⊥BC于点M,连接PM.则四棱锥的体积能用AB的长度表示,即可建立体积与AB的函数,借助二次函数知识求最值;此时可建立空间直角坐标系,利用坐标法求解.【解析】(1)因为ABCD为矩形,所以AB⊥AD,又因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以AB⊥平面PAD,又PD⊂平面PAD,所以AB⊥PD.(2)过点P作PO⊥AD于点O,则PO⊥平面ABCD,过点O作OM⊥BC于点M,连接PM.则PM⊥BC,因为∠BPC=90°,PB=,PC=2,所以BC=,PM=,设AB=t,则在Rt△POM中,PO=,所以VP-ABCD=·t··=,所以当t2=,即t=时,VP-ABCD最大为.此时PO=AB=,且PO,OA,OM两两垂直,以OA,OM,OP所在直线为x,y,z轴建立空间直角坐标系Oxyz, 则P,D,C,B.所以=,=,=.设平面PCD的一个法向量m=(x1,y1,z1),则即令x1=1,则m=(1,0,-2),|m|=;同理设平面PBC的一个法向量n=(x2,y2,z2),即令y2=1,则n=(0,1,1),|n|=,设平面PBC与平面DPC夹角为θ,显然θ为锐角,且cosθ===..。

2019年高考专题：立体几何试题1．【2019年高考全国Ⅱ卷文数】设α，β为两个平面，则α∥β的充要条件是A ．α内有无数条直线与β平行B ．α内有两条相交直线与β平行C ．α，β平行于同一条直线D ．α，β垂直于同一平面【解析】由面面平行的判定定理知：α内两条相交直线都与β平行是αβ∥的充分条件，由面面平行性质定理知，若αβ∥，则α内任意一条直线都与β平行，所以α内两条相交直线都与β平行是αβ∥的必要条件，故选B ．2．【2019年高考江苏卷】如图，长方体1111ABCD A B C D -的体积是120，E 为1CC 的中点，则三棱锥E −BCD 的体积是 .【解析】因为长方体1111ABCD A B C D -的体积为120，所以1120AB BC CC ⋅⋅=，因为E 为1CC 的中点，所以112CE CC =， 由长方体的性质知1CC ⊥底面ABCD ，所以CE 是三棱锥E BCD -的底面BCD 上的高， 所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=.3．【2019年高考全国Ⅰ卷文数】如图，直四棱柱ABCD –A 1B 1C 1D 1的底面是菱形，AA 1=4，AB =2，∠BAD =60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点.（1）证明：MN ∥平面C 1DE ；（2）求点C 到平面C 1DE 的距离．【解析】（1）连结1,B C ME .因为M ，E 分别为1,BB BC 的中点，所以1 ME B C ∥，且112ME B C =. 又因为N 为1A D 的中点，所以112ND A D =. 由题设知11=A B DC ∥，可得11=BC A D ∥，故=ME ND ∥， 因此四边形MNDE 为平行四边形，MN ED ∥. 又MN ⊄平面1C DE ，所以MN ∥平面1C DE .（2）过C 作C 1E 的垂线，垂足为H .由已知可得DE BC ⊥，1DE C C ⊥，所以DE ⊥平面1C CE ，故DE ⊥CH.从而CH ⊥平面1C DE ，故CH 的长即为C 到平面1C DE 的距离，由已知可得CE =1，C 1C =4，所以117C E =，故417CH =. 从而点C 到平面1C DE 的距离为1717. 4．【2019年高考全国Ⅱ卷文数】如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1．（1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，AB =3，求四棱锥11E BB C C -的体积．【解析】（1）由已知得B 1C 1⊥平面ABB 1A 1，BE ⊂平面ABB 1A 1，故11B C BE ⊥．又1BE EC ⊥，所以BE ⊥平面11EB C ．（2）由（1）知∠BEB 1=90°. 由题设知Rt △ABE ≌Rt △A 1B 1E ，所以1145AEB A EB ︒∠=∠=，故AE =AB =3，126AA AE ==. 作1EF BB ⊥，垂足为F ，则EF ⊥平面11BB C C ，且3EF AB ==．所以，四棱锥11E BB C C -的体积1363183V =⨯⨯⨯=． 5．【2019年高考全国Ⅲ卷文数】图1是由矩形ADEB ，Rt △ABC 和菱形BFGC 组成的一个平面图形，其中AB =1，BE =BF =2，∠FBC =60°．将其沿AB ，BC 折起使得BE 与BF 重合，连结DG ，如图2．（1）证明：图2中的A ，C ，G ，D 四点共面，且平面ABC ⊥平面BCGE ；（2）求图2中的四边形ACGD 的面积.【解析】（1）由已知得AD BE ，CG BE ，所以AD CG ，故AD ，CG 确定一个平面，从而A ，C ，G ，D 四点共面．由已知得AB ⊥BE ，AB ⊥BC ，故AB ⊥平面BCGE ．又因为AB ⊂平面ABC ，所以平面ABC ⊥平面BCGE ．（2）取CG 的中点M ，连结EM ，DM.因为AB ∥DE ，AB ⊥平面BCGE ，所以DE ⊥平面BCGE ，故DE ⊥CG .由已知，四边形BCGE 是菱形，且∠EBC =60°得EM ⊥CG ，故CG ⊥平面DEM ．因此DM ⊥CG ．在Rt △DEM 中，DE =1，EM =3，故DM =2．所以四边形ACGD 的面积为4．6．【2019年高考北京卷文数】如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底部ABCD 为菱形，E 为CD 的中点．（1）求证：BD ⊥平面PAC ；（2）若∠ABC =60°，求证：平面PAB ⊥平面PAE ；（3）棱PB 上是否存在点F ，使得CF ∥平面PAE ？说明理由．【解析】（1）因为PA ⊥平面ABCD ，所以PA BD ⊥．又因为底面ABCD 为菱形，所以BD AC ⊥．所以BD ⊥平面PAC ．（2）因为PA ⊥平面ABCD ，AE ⊂平面ABCD ，所以PA ⊥AE ．因为底面ABCD 为菱形，∠ABC =60°，且E 为CD 的中点，所以AE ⊥CD ．所以AB ⊥AE ．所以AE ⊥平面PAB ．所以平面PAB ⊥平面PAE ．（3）棱PB 上存在点F ，使得CF ∥平面PAE ．取F 为PB 的中点，取G 为PA 的中点，连结CF ，FG ，EG ．则FG ∥AB ，且FG =12AB ．因为底面ABCD 为菱形，且E 为CD 的中点， 所以CE ∥AB ，且CE =12AB ．所以FG ∥CE ，且FG =CE ． 所以四边形CEGF 为平行四边形．所以CF ∥EG ．因为CF ⊄平面PAE ，EG ⊂平面PAE ，所以CF ∥平面PAE ．7．【2019年高考天津卷文数】如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形，PCD △为等边三角形，平面PAC ⊥平面PCD ，,2,3PA CD CD AD ⊥==.（1）设G ，H 分别为PB ，AC 的中点，求证：GH ∥平面PAD ；（2）求证：PA ⊥平面PCD ；（3）求直线AD 与平面PAC 所成角的正弦值.【解析】（1）连接BD ，易知ACBD H =，BH DH =.又由BG=PG ，故GH PD ∥.又因为GH ⊄平面P AD ，PD ⊂平面P AD ，所以GH ∥平面P AD .（2）取棱PC 的中点N ，连接DN .依题意，得DN ⊥PC ，又因为平面PAC ⊥平面PCD ，平面PAC 平面PCD PC =， 所以DN ⊥平面P AC ，又PA ⊂平面P AC ，故DN PA ⊥.又已知PA CD ⊥，CD DN D =，所以PA ⊥平面PCD .（3）连接AN ，由（2）中DN ⊥平面P AC ，可知DAN ∠为直线AD 与平面P AC 所成的角， 因为PCD △为等边三角形，CD =2且N 为PC 的中点， 所以3DN =.又DN AN ⊥，在Rt AND △中，3sin 3DN DAN AD ∠==. 所以，直线AD 与平面P AC 所成角的正弦值为33. 8．【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．【解析】（1）因为D ，E 分别为BC ，AC 的中点，所以ED ∥AB .在直三棱柱ABC−A 1B 1C 1中，AB ∥A 1B 1，所以A 1B 1∥ED .又因为ED ⊂平面DEC 1，A 1B 1⊄平面DEC 1，所以A 1B 1∥平面DEC 1.（2）因为AB =BC ，E 为AC 的中点，所以BE ⊥AC .因为三棱柱ABC−A 1B 1C 1是直棱柱，所以CC 1⊥平面ABC .又因为BE ⊂平面ABC ，所以CC 1⊥BE .因为C 1C ⊂平面A 1ACC 1，AC ⊂平面A 1ACC 1，C 1C ∩AC =C ，所以BE ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1，所以BE ⊥C 1E .9．【2019年高考浙江卷】如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ,90ABC ∠=︒，1130,,,BAC A A AC AC E F ∠=︒==分别是AC ，A 1B 1的中点.（1）证明：EF BC ⊥；（2）求直线EF 与平面A 1BC 所成角的余弦值.【解析】（1）连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥AC ． 又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1，平面A 1ACC 1∩平面ABC =AC ，所以，A 1E ⊥平面ABC ，则A 1E ⊥BC ．又因为A 1F ∥AB ，∠ABC =90°，故BC ⊥A 1F ．所以BC ⊥平面A 1EF ．因此EF ⊥BC ．（2）取BC 中点G ，连接EG ，GF ，则EGFA 1是平行四边形．由于A 1E ⊥平面ABC ，故A 1E ⊥EG ，所以平行四边形EGFA 1为矩形．由（1）得BC ⊥平面EGFA 1，则平面A 1BC ⊥平面EGFA 1， 所以EF 在平面A 1BC 上的射影在直线A 1G 上．连接A 1G 交EF 于O ，则∠EOG 是直线EF 与平面A 1BC 所成的角（或其补角）． 不妨设AC =4，则在Rt △A 1EG 中，A 1E =23，EG =3.由于O 为A 1G 的中点，故11522A G EO OG ===， 所以2223cos 25EO OG EG EOG EO OG +-∠==⋅．因此，直线EF 与平面A 1BC 所成角的余弦值是35。

垂直的证明【方法总结】1、证明线面垂直的方法：①利用线面垂直定义：如果一条直线垂直于平面内任一条直线，则这条直线垂直于该平面；②用线面垂直判定定理：如果一条直线与平面内的两条相交直线都垂直，则这条直线与平面垂直；③用线面垂直性质：两条平行线中的一条垂直于一个平面，则另一条也必垂直于这个平面．2、证明线线（或线面）垂直有时需多次运用线面垂直的定义和线面垂直的判定定理，实现线线垂直与线面垂直的相互转化．3、证明面面垂直一般要先找到两个面的交线，然后再在两个面内找能与交线垂直的直线，最后通过证明线面垂直证明面面垂直。

【分类练习】考向一线面垂直例1、在四棱锥P ABCD -中，PA ⊥底面ABCD ，//AB CD ，AB BC ⊥，1AB BC ==，2DC =，点E 在PB 上求证：CA ⊥平面PAD ；【答案】(1)证明见解析；(2)2.【解析】(1)过A 作AF ⊥DC 于F ,则CF =DF =AF ,所以∠DAC =90°,即AC ⊥DA ，又PA ⊥底面ABCD ，AC ⊂面ABCD ，所以AC ⊥PA ，因为PA 、AD ⊂面PAD ，且PA ∩AD =A ，所以AC ⊥平面PAD .例2、如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1.（1）证明：BE ⊥平面EB 1C 1；解析：（1）由已知得，11B C ⊥平面11ABB A ，BE ⊂平面11ABB A ，故11B C ⊥BE ．又1BE EC ⊥，所以BE ⊥平面11EB C ．例3、如图，在三棱柱111ABC A B C -中，1CC ⊥平面ABC ，D ，E ，F ，G 分别为1AA ，AC ，11A C ，1BB 的中点求证：AC ⊥平面BEF ；【解析】(1)在三棱柱111ABC A B C -中，∵1CC ⊥平面ABC ，∴四边形11A ACC 为矩形．又E ，F 分别为AC ，11A C 的中点，∴AC ⊥EF ．∵AB BC =．∴AC ⊥BE ，∴AC ⊥平面BEF ．例4、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，CD ⊥AD ，BC ∥AD ，12BC CD AD ==.（Ⅰ）求证：BD ⊥平面PAB ；【解析】因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD ⊥PA .所以222AD AB BD =+，所以BD AB ⊥.因为PA AB A = ，所以BD ⊥平面PAB .【巩固练习】1、如图，在三棱柱ABC－A 1B 1C 1中，AB＝AC，A 1在底面ABC 的射影为BC 的中点，D 是B 1C 1的中点．证明：A 1D⊥平面A 1BC；【答案】见解析【解析】证明：设E 为BC 的中点，连接A 1E，AE.由题意得A 1E⊥平面ABC，所以A 1E⊥AE.因为AB＝AC，所以AE⊥BC.故AE⊥平面A 1BC.连接DE，由D，E 分别为B 1C 1，BC 的中点，得DE∥B 1B 且DE＝B 1B，从而DE∥A 1A 且DE ＝A 1A，所以AA 1DE 为平行四边形．于是A 1D∥AE.因为AE⊥平面A 1BC，所以A 1D⊥平面A 1BC.2．（2019·上海格致中学高三月考）如图，在四棱锥P ABCD -中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD DC =，E 是PC 的中点，作EF PB ⊥交PB 于点F .（1）证明：PA ∥平面EDB ；（2）证明：PB ⊥平面EFD .【答案】（1）详见解析；（2）详见解析.【解析】（1）设AC 与BD 相交于O ，连接OE ，由于O 是AC 中点，E 是PC 中点，所所以PA ∥平面EDB .（2）由于PD ⊥底面ABCD ，所以PD BC ⊥，由于,BC CD PD CD D ⊥⋂=，所以BC ⊥平面PCD ，所以BC DE ⊥.由于DP DC =且E 是PC 中点，所以DE PC ⊥，而PC BC C ⋂=，所以DE ⊥平面PBC ，所以DE PB ⊥.依题意EF PB ⊥，DE EF E = ，所以PB ⊥平面EFD .3．（2019·江苏高三月考）如图，在四棱锥P ABCD -中，四边形ABCD 是平行四边形，AC ，BD 相交于点O ，OP OC =，E 为PC 的中点，PA PD ⊥.（1）求证：//PA 平面BDE ；（2）求证：PA ⊥平面PCD【答案】（1）详见解析（2）详见解析【解析】（1）连结OE .因为四边形ABCD 是平行四边形，AC ，BD 相交于点O ，所以O 为AC 的中点.因为E 为PC 的中点，所以//OE PA .因为OE ⊂平面BDE ，PA ⊄平面BDE ，所以//PA 平面BDE .（2）因为OP OC =，E 为PC 的中点，所以OE PC ⊥.由（1）知，//OE PA ，所以PA PC ⊥.因为PA PD ⊥，PC ，PD ⊂平面PCD ，PC PD P ⋂=，所以PA ⊥平面PCD .考向二面面垂直例1、如图，在四棱锥P ABCD -中，已知底面ABCD 为矩形，且AB =，1BC =，E ，F 分别是AB ，PC 的中点，PA DE ⊥.(1)求证：//EF 平面PAD ；(2)求证：平面PAC ⊥平面PDE ．【答案】（1）详见解析（2）详见解析【解析】证明：(1)取PD 中点G ，连AG ，FG ，F ，G 分别是PC ，PD 的中点又E 为AB 中点//AE FG ∴，AE FG=四边形AEFG 为平行四边形//EF AG ∴，又EF ⊄平面PAD ，AG ⊂平面PAD//EF ∴平面PAD(2)设AC DE H= 由AEH CDH ∆∆ 及E 为AB 中点又BAD ∠为公共角GAE BAC∴∆∆ 90AHE ABC ∴∠=∠=︒即DE AC ⊥又DE PA ⊥，PA AC A= DE ⊥平面PAC ，又DE ⊂平面PDE∴平面PAC ⊥平面PDE例2、如图，边长为2的正方形ABCD 所在的平面与半圆弧 CD所在平面垂直，M 是 CD 上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC ；【解析】(1)由题设知，平面CMD ⊥平面ABCD ，交线为CD ．因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM ．因为M 为 CD上异于C ，D 的点，且DC 为直径，所以DM ⊥CM ．又BC CM =C ，所以DM ⊥平面BMC ．而DM ⊂平面AMD ，故平面AMD ⊥平面BMC ．例3、如图，在梯形ABCD 中，AB ∥CD ，AD=DC=CB=a ，∠ABC=3π，平面ACFE ⊥平面ABCD ，四边形ACFE 是矩形，AE=AD ，点M 在线段EF 上。

专题04 立体几何1．【2019年高考全国Ⅱ卷文数】设α，β为两个平面，则α∥β的充要条件是A．α内有无数条直线与β平行B．α内有两条相交直线与β平行C．α，β平行于同一条直线D．α，β垂直于同一平面2．【2019年高考全国Ⅲ卷文数】如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则A．BM=EN，且直线BM，EN是相交直线B．BM≠EN，且直线BM，EN是相交直线C．BM=EN，且直线BM，EN是异面直线D．BM≠EN，且直线BM，EN是异面直线3．【2019年高考浙江卷】祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V柱体=Sh，其中S是柱体的底面积，h是柱体的高．若某柱体的三视图如图所示（单位：cm），则该柱体的体积（单位：cm3）是A．158 B．162C．182 D．3244．【2019年高考浙江卷】设三棱锥V –ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点）．记直线PB 与直线AC 所成的角为α，直线PB 与平面ABC 所成的角为β，二面角P –AC –B 的平面角为γ，则 A ．β<γ，α<γB ．β<α，β<γC ．β<α，γ<αD ．α<β，γ<β5．【2019年高考全国Ⅰ卷文数】已知∠ACB=90°，P 为平面ABC 外一点，PC =2，点P 到∠ACB 两边AC ，BC P 到平面ABC 的距离为___________．6．【2019年高考全国Ⅱ卷文数】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．（本题第一空2分，第二空3分．）7．【2019年高考全国Ⅲ卷文数】学生到工厂劳动实践，利用3D 打印技术制作模型．如图，该模型为长方体1111ABCD A B C D 挖去四棱锥O −EFGH 后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H 分别为所在棱的中点，16cm 4cm AB =BC =AA =，，3D 打印所用原料密度为0.9 g/cm 3，不考虑打印损耗，制作该模型所需原料的质量为___________g.8．【2019年高考北京卷文数】某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为1，那么该几何体的体积为__________．9．【2019年高考北京卷文数】已知l ，m 是平面α外的两条不同直线．给出下列三个论断：①l ⊥m ；②m ∥α；③l ⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．10．【2019若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为__________.11．【2019年高考江苏卷】如图，长方体1111ABCD A B C D -的体积是120，E 为1CC 的中点，则三棱锥E −BCD的体积是 ▲ .12．【2019年高考全国Ⅰ卷文数】如图，直四棱柱ABCD –A 1B 1C 1D 1的底面是菱形，AA 1=4，AB =2，∠BAD =60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点.（1）证明：MN ∥平面C 1DE ； （2）求点C 到平面C 1DE 的距离．13．【2019年高考全国Ⅱ卷文数】如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1．（1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，AB =3，求四棱锥11E BB C C 的体积．14．【2019年高考全国Ⅲ卷文数】图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°．将其沿AB，BC折起使得BE与BF重合，连结DG，如图2．（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的四边形ACGD的面积.-中，PA⊥平面ABCD，底部ABCD为菱形，E 15．【2019年高考北京卷文数】如图，在四棱锥P ABCD为CD的中点．（1）求证：BD⊥平面PAC；（2）若∠ABC=60°，求证：平面PAB⊥平面PAE；（3）棱PB上是否存在点F，使得CF∥平面PAE？说明理由．16．【2019年高考天津卷文数】如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形，PCD △为等边三角形，平面PAC ⊥平面PCD ，,2,3PA CD CD AD ⊥==.（1）设G ，H 分别为PB ，AC 的中点，求证：GH ∥平面PAD ； （2）求证：PA ⊥平面PCD ；（3）求直线AD 与平面PAC 所成角的正弦值.17．【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1； （2）BE ⊥C 1E ．18．【2019年高考浙江卷】如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ,90ABC ∠=︒，1130,,,BAC A A AC AC E F ∠=︒==分别是AC ，A 1B 1的中点. （1）证明：EF BC ⊥；（2）求直线EF 与平面A 1BC 所成角的余弦值.19．【云南省昆明市2019届高三高考5月模拟数学试题】已知直线l ⊥平面α，直线m ∥平面β，若αβ⊥，则下列结论正确的是 A ．l β∥或l β⊄ B ．//l m C ．m α⊥D ．l m ⊥20．【陕西省2019届高三年级第三次联考数学试题】已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为A B ．34C ．4D ．5421．【四川省宜宾市2019届高三第三次诊断性考试数学试题】如图，边长为2的正方形ABCD 中，,E F 分别是,BC CD 的中点，现在沿,AE AF 及EF 把这个正方形折成一个四面体，使,,B C D 三点重合，重合后的点记为P ，则四面体P AEF -的高为A ．13 B ．23C ．34D ．122．【广东省深圳市高级中学2019届高三适应性考试（6月）数学试题】在三棱锥P ABC -中，平面PAB ⊥平面ABC ，ABC △是边长为6的等边三角形，PAB △是以AB 为斜边的等腰直角三角形，则该三棱锥外接球的表面积为_______．23．【河南省洛阳市2019年高三第三次统一考试（5月）数学试题】在四棱柱1111ABCD A B C D -中，四边形ABCD 是平行四边形，1A A ⊥平面ABCD ， 60BAD ∠=︒，12,1,AB BC AA ===，E 为11A B 中点.（1）求证：平面1A BD ⊥平面1A AD ； （2）求多面体1A E ABCD -的体积.。

2019-2020年高考数学大题专题练习——立体几何（二）27.如图，四边形ABCD 与BDEF 均为菱形，，且FA =FC . 60DAB DBF ∠=∠=︒（1）求证：AC ⊥平面BDEF ；（2）求直线AF 与平面BCF 所成角的正弦值.28.如图（甲），在直角梯形ABED 中，，，，且，//AB DE AB BE ⊥AB CD ⊥BC CD =，F 、H 、G 分别为AC 、AD 、DE 的中点，现将沿折起，使平面ACD ⊥平2AB =ACD ∆CD 面CBED ，如图（乙）．（1）求证：平面FHG ∥平面ABE ；（2）若，求二面角D -AB -43BC =C的余弦值．29.如图,在四棱锥中,平面平面P ABCD -PAB ⊥,,90,ABCD AD BC ABC ∠=A PA =为的中点.3,1,2,3,PB BC AB AD O ====AB （1）证明:PO CD ⊥；（2）求二面角的余弦值.C PD O --30.如图所示的几何体中，为三棱柱，且，111ABC A B C -1AA ABC⊥平面四边形ABCD 为平行四边形，，.2AD CD =060ADC ∠=（1）求证：；11//C D AB C平面（2）若，求证：；1AA AC =111AC A B CD⊥平面（3）若，二面角2CD =1A C D C--，求三棱锥的体积．11C A CD-31.如图，四边形ABCD 中，AB ⊥AD ，AD ∥BC ，AD =6，BC =2AB =4，E 、F 分别在BC 、AD 上，EF ∥A B ，现将四边形ABCD 沿EF 折起，使平面ABEF ⊥平面EFDC ．（1）若BE =1，是否存在折叠后的线段AD 上存在一点P ，且，使得CP ∥平面ABEAP PD λ=F ？若存在，求出的值；若不存在，说明理由．λ（2）求三棱锥A -CDF 的体积的最大值，并求此时点F 到平面ACD 的距离．FECBA DFECBAD32.已知在四棱锥P-ABCD 中，底面ABCD 为矩形，且AD =2，AB =1，PA ⊥平面ABCD ，E ，F 分别是线段AB ，BC 的中点.（1）证明：PF ⊥DF ；（2）在线段PA 上是否存在点G ，使得EG ∥平面PFD ？若存在，确定点G 的位置；若不存在，说明理由.（3）若PB 与平面ABCD 所成的角为45°,求二面角A - PD -F 的余弦值.33.如图所示，在直三棱柱ABC－A1B1C1中，CA＝4，CB＝4，CC1＝2，∠ACB＝90°，点M在线段A1B1上.2(1)若A1M＝3MB1，求异面直线AM和A1C所成角的余弦值；(2)若直线AM与平面ABC1所成角为30°，试确定点M的位置．34.如图，几何体EF﹣ABCD中，CDEF为边长为2的正方形，ABCD为直角梯形，AB∥CD，AD⊥DC，AD=2，AB=4，∠ADF=90°．（Ⅰ）求证：AC⊥FB（Ⅱ）求二面角E﹣FB﹣C的大小．35.如图，在四棱锥中，是的中点，底面P ABCD -E PC 为矩形，，，，且平面ABCD 4AB =2AD =PA PD =PAD ⊥平面，平面与棱交于点，平面与平面ABCD ABE PD F PCD 交于直线.PAB l （1）求证：；l EF ∥（2）求与平面PB ABCD 的余弦值.P AE B --36.在四棱锥P ﹣ABCD 中，AD ∥BC ，AD =AB =DC =BC 21=1，E 是PC 的中点，面PA C ⊥面ABCD ．（Ⅰ）证明：ED ∥面PAB ；（Ⅱ）若PC =2，PA =，求二面角A ﹣PC ﹣D 的余弦值3．37.如图，在四棱锥P ﹣ABCD 中，∠ABC =∠ACD =90°，∠BAC =∠CAD =60°，PA ⊥平面ABCD ，PA =2，AB =1．（1）设点E为PD 的中点，求证：CE ∥平面PAB ；（2）线段PD 上是否存在一点N ，使得直线CN 与平面PAC 所成的角θ的正弦值为？若存515在，试确定点N 的位置，若不存在，请说明理由．38.如图，已知四棱锥的底面为菱形，且，，E ABCD -60ABC ∠=︒2AB EC ==AE BE ==（1）求证：平面EAB ⊥平面ABCD .（2）求二面角A -EC -D 的余弦值.39.如图，在三棱锥P -ABC 中，侧面PAB 为边长为ABC 为以AB 为斜边的等腰直角三角形， PC ⊥AC ．（Ⅰ）求证：PC ⊥平面ABC ；（Ⅱ）求二面角B -AP -C 的的余弦值.40.在四棱锥P ﹣ABCD 中，底面是边长为2的菱形，∠BA D =60°，PB =PD =2，AC ∩BD =O ．（Ⅰ）证明：PC ⊥BD（Ⅱ）若E 是PA 的中点，且BE 与平面PAC 所成的角的正切值为，求二面角A﹣EC﹣B 的余36弦值．41. 如图，四棱锥中，侧面为等边三角形且垂直于底面，ABCD P -PAD ABCD ,22==BC AD .90=∠=∠ABC BAD （1）证明：；BC PC ⊥（2）若直线与平面所成角为30°，求二PC PAD 面角的余弦值.D PC B --42.如图，在底面为矩形的四棱锥中，.P ABCD -PB AB ⊥（1）证明：平面平面；PBC ⊥PCD （2）若异面直线与所成角为，，，求二面角PC BD 60PB AB =PB BC ⊥的大小.B PDC --43.如图，已知四棱锥的底面是菱形，，，P ABCD -3BAD π∠=2AB PD ==.PB PC ==（1）求证：平面平面；PBC ⊥ABCD （2）求直线与平面所成角的正弦值.PC PAB 44.如图，矩形ABCD 所在的平面和平面互相垂直，ABEF 等腰梯形中， ，，1AD AF ==，ABEF EF AB //2=AB ,分别为的中点，为底面060=∠BAF P O ,CB AB ,M 的重心.OBF ∆（Ⅰ）求证：∥平面；PM AFC （Ⅱ）求直线与平面所成角的正弦值.ACCEFa 45.如图，在四棱锥中，面，，，P ABCD -PA ⊥ABCD //AB CD CD AD ⊥，，分别为，的中点．22AD CDAB ===E F PC CD （Ⅰ）求证：平面平面；ABE ⊥BEF （Ⅱ）设，若平面与平面所成锐二面角，求的取值范PA a =EBD ABCD ,43ππθ⎡⎤∈⎢⎥⎣⎦a 围．46.如图所示中，，，，将三角形ABCD //AD BC AD DC AB ==60ABC ∠=︒ABD 沿折起，使点在平面上的投影落在上.BD A BCD G BD （Ⅰ）求证：平面平面；ACD ⊥ABD （Ⅱ）求二面角的平面角的余弦值.G AC D --47.如图，在三棱锥中，，，为的中点.P ABC -AB BC ⊥PA PB =E AC （1）求证：；PE AB ⊥（2）设平面平面，，，求二面角的平面PAB ⊥ABC 2PB BC ==4AC =B PA C --角的正弦值.48.如图，在三棱锥中，平面平面，为等边三角形，P ABC -PAC ⊥PAB PAC ∆且为的中点，点在上.AB PB ⊥AB PB ==O PA M AC （1）求证：平面平面；BOM ⊥PAC （2）求点到平面的距离.P ABC49.如图，在四棱锥中，底面P ABCD -PA ⊥ABCD ，底面为直角梯形，，ABCD AD BC ∥90BAD ∠=︒，，为的中点，平面交于点.22PA AD AB BC ====M PB ADM PC N （1）求证：；PB DN ⊥（2）求二面角的余弦值.P DN A --50.如图1，在直角梯形ABCD 中，∠ADC =90°，CD ∥AB ，AB =4，AD =CD =2，M 为线段AB 的中点．将△ADC 沿AC 折起，使平面ADC ⊥平面ABC ，得到几何体D ﹣ABC ，如图2所示．（Ⅰ）求证：BC ⊥平面ACD ；（Ⅱ）求二面角A ﹣CD ﹣M的余弦值．51.已知四边形ABCD 为直角梯形，∠BCD =90°，AB ∥CD ，且AD =3，BC =2CD =4，点E ，F 分别在线段AD 和BC 上，使FECD 为正方形，将四边形ABFE 沿EF 翻折至使二面角B ﹣EF ﹣C 的所成角为60°（Ⅰ）求证：CE ∥面A ′DB ′（Ⅱ）求直线A ′B ′与平面FECD所成角的正弦值52.如图，在四棱锥中，底面是P ABCD -ABCD 矩形，M 是的中点，平面，且PA PD ⊥ABCD 4PD CD ==，．2AD =（）求与平面所成角的正弦．1AP CMB （）求二面角的余弦值．2M CB P --D PABCMAl l试卷答案27.（1）设与相交于点，连接，AC BD O FO ∵四边形为菱形，∴，且为中点，ABCD AC BD ⊥O AC ∵，∴,FA FC =AC FO ⊥又，∴平面.FO BD O ⋂=AC ⊥BDEF （2）连接，∵四边形为菱形，且，∴为等边三角形，DF BDEF 60DBF ∠=︒DBF ∆∵为中点，∴，又，∴平面.O BD FO BD ⊥AC FO ⊥FO ⊥ABCD ∵两两垂直，∴建立空间直角坐标系，如图所示，,,OA OB OF O xyz -设，∵四边形为菱形，，∴2AB =ABCD 60DAB ∠=︒2,BD AC ==∵为等边三角形，∴.DBF ∆OF =∴，)()()(,0,1,0,,AB C F ∴.(),,AF CF CB ===设平面的法向量为，则，BCF (),,n x y z = 00CF n CB n y ⎧⋅==⎪⎨⋅=+=⎪⎩取，得.1x =()1,1n =-设直线与平面所成角为，AF BCF θ则.sin cos ,AF n AF n AF nθ⋅===⋅ 28.（1）证明：由图（甲）结合已知条件知四边形为正方形，如图（乙），CBED ∵分别为的中点，∴．F HG 、、AC AD DE 、、//,//FH CD HG AE ∵，∴．//CD BE //FH BE ∵面，面．∴面．BE ⊂ABE FH ⊄ABE //FH ABE 同理可得面，//HG ABE 又∵,∴平面平面．FH HG H ⋂=//FHG ABE（2）这时，43BC =23AC =从而，AB ==过点作于，连结．C CM AB ⊥M MD ∵，∴面．,,CD AC CD BC AC BC C ⊥⊥⋂=CD ⊥ABC ∵面，∴,∴面，CM ⊂ABC CM CD ⊥AB ⊥MCD ∵面，∴， MD ⊂MCD AB MD ⊥∴是二面角的平面角，CMD ∠D AB C --由得，AB CM AC BC ⋅=⋅AC BC CM AB ⋅==∴，MD ==在中Rt MCD∆cos MC CMD MD ∠===29.解：（1）联结因为为的中点,,PO 3,PA PB ==O AB 所以又平面平面交线为.PO AB ⊥PAB ⊥,ABCD ,AB 平面所以又PO ⊆,PAB .PO ABCD ⊥平面CD ⊆平面所以,ABCD .PO CD ⊥（2）取线段的中点因为所以CD ,E 2OE =，,OE BC A 90,ABC ∠= 由（1）知,故可以为原点,,.AB BC AB OE ⊥⊥.PO ABCD ⊥平面O 射线分别为的正半轴建立空间直角坐标系则,,OB OE OP ,x y z 轴,轴轴.O xyz -(0,0,0),(1,1,0),(0,0,(1,3,0).O C P D -于是(1,1,(2,2,0),(0,0,CP CD OP =--=-=设平面的一个法向量为由得CPD 111(,,),x y z =m 0,0CP CD ⋅=⋅=m m 令得111110,220x y x y ⎧--+=⎪⎨-+=⎪⎩11,z==m 设平面的法向量为由得OPD 222(,,),x y z =n 0,0OP OD ⋅=⋅=n n 令得2220,30x y ⎧=⎪⎨-+=⎪⎩23,x =(3,1,0).=n 所以易知二面角的平面角为锐角,所以二4cos ,.5⋅<>===m n m n m n C PD O --面角的余弦值为C PD O --4.530.（1）【证明】连交于点，连交于点，则.1BC 1B CM BD AC N 1MN AB C⊂平面由平几知：为的中点，为的中点，M 1BC N BD 即为的中位线..MN 1BC D∆1//MN C D∴又.……………3分1111,//C D AB CC D AB C⊄∴平面平面（2）【证明】.111,,,AA ABCD AC ABCD AA AC AA CD⊥⊂∴⊥⊥ 平面平面又.11111,,AA AC AA C C AC A C=∴⊥ 知为正方形在中由余弦定理知：.ACD ∆222,AC AD AC CD CD AC ==+∴⊥得又.111,AC AA A CD A ACC =∴⊥ 平面又.1111,AC A ACC CD AC ⊂∴⊥平面又.……………………7分1111,A C CD C AC A B CD=∴⊥ 平面（3）【解】作交于，连，由（2）知：.1CH C D⊥1C DH AG 1AC CC D⊥平面t b . ……9分111,,AC C D C D ACH AHC A C D C∴⊥∴⊥∴∠--平面为二面角的平面角；由知：；cos ,tan 2ACAHC AHC CH ∴∠=∠==2CD =AC =CH =在中由平几知：，于是得为正方形.1C CD∆1CC =11AA C C由（2）知：. ………………………12分111111(2432C A CD D A CC V V --==⨯⨯⨯=31.解：（1）存在P ，使得CP ∥平面ABEF ，此时．32λ=证明：当，此时，32λ=35AP AD =过P 作，与AF 交M ，则，MP FD ∥35MP FD =又，故，5FD =3MP =∵，，3EC =MP FD EC ∥∥∴，且，故四边形MPCE 为平行四边形，MP EC ∥MP EC =∴，PC ME ∥∵平面ABEF ，平面ABEF ，CP ØME ⊂∴平面ABEF 成立．CP ∥（2）∵平面ABEF ⊥平面EFDC ，ABEF ∩平面EFDC =EF ，，AF EF ∥∴AF ⊥平面EFDC ，∵，BE x =∴，，，AF x =(04)x <<6FD x =-故三棱锥A -CDF 的体积，2111162(6)(6)332332x x V x x x x +-⎛⎫=⨯⨯⨯-=-⨯= ⎪⎝⎭≤∴时，三棱锥的体积V 有最大值，最大值为3．3x =建立如图所示的空间直角坐标系，则，，，．(0,0,0)F (0,0,3)A (2,1,0)C (0,3,0)D ，，．(0,3,3)AD =- (2,2,0)CD =-(0,0,3)FA =设平面ACD 的法向量为，则，(,,)n x y z = 00n AD n CD ⎧⋅=⎪⎨⋅=⎪⎩∴，取，则，，330220y z x y -=⎧⎨-+=⎩1y =1x =1z =∴．(1,1,1)n =∴点F 到平面ACD 的距离||||n FA d n ⋅==32.（1）连接，则.AF AF =DF =又，∴，∴2AD =222DF AF AD +=DF AF ⊥又∵平面，∴.又.PA ⊥ABCD DF PA ⊥PA AF A = ∴平面.DF ⊥PAF ∵平面，∴.PF ⊂PAF DF PF ⊥（2）过点作交于点，则平面，且有.E EH FD ∥AD H EH ∥PFD 14AH AD =再过点作交于点，连接，则平面且.H HG DP ∥PA G EG HG ∥PFD 14AG AP =∴平面平面.∴平面.EHG ∥PFD EG ∥PFD ∴当为的一个四等分点（靠近点）时，平面G PA A EG ∥PFD（3）∵平面，∴是与平面所成的角，且，∴PA ⊥ABCD PBA ∠PB ABCD 45PBA ∠=︒.1PA AB ==取的中点，连接，则，平面，∴.AD M FM FM AD ⊥FM ⊥PAD FM PD ⊥在平面中，过点作于点，连接则平面，则为PAD M MN PD ⊥N FN PD ⊥FMN MNF ∠二面角的平面角.A PD F --∵，∴Rt MND RtPAD △∽△MN MDPA PD=∵，，，且，1PA =1MD =PD =90FMN ∠=︒h ng sn ∴，，∴MN =FN =cos MN MNF FN ∠==故二面角A PD F -- 33.解:以C 为坐标原点，分别以CA ，CB ，CC 1所在直线为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则C (0,0,0)，A (4,0,0)，A 1(4,0,2)，B 1(0,4，2).22(1)因为A 1M ＝3MB 1，所以M (1,3,2).2所以＝(4,0,2)，＝(－3,3,2).1CA 2AM 2所以cos 〈，＝＝－.1CA AM AMCA 26244⋅-3939所以异面直线AM 和A 1C 所成角的余弦值为.-------------------------8分3939(2)由A (4,0,0)，B (0,4,0)，C 1(0,0,2)，知＝(－4,4,0)，＝(－4,0,2).2AB 1AC 2设平面ABC 1的法向量为n ＝(a ，b ，c )，由得，⎪⎩⎪⎨⎧=⋅=⋅001AC n AB n ⎪⎩⎪⎨⎧=+-=+-0224044c a b a 令a ＝1，则b ＝1，c ＝，所以平面ABC 1的一个法向量为n ＝(1,1，).22因为点M 在线段A 1B 1上，所以可设M (x,4－x,2)，所以＝(x －4,4－x,2).2AM 2因为直线AM 与平面ABC 1所成角为30°，所以|cos 〈n ，〉|＝sin 30°＝.AM 21e 由|n ·|＝|n ||||cos 〈n ，〉|，得|1·(x －4)＋1·(4－x )＋·2|AM AM AM 22＝2· ·， 解得x ＝2或x ＝6.8)4()4(22+-+-x x 21因为点M 在线段A 1B 1上，所以x ＝2，即点M (2,2,2)是线段A 1B 1的中点. -------------------------14分234.（Ⅰ）证明：由题意得，AD ⊥DC ，AD ⊥DF ，且DC ∩DF =D ，∴AD ⊥平面CDEF ，∴AD ⊥FC ，……………………………………2分∵四边形CDEF 为正方形．∴DC ⊥FC由DC ∩AD =D ∴FC ⊥平面ABCD ，∴FC ⊥AC ……………………4分又∵四边形ABCD 为直角梯形，AB ∥CD ，AD ⊥DC ，AD =2，AB =4∴，，则有AC 2+BC 2=AB 2∴AC ⊥BC22=AC 22=BC 由BC ∩FC =C ，∴AC ⊥平面FCB ，∴AC ⊥FB ．……………………6分（Ⅱ）解：由（I ）知AD ，DC ，DE 所在直线相互垂直，故以D 为原点，以的方向分别为x ，y ，z 轴的正方向，建立如图所示的空间直角坐标系D-DADC DE ，，xyz…………………………………7分可得D （0，0，0），F （0，2，2），B （2，4，0），E （0，0，2），C （0，2，0），A （2，0，0），由（Ⅰ）知平面FCB 的法向量为)0,2,2(-=AC ∵，……………………………………………………8分)0,2,0(=EF )2,2,2(-=FB 设平面EFB 的法向量为则有即),,(z y x n =⎪⎩⎪⎨⎧=⋅=⋅00FB n EF n ⎩⎨⎧=-+=022202z y x y 令则……………………………………………………………………10分1=z )1,0,1(=n设二面角E ﹣FB ﹣C 的大小为θ，有图易知为锐角θ21cos θ所以二面角E ﹣FB ﹣C 的大小为……………………………………………………12分3π35.解：（1）矩形中，ABCD AB CD ∥∵面，平面，AB ⊄PCD CD ⊂PCD ∴平面，AB ∥PCD 又平面，AB ⊂ABE 平面平面，∴，PCD ABE EF =AB EF ∥又平面平面，∴PAB PCD l =AB l ∥∴.l EF ∥（2）取中点，连接，∵，∴，AD O PO PA PD =PO AD ⊥又平面平面，且平面平面，PAD ⊥ABCD PAD ABCD AD =∴平面，连接，则为在平面内的射影，PO ⊥ABCD OB OB PB ABCD ∴为与平面所成角，∴PBO ∠PB ABCD sin PBO ∠=∴，由题，∴tan PBO ∠=OB =2PO =取中点，连接，以为坐标原点，分别以，的方向分别为，，BC G OG O OA OG OP x y z轴的正方向建立如图所示的空间直角坐标系：则：，，，，则，(002)P ∥∥(100)A ∥∥(140)B ∥∥(140)C -∥∥1212E ⎛⎫- ⎪⎝⎭∥∥，(102)PA =-∥∥3212AE ⎛⎫=- ⎪⎝⎭∥∥设平面的法向量为，于是，∴，令，PAE ()n x yz =∥∥00n PA n AE ⋅=⎧⋅=⎪⎨⎪⎩203202x z x y z -=⎧⎪⎨-++=⎪⎩2x =则，1y =1z =∴平面的一个法向量PAE (211)n =∥∥同理平面的一个法向量为，ABE (203)m =∥∥∴cos ||||n m n m n m ⋅===∥可知二面角为钝二面角P AE B --所以二面角的余弦值为P AEB --36.【分析】（Ⅰ）取PB 的中点F ，连接AF ，EF ，由三角形的中位线定理可得四边形ADEF 是平行四边形．得到DE ∥AF ，再由线面平行的判定可得ED ∥面PAB ；（Ⅱ）法一、取BC 的中点M ，连接AM ，由题意证得A 在以BC 为直径的圆上，可得AB ⊥AC，找出二面角A ﹣PC ﹣D 的平面角．求解三角形可得二面角A ﹣PC ﹣D 的余弦值．法二、由题意证得AB ⊥AC ．又面PAC ⊥平面ABCD ，可得AB ⊥面PAC ．以A 为原点，方向分别为x 轴正方向，y 轴正方向建立空间直角坐标系．求出P 的坐标，再求出平面PDC 的一个法向量，由图可得为面PAC 的一个法向量，由两法向量所成角的余弦值可得二面角A ﹣PC ﹣D 的余弦值．【解答】（Ⅰ）证明：取PB 的中点F ，连接AF ，EF ．∵EF 是△PBC 的中位线，∴EF ∥BC ，且EF=．又AD=BC ，且AD=，∴AD ∥EF 且AD=EF ，则四边形ADEF 是平行四边形．∴DE ∥AF ，又DE ⊄面ABP ，AF ⊂面ABP ，∴ED ∥面PAB ；（Ⅱ）解：法一、取BC 的中点M ，连接AM ，则AD ∥MC 且AD=MC ，∴四边形ADCM 是平行四边形，∴AM=MC=MB，则A在以BC为直径的圆上．∴AB⊥AC ，可得．过D作DG⊥AC于G，∵平面PAC⊥平面ABCD，且平面PAC∩平面ABCD=AC，∴DG⊥平面PAC，则DG⊥PC．过G作GH⊥PC于H，则PC⊥面GHD，连接DH，则PC⊥DH，∴∠GHD是二面角A﹣PC﹣D的平面角．在△ADC中，，连接AE ，．在Rt△GDH中，，∴，即二面角A﹣PC﹣D 的余弦值．法二、取BC的中点M，连接AM，则AD∥MC，且AD=MC．∴四边形ADCM是平行四边形，∴AM=MC=MB，则A在以BC为直径的圆上，∴AB⊥AC．∵面PAC⊥平面ABCD，且平面PAC∩平面ABCD=AC，∴AB⊥面PAC．如图以A 为原点，方向分别为x轴正方向，y轴正方向建立空间直角坐标系．可得，．设P（x，0，z），（z＞0），依题意有，，解得．则，，．设面PDC 的一个法向量为，由，取x0=1，得．为面PAC 的一个法向量，且，设二面角A﹣PC﹣D的大小为θ，则有，即二面角A﹣PC﹣D 的余弦值．37.【分析】（1）取AD中点M，利用三角形的中位线证明EM∥平面PAB，利用同位角相等证明MC∥AB，得到平面EMC∥平面PAB，证得EC∥平面PAB；（2）建立坐标系，求出平面PAC的法向量，利用直线CN与平面PAC所成的角θ的正弦值为，可得结论．【解答】（1）证明：取AD中点M，连EM，CM，则EM∥PA．∵EM⊄平面PAB，PA⊂平面PAB，∴EM∥平面PAB．在Rt△ACD中，∠CAD=60°，AC=AM=2，∴∠ACM=60°．而∠BAC=60°，∴MC∥AB．∵MC⊄平面PAB，AB⊂平面PAB，∴MC∥平面PAB．∵EM∩MC=M，∴平面EMC∥平面PAB．∵EC⊂平面EMC，∴EC∥平面PAB．（2）解：过A作AF⊥AD，交BC于F，建立如图所示的坐标系，则A（0，0，0），B （，﹣，0），C（，1，0），D（0，4，0），P（0，0，2），设平面PAC 的法向量为=（x ，y ，z），则，取=（，﹣3，0），设=λ（0≤λ≤1），则=（0，4λ，﹣2λ），=（﹣λ﹣1，2﹣2λ），∴|cos ＜，＞|==，∴，∴N 为PD 的中点，使得直线CN 与平面PAC 所成的角θ的正弦值为．38.（1）证明：取AB 的中点O ，连接EO ，COAE EB ==AEB ∆为等腰直角三角形∴EO AB ⊥，1EO =又∵AB BC =，60ABC ∠=︒，∴ABC ∆是等边三角形.∴CO =，2EC =，∴222EC EO CO =+∴EO CO⊥∵EO ⊥平面ABCD ，又EO ⊂平面EAB ，∴平面EAB ⊥平面ABCD（2）解：以AB 的中点O 为坐标原点，OB 所在直线为y 轴，OE 所在直线为z 轴，如图建系则()0,1,0A -，)C，)2,0D -，()0,0,1Ed)AC =u u u r，)1EC =-u u u r，()0,2,0DC =u u u r设平面DCE 的法向量为(),,1n x y =r ，则00EC n DCn ⎧⋅=⎪⎨⋅=⎪⎩u u u r r u u u r r，即1020y -==⎪⎩，解得：0x y ⎧=⎪⎨⎪=⎩∴n ⎫=⎪⎪⎭r 同理求得平面EAC 的一个法向量为1,1m ⎫=-⎪⎪⎭u r cos ,m n m n m n⋅==u r ru r r u r r ，所以二面角A EC D --.39.证明：（Ⅰ）取中点，连结．AB D PD CD ，，．AP BP =Q PD AB ∴⊥，．，AC BC =Q CD AB ∴⊥PD CD D =Q I 平面．----3分AB ∴⊥PCD 平面，PC ⊂Q PCD ，又∵，∴- ----6分PC AB ∴⊥PC AC ⊥PC ABC ⊥平面解：（Ⅱ）如图，以为原点建立空间直角坐标系．C C xyz -则．设．---8分(000)(020)(200)C A B ，，，，，，，，(00)P t ，，，，． ----9分PB AB == 2t ∴=(002)P ，，取中点，连结．，，AP E BE CE ，AC PC = AB BP =，．CE AP ∴⊥BE AP ⊥是二面角的平面角．BEC ∴∠B AP C --，，， ---10分(011)E ，，(011)EC =--u u u r ，，(211)EB =--u u r，，cos EC EB BEC EC EB∴∠===u u u r u u r g u u u r u u r g二面角． -------- -12分∴B AP C --40.【分析】（Ⅰ）证明BD ⊥AC ，BD ⊥PO ，推出BD ⊥面PAC ，然后证明BD ⊥PC ．（Ⅱ）说明OE 是BE 在面PAC 上的射影，∠OEB 是BE 与面PAC 所成的角．利用Rt △BOE ，在Rt △PEO 中，证明PO ⊥AO ．推出PO ⊥面ABCD ．方法一：说明∠OHB 是二面角A ﹣EC ﹣B 的平面角．通过求解三角形求解二面角A ﹣EC ﹣B 的余弦值．方法二：以建立空间直角坐标系，求出平面BEC的法向量，平面AEC 的一个法向量，利用空间向量的数量积求解即可．【解答】（本小题满分12分）证明：（Ⅰ）因为底面是菱形，所以BD ⊥AC ．（1分）又PB=PD ，且O 是BD 中点，所以BD ⊥PO ．（2分）PO∩AC=O ，所以BD ⊥面PAC ．（3分）又PC ⊂面PAC ，所以BD ⊥PC ．（4分）（Ⅱ）由（Ⅰ）可知，OE 是BE 在面PAC 上的射影，所以∠OEB 是BE 与面PAC 所成的角．在Rt △BOE 中，，BO=1，所以．在Rt △PEO 中，，，所以．所以，又，所以PO 2+AO 2=PA 2，所以PO ⊥AO ．（6分）又PO ⊥BD ，BD∩AO=O ，所以PO ⊥面ABCD ．（7分）方法一：过O 做OH ⊥EC 于H ，由（Ⅰ）知BD ⊥面PAC ，所以BD ⊥EC ，所以EC ⊥面BOH ，BH ⊥EC ，所以∠OHB 是二面角A ﹣EC ﹣B 的平面角．（9分）在△PAC 中，，所以PA 2+PC 2=AC 2，即AP ⊥PC ．所以．（10分），得，（11分），，所以二面角A﹣EC﹣B的余弦值为．（12分）方法二：如图，以建立空间直角坐标系，，B（0，1，0），，，，，．（9分）设面BEC 的法向量为，则，即，得方程的一组解为，即．（10分）又面AEC 的一个法向量为，（11分）所以，所以二面角A﹣EC﹣B的余弦值为．（12分）【点评】本题考查二面角的平面角的求法，直线与平面垂直的判定定理的应用，考查空间想象能力以及计算能力．41.（1）取AD的中点为O，连接COPO,，PAD∆为等边三角形，ADPO⊥∴.底面ABCD中，可得四边形ABCO为矩形，AD CO ⊥∴，⊥∴=⋂AD CO PO ,0 平面POC ，⊂PC 平面PC AD POC ⊥,.又BC AD //，所以PC AD ⊥.（2）由面⊥PAD 面AD PO ABCD ⊥,知，⊥∴PO 平面ABCD ，OC OD OP ,,两两垂直，直线PC 与平面PAD 所成角为30，即30=∠CPO ，由2=AD ，知3=PO ，得1=CO .分别以→→→OP OD OC ,,的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系xyz O -，则),3,0,0(P ),0,1,0(D )0,1,1(),0,0,1(-B C ，),0,1,0(=→BC )0,1,1(),3,0,1(-=-=→→CD PC ，设平面PBC 的法向量为),,(z y x n =.⎩⎨⎧=-=∴030z x y ，则)1,0,3(=n，设平面PDC 的法向量为),,(z y x m =，⎩⎨⎧=-=-∴030z x y x ，则)1,3,3(=m，772724||||,cos ==⋅>=<n m n m n m,∴由图可知二面角C SB A --的余弦值772-.42.（1）证明：由已知四边形为矩形，得，ABCD AB BC ⊥∵，，∴平面.PB AB ⊥PB BC B = AB ⊥PBC 又，∴平面.//CD AB CD ⊥PBCsi na r∵平面，∴平面平面.CD ⊂PCD PBC ⊥PCD （2）解：以为坐标原点，建立如图所示的空间直角坐标系.B B xyz -设，，则，，，，1PB AB ==(0)BC a a =>(0,0,0)B (0,0,)C a(1,0,0)P (0,1,)D a 所以，，则，即，(1,0,)PC a =- (0,1,)BD a = ||cos 60||||PC BD PC BD ∙=22112a a =+解得（舍去）.1a =1a =-设是平面的法向量，则，即，111(,,)n x y z = PBD 00n BP n BD ⎧∙=⎪⎨∙=⎪⎩11100x y z =⎧⎨+=⎩可取.(0,1,1)n =-设是平面的法向量，则即，222(,,)m x y z = PCD 00m PD m CD ⎧∙=⎪⎨∙=⎪⎩222200x y z y -++=⎧⎨=⎩可取，所以，(1,0,1)m = 1cos ,2||||n m n m n m ∙<>==-由图可知二面角为锐角，所以二面角的大小为.B PDC --B PD C --6043.（1）证明：如图，取中点，连接、、，则和分别是等边三角形、等腰直BC M PM DM DB BCD ∆PBC ∆角三角形.故，，且，PM BC ⊥DM BC ⊥1PM =DM =所以，222DM PM PD +=故，PM DM ⊥所以平面.PM ⊥ABCD 又平面，从而平面平面.PM ⊂PBC PBC ⊥ABCD （2）如图，建立空间直角坐标系.M xyz -，，，，，，(0,0,1)P 2,0)A (0,1,0)B (0,1,0)C -(1,0)AB =- (0,1,1)PB =-，(0,1,1)PC =--设平面的法向量为，则，ABP (,,)n x y z = 00y y z ⎧-=⎪⎨-+=⎪⎩令，解得，，即，1x =-y =z =(n =-记直线与平面所成角的平面角为，则PC PAB θ||sin ||||n PC n PC θ∙===即直线与平面.PC PAB 44.（Ⅰ）连结OM 延长交F B 于H ，则H 为F B 的中点，又P 为C B 的中点，∴PH ∥CF ，又∵CF ⊂平面FC A ，∴PH ∥平面FC A 连结PO ，则PO ∥C A ，C A ⊂平面FC A ，∴PO ∥平面FC APO PH =P ∴平面POH ∥平面FC A ，PM ⊂平面POH∴//PM 平面FCA （Ⅱ）作AQ ⊥EF 交EF 延长线于Q,作AH ⊥DQ 交DQ 于H ，则AH ⊥面EQDC∴∠ACH 就是直线AC 与平面CEF 所成角在Rt ∆ADQ 中，AH=7327231=⨯在Rt ∆ACH 中，sin ∠ACH=35105=AC AH 直线AC 与平面CEF 所成角正弦值为3510545.（Ⅰ）证明：如图，∵，，，为的中点//AB CD CD AD ⊥22AD CD AB ===F CD ，∴为矩形，，ABFD AB BF ⊥又由平面，AB ⊥PAD ∴，AB PD ⊥又∵，∴，//EF PD AB EF ⊥∵，∴平面，BF EF F = AB ⊥BEF 又平面，∴平面平面．AE ⊂ABE ABE ⊥BEF （Ⅱ）由条件以所在直线为轴，所在直线为轴，所在直线为轴建立空AB x AD y AP z 间坐标系，则，，，，，(1,0,0)B (0,2,0)D (0,0,)P a (2,2,0)C (1,1,)2aE ，，(1,2,0)BD =- (0,1,2a BE = 平面的法向量，设平面的法向量为，BCD 1(0,0,1)n = EBD 2(,,)n x y z =由即，即取，得，，22,,n BD n BE ⎧⊥⎪⎨⊥⎪⎩ 22,,n BD n BE ⎧⋅⎪⎨⋅⎪⎩ 20,0,2x y azy -+=⎧⎪⎨+=⎪⎩1y =2x =2z a =-则，所以，22(2,1,)n a=- cos θ==因为平面与平面所成锐二面角，EBD ABCD ,43ππθ⎡⎤∈⎢⎥⎣⎦所以，得1cos 2θ⎡∈⎢⎣12⎡⎢⎣12≥，得或a≤≤≤a≤a≥所以的取值范围是．a46.（Ⅰ）证明：在等腰梯形ABCD中，可设2AD CD AB===，可求出BD=，4BC=，在BCD∆中，222BC BD DC=+，∴BD DC⊥，∵点A在平面BCD上的投影G落在BD上，∴AG⊥平面BCD，∴AG CD⊥，又BD DC⊥，AG BD G=∴CD⊥平面ABD，而CD⊂平面ACD，∴CD⊥平面ABD.（Ⅱ）由（Ⅰ）知BD CD⊥，AG BD⊥，G为BD中点，建立如图所示的空间坐标系，设2AD CD AB===，结合（Ⅰ）计算可得：(0,0,0)D，(0,2,0)C，G，A，(0,0,1)GA=，(2,1)GC=，设1111(,,)n x y z=是平面AGC的法向量，则11120zy=⎧⎪⎨+=⎪⎩，取1n=.(0,2,0)DC=，设2222(,,)n x y z=是平面ACD的法向量，则222yz=⎧⎪+=，取2n=.设二面角G AC D --的平面角为，则12cos cos ,n n θ=<>==47.（1）设AB 中点为O ，连接PO ，EO ，因为PA PB =，所以PO AB ⊥，又E 为AC 的中点，所以EO BC ∥.因为AB BC ⊥，所以EO AB ⊥，因为PO OE O =I ，所以AB ⊥平面POE ，又PE ⊂平面POE ，所以PE AB⊥（2）由（1）知PO AB ⊥，因为平面PAB ⊥平面ABC ，平面PAB I 平面ABC AB =，PO ⊂平面PAB ，所以PO ⊥平面ABC ，又EO AB ⊥.以O 为坐标原点，分别以OE u u u r ，OB u u u r ，OP u u u r为x 轴，y 轴，z 轴的正方向建立空间直角坐标系O xyz -，如图所示，因为AB BC ⊥，4AC =，2BC =，所以AB ==由O 为AB 中点，PO AB ⊥，2PB =，得OA OB ==1PO ==，则，()0,0,0O ，()1,0,0E ，()0,0,1P，()0,A，()B，()C 设平面PAC 的一个法向量为(),,n x y z =r，由00n PA n PC ⎧⋅=⎪⎨⋅=⎪⎩r u u r r u u u r，即020z x z ⎧-=⎪⎨+-=⎪⎩取y =，可得()3,n =r ，因为平面PAB ⊥平面ABC ，平面PAB I 平面ABC AB =，OE ⊂平面ABC ，所以EO ⊥平面PAB ，所以平面PAB 的一个法向量为()1,0,0OE =u u u r，∴cos,OE nOE nOE n⋅=u u u r ru u u r ru u u r r==，设二面角B PA C--的大小为θ，则cos=θ所以sin==θ，∴二面角B PA C--.48.（1），为的中点，.AB PB=O AB OB PA∴⊥又平面平面，且平面，PAC⊥PAB OB⊂ABP平面，而平面，BO∴⊥PAC OB⊂BOM平面平面.∴BOM⊥PAC（2）由已知得，为等腰直角三角形，，PAB∆AB PB==，等边的面积，2,1AP BO∴==PAC∆PACS∆=，13B PAC PACV S BO-∆∴=⨯⨯=113=由（1）易知平面，，OC⊥APB2AC BC∴==在中，∴ABC∆AB12ABCS∆∴==设点到平面的距离为，P ABC h则有，13P ABC ABCV S h-∆=⨯⨯=，即点到平面.h∴=P ABC49.证明：（1）因为M ，N 分别为PB ，PC 的中点，PA AB =，所以PB MA ⊥.因为90BAD ∠=︒，所以DA AB ⊥.因为PA ⊥底面ABCD ，所以DA PA ⊥.因为PA AB A =I ，所以DA ⊥平面PAB .所以PB DA ⊥.因为AM DA A =I ，所以PB ⊥平面ADNM 因为DN ⊂平面ADNM ，所以PB DN ⊥.（2）如图，以A 为坐标原点，建立空间直角坐标系A xyz -.则()0,0,0A ，()2,0,0B ，()2,1,0C ，()0,2,0D ，()0,0,2P .由（1）可知，PB ⊥平面ADNM ，所以平面ADMN 的法向量为()2,0,2BP =-u u r.设平面PDN 的法向量为(),,n x y z =r因为()2,1,2PC =-u u u r ，()0,2,2PD =-u u u r，所以00n PC n PD ⎧⋅=⎪⎨⋅=⎪⎩r u u u r r u u u r即220220x y z y z +-=⎧⎨-=⎩令2z =，则2y =，1x =，所以()1,2,2n =，所以cos ,n BP n BP n BP ⋅==r u u rr u u r r u u r =所以二面角P DN A --.50.【考点】直线与平面垂直的判定；与二面角有关的立体几何综合题．【分析】（Ⅰ）要证BC ⊥平面ACD ，只需证明BC 垂直平面ACD 内的两条相交直线AC 、OD即可；（Ⅱ）建立空间直角坐标系，求出两个平面的法向量，利用向量的数量积，求二面角A﹣CD﹣M的余弦值．【解答】解：（Ⅰ）在图1中，可得，从而AC2+BC2=AB2，故AC⊥BC取AC中点O连接DO，则DO⊥AC，又面ADC⊥面ABC，面ADC∩面ABC=AC，DO⊂面ACD，从而OD⊥平面ABC，∴OD⊥BC又AC⊥BC，AC∩OD=O，∴BC⊥平面ACD另解：在图1中，可得，从而AC2+BC2=AB2，故AC⊥BC∵面ADC⊥面ABC，面ADE∩面ABC=AC，BC⊂面ABC，从而BC⊥平面ACD（Ⅱ）建立空间直角坐标系O﹣xyz如图所示，则，，，设为面CDM的法向量，则即，解得令x=﹣1，可得又为面ACD的一个法向量∴∴二面角A﹣CD﹣M 的余弦值为．51.【考点】点、线、面间的距离计算；直线与平面平行的判定．【分析】（I）如图所示，取FB′的中点M，连接CM，A′M．可得四边形A′EMB′是平行四边形．A′B′∥EM．同理可得A′D∥CM，可得平面EMC∥平面A′DB′，即可证明CE∥面A′DB′．（II）取DE的中点O，建立如图所示的空间直角坐标系．∠A′ED=∠B′FC=60°．平面EFCD的一个法向量为=（0，0，1）．可得=．可得直线A′B′与平面FECD所成角的正弦值=||．【解答】（I）证明：如图所示，取FB′的中点M，连接CM，A′M．∵A′E B′M，∴四边形A′EMB′是平行四边形．∴A′B′∥EM．∵A′M CD，∴四边形A′MCD是平行四边形，∴A′D∥CM，又∵CM∩EM=M，A′B′∩A′D=A′，∴平面EMC∥平面A′DB′，由CE⊂平面CME．∴CE∥面A′DB′．（II）解：取DE的中点O，建立如图所示的空间直角坐标系．∠A′ED=∠B′FC=60°．则，A′， =．平面EFCD的一个法向量为=（0，0，1）．∴===﹣．∴直线A′B′与平面FECD 所成角的正弦值=||=．52.见解析．解：（）∵是矩形，1ABCD ∴，AD CD ⊥又∵平面，PD ⊥ABCD ∴，，即，，两两垂直，PD AD ⊥PD CD ⊥PD AD CD ∴以为原点，，，分别为轴，轴，轴建立如图空间直角坐标系，D DA DC DP x y z 由，，得，，，，，4PD CD ==2AD =(2,0,0)A (2,4,0)B (0,4,0)C (0,0,0)D (0,0,4)P ，(1,0,2)M 则，，，(2,0,4)AP =- (2,0,0)BC =- (1,4,2)MB =-设平面的一个法向量为，CMB 1111(,,)n x y z =则，即，令，得，，1100BC n MB n ⎧⋅=⎪⎨⋅=⎪⎩ 111120420x x y z -=⎧⎨+-=⎩11y =10x =12z =∴，1(0,1,2)n =∴，1114cos ,5||||AP n AP n AP n ⋅<>==⋅故与平面所成角的正弦值为．AP CMB 45（）由（1）可得(0,4,4)PC =-，2设平面PBC 的一个法向量为2222(,,)n x y z =，则2200BC n PC n ⎧⋅=⎪⎨⋅=⎪⎩，即22220440x y z -=⎧⎨-=⎩，令21y =，得20x =，21z =，∴2(0,1,1)n =，∴12cos ,n n <>=，故二面角M CB P --。

立体几何1．[四川省宜宾市第四中学高2020届一诊模拟考试理科数学]若某空间几何体的三视图如图所示，则该几何体的体积是A ．2B ．1C ．D ．【答案】B2．[湖南省衡阳县2020届高三12月联考数学（理）试题]【答案】D 【解析】3．[【全国百强校首发】四川省棠湖中学2020届高三一诊模拟考试数学（理）试题] 在正方体1111ABCD A B C D -中，动点E 在棱1BB 上，动点F 在线段11A C 上，O 为底面ABCD 的中心，若1,BE x A F y ==，则四面体O AEF -的体积 A ．与,x y 都有关 B ．与,x y 都无关 C ．与x 有关，与y 无关D ．与y 有关，与x 无关【答案】B4．[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学（理）试题]5．[四川省宜宾市第四中学高2020届一诊模拟考试理科数学] 一个圆锥SC的高和底面直径相等，且这个圆锥SC和圆柱OM的底面半径及体积也都相等，则圆锥SC和圆柱OM的侧面积的比值为A．322B．23C．35D．45【答案】C6．[辽宁葫芦岛锦化高中协作校高三上学期第二次考试数学理科试题]【答案】D【解析】7．[广东省三校（广州真光中学、深圳市第二中学、珠海市第二中学）2020届高三上学期第一次联考数学（理）试题] 在如图直二面角A­BD­C中，△ABD、△CBD均是以BD为斜边的等腰直角三角形，取AD的中点E，将△ABE 沿BE 翻折到△A1BE，在△ABE的翻折过程中，下列不可能成立的是A．BC与平面A1BE内某直线平行B．CD∥平面A1BEC．BC与平面A1BE内某直线垂直D．BC⊥A1B【答案】D8．[湖南省衡阳县2020届高三12月联考数学（理）试题]【答案】D【解析】9．[陕西省汉中市2020届高三教学质量第一次检测考试理科数学试题] 圆锥的侧面展开图是半径为R 的半圆，则该圆锥的体积为________. 【答案】33πR 10．[辽宁省本溪高级中学2020届高三一模考试数学（理）试卷]【答案】4π11．[安徽省合肥一中、安庆一中等六校教育研究会2020届高三上学期第一次素质测试数学（理)试题] 如图，在棱长为 1 的正方体1111ABCD A B C D -中，点M 是AD 的中点，动点P 在底面ABCD 内（不包括边界），若1B P ∥平面1A BM ，则1C P 的最小值是________．【答案】305【解析】 【分析】由面面平行找到点P 在底面ABCD 内的轨迹为线段DN ，再找出点P 的位置，使1C P 取得最小值，即1C P 垂直DN 于点O ，最后利用勾股定理求出最小值. 【详解】取BC 中点N ，连接11,,B D B N DN ，作CO DN ⊥，连接1C O ，因为平面1B DN ∥平面1A BM ，所以动点P 在底面ABCD 内的轨迹为线段DN ，当点P 与点O 重合时，1C P 取得最小值，因为11152225DN CO DC NC CO ⋅=⋅⇒==，所以221min 11130()155C P C O CO CC ==+=+=. 故1C P 的最小值是305. 【点睛】本题考查面面平行及最值问题，求解的关键在于确定点P 的位置，再通过解三角形的知识求最值.12．[四川省成都外国语学校2019-2020学年高三（上）期中数学试卷（理科）]已知某几何体的三视图如图所示，则该几何体的外接球的半径为________．21【答案】【解析】【分析】根据三视图还原几何体，设球心为O，根据外接球的性质可知，O与PAB△和正方形ABCD中心的连线分别与两个平面垂直，从而可得到四边形OGEQ 为矩形，求得OQ和PQ后，利用勾股定理可求得外接球半径.【详解】由三视图还原几何体如下图所示：设PAB△的中心为Q，正方形ABCD的中心为G，外接球球心为O，则OQ⊥平面PAB，OG⊥平面ABCD，E为AB中点，∴四边形OGEQ为矩形，112OQ GE BC ∴===，2233PQ PE ==， ∴外接球的半径：22213R GE PQ =+=. 故答案为21. 【点睛】本题考查多面体外接球半径的求解，关键是能够根据球的性质确定球心的位置，从而根据长度关系利用勾股定理求得结果. 13．[湖南省衡阳县2020届高三12月联考数学（理）试题]【答案】【解析】14．[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学（理）试题]【答案】1 315．[江苏省南通市2020届高三第一学期期末考试第一次南通名师模拟试卷数学试题]如图，在四棱锥P ABCD-中，底面ABCD是平行四边形，平面ABP⊥平面BCP，90APB=，M为CP的中点．求证：∠=︒，BP BC（1）AP//平面BDM；（2）BM ACP⊥平面．【解析】（1）设AC 与BD 交于点O ，连接OM ， 因为ABCD 是平行四边形，所以O 为AC 中点， 因为M 为CP 的中点，所以AP ∥OM ， 又AP ⊄平面BDM ，OM ⊂平面BDM ， 所以AP ∥平面BDM ．（2）平面ABP ⊥平面BCP ，交线为BP ， 因为90APB ∠=︒，故AP BP ⊥，因为AP ⊂平面ABP ，所以AP ⊥平面BCP ， 因为BM ⊂平面BCP ，所以AP ⊥BM ． 因为BP BC =，M 为CP 的中点，所以BM CP ⊥． 因为AP CP P =I ，AP CP ⊂，平面ACP ， 所以BM ⊥平面ACP .16．[河南省新乡市高三第一次模拟考试（理科数学）] 如图，在四棱锥ABCDV -中，二面角D BC V --为︒60，E 为BC 的中点. （1）证明：VE BC =；（2）已知F 为直线VA 上一点，且F 与A 不重合，若异面直线BF 与VE 所成角为︒60，求.VA VFABCDPMABCDPMO【解析】17．[四川省成都外国语学校2019-2020学年高三（上）期中数学试卷（理科）]如图，在底面是菱形的四棱锥P-ABCD中，PA⊥平面ABCD，∠ABC=60°，PA=AB=2，点E，F分别为BC，PD的中点，设直线PC与平面AEF交于点Q．（1）已知平面PAB∩平面PCD=l，求证：AB∥l．（2）求直线AQ 与平面PCD 所成角的正弦值． 【解析】 【分析】（1）证明AB ∥平面PCD ，然后利用直线与平面平行的性质定理证明AB ∥l ； （2）以点A 为原点，直线AE 、AD 、AP 分别为轴建立空间直角坐标系，求出平面PCD 的法向量和直线AQ 的方向向量，然后利用空间向量的数量积求解直线AQ 与平面PCD 所成角的正弦值即可．【详解】（1）证明：∵AB ∥CD ，AB ⊄平面PCD ，CD ⊂平面PCD ． ∴AB ∥平面PCD ，∵AB ⊂平面PAB ，平面PAB ∩平面PCD =l ， ∴AB ∥l ；（2）∵底面是菱形，E 为BC 的中点，且AB =2， ∴13BE AE AE BC ==⊥,,， ∴AE ⊥AD ，又PA ⊥平面ABCD ，则以点A 为原点，直线AE 、AD 、AP 分别为x 、y 、z 轴建立如图所示空间直角坐标系，则()()()()020,002,30,300D P C E,,,,,,,,，∴()0,1,1F ，()()()()3000,11310022AE AF DC DP ===-=-u u u r u u u r u u u r u u u r,,,,,,,,,,，设平面PCD 的法向量为(),,x y z =n ，有0PD ⋅=u u u r n ，0CD ⋅=u u u rn ，得()133=，，n ，设()1AQ AC AP λλ=+-u u u r u u u r u u u r，则()()321AQ λλλ=-u u u r ,,，再设(3,,)AQ mAE n m n n AF =+=u u u r u u u r u u u r，则()3321m n nλλλ⎧=⎪=⎨⎪-=⎩，解之得23m n λ===，∴2223333AQ ⎛⎫=⎪⎝⎭u u u r ,,， 设直线AQ 与平面PCD 所成角为α，则3105sin cos ,AQ AQ AQα⋅>=<==u u u r u u u r u u u r n n n ，∴直线AQ 与平面PCD 所成角的正弦值为3105． 【点睛】本题考查直线与平面平行的判定定理以及性质定理的应用，直线与平面所成角的向量求法，合理构建空间直角坐标系是解决本题的关键，属中档题.18．[安徽省合肥一中、安庆一中等六校教育研究会2020届高三上学期第一次素质测试数学（理)试题] 已知三棱柱111ABC A B C -中，1AB AC AA ==，侧面11ABB A ⊥底面ABC ，D 是BC 的中点，160B BA ∠=︒，1B D AB ⊥.（1）求证：ABC △为直角三角形；（2）求二面角1C AD B --的余弦值． 【解析】（1）取AB 中点O ，连接OD ，1B O ，易知1ABB △为等边三角形，从而得到1B O AB ⊥，结合1B D AB ⊥，可根据线面垂直判定定理得到AB ⊥平面1B OD ，由线面垂直的性质知AB OD ⊥，由平行关系可知AB AC ⊥，从而证得结论；（2）以O 为坐标原点可建立空间直角坐标系，根据空间向量法可求得平面1ADC 和平面ADB 的法向量的夹角的余弦值，根据所求二面角为钝二面角可得到最终结果. 【详解】（1）取AB 中点O ，连接OD ，1B O ，在1ABB △中，1AB B B =，160B BA ∠=︒，1ABB ∴△是等边三角形， 又O 为AB 中点，1B O AB ∴⊥，又1B D AB ⊥，111B O B D B =I ，11,B O B D ⊂平面1B OD ，AB ∴⊥平面1B OD ，OD ⊂Q 平面1B OD ，AB OD ∴⊥， 又OD AC ∥，AB AC ∴⊥， ∴ABC △为直角三角形.（2）以O 为坐标原点，建立如下图所示的空间直角坐标系：令12AB AC AA ===，则()1,2,0C -，()1,0,0A -，()0,1,0D ，()1,0,0B ，()10,0,3B ，()11,0,3BB ∴=-u u u v ，()0,2,0AC =u u u v ，()1,1,0AD =u u u v，()1111,2,3AC AC CC AC BB =+=+=-u u u u v u u u v u u u u v u u u v u u u v，设平面1ADC 的法向量为(),,x y z =m ，10230AD x y AC x y z ⎧⋅=+=⎪∴⎨⋅=++=⎪⎩u u u v u u u u v m m ，令1x =，则1y =-，3z =，()1,1,3∴=-m ， 又平面ADB 的一个法向量为()0,0,1=n ，315cos ,5113∴<>==++m n ， Q 二面角1C AD B --为钝二面角，∴二面角1C AD B --的余弦值为15-.【点睛】本题考查立体几何中垂直关系的证明、空间向量法求解二面角的问题，涉及到线面垂直判定定理和性质定理的应用；证明立体几何中线线垂直关系的常用方法是通过证明线面垂直得到线线垂直的关系.19．[江西省宜春市上高二中2020届高三上学期第三次月考数学（理）试题]20．[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学（理）试题]21．[辽宁葫芦岛锦化高中协作校高三上学期第二次考试数学理科试题]【解析】22．[【全国百强校首发】四川省棠湖中学2020届高三一诊模拟考试数学（理）试题] 如图，在四棱锥P ABCD-中，底面ABCD为矩形，平面PCD⊥平面ABCD,2AB=,1BC=，2PC PD==，E为PB中点．（1）求证：PD∥平面ACE；（2）求二面角E AC D--的余弦值；（3）在棱PD上是否存在点M，使得AM⊥BD？若存在，求PMPD的值；若不存在，说明理由．【解析】（1）设BD交AC于点F，连接EF. 因为底面ABCD是矩形，所以F为BD中点 . 又因为E为PB中点，所以EF∥PD.因为PD ⊄平面,ACE EF ⊂平面ACE ，所以PD ∥平面ACE.（2）取CD 的中点O ，连接PO ，FO .因为底面ABCD 为矩形，所以BC CD ⊥.因为PC PD =，O CD 为中点，所以,PO CD OF ⊥∥BC ，所以OF CD ⊥. 又因为平面PCD ⊥平面ABCD ，PO ⊂平面,PCD 平面PCD ∩平面ABCD =CD . 所以PO ⊥平面ABCD ，如图，建立空间直角坐标系O xyz -， 则111(1,1,0)(0,1,0)(1,1,0),(0,0,1),(,,)222A C B P E -，,， 设平面ACE 的法向量为(,,)x y z =m ，131(1,2,0),(,,)222AC AE =-=-u u u r u u u r ， 所以20,2,0,131.00222x y x y AC z y x y z AE -+=⎧⎧=⎧⋅=⎪⇒⇒⎨⎨⎨=--++=⋅=⎩⎩⎪⎩u u u v u u u v m m 令1y =，则2,1x z ==-，所以2,11=-（，）m .平面ACD 的法向量为(0,0,1)OP =u u u r ，则6cos ,OP OP OP⋅<>==-⋅u u u r u u u r u u u r m m |m |. 如图可知二面角E AC D --为钝角，所以二面角E AC D --的余弦值为66-. （3）在棱PD 上存在点M ，使AM BD ⊥.设([0,1]),(,,)PM M x y z PD=∈λλ，则,01,0PM PD D =-u u u u r u u u r λ（，）.因为(,,1)(0,1,1)x y z -=--λ，所以(0,,1)M --λλ. (1,1,1),(1,2,0)AM BD =---=--u u u u r u u u r λλ.因为AM BD ⊥，所以0AM BD ⋅=u u u u r u u u r .所以12(1)0λ--=，解得1=[0,1]2∈λ. 所以在棱PD 上存在点M ，使AM BD ⊥，且12PM PD =。

8.1 基本立体图形(精练)【题组一多面体】1．(2020·广西崇左市·崇左高中)下列几何体中是棱锥的有( )A．0个B．1个C．2个D．3个【答案】C【解析】由棱锥的定义可得，只有几何体⑤、⑥为棱锥.故选：C.2．(2020·广西桂林市·桂林十八中)下列命题正确的是( )A．棱柱的底面一定是平行四边形B．棱锥的底面一定是三角形C．棱锥被平面分成的两部分不可能都是棱锥D．棱柱被平面分成的两部分可以都是棱柱【答案】D【解析】对于选项,A棱柱的底面也可以是三角形，五边形等，不一定是平行四边形，所以该选项错误；对于选项B，棱锥的底面不一定是三角形，也可以是四边形，五边形等，所以该选项错误；对于选项C，棱锥被平面分成的两部分可能都是棱锥，所以该选项错误；对于选项D，棱柱被平面分成的两部分可以都是棱柱，所以该选项正确.故选：D3．(2020·全国高三专题练习)一个棱锥所有的棱长都相等，则该棱锥一定不是( )A．正三棱锥B．正四棱锥C．正五棱锥D．正六棱锥【答案】D【解析】因为正六变形的中心到底面顶点的距离等于边长，所以正六棱锥的侧棱必大于底面棱长，故选：D.4．(2021·江苏高一课时练习)棱台不具备的特点是( )A．两底面相似B．侧面都是梯形C．侧棱都相等D．侧棱延长后都交于一点【答案】C【解析】根据棱台的定义，由平行于棱锥底面的平面截棱锥，截面与底面之间的部分叫棱台．棱台的两底面是相似多边形，A正确；侧面的上下底边平行，侧面都是梯形，B正确；侧棱延长后交于一点，D正确；由于棱锥的侧棱不一定相等，所以棱台的侧棱也不一定相等，C不一定成立，故选：C．5．(2021·河南焦作市)某几何体有6个顶点，则该几何体不可能是( )A．五棱锥B．三棱柱C．三棱台D．四棱台【答案】D【解析】四棱台有8个顶点，不符合题意.，其他都是6个顶点．故选：D．6．(2020·全国高三专题练习(文))下列说法中正确的是( )A．有两个面平行，其余各面都是四边形的几何体叫棱柱B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱C．有一个面是多边形，其余各面都是梯形的几何体叫棱台D．有一个面是多边形，其余各面都是有一个公共顶点的三角形的几何体叫棱锥【答案】D【解析】因为有两个面平行，其余各面是相邻的公共边都相互平行的平行四边形的几何体叫棱柱，所以A、B错误；而一个平行于底面的平面截棱锥，底面与截面之间的部分叫棱台，所以棱台各侧棱的延长线交于一点，所以C错误；因为有一个面是多边形，其余各面都是有公共顶点的三角形的几何体叫棱锥，所以D正确.故选：D.7．(2020·朝阳县柳城高级中学)下列说法正确的是( )A．棱柱的侧棱都相等，侧面都是全等的平行四边形B．用一个平面去截棱锥，棱锥底面与截面之间的部分是棱台C．若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直D．棱台的侧棱延长后交于一点，侧面是等腰梯形【答案】C【解析】A. 棱柱的侧棱都相等，侧面是平行四边形,但不一定全等，故错误；B.用一个平面去截棱锥，当棱锥底面与截面平行时，才是棱台，故错误；C.若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直，如正方体共顶点的三个相邻平面，故正确；D.棱台的侧棱延长后交于一点，但侧面不一定是等腰梯形，故错误；故选：C8．(2021·江苏高一课时练习)下列说法正确的是________(填序号).①底面是正多边形的棱锥为正棱锥；②各侧棱都相等的棱锥为正棱锥；③各侧面都是等腰三角形的棱锥为正棱锥；④各侧面都是全等的等腰三角形的棱锥是正棱锥；⑤底面是正多边形且各侧面全等的棱锥为正棱锥.【答案】⑤【解析】对于①，如果棱锥的顶点在底面上的射影不是正多边形的中心，则此棱锥不是正棱锥，故①错误.对于②，如图(1)，棱锥的顶点是圆锥的顶点，而底面多边形是圆锥底面圆的内接非正多边形，此时棱锥满足各侧棱都相等，但不是正棱锥，故②错误.对于③④，如图(2)，侧面都是等腰三角形，且它们全等，但该三棱锥不是正棱锥，故③④错误.对于⑤，因为底面是正多边形且各侧面全等的棱锥为正棱锥，故顶点底面上的射影O为正多边形的中心，此时棱锥为正棱锥，故⑤正确.故答案为：⑤9．(2020·全国高三专题练习)给出下列命题：①棱柱的侧棱都相等，侧面都是全等的平行四边形；②若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直；③在四棱柱中，若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱；④存在每个面都是直角三角形的四面体.其中正确命题的序号是________.【答案】②③④【解析】①不正确，根据棱柱的定义，棱柱的各个侧面都是平行四边形，但不一定全等；②正确，若三棱锥的三条侧棱两两垂直，则三个侧面构成的三个平面的二面角都是直二面角；③正确，因为两个过相对侧棱的截面的交线平行于侧棱，又垂直于底面；④正确，如图，正方体1111ABCD A B C D-中的三棱锥1C ABC-，四个面都是直角三角形.故答案为：②③④10．(2020·全国高三专题练习)下列关于棱锥、棱台的说法中，正确说法的序号是________ ①用一个平面去截棱锥，底面和截面之间的部分组成的几何体叫棱台；②棱台的侧面一定不会是平行四边形；③棱锥的侧面只能是三角形；④棱台的各侧棱延长后必交于一点；⑤棱锥被平面截成的两部分不可能都是棱锥.【答案】②③④【解析】①错，若平面不与棱锥底面平行，用这个平面去截棱锥，则棱锥底面和截面之间的部分不是棱台；②对，棱台的侧面一定是梯形，而不是平行四边形；③对，由棱锥的定义知棱锥的侧面只能是三角形；④对，棱台是由平行于棱锥底面的平面截得的，故棱台的各侧棱延长后必交于一点；⑤错，如图所示四棱锥被平面PBD截成的两部分都是棱锥.故答案为：②③④11．(2021·江苏高一课时练习)如图，下列几何体中，_______是棱柱，_______是棱锥，_______是棱台(仅填相应序号).【答案】①③④⑥⑤【解析】结合棱柱、棱锥和棱台的定义可知①③④是棱柱，⑥是棱锥，⑤是棱台.故答案为：①③④；⑥；⑤.【题组二旋转体】1．(2020·浙江)以下空间几何体是旋转体的是( )A．圆台B．棱台C．正方体D．三棱锥【答案】A【解析】由封闭的旋转面围成的几何体叫作旋转体可知，只有A项满足题意故选：A2．(2020·东台创新高级中学高一月考)给出下列命题：①圆柱的母线与它的轴可以不平行；②圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线都可以构成直角三角形；③在圆台的上、下两底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的．其中正确的是( )A．①③B．②④C．①④D．②③【答案】B【解析】圆柱的母线与它的轴平行，故①错误；圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线都可以构成直角三角形，故②正确；在圆台的上、下两底面圆周上各取一点，则这两点的连线不一定是圆台的母线，故③错误；圆柱的任意两条母线所在的直线是互相平行的，故④正确；故选：B3．(2020·全国高一课时练习)如图所示，观察下面四个几何体，其中判断正确的是( )A．①是圆台B．②是圆台C．③是圆锥D．④是圆台【答案】C【解析】图①不是由圆锥截得的,所以①不是圆台;图②上下两个面不平行，所以②不是圆台;图④不是由圆锥截得的，所以④不是圆台;很明显③是圆锥，故选：C.4．(2032·上海市)有下列命题：①在圆柱的上、下底面的圆周上各取一点，则这两点连线的长度是母线的长度；②圆锥顶点与底面圆周上任意一点连线的长度是母线的长度；③圆柱的任意两条母线所在直线互相平行；④过球上任意两点有且只有一个大圆；其中正确命题的序号是_____【答案】②③【解析】①若上下顶面两点连线不垂直于底面，则两点连线长度不是母线的长度，①错误；②由圆锥的特点可知，圆锥顶点到底面圆周上任意一点长度相等，均为母线长度，②正确；③圆柱的母线均垂直于底面，所以任意两条母线所在直线互相平行，③正确；④若两点连线为球的直径，则过两点有两个大圆，④错误.故答案为②③【题组三组合体】1．(2020·全国高一课时练习)说出图中物体的主要结构特征.【答案】详见解析【解析】(1)一个圆柱与一个圆锥的组合体，上部分为圆锥，下部分为圆柱；(2)一个六棱柱里面挖去了一个圆柱.2．(2020·全国高一课时练习)如图，以直角梯形ABCD的下底AB所在直线为轴，其余三边旋转一周形成的面围成一个几何体，说出这个几何体的结构特征.【答案】详见解析【解析】几何体如图(2)所示，其中DE AB，垂足为E.这个几何体是由圆柱BE和圆锥AE组合而成的.其中圆柱BE的底面分别是B和E，侧面是由梯形的上底CD绕轴AB旋转形成的；圆锥AE的底面是E，侧面是由梯形的边AD绕轴AB旋转而成的. 3．(2020·全国高一课时练习)如图，说出图中两个几何体的结构特征.【答案】(1)由圆锥和圆台组合而成的简单组合体.(2)由四梭柱和四棱锥组合而成的简单组合体.【解析】几何体(1)是圆台上拼接了一个与圆台上底同底的圆锥；几何体(2)是长方体上拼接了一个同底的四棱锥；4．(2020·全国高一课时练习)试指出图中组成各几何体的基本元素.【答案】(1)几何体由6个顶点、12条棱和8个面组成(2)几何体由6个顶点、10条棱和6个面组成【解析】(1) 是由两个四棱锥组成的，有6个顶点、12条棱和8个面组成.(2)是由两个锥体组合而成，有6个顶点、10条棱和6个面组成.【题组四截面问题】1．(2020·江西吉安市·高三其他模拟(文))如图是一个正方体的表面展开图，则图中“0”在正方体中所在的面的对面上的是( )A．2 B．1 C．高D．考【答案】C【解析】将展开图还原成正方体可知，“0”在正方体中所在的面的对面上的是“高”，故选:C.2．(2021·江苏高一课时练习)如图所示，在三棱台A′B′C′－ABC中，截去三棱锥A′－ABC，则剩余部分是( )A．三棱锥B．四棱锥C．三棱柱D．组合体【答案】B【解析】根据棱锥的结构特征可判断，余下部分是四棱锥A′－BCC′B′．故选：B.3．(2020·唐山市第十一中学高二期中)用一个平面去截一个几何体，得到的截面是三角形面，这个几何体不可能是( )A．棱锥B．圆锥C．圆柱D．正方体【答案】C【解析】圆柱的截面的图形只有矩形或圆形，如果截面是三角形，那么这个几何体不可能是圆柱.故选：C4．(2021·江苏高一课时练习)如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面，下底面圆心为顶点的圆锥而得到的组合体，现用一个竖直的平面去截这个组合体，则截面图形可能是( )A．①②B．①③C．①④D．①⑤【答案】D【解析】一个圆柱挖去一个圆锥后，剩下的几何体被一个竖直的平面所截后，圆柱的轮廓是矩形除去一条边，当截面经过圆柱上下底面的圆心时，圆锥的截面为三角形除去一条边，所以①正确；当截面不经过圆柱上下底面的圆心时，圆锥的截面为抛物线的一部分，所以⑤正确；故选:D。

2019--2020年高考数学试题分类汇编立体几何一、选择题.1、（2019年高考全国I 卷理科12）已知三棱锥P −ABC 的四个顶点在球O 的球面上，P A =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是P A ，AB 的中点，∠CEF =90°，则球O 的体积为A ．68πB ．64πC ．62πD ．6π 答案：D解析：如图，三棱锥ABC P -为正三棱锥，不妨设a PC PB PA 2||||||===，底面外接圆半径为r ，由题意可得3||,||==CF a EF .在PAC ∆中，由余弦定理可得aa a a PAC 21222444cos 22=⨯⨯-+=∠， 所以在EAC ∆中22124||222+=⨯⨯⨯-+=a aa a a EC 又︒=∠90CEF ，根据勾股定理可得222||||||CF EF EC =+，即2||=PC 在直角POC ∆中，332||=OC ,36||||22=-=r PC OP 由正三棱锥外接球半径公式可得26||2||222=+=OP OP r R ，故体积为π6 2、（2019年高考全国II 卷文理科7）设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行B ．α内有两条相交直线与β平行C ．α，β平行于同一条直线D ．α，β垂直于同一平面答案：B解析：由“判定定理:如果一个平面内有两条相交直线分别与另一个平面内两条相交直线平行,那么这两个平面平行”可知答案选B3、（2019年高考全国II 卷文理科16）．中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．（本题第一空2分，第二空3分．） 答案：A解析：(1)上层8个,中层8个,下层8个上下底各1个(2)设棱长为a ,如图作出该几何体的截面,1,21=-=CE a CD 又△CDE 为等腰直角三角形,则a a =-⨯212，解得12-=a .则棱长为12- 4、（2019年高考全国III 卷文理科8）如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则A ．BM =EN ，且直线BM 、EN 是相交直线B ．BM ≠EN ，且直线BM ，EN 是相交直线C ．BM =EN ，且直线BM 、EN 是异面直线D ．BM ≠EN ，且直线BM ，EN 是异面直线答案：B解析：建系如图)23,0,23(),0,11,1(),3,0,1(),0,2,0(M N E B 所以7)023()20()023(||222=-+-+-=BM , 2)300()01()11(||222=-+-+-=EN又因为BN BE BM +=21 所以B 、M 、E 、N 四点共面。