《排队论》习题解答

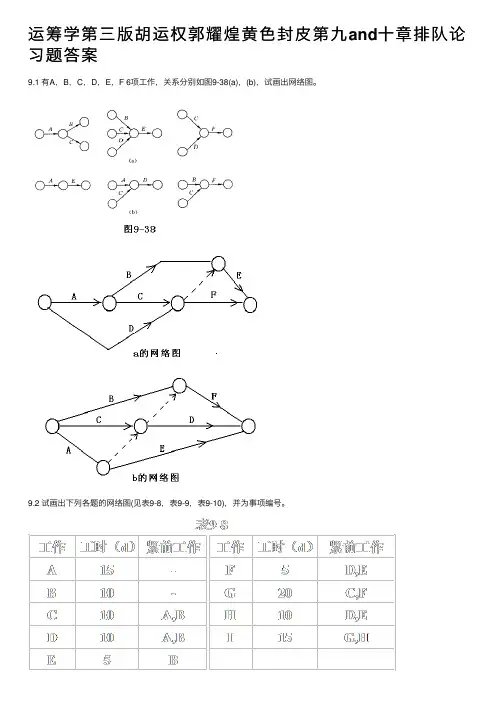
运筹学第三版胡运权郭耀煌黄⾊封⽪第九and⼗章排队论习题答案9.1 有A，B，C，D，E，F 6项⼯作，关系分别如图9-38(a)，(b)，试画出⽹络图。

9.2 试画出下列各题的⽹络图(见表9-8，表9-9，表9-10)，并为事项编号。

9.3 设有如图9-39，图9-40⽹络图，⽤图上计算法计算时间参数，并求出关键路线。

9.4 绘制表9-11，表9-12所⽰的⽹络图，并⽤表上计算法计算⼯作的各项时间参数、确定关键路线。

9.5 某⼯程资料如表9-13所⽰。

要求：(1)画出⽹络图。

(2)求出每件⼯作⼯时的期望值和⽅差。

(3)求出⼯程完⼯期的期望值和⽅差。

(4)计算⼯程期望完⼯期提前3天的概率和推迟5天的概率。

解：每件⼯作的期望⼯时和⽅差见表9-13的左部。

⼯程完⼯期的期望值为32个⽉，⽅差为5（1+1+1+1+1）。

⼯程期望完⼯期提前3天的概率为0.09，推迟5天的概率为0.987。

9.6 对图9-41所⽰⽹络，各项⼯作旁边的3个数分别为⼯作的最乐观时间、最可能时间和最悲观时间，确定其关键路线和最早完⼯时间的概率。

根据关键线路，再考虑到其他线路上的时差很多，可知最早完⼯时间应该等于关键线路上各个⼯作最早完⼯时间之和:4+2+6+2+3=2=19 。

概率为0.005 。

9.7 某项⼯程各道⼯序时间及每天需要的⼈⼒资源如图9-42所⽰。

图中，箭线上的英⽂字母表⽰⼯序代号，括号内数值是该⼯序总时差，箭线下左边数为⼯序⼯时，括号内为该⼯序每天需要的⼈⼒数。

若⼈⼒资源限制每天只有15⼈，求此条件下⼯期最短的施⼯⽅案。

解:最短⼯期还是15天。

各个⼯作的开始时间如下图所⽰：9.8 已知下列⽹络图有关数据如表9-14，设间接费⽤为15元／天，求最低成本⽇程。

解：将①→②缩短两天，总⼯期为25天，直接费⽤7420元，间接费⽤375元，最⼩总费⽤为7795元。

⽹络图和关键线路如下：9.9 ⼀项⼩修计划包括的⼯作如表9-15所⽰。

排队论习题及答案排队论习题及答案排队论是概率论和数学统计中的一个重要分支，研究的是随机事件的排队问题。

在现实生活中，我们经常会遇到排队的情况，如等候乘坐公交车、购物结账等。

排队论的研究可以帮助我们更好地理解和优化排队过程，提高效率和服务质量。

下面，我们将介绍几个排队论的习题及其解答。

习题一：某银行有两个窗口，顾客到达银行的时间服从平均到达率为λ的泊松分布，每个顾客在窗口办理业务的时间服从平均服务率为μ的指数分布。

求平均等待时间和平均排队长度。

解答：首先，我们可以根据泊松分布和指数分布的性质，得到顾客到达时间和服务时间之间的关系。

假设顾客到达时间服从泊松分布，到达率为λ，那么两个顾客到达时间之间的时间间隔服从参数为λ的指数分布。

同样，假设顾客的服务时间服从指数分布，服务率为μ，那么两个顾客的服务时间之间的时间间隔服从参数为μ的指数分布。

根据排队论的基本原理，平均等待时间等于平均排队长度除以到达率。

平均排队长度可以通过利用排队论的公式计算得到。

在本题中，根据M/M/2模型，可以得到平均排队长度的公式为：Lq = λ^2 / (2μ(μ - λ))其中，Lq表示平均排队长度，λ表示到达率，μ表示服务率。

接下来，我们可以计算平均等待时间。

根据排队论的公式，平均等待时间等于平均排队长度除以到达率。

所以，平均等待时间的公式为：Wq = Lq / λ综上所述，我们可以通过计算得到平均等待时间和平均排队长度。

习题二：某餐厅有4个服务台，每个服务台的服务时间服从平均服务率为μ的指数分布，顾客到达时间服从平均到达率为λ的泊松分布。

求平均等待时间和平均排队长度。

解答：在这个问题中，我们可以使用M/M/4模型来求解。

根据M/M/4模型，平均排队长度的公式为：Lq = (λ/μ)^4 * (1/(4! * (1 - ρ)))其中，Lq表示平均排队长度，λ表示到达率，μ表示服务率，ρ表示系统繁忙度。

平均等待时间的公式为：Wq = Lq / λ通过计算可以得到平均等待时间和平均排队长度。

《运筹学》第六章排队论习题转载请注明1. 思考题（1）排队论主要研究的问题是什么；（2）试述排队模型的种类及各部分的特征；（3）Kendall 符号C B A Z Y X /////中各字母的分别代表什么意义；（4）理解平均到达率、平均服务率、平均服务时间和顾客到达间隔时间等概念； （5）分别写出普阿松分布、负指数分布、爱尔朗分布的密度函数，说明这些分布的主要性质；（6）试述队长和排队长；等待时间和逗留时间；忙期和闲期等概念及他们之间的联系与区别。

2．判断下列说法是否正确（1）若到达排队系统的顾客为普阿松流，则依次到达的两名顾客之间的间隔时间服从负指数分布；（2）假如到达排队系统的顾客来自两个方面，分别服从普阿松分布，则这两部分顾客合起来的顾客流仍为普阿松分布；（3）若两两顾客依次到达的间隔时间服从负指数分布，又将顾客按到达先后排序，则第1、3、5、7，┉名顾客到达的间隔时间也服从负指数分布； （4）对1//M M 或C M M //的排队系统，服务完毕离开系统的顾客流也为普阿松流； （5）在排队系统中，一般假定对顾客服务时间的分布为负指数分布，这是因为通过对大量实际系统的统计研究，这样的假定比较合理；（6）一个排队系统中，不管顾客到达和服务时间的情况如何，只要运行足够长的时间后，系统将进入稳定状态；（7）排队系统中，顾客等待时间的分布不受排队服务规则的影响；（8）在顾客到达及机构服务时间的分布相同的情况下，对容量有限的排队系统，顾客的平均等待时间少于允许队长无限的系统；（9）在顾客到达分布相同的情况下，顾客的平均等待时间同服务时间分布的方差大小有关，当服务时间分布的方差越大时，顾客的平均等待时间就越长； （10）在机器发生故障的概率及工人修复一台机器的时间分布不变的条件下，由1名工人看管5台机器，或由3名工人联合看管15台机器时，机器因故障等待工人维修的平均时间不变。

3．某店有一个修理工人，顾客到达过程为Poisson 流，平均每小时3人，修理时间服从负指数分布，平均需19分钟，求： （1）店内空闲的时间； （2）有4个顾客的概率； （3）至少有一个顾客的概率； （4）店内顾客的平均数； （5）等待服务的顾客数； （6）平均等待修理的时间；（7）一个顾客在店内逗留时间超过15分钟的概率。

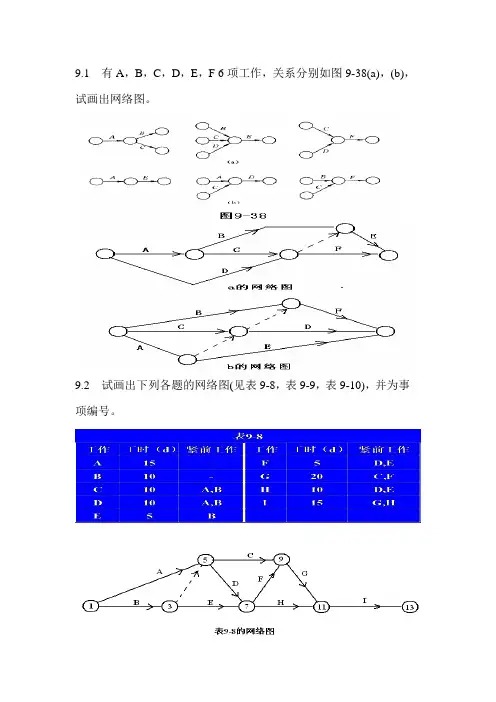
9.1 有A，B，C，D，E，F 6项工作，关系分别如图9-38(a)，(b)，试画出网络图。

9.2 试画出下列各题的网络图(见表9-8，表9-9，表9-10)，并为事项编号。

9.3 设有如图9-39，图9-40网络图，用图上计算法计算时间参数，并求出关键路线。

9.4 绘制表9-11，表9-12所示的网络图，并用表上计算法计算工作的各项时间参数、确定关键路线。

9.5 某工程资料如表9-13所示。

要求：(1)画出网络图。

(2)求出每件工作工时的期望值和方差。

(3)求出工程完工期的期望值和方差。

(4)计算工程期望完工期提前3天的概率和推迟5天的概率。

解：每件工作的期望工时和方差见表9-13的左部。

工程完工期的期望值为32个月，方差为5（1+1+1+1+1）。

工程期望完工期提前3天的概率为0.09，推迟5天的概率为0.987。

9.6 对图9-41所示网络，各项工作旁边的3个数分别为工作的最乐观时间、最可能时间和最悲观时间，确定其关键路线和最早完工时间的概率。

根据关键线路，再考虑到其他线路上的时差很多，可知最早完工时间应该等于关键线路上各个工作最早完工时间之和: 4+2+6+2+3=2=19 。

概率为0.005 。

9.7 某项工程各道工序时间及每天需要的人力资源如图9-42所示。

图中，箭线上的英文字母表示工序代号，括号内数值是该工序总时差，箭线下左边数为工序工时，括号内为该工序每天需要的人力数。

若人力资源限制每天只有15人，求此条件下工期最短的施工方案。

解:最短工期还是15天。

各个工作的开始时间如下图所示：9.8 已知下列网络图有关数据如表9-14，设间接费用为15元／天，求最低成本日程。

解：将①→②缩短两天，总工期为25天，直接费用7420元，间接费用375元，最小总费用为7795元。

网络图和关键线路如下：9.9 一项小修计划包括的工作如表9-15所示。

(1)正常计划工期与最小工期各是多少天?(2)日常经营费为50元／天，最佳工期应是多少天?列出每项工作的相应工时。

排队论习题解10.1某修理店只有一个修理工人, 来修理的顾客到达次数服从普阿松分布,平均每小时3人,修理时间服从负指数分布,平均需10分钟, 求(1) 修理店空闲时间概率; (2) 店内有4个顾客的概率; (3) 店内至少有一个顾客的概率; (4) 在店内顾客平均数; (5) 等待服务的顾客平均数; (6) 在店内平均逗留时间; (7) 平均等待修理(服务)时间;(8) 必须在店内消耗15分钟以上的概率.04440s q s q 60M /M /1//3 6.1031(1)p 1162111(2)p (1)(1)()223211(3)1p 1223(4)L 1()631312(5)L ()632111(6)()633112(7)()636(8)1-F()W W λμρρρλμλρλμλμλρμλω∞∞====-=-==-=-=-=-====--⋅===--===--===--解：该系统为（）模型，，；；；人；人；小时；小时；1515-(6-3)--(-)6020eee .μλω⨯===11(1)(2)(3)23211(4)(5)2211(6)(7)(8)3615.15-20答：修理店空闲时间概率为；店内有三个顾客的概率为；店内至少有一个顾客的概率为；店内顾客平均数为1人；等待服务顾客平均数为人；在店内平均逗留时间分钟；平均等待修理时间为分钟；必须在店内消耗分钟以上的概率为e10.22015(1)(2)(3)(4) 1.25M /M /1.603(/20λ==设有一单人打字室，顾客的到达为普阿松流，平均到达时间间隔为分钟，打字时间服从指数分布，平均时间为分钟，求顾客来打字不必等待的概率；打字室内顾客的平均数；顾客在打字室内平均逗留时间；若顾客在打字室内的平均逗留时间超过小时，则主人将考虑增加设备及打字员，问顾客的平均到达概率为多少时，主人才会考虑这样做？解：该题属模型人小时0s s s 60)4(/).1531(1)p 11443(2)L 3()4311(3)1()431(4)1.2511.25 3.23.230.2(/).4W W μρλμλμλμλλλ===-=-====--===--=>-≥>-=-Q ，人小时；人；小时；；，，人小时1(1)(2)3(3)41(4)0.2/.答：顾客来打字不必等待的概率为；打字室内顾客平均数为人；顾客在打字室内平均逗留时间为小时；平均到达率为人小时时，店主才会考虑增加设备及打字员 10.3 汽车按平均90辆/h 的poission 流到达高速公路上的一个收费关卡，通过关卡的平均时间为38s 。

排队论习题答案排队论习题答案排队论是运筹学中的一个重要分支，研究的是排队系统中的等待时间、服务时间以及系统的稳定性等问题。

在实际生活中，我们经常会遇到排队的情况，比如超市、银行、医院等地方。

那么，如何有效地解决排队问题，减少等待时间呢？下面我将通过几个习题来探讨排队论的解题方法。

习题一：某银行有两个窗口，分别为A窗口和B窗口，顾客到达的时间间隔服从指数分布，平均每10分钟到达一人。

A窗口的服务时间服从均值为5分钟的指数分布，B窗口的服务时间服从均值为7分钟的指数分布。

求顾客平均等待时间和平均逗留时间。

解答一：首先，我们需要计算平均到达率λ和平均服务率μ。

根据题目给出的信息，平均到达率λ=1/10=0.1人/分钟，平均服务率μA=1/5=0.2人/分钟，平均服务率μB=1/7≈0.1429人/分钟。

根据排队论的基本原理，当λ<μ时，系统稳定，顾客平均等待时间为0。

当λ>μ时，系统不稳定，顾客平均等待时间为ρ/(μ-λ)，其中ρ为系统繁忙率。

由于该题目中有两个窗口，所以我们需要计算两个窗口的繁忙率ρA和ρB。

ρA=λ/μA=0.1/0.2=0.5，ρB=λ/μB=0.1/0.1429≈0.7。

由于两个窗口的繁忙率不相等，我们需要使用排队网络的方法来求解。

根据排队网络的基本原理，顾客平均逗留时间等于顾客在每个窗口的平均逗留时间之和。

根据排队网络的公式，顾客在A窗口的平均逗留时间为1/(μA-λ)≈5分钟，顾客在B窗口的平均逗留时间为1/(μB-λ)≈7.5分钟。

所以，顾客平均逗留时间为5+7.5=12.5分钟。

习题二：某医院门诊部有一个窗口，顾客到达的时间间隔服从泊松分布，平均每10分钟到达一人。

窗口的服务时间服从均值为8分钟的指数分布。

求顾客平均等待时间和平均逗留时间。

解答二：同样地，我们需要计算平均到达率λ和平均服务率μ。

根据题目给出的信息，平均到达率λ=1/10=0.1人/分钟，平均服务率μ=1/8=0.125人/分钟。

《运筹学》第六章排队论习题1. 思考题（1）排队论主要研究的问题是什么；（2）试述排队模型的种类及各部分的特征；（3）Kendall 符号C B A Z Y X /////中各字母的分别代表什么意义；（4）理解平均到达率、平均服务率、平均服务时间和顾客到达间隔时间等概念； （5）分别写出普阿松分布、负指数分布、爱尔朗分布的密度函数，说明这些分布的主要性质；（6）试述队长和排队长；等待时间和逗留时间；忙期和闲期等概念及他们之间的联系与区别。

2．判断下列说法是否正确（1）若到达排队系统的顾客为普阿松流，则依次到达的两名顾客之间的间隔时间服从负指数分布；（2）假如到达排队系统的顾客来自两个方面，分别服从普阿松分布，则这两部分顾客合起来的顾客流仍为普阿松分布；（3）若两两顾客依次到达的间隔时间服从负指数分布，又将顾客按到达先后排序，则第1、3、5、7，┉名顾客到达的间隔时间也服从负指数分布； （4）对1//M M 或C M M //的排队系统，服务完毕离开系统的顾客流也为普阿松流； （5）在排队系统中，一般假定对顾客服务时间的分布为负指数分布，这是因为通过对大量实际系统的统计研究，这样的假定比较合理；（6）一个排队系统中，不管顾客到达和服务时间的情况如何，只要运行足够长的时间后，系统将进入稳定状态；（7）排队系统中，顾客等待时间的分布不受排队服务规则的影响；（8）在顾客到达及机构服务时间的分布相同的情况下，对容量有限的排队系统，顾客的平均等待时间少于允许队长无限的系统；（9）在顾客到达分布相同的情况下，顾客的平均等待时间同服务时间分布的方差大小有关，当服务时间分布的方差越大时，顾客的平均等待时间就越长； （10）在机器发生故障的概率及工人修复一台机器的时间分布不变的条件下，由1名工人看管5台机器，或由3名工人联合看管15台机器时，机器因故障等待工人维修的平均时间不变。

3．某店有一个修理工人，顾客到达过程为Poisson 流，平均每小时3人，修理时间服从负指数分布，平均需19分钟，求： （1）店内空闲的时间； （2）有4个顾客的概率； （3）至少有一个顾客的概率； （4）店内顾客的平均数； （5）等待服务的顾客数； （6）平均等待修理的时间；（7）一个顾客在店内逗留时间超过15分钟的概率。

习题五[5-1] 设某地铁站口顾客流是泊松流，每小时平均有120人乘车，求在1分钟内无人乘车，有1、2、3、4人乘车的概率，1分钟内有超过1人乘车的概率。

[5-2] 设货车按泊松流到达车站，平均每天到达2辆，装卸货物时间服从负指数分布，平均每天可装卸3车。

求每辆货车在车站平均停留时间，平均有多少车在排队等待装卸。

[5-3] 设某个售票点只有一个窗口，顾客到达服从泊松分布，平均每分钟到达1人，窗口售票时间服从负指数分布，平均每分钟可服务2人。

求系统平稳状态下的平均队长、平均等待队长、平均等待时间、顾客逗留时间、顾客不等待的概率以及等待队长超过5人时的概率。

[5-4] 某超市的顾客按泊松流到达，平均每小时12人，收款台收费时间服从负指数分布，平均每位顾客需要4分钟。

求该超市的效益指标。

[5-5] 设某产品是生产过程中需要的，若进货过多，会造成保管费增加，若存货不足会影响生产，因此需要找到合理的库存量S ，使得库存费用与缺货损失的总和最小。

设对这种产品的需求量是泊松分布，参数为λ，生产这种产品的时间服从负指数分布，参数为μ。

库存一件该产品单位时间费用为C ，缺少一个该产品造成损失H ，求最优库存S 。

[5-6] 设某单位需要购置计算机，一种方案是购置一台大型计算机，一种方案是购置n 台微型计算机，每台微型计算机是大型计算机处理能力的1/n 。

设要求上机的题目是参数为λ的泊松流，大型与微型计算机计算题目时间是服从负指数分布，大型计算机的参数为μ，试从平均逗留时间、平均等待时间分析，选择哪种方案合适。

[5-7] 设某信访部门的接待人员每天工作10小时，来访人员的到来和接待时间都是随机的，每天平均有90人到来，接待的平均速率为10人/小时。

求排队等待的平均人数，等待接待的人多于2人的概率，若要使等待的人平均为2人，接待的速率应提高多少？[5-8] 设[0,t )内到达的顾客服从泊松分布，参数为λ。

只有单个服务员、服务时间为负指数分布，平均服务时间为1/μ。

通用版六年级奥数专项精品讲义及常考易错题汇编计数问题-排队论问题【知识点归纳】1．排队论问题解决方法：要使等候时间最短，应该从等候时间较少的事情做起．2．举例说明：四（1）班的3个同学各拿一只水桶去接水，水龙头给3只桶注满水所需的时间分别是4分钟、3分钟、1分钟，现在只有1个水龙头可以接水，怎样安排能使他们总的等候时间最短？这个最短的时间是多少？【常考题型】例1：小朋友排队做早操，无论从左数还是从右手笑笑都排在第5位，这排小朋友有（）人．A、8B、9C、10D、11分析：无论从左数还是从右手笑笑都排在第5位，说明笑笑的左右各有4个人，再加上她自己一共有4×2+1=9人，据此解答．解：（5-1）×2+1，=4×2+1，=9（人）；答：这排小朋友有9人．故选：B点评：本题关键是理解“笑笑都排在第5位”的意思是：她的左右各有4个人，注意：求这一排的总人数时不要忘了加上她自己．一．选择题1．同学们排队领书，小明前面有3人，后面有4人．一共有几人排队？() A．7人B．9人C．8人2．小朋友排队，从前数，小小是第4个人，从后数，她是第3个人，这一队共有() A．5人B．6人C．7人D．8人3．40个小朋友排队，笑笑前面有7人，后边有()人。

A．32B．23C．334．同学们排队做操从前面数小明是第5个，从后面数小明是第8个，这一列共有()人．A．12B．13C．145．24个小朋友站在一起，从左数笑笑排第10，从右数淘气排第8，笑笑和淘气中间有( )人．A．5B．7C．66．小朋友排队，从前往后数，红红排在第8个，从后往前数，红红排在第10个，这队共有( )人．A．18B．17C．197．一排小动物共有20只，从左往右数大象排第16，从右往左数小猫排第18，大象和小猫之间相隔()只动物．A．1B．2C．11D．128．小芳排队去大食堂打饭，她发现从前往后数，自己排第7，倒数也是第7，这个队伍一共有()A．14人B．15人C．13人二．填空题9．小朋友们排队做操，小明前面有6个人，后面有5个人，这一排一共有人10．28位小朋友排成一行，从左边开始数第10位是小雨，从右边开始数他是第位。

排队论例1题目：某火车站的售票处设有一个窗口,若购票者是以最简单流到达,平均每分钟到达1人,假定售票时间服从负指数分布,平均每分钟可服务2人,试研究售票窗口前排队情况解:由题设λ=1(人/分),μ=2(人/分),ρ=λμ=12平均队长L=1ρρ-=1(人)平均等待队长Lq=21ρρ-=12(人)平均等待时间Wq=λμμ（-1）=12(分)平均逗留时间W=1μλ-=1(分)顾客不需要等待的概率为P o=12,等待的顾客人数超过5人的概率为P(N≥6)=1766666111111()(1)()()()()222222n n nnn n n nPρ-∞∞∞∞=====-===∑∑∑∑1例2题目：在某工地卸货台装卸设备的设计方案中,有三个方案可供选择,分别记作甲、乙、丙。

目的是选取使总费用最小的方案，有关费用（损失）如下表所示设货车按最简单流到达，平均每天（按10小时计算）到达15车，每车平均装货500袋，卸货时间服从负指数分布，每辆车停留1小时的损失为10元。

解：平均到达率λ=1.5车/小时,服务率μ依赖于方案μ甲=1000/500/袋小时袋车=2车/小时μ乙=2000/500/袋小时袋车=4车/小时μ丙=6000/500/袋小时袋车=12车/小时由(7.2.6),1辆车在系统内平均停留时间为W甲=12-1.5=2(小时/车)W乙=14-1.5=0.4(小时/车)W丙=112-1.5=0.095(小时/车)每天货车在系统停留的平均损失费为W⨯10⨯15,每天的实际可变费用(如燃料费等)为(可变操作费/天)⨯设备忙的概率=c p(元/天)而ρ甲=0.75 , ρ乙=0.375 , ρ丙=0.125,所以每个方案的费用综合如下表所示:23例3 题目：要购置计算机,有两种方案.甲方案是购进一大型计算机,乙方案是购置n 台小型计算机.每台小型计算机是大型计算机处理能力的1n设要求上机的题目是参数为λ的最简单流,大型计算机与小型计算机计算题目的时间是负指数分布,大型计算机的参数是μ.试从平均逗留时间、等待时间看，应该选择哪一个方案 解：设ρ=λμ，按甲方案，购大型计算机 平均等待时间 q W 甲=ρμρ（1-）=λμμλ（-）平均逗留时间 W 甲=1μλ- 按乙方案，购n 台小型计算机，每台小计算机的题目到达率为n λ，服务率为nμ, ρ=//n n λμ=λμ平均等待时间 W q 乙=nρμρ（1-）=n ρμρ（1-）=nW q 甲平均逗留时间 W 乙=1n nμλ-=n μλ-=nW 甲所以只是从平均等待时间，平均逗留时间考虑，应该购置大型计算机4例4题目：设船到码头，在港口停留单位时间损失c 1 元，进港船只是最简单流，参数为λ，装卸时间服从参数为μ的负指数分布，服务费用为c μ2，c 2是一个正常数.求使整个系统总费用损失最小的服务率μ 解:因为平均队长L λμλ=-,所以船在港口停留的损失费为1c λμλ-,服务费为c μ1,因此总费用为 1c F c λμμλ=+-2 求μ使F 达到最小,先求F 的导数12()c dF c d λμμλ=-+-2 让dF d μ=0,解出2μλ=因为 22F u μμ*=∂∂=22()c λμλ*-1>0 (μ>λ) 最优服务率是μ*,当μμ*=时, 12()[c F c c λμλ*=+5例5题目：一个理发店只有一个理发师,有3个空椅供等待理发的人使用,设顾客以最简单流来到,平均每小时5人,理发师的理发时间服从负指数分布,平均每小时6人.试求L ,q L ,W ,q W解:λ=5(人/小时) , μ=5(人/小时) , k =4 , 56ρ= 用公式(7.2.10),(7.2.11),(7.2.12),(7.2.13)得到565555[16()5()]666 1.9715[1()]66L -+==- 5555(1)[16()]66 1.97 1.2251()6q L -=+=- 55555()[1()]660.101()6P -==- 5(1)z LLW P λλ==-=1.9750.9=0.438(小时)0.271qq zL W λ==(小时)6例6题目：给定一个//1/M M k 系统,具有λ=10(人/小时), μ=30（人/小时），k =2.管理者想改进服务机构.方案甲是增加等待空间,使k =3.方案乙是将平均服务率提高到μ=40(人/小时),设服务每个顾客的平均收益不变,问哪个方案获得更大收益,当λ增加到每小时30人,又将有什么结果?解:由于服务每个顾客的平均收益不变,因此服务机构单位时间的收益与单位时间内实际进入系统的平均人数k n 成正比(注意,不考虑成本)!(1)(1)1k k k k n p λρλρ+-=-=- 方案甲:k=3, λ=10, μ=3033411()310[]11()3n -=-=9.75 方案乙: k=2, λ=10, μ=40223110(1())311()4n -=-=9.5 因此扩大等待空间收益更大 当λ增加到30人/小时时,λρμ==1.这时方案甲有3330()31n =+=22.5(人/小时) 而方案乙是把μ提高到μ=40人/小时. λρμ==3040<1, k=2 2233(1())430[]31()4n -=-=22.7(人/小时) 所以当λ=30人/小时时,提高服务效益的收益比扩大等待空间的收益大7例7题目：一个大型露天矿山,考虑建设矿山卸矿场,是建一个好呢?还是建两个好.估计矿车按最简单流到达,平均每小时到达15辆,卸车时间也服从负指数分布,平均卸车时间是3分钟,每辆卡车售价8万元,建设第二个卸矿场需要投资14万元解:平均到达率 λ=15(辆/小时) 平均服务率 μ=20(辆/小时) 只建一个卸矿场的情况:1ρρ==1520=0.75 在卸矿场停留的平均矿车数0,,,,,,q q q q p p L L W W λμL λμλ=-=152015-=3(辆)建两个卸矿场的情况:ρ=0.75,2μ=2λμ=0.375 2101220[10.75(0.75)]0.452!22015P -=++=- 220.451520(0.75)0.750.120.750.871!(22015)L +=+=+=-因此建两个卸矿场可减少在卸矿场停留的矿车数为:3-0.87=2.13辆.就是相当于平均增加2.13辆矿车运矿石.而每辆卡车的价格为8万元,所以相当于增加2.13⨯8=17.04万元的设备,建第二个卸矿场的投资为14万元,所以建两个卸矿场是合适的.8例8题目：有一个///M M c ∞系统,假定每个顾客在系统停留单位时间的损失费用为c 1元,每个服务设备单位时间的单位服务率成本为c 2元.要求建立几个服务台才能使系统单位时间平均总损失费用最小解:单位时间平均损失费为F c L c c μ=+12要求使F 达到最小的正整数解c *,通常用边际分析法:找正整数c *,使其满足{()(1)()(1)F c F c F c F c ****≤+≤-由()(1)F c F c **≤+,得到122()(1)(1)c L c c c c L c c c μμ****+≤+++所以 21()(1)c L c L c c μ**-+≤ 同样,由()(1)F c F c **≤-得到21(1)()c L c L c c μ**--≥因此c *必须满足不等式21()(1)c L c L c c μ**-+≤≤(1)()L c L c **-- 取c =1,2,…,计算()L c 与(1)L c +之差,若21c c μ落在()(1)L c L c **-+,(1)()L c L c **--之间,c *就是最优解9例9题目：某公司中心实验室为各工厂服务,设做实验的人数按最简单流到来.平均每天48(人次/天),1c =6(元).作实验时间服从负指数分布,平均服务率为μ=25(人次/天),2c =4(元),求最优实验设备c *,使系统总费用为最小. 解:λ= 48(人次/天)，μ=25(人次/天)，λμ＝1.92 按///M M c ∞计算0P ,()L c 等(注意以下公式只对0 1.92cρ=<1成立). 201100(1.92)(1.92)[]!(1)!( 1.92)n P n c c ρ--==+--∑12(1.92)() 1.92(1)!( 1.92)c L c P c c +=+-- 将计算结果列成下表21c c μ=1006=16.67 所以取c *=3,总费用最小10例10题目：设有2个工人看管5台自动机,组成//2/5/5M M 系统,λ=1(次/运转小时),μ=4(次/小时),求平均停止运转机器数L 、平均等待修理数q L 以及每次出故障的平均停止运转时间W 、平均等待修理时间q W解：14λμ=，18c λμ=由（7.3.1）,(7.3.2)有 0P =0.3149 1P =0.391 2P =0.197 由（7.3.3）,(7.3.4)有 q L =0.118,L =1.094,c λ=3.906 由（7.3.5）,(7.3.6)有W =0.28(小时),q W =0.03(小时)实际上,这些数量指标有表可查例11题目：设某厂有自动车床若干台,各台的质量是相同的,连续运转时间服从负指数分布,参数为λ,工人的技术也差不多,排除故障的时间服从负指数分布,参数为μ.设λμ=0.1,有两个方案.方案一:3个工人独立地各自看管6台机器.方案二,3个工人共同看管20台机器,试比较两个方案的优劣解:方案一.因为是分别看管,可以各自独立分析,是3个//1/6M M 系统.由上面的公式可求出01P -=0.5155,c =0.5155, a =5.155Lq =0.3295, L =0.845,(1)q =0.4845,(1)r =0.0549方案二.m =20,c =3,λμ=0.1,可求得c =1.787,a =17.87,q L =0.339 L =2.126,(3)q =0.4042,(3)r =0.01695机器损失系数,修理工人损失系数都小于方案一,所以方案二较好11例12题目：某露天铁矿山,按设计配备12辆卡车参加运输作业(每辆载重160吨,售价72万元),备用车8辆,要求保证同时有12辆车参加运输的概率不低于0.995.设每辆平均连续运输时间为3个月,服从负指数分布.有两个修理队负责修理工作,修理时间服从负指数分布.平均修复时间为5天.问这个设计是否合理.解:由假设知,这是////M M c m N m +系统,m =12,1λ=3,1μ=6(月)c =2我们有m c λμ=0.3333,c μλ=36用c N ≤的公式,求N ,要求00.995Nn n p =≥∑设N =2,有Nnn p=∑=0.9474,当N =3时,有Nnn p=∑=0.9968.所以3辆备用车就能达到要求,原设计用的备用车太多当N =3时,卡车的利用律(2)q =0.793712例13题目：假定例2.1中工人的到达服从泊松分布，λ=8人/小时，试分别计算1h 内到达4，5，6，…，12个工人的概率。

《运筹学》第六章排队论习题1. 思考题（1）排队论主要研究的问题是什么；（2）试述排队模型的种类及各部分的特征；（3）Kendall 符号C B A Z Y X /////中各字母的分别代表什么意义；（4）理解平均到达率、平均服务率、平均服务时间和顾客到达间隔时间等概念； （5）分别写出普阿松分布、负指数分布、爱尔朗分布的密度函数，说明这些分布的主要性质；（6）试述队长和排队长；等待时间和逗留时间；忙期和闲期等概念及他们之间的联系与区别。

2．判断下列说法是否正确（1）若到达排队系统的顾客为普阿松流，则依次到达的两名顾客之间的间隔时间服从负指数分布；（2）假如到达排队系统的顾客来自两个方面，分别服从普阿松分布，则这两部分顾客合起来的顾客流仍为普阿松分布；（3）若两两顾客依次到达的间隔时间服从负指数分布，又将顾客按到达先后排序，则第1、3、5、7，┉名顾客到达的间隔时间也服从负指数分布； （4）对1//M M 或C M M //的排队系统，服务完毕离开系统的顾客流也为普阿松流； （5）在排队系统中，一般假定对顾客服务时间的分布为负指数分布，这是因为通过对大量实际系统的统计研究，这样的假定比较合理；（6）一个排队系统中，不管顾客到达和服务时间的情况如何，只要运行足够长的时间后，系统将进入稳定状态；（7）排队系统中，顾客等待时间的分布不受排队服务规则的影响；（8）在顾客到达及机构服务时间的分布相同的情况下，对容量有限的排队系统，顾客的平均等待时间少于允许队长无限的系统；（9）在顾客到达分布相同的情况下，顾客的平均等待时间同服务时间分布的方差大小有关，当服务时间分布的方差越大时，顾客的平均等待时间就越长； （10）在机器发生故障的概率及工人修复一台机器的时间分布不变的条件下，由1名工人看管5台机器，或由3名工人联合看管15台机器时，机器因故障等待工人维修的平均时间不变。

3．某店有一个修理工人，顾客到达过程为Poisson 流，平均每小时3人，修理时间服从负指数分布，平均需19分钟，求： （1）店内空闲的时间； （2）有4个顾客的概率； （3）至少有一个顾客的概率； （4）店内顾客的平均数； （5）等待服务的顾客数； （6）平均等待修理的时间；（7）一个顾客在店内逗留时间超过15分钟的概率。

排队论习题解10.1某修理店只有一个修理工人, 来修理的顾客到达次数服从普阿松分布,平均每小时3人,修理时间服从负指数分布,平均需10分钟, 求(1) 修理店空闲时间概率; (2) 店内有4个顾客的概率; (3) 店内至少有一个顾客的概率; (4) 在店内顾客平均数; (5) 等待服务的顾客平均数; (6) 在店内平均逗留时间; (7) 平均等待修理(服务)时间;(8) 必须在店内消耗15分钟以上的概率.04440s q s q 60M /M /1//3 6.1031(1)p 1162111(2)p (1)(1)()223211(3)1p 1223(4)L 1()631312(5)L ()632111(6)()633112(7)()636(8)1-F()W W λμρρρλμλρλμλμλρμλω∞∞====-=-==-=-=-=-====--⋅===--===--===--解：该系统为（）模型，，；；；人；人；小时；小时；1515-(6-3)--(-)6020eee .μλω⨯===11(1)(2)(3)23211(4)(5)2211(6)(7)(8)3615.15-20答：修理店空闲时间概率为；店内有三个顾客的概率为；店内至少有一个顾客的概率为；店内顾客平均数为1人；等待服务顾客平均数为人；在店内平均逗留时间分钟；平均等待修理时间为分钟；必须在店内消耗分钟以上的概率为e10.22015(1)(2)(3)(4) 1.25M /M /1.603(/20λ==设有一单人打字室，顾客的到达为普阿松流，平均到达时间间隔为分钟，打字时间服从指数分布，平均时间为分钟，求顾客来打字不必等待的概率；打字室内顾客的平均数；顾客在打字室内平均逗留时间；若顾客在打字室内的平均逗留时间超过小时，则主人将考虑增加设备及打字员，问顾客的平均到达概率为多少时，主人才会考虑这样做？解：该题属模型人小时0s s s 60)4(/).1531(1)p 11443(2)L 3()4311(3)1()431(4)1.2511.25 3.23.230.2(/).4W W μρλμλμλμλλλ===-=-====--===--=>-≥>-=-Q ，人小时；人；小时；；，，人小时1(1)(2)3(3)41(4)0.2/.答：顾客来打字不必等待的概率为；打字室内顾客平均数为人；顾客在打字室内平均逗留时间为小时；平均到达率为人小时时，店主才会考虑增加设备及打字员 10.3 汽车按平均90辆/h 的poission 流到达高速公路上的一个收费关卡，通过关卡的平均时间为38s 。