搜索剪枝(魔方为例)

剪枝技术的技巧
剪枝技术是在搜索算法中用来减少搜索空间以提高效率的一种技术。

以下是一些常见的剪枝技巧：
1. 回溯剪枝：当进行回溯搜索时，可以通过判断当前搜索路径是否符合要求，如果不符合则可以提前终止当前路径的搜索，从而减少不必要的搜索。

2. 前向剪枝：在搜索过程中，可以通过一些策略来判断一些分支是否有必要继续搜索下去。

比如，通过估计某个分支的上下界来判断该分支是否可能包含最优解，如果不包含则可以直接剪掉该分支，从而减少搜索空间。

3. 对称剪枝：当问题存在对称性质时，可以利用对称性质来减少搜索空间。

比如，棋盘游戏中，如果对称的局面是等价的，则可以只搜索其中一部分的局面，然后利用对称性质进行复制和旋转，得到其他等价的局面。

4. 剪枝函数的设计：在问题中，可以通过设计剪枝函数来减少搜索空间。

剪枝函数可以根据问题的特性和要求来判断某个搜索节点下的子节点是否需要继续搜索。

比如，在搜索字典树的时候，可以使用剪枝函数判断某个前缀是否是合法的单词，如果不是则可以剪掉该分支。

5. 启发式搜索：启发式搜索是一种基于问题特性和经验的搜索技术，可以通过估计搜索节点的优劣程度来决定搜索优先级。

在搜索过程中，可以通过选择优先
级高的节点来先进行搜索，从而提高效率。

比如，在迷宫问题中，可以通过估计每个节点到目标点的距离来进行搜索，选择距离最短的节点先进行搜索。

这些技巧可以根据具体的问题和算法进行灵活运用，以提高搜索效率。

参数空间剪枝
剪枝是一种常见的技术手段，用于减少参数空间的大小，从而提高算法的效率和性能。

参数空间剪枝可以应用于各种领域，包括机器学习、优化算法等。

在机器学习中，参数空间剪枝可以用于减少模型的复杂度，提高训练速度和泛化能力。

在训练模型时，通常需要搜索一定的参数空间，以找到最优的参数组合。

然而，参数空间往往非常庞大，搜索起来非常耗时。

因此，剪枝技术可以用来缩小参数空间，减少搜索的时间和计算量。

在优化算法中，参数空间剪枝可以用于减少搜索空间，加速求解过程。

优化问题通常可以转化为在参数空间中搜索最优解的问题。

然而，参数空间往往非常庞大，搜索起来非常困难。

因此，剪枝技术可以用来减少搜索空间，提高求解效率。

剪枝技术有很多种方法，包括基于规则的剪枝、基于启发式的剪枝、基于模型的剪枝等。

基于规则的剪枝方法通常通过定义一些规则，来剪除一些不符合规则的参数组合。

基于启发式的剪枝方法通常通过一些启发式的方法，来剪除一些不可能是最优解的参数组合。

基于模型的剪枝方法通常通过训练一个模型，来预测哪些参数组合是不可能是最优解的。

在实际应用中，剪枝技术能够显著提高算法的效率和性能。

通过剪
枝，可以减少搜索的时间和计算量，从而加快求解过程。

同时，剪枝还可以减少模型的复杂度，提高模型的泛化能力。

因此，参数空间剪枝是一种非常有用的技术手段，值得在各种应用中广泛使用。

12图1 魔方底层架十字可以无师自通，只是我们这一步要复原的四个棱块的相对位置顺序要注意，由于我们以白色中心块做底层，按照我们现在的主流魔方的贴纸的帖法（上黄下白，前蓝后緑，左橙右红），如果我们先复原了白蓝这个棱块，那我们在保持白色中心块在底部的情况下，白红的棱块就一点要放在白蓝棱块的右边，白橙棱块放在白蓝棱块的左边，白緑棱块放在白蓝棱块的对面，由于魔方的中心块不会发生变化，所以在复原的过程中，我们是以中心块为参照物的，第一步我们在复原白蓝、白红、白绿、白橙这四个棱块的时候，我们可以先把白色面旋转到顶层，和黄色中心块同一个平面，然后再把他对应的另一个颜色（蓝或红或緑或橙）经过旋转最上层，使之和对应的中心块的颜色同色，这样我们再旋转180度，对应的棱块就正确复原到底部了。

注意：图101的情况是没有正确归位的情况，需要调整白蓝和白红两个棱块的位置，才是正确的完成了底棱归位图101第二步：底角归位（复原魔方第一层四个角块）图2 魔方的四个底角正确归位以后一定会出现倒T字型，如图2所示，如果不是这样肯定是底面角块没有正确归位（位置错了，重新来过）。

底角归位也可无师自通，有兴致的朋友可以自己琢磨一些技巧和完成这一步。

有难度的朋友可参考我下面介绍的一种技巧来完成，我们先看图2-1和图2-2，首先我们先确定目标块的位置是在他要正确归位的正上面的位置，然后我们再看白色的面朝向何方，就很快的能快速判断出来是下图几种情况中的哪一种了。

复原基本思想：先将目标角块调至顶层侧面，再转动能与之相连形成顺色整体的面，使目标角与底棱连成一个(1×1×2)的归位整体，再转至正确的位置。

因此，下列的五个实例并没有必要当成公式来死记。

3图2-1 图2-2 公式2-1：（R U R'）公式2-2：（F'U'F）记忆技巧：白色朝右，第一步就旋转右层记忆技巧：白色朝前，第一步就旋转前层图201 图202 图203 用两次公式2-1 用两次公式2-2 用三次公式2-1（R U R'） U' （R U R'）（F'U'F）U （F'U'F）（R U R'）（R U R'） U' （R U R'）第三步：中棱归位（复原魔方中层四个棱块的步骤）4图3 魔方中间层共有四个棱块，也只是四个棱块需要复原（注意中间层没有角块哟），图3-1和图3-2是两个比较常见的情形，我们主要介绍的就是这两种情况的复原方法，仔细分析比较这两个公式，步骤虽然有点多，可是很好记忆哟。

魔方速解法-桥式桥式魔方，又称北桥魔方，源自于美国小伍德斯托克特 (Woodstock) 县一位古典魔方高手 Peter Comier 所发明，它以其独特又神秘的外形，迅速赢得了魔友们的喜爱，在很短的时间里即成为独特的收藏品及拼图玩具。

桥式魔方的样式特点主要为特殊的立体桥形状，组合出六面立体的三维魔方，且不仅具有旋转的空间维度，橫向亦有移动的特色，它所具有的特殊复杂的几何设计，更加将魔方推向极致，是玩家们需要重新梳理六面立体桥魔方进行速解的不二之选，其所承载的独特文化更是吸引众多爱好玩家的喜爱，成为当下数字魔方领域迷人的存在。

桥式魔方的解法和其它魔方的解法一样，也可以采用通用的式法来完成。

第一步，把桥式魔方展开，方便熟悉桥体的形状，包括桥头（mouth）、桥面（face）以及桥的两侧（right side and left side），亦可熟悉魔方解法的基本概念（cross、f2l、oll、pll）；第二步，整体不动的情况下，根据特定的步骤方法摆放每个角块（corner cube）以及正中心块（edge cube），只能够旋转每一层所对应的魔方，而不能够勾动任何隔离的块，完成角块和正中央块的装订；第三步，在每一层魔方大致形成正确形状以后，便可将其与中心块（center cube）旋转搭配在正确摆立；最后一步，在保持每一层魔方不动的基础下，使用一系列的套路连结六面的魔方，完成六面立体桥魔方的速解，完成难度较高，但也在可接受范围内的解题流程。

通过上述步骤，理解桥式魔方六面立体解法，桥式魔方可以在不分层次提取每个旋转块具体位置的前提下，完成六面立体整合，而解法上非常类似普通的三维立体魔方，只需要简单熟悉特殊部件的空间结构，即可完成桥式魔方的立体速解。

桥式魔方在速解上较普通的魔方突显出自己的独特性，这正因为桥的整体结构，使其表现出一种让用户更容易完成速解的多面模型，而解法上也需要一定的反复观察，才能完成一个完美的立体桥结构，追求完美解题是玩家们需要努力探寻的答案，并在更多时间内完成魔方的速解，通过这样的精细解题，可以最大程度的强化习得熟练的解题技能，在有趣的魔方游戏中，赢之未敢忘。

魔方的解法（初學者）魔方的解法很多，主要分為2個類別：層先歸位（逐層完成）及角塊先歸位（先完成角位）；以這2個方法為基礎，發展出很多不同的解法。

而現在所用的快速解法是以層先歸位的方法。

這個方法：● 先在其中一面做1個“十”字，完成第1層 ● 然後再做第2層 ● 最後做第3層這是個初階的方法，要記熟幾個步驟。

若能熟練的話，可以在60秒以內完成。

有些人甚至可以在20-30秒內完成。

但初學者不用太介懷時間，只要掌握步驟就可以，並加以練習，就可以熟練，然後再學其他高級的方法。

這個方法除了不用記太多步驟外，還有其他好處，是容易知道自己在哪兒出錯。

若你想學習更多高級的解法的話，就可以再多記其他步驟，成為魔方的高級專家。

魔方的經構三階魔方共有27棱塊（3 x 3 x 3）；有6個中心點、8個角塊、12條棱邊。

中心點可以在自己的軸上自由轉動，而角和棱邊可以繞著中心點轉動。

術語要了解以後所述的魔方解法，先行了解簡單的術語。

魔方有6面：前（F ）、後（B ）、上（U ）、下（D ）、左（L ）、右（R ）。

魔方還有2個主要術語：棱塊、角塊。

注意下列要點：● 1個英文字母代表要把該面順時針方向轉動 ● 1個英文字母上加上小撇（’），代表要逆時針方向轉動 ● 若在英文字母後加上2，代表要轉180°● 括號代表要把有關步驟組合成一組，方便學習較長的步驟例如：RU ’L2這個步驟代表要把右面往順時針方向轉90°，然後上層往逆時針方向轉90°，最後左面順時針方向轉180°。

下後上 右上 左 棱塊 角塊解法第1層要使第1層歸位，有2個階段： ● 先做出“十”字（解決棱塊） ● 使角塊歸位緊記：每塊棱塊和角塊在不同面上的顏色都不同，這個就是代表不同的棱塊和角塊其實是有特定位置。

首先做“十”字解法的第1步是先要使上層轉出1個白色“十”字，使棱塊都是白色向上。

第1步要做出“十”字，要因應不同情況而轉動魔方，使棱塊轉到X 的位置。

剪枝搜索法求解选择问题1.问题的描述选择问题：给定n个元素，要求确定其中的第k小元素。

解决该问题的一种方法是先将n 个元素排序，然后从有序序列中确定第k小元素。

因为排序算法的时间复杂度是O(nlogn)，所以这也决定了该方法在最坏情况下的时间复杂度是O(nlogn)。

应用剪枝搜索策略可以在线性时间内解决选择问题(select problem)。

2.通过剪枝搜索法求解选择问题的算法思想确定不包含第k小元素的那部分元素，在每次迭代时将该部分剪除。

要得到O(n)时间的算法，必须在每次迭代时用O(n)时间剪去部分元素。

令S表示输入数据集合，p为S中某元素。

可以把S分成S1、S2和S3三个子集，其中S1中包含所有小于p的元素，S2中包含所有等于p的元素，S3中包含所有大于p的元素。

如果S1集合中的元素个数大于k,那么可以确定S的第k小元素就在S1中，并且在接下来的迭代中可以剪去S2和S3; 否则，如果S1和S2元素个数之和大于k,那么p就是S的第k小元素;如果上面情况均不满足，那么S的第k小元素必大于p。

这样，可以丢弃S1和S2，在下次迭代时，重新开始从S3中找出第(k−|S1|−|S2|)小元素。

关键点是如何选择p，使在每--次迭代时都能丢弃S的一部分，不管该部分是S1、S2还是S3。

可以按如下方法选择p:首先，将n个元素分成每5个元素形成一个集合的[n/5]个子集。

如果需要，可以在最后的子集中加入虚拟元素∞。

然后，对每个5元素子集排序，从每个子集中选出中位数形成新序列M={m1,m2,…,muisp},并令p为M中位数。

如图1所示，S中至少有1/4元素小于或等于p，至少1/4的元素大于或等于p。

这样，如果按照这种方法选择p，那么在每次迭代时总能剪去S中至少n/4的元素。

图 13.算法描述输入元素个数后，使其索引从0开始，那么第k小的元素就是把所有数组元素从小到大排序后索引在k−1位置上的元素。

Partition函数：将给定的数组元素根据第一个元素进行划分。

應用Freemat軟件---結合剪枝法解出六角幻方的答案何耀堂劉冠靈一、前言由1910年至1962，共花了52年時間，通過不斷嘗試，終於找出二階六角幻方(圖3)的答案；在1969年滑鐵盧大學二年級學生阿萊爾對特裡格的結論作了簡單而又巧妙的證明[2]，他又把六角幻方的可能選擇輸入電子計算機測試，結果用了17秒時間，得出了與阿當斯完全相同的結果。

由此可見利用適當的條件，結合計算機的力量，節省不少時間，因此本文嘗試用這個角度來進行，本文主要介紹六角幻方怎樣用窮舉法，結合適當的數學條件(剪枝法)，通過FreeMath計算出它的唯一解。

二、六角幻方------建模過程每條直線上的數字之和相等。

如圖，橫行有5行，故每一直線的數字之和是190538÷=。

因每一直線的數字之和是38，結合圖(1a)，則滿足以下十五條條件為﹕38A B C ++= …………(1) 38C G L ++= …………(2) 38L P S ++= …………(3) 38S R Q ++= …………(4) 38Q M H ++= (5)38H D A ++=…………(6) 38D E F G +++=…………(7) 38D I N R +++=…………(8) 38G K O R +++= …………(9) 38B E I M +++= …………(10) 38B F K P +++=…………(11) 38M N O P +++= (12)38A E J O S ++++= …………(13) 38C F J N Q ++++=…………(14) 38H I J K L ++++= (15)如右圖，如果得知E 、F 、K 、O 、N 、I 的數值，便能計算出B 、G 、P 、R 、M 、D 和J 的數值。

由(7)(8)(9)+-得238D E F I N K O ++++--=整理得[]138()()()2D E F I N K O =-+-+++ (16)同理可得[]138()()()2G E F K O I N =-+-+++ …………(17) []138()()()2R IN K O E F =-+-+++ (18)[]138()()()2B E I F K N O =-+-+++ …………(19) []138()()()2M EI N O F K =-+-+++ …………(20) []138()()()2P FK N O E I =-+-+++ (21)已知E 、F 、K 、O 、N 、I ，計算J 的步驟比較複雜，如下﹕ 由(13)得 38()()J E O A S =-+-+ …………(*)由(1)(3)(2)+-得 38()A S B P G +=-++ …………(**) 由(11)得 38()B P F K +=-+ 代入(**)得 ()A S F K G +=++ 代入(*)得38()()J E O F K G=-+-++ 以(17)的G 值代入上式得 []138()()38()()()2J E O F K E FK OI N =-+-+--+-+++整理得119()2J E F K O N I =-+++++ (22)因為在J 的圓圈中只能填入1-19，所以119J ≤≤，故由(22)得0()36E F K O N I ≤+++++≤ (23)三、六角幻方------利用計算機過程我們會用開源軟件freemat 幫助篩選出合適的答案，首先找出要符合條件的E 、F 、K 、O 、N 、I 的所有組合，從19個取6個數的組合數為61927132C =(種)利用條件(23)和根據(22)計算出J 的值，因J 必須為整數的條件篩選後，剩下78種組合(經過運行test_step1.m 代碼運算所得，需時約39秒)。

下面我们举一个例子——Betsy 的旅行(USACO)。

题目简述：一个正方形的小镇被分成N 2个小方格，Betsy 要从左上角的方格到达左下角的方格，并且经过每个方格恰好一次。

编程对于给定的N ，计算出Betsy 能采用的所有的旅行路线的数目。

实际上，由于Betsy 的每一次移动，只会影响到附近的格子，所以每次执行剪枝判断时，应当只对她附近的格子进行检查：对于第一个剪枝条件，我们可以设一个整型标志数组，分别保存与每个格子相邻的没被经过的格子的数目，Betsy 每次移动到一个新位置，都只会使与之相邻的至多4个格子的标志值发生变化，只要检查它们的标志值即可。

而对于第二个剪枝条件，处理就稍稍麻烦一些。

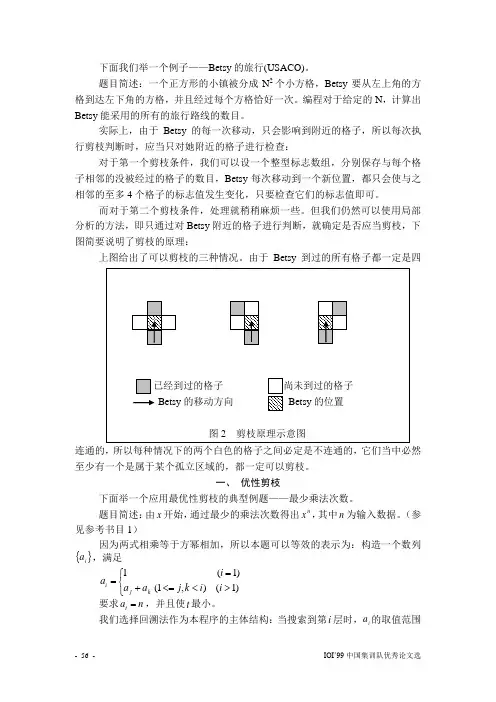
但我们仍然可以使用局部分析的方法，即只通过对Betsy 附近的格子进行判断，就确定是否应当剪枝，下图简要说明了剪枝的原理：上图给出了可以剪枝的三种情况。

由于Betsy 到过的所有格子都一定是四连通的，所以每种情况下的两个白色的格子之间必定是不连通的，它们当中必然至少有一个是属于某个孤立区域的，都一定可以剪枝。

一、 优性剪枝下面举一个应用最优性剪枝的典型例题——最少乘法次数。

题目简述：由x 开始，通过最少的乘法次数得出n x ，其中n 为输入数据。

（参见参考书目1）因为两式相乘等于方幂相加，所以本题可以等效的表示为：构造一个数列{}i a ，满足⎩⎨⎧><<=+==)1(),1()1(1i i k j a a i a k ji 要求n a t =，并且使t 最小。

我们选择回溯法作为本程序的主体结构：当搜索到第i 层时，i a 的取值范围搜索中的剪枝优化在11+-i a 到2*1-i a 之间，为了尽快接近目标n ，应当从2*1-i a 开始从大到小为i a 取值，当然，选取的数都不能大于n 。

当搜索到n 出现时，就得到了一个解，与当前保存的解比较取优。

最终搜索结束之后，即得到最终的最优解。

DFS（四）：剪枝策略顾名思义，剪枝就是通过⼀些判断，剪掉搜索树上不必要的⼦树。

在采⽤DFS算法搜索时，有时候我们会发现某个结点对应的⼦树的状态都不是我们要的结果，这时候我们没必要对这个分⽀进⾏搜索，砍掉这个⼦树，就是剪枝。

在DFS搜索算法中，剪枝策略就是寻找过滤条件，提前减少不必要的搜索路径。

应⽤剪枝策略的核⼼问题是设计剪枝判断⽅法，即确定哪些枝条应当舍弃，哪些枝条应当保留的⽅法。

剪枝策略按照其判断思路可⼤致分成两类：可⾏性剪枝及最优性剪枝。

1.可⾏性剪枝可⾏性剪枝就是把能够想到的不可能出现的情况给它剪掉。

该⽅法判断继续搜索能否得出答案，如果不能直接回溯。

【例1】Sum It Up （POJ 1564）DescriptionGiven a specified total t and a list of n integers, find all distinct sums using numbers from the list that add up to t. For example, if t = 4, n = 6, and the list is [4, 3, 2, 2, 1, 1], then there are four different sums that equal 4: 4, 3+1, 2+2, and 2+1+1. (A number can be used within a sum as many times as it appears in the list, and a single number counts as a sum.) Your job is to solve this problem in general.InputThe input will contain one or more test cases, one per line. Each test case contains t, the total, followed by n, the number of integers in the list, followed by n integers x 1 , . . . , x n . If n = 0 it signals the end of the input; otherwise, t will be a positive integer less than 1000, n will be an integer between 1 and 12 (inclusive), and x 1 , . . . , x n will be positive integers less than 100. All numbers will be separated by exactly one space. The numbers in each list appear in nonincreasing order, and there may be repetitions.OutputFor each test case, first output a line containing `Sums of', the total, and a colon. Then output each sum, one per line; if there are no sums, output the line `NONE'. The numbers within each sum must appear in nonincreasing order. A number may be repeated in the sum as many times as it was repeated in the original list. The sums themselves must be sorted in decreasing order based on the numbers appearing in the sum. In other words, the sums must be sorted by their first number; sums with the same first number must be sorted by their second number; sums with the same first two numbers must be sorted by their third number; and so on. Within each test case, all sums must be distinct; the same sum cannot appear twice.Sample Input4 6 4 3 2 2 1 15 3 2 1 1400 12 50 50 50 50 50 50 25 25 25 25 25 250 0Sample OutputSums of 4:43+12+22+1+1Sums of 5:NONESums of 400:50+50+50+50+50+50+25+25+25+2550+50+50+50+50+25+25+25+25+25+25（1）编程思路。

算法笔记--极⼤极⼩搜索及alpha-beta剪枝极⼩极⼤搜索算法即minimax搜索算法主要应⽤于零和博弈（⾮胜即负，如围棋，象棋，井⼦棋等），完全信息（玩家知道之前所有的步骤。

象棋就是完全信息，因为玩家是交替着落⼦，且之前的步骤都能在棋盘上体现）这个算法采⽤搜索算法递归实现，⼀层为先⼿，记为a, ⼀层为后⼿，记为b, 交替出现对于最终局⾯，有⼀个分数（⽐如：先⼿胜分数为1，平局分数为0，先⼿输分数为-1）先⼿a想要让这个分数越⼤越好，后⼿b想要让这个分数越⼩越好，于是搜索到先⼿这⼀层，取最⼤返回，搜索到后⼿这⼀层，取最⼩返回如下图：于是伪代码为：int MaxMin(position,int d){int bestvalue,value;if(game over) //检查游戏是否结束return evaluation(p);// 游戏结束，返回估值if(depth<=0) //检查是否是叶⼦节点return evaluation(p);//叶⼦节点，返回估值if(max) //极⼤值点bestvalue=-INFINTY;else//极⼩值点bestvalue=INFINTY;for(each possibly move m){MakeMove(m); //⾛棋value=MaxMin(p,d-1);UnMakeMove(m); //恢复当前局⾯if(max)bestvalue=max(value,bestvalue);//取最⼤值elsebestvalue=min(value,bestvalue);//取最⼩值}return bestvalue;}关于alpha-beta剪枝：如果当前层为取最⼩，如果取最⼩后⽐上⼀层当前最⼤值还⼩，则不需要往下搜索，因为上⼀层根本不会选择当前节点往下搜，还有更好的选择同理，如果当前层为取最⼤，如果取最⼤后⽐上⼀层当前最⼩值还⼤，则不需要往下搜索，因为上⼀层根本不会选择当前节点往下搜具体推荐看最上⾯的知乎链接点赞最多的回答。

魔方全解(比较简单的几种解法)LT三阶魔方一、魔方构造1．魔方共六个面，每个面有一种颜色，若以红面为正面，绿面为底面，则橙面为背面，蓝面为顶面，白面为左面，黄面为右面。

2．三阶魔方由3×3×3=27块小正方体构成，其中一块在内部，没有颜色；6块只有一种颜色，叫做中心块；12块有两种颜色，叫做边块；8块有三种颜色，叫做角块。

3．只要魔方任意三块小正方体连成一线，就能旋转。

4．三阶魔方中心块的位置不会改变。

5．魔方还原的前提是有一个被转乱的魔方。

二、转向表示为了方便表示魔方的转向，使用以下字母。

（箭头所指为前面）1．一层旋转F （Front ） 中心块边块F 将魔方前面一层顺时针旋转90度。

Fi 将魔方前面一层逆时针旋转90度。

B （Back ）B 将魔方后面一层顺时针旋转90度。

Bi 将魔方后面一层逆时针旋转90度。

L （Left ）L 将魔方左面一层顺时针旋转90度。

Li 将魔方左面一层逆时针旋转90度。

R （Right ）R 将魔方右面一层顺时针旋转90度。

Ri 将魔方右面一层逆时针旋转90度。

U （Up ）U 将魔方上面一层顺时针旋转90度。

Ui 将魔方上面一层逆时针旋转90度。

D （Down ）D 将魔方下面一层顺时针旋转90度。

Di 将魔方下面一层逆时针旋转90度。

2．中间层旋转F Fi B BiL Li R Ri U Ui D Di·通常，单个字母表示顺时针旋转，加i或ˊ表示逆时针旋转。

·双写转向或在转向后加2表示在这个方向上旋转180度。

·()×n表示重复括号内的步骤n次。

三、魔方还原1．一面（一层）还原1）还原一面边块①选择好一种颜色的中间块作为要还原的一面，将其作为前面，记住它的背面中间块颜色。

②先恢复一个色块，以这个色块为准，旋转前面使上、下、左、右四面中心块正位。

③旋转后面一层或第二层使其出现下面情况，逐个恢复色块，直到前面形成十字。

魔方指法练习FSC关于魔方指法练习(FSC)FSC：finger shortcut“手指捷径”，指魔方速度还原中的基本手法。

就是利用手指头来转动方块，减少换手所产生的时间，以往我们都是用手腕来转动方块，在换方向时，我们习惯把手拿起来换位置，这时已经造成时间的浪费了，玩方块若以「速度」为目标的话，那么FSC就为必要的一项技能。

基本用法然后我们作「U'」，这时就是用左手的食指来推方块。

当我们作「U」时，则是用右手食指来推方块。

以上为最基本的用法，其实FSC的变化非常的多，需要靠每个人自己去探索，找出自己顺的手法，更进阶的还会有「大拇指的FSC」，或是变换角度然后左右手同时用...等等。

(R U R') U用右手食指推(R' U' R) U'用左食指推(R' U R') 三步全用右食指一气呵成(R U' R') U'用左食指推(R U' R) 三步全用右大拇指一气呵成(R' U2) 第一手R'和第二手U2中的一半用右食指。

第二手剩下来的用右中指。

(R U2') 第一手R'和第二手U2'中的一半U'用右大拇指。

第二手剩下来的U'用左食指。

(R2 U') 全用右大拇指一气呵成。

(R' F' R) (F' R)用右大拇指一气呵成。

(R' F R F') (R F' )用右大拇指一气呵成。

(U U' u u' U2 U2' u2 u2') U、U'等系列是魔术方块极为重要的手法。

平常多转U、U'等系列来练习吧。

(R U R' U')*6(R U' R' U )*6(R' F R F')*6下面是详解3阶魔方手法要点如果你有一个国甲之类的专业型魔方，你就可以做到高手录像中用手指拨动魔方的动作，以下为3阶魔方手法中的要点。

DFS剪枝经典例题包括「木棍加工」和「最小矩形覆盖」等。

「木棍加工」问题描述：给定一个长度为n的数组，表示n根木棍的长度。

现在需要将这些木棍加工成一些小段，要求每个小段的长度都相同，并且这些小段的数量要尽可能多。

求这些小段的最大可能长度。

这个问题可以使用DFS搜索+剪枝来解决。

具体做法是先对木棍长度进行排序，然后从大到小枚举每个长度作为小段的可能长度，使用DFS搜索来检查是否能够将所有木棍切割成这个长度的小段。

在DFS搜索的过程中，可以使用一些剪枝技巧来提前结束搜索，例如：如果当前搜索到的木棍长度已经大于剩余未搜索的木棍的总长度，那么就可以直接返回false。

「最小矩形覆盖」问题描述：给定一个平面上的n个点，求一个最小的矩形，使得这n个点都在矩形内部或者矩形的边上。

这个问题也可以使用DFS搜索+剪枝来解决。

具体做法是先枚举矩形的两个相对顶点，然后使用DFS搜索来找到另外两个顶点。

在DFS搜索的过程中，可以使用一些剪枝技巧来提前结束搜索，例如：如果当前搜索到的两个点构成的线段已经包含了所有点，那么就可以直接计算矩形的面积并更新答案。

以上两个例子都是DFS搜索+剪枝的经典应用，可以帮助理解DFS剪枝的思路和技巧。