第二章 课后作业参考答案

第二章劳动合同与社会保险法律制度（课后作业）一、单项选择题1.根据劳动合同法律制度的规定，下列选项中，不属于劳动者与用人单位签订劳动合同时应遵循的原则的是（）。

A.平等自愿原则B.诚实信用原则C.从属原则D.协商一致原则2.根据劳动合同法律制度的规定，除文艺、体育和特种工艺单位录用的人员外，用人单位招用的劳动者须年满（）周岁。

A.10B.12C.16D.183.甲公司招聘了5名服务人员，在签订劳动合同时要求该5名聘用人员每人缴纳500元的服装押金。

劳动行政部门发现甲公司这一违法行为后对其进行了处罚，下列处罚措施中，不符合规定的是（）。

A.责令限期向5名劳动者每人退还收取的500元押金B.处以总额为2000元的罚款C.处以总额为2500元的罚款D.处以总额为10000元的罚款4.2014年3月1日，钱某开始在P公司工作（全日制用工），3月10日，P公司书面通知钱某签订劳动合同，但是钱某拒绝签订。

3月20日，P公司通知钱某终止劳动关系。

根据劳动合同法律制度的规定，下列表述正确的是（）。

A.P公司无需向钱某支付经济补偿B.P公司可以口头通知钱某终止劳动关系C.P公司可以与钱某不签订书面劳动合同而订立口头协议D.P公司可以拒绝向钱某支付其实际工作时间的劳动报酬5.根据劳动合同法律制度的规定，关于无效劳动合同法律后果，下列表述不正确的是（）。

A.无效劳动合同，从订立时起就没有法律效力B.劳动合同部分无效的，不影响其他部分的效力，其他部分仍然有效C.对劳动合同的无效或者部分无效有争议的，只能由劳动争议仲裁机构确认D.劳动合同被确认无效，劳动者已付出劳动的，用人单位应当向劳动者支付劳动报酬6.根据劳动合同法律制度的规定，因特殊原因需要延长工作时间的，在保障劳动者身体健康的条件下延长工作时间，除有特殊情况外，每日不得超过（）小时，每月不得超过（）小时。

A.1小时 36小时B.1小时 40小时C.3小时 36小时D.3小时 40小时7.周某为R公司职工，月工资1800元，当地月最低工资标准为1600元。

高分子化学第二章课后作业（共100分）1、简述逐步聚合的实施方法。

（10分）答案：2、影响线形缩聚物聚合度的因素有哪些？两单体非等化学计量，如何控制聚合度？（10分）备注：影响线形缩聚物聚合度中的第四个因素（反应条件）未回答的也可以给予满分。

另外批改时注意两单体非等化学计量的公式（应该有部分写成两单体等化学计量公式）3、己二酸与下列化合物反应，哪些能形成聚合物并说明原因。

（10分）A.乙醇B.乙二醇C.甘油D.苯胺E.己二胺答案：己二酸（f=2）为2官能度单体，因此能与己二酸形成聚合物的化合物有：乙二醇（f=2）、甘油（f=3）、己二胺（f=2）。

其中与乙二醇（f=2）、己二胺（f=2）形成线形缩聚物，与甘油（f=3）形成体形缩聚物。

答案解释：4、聚酯化和聚酰胺化的平衡常数有何差别？对缩聚条件有何影响？（10分）答案：(1)聚酯化反应平衡常数小，K=4，低分子副产物水的存在限制了聚合物分子量的提高，对聚合反应的条件要求较高，反应须在高温和高真空条件下进行，体系中水的残留量应尽量低，这样才能得到高聚合度的聚合物。

（2）聚酰胺化反应平衡常数中等，K=300-400,水对分子量有所影响，对聚合反应的条件要求相对温和。

聚合早期，可在水介质中进行；聚合后期，须在一定的减压条件下脱水，提高反应程度。

5、分别按Carothers法和Flory统计法计算下列混合物的凝胶点：（10分）（1）邻苯二甲酸酐和甘油按照摩尔比为1.5:0.98进行缩聚（2）邻苯二甲酸酐、甘油、乙二醇按照摩尔比为1.5:0.99:0.002进行缩聚答案：（1）Carothers法：邻苯二甲酸酐（f=2）官能度为2，甘油（f=3）官能度为3，邻苯二甲酸酐和甘油按照摩尔比为1.5：0.98进行缩聚的情况下，属于两基团不相等平均官能度=（2*3*0.98）/(1.5+0.98)=2.371，凝胶点=2/2.371=0.844Flory统计法：由题可知甘油（f=3）官能度为3，则支化单元分率ρ=1，基团比r=（0.98*3）/ (1.5*2)=0.98,f=3则凝胶点=1/[0.98+0.98*1*(3-2)]1/2=0.714（2）Carothers法：邻苯二甲酸酐（f=2）官能度为2，甘油（f=3）官能度为3，乙二醇（f=2）官能度为2，邻苯二甲酸酐、甘油、乙二醇按照摩尔比为1.5:0.99:0.002进行缩聚的情况下，属于两基团不相等平均官能度=2*（0.99*3+0.002*2）/(1.5+0.99+0.002)=2.387，凝胶点=2/2.387=0.838Flory统计法：由题可知甘油（f=3）官能度为3，则支化单元分率ρ=0.99*3/(0.99*3+0.002*2) =0.999，基团比r=（0.99*3+0.002*2）/(1.5*2)=0.991,f=3则凝胶点=1/[0.991+0.991*0.999*(3-2)]1/2=0.71解题思路：（1）首先判断该体系是属于两基团数相等还是两基团数不等；（2）Carothers法：根据体系的类型选择合适的公式计算出平均官能度，进而计算出凝胶点；（3）Flory统计法：根据体系的类型，得到官能度f为多少（此处注意与平均官能度不是一个概念，官能度f为多官能度单体的官能度），选择合适的公式计算出支化单元分率、基团比，进而计算出凝胶点。

第二章新民主主义革命理论1、什么是新民主主义革命的总路线？如何理解新民主主义革命的领导权问题？(1)1948年，毛泽东在《晋绥干部会议上的讲话》中完整地表述了新民主主义革命总路线的内容，即无产阶级领导的，人民大众的，反对帝国主义、封建主义和官僚资本主义的革命。

新民主主义的政治、经济、文化纲领是新民主主义革命总路线的展开和具体化，指明了新民主主义革命的发展方向。

中国革命必须走农村包围城市、武装夺取政权的革命道路。

新民主主义革命的总路线指明了革命的目的、对象、动力、领导力量以及革命的性质和前途。

具体内容如下：①新民主主义革命的目的新民主主义革命的目的是推翻买办的封建的生产关系以及腐朽的政治上层建筑,从根本上解放被束缚的生产力。

②新民主主义革命的对象近代中国社会的性质和主要矛盾，决定了中国革命的主要敌人就是帝国主义、封建主义和官僚资本主义。

帝国主义是中国革命的首要对象，是中国社会进步和发展的最大障碍，是近代中国贫困落后和一切灾难祸害的总根源。

封建地主阶级是帝国主义统治中国和封建军阀实行专制统治的社会基础,是中国经济现代化和政治民主化的主要障碍。

官僚资本主义是依靠帝国主义、勾结封建势力、利用国家政权力量而发展起来的买办的封建的国家垄断资本主义。

官僚资本主义对广大劳动人民的残酷剥削和对民族工商业的巧取豪夺，严重地束缚了中国社会生产力的发展，因此也是中国革命的对象。

③新民主主义革命的动力新民主主义革命的动力包括无产阶级、农民阶级、城市小资产阶级和民族资产阶级。

无产阶级是中国革命最基本的动力。

中国无产阶级是新的社会生产力的代表,是近代中国最进步的阶级，是中国革命的领导力量。

农民是中国革命的主力军，其中的贫农是无产阶级最可靠的同盟军，而中农是无产阶级可靠的同盟军。

城市小资产阶级是无产阶级的可靠同盟者。

民族资产阶级也是中国革命的动力之一。

④新民主主义革命的领导力量无产阶级的领导权是中国革命的中心问题，也是新民主主义革命理论的核心问题。

第二章 流体静力学2-1 密闭容器测压管液面高于容器内液面h=1.8m,液体密度为850kg/m3, 求液面压强。

解：08509.8 1.814994Pa p gh ρ==⨯⨯=2-2 密闭水箱，压力表测得压强为4900Pa,压力表中心比A 点高0.4米，A 点在液面下1.5m ，液面压强。

解：0()490010009.8(0.4 1.5) 49009800 1.15880PaM B A p p g h h ρ=+-=+⨯⨯-=-⨯=-2-3 水箱形状如图，底部有4个支座。

试求底面上的总压力和四个支座的支座反力，并讨论总压力和支座反力不相等的原因。

解：底面上总压力（内力，与容器内的反作用力平衡）()10009.81333352.8KN P ghA ρ==⨯⨯+⨯⨯=支座反力支座反力（合外力）3312()10009.8(31)274.4KN G g V V ρ=+=⨯⨯+=2-4盛满水的容器顶口装有活塞A ，直径d=0.4m ，容器底直径D=1.0m ，高h=1.8m 。

如活塞上加力为2520N(包括活塞自重)。

求容器底的压强和总压力。

解：压强2252010009.8 1.837.7kPa (0.4)/4G p gh A ρπ=+=+⨯⨯= 总压力 237.71/429.6KN P p A π=⋅=⨯⋅=2-5多管水银测压计用来测水箱中的表面压强。

图中高程单位为m ，试求水面的绝对压强。

解：对1-1等压面02(3.0 1.4)(2.5 1.4)p g p g ρρ+-=+-汞对3-3等压面 2(2.5 1.2)(2.3 1.2)a p g p g ρρ+-=+-汞将两式相加后整理0(2.3 1.2)(2.5 1.4)(2.5 1.2)(3.0 1.4)264.8kPap g g g g ρρρρ=-+-----=汞汞绝对压强 0.0264.8+98=362.8kPa abs a p p p =+=2-6水管A 、B 两点高差h 1=0.2m ，U 形管压差计中水银液面高差h 2=0.2m 。

有机化学课后习题答案第⼆章2章思考题2.1 分析共轭效应和超共轭效应的异同点，重点阐述σ-π和p-π共轭。

2.2 请举例说明同分异构体中各种异构体的定义及其异同点。

2.3解释甲烷氯化反应中观察到的现象：（1）（1）甲烷和氯⽓的混合物于室温下在⿊暗中可以长期保存⽽不起反应。

（2）（2）将氯⽓先⽤光照射，然后迅速在⿊暗中与甲烷混合，可以得到氯化产物。

（3）（3）将氯⽓⽤光照射后在⿊暗中放⼀段时期,再与甲烷混合，不发⽣氯化反应。

（4）（4）将甲烷先⽤光照射后，在⿊暗中与氯⽓混合，不发⽣氯化反应。

（5）（5）甲烷和氯⽓在光照下起反应时，每吸收⼀个光⼦产⽣许多氯化甲烷分⼦。

2.4 3-氯-1,2-⼆溴丙烷是⼀种杀根瘤线⾍的农药，试问⽤什么原料，怎样合成？2.5 写出烯烃C5H10的所有同分异构体，命名之，并指出哪些有顺反异构体。

2.6 找出下列化合物的对称中⼼.(1)⼄烷的交叉式构象(2)丁烷的反交叉式构象(3)反-1,4-⼆甲基环已烷(椅式构象)(4)写出1,2,3,4,5,6-六氯环已烷有对称中⼼的异构体的构象式(椅式)。

2.7 ⼀个化合物的氯仿溶液的旋光度为+10o, 如果把溶液稀释⼀倍, 其旋光度是多少? 如化合物的旋光度为-350o, 溶液稀释⼀倍后旋光度是多少?2.8 ⼄烯、丙烯、异丁烯在酸催化下与⽔加成，⽣成的活性中间体分别为、、，其稳定性＞＞, 所以反应速度是＞＞。

解答2.1 答：在离域体系中，键长趋于平均化，体系能量降低⽽使分⼦稳定性增加。

共轭体所表现出来的这种效应叫共轭效应。

共轭体系分为π-π共轭体系和p-π共轭体系。

超共轭效应是当C—H键与相邻的π键处于能重叠位置时，C—H键的轨道与π轨道也有⼀定程度的重叠，发⽣电⼦的离域现象，此时，键向π键提供电⼦，使体系稳定性提⾼。

它分为-p 和-π超共轭。

超共轭效应⽐共轭效应⼩。

异构现象异同点举例构造异构分了中原互相联结的⽅式和次序不同1. 碳链异构碳链不同2. 位置异构取代基在碳链或环上的位置不同3.官能团异构官能团不同⽴体异构分⼦中原⼦在空间2.3 答：（1）⽆引发剂⾃由基产⽣（2）光照射，产⽣Cl·，氯⾃由基⾮常活泼与甲烷⽴即反应。

第二章课后习题答案第二章牛顿定律2-1如图(a)所示,质量为m的物体用平行于斜面的细线联结置于光滑的斜面上,若斜面向左方作加速运动,当物体刚脱离斜面时,它的加速度的大小为()(A)ginθ(B)gcoθ(C)gtanθ(D)gcotθ分析与解当物体离开斜面瞬间,斜面对物体的支持力消失为零,物体在绳子拉力FＴ(其方向仍可认为平行于斜面)和重力作用下产生平行水平面向左的加速度a,如图(b)所示,由其可解得合外力为mgcotθ,故选(D)．求解的关键是正确分析物体刚离开斜面瞬间的物体受力情况和状态特征．2-2用水平力FN把一个物体压着靠在粗糙的竖直墙面上保持静止．当FN逐渐增大时,物体所受的静摩擦力Ff的大小()(A)不为零,但保持不变(B)随FN成正比地增大(C)开始随FN增大,达到某一最大值后,就保持不变(D)无法确定分析与解与滑动摩擦力不同的是,静摩擦力可在零与最大值μFN范围内取值．当FN增加时,静摩擦力可取的最大值成正比增加,但具体大小则取决于被作用物体的运动状态．由题意知,物体一直保持静止状态,故静摩擦力与重力大小相等,方向相反,并保持不变,故选(A)．2-3一段路面水平的公路,转弯处轨道半径为R,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率()μgR(B)必须等于μgR(C)不得大于μgR(D)还应由汽车的质量m决定(A)不得小于分析与解由题意知,汽车应在水平面内作匀速率圆周运动,为保证汽车转弯时不侧向打滑,所需向心力只能由路面与轮胎间的静摩擦力提供,能够提供的最大向心力应为μFN．由此可算得汽车转弯的最大速率应为v＝μRg．因此只要汽车转弯时的实际速率不大于此值,均能保证不侧向打滑．应选(C)．2-4一物体沿固定圆弧形光滑轨道由静止下滑,在下滑过程中,则()(A)它的加速度方向永远指向圆心,其速率保持不变(B)它受到的轨道的作用力的大小不断增加(C)它受到的合外力大小变化,方向永远指向圆心(D)它受到的合外力大小不变,其速率不断增加分析与解由图可知,物体在下滑过程中受到大小和方向不变的重力以及时刻指向圆轨道中心的轨道支持力FN作用,其合外力方向并非指向圆心,其大小和方向均与物体所在位置有关．重力的切向分量(mgcoθ)使物体的速率将会不断增加(由机械能守恒亦可判断),则物体作圆周运动的向心力(又称法向力)将不断增大,由轨道法向方向上的动力学方程v2FNmginθm可判断,随θ角的不断增大过程,轨道支持力FN也将不R断增大,由此可见应选(B)．2-5图(a)示系统置于以a＝1/4g的加速度上升的升降机内,A、B两物体质量相同均为m,A所在的桌面是水平的,绳子和定滑轮质量均不计,若忽略滑轮轴上和桌面上的摩擦,并不计空气阻力,则绳中张力为()(A)58mg(B)12mg(C)mg(D)2mg分析与解本题可考虑对A、B两物体加上惯性力后,以电梯这个非惯性参考系进行求解．此时A、B两物体受力情况如图(b)所示,图中a′为A、B两物体相对电梯的加速度,ma′为惯性力．对A、B两物体应用牛顿第二定律,可解得FＴ＝5/8mg．故选(A)．讨论对于习题2-5这种类型的物理问题,往往从非惯性参考系(本题为电梯)观察到的运动图像较为明确,但由于牛顿定律只适用于惯性参考系,故从非惯性参考系求解力学问题时,必须对物体加上一个虚拟的惯性力．如以地面为惯性参考系求解,则两物体的加速度aA和aB均应对地而言,本题中aA和aB的大小与方向均不相同．其中aA应斜向上．对aA、aB、a和a′之间还要用到相对运动规律,求解过程较繁．有兴趣的读者不妨自己尝试一下．2-6图示一斜面,倾角为α,底边AB长为l＝2.1m,质量为m的物体从题2-6图斜面顶端由静止开始向下滑动,斜面的摩擦因数为μ＝0.14．试问,当α为何值时,物体在斜面上下滑的时间最短？其数值为多少？解取沿斜面为坐标轴O某,原点O位于斜面顶点,则由牛顿第二定律有mginαmgμcoαma(1)又物体在斜面上作匀变速直线运动,故有l11at2ginαμcoαt2coα22则t2l(2)gcoαinαμcoα为使下滑的时间最短,可令dt0,由式(2)有dαinαinαμcoαcoαcoαμinα0则可得tan2α1o,49μ此时t2l0.99gcoαinαμcoα2-7工地上有一吊车,将甲、乙两块混凝土预制板吊起送至高空．甲块质量为m1＝2.00某102kg,乙块质量为m2＝1.00某102kg．设吊车、框架和钢丝绳的质量不计．试求下述两种情况下,钢丝绳所受的张力以及乙块对甲块的作用力：(1)两物块以10.0m·ｓ-2的加速度上升；(2)两物块以1.0m·ｓ-2的加速度上升．从本题的结果,你能体会到起吊重物时必须缓慢加速的道理吗？解按题意,可分别取吊车(含甲、乙)和乙作为隔离体,画示力图,并取竖直向上为Oy轴正方向(如图所示)．当框架以加速度a上升时,有FＴ-(m1＋m2)g＝(m1＋m2)a(1)FN2-m2g＝m2a(2)解上述方程,得FＴ＝(m1＋m2)(g＋a)(3)FN2＝m2(g＋a)(4)(1)当整个装置以加速度a＝10m·ｓ-2上升时,由式(3)可得绳所受张力的值为FＴ＝5.94某103N乙对甲的作用力为F′N2＝-FN2＝-m2(g＋a)＝-1.98某103N(2)当整个装置以加速度a＝1m·ｓ-2上升时,得绳张力的值为FＴ＝3.24某103N此时,乙对甲的作用力则为F′N2＝-1.08某103N由上述计算可见,在起吊相同重量的物体时,由于起吊加速度不同,绳中所受张力也不同,加速度大,绳中张力也大．因此,起吊重物时必须缓慢加速,以确保起吊过程的安全．2-8如图(a)所示,已知两物体A、B的质量均为m＝3.0kg物体A以加速度a＝1.0m·ｓ-2运动,求物体B与桌面间的摩擦力．(滑轮与连接绳的质量不计)分析该题为连接体问题,同样可用隔离体法求解．分析时应注意到绳中张力大小处处相等是有条件的,即必须在绳的质量和伸长可忽略、滑轮与绳之间的摩擦不计的前提下成立．同时也要注意到张力方向是不同的．解分别对物体和滑轮作受力分析［图(b)］．由牛顿定律分别对物体A、B及滑轮列动力学方程,有mAg-FＴ＝mAa(1)F′Ｔ1-Fｆ＝mBa′(2)F′Ｔ-2FＴ1＝0(3)考虑到mA＝mB＝m,FＴ＝F′Ｔ,FＴ1＝F′Ｔ1,a′＝2a,可联立解得物体与桌面的摩擦力Ffmgm4ma7.2N2讨论动力学问题的一般解题步骤可分为：(1)分析题意,确定研究对象,分析受力,选定坐标；(2)根据物理的定理和定律列出原始方程组；(3)解方程组,得出文字结果；(4)核对量纲,再代入数据,计算出结果来．2-9质量为m′的长平板A以速度v′在光滑平面上作直线运动,现将质量为m的木块B轻轻平稳地放在长平板上,板与木块之间的动摩擦因数为μ,求木块在长平板上滑行多远才能与板取得共同速度？分析当木块B平稳地轻轻放至运动着的平板A上时,木块的初速度可视为零,由于它与平板之间速度的差异而存在滑动摩擦力,该力将改变它们的运动状态．根据牛顿定律可得到它们各自相对地面的加速度．换以平板为参考系来分析,此时,木块以初速度-v′(与平板运动速率大小相等、方向相反)作匀减速运动,其加速度为相对加速度,按运动学公式即可解得．该题也可应用第三章所讲述的系统的动能定理来解．将平板与木块作为系统,该系统的动能由平板原有的动能变为木块和平板一起运动的动能,而它们的共同速度可根据动量定理求得．又因为系统内只有摩擦力作功,根据系统的动能定理,摩擦力的功应等于系统动能的增量．木块相对平板移动的距离即可求出．解1以地面为参考系,在摩擦力Fｆ＝μmg的作用下,根据牛顿定律分别对木块、平板列出动力学方程Fｆ＝μmg＝ma1F′ｆ＝-Fｆ＝m′a2a1和a2分别是木块和木板相对地面参考系的加速度．若以木板为参考系,木块相对平板的加速度a＝a1＋a2,木块相对平板以初速度-v′作匀减速运动直至最终停止．由运动学规律有-v′2＝2a由上述各式可得木块相对于平板所移动的距离为mv22μgmm解2以木块和平板为系统,它们之间一对摩擦力作的总功为W＝Fｆ(＋l)-Fｆl＝μmg式中l为平板相对地面移动的距离．由于系统在水平方向上不受外力,当木块放至平板上时,根据动量守恒定律,有m′v′＝(m′＋m)v″由系统的动能定理,有μmg由上述各式可得11mv2mmv222mv22μgmm2-10如图(a)所示,在一只半径为R的半球形碗内,有一粒质量为m的小钢球,当小球以角速度ω在水平面内沿碗内壁作匀速圆周运动时,它距碗底有多高？分析维持钢球在水平面内作匀角速度转动时,必须使钢球受到一与向心加速度相对应的力(向心力),而该力是由碗内壁对球的支持力FN的分力来提供的,由于支持力FN始终垂直于碗内壁,所以支持力的大小和方向是随ω而变的．取图示O某y坐标,列出动力学方程,即可求解钢球距碗底的高度．解取钢球为隔离体,其受力分析如图(b)所示．在图示坐标中列动力学方程FNinθmanmRω2inθ(1)Rh(3)且有coθR由上述各式可解得钢球距碗底的高度为hR可见,h随ω的变化而变化．gω22-11火车转弯时需要较大的向心力,如果两条铁轨都在同一水平面内(内轨、外轨等高),这个向心力只能由外轨提供,也就是说外轨会受到车轮对它很大的向外侧压力,这是很危险的．因此,对应于火车的速率及转弯处的曲率半径,必须使外轨适当地高出内轨,称为外轨超高．现有一质量为m的火车,以速率v沿半径为R的圆弧轨道转弯,已知路面倾角为θ,试求：(1)在此条件下,火车速率v0为多大时,才能使车轮对铁轨内外轨的侧压力均为零？(2)如果火车的速率v≠v0,则车轮对铁轨的侧压力为多少？分析如题所述,外轨超高的目的欲使火车转弯的所需向心力仅由轨道支持力的水平分量FNinθ提供(式中θ角为路面倾角)．从而不会对内外轨产生挤压．与其对应的是火车转弯时必须以规定的速率v0行驶．当火车行驶速率v≠v0时,则会产生两种情况：如图所示,如v＞v0时,外轨将会对车轮产生斜向内的侧压力F1,以补偿原向心力的不足,如v＜v0时,则内轨对车轮产生斜向外的侧压力F2,以抵消多余的向心力,无论哪种情况火车都将对外轨或内轨产生挤压．由此可知,铁路部门为什么会在每个铁轨的转弯处规定时速,从而确保行车安全．解(1)以火车为研究对象,建立如图所示坐标系．据分析,由牛顿定律有v2FNinθm(1)解(1)(2)两式可得火车转弯时规定速率为v0gRtanθ(2)当v＞v0时,根据分析有v2FNinθF1coθm(3)RFNcoθF1inθmg0(4)解(3)(4)两式,可得外轨侧压力为v2F1mcoθginθR当v＜v0时,根据分析有v2FNinθF2coθm(5)RFNcoθF2inθmg0(6)解(5)(6)两式,可得内轨侧压力为v2F2mginθcoθR2-12一杂技演员在圆筒形建筑物内表演飞车走壁．设演员和摩托车的总质量为m,圆筒半径为R,演员骑摩托车在直壁上以速率v作匀速圆周螺旋运动,每绕一周上升距离为h,如图所示．求壁对演员和摩托车的作用力．分析杂技演员(连同摩托车)的运动可以看成一个水平面内的匀速率圆周运动和一个竖直向上匀速直线运动的叠加．其旋转一周所形成的旋线轨迹展开后,相当于如图(b)所示的斜面．把演员的运动速度分解为图示的v1和v2两个分量,显然v1是竖直向上作匀速直线运动的分速度,而v2则是绕圆筒壁作水平圆周运动的分速度,其中向心力由筒壁对演员的支持力FN的水平分量FN2提供,而竖直分量FN1则与重力相平衡．如图(c)所示,其中φ角为摩托车与筒壁所夹角．运用牛顿定律即可求得筒壁支持力的大小和方向解设杂技演员连同摩托车整体为研究对象,据(b)(c)两图应有FN1mg0(1)FN2v2m(2)Rv2vcoθv2πR2πR2h2(3)22FNFN1FN2(4)以式(3)代入式(2),得FN2m4π2R2v24π2Rmv222(5)2222R4πRh4πRh将式(1)和式(5)代入式(4),可求出圆筒壁对杂技演员的作用力(即支承力)大小为22FNFN1FN224π2Rv22mg4π2R2h2与壁的夹角φ为FN24π2Rv2arctanarctan222FN14πRhg讨论表演飞车走壁时,演员必须控制好运动速度,行车路线以及摩托车的方位,以确保三者之间满足解题用到的各个力学规律．2-13一质点沿某轴运动,其受力如图所示,设t＝0时,v0＝5m·ｓ-1,某0＝2m,质点质量m＝1kg,试求该质点7ｓ末的速度和位置坐标．分析首先应由题图求得两个时间段的F(t)函数,进而求得相应的加速度函数,运用积分方法求解题目所问,积分时应注意积分上下限的取值应与两时间段相应的时刻相对应．解由题图得0t52t,Ft5t7355t,由牛顿定律可得两时间段质点的加速度分别为a2t,0t5a355t,5t7对0＜t＜5ｓ时间段,由adv得dtvtv00dvadt积分后得v5t再由v2d某得dtd某vdt某00某t积分后得某25tt将t＝5ｓ代入,得v5＝30m·ｓ-1和某5＝68.7m对5ｓ＜t＜7ｓ时间段,用同样方法有133dvv0vt5a2dt得v35t2.5t82.5t再由得某＝17.5t2-0.83t3-82.5t＋147.87将t＝7ｓ代入分别得v7＝40m·ｓ-1和某7＝142m2-14一质量为10kg的质点在力F的作用下沿某轴作直线运动,已知F ＝120t＋40,式中F的单位为N,t的单位的ｓ．在t＝0时,质点位于某＝5.0m处,其速度v0＝6.0m·ｓ-1．求质点在任意时刻的速度和位置．分析这是在变力作用下的动力学问题．由于力是时间的函数,而加速度a＝dv/dt,这时,动力学方程就成为速度对时间的一阶微分方程,解此微分方程可得质点的速度v(t)；由速度的定义v＝d某/dt,用积分的方法可求出质点的位置．解因加速度a＝dv/dt,在直线运动中,根据牛顿运动定律有2某某5d某vdt5t120t40mdvdt依据质点运动的初始条件,即t0＝0时v0＝6.0m·ｓ-1,运用分离变量法对上式积分,得vv0dv12.0t4.0dt0tv＝6.0+4.0t+6.0t2又因v＝d某/dt,并由质点运动的初始条件：t0＝0时某0＝5.0m,对上式分离变量后积分,有d某6.04.0t6.0tdt某t2某00某＝5.0+6.0t+2.0t2+2.0t32-15轻型飞机连同驾驶员总质量为1.0某103kg．飞机以55.0m·ｓ-1的速率在水平跑道上着陆后,驾驶员开始制动,若阻力与时间成正比,比例系数α＝5.0某102N·ｓ-1,空气对飞机升力不计,求：(1)10ｓ后飞机的速率；(2)飞机着陆后10ｓ内滑行的距离．分析飞机连同驾驶员在水平跑道上运动可视为质点作直线运动．其水平方向所受制动力F为变力,且是时间的函数．在求速率和距离时,可根据动力学方程和运动学规律,采用分离变量法求解．解以地面飞机滑行方向为坐标正方向,由牛顿运动定律及初始条件,有dvαtdtvtαtdvv00mdtα2t得vv02mFmam因此,飞机着陆10ｓ后的速率为v＝30m·ｓ-1又tα2d某vdt某0002mt某故飞机着陆后10ｓ内所滑行的距离某某0v0tα3t467m6m2-16质量为m的跳水运动员,从10.0m高台上由静止跳下落入水中．高台距水面距离为h．把跳水运动员视为质点,并略去空气阻力．运动员入水后垂直下沉,水对其阻力为bv2,其中b为一常量．若以水面上一点为坐标原点O,竖直向下为Oy轴,求：(1)运动员在水中的速率v与y的函数关系；(2)如b/m＝0.40m-1,跳水运动员在水中下沉多少距离才能使其速率v减少到落水速率v0的1/10？(假定跳水运动员在水中的浮力与所受的重力大小恰好相等)分析该题可以分为两个过程,入水前是自由落体运动,入水后,物体受重力P、浮力F和水的阻力Fｆ的作用,其合力是一变力,因此,物体作变加速运动．虽然物体的受力分析比较简单,但是,由于变力是速度的函数(在有些问题中变力是时间、位置的函数),对这类问题列出动力学方程并不复杂,但要从它计算出物体运动的位置和速度就比较困难了．通常需要采用积分的方法去解所列出的微分方程．这也成了解题过程中的难点．在解方程的过程中,特别需要注意到积分变量的统一和初始条件的确定．解(1)运动员入水前可视为自由落体运动,故入水时的速度为v02gh运动员入水后,由牛顿定律得P-Fｆ-F＝ma由题意P＝F、Fｆ＝bv2,而a＝dv/dt＝v(dv/dy),代入上式后得-bv2＝mv(dv/dy)考虑到初始条件y0＝0时,v0t2gh,对上式积分,有vdvmdy0v0vbvv0eby/m2gheby/m(2)将已知条件b/m＝0.4m-1,v＝0.1v0代入上式,则得ymvln5.76mbv0某2-17直升飞机的螺旋桨由两个对称的叶片组成．每一叶片的质量m＝136kg,长l＝3.66m．求当它的转速n＝320r/min 时,两个叶片根部的张力．(设叶片是宽度一定、厚度均匀的薄片)分析螺旋桨旋转时,叶片上各点的加速度不同,在其各部分两侧的张力也不同；由于叶片的质量是连续分布的,在求叶片根部的张力时,可选取叶片上一小段,分析其受力,列出动力学方程,然后采用积分的方法求解．解设叶片根部为原点O,沿叶片背离原点O的方向为正向,距原点O为r处的长为dr一小段叶片,其两侧对它的拉力分别为FＴ(r)与FＴ(r＋dr)．叶片转动时,该小段叶片作圆周运动,由牛顿定律有dFTFTrFTrdr由于r＝l时外侧FＴ＝0,所以有m2ωrdrltFTrdFTlrmω2rdrlmω2222πmn222FTrlrlr2ll上式中取r＝0,即得叶片根部的张力FＴ0＝-2.79某105N负号表示张力方向与坐标方向相反．2-18一质量为m的小球最初位于如图(a)所示的A点,然后沿半径为r 的光滑圆轨道ADCB下滑．试求小球到达点C时的角速度和对圆轨道的作用力．分析该题可由牛顿第二定律求解．在取自然坐标的情况下,沿圆弧方向的加速度就是切向加速度aｔ,与其相对应的外力Fｔ是重力的切向分量mginα,而与法向加速度an相对应的外力是支持力FN和重力的法向分量mgcoα．由此,可分别列出切向和法向的动力学方程Fｔ＝mdv/dt和Fn＝man．由于小球在滑动过程中加速度不是恒定的,因此,需应用积分求解,为使运算简便,可转换积分变量．倡该题也能应用以小球、圆弧与地球为系统的机械能守恒定律求解小球的速度和角速度,方法比较简便．但它不能直接给出小球与圆弧表面之间的作用力．解小球在运动过程中受到重力P和圆轨道对它的支持力FN．取图(b)所示的自然坐标系,由牛顿定律得Ftmginαmdv(1)dtmv2FnFNmgcoαm(2)R由vdrdαrdα,得dt,代入式(1),并根据小球从点A运动到点Cdtdtv的始末条件,进行积分,有vv0vdvα90orginαdα得v则小球在点C的角速度为2rgcoαωv2gcoα/rrmv2mgcoα3mgcoα由式(2)得FNmr由此可得小球对圆轨道的作用力为FN3mgcoαFN负号表示F′N与en反向．2-19光滑的水平桌面上放置一半径为R的固定圆环,物体紧贴环的内侧作圆周运动,其摩擦因数为μ,开始时物体的速率为v0,求：(1)t时刻物体的速率；(2)当物体速率从v0减少到12v0时,物体所经历的时间及经过的路程．解(1)设物体质量为m,取图中所示的自然坐标,按牛顿定律,有mv2FNmanRFfmatdvdt由分析中可知,摩擦力的大小Fｆ＝μFN,由上述各式可得v2dvμRdt取初始条件t＝0时v＝v0,并对上式进行积分,有t0dtRvdvμv0v2vRv0Rv0μt(2)当物体的速率从v0减少到1/2v0时,由上式可得所需的时间为t物体在这段时间内所经过的路程Rμv0vdt0tt0Rv0dtRv0μtRln2μ2-20质量为45.0kg的物体,由地面以初速60.0m·ｓ-1竖直向上发射,物体受到空气的阻力为Fr＝kv,且k＝0.03N/(m·ｓ-1)．(1)求物体发射到最大高度所需的时间．(2)最大高度为多少？分析物体在发射过程中,同时受到重力和空气阻力的作用,其合力是速率v的一次函数,动力学方程是速率的一阶微分方程,求解时,只需采用分离变量的数学方法即可．但是,在求解高度时,则必须将时间变量通过速度定义式转换为位置变量后求解,并注意到物体上升至最大高度时,速率应为零．解(1)物体在空中受重力mg和空气阻力Fr＝kv作用而减速．由牛顿定律得mgkvmdv(1)dt某2-25如图(a)所示,电梯相对地面以加速度a竖直向上运动．电梯中有一滑轮固定在电梯顶部,滑轮两侧用轻绳悬挂着质量分别为m1和m2的物体A和B．设滑轮的质量和滑轮与绳索间的摩擦均略去不计．已知m1＞m2,如以加速运动的电梯为参考系,求物体相对地面的加速度和绳的张力．分析如以加速运动的电梯为参考系,则为非惯性系．在非惯性系中应用牛顿定律时必须引入惯性力．在通常受力分析的基础上,加以惯性力后,即可列出牛顿运动方程来．解取如图(b)所示的坐标,以电梯为参考系,分别对物体A、B作受力分析,其中F1＝m1a,F2＝m2a分别为作用在物体A、B上的惯性力．设ar为物体相对电梯的加速度,根据牛顿定律有m1gm1aFT1m1ar(1)m2gm2aFT2m2ar(2)FT2FT2(3)由上述各式可得arm1m2gam1m22m1m2gam1m2FT2FT2由相对加速度的矢量关系,可得物体A、B对地面的加速度值为a1aram1m2g2m2am1m22m1am1m2gm1m2a2araa2的方向向上,a1的方向由ar和a的大小决定．当ar＜a,即m1g-m2g-2m2a＞0时,a1的方向向下；反之,a1的方向向上．某2-26如图(a)所示,在光滑水平面上,放一质量为m′的三棱柱A,它的斜面的倾角为α．现把一质量为m的滑块B放在三棱柱的光滑斜面上．试求：(1)三棱柱相对于地面的加速度；(2)滑块相对于地面的加速度；(3)滑块与三棱柱之间的正压力．分析这类问题可应用牛顿定律并采用隔离体法求解．在解题的过程中必须注意：(1)参考系的选择．由于牛顿定律只适用于惯性系,可选择地面为参考系(惯性系)．因地面和斜面都是光滑的,当滑块在斜面上下滑时,三棱柱受到滑块对它的作用,也将沿地面作加速度为aA的运动,这时,滑块沿斜面的加速度aBA,不再是它相对于地面的加速度aB了．必须注意到它们之间应满足相对加速度的矢量关系,即aB＝aA＋aBA．若以斜面为参考系(非惯性系),用它求解这类含有相对运动的力学问题是较为方便的．但在非惯性系中,若仍要应用牛顿定律,则必须增添一惯性力F,且有F＝maA．(2)坐标系的选择．常取平面直角坐标,并使其中一坐标轴方向与运动方向一致,这样,可使解题简化．(3)在分析滑块与三棱柱之间的正压力时,要考虑运动状态的影响,切勿简单地把它视为滑块重力在垂直于斜面方向的分力mgcoα,事实上只有当aA＝0时,正压力才等于mgcoα．解1取地面为参考系,以滑块B和三棱柱A为研究对象,分别作示力图,如图(b)所示．B受重力P1、A施加的支持力FN1；A受重力P2、B施加的压力FN1′、地面支持力FN2．A的运动方向为O某轴的正向,Oy轴的正向垂直地面向上．设aA为A对地的加速度,aB为B对的地加速度．由牛顿定律得FN1inαmaA(1)FN1inαmaB某(2)FN1coαmgmaBy(3)FN1FN1(4)设B相对A的加速度为aBA,则由题意aB、aBA、aA三者的矢量关系如图(c)所示．据此可得aB某aAaBAcoα(5)aByaBAinα(6)解上述方程组可得三棱柱对地面的加速度为aAmginαcoα2mminαmginαcoαmmin2α滑块相对地面的加速度aB在某、y轴上的分量分别为aB某aBymmgin2αmmin2α则滑块相对地面的加速度aB的大小为aBaa2B某2Bym22mmm2in2αginαmmin2α其方向与y轴负向的夹角为amcotαθarctanB某arctanaBymmA与B之间的正压力FN1mmgcoα2mminα解2若以A为参考系,O某轴沿斜面方向［图(d)］．在非惯性系中运用牛顿定律,则滑块B的动力学方程分别为mginαmaAcoαmaBA(1)mgcoαFN1maAinα0(2)又因FN1inαmaA0(3)FN1FN1(4)由以上各式可解得aAaBAmginαcoαmmin2αmmginαmmin2α由aB、aBA、aA三者的矢量关系可得m22mmm2in2αaBginαmmin2α以aA代入式(3)可得FN1mmgcoαmmin2α。

10 2 10
1R
Rx
r
r
Rx
Rx
7.5 7.5 ......
Rx
r
Rx
1'
3'
2'
(a)
2' (b)
1'
(a-1)
图 2.6
解：（a）设 R 和 r 为 1 级，则图题 2.6(a)为 2 级再加 Rx 。将 22 端 Rx 用始端
11 Rx 替代，则变为 4 级再加 Rx ，如此替代下去，则变为无穷级。从始端11 看等
30
40
30
40
30
40
30
40
R
R
(a 1)
(a 2)
由图(a-1)得：
R (30 40) 35 2
或由图(a-2)得
R 30 40 35 22
(b) 对图(b)电路，将 6Ω和 3Ω并联等效为 2Ω,2Ω和 2Ω并联等效为 1Ω,4Ω 和 4Ω并联等效为 2Ω，得图(b-1)所示等效电路：
Im1 20 Im2 6V m1 41 Im2 9.2V
答案 2.18
解：以节点①为参考点的各节点电压相对以节点④为参考点的节点电压降低了
U Un1 Un4 7V 。 则
Un1 0 Un2 Un2 U 5V 7V 2V Un3 Un3 U 4V 7V 3V
(1
(0.5 1) 0.5) Im1
Im1 (0.5 1) Im2 1 (0.5 1 2 1) Im2
Im3 5V 3 Im3
0
Im3 2I
由图可见，控制量和待求电流支路所在回路均只有一个回路电流经过，即
I m2 I ， Im1 Ix 。这样上式可整理成

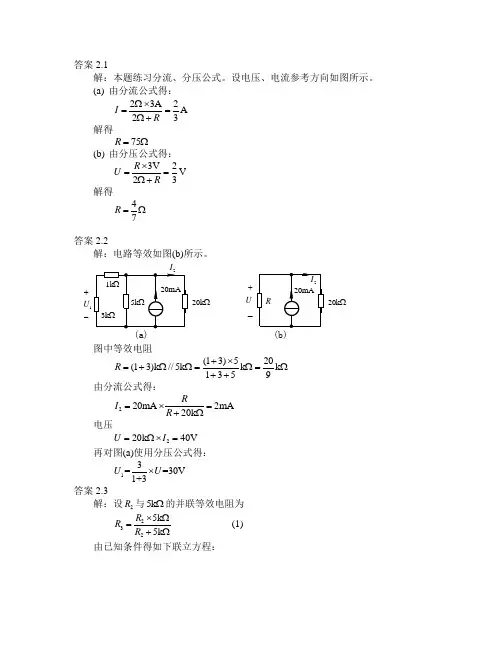
习题2.11.设随机变量X 的分布律为P{X=k}=,k=1, 2,N,求常数a.aN 解:由分布律的性质=1得∑∞k =1p kP(X=1) + P(X=2) +…..+ P(X=N) =1N*=1,即a=1aN 2.设随机变量X 只能取-1,0,1,2这4个值,且取这4个值相应的概率依次为,,求常数c.12c 34c ,58c ,716c 解:12c +34c +58c +716c =1C=37163.将一枚骰子连掷两次,以X 表示两次所得的点数之和,以Y 表示两次出现的最小点数,分别求X,Y 的分布律.注: 可知X 为从2到12的所有整数值．可以知道每次投完都会出现一种组合情况，其概率皆为(1/6)*(1/6)=1/36，故P(X=2)=(1/6)*(1/6)=1/36(第一次和第二次都是1)P(X=3)=2*(1/36）＝1/18(两种组合(1,2)(2,1))P(X=4)=3*(1/36）＝1/12(三种组合(1,3)(3,1)(2,2))P(X=5)=4*(1/36）＝1/9(四种组合(1,4)(4,1)(2,3)(3,2))P(X=6)=5*(1/36＝5/36(五种组合(1,5)(5,1)(2,4)(4,2)(3,3))P(X=7)=6*(1/36)＝1/6(这里就不写了,应该明白吧)P(X=8)=5*(1/36)＝5/36P(X=9)=4*(1/36)＝1/9P(X=10)=3*(1/36)＝1/12P(X=11)=2*(1/36)＝1/18P(X=12)=1*(1/36)＝1/36以上是X 的分布律投两次最小的点数可以是1到6里任意一个整数,即Y 的取值了.P(Y=1)=(1/6)*1=1/6 一个要是1,另一个可以是任何值P(Y=2)=(1/6)*(5/6)=5/36 一个是2,另一个是大于等于2的5个值P(Y=3)=(1/6)*(4/6)=1/9 一个是3,另一个是大于等于3的4个值P(Y=4)=(1/6)*(3/6)=1/12一个是4,另一个是大于等于4的3个值P(Y=5)=(1/6)*(2/6)=1/18一个是5,另一个是大于等于5的2个值P(Y=6)=(1/6)*(1/6)=1/36一个是6,另一个只能是6以上是Y 的分布律了.4.设在15个同类型的零件中有2个是次品,从中任取3次,每次取一个,取后不放回.以X 表示取出的次品的个数,求X 的分布律.解:X=0,1,2X=0时,P=C 313C 315=2235X=1时,P=C 213∗C 12C 315=1235X=2时,P=C 013∗C 22C 315=1355.抛掷一枚质地不均匀的硬币,每次出现正面的概率为,连续抛掷8次,以X 表示出现正面的次数,求23X 的分布律.解:P{X=k}=, k=1, 2, 3, 8C k 8(23)k (13)8‒k 6.设离散型随机变量X 的分布律为X -123P141214解:求P {X ≤12}, P {23<X ≤52}, P {2≤X ≤3}, P {2≤X <3}P {X ≤12}=14P {23<X ≤52}=12P {2≤X ≤3}=12+14=34P {2≤X <3}=127.设事件A 在每一次试验中发生的概率分别为0.3.当A 发生不少于3次时,指示灯发出信号,求:(1)进行5次独立试验,求指示灯发出信号的概率;(2)进行7次独立试验,求指示灯发出信号的概率.解:设X 为事件A 发生的次数,(1)P {X ≥3}=P {X =3}+P {X =4}+P {X =5}=C 35(0.3)3(0.7)2+C 45(0.3)4(0.7)1+C 55(0.3)5(0.7)0=0.1323+0.02835+0.00243=0.163(2) P{X≥3}=1‒P{X=0}‒P{X=1}‒P{X=2}=1‒C07(0.3)0(0.7)7‒C17(0.3)1(0.7)6‒C27(0.3)2(0.7)5=1‒0.0824‒0.2471‒0.3177=0.3538.甲乙两人投篮,投中的概率分别为0.6,0.7.现各投3次,求两人投中次数相等的概率.解:设X表示各自投中的次数P{X=0}=C03(0.6)0(0.4)3∗C03(0.7)0(0.3)3=0.064∗0.027=0.002P{X=1}=C13(0.6)1(0.4)2∗C13(0.7)1(0.3)2=0.288∗0.189=0.054P{X=2}=C23(0.6)2(0.4)1∗C23(0.7)2(0.3)1=0.432∗0.441=0.191P{X=3}=C33(0.6)3(0.4)0∗C33(0.7)3(0.3)0=0.216∗0.343=0.074投中次数相等的概率= P{X=0}+P{X=1}+P{X=2}+P{X=3}=0.3219.有一繁忙的汽车站,每天有大量的汽车经过,设每辆汽车在一天的某段时间内出事故的概率为0.0001.在某天的该段时间内有1000辆汽车经过,问出事故的次数不小于2的概率是多少?(利用泊松分布定理计算)解:设X表示该段时间出事故的次数,则X~B(1000,0.0001),用泊松定理近似计算=1000*0.0001=0.1λP{X≥2}=1‒P{X=0}‒P{X=1}=1‒C01000(0.0001)0(0.9999)1000‒C11000(0.0001)1(0.9999)999=1‒e‒0.1‒0.1e‒0.1=1‒0.9048‒0.0905=0.004710.一电话交换台每分钟收到的呼唤次数服从参数为4的泊松分别,求:(1)每分钟恰有8次呼唤的概率;(2)每分钟的呼唤次数大于10的概率.解: (1) P{X=8}=P{X≥8}‒P{X≥9}=0.051134‒0.021363=0.029771(2) P{X>10}=P{X≥11}=0.002840习题2.21.求0-1分布的分布函数.解:F(x)={0, x<0q, 0≤x<11,x≥12.设离散型随机变量X的分布律为:3 OF 18X -123P0.250.50.25求X 的分布函数,以及概率,.P {1.5<X ≤2.5} P {X ≥0.5}解:當x <‒1時,F (x )=P {X ≤x }=0;當‒1≤x <2時,F (x )=P {X ≤x }=P {X =‒1}=0.25;當2≤x <3時,F (x )=P {X ≤x }=P {X =‒1}+P {X =2}=0.25+0.5=0.75;當x ≥3時,F (x )=P {X ≤x }=P {X =‒1}+P {X =2}+P {X =3}=0.25+0.5+0.25=1;则X 的分布函数F(x)为:F (x )={0, x <‒10.25, ‒1≤x <20.75, 2≤x <31, x ≥3P {1.5<X ≤2.5}=F (2.5)‒F (1.5)=0.75‒0.25=0.5 P {X ≥0.5}=1‒F (0.5)=1‒0.25=0.753.设F 1(x),F 2(x)分别为随机变量X 1和X 2的分布函数,且F(x)=a F 1(x)-bF 2(x)也是某一随机变量的分布函数,证明a-b=1.证: F (+∞)=aF (+∞)‒bF (+∞)=1,即a ‒b =14.如下4个函数,哪个是随机变量的分布函数:(1)F 1(x )={0, x <‒212, ‒2≤x <02, x ≥0(2)F 2(x )={0, x <0sinx, 0≤x <π1, x ≥π(3)F 3(x )={0, x <0sinx, 0≤x <π21, x ≥π2(4)F 4(x )={0, x <0x +13, 0<x <121, x ≥125.设随机变量X 的分布函数为F(x) =a+b arctanx ,‒∞<x <+∞,求(1)常数a,b;(2) P {‒1<X ≤1}解: (1)由分布函数的基本性质 得:F (‒∞)=0,F (+∞)=1{a +b ∗(‒π2)=0a +b ∗(π2)=1of backbone backbone role; to full strengthening members youth work, full play youth employees in company development in the of force role; to improve independent Commission against corruption work level, strengthening on enterprise business key link of effectiveness monitored. , And maintain stability. To further strengthen publicity and education, improve the overall legal system. We must strengthen safety management, establish and improve the education, supervision, and evaluation as one of the traffic safety management mechanism. To conscientiously sum up the Olympic security controls, promoting integrated management to a higher level, higher standards, a higher level of development. Employees, today is lunar calendar on December 24, the ox Bell is about to ring, at this time of year, we clearly feel the pulse of the XX power generation company to flourish, to more clearly hear XX power generation companies mature and symmetry breathing. Recalling past one another across a railing, we are enthusiastic and full of confidence. Future development opportunities, we more exciting fight more spirited. Employees, let us together across 2013 full of challenges and opportunities, to create a green, low-cost operation, fullof humane care of a world-class power generation company and work hard! The occasion of the Spring Festival, my sincere wish that you and the families of the staff in the new year, good health, happy, happy5 OF 18解之a=, b=121π(2)P {‒1<X ≤1}=F (1)‒F (‒1)=a +b ∗π4‒(a +b ∗‒π4)=b ∗π2=12(将x=1带入F(x) =a+b arctanx )注: arctan 为反正切函数,值域(), arctan1=‒π2,π2 π46.设随机变量X 的分布函数为F (x )={0, x <1lnx, 1≤x <e1, x ≥e求P {X ≤2},P {0<X ≤3},P {2<X ≤2.5}解: 注: P {X ≤2}=F(2)=ln2 F(x)=P {X ≤x }P {0<X ≤3}=F (3)‒F (0)=1‒0=1;P {2<X ≤2.5}=F (2.5)‒F (2)=ln2.5‒ln2=ln2.52=ln1.25习题2.31.设随机变量X 的概率密度为:f (x )={acosx, |x |≤π20, 其他.求: (1)常数a; (2);(3)X 的分布函数F(x).P {0<X <π4}解:(1)由概率密度的性质∫+∞‒∞f (x )dx =1,∫π2‒π2acosxdx =a sinx |π2‒π2=asin π2‒asin (‒π2)=asin π2+asin π2=a +a =1A =12(2)P {0<X <π4}=(12)sin(π4)‒(12)sin (0)=12∗22+12∗0=24一些常用特殊角的三角函数值正弦余弦正切余切0010不存在π/61/2√3/2√3/3√3π/4√2/2√2/211of backbone backbone role; to full strengthening members youth work, full play youth employees in company development in the of force role; to improve independent Commission against corruption work level, strengthening on enterprise business key link of effectiveness monitored. , And maintain stability. To further strengthen publicity and education, improve the overall legal system. We must strengthen safety management, establish and improve the education, supervision, and evaluation as one of the traffic safety management mechanism. To conscientiously sum up the Olympic security controls, promoting integrated management to a higher level, higher standards, a higher level of development. Employees, today is lunar calendar on December 24, the ox Bell is about to ring, at this time of year, we clearly feel the pulse of the XX power generation company to flourish, to more clearly hear XX power generation companies mature and symmetry breathing. Recalling past one another across a railing, we are enthusiastic and full of confidence. Future development opportunities, we more exciting fight more spirited. Employees, let us together across 2013 full of challenges and opportunities, to create a green, low-cost operation, full of humane care of a world-class power generation company and work hard! The occasion of the Spring Festival, my sincere wish that you and the families of the staff in the new year, good health, happy, happy(3)X 的概率分布为:F (x )={0, x <‒π212(1+sinx ), ‒π2≤x <π21, x ≥π2 2.设随机变量X 的概率密度为f (x )=ae ‒|x |, ‒∞<x <+∞,求: (1)常数a; (2); (3)X 的分布函数. P {0≤X ≤1}解:(1),即a=∫+∞‒∞f(x)dx =∫0‒∞ae x dx +∫+∞ae ‒x dx =a +a =112(2)P {0≤X ≤1}=F (1)‒F (0)=12(1‒e ‒1)(3)X 的分布函数F (x )={12e x, x ≤01‒12e ‒x, x >03.求下列分布函数所对应的概率密度:(1)F 1(x )=12+1πarctanx , ‒∞<x <+∞;解:(柯西分布)f 1(x )=1π(1+x 2)(2)F 2(x )={1‒e ‒x 22, x >00, x ≤0π/3√3/21/2√3√3/3π/210不存在0π-1不存在7 OF 18解:(指数分布) f 2(x )={x e ‒x 22, x >00, x ≤0(3)F 3(x )={0, x <0sinx , 0≤ x ≤π21, x >π2解: (均匀分布)f 3(x )={cosx , 0≤ x ≤π20, 其他4.设随机变量X 的概率密度为f (x )={x, 0≤x <12‒x, 1≤ x <20, 其他.求: (1); (2)P {X ≥12} P {12<X <32}.解:(1)P {X ≥12}=1‒F (12)=1‒1222=1‒18=78(2)(2)P {12<X <32}=F(32)‒F(12)=(2∗32‒1‒3222)‒(3222)=345.设K 在(0,5)上服从均匀分布,求方程(利用二次式的判别式)4x 2+4Kx +K +2=0有实根的概率.解: K~U(0,5)f (K )={15 , 0≤x ≤50, 其他方程式有实数根,则Δ≥0,即(4K)2‒4∗4∗(K +2)=16K 2‒16(K +2)≥02≤K ≤‒1故方程有实根的概率为:P {K ≤‒1}+P {K ≥2}=∫5215dx =0.66.设X ~ U(2,5),现在对X 进行3次独立观测,求至少有两次观测值大于3的概率.解:P {K >3}=1‒F (3)=1‒3‒25‒2=23至少有两次观测值大于3的概率为:C 23(23)2(13)1+C 33(23)3(13)0=20277.设修理某机器所用的时间X 服从参数为λ=0.5(小时)指数分布,求在机器出现故障时,在一小时内可以修好的概率.解: P {X ≤1}=F (1)=1‒e‒0.58.设顾客在某银行的窗口等待服务的时间X(以分计)服从参数为λ=的指数分布,某顾客在窗口等待159 OF 18服务,若超过10分钟,他就离开.他一个月要到银行5次,以Y 表示他未等到服务而离开窗口的次数.写出Y 的分布律,并求P {Y ≥1}.解:“未等到服务而离开的概率”为P {X ≥10}=1‒F (10)=1‒(1‒e‒15∗10)=e ‒2P {Y =k }=C k 5(e ‒2)k(1‒e ‒2)5‒k , (k =0,1,2,3,4,5)Y 的分布律:Y 012345P0.4840.3780.1180.0180.0010.00004P {Y ≥1}=1‒P {Y =0}=1‒0.484=0.5169.设X ~ N(3,),求:22(1);P {2<X ≤5}, P {‒4<X ≤10}, P {|X |>2}, P {X >3}(2).常数c,使P {X >c }=P {X ≤c }解: (1)P {2<X ≤5}=Φ(5‒32)‒Φ(2‒32)=Φ(1)‒[1‒Φ(12)]=0.8413‒(1‒0.6915)=0.5328P {‒4<X ≤10}=Φ(10‒32)‒Φ(‒4‒32)=Φ(3.5)‒[1‒Φ(3.5)]=0.9998‒0.0002=0.9996 P {|X |>2}= 1‒P {‒2≤X ≤2}=1‒[Φ(2‒32)‒Φ(‒2‒32)]=1‒(0.3085‒0.0062)=0.6977P {X >3}= P {X ≥3}=1‒Φ(3‒32)=1‒Φ(0)=1‒0.5=0.5(2)P {X >c }=P {X ≤c }P {X >c }=1‒P {X ≥c }P {X >c }+P {X ≥c }=1Φ(c ‒32)+Φ(c ‒32)=1Φ(c ‒32)=0.5经查表,即C=3c ‒32=010.设X ~ N(0,1),设x 满足P {|X |>x }<0.1.求x 的取值范围.解:P {|X |>x }<0.12[1‒Φ(x )]<0.1‒Φ(x )<‒1920Φ(x )≥1920Φ(x )≥0.95经查表当 1.65时x ≥Φ(x )≥0.95即 1.65时x ≥P {|X |>x }<0.111.X ~ N(10,),求:22(1)P {7<X ≤15};(2)常数d,使P {|X ‒10|<d }<0.9.解: (1)P {7<X ≤15}=Φ(15‒102)‒Φ(7‒102)=Φ(2.5)‒[1‒Φ(1.5)]=0.9938‒0.0668=0.927(2)P {|X ‒10|<d }=P {10‒d <X <10+d }<0.9=Φ(10+d ‒102)‒Φ(10‒d ‒102)<0.9=Φ(d2)<0.95经查表,即d=3.3d2=1.6512.某机器生产的螺栓长度X(单位:cm)服从正态分布N(10.05,),规定长度在范围10.050.12内 0.062±为合格,求一螺栓不合格的概率.解:螺栓合格的概率为:P {10.05‒0.12<X <10.05+0.12}=P {9.93<X <10.17}=Φ(10.17‒10.050.06)‒Φ(9.93‒10.050.06)=Φ(2)‒[1‒Φ(2)]=0.9772∗2‒1=0.9544螺栓不合格的概率为1-0.9544=0.045613.测量距离时产生的随机误差X(单位:m)服从正态分布N(20,).进行3次独立测量.求:402(1)至少有一次误差绝对值不超过30m 的概率;(2)只有一次误差绝对值不超过30m的概率.解:(1)绝对值不超过30m的概率为:P{‒30<X<30}=Φ(30‒2040)‒Φ(‒30‒2040)=Φ(0.25)‒[1‒Φ(1.25)]=0.4931至少有一次误差绝对值不超过30m的概率为:1−C 03(0.4931)0(1‒0.4931)3=1‒0.1302=0.8698(2)只有一次误差绝对值不超过30m的概率为:C13(0.4931)1(1‒0.4931)2=0.3801习题2.41.设X的分布律为X-2023P0.20.20.30.3求(1)的分布律.Y1=‒2X+1的分布律; (2)Y2=|X|解: (1)的可能取值为5,1,-3,-5.Y1由于P{Y1=5}=P{‒2X+1=5}=P{X=‒2}=0.2P{Y1=1}=P{‒2X+1=1}=P{X=‒2}=0.2P{Y1=‒3}=P{‒2X+1=‒3}=P{X=2}=0.3P{Y1=‒5}=P{‒2X+1=‒5}=P{X=3}=0.3从而的分布律为:Y1X-5-315Y10.30.30.20.2(2)的可能取值为0,2,3.Y2由于P{Y2=0}=P{|X|=0}=P{X=0}=0.2P{Y2=2}=P{|X|=0}=P{X=‒2}+P{X=2}=0.2+0.3=0.5P{Y2=3}=P{|X|=3}=P{X=3}=0.3从而的分布律为:Y2X023Y20.20.50.32.设X的分布律为X-1012P0.20.30.10.411 OF 18求Y=(X‒1)2的分布律.解:Y的可能取值为0,1,4.由于P{Y=0}=P{(X‒1)2=0}=P{X=1}=0.1P{Y=1}=P{(X‒1)2=1}=P{X=0}+P{X=2}=0.7P{Y=4}=P{(X‒1)2=4}=P{X=‒1}=0.2从而的分布律为:YX014Y0.10.70.23.X~U(0,1),求以下Y的概率密度:(1)Y=‒2lnX; (2)Y=3X+1; (3)Y=e x.解: (1) Y=g(x)=‒2lnX, 值域為(0,+∞),X=ℎ(y)=e‒Y2, ℎ'(y)=12e‒Y2 f Y(y)=f x(ℎ(y))| ℎ'(y)|=1∗12e‒Y2=12e‒Y2.即f Y(y)={12e‒Y2, y>0,0, y≤0(2) Y=g(x)=3X+1,值域為(‒∞,+∞), X=ℎ(y)=Y‒13, ℎ'(y)=13f Y(y)=f x(ℎ(y))| ℎ'(y)|=1∗13=13即f Y(y)={13, 1< y<4,0, 其他注: 由X~U(0,1),,当X=0时,Y=3*0+1=1; ,当X=1时,Y=3*1+1=4 Y=3X+1(3) Y=g(x)=e x, X=ℎ(y)=lny, ℎ'(y)=1yf Y(y)=f x(ℎ(y))| ℎ'(y)|=1∗1y=1y即f Y(y)={1y, 0< y<e,0, 其他注: ,当X=0时,; ,当X=1时,Y=e0=0 Y=e1=e4.设随机变量X的概率密度为f X(x)={32x2, ‒1<x<00, 其他.of backbone backbone role; to full strengthening members youth work, full play youth employees in company development in the of force role; to improve independent Commission against corruption work level, strengthening on enterprise business key link of effectiveness monitored. , And maintain stability. To further strengthen publicity and education, improve the overall legal system. We must strengthen safety management, establish and improve the education, supervision, and evaluation as one of the traffic safety management mechanism. To conscientiously sum up the Olympic security controls, promoting integrated management to a higher level, higher standards, a higher level of development. Employees, today is lunar calendar on December 24, the ox Bell is about to ring, at this time of year, we clearly feel the pulse of the XX power generation company to flourish, to more clearly hear XX power generation companies mature and symmetry breathing. Recalling past one another across a railing, we are enthusiastic and full of confidence. Future development opportunities, we more exciting fight more spirited. Employees, let us together across 2013 full of challenges and opportunities, to create a green, low-cost operation, fullof humane care of a world-class power generation company and work hard! The occasion of the Spring Festival, my sincere wish that you and the families of the staff in the new year, good health, happy, happy13 OF 18求以下Y 的概率密度:(1)Y=3X; (2) Y=3-X; (3)Y =X 2.解: (1) Y=g(x)=3X,X =ℎ(y )=Y 3, ℎ'(y)=13f Y (y )=f x (ℎ(y ))| ℎ'(y)|=Y 26∗13=Y218即f Y (y )={Y 218, ‒3< y <0,0, 其他(2)Y=g(x) =3-X, X=h(y) =3-Y,-1ℎ'(y)=f Y (y )=f x (ℎ(y ))| ℎ'(y)|=32∗(3‒Y)2+1=3(3‒Y)22即f Y (y )={3(3‒Y)22, 3< y <4,0, 其他(3), X=h(y)=,Y =g(x)=X 2Y ℎ'(y)=12Y,即f Y (y )=f x (ℎ(y ))| ℎ'(y)|=3Y 22∗1 2Y=3Y4f Y (y )={3Y4, 0< y <1,0, 其他5.设X 服从参数为λ=1的指数分布,求以下Y 的概率密度:(1)Y=2X+1; (2)(3) Y =e x; Y =X 2.解: (1) Y=g(x)=2X+1,X =ℎ(y )=Y ‒12, ℎ'(y )=12X 的概率密度为:f X (x )={λe ‒λx, x >0,0, x ≤0f Y (y )=f x (ℎ(y ))| ℎ'(y)|=λe ‒λ∗Y ‒12∗12=12e ‒Y ‒12即f Y (y )={12e ‒Y ‒12, y >00, 其他(2)Y =g (x )=e x , X =ℎ(y )=lnY,ℎ'(y )= 1Y注意是绝对值 ℎ'(y)of backbone backbone role; to full strengthening members youth work, full play youth employees in company development in the of force role; to improve independent Commission against corruption work level, strengthening on enterprise business key link of effectiveness monitored. , And maintain stability. To further strengthen publicity and education, improve the overall legal system. We must strengthen safety management, establish and improve the education, supervision, and evaluation as one of the traffic safety management mechanism. To conscientiously sum up the Olympic security controls, promoting integrated management to a higher level, higher standards, a higher level of development. Employees, today is lunar calendar on December 24, the ox Bell is about to ring, at this time of year, we clearly feel the pulse of the XX power generation company to flourish, to more clearly hear XX power generation companies mature and symmetry breathing. Recalling past one another across a railing, we are enthusiastic and full of confidence. Future development opportunities, we more exciting fight more spirited. Employees, let us together across 2013 full of challenges and opportunities, to create a green, low-cost operation, full of humane care of a world-class power generation company and work hard! The occasion of the Spring Festival, my sincere wish that you and the families of the staff in the new year, good health, happy, happyf Y (y )=f x (ℎ(y ))| ℎ'(y)|=e‒lnY∗1Y =1e lnY ∗1Y =1Y ∗1Y =1Y 2即f Y (y )={1Y2, y >10, 其他(3)Y =g (x )=X 2,X =ℎ(y )=Y , ℎ'(y )=12Y,,f Y (y )=f x (ℎ(y ))| ℎ'(y)|=e ‒Y∗12Y=12Ye ‒Y即f Y (y )={12Ye ‒Y, y >00, 其他6.X~N(0,1),求以下Y 的概率密度:(1) Y =|X |; (2)Y =2X 2+1解: (1) Y =g (x )=|X |, X =ℎ(y )=±Y, ℎ'(y )=1f X (x )=12πσe‒(x ‒μ)22σ2‒∞<x <+∞当X=+Y 时:f Y (y )=f x (ℎ(y ))| ℎ'(y)|=12πe‒y 22当X=-Y 时: f Y (y )=f x (ℎ(y ))| ℎ'(y)|=12πe ‒y 22故f Y (y )=12πe ‒y 22+12πe‒y 22=22πe ‒y 22=42πe‒y 22=2πe ‒y 22f Y (y )={2πe ‒y 22, y >00, y ≤0(2)Y =g (x )=2X 2+1, X =ℎ(y )=Y ‒12,ℎ'(y )=12Y ‒12永远大于0.e x 当x>0是,>1e xof backbone backbone role; to full strengthening members youth work, full play youth employees in company development in the of force role; to improve independent Commission against corruption work level, strengthening on enterprise business key link of effectiveness monitored. , And maintain stability. To further strengthen publicity and education, improve the overall legal system. We must strengthen safety management, establish and improve the education, supervision, and evaluation as one of the traffic safety management mechanism. To conscientiously sum up the Olympic security controls, promoting integrated management to a higher level, higher standards, a higher level of development. Employees, today is lunar calendar on December 24, the ox Bell is about to ring, at this time of year, we clearly feel the pulse of the XX power generation company to flourish, to more clearly hear XX power generation companies mature and symmetry breathing. Recalling past one another across a railing, we are enthusiastic and full of confidence. Future development opportunities, we more exciting fight more spirited. Employees, let us together across 2013 full of challenges and opportunities, to create a green, low-cost operation, fullof humane care of a world-class power generation company and work hard! The occasion of the Spring Festival, my sincere wish that you and the families of the staff in the new year, good health, happy, happy15 OF 18f Y (y )=f x (ℎ(y ))| ℎ'(y)|=12πe‒(Y ‒12)22∗12Y ‒12=12π(y ‒1)e‒y ‒14即f Y (y )={12π(y ‒1)e ‒y ‒14, y >10, y ≤1自测题一,选择题1,设一批产品共有1000件,其中有50件次品,从中随机地,有放回地抽取500件产品,X 表示抽到次品的件数,则P{X=3}= C .A. B.C. D.C 350C 497950C 5001000A 350A 497950A 5001000C 3500(0.05)3(0.95)497 35002.设随机变量X~B(4,0.2),则P{X>3}= A .A. 0.0016B. 0.0272C. 0.4096D. 0.8192解:P{X>3}= P{X=4}= (二项分布)C 44(0.2)4(1‒0.2)03.设随机变量X 的分布函数为F(x),下列结论中不一定成立的是D .A. B. C. D. F(x) 为连续函数F (+∞)=1 F (‒∞)=00≤F (x )≤14.下列各函数中是随机变量分布函数的为 B .A. B.F 1(x )=11+x 2, ‒∞<x <+∞F 2(x )={0, x ≤0x 1+x , x >0C.D.F 3(x )=e ‒x, ‒∞<x <+∞F 4(x )=34+12πarctanx, ‒∞<x <+∞5.设随机变量X 的概率密度为 则常数a= A .f (x )={a x 2, x >100, x ≤10A. -10B.C.D. 10解: F(x) =‒15001500∫+∞‒∞a x2dx =‒ax =16.如果函数是某连续型随机变量X 的概率密度,则区间[a,b]可以是 C f (x )={x, a<x <b0, 其他A. [0, 1]B. [0, 2]C. D. [1, 2][0,2]不晓得为何课后答案为Dof backbone backbone role; to full strengthening members youth work, full play youth employees in company development in the of force role; to improve independent Commission against corruption work level, strengthening on enterprise business key link of effectiveness monitored. , And maintain stability. To further strengthen publicity and education, improve the overall legal system. We must strengthen safety management, establish and improve the education, supervision, and evaluation as one of the traffic safety management mechanism. To conscientiously sum up the Olympic security controls, promoting integrated management to a higher level, higher standards, a higher level of development. Employees, today is lunar calendar on December 24, the ox Bell is about to ring, at this time of year, we clearly feel the pulse of the XX power generation company to flourish, to more clearly hear XX power generation companies mature and symmetry breathing. Recalling past one another across a railing, we are enthusiastic and full of confidence. Future development opportunities, we more exciting fight more spirited. Employees, let us together across 2013 full of challenges and opportunities, to create a green, low-cost operation, fullof humane care of a world-class power generation company and work hard! The occasion of the Spring Festival, my sincere wish that you and the families of the staff in the new year, good health, happy, happy7.设随机变量X 的取值范围是[-1,1],以下函数可以作为X 的概率密度的是 A A. B. {12, ‒1< x <10, 其他{2, ‒1< x <10, 其他C.D. {x, ‒1< x <10, 其他{x 2, ‒1< x <10, 其他8.设连续型随机变量X 的概率密度为 则= B .f (x )={x2, 0< x <20, 其他P{‒1≤ X ≤1}A. 0 B. 0.25 C. 0.5 D. 1解:P {‒1≤ X ≤1}=∫1‒1x2dx =x 24|1‒1=149.设随机变量X~U(2,4),则= A . (需在区间2,4内)P{3< x <4}A. B. P{2.25< x <3.25}P{1.5< x <2.5}C. D. P{3.5< x <4.5}P{4.5< x <5.5}10. 设随机变量X 的概率密度为 则X~ A .f (x )=122πe ‒(x ‒1)28A. N (-1, 2)B. N (-1, 4)C. N (-1, 8)D. N (-1, 16)11.已知随机变量X 的概率密度为fx(x),令Y=-2X,则Y 的概率密度fy(y)为 D .A.B.C.D. 2f X (‒2y)f X (‒y2)12f X(‒y2)12f X (y 2)二,填空题1.已知随机变量X 的分布律为X 12345P2a0.10.3a0.3则常数a= 0.1 .解:2a+0.1+0.3+a+0.3=12.设随机变量X 的分布律为X 123P162636记X 的分布函数为F(x)则F(2)=.解: 1216+263.抛硬币5次,记其中正面向上的次数为X,则=.P{ X ≤4}3132解:P { X ≤4}=1‒P { X =5}=1‒C 55(12)5(12)自己算的结果是12f X(‒y2)17 OF 184.设X 服从参数为λ(λ>0)的泊松分布,且,则λ= 2 .P { X =0}=12P { X =2}解:分别将.P { X =0},P { X =2}帶入P k =P { X =k }=λk k!e ‒λ5.设随机变量X 的分布函数为F (x )={0, x <a0.4, a ≤x <b1, x ≥b其中0<a<b,则= 0.4.P {a2<X <a +b 2}解:P { a 2<X <a +b 2}=F (a +b 2)‒F (a 2)=0.4‒0=0.46.设X 为连续型随机变量,c 是一个常数,则= 0.P { X =c }7. 设连续型随机变量X 的分布函数为F (x )={13e x, x <013(x +1), 0≤x <21, x ≥2则X 的概率密度为f(x),则当x<0是f(x)=.13e x 8. 设连续型随机变量X 的分布函数为其中概率密度为f(x),F (x )={1‒e ‒2x , x >00, x ≤0则f(1)= .2e ‒29. 设连续型随机变量X 的概率密度为其中a>0.要使,则常数a=f (x )={12a, ‒a < x <a 0, 其他P { X >1}=13 3 .解:P { X >1}=1‒P { X ≤1}=13,P { X ≤1}=23=12a10.设随机变量X~N(0,1),为其分布函数,则= 1 .Φ(x)Φ(x )+Φ(‒x)11.设X~N ,其分布函数为为标准正态分布函数,则F(x)与之间的关系是(μ,σ2)F (x ),Φ(x)Φ(x)=.F (x )Φ(x ‒μσ)12.设X~N(2,4),则= 0.5 .P { X ≤2}13.设X~N(5,9),已知标准正态分布函数值,为使,则Φ(0.5)=0.6915P { X <a }<0.6915常数a< 6.5. 解:, F (a )=Φ(a ‒μσ)=a ‒53a ‒53<0.514. 设X~N(0,1),则Y=2X+1的概率密度= .f Y (y )122πe‒(Y ‒1)28解:Y =g (x )=2X +1, X =ℎ(y )=Y ‒12,ℎ'(y )=12f Y (y )=f x (ℎ(y ))| ℎ'(y)|=12πe‒(Y ‒12)22∗12=122πe‒(Y ‒1)28三.袋中有2个白球3个红球,现从袋中随机地抽取2个球,以X 表示取到红球的数,求X 的分布律.解: X=0,1,2当X=0时,P { X =0}=C 03∗C 22C 25=110当X=1时,P { X =1}=C 13∗C 12C 25=610当X=2时,P { X =2}=C 23∗C 02C 25=310X 的分布律为:X 012P110610310四.设X 的概率密度为求: (1)X 的分布函数F(x);(2).f (x )={|x|, ‒1≤ x ≤10, 其他 P { X <0.5},P { X >‒0.5}解: (1)当x <-1时. F(x)=0;;当‒1≤x <0时,F(x)=∫x‒1‒x dx =‒x 22|x ‒1=12‒x 22当0≤x <1时,F (x )=1‒ 1∫xx dx =1‒x 22|1x =12+x 22当x ≥1时. F(x)=1F (X )={0, X <‒112‒x22, ‒1≤X <012+x22, 0≤X <11, X ≥1(2)P { X <0.5}=F (0.5)=12+0.522=58;P { X >‒0.5}=1‒F (‒0.5)=1‒(12‒0.522)=58五.已知某种类型电子组件的寿命X(单位:小时)服从指数分布,它的概率密度为f (x )={12000e ‒x 2000, x >00, x ≤0We will continue to improve the company's internal control system, and steady improvement in ability to manage and control, optimize business processes, to ensure smooth processes, responsibilities in place; to further strengthen internal controls, play a control post independent oversight role of evaluation complying with third-party responsibility; to actively make use of internal audit tools detect potential management, streamline, standardize related transactions, strengthening operations in accordance with law. Deepening the information management to ensure full communication "zero resistance". To constantly perfect ERP, and BFS++, and PI, and MIS, and SCM, information system based construction, full integration information system, achieved information resources shared; to expand Portal system application of breadth and depth, play information system on enterprise of Assistant role; to perfect daily run maintenance operation of records, promote problem reasons analysis and system handover; to strengthening BFS++, and ERP, and SCM, technology application of training, improve employees application information system of capacity and level. Humanistic care to ensure "zero." To strengthening Humanities care,continues to foster company wind clear, and gas are, and heart Shun of culture atmosphere; strengthening love helped trapped, care difficult employees; carried out style activities, rich employees life; strengthening health and labour protection, organization career health medical, control career against; continues to implementation psychological warning prevention system, training employees health of character, and stable of mood and enterprising of attitude, created friendly fraternity of Humanities environment. To strengthen risk management, ensure that the business of "zero risk". To strengthened business plans management, will business business plans cover to all level, ensure the business can control in control; to close concern financial, and coal electric linkage, and energy-saving scheduling, national policy trends, strengthening track, active should; to implementation State-owned assets method, further specification business financial management; to perfect risk tube control system, achieved risk recognition, and measure, and assessment, and report, and control feedback of closed ring management, improve risk prevention capacity. To further standardize trading, and strive to achieve "according to law, standardize and fair." Innovation of performance management, to ensure that potential employees "zero fly". To strengthen performance management, process control, enhance employee evaluation and levels of effective communication to improve performance management. To further quantify and refine employee standards ... Work, full play party, and branch, and members in "five type Enterprise" construction in the of core role, and fighting fortress role and pioneer model role; to continues to strengthening "four good" leadership construction, full play levels cadres in enterprise development in theof backbone backbone role; to full strengthening members youth work, full play youth employees in company development in the of force role; to improve independent Commission against corruption work level, strengthening on enterprise business key link of effectiveness monitored. , And maintain stability. To further strengthen publicity and education, improve the overall legal system. We must strengthen safety management, establish and improve the education, supervision, and evaluation as one of the traffic safety management mechanism. To conscientiously sum up the Olympic security controls, promoting integrated management to a higher level, higher standards, a higher level of development. Employees, today is lunar calendar on December 24, the ox Bell is about to ring, at this time of year, we clearly feel the pulse of the XX power generation company to flourish, to more clearly hear XX power generation companies mature and symmetry breathing. Recalling past one another across a railing, we are enthusiastic and full of confidence. Future development opportunities, we more exciting fight more spirited. Employees, let us together across 2013 full of challenges and opportunities, to create a green, low-cost operation, fullof humane care of a world-class power generation company and work hard! The occasion of the Spring Festival, my sincere wish that you and the families of the staff in the new year, good health, happy, happy19 OF 18一台仪器装有4个此种类型的电子组件,其中任意一个损坏时仪器便不能正常工作,假设4个电子组件损坏与否相互独立.试求: (1)一个此种类型电子组件能工作2000小时以上的概率;(2)一台仪器能正p 1常工作2000小时以上的概率.p 2解: (1)P 1=P {X ≥2000}=∫+∞200012000e‒x 2000dx=12000∗‒2000∗e‒x2000|+∞2000=‒e‒x 2000|+∞2000=0‒(‒e ‒1)=e ‒1(2)因4个电子组件损坏与否相互独立,故:P 2=P 14=(e ‒1)4=e ‒4当+∞带入‒x2000时变成负无穷大,e ‒∞=0。

第二章心理辅导的理论基础一、理论测试题（一）单项选择题1．（）是根据操作性条件反射原理，强调行为的改变是依据行为后果而定的。

A．强化法B．系统脱敏法C．代币法D．来访者中心疗法2．在对学生进行心理辅导时，常使用的“强化法”属于（）。

A．行为改变技术B．认知改变法C．运动改变法D．精神分析法3．在心理辅导的行为演练中，系统脱敏法是由（）首创。

A．皮亚杰B．沃尔帕C．艾利斯D．罗杰斯4．心理辅导老师帮李晓明建立焦虑等级，让他想象引起焦虑的情境，然后逐渐减少焦虑等级，直至完全放松，以缓解其考试焦虑，这种方法是（）。

A．强化法B．系统脱敏法C．理性一情绪疗法D．来访者中心疗法5．行为塑造法是根据（）的操作条件反射研究结果而设计的培育和养成新反应或行为模式的一项行为治疗技术，是操作条件作用法强化原则的有力应用之一。

A．皮亚杰B．斯金纳C．艾利斯D．奥苏贝尔6．（）就是运用代币并编制一套相应的激励系统来对符合要求的目标行为的表现进行肯定和奖励。

A．强化法B．理性一情绪疗法C．代币法D．来访者中心疗法7．李老师通过奖励小红花来表扬学生的行为，这种心理辅导方法属于（）。

A．系统脱敏法B．代币法C．行为塑造法D．来访者中心疗法8.晓红是韩老师班上的学生，她孤僻、羞涩，当她主动与同学交谈或请教老师时，韩老师就给予肯定或激励。

这种心理辅导方法是（）。

A．强化法B．系统脱敏法C．来访者中心法D．理性一情绪疗法9．（）不是行为改变的基本方法。

A．强化法B．代币法C．自我控制法D．演练法10．小伟过分害怕狗，通过让他看狗的照片，谈论狗，远看狗到近看狗、摸狗、抱狗，消除对狗的惧怕反应，这是行为训练的（）。

A．全身松弛训练B．系统脱敏法C．行为塑造法D．肯定性训练11．当一位胆小的学生敢于主动向教师提问时，教师耐心解答并给予表扬和鼓励。

教师的这种做法属于行为改变方法中的（）。

A．强化法B．示范法C．消退法D．行为塑造法12．认知疗法于20世纪六七十年代在（）产生。

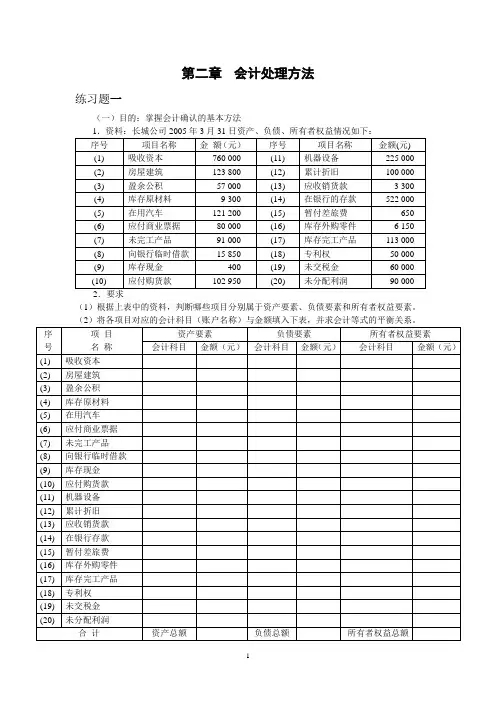
第二章会计处理方法练习题一（一）目的：掌握会计确认的基本方法（1）根据上表中的资料，判断哪些项目分别属于资产要素、负债要素和所有者权益要素。

练习题一参考答案要点（1）资产要素的有：(2)；(4)；(5)；(7)；(9)；(11)；(12)；(13)；(14)；(15)；(16)；(17)；(18) 负债要素的有：(6)；(8)；(10)；(19)所有者权益要素的有：(1)；(3)；(20)（2）负债表存货项目中。

严格来说，此处是不对的。

因为“生产成本”是费用类账户。

练习题二（二）目的：掌握权责发生制与收付实现制1．资料绿叶公司2005年10月份发生如下经济业务：（1）支付本月的水电费300元。

（2）预付下个月房屋租金2 000元。

（3）支付上月工商部门罚款500元。

（4）销售商品收入20 000元，款项尚未收到。

（5）支付上月购货款38 000元。

（6）采购员报销差旅费2 500元，退回多余现金500元（出差前预借3 000元）。

（7）收到上月销售货款500 000，存入银行。

2．要求分别根据权责发生制和现金收付制，确认和计算本月收入与费用（将结果填入下表）。

练习题二参考答案要点练习题三（三）目的：掌握会计确认的基本方法1．资料上扬公司2005年12月发生如下经济交易与事项：（1）10日，与甲公司签订购货合同，协议购买A材料50万元，约定合同签订之日起10日内预付购货定金10万元。

（2）12日，有一批产品完工验收入库，这批产品的生产成本为20万元。

（3）18日，根据购货合同预付甲公司购货定金10万元。

（4）20日，公司发生失窃事件，丢失现金5万元。

（5）25日，以银行存款预付下年度财产保险费3万元。

（6）28日，以银行存款支付本季度贷款利息费用9万元，其中前两个月已预提6万元。

（7）31日，计算出本月产品销售应缴纳的税金5万元，但尚未实际缴纳。

（8）31日，计算出本月应负担的工资费用15万元，其中管理人员5万元，生产工人10万元，公司每月的工资在下月上旬发放。

第二章1. (Q2) For a communication session between a pair of processes, which process is the client and which is the server?Answer: The process which initiates the communication is the client; the process that waits to be contacted is the server..2. (Q3) What is the difference between network architecture and application architecture?Answer: Network architecture refers to the organization of the communication process into layers (e.g., the five-layer Internet architecture). Application architecture, on the other hand, is designed by an application developer and dictates the broad structure of the application(e.g., client-server or P2P)3. (Q4) What information is used by a process running on one host to identify a process running on another host?Answer: The IP address of the destination host and the port number of the destination socket.4. (Q6) Referring to Figure 2.4, we see that none of the application listed in Figure 2.4 requires both no data loss and timing. Can you conceive of an application that requires no data loss and that is also highly time-sensitive?Answer: There are no good example of an application that requires no data loss and timing.If you know of one, send an e-mail to the authors5. (Q9) Why do HTTP, FTP, SMTP, and POP3 run on top of TCP rather than on UDP?Answer: The applications associated with those protocols require that all application data be received in the correct order and without gaps. TCP provides this service whereas UDP does not.6. (Q11) What is meant by a handshaking protocol?Answer: A protocol uses handshaking if the two communicating entities first exchange control packets before sending data to each other. SMTP uses handshaking at the application layer whereas HTTP does not.7. (Q13) Telnet into a Web server and send a multiline request message. Include in the request message the If-modified-since: header line to force a response message with the 304 Not Modified status code.Answer: Issued the following command (in Windows command prompt) followed by the HTTP GET message to the “” web server:> telnet 80Since the index.html page in this web server was not modified since Fri, 18 May 2007 09:23:34 GMT, the following output was displayed when the above commands were issued on Sat, 19 May 2007. Note that the first 4 lines are the GET message and header lines input by the user and the next 4 lines (starting from HTTP/1.1 304 Not Modified) is the response from the web server.8. (Q14) Consider an e-commerce site that wants to keep a purchase record for each of its customers. Describe how this can be done with cookies.Answer: When the user first visits the site, the site returns a cookie number. This cookie number is stored on the user’s host and is managed by the browser. During each subsequent visit (and purchase), the browser sends the cookie number back to the site. Thus the site knows when this user (more precisely, this browser) is visiting the site.9. (Q15) Suppose Alice, with a Web-based e-mail account (such as Hotmail or gmail), sends a message to Bob, who accesses his mail from his mail server using POP3. Discuss how the message gets from Alice’s host to Bob’s host. Be sure to list the series of application-layer protocols that are used to move the message between the two hosts.Answer: Message is sent from Alice’s host to her mail server over HTTP. Alice’s mail server then sends the message to Bob’s mail server over SMTP. Bob then transfers the message from his mail server to his host over POP3.10. (Q10) Recall that TCP can be enhanced with SSL to provide process-to-process securityservices, including encryption. Does SSL operate at the transport layer or the application layer? If the application developer wants TCP to be enhanced with SSL, what does the developer have to do?Answer: SSL operates at the application layer. The SSL socket takes unencrypted data from the application layer, encrypts it and then passes it to the TCP socket. If the application developer wants TCP to be enhanced with SSL, she has to include the SSL code in the application.11. (Q16) Print out the header of an e-mail message you have recently received. How manyReceived: header lines are there? Analyze each of the header lines in the message.Answer: from 65.54.246.203 (EHLO )Received：(65.54.246.203) by with SMTP; Sat, 19 May 2007 16:53:51 -0700from ([65.55.135.106]) by Received: with Microsoft SMTPSVC(6.0.3790.2668); Sat, 19 May 2007 16:52:42 -0700 Received: from mail pickup service by with Microsoft SMTPSVC; Sat,19 May 2007 16:52:41 -0700Message-ID: <BAY130-************************************>Received: from 65.55.135.123 by with HTTP; Sat, 19 May 2007 23:52:36 GMTFrom: "prithuladhungel"<***************************>To: ******************Bcc:Subject: Test mailDate: Sat, 19 May 2007 23:52:36 +0000Mime-Version:1.0Content-Type: Text/html; format=flowedReturn-Path: ***************************Figure: A sample mail message headerReceived: This header field indicates the sequence in which the SMTP servers send and receive the mail message including the respective timestamps.In this example there are 4 “Received:” header lines. This means the mail message passed through 5 different SMTP servers before being delivered to the receiver’s mail box. The last (forth) “Received:” header indicates the mail message flow from the SMTP server of the sender to the second SMTP server in the chain of servers. The sender’s SMTP server is at address 65.55.135.123 and the second SMTP server in the chain is . The third “Received:” header indicates the mail message flow from the second SMTP server in the chain to the third server, and so on.Finally, the first “Received:” header indicates the flow of the mail message from the forth SMTP server to the last SMTP server (i.e. the receiver’s mail server) in the chain.Message-id: The message has been given this numberBAY130-************************************(by .Message-id is a unique string assigned by the mail system when the message is first created.From: This indicates the email address of the sender of the mail. In the givenexample,**************************************To: This field indicates the email address of the receiver of the mail. In the example, the ****************************Subject: This gives the subject of the mail (if any specified by the sender). In the example, the subject specified by the sender is “Test mail”Date: The date and time when the mail was sent by the sender. In the example, the sender sent the mail on 19th May 2007, at time 23:52:36 GMT.Mime-version: MIME version used for the mail. In the example, it is 1.0.Content-type: The type of content in the body of the mail message. In the example, it is “text/html”.Return-Path: This specifies the email address to which the mail will be sent if thereceiver of this mail wants to reply to the sender. This is also used by the sender’smail server for bouncing back undeliverable mail messages of mailer-daemonerror messages. In the example, the return path is“***************************”.12. (Q18) Is it possible for an organization’s Web server and mail server to have exactly thesame alias for a hostname (for example, )? What would be the type for the RR that contains the hostname of the mail server?Answer: Yes an organization’s mail server and Web server can have the same alias for a host name. The MX record is used to map the mail server’s host name to its IP address.13. (Q19) Why is it said that FTP sends control information “out-of-band”?Answer: FTP uses two parallel TCP connections, one connection for sending control information (such as a request to transfer a file) and another connection for actually transferring the file. Because the control information is not sent over the same connection that the file is sent over, FTP sends control information out of band.14. (P6) Consider an HTTP client that wants to retrieve a Web document at a given URL. The IPaddress of the HTTP server is initially unknown. What transport and application-layer protocols besides HTTP are needed in this scenario?Answer:Application layer protocols: DNS and HTTPTransport layer protocols: UDP for DNS; TCP for HTTP15. (P9) Consider Figure2.12, for which there is an institutional network connected to theInternet. Suppose that the average object size is 900,000 bits and that the average requestrate from the institution’s browsers to the origin servers is 10 requests per second. Also suppose that the amount of time it takes from when the router on the Internet side of the access link forwards an HTTP request until it receives the response is two seconds on average (see Section 2.2.5). Model the total average response times as the sum of the average access delay (that is, the delay from Internet router to institution router) and the average Internet delay. For the average access delay, use △/(1-△β), where △is the average time required to send an object over the access link and βis the arrival rate of objects to the access link.a. Find the total average response time.b. Now suppose a cache is installed in the institutional LAN. Suppose the hit rate is 0.6. Findthe total response time.Answer:a.The time to transmit an object of size L over a link or rate R is L/R. The average time isthe average size of the object divided by R:Δ= (900,000 bits)/(1,500,000 bits/sec) = 0.6 secThe traffic intensity on the link is (1.5 requests/sec)(0.6 sec/request) = 0.9. Thus, the average access delay is (0.6 sec)/(1 - 0.9) = 6 seconds. The total average response time is therefore 6 sec + 2 sec = 8 sec.b.The traffic intensity on the access link is reduced by 40% since the 40% of the requestsare satisfied within the institutional network. Thus the average access delay is(0.6 sec)/[1 – (0.6)(0.9)] = 1.2 seconds. The response time is approximately zero if therequest is satisfied by the cache (which happens with probability 0.4); the average response time is 1.2 sec + 2 sec = 3.2 sec for cache misses (which happens 60% of the time). So the average response time is (0.4)(0 sec) + (0.6)(3.2 sec) = 1.92 seconds. Thus the average response time is reduced from 8 sec to 1.92 sec.16. (P12) What is the difference between MAIL FROM: in SMTP and From: in the mail messageitself?Answer: The MAIL FROM: in SMTP is a message from the SMTP client that identifies the sender of the mail message to the SMTP server. The From: on the mail message itself is NOT an SMTP message, but rather is just a line in the body of the mail message.17. (P16) Consider distributing a file of F = 5 Gbits to N peers. The server has an upload rate ofu s = 20 Mbps, and each peer has a download rate of d i =1 Mbps and an upload rate of u. For N = 10, 100, and 1,000 and u = 100 Kbps, 250 Kbps, and 500 Kbps, prepare a chart giving the minimum distribution time for each of the combinations of N and u for both client-server distribution and P2P distribution.Answer: For calculating the minimum distribution time for client-server distribution, we usethe following formula:D cs = max {NF/u s , F/d min }Similarly, for calculating the minimum distribution time for P2P distribution, we use the following formula:D P2P = max{F/u s ,F/d min ,NF/( u s +∑u i n i=1 )} Where,F = 5 Gbits = 5 * 1024 Mbits u s = 20 Mbps d min = d i = 1 MbpsClient Server:N 10 100 1000 200 Kbps10240 51200 512000 u 600 Kbps10240 51200 512000 1Mbps10240 51200 512000Peer to Peer:N 10 100 1000 200 Kbps10240 25904.3 47559.33 U 600 Kbps10240 13029.6 16899.64 1 Mbps10240 10240 10240。

第二章 导数与微分1. ()().1,102-'=f x x f 试按定义求设200200(1)(1)10(1)10'(1)lim lim1020lim lim(1020)20x x x x f x f x f x xx x x x∆→∆→∆→∆→-+∆--∆---==∆∆∆-∆==∆-=-∆2. 下列各题中均假定()0x f '存在，按导数定义观察下列极限，指出此极限表示什么, 并将答案填在括号内。

⑴ ()()=∆-∆-→∆xx f x x f x 000lim（0'()f x -）； ⑵ ()=→∆xx f x 0lim （'(0)f ）， 其中()()存在；且0,00f f '= ⑶ ()()=--+→hh x f h x f h 000lim（02'()f x ）.3. 求下列函数的导数：⑴ ='=y x y ,4则34x ⑵ ='=y x y ,32则1323x -⑶ ='=y xy ,1则3212x -- ⑷ ='=y x x y ,53则115165x 4． 求曲线. 21,3 cos 程处的切线方程和法线方上点⎪⎭⎫⎝⎛=πx y'sin ,'()32y x y π=-=-所以切线方程为1()223y x π-=--2(1)03y +-+=班级 姓名学号法线方程为1)23y x π-=-化简得3)0x π+-= 5. 讨论函数⎪⎩⎪⎨⎧=≠=0 001sin 2x x xx y 在0=x 处的连续性和可导性. 20(0)01lim sin 0(0)()x f x f x→===因为有界量乘以无穷小 所以函数在0x =处连续因为 20001s i n(0)(0)1l i m l i m l i ms i n 0x x x x f x f x x x xx∆→∆→∆→∆+∆-==∆=∆∆∆ 所以函数在0x =处可导.6. 已知()()()()是否存在？又及求 0 ,0 0 ,0 2f f f x x x x x f '''⎩⎨⎧<-≥=-+ 2'00(0)(0)(0)lim lim 0h h f h f h f hh +→+→++-==='00(0)(0)(0)limlim 1h h f h f hf hh -→-→++--===- ''(0)(0)f f +-≠ '(0)f ∴不存在7. ()(). , 0 0sin x f x x x x x f '⎩⎨⎧≥<=求已知当0x <时, '()(sin )'cos f x x x ==; 当0x >时, '()()'1f x x ==;班级 姓名学号当0x =时'00(0)(0)(0)limlim 1h h f h f hf hh +→→+-===＋＋ '00(0)(0)sin (0)limlim 1h h f h f h f h h-→-→+-===－ '(0)1f ∴=综上，cos ,0'()1,0x x f x x <⎧=⎨≥⎩8. 求下列函数的导数：（1）;54323-+-=x x x y （2）;1227445+-+=x xx y 2222222232242222csc cot (1)2csc 2'(1)2(1)csc cot 4csc (1)23(3)(3ln )(2ln )(2)'(3ln )(94)ln 32(3ln )x x x x xy x x x x x x x x x x x x x x x y x x x x x x x x x x -+-=+-+-=+++-++=+-+-+=+ 2'364y x x =-+652'20282y x x x ---=--+ （3）;3253xx e x y +-= （4）;1sec tan 2-+=x x y2'152ln 23x x y x e =-+ 2'2s e c s e c t a ny x x x =+班级 姓名学号（5）;log 3lg 2ln 2x x x y +-= （6）()();7432x x y -+=123'ln10ln 2y x x x =-+ '422y x =--（7）;ln x xy =（8）;cos ln 2x x x y = 21ln 'x xx y x-= 221'2ln cos cos ln sin y x x x x x x x x x =+- 21ln x x-= 22l n c o s c o s l n s i n x x x x x x x x =+- （9）;1csc 22xxy +=2222csc cot (1)2csc 2'(1)x x x x xy x -+-=+ 2222(1)csc cot 4csc (1)x x x x xx -+-=+ （10）.ln 3ln 223x x x x y ++=2232223(3)(3ln )(2ln )(2)'(3ln )x x x x x x x x y x x ++-++=+ 4222(94)ln 32(3ln )x x x x x xx x -+-+=+ 9. 已知. ,cos 21sin 4πϕϕρϕϕϕρ=+=d d 求因为1s i n c o s s i n2d d ρϕϕϕϕϕ=+-班级 姓名学号所以4222422284d d πϕρπϕ==+-=+10. .1轴交点处的切线方程与写出曲线x xx y -= 令0y =，得11x x ==-或 因为2'1y x -=+， 所以 11'2,'2x x y y ==-==曲线在(1,0)处的切线方程为2(1)y x =-，即220x y --=； 曲线在(1,0)-处的切线方程为2(1)y x =+，即220x y -+=。

第2章人工智能与知识工程初步1. 设有如下语句，请用相应的谓词公式分别把他们表示出来：s(1)有的人喜欢梅花，有的人喜欢菊花，有的人既喜欢梅花又喜欢菊花。

解：定义谓词dP(x)：x是人L(x,y)：x喜欢y其中，y的个体域是{梅花，菊花}。

将知识用谓词表示为：(∃x )(P(x)→L(x, 梅花)∨L(x, 菊花)∨L(x, 梅花)∧L(x, 菊花))(2)有人每天下午都去打篮球。

解：定义谓词P(x)：x是人B(x)：x打篮球A(y)：y是下午将知识用谓词表示为：a(∃x )(∀y) (A(y)→B(x)∧P(x))(3)新型计算机速度又快，存储容量又大。

解：定义谓词NC(x)：x是新型计算机F(x)：x速度快B(x)：x容量大将知识用谓词表示为：(∀x) (NC(x)→F(x)∧B(x))(4)不是每个计算机系的学生都喜欢在计算机上编程序。

解：定义谓词S(x)：x是计算机系学生L(x, pragramming)：x喜欢编程序U(x,computer)：x使用计算机将知识用谓词表示为：¬(∀x) (S(x)→L(x, pragramming)∧U(x,computer))(5)凡是喜欢编程序的人都喜欢计算机。

解：定义谓词P(x)：x是人L(x, y)：x喜欢y将知识用谓词表示为：(∀x) (P(x)∧L(x,pragramming)→L(x, computer))2请对下列命题分别写出它们的语义网络： (1) 每个学生都有一台计算机。

解：(2) 高老师从3月到7月给计算机系学生讲《计算机网络》课。

解：(3) 学习班的学员有男、有女、有研究生、有本科生。

解：参例2.14(4) 创新公司在科海大街56号，刘洋是该公司的经理，他32岁、硕士学位。

解：参例2.10(5) 红队与蓝队进行足球比赛，最后以3：2的比分结束。

解：2.19 请把下列命题用一个语义网络表示出来： (1) 树和草都是植物； 解：(2) 树和草都有叶和根； 解：(3) 水草是草，且生长在水中； 解：(4) 果树是树，且会结果； 解：(5) 梨树是果树中的一种，它会结梨。

1. 已知某一时期内某商品的需求函数为Q =50-5P ，供给函数为Qs=-10+5p。

（1）求均衡价格Pe和均衡数量Qe，并作出几何图形。

（2）假定供给函数不变，由于消费者收入水平提高，使需求函数变为Qd=60-5P。

求出相应的均衡价格Pe 和均衡数量Qe ，并作出几何图形。

（3）假定需求函数不变，由于生产技术水平提高，使供给函数变为Qs=-5+5p。

求出相应的均衡价格Pe 和均衡数量Qe ，并作出几何图形。

（4）利用（1）（2 ）（3），说明静态分析和比较静态分析的联系和区别。

（5）利用（1）（2 ）（3），说明需求变动和供给变动对均衡价格和均衡数量的影响.解答: (1)将需求函数Qd = 50-5P和供给函数Qs =-10+5P 代入均衡条件Qd = Qs ,有: 50- 5P= -10+5P得: Pe=6以均衡价格Pe =6 代入需求函数Qd =50-5p ,得: Qe=20所以,均衡价格和均衡数量分别为Pe =6 , Qe=20 (图略)(2)将由于消费者收入提高而产生的需求函数Qd=60-5p 和原供给函数Qs=-10+5P, 代入均衡条件Q d= Qs ,有: 60-5P=-10+5P 得Pe=7以均衡价格Pe=7代入Qd方程，得Qe=25所以,均衡价格和均衡数量分别为Pe =7 , Qe=25 (图略)(3) 将原需求函数Qd =50-5p和由于技术水平提高而产生的供给函数Q =-5+5p ,代入均衡条件Qd =Qe ,有: 50-5P=-5+5P得Pe= 5.5以均衡价格Pe= 5.5 代入Qd =50-5p ,得22.5所以,均衡价格和均衡数量分别为Pe=5.5 Qe=22.5(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征.也可以说,静态分析是在一个经济模型中根据所给的外生变量来求内生变量的一种分析方法.以(1)为例,在图中,均衡点 E 就是一个体现了静态分析特征的点.它是在给定的供求力量的相互作用下所达到的一个均衡点.在此,给定的供求力量分别用给定的供给函数Q=-10+5P 和需求函数Q=50-5P表示，均衡点具有的特征是:均衡价格P=6 且当P =6 时,有Q= Q d= Qe =20 ，同时,均衡数量Qe= 20 ,且当Qe=20 时,有Pd=Ps=Pe=6 ，也可以这样来理解静态分析:在外生变量包括需求函数的参数(50,-5) 以及供给函数中的参数(-10,5)给定的条件下,求出的内生变量分别为P= 6 ，Qe =20依此类推,以上所描素的关于静态分析的基本要点,在(2)及其图和(3)及其图中的每一个单独的均衡点上都得到了体现。

第二章进程和线程作业答案1，2，4，6，7，10，11，12，14, 211.在操作系统中为什么要引入进程概念？它与程序的差别和关系是怎样的？答：由于多道程序的并发执行时共享系统资源，共同决定这些资源的状态，因此系统中各程序在执行过程中就出现了相互制约的新关系，程序的执行出现“走走停停”的新状态。

用程序这个静态概念已经不能如实反映程序并发执行过程中的这些特征。

为此，人们引入“进程（Process）”这一概念来描述程序动态执行过程的性质。

进程和程序是两个完全不同的概念。

进程与程序的主要区别：进程和程序之间存在密切的关系：进程的功能是通过程序的运行得以实现的，进程活动的主体是程序，进程不能脱离开具体程序而独立存在。

2.PCB的作用是什么？它是怎样描述进程的动态性质的？答：PCB是进程组成中最关键的部分。

每个进程有惟一的进程控制块；操作系统根据PCB对进程实施控制和管理，进程的动态、并发特征是利用PCB表现出来的；PCB是进程存在的唯一标志。

PCB中有表明进程状态的信息，该进程的状态包括运行态、就绪态和阻塞态，它利用状态信息来描述进程的动态性质。

4. 用如图2-26所示的进程状态转换图能够说明有关处理机的大量容。

试回答：①什么事件引起每次显著的状态变迁？②下述状态变迁因果关系能否发生？为什么？（A）2→1 （B）3→2 （C）4→1答：（1）就绪→运行：CPU空闲，就绪态进程被调度程序选中运行→阻塞：运行态进程因某种条件未满足而放弃CPU的占用。

阻塞→就绪：阻塞态进程所等待的事件发生了。

运行→就绪：正在运行的进程用完了本次分配给它的时间片（2）下述状态变迁（A）2→1，可以。

运行进程用完了本次分配给它的时间片，让出CPU，从就绪队列中选一个进程投入运行。

（B）3→2，不可以。

任何时候一个进程只能处于一种状态，它既然由运行态变为阻塞态，就不能再变为就绪态。

（C）4→1，可以。

某一阻塞态进程等到的事件出现了，而且此时就绪队列为空，该进程进入就绪队列后马上又被调度运行。

第二章注册会计师管理制度一、单项选择题1．申请人申请注册会计师的，必须满足从事（）工作两年以上。

A．审阅业务 B．税务代理业务 C．审计业务 D．代理记账业务2．申请人申请注册会计师，以下说法中正确的是（）。

A．申请人必须取得注册会计师证书，并从事税务服务工作两年以上B．申请人可以向省财政厅申请注册，并报经中国注册会计师协会备案C．申请人必须具备完全民事行为能力D．申请人必须具有本科学历3．验证企业资本，出具验资报告，是（）业务。

A．审计 B．审阅 C．其他鉴证业务 D．相关服务4．下列选项中，不属于注册会计师的其他审计业务的是（）。

A．对财务信息执行商定程序B．按照特殊目的编制基础编制的财务报表审计C．单一财务报表或财务报表特定要素审计D．简要财务报表审计5．当今世界中，成为注册会计师职业界组织形式发展的一大趋势的是（）。

A．独资会计师事务所 B．普通合伙会计师事务所C．有限责任会计师事务所 D．有限责任合伙会计师事务所6．设立合伙会计师事务所的条件是（）。

A．合伙人共同制定的章程 B．有会计师事务所的名称C．有不少于人民币30万元的注册资本 D．有5名以上的专职从业人员二、多项选择题1．申请人申请注册会计师的，不予注册的情形有（）。

A．不具有完全民事行为能力B．因为抢劫，被判以刑事处罚C．因在学校上学时打伤同学，被判以行政拘留D．自行停止执行注册会计师业务满半年的2．常见的其他鉴证业务有（）。

A．审阅业务 B．简要财务报表审计C．预测性财务信息审核 D．系统鉴证3．常见的相关服务业务有（）。

A．对财务信息执行商定程序 B．税务筹划C．验资 D．会计咨询4．各国会计师事务所的组织形式有（）。

A．独资会计师事务所 B．普通合伙会计师事务所C．有限责任会计师事务所 D．有限责任合伙会计师事务所5．下列关于注册会计师业务范围和会计师事务所责任的说法，不正确的有（）。

A．我国普通合伙会计师事务所以事务所的全部资产对其债务承担责任，不足部分由当事合伙人承担无限责任B．有限责任会计师事务所的出资人对事务所的债务承担全部责任C．有限责任会计师事务所的出资人对事务所的债务按照协议承担全部责任D．我国普通合伙会计师事务所的合伙人对会计师事务所的债务承担无限连带责任6．设立有限责任会计师事务所的条件有（）。

第二章课后习题思考题1.管理会计对成本是如何进行分类的？各种分类的主要目的是什么？管理会计将成本按各种不同的标准进行分类，以适应企业经营管理的不同需求。

1.按成本经济用途分类：制造成本和非制造成本。

主要目的是用来确定存货成本和期间损益，满足对外财务报告的需要。

2.按性态分类：固定成本、变动成本和混合成本。

按性态进行划分是管理会计这一学科的基石，管理会计作为决策会计的角色，其许多决策方法尤其是短期决策方法都需要借助成本性态这一概念。

3.按可控性分类：可控成本和不可控成本4.按是否可比分类：可比成本和不可比成本5.按特定的成本概念分类：付现成本和沉没成本、原始成本和重置成本、可避免成本和不可避免成本、差别成本和边际成本、机会成本6.按决策相关性分类：相关成本和无关成本2.按成本性态划分，成本可分为几类？各自的含义、构成和相关范围是什么？按成本性态可以将企业的全部成本分为固定成本、变动成本和混合成本三类。

（1）固定成本是指其总额在一定期间和一定业务量范围内，不受业务量变动的影响而保持固定不变的成本。

但是符合固定成本概念的支出在“固定性”的强弱上还是有差别的，所以根据这种差别又将固定成本细分为酌量性固定成本和约束性固定成本。

酌量性固定成本也称为选择性固定成本或者任意性固定成本，是指管理当局的决策可以改变其支出数额的固定成本。

约束性固定成本与酌量性固定成本相反，是指管理当局的决策无法改变其支出数额的固定成本，因而也称为承诺性固定成本，它是企业维持正常生产经营能力所必须负担的最低固定成本，其支出的大小只取决于企业生产经营的规模与质量，因而具有很大的约束性，企业管理当局不能改变其数额。

固定成本的“固定性”不是绝对的，而是有限定条件的，这种限定条件在管理会计中叫做相关范围，表现为一定的期间范围和一定的空间范围。

就期间范围而言，固定成本表现为在某一特定期间内具有固定性。

从较长时间看，所有成本都具有变动性，即使“约束性”很强的约束性固定成本也是如此。