人教版初中数学九年级：圆周角和圆心角的关系(1)1PPT课件

格式：pptx
大小：2.03 MB
文档页数：15

下载文档原格式

圆周角和圆心角的关系第一课时-ppt (1)

1、圆周角定义
顶点在圆上
D 这样的角叫圆周角。
两边都与圆相交
F
C
.O
E
想一想:
A
B
1.劣弧AB所对的圆心角有几个？
劣弧AB所对的圆周角有几个？
2.圆心O与圆周角的位置关系有哪几种？
探索：判断下列各图中，哪些是圆周角，为什么？
找出劣弧BC所对的圆周角
D A
B
C
2、圆心与圆周角的位置关系:
则⊙O的半径是 2 。
C
解：连接OA、OB ∵∠C=30 ° ，∴∠AOB=60 °
O
A B
又∵OA=OB ，∴△AOB是等边三角形
∴OA=OB=AB=2，即半径为2。
O
C
D
A B
变式：
5.若OA//BC, ∠C= 25°, 则 ∠ADB=_______
6.若 ∠C= 25°,点P在AB间滑动则∠AOP的取值范围______
A O
A O
B
C
B
C
点O在∠BAC的一边上点O在∠BAC内部
A O
C B
点O在∠BAC外部
1.三种情况进行证明：
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角， ∴∠AOC=∠B+∠A. ∵OA=OB， ∴∠A=∠B.
∴∠AOC=2∠B. 即 ∠ABC = 12∠AOC.
C
O
A
B
P
已知⊙O中弦AB等于半径，弦AB所对的圆心角的度数为 6,0°圆周角的度数为 30 °或 150。°
O
A
BLeabharlann 7.如图,OA，OB，OC都是⊙O的半径，∠ AOB=2∠ BOC，

人教版数学九年级上册圆周角课件PPT

24.1.4 圆周角（1）
1、复习提问:
(1)什么是圆心角？ (2)圆心角，弧，弦，弦心
距关系定理是什么？
名师课件免费课件下载优秀公开课课件人教版数学九年级上册24. 1.4圆周角课件
∠ACB与 ∠AOB 有何异同点？你知道∠ACB这一类的角名字吗？
圆周角的概念： C
顶点在圆上，两边与
定理
一条弧所对的圆周角等于它所对的圆心角的一半．
推论
在同圆或等圆中，同弧或等弧所
C2
对的圆周角相等
C1
C3
半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦 A 是直径．
·O
B
名师课件免费课件下载优秀公开课课件人教版数学九年级上册24. 1.4圆周角课件
名师课件免费课件下载优秀公开课课件人教版数学九年级上册24. 1.4圆周角课件
A
A
A
C
C
C
●O
●O
●O
B
B B
n 为了解决这个问题,我们先探究一条弧所对的圆周角和圆心角之间的关系.
名师课件免费课件下载优秀公开课课件人教版数学九年级上册24. 1.4圆周角课件
名师课件免费课件下载优秀公开课课件人教版数学九年级上册24. 1.4圆周角课件
议圆一议周角和圆心角的关系
为了进一步探究上面的发现，如图在⊙O任取一个圆周角 ∠BAC，将圆对折，使折痕经过圆心O和∠BAC的顶点 A．由于点A的位置的取法可能不同，这时折痕可能会；
（1）在圆周角的一条边上；
∵OA=OC，
A
O·
B
C
∴∠A=∠C．又∠BOC=∠A+∠C ∴∠BOC=2∠A

圆周角和圆心角的关系ppt课件

50°，则∠EBC+∠ADC 的度数为 _______.
-18-
3.4 圆周角和圆心角的关系
解析：如解析图，连接 AB，DE，则∠ABE=∠ADE. ∵ 所对的圆心角的度数为 50°，∴∠ABE= ∠ADE =25°. ∵ 点 A，B，C，D 在 ⊙O 上，∴四边形 ABCD 是圆内接四边形， ∴∠ABC+∠ADC=180°， ∴∠ABE+∠EBC+∠ADC=180°， ∴∠EBC+∠ADC=180°-∠ABE=180°-25°=155°．答案：155° 题型解法：本题考查了圆周角定理和圆内接四边形的性质，作出辅助线构建圆内接四边形是解题的关键．
-10-
3.4 圆周角和圆心角的关系
■考点四圆内接四边形
定义
四边形的四个顶点都在同一个圆上，这个四边形叫做圆内接四边形，这个圆叫做四边形的外接圆
推论圆内接四边形的对角互补
拓展圆内接四边形的任何外角等于内对角
注意并不是所有的四边形都存在外接圆，只有对角互补的四边形才存在外接圆
-11-
3.4 圆周角和圆心角的关系
A． 20° B． 40°
C． 50° D． 70°
-7-
3.4 圆周角和圆心角的关系
3. 如图，已知△ABC 的三个顶点都在同一圆上，且 AC=6，BC=8，AB=10，则该圆的半径长是 ________.
（第 3 题图）
（第 4 题图）
4. 如图，AB=BC，∠ABC =120°，AD 为 ⊙O 的直径，AD=6，那么 AB 的
值为 ______.
-8-
3.4 圆周角和圆心角的关系
5. 如图，AB=AC，AB 是直径，求证：BC=2DE．（第 5 题图）

圆周角和圆心角、弧的关系ppt课件

∵ OA = OC，∴ ∠ A = ∠ C. ∴ ∠ AOB = 2 ∠ C,
即 ∠ C = 1 ∠ AOB. 2
请你完成图 (2)和图 (3)两种情况的证明.
ppt课件
13
2. 圆周角定理：
知2－讲
圆周角的度数等于它所对弧上的圆心角度数的一半．
要点精析：
(1)圆周角相对于圆心的位置关系有三种，因此定理的证明
ppt课件
（来自《典中点》）
21
知2－练
4 (2015·海南)如图，将⊙O沿弦AB折叠，圆弧恰好经过圆心O，点P是 ¼ AMB 上一点，则∠APB的度数为( ) A．45° B．30° C．75° D．60°
ppt课件
（来自《典中点》）
22
知识点 3 同弧或等弧所对的圆周角
知3－导
想一想在如图的射门游戏中，当球员在B ， D，E处射门
ppt课件
（来自《典中点》）
19
知2－练
2 (2016·绍兴)如图，BD是⊙O的直径，点A，C在⊙O上， »AB »BC ，∠AOB＝60°，则∠BDC的度数是( ) A．60° B．45° C．35° D．30°
ppt课件
（来自《典中点》）
20
知2－练
3 (2015·珠海)如图，在⊙O中，直径CD垂直于弦AB，若 ∠C＝25°，则∠BOD的度数是( ) A．25° B．30° C．40° D．50°
圆周角定理：圆周角的度数等于它所对弧上的圆心角度数的一半.
（来自教材）
ppt课件
11
知2－讲
1. 圆周角定理的证明：已知：如图, ∠ C是 »AB 所对的圆周角， ∠ AOB是 »AB 所对的圆心角. 求证： ∠ C= 1 ∠ AOB 2 分析：根据圆周角和圆心的位置关系，分三种情况讨论：

《圆心角和圆周角(1)》ppt课件PPT课件

连接OD，OE，∵∠B＝60°，OD＝OB，∴△OBD为等边三角形， ∴BD＝OD，∴同理DE＝EC＝OD，∴BD＝DE＝EC
• 谢谢大家
• 再见
谢谢
• 十分感谢大家，再见！
10．(4分)在⊙ O与⊙ O′中，若∠AOB＝∠A′O′B′，则AB与A′B′ 的关
系为( )
D
A．AB＝A′B′
B．AB＞A′B′
C．AB＜A′B′
D．无法确定知A，B，C，D是⊙ O上四点，若AC＝BD，求证： AB＝CD.
15．(10分)如图，以⊙ O的直径BC为边作等边△ABC，AB，AC分别交⊙ O于点D，E. 求证：BD＝DE＝EC.
PPT图表：./tubiao/
PPT下载：./xiazai/
PPT教程： ./powerpoint/
资料下载：./ziliao/
范文下载：./fanwen/
试卷下载：./shiti/
教案下载：./jiaoan/
PPT论坛：
PPT课件：./kejian/
语文课件：./kejian/yuwen/ 数学课件：./kejian/shuxue/
28.3 圆心角和圆周角(一)
PPT教学课件
1．顶点在圆心的角叫做___圆__心__角_． 2．在同圆或等圆中，相等的圆心角所对的弦___相__等___，所对的弧也 ___相__等___；相等的弦或相等的弧所对的圆心角___相__等___．
1．(4分)已知，如图⊙ O的半径OA＝5 cm，弦CD＝5 cm，则弦CD所对圆心角为____6_0_°__． 2．(4分)下列说法正确的是( C ) A．如果一个角的一边过圆心，则这个角就是圆心角 B．圆心角α的取值范围是0°＜α＜180° C．圆心角就是顶点在圆心，且角的两边是两半径所在的射线的角 D．圆心角就是在圆心的角

圆周角和圆心角的关系精品PPT课件

演讲人：XXXXXX
时间：XX年XX月XX日
2、练习
①②
顶两
点边
A
在分
圆别
上与
圆
还
有
另
一
个
交
点
A
二、认识圆周角
A
P
B
P
B
O
O
P O
B
P
O
A
B
P O
A
B
三、探究圆周角与圆心角的关系
环节一：作图
.A B.
●O
我们今天就研究一条弧所对圆周角与圆心角的大小关系
一条弧对1个圆心角，对无数个圆周角从圆心与圆周角的位置关系来看，我们可以将这无数个圆心角分成三类：圆心在圆周角的边上，圆心在圆周角的内部，圆心在圆周角的外部。
∠ABC=
1 2
∠AOC
三、探究圆周角与圆心角的关系环节四：得出结论圆周角定理圆周角的度数等于它所对弧上的圆心角度数的_一__半__。
推论
同弧或等弧所对的圆周角______相__等。
三、探究圆周角与圆心角的关系
环节五：针对练习
1、如图，在⊙O中，∠BOC=50°，则∠BAC=
。
2、如图，点A，B，C是⊙O上的三点，∠BAC=40°，则∠BOC=
所用知识：①外角等于不相邻的两个内角之和；②圆的半径相等
三、探究圆周角与圆心角的关系
环节三：推理证明
AD C
O
连接BO并延长作直径，将问题
转化为第一种情况解答，转化
B
是一种很重要的数学方法
∠B=
1 2
∠AOC
三、探究圆周角与圆心角的关系环节三：推理证明
A C

圆周角和圆心角的关系(第1课时)课件

第三章圆
第三章圆
3.4 圆周角和圆心角的关系（第1课时）
学习目标
1.理解圆周角的概念，会叙述并证明圆周角定理. 2.理解圆周角与圆心角的关系并能运用圆周角定理及推
论解决简单的几何问题.（重点） 3.了解圆周角的分类，会推理验证“圆周角与圆心角的
关系”.（难点）
情景导入
如图，在足球射门的游戏中，球员射中球门的难易程度与他所处的位置B对球门AC的张角（∠BAC）有关．当球员在B 、D、E三点射门时，他所处的位置对球门AC分别形成三个张角∠BAC，∠BAC，∠BAC．这三个角的大小有什么关系？在这三点射门的效果一样吗？
B
O
C
B
（2）圆心角
O （3）
B
C
A（5）Biblioteka CO·B （6）
边AC没有与圆相交
圆周角 A
合作探究
活动1：圆周角与圆心角的关系
做一做: 如图，∠AOB=80°．
（1）请你画几个 A B 所对的圆周角？这几个圆
周角有什么关系？与同伴进行交流．（2）这些圆周角和圆心角∠AOB的大小有什么
关系？你是怎么发现的？与同伴进行交流．
求证： ∠C= 1 ∠AOB ． 2
分析：根据圆周角和圆心角的位置关系，分三种情况讨论：（1）圆心O在圆周角∠C的一边上，如图（1）；（2）圆心O在圆周角∠C的内部，如图（2）；（3）圆心O在圆周角∠C的外部，如图（3）．
证明：（1）当圆心O在圆周角∠C的一边上时，如图（1）．
∵∠AOB是△ACO的外角，
∠1=∠4，∠2=∠7， ∠3=∠6，∠5=∠8，
△AEB∽△DEC △AED∽△BEC
课堂小结
1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角. 2.圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半. 3.圆周角定理推论:同弧（或等弧）所对的圆周角相等 .

3.4圆周角和圆心角的关系-ppt

自检互评如图，AB是⊙O的直径，弦CD⊥AB 于点E,点P在⊙O上，∠1=∠C。（1）求证：CB∥PD （2）若BC=3，sinP=0.6，求⊙O的直径。
点O在∠BAC 外部
分别测量图中BC弧所对的圆周角BAC和圆心角∠AOC的度数，我们能发现什么结论？
1.首先考虑特殊情况：
当圆心(O)在圆周角(∠ABC)的一边(BC) 上时,圆周角∠ABC与圆心角∠AOC的大小关系.
A
∵OA=OB
C
∴∠ABC=∠BAO,
●O
又 ∵∠AOC=∠BAO+∠ABC, B
复习回顾
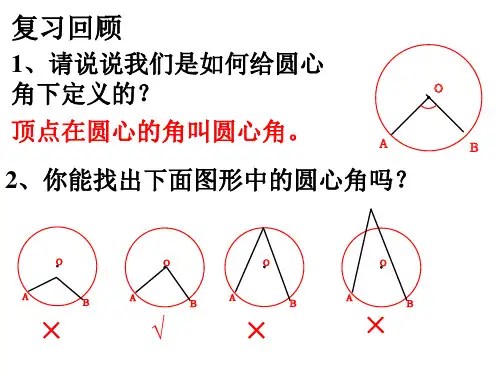
1、请说说我们是如何给圆心角下定义的？顶点在圆心的角叫圆心角。
2、你能找出下面图形中的圆心角吗？
×
√
×
×
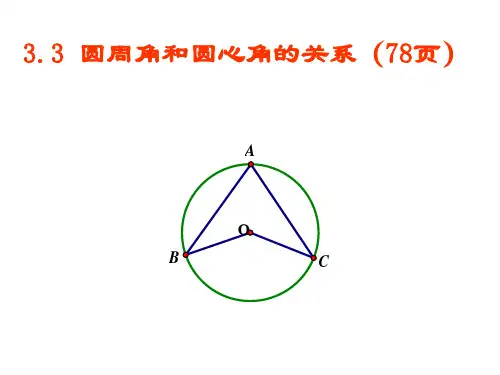
3.3 圆周角和圆心角的关系
3.在射门游戏中，球员射中球门的难易与他所处的位置B对球门的张角（∠ABC）有关，如图，当他站在B,D,E的位置射球时，对球门AC的大小相等吗？
B
（2）角的两边都与圆相交的角是 A
圆周角吗？
圆周角的特征：（1）角的顶点在圆上，（2）两边在圆内的部分是圆的两条弦
·
O C
1.判断下列各图中，哪些是圆周角，为什么？
图1 图2 图3
2.如图，A,B,C,D,E,是圆上的五个点，则图中共有____4______个圆周角，分别是
_∠__B_A_C_,∠_A_B_D_，_∠__A_C_E_，_∠_B_D. E,∠CED
A C D
O B
A
C
O
B ①
如图，连接BO并延长，与相交于点D。（此时我们得到与图①同
样的情形） ∵ ∠AOD是△ABO的外角， ∴ ∠ABD=∠A+∠ABO。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

⌒ ⌒
有没有圆周角？有没有圆心角？它们有什么共同的特点？
C 它们都对着同一条弧
下列图形中，哪些图形中的圆心角∠BOC和圆周角∠A是同对一条弧。
A
AO BAFra bibliotekA OB
C
C
O
D
C
B
C
A
B
A
O
B
D C
D
O
B
C
E
自己动手量一量同一条弧所对的圆心角和圆周角分别是多少度？
A A
O
O
B
C
B
C
一条弧所对的圆周角等于它所对的圆心角的一半
3.3 圆周角和圆心角的关系(1)
圆心角、弧、弦、弦心距之间的关系
D B
C O A
B
O
A
B'
O'
A'
在同圆或等圆中，
相等的圆心角所对的弧相等，所对的弦相等
圆心角、弧、弦、弦心距之间的关系
D B
C O A
B
O
A
B'
O'
A'
在同圆或等圆中，如果两个圆心角、两条弧、两条弦
中有一组量相等，那么它们所对应的其余各组量都分别相等
点与圆的位置关系有哪些?
当角的顶点发生变化时，这个角的位置有哪几种情况?
圆周角
A.
A.
A.
O.
O.
O.
B
C
B
C
B
C
圆周角定义: 顶点在圆上,
并且两边都和圆相交的角
A
叫圆周角.
特征：
① 角的顶点在圆上.
② 角的两边都与圆相交. B
.
O C
1.判别下列各图形中的角是不是圆周角。
A
B
C
D
E
F
G
A
O B
1.圆心角的定义? 答:顶点在圆心的角叫圆心角.
O.
B
C
在同圆或等圆中，
圆心角的度数和它所对的弧的度数的关系
我们把顶点在圆心的周角等分
成360份时，每一份的圆心角是 1°的角。
O.
因为同圆中相等的圆心角所对
的弧相等，所以整个圆也被等分 B
C
成360份。我们把每一份这样的
弧叫做1°的弧。
在同圆或等圆中，圆心角的度数和它所对的弧的度数相等。
A
O
B
C
A O
B
C
练习：
1.求圆中角X的度数
.O
C
70° x
A
B
A
D
C 120°
O.
XB
2.如图，圆心角∠AOB=100°，则∠ACB=___。
O
A
B
本课件可任意编辑，请在下载后
根据实际需求进行修改。
This courseware can be edited freely, please modify according to the actual needs after downloading.