当前位置：文档之家 › 解析几何第四版吕林根课后习题集规范标准答案第一章

解析几何第四版吕林根课后习题集规范标准答案第一章

  • 格式：doc
  • 大小：2.65 MB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

《解析几何》(第四版)吕林根许子道编第一章向量与坐标1.8两向量的向量积

《解析几何》(第四版)吕林根许子道编第一章向量与坐标1.8两向量的向量积

j
i
a
bYX(1XX1X12i(2(jiY1kiji))ZY1X1kY1)2Y(2j((iXk2ji)j) YY21XZj
(a
b)
c
a
c
b
c.
(1.8-5)
证
若
a,
b,
c中至少有一个是零矢
,
或a,
b,
c为一组
共线矢, (1.8 5)成立.
现假设不是上述情况.
设c 为c的单(a位矢b )，先c 证
a
c
b
c
.
证明向量积的分配律: (a+b)c=(a c)+(b c)
引理 a c a2
证明 两矢方向: 一致；引入
成立;
若
a
//
b ，则
a
b
a
b
b
sin (a, b )
a
ba
b a sin (a, b ),
即
a
b 与b
a模相等.
又由向量积定义，a
b 与b
a同时垂直于
a与b,
所其以次, a因 从 b与abba的共终线点. 来看
a,
b 决定的平面
,
顺序
b,
a,
b
a构成右手标架
o; b, a,b a
,
所以a
b与
b
a的方向相反 ,
从而得
a b b a.
定理1.8.4 向量积满足数因子的结 合律,即
为数，(a,ab)为 b任 意a向(量b.)
(a
b ).
(1.8-3)
推论 , 为任意实数，则
(a) (b ) ( )(a b ).

解析几何教程习题答案

解析几何教程习题答案

第一章 向量代数习题1.11. 试证向量加法的结合律，即对任意向量,,a b c 成立()().a b c a b c ++=++证明：作向量,,AB a BC b CD c ===（如下图），则 ()(),a b c AB BC CD AC CD AD ++=++=+=()(),a b c AB BC CD AB BD AD ++=++=+=故()().a b c a b c ++=++2. 设,,a b c 两两不共线，试证顺次将它们的终点与始点相连而成一个三角形的充要条件是0.a b c ++=证明：必要性，设,,a b c 的终点与始点相连而成一个三角形ABC ∆，则0.a b c AB BC CA AC CA AA ++=++=+== 充分性，作向量,,AB a BC b CD c ===，由于ABCabcABCDabca b +b c +0,a b c AB BC CD AC CD AD =++=++=+=所以点A 与D 重合，即三向量,,a b c 的终点与始点相连构成一个三角形。

3. 试证三角形的三中线可以构成一个三角形。

证明：设三角形ABC ∆三边,,AB BC CA 的中点分别是,,D E F （如下图），并且记,,a AB b BC c CA ===，则根据书中例 1.1.1，三条中线表示的向量分别是111(),(),(),222CD c b AE a c BF b a =-=-=- 所以，111()()()0,222CD AE BF c b a c b a ++=-+-+-=故由上题结论得三角形的三中线,,CD AE BF 可以构成一个三角形。

4. 用向量法证明梯形两腰中点连线平行于上、下底且等于它们长度和的一半。

证明：如下图，梯形ABCD 两腰,BC AD 中点分别为,E F ，记向量,AB a FA b ==，则,DF b =而向量DC 与AB 共线且同向，所以存在实数0,λ>使得.DC AB λ=现在,FB b a =+,FC b a λ=-+由于E 是BC 的中点，所以1111()()(1)(1).2222FE FB FC b a a b a AB λλλ=+=++-=+=+且A BabcE FD C111(1)()().222FE AB AB AB AB DC λλ=+=+=+ 故梯形两腰中点连线平行于上、下底且等于它们长度和的一半。

解析几何 第四版 课后答案

解析几何 第四版 课后答案

由上题结论知： AL + BM + CN = 0
∴OA + OB + OC = OL + OM + ON
4. 用矢量法证明，平行四边行的对角线互相平分. [证明]：如图 1-4，在平行四边形 ABCD 中，O 是对角线 AC，BD 的交点
∵ AD = OD − OA
BC = OC − OB
但 AD = BC
BM = 1 (BA + BC) 2
CN = 1 (CA + CB) 2
∴ AL + BM + CN = 1 ( AB + AC + BA + BC + CA + CB) = 0 2
从而三中线矢量 AL, BM ,CN 构成一个三角形。
3. 设 L、M、N 是△ABC 的三边的中点，O 是任意一点，证明
第 1 章 矢量与坐标
§1.1 矢量的概念
1.下列情形中的矢量终点各构成什么图形？
（1）把空间中一切单位矢量归结到共同的始点；
（2）把平行于某一平面的一切单位矢量归结到共同的始点；
（3）把平行于某一直线的一切矢量归结到共同的始点；
（4）把平行于某一直线的一切单位矢量归结到共同的始点.
[解]：（1Байду номын сангаас单位球面； （2）单位圆
＝3 PiGi ,
从而 OPi
＝ OAi + 3OGi 1+ 3
，
设 Ai (xi, yi, zi)(i＝1, 2, 3, 4)，则
G1
⎜⎛ ⎝
x2
+
x3 3
+
x4
,
y2 + y3 + y4 , 3

解析几何第四版吕林根课后习题答案一至三章

解析几何第四版吕林根课后习题答案一至三章

PA1 PO PA2 PO PAn PO 0





即
PA1 PA2 PAn n PO
§1.4 向量的线性关系与向量的分解
1．在平行四边形 ABCD 中， （1）设对角线 AZ a, BD b, 求 AB, BC , CD, DA. 解： AB
解?a?b?b?a?b?a?b?a?b?a?b?a?b?a?????????????????yxyyxxyyxxyxyx22?e?e?e?e?e?e?e?e?b?a?????????3132132142232?e?e?e?e?e?e?e?e?e?b?a???????????3213213213422232?e?e?e?e?e?e?e?e?e?b?a???????????321321321710322322323
OA OB + OC = OL + OM + ON .
7. 设 L、M、N 是△ABC 的三边的中点，O 是任意一点，证明 [证明] OA OL LA
OB OM MB OC ON NC OA OB OC OL OM ON ( LA MB NC )
1 1 1 1 b a , BC b a , CD b a , DA b a ．设边 BC 和 CD 的 2 2 2 2






（2）中点 M 和 N，且 AM P, AN q 求 BC , CD 。 解： AC
1 1 q P , BC 2MC 2 q P P q 3P 2 2








解析几何 第四版 课后答案

解析几何 第四版 课后答案
本文档为解析几何第四版课后答案的汇总，主矢量终点构成的图形，如单位球面、单位圆等。对于正六边形中的矢量相等问题，给出了详细的解答。在四边形中点连线矢量的证明题中，证明了平面和空间四边形中点的连线矢量关系。此外，还涉及了平行六面体中的矢量相等与相反关系的判断。在数量乘矢量部分，解答了使各式成立的矢量条件，如矢量垂直、同向、反向等。同时，提供了三角形中线矢量构成三角形的证明，以及平行四边形对角线互相平分的矢量法证明。最后，解答了关于平行四边形中心和任意一点矢量关系的问题。这些答案详细、准确，可供学习者对照检查自己的解题过程和结果，有助于加深对解析几何知识的理解。

吕林根解析几何(第四版)(完整课件)(1)

吕林根解析几何(第四版)(完整课件)(1)

即( ,但 e 0 ,则 x .即 x ' 0 x xe ' ) 0
xx'.
定理1.4.2 如果向量 e1 , e 2 不共线, 则向量
r 与 e1 , e 2 共面的充分必要条件是 r 可以用向
量 e1 , e 2 线性表示,即
r x e y e 1 2
并且系数 x , y 被 e1,e2, r 唯一确定.
而O M a ,O N b ,
O
M P m M B m ( O B O M ) m ( b a ) ,
N P n N A n ( O A O N ) n () a b ,

p a m () b am ( 1 ) a m b ,
10 ,所以 aa ,2 , , a 因为 1 n线性相关.
定理1.4.5 如果一组向量中的一部分向量
线性相关那么这一组向量就线性相关.
证明: 设有一组向量 a , , a , , a , , a ( s r ) 1 2 s r 其中一部分,如 aa 线性相关 , 即存在不 , , , a 1 2 s 全为0的 ,使得 ( i 1 , 2 , s )
F
C
P1
B
定义1.4.2 对于 n(n 1) 个向量 aa , ,2 , , a 1 n 如果存在不全为零的 n 个数 使得 , , , 1 2 n
a a a 0 .
1 1 2 2 n n
1 2 n
那么 n 个向量 aa 叫做线性相关,不是 ,2 , , a 1 n
充分性 设 a 中有一个向量是其 ( i 1 , 2 , n ) i 余向量的线性组合.设这个向量为 a n ,即 则

吕林根解析几何(第四版)(完整课件)1.7

吕林根解析几何(第四版)(完整课件)1.7

cC
AB PC
所以三高交于一点.
直角坐标系下数量积的坐标运算
定理1.7.3 设 a X1i Y1 j Z1k,b X 2i Y2 j Z2 k, 则 a b X1X 2 Y1Y2 Z1Z2.
证明: a b ( X1i Y1 j Z1k )( X 2i Y2 j Z2 k )
若 a,b 中没有 0 ,则(1)和(4)显然成立.
(2) 若 0 ,则等式成立.若 0,则
(a) b | b |射影 (a) | b | ( 射影 a )
b
b
( | b | 射影 b a) (a b) .
又 a (b) (b) a (b a) (a b), 所以
(a) b a (b) (a b).
2
X1X 2 i X1Y2i j X1Z1i k
2
Y1X 2 j i Y1Y2 j Y1Z2 j k
2
Z1X 2 k i Z1Y2 k j Z1Z2 k .
而 i, j,k是两两垂直的单位向量,则有
i j j i 0, j k k j 0, i k k i 0,
于各边平方和.
B
C
证明: 如图, OACB 中,
设 OA a,OB b,OC m, O
A
BA n ,则有 m a b,n a b ,所以
2
2
2
2
2
2
m a 2a b b , n a 2a b b .
所以
2
m
2
n
2
2a
2b2 ,即|
m
|2
|
n
|2
2
|
a
|2
2
|
b
|2
例2 证明: 如果一条直线与一个平面内的

解析几何版吕林根课后习题答案

解析几何版吕林根课后习题答案

第四章 柱面、锥面、旋转曲面与二次曲面§ 4.1柱面1、已知柱面的准线为：⎩⎨⎧=+-+=-+++-0225)2()3()1(222z y x z y x 且（1）母线平行于x 轴；（2）母线平行于直线c z y x ==,，试求这些柱面的方程。

解：（1）从方程⎩⎨⎧=+-+=-+++-0225)2()3()1(222z y x z y x 中消去x ，得到：25)2()3()3(222=-+++--z y y z 即：0235622=----+z y yz z y 此即为要求的柱面方程。

（2）取准线上一点),,(0000z y x M ，过0M 且平行于直线⎩⎨⎧==c z yx 的直线方程为：⎪⎩⎪⎨⎧=-=-=⇒⎪⎩⎪⎨⎧=+=+=z z t y y tx x zz t y y tx x 000000 而0M 在准线上，所以⎩⎨⎧=+--+=-++-+--02225)2()3()1(222t z y x z t y t x 上式中消去t 后得到：02688823222=--+--++z y x xy z y x 此即为要求的柱面方程。

2、设柱面的准线为⎩⎨⎧=+=z x z y x 222，母线垂直于准线所在的平面，求这柱面的方程。

解：由题意知：母线平行于矢量{}2,0,1- 任取准线上一点),,(0000z y x M ，过0M 的母线方程为：⎪⎩⎪⎨⎧+==-=⇒⎪⎩⎪⎨⎧-==+=t z z y y tx x tz z y y tx x 2200000而0M 在准线上，所以：⎩⎨⎧+=-++=-)2(2)2(22t z t x t z y t x 消去t ，得到：010*******22=--+++z x xz z y x 此即为所求的方程。

3、求过三条平行直线211,11,-=+=--==+==z y x z y x z y x 与的圆柱面方程。

解：过原点且垂直于已知三直线的平面为0=++z y x ：它与已知直线的交点为())34,31,31(),1,0,1(,0,0,0--，这三点所定的在平面0=++z y x 上的圆的圆心为)1513,1511,152(0--M ，圆的方程为： ⎪⎩⎪⎨⎧=++=-++++07598)1513()1511()152(222z y x z y x 此即为欲求的圆柱面的准线。

解析几何第四版吕林根 期末复习 课后习题(重点)详解

解析几何第四版吕林根 期末复习 课后习题(重点)详解

第一章 矢量与坐标§ 数量乘矢量4、 设→→→+=b a AB 5，→→→+-=b a BC 82，)(3→→→-=b a CD ，证明：A 、B 、D 三点共线． 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线，又∵B 为公共点，从而A 、B 、D 三点共线．6、 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点，证明：三中线矢量AL , BM , CN 可 以构成一个三角形. 证明： )(21AC AB AL +=Θ )(21+=)(21CB CA CN +=0)(21=+++++=++∴7.、设L 、M 、N 是△ABC 的三边的中点，O 是任意一点，证明 OB OA ++OC =OL ++.[证明] LA OL OA +=Θ MB OM OB += NC ON OC +=)(OM +++++=++∴ =)(CN BM AL ON OM OL ++-++ 由上题结论知：0=++ ON OM OL OC OB OA ++=++∴ 从而三中线矢量,,构成一个三角形。

8.、如图1-5，设M 是平行四边形ABCD 的中心，O 是任意一点，证明OA +OB ++OD ＝4OM .[证明]：因为OM ＝21(OA +), OM ＝21(OB +OD ), 所以 2＝21(OA +OB +OC +) 所以OA +OB ++OD ＝4OM .10、用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半．图1-5证明 已知梯形ABCD ，两腰中点分别为M 、N ，连接AN 、BN ． →→→→→→++=+=DN AD MA AN MA MN ，→→→→→→++=+=CN BC MB BN MB MN ，∴ →→→+=BC AD MN ，即§ 矢量的线性关系与矢量的分解3.、设一直线上三点A , B , P 满足AP ＝(－1),O 是空间任意一点，求证：OP ＝λλ++1[证明]：如图1-7，因为＝－OA ,PB ＝OB －,所以 －OA ＝ (OB －),(1+)OP ＝+,从而 OP ＝λλ++1OB.4.、在ABC ∆中,设,1e =2e =.(1) 设E D 、是边BC 三等分点,将矢量,分解为21,e e 的线性组合; （2）设AT 是角A 的平分线(它与BC 交于T 点),将分解为21,e e 的线性组合 解：（1）()12123131,e e e e -==-=-=Θ， 2111231323131e e e e e BD AB AD +=-+=+=，同理123132e e AE +=（2）因为||||TC ||11e e , 且 BT 与方向相同， 所以 BT ||21e e .由上题结论有AT ||||1||212211e e e e e +||||212112e e e e e e +.5．在四面体OABC 中，设点G 是ABC ∆的重心（三中线之交点），求矢量对于矢量,,,的分解式。

(完整版)解析几何课件(吕林根许子道第四版)(精)

(完整版)解析几何课件(吕林根许子道第四版)(精)

任意向量 r可以由向量 e1 , e2 , e3线性表示，或说空间
任意向量 r可以分解成向量 e1 , e2 , e3的线性组合，即
r xe1 ye2 ze3 ,
(1.4 3) 上一页 下一页
并且其中系数 x, y, z被e1 , e2 , e3 , r唯一确定.
返回
第一章 向量与坐标 §1.4向量的线性关系与向量的分解
这时e1 , e2 , e3叫做空间向量的基底 .
例2 证明四面体对边中点的连线交于一点，且
互相平分.
证 设四面体ABCD一组
D
对边AB,CD的中点E, F的连
线为EF ,它的中点为P1,其余
e3
两组对边中点分别为 P2 , P3 ,
下只需证P1 , P2 , P3三点重合
就可以了.取不共面的三向量 A
设 是一个数，向量a与 的乘积a规定为
(1) 0, (2) 0,
aa与a0同向，| a| | a|
(3) 0, a与a反向，| a|| | | a|
a 2a
1 a 2
下一页
返回
第一章 向量与坐标 §1.3 数乘向量

|
a a|

ea .
上式表明：一个非零向量除以它的模的结果是 一个与原向量同方向的单位向量.
上一页 下一页
返回
第一章 向量与坐标 §1.3 数乘向量
例1设AM是三角形ABC的中线，求证:
uuuur AM

1
uuur ( AB

uuuur AC)
2
如图
证
uuuur uuur uuuur uuuur uuur uuuur
D

解析几何课件(吕林根许子道第四版)(精)

解析几何课件(吕林根许子道第四版)(精)

空间中点与平面的关系
点在平面内：点 位于平面内满足 平面的定义和性 质
点在平面外：点 不在平面内与平 面平行或与平面 相交
点的轨迹：点按 照某种规律在平 面上移动形成轨 迹
点的射影：点在 平面上的投影与 原点连线与平面 的夹角关系
空间中直线与平面的关系
直线与平面的位置关系：直线要么在平面上要么与平面平行要么与平面相交 直线与平面的交点：直线与平面的交点称为直线在平面上的投影 直线与平面的角度：直线与平面之间的角度称为线面角可以通过几何或向量方法求解 直线与平面的距离：直线到平面的最短距离称为线到面的距离可以通过几何或向量方法求解
05
解析几何中的投影与透视
投影的基本概念
投影的定义：通过光线将物体投射到平面上生成影子。 投影的分类：中心投影、平行投影。 投影的应用：建筑设计、工程制图、动画制作等领域。 投影的性质：与光源、物体和投影面的位置关系有关。
透视的基本概念
透视的定义：通过透明平面观察物体研究物体在平面上的投影从而表现出物体的三维空间 感。
应用：在解析几何中坐标变换被广泛应用于解决各种实际问题如平面几何、 立体几何、曲线和曲面等。 意义：通过坐标变换可以深入理解几何图形的内在性质和规律进一步探索 几何图形的变换和对称等特性。
图形变换
平移变换：将图形在平面内沿某一方向移动一定的距离而不改变其形状和大小。 旋转变换：将图形绕某一点旋转一定的角度而不改变其形状和大小。 伸缩变换：将图形按一定的比例进行放大或缩小而不改变其形状和大小。 对称变换：将图形关于某一直线或点进行翻转或反射而不改变其形状和大小。
第四 版)(精).ppt
单击此处添加副标题
汇报人：
目录
01 课件概览 02 解析几何基础知识 03 解析几何中的曲线与方程 04 解析几何中的平面与空间 05 解析几何中的投影与透视 06 解析几何中的变换与对称

解析几何教程习题答案

解析几何教程习题答案

第一章 向量代数习题1.11. 试证向量加法的结合律，即对任意向量,,a b c 成立()().a b c a b c ++=++证明：作向量,,AB a BC b CD c ===（如下图），则 ()(),a b c A B B C C D A C C D A D++=++=+= ()(),a b c AB BC CD AB BD AD ++=++=+=故()().a b c a b c ++=++2. 设,,a b c 两两不共线，试证顺次将它们的终点与始点相连而成一个三角形的充要条件是0.a b c ++=证明：必要性，设,,a b c 的终点与始点相连而成一个三角形ABC ∆，则0.a b c AB BC CA AC CA AA ++=++=+== 充分性，作向量,,AB a BC b CD c ===，由于0,a b c AB BC CD AC CD AD =++=++=+=所以点A 与D 重合，即三向量,,a b c 的终点与始点相连构成一个三角形。

ABCabcABCDabca b +b c +3. 试证三角形的三中线可以构成一个三角形。

证明：设三角形ABC ∆三边,,AB BC CA 的中点分别是,,D E F （如下图），并且记,,a AB b BC c CA ===，则根据书中例 1.1.1，三条中线表示的向量分别是111(),(),(),222CD c b AE a c BF b a =-=-=- 所以，111()()()0,222CD AE BF c b a c b a ++=-+-+-=故由上题结论得三角形的三中线,,CD AE BF 可以构成一个三角形。

4. 用向量法证明梯形两腰中点连线平行于上、下底且等于它们长度和的一半。

证明：如下图，梯形ABCD 两腰,BC AD 中点分别为,E F ，记向量,AB a FA b ==，则,DF b =而向量DC 与AB 共线且同向，所以存在实数0,λ>使得.DC AB λ=现在,FB b a =+,FC b a λ=-+由于E 是BC 的中点，所以1111()()(1)(1).2222FE FB FC b a a b a AB λλλ=+=++-=+=+且 111(1)()().222FE AB AB AB AB DC λλ=+=+=+ 故梯形两腰中点连线平行于上、下底且等于它们长度和的一半。

解析几何第一章答案

解析几何第一章答案

习题1答案1.(1) 有两个分量为零；（2）有一个分量为零；（3）y 坐标为3；（4）z 坐标为±5.2.A 位于xOz 面上；B 位于yOz 面上；C 位于z 轴上；D 位于y 轴上.3.A 在Ⅳ卦限；B 在Ⅴ卦限；C 在Ⅷ卦限；D 在Ⅲ卦限.4. (1) （2，-3，1）,（-2，-3，-1）,（2，3，-1）;(2) （2，3，1）,（-2，-3，1）,（-2，3，-1）;(3) （-2，3，1）;(1)（a , b , -c ）, （-a , b , c ）, （a , -b , c ）;(2) （a , -b , -c ）,（-a , b , -c ）,（-a , -b , c ）;(3) （-a , -b , -c ）;5. 提示：CA =CB =66.（0，1，-2）.7. 134+e e ; 123243-+-e e e ; 3243107-+-e e e .8. 提示：2102AB BC CD AB ++=+=a b .9. B （-2，4，-3） 10. 21P P = (-2, -2, -2)； 521P P = (-10, -10, -10). 11. =a 3, =b 38, =c 3; 333(,,)333=a , 235(,,)383838-=b ,212(,,)333--=c ;12()()()()1111,,,2222AB BC CD DA =-=+=-=-+a b a b b a a b ..13.24334233CD BC ⎧=-⎪⎪⎨⎪=-⎪⎩l kl k.14.方法1：→+→=→AM OA OM .方法2：提示：延长 O M 至 N ，使 2ON OM =.15.提示：方法1：()()1123OM OA OB OC AM BM CM =+++++.方法2：坐标法.16.提示：→→→+=AM OA OM ,→→→+=BM OB OM ,→→→+=CM OC OM ,→→→+=DM OD OM17.提示：取AC 的中点O ，则OM ，ON 分别为中位线.18.1))(21→→→+=AC AB AD ,→→→-=AB AC BE 21,→→→-=AC AB CF 21.2) 0=++→→→CF BE AD .19．提示：→→+→-=+i 11OP OP OP i i λ.（其中2 λ）20. 提示：A ，B ，C 三点共线,→→→+=OB OA OC μλ其中21．提示：A ,B ,C ,D 四点共面→→→+=CA k BC k AD 21. 22．)(32321r r r ++=→ED 23.提示：过L 作LD=BM .24．提示：证向量共线.25.1)3a -2b +c =，2)5a +6b +c 26.→AB (1,3,3)27.B （3，4，4）28. A （-1，2，4）; B （8，-4，-2）.29. (1) 3,57++i j k ; (2) 18,10214-++i j k ;(3) cos ∠（a ，b ）=3221; sin ∠（a ，b ）= 527; tan ∠（a ，b ）=533. 30. (1) 10l =; (2) 2l =-.31. (1) 824j k --; (2) j k --; (3) 2 32. (1) 36; (2)3217, 3677. 33. 1.34.（1） 提示：()()()()[]⋅⋅-=-a a b c ac b a ab c a ac b .（2）提示： 因为 m 1m 2,所以，对该平面上任意矢量c ＝λm 1＋μm 2.（3）提示： BC AC AB =-, AD CD CA =- .35．(1)5；(2)-3；(3)72-；(4)11. 36.(1) 32-(2) 222123=++r 14=, r 与a ,b ,c 的夹角分别为arccos 1414，14arccos 7，314arccos .14(3)cos (,)∠=a b 3π (4)40λ=37.解：1)向量a ,b ,c 不共面，c 不能表成a ,b 的线性组合.2)向量a ,b ,c 共面,b a c 3221+= 3)向量a ,b ,c 共面,c 不能表成a ,b 的线性组合.38. B (10,0，513) 39.|AB |=149,AB 边上的中线长：2461,|BC |=292,BC 边上的中线长：352, |AC |=212,AC 边上的中线长：2341.40.1）20 2）11.41.1）x ·y =354,105,2310==y x ， 354(,)arccos242550∠=x y 2）x ·y =929,426,2237==y x ， 929(,)arccos 952962∠=x y42.(3a +2b )·(2a -5b ）=633314-，两向量间的夹角为π43. 43.略. 44.3=OL ，321531+=→OM ，(,)OL OM ∠3215633arccos --=45.D 分AB 的比为1，T 分AB 的中为b a .H 分AB 的线为θθcos 2cos 2ab b ab a--. 46．略.47．略.48. 略.49.1) a ×b=(6, 3 3), S=63;2） a ×b =(12,26, 8) , =2221S ; 3） a ×b = (72, 24, 0),=2410S . . 50．1) (2,1,2), (2, 1, 2).2) (16, 4, 16). 3) 2, 2.4) (3,4,5), (1, 2, 1).51.略.52.四面体的体积596V =. 53.提示：(a, b , c )=0.自我测验题1一、填空题.1.Ⅵ，(4,2,-6), (4,-2,-6)，(8,-4,8).2．68,(-5,15,-7),-34,9299.3.求面积、求垂直向量、证明平行问题.4.0⋅=a b ，(),,0=a b c5.在三轴上的射影，1-1对应.二、判断题.1.√2.×3.√4. ×5.×三、计算题.1.1) x 与 y 共线或 x 与 y 中至少有一个为 0 . 2） x 与 y 共线或 x 与 y 中至少有一个为 0 . .2. 3a +3b -5c .3.x =2||b a b b ⨯-a .4.x =ba c ab ⋅⨯+α. 5..096172,22,63=+--z y x四、证明题.1.提示：证AD AB 与共线.2.略.。

5-7解析几何吕林根第四版

5-7解析几何吕林根第四版

利用三角函数关系
cos2 α = 1 + cos 2α , sin2 α = 1 − cos 2α ,
2
2
sinα ⋅ cosα = sin 2α ,
2
(2)可化为：
a
'11
= a11 + a22 2
+
a11
− 2
a12
cos 2α
+
a12
sin 2α ,
a
'22
= a11 + a22 2
−
a11
5 −3 −3 2
I3 = −3 5 2 = −128. −3 2 2 −4
所以
I3 = −128 = −8, I2 16
而特征方程λ 2 − 10λ + 16 = 0 的两根为 = λ1 2= , λ2 8,
所以曲线的简化方程(略去撇号)为：
2x2 + 8 y2 − 8 =0,
曲线的标准方程(略去撇号)为
I '1 = a '11 + a '22 = a11 + a22 = I1,
= I '2
a '1= 1 a '12 a '12 a '22
a= 11 a12 a12 a22
I2;
而
a '11 a '12 a '13
I '3 = a '12 a '22 a '23
a '13 a '23 a '33
a11 a12 a11x0 + a12 y0 + a13
a22 ( y '+ y0 )2 + a33= a22 y '2 + 2a22 y0 y '+ a22 y02 + a33
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

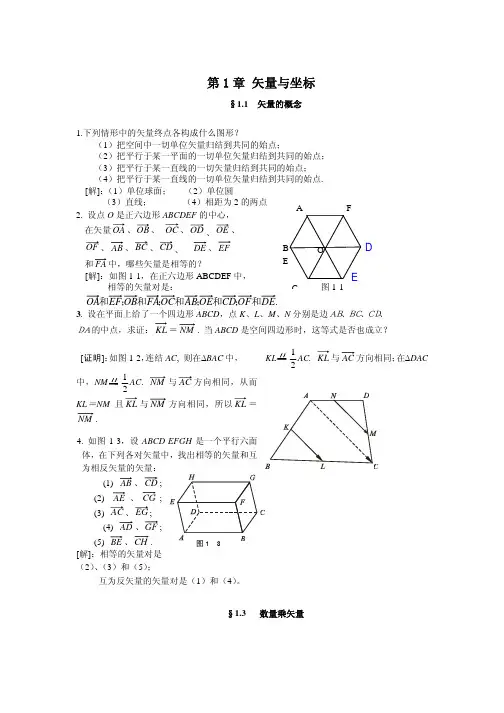
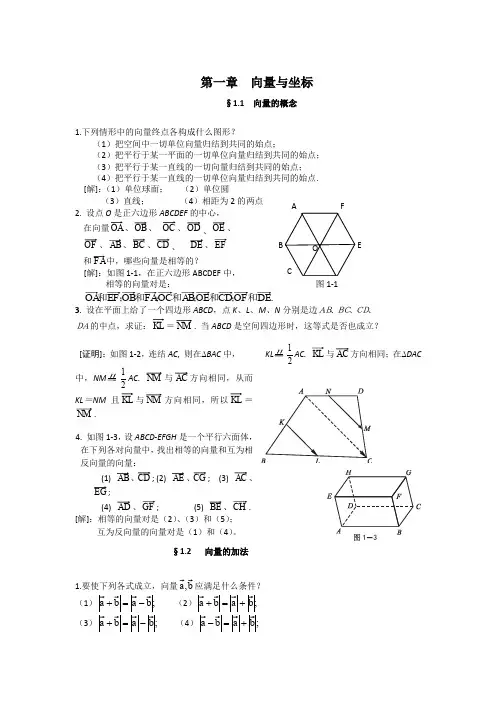
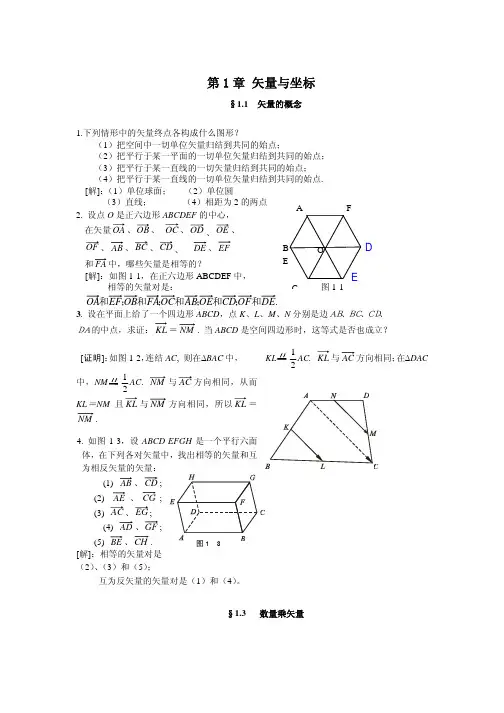
第一章 矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形？（1）把空间中一切单位矢量归结到共同的始点；（2）把平行于某一平面的一切单位矢量归结到共同的始点； （3）把平行于某一直线的一切矢量归结到共同的始点；（4）把平行于某一直线的一切单位矢量归结到共同的始点. [解]：（1）单位球面； （2）单位圆（3）直线； （4）相距为2的两点2. 设点O 是正六边形ABCDEF 的中心，在矢量、OB 、 、OD 、OE 、OF 、AB 、BC 、CD 、 DE 、 和中，哪些矢量是相等的？[解]：如图1-1，在正六边形ABCDEF 中，相等的矢量对是： 图1-1 .和和和和和3. 设在平面上给了一个四边形ABCD ，点K 、L 、M 、N 分别是边ＡＢ、ＢＣ、ＣＤ、ＤＡ的中点，求证：KL ＝NM . 当ABCD 是空间四边形时，这等式是否也成立？[证明]：如图1-2，连结AC , 则在∆BAC 中，21AC. KL 与方向相同；在∆DAC 中，21AC . NM 与AC 方向相同，从而KL ＝NM 且KL 与NM 方向相同，所以KL ＝NM .4. 如图1-3，设ABCD -EFGH 是一个平行六面体，在下列各对矢量中，找出相等的矢量和互为相反矢量的矢量：(1) AB 、; (2) AE 、;(3) 、;(4) AD 、GF ; (5) BE 、CH . [解]：相等的矢量对是（2）、（3）和（5）；互为反矢量的矢量对是（1）和（4）。

§1.2 矢量的加法1.要使下列各式成立，矢量b a ,应满足什么条件？C（1-=+ （2+=+ （3-=+ （4+= （5-=-[解]：（1）,-=+；（2）,+=+（3≥且,=+ （4）,+=（5）,≥-=-§1.3 数量乘矢量1 试解下列各题．⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x ．⑵ 已知→→→→-+=3212e e e a ，→→→→+-=321223e e e b ，求→→+b a ，→→-b a 和→→+b a 23．⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243，解出矢量→x ，→y ．解 ⑴→→→→→→→→→→→→→→-=+-+---+=-⋅+--⋅-ay b x b y a y b x a x b y a y b x a x b a y x b a y x 22)()()()(⑵ →→→→→→→→→→+=+-+-+=+3132132142232e e e e e e e e b a ，→→→→→→→→→→→-+-=+---+=-321321321342)223(2e e e e e e e e e b a ， →→→→→→→→→→→-+-=+---+=-3213213217103)223(2)2(323e e e e e e e e e b a ． 2 已知四边形ABCD 中，→→→-=c a AB 2，→→→→-+=c b a CD 865，对角线→AC 、→BD 的中点分别为E 、F ，求→EF ．解 →→→→→→→→→→→-+=-+-+=+=c b a c a c b a AB CD EF 533)2(21)865(212121．3 设→→→+=b a AB 5，→→→+-=b a BC 82，)(3→→→-=b a CD ，证明：A 、B 、D 三点共线． 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线，又∵B 为公共点，从而A 、B 、D 三点共线．4 在四边形ABCD 中，→→→+=b a AB 2，→→→--=b a BC 4，→→→--=b a CD 35，证明ABCD 为梯形．证明∵→→→→→→→→→→→→→=--=-+--++=++=BC b a b a b a b a CD BC AB AD 2)4(2)35()4()2( ∴→AD ∥→BC ，∴ABCD 为梯形．6. 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点，证明：三中线矢量AL , BM ,可 以构成一个三角形.[证明]： )(21AC AB AL +=Θ )(21BC BA BM +=)(21CB CA CN +=0)(21=+++++=++∴CB CA BC BA AC AB CN BM AL从而三中线矢量,,构成一个三角形。

7. 设L 、M 、N 是△ABC 的三边的中点，O 是任意一点，证明 OB OA ++OC =OL ++.[证明] LA OL OA +=Θ OM += NC ON OC +=)(NC MB LA ON OM OL OC OB OA +++++=++∴ =)(OM ++-++ 由上题结论知：0=++CN BM ALOM ++=++∴8. 如图1-5，设M 是平行四边形ABCD 的中心，O 是任意一点，证明OA +OB ++OD ＝4OM .[证明]：因为OM ＝21(OA +OC ), ＝21(OB +), 所以 2OM ＝21(OA +OB ++OD ) 所以OA +OB +OC +＝4.9 在平行六面体ABCDEFGH （参看第一节第4题图）中，证明图1-5→→→→=++AG AH AF AC 2．证明 →→→→→→→→→→→→=+++=+++=++AG CG FG AF AC DH AD AF AC AH AF AC 2． 10. 用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半． 证明 已知梯形ABCD ，两腰中点分别为M 、N ，连接AN 、BN ． →→→→→→++=+=DN AD MA AN MA MN ，→→→→→→++=+=CN BC MB BN MB MN ，∴ →→→+=BC AD MN ，即)(21→→→+=BC AD MN ，故→MN 平行且等于)(21→→+BC AD ．11. 用矢量法证明，平行四边行的对角线互相平分.[证明]：如图1-4，在平行四边形ABCD 中，O 是对角线AC ，BD的交点但 OB OCOA OD BCAD OBOC BC OA OD AD +=+-=-∴=-=-=Θ由于)(OC OA +∥,AC )(OD OB +∥,BD 而AC 不平行于BD ，∴0=+=+OB OD OC OA ，从而OA=OC ，OB=OD 。

12. 设点O 是平面上正多边形A 1A 2…A n 的中心，证明: 1OA +2OA +…+n OA ＝0ρ.[证明]：因为1OA ＋3OA ＝λ2OA , 2OA ＋4OA ＝λ3OA , ……1-n OA +1OA ＝λn OA ,n OA ＋2OA ＝λ1OA ,所以 2(1OA +2OA +…+n OA )＝λ(1OA +2OA +…+n OA ),所以 (λ－2)(1OA +2OA +…+n OA )＝0ρ. 显然 λ≠2, 即 λ－2≠0.所以 1OA +2OA +…+n OA ＝0ρ.13．在12题的条件下，设P 是任意点，证明：n PA PA PA n =+++K 21图1-4证明：21=+++n OA OA OA ΛΘ()()()21=-++-+-∴PA PA n Λ 即 n PA PA n =+++Λ21§1.4 矢量的线性关系与矢量的分解 1．在平行四边形ABCD 中，（1）设对角线,,==求.,,, 解：()()()()+-=-=+=--=21,21,21,21．设边BC 和CD 的（2）中点M 和N ，且==,求,。

解：()()P q P P q MC BC P q AC 32122,21-=⎪⎭⎫⎝⎛--==-=()+=⎪⎭⎫ ⎝⎛++-=-==21212222．在平行六面体ABCD-EFGH 中，设,,,321e e e ===三个面上对角线矢量设为,,,r AF q AH p AC ===试把矢量r q p a γμλ++=写成321,,e e e 的线性组合。

证明：2312,e e e e -==-==， 13e e r AF -==，γμλ++=()()()321e e e γμμλγλ++-++-=3. 设一直线上三点A , B , P 满足AP ＝λ(λ≠－1),O 是空间任意一点，求证：OP ＝λλ++1OBOA[证明]：如图1-7，因为AP ＝OP －,PB ＝－OP ,所以 OP －＝λ (－OP ),(1+λ)＝OA +λOB ,从而 OP ＝λλ++1OBOA .4. 在ABC ∆中,设,1e =2e =.(1) 设E D 、是边BC 三等分点,将矢量,分解为21,e e 的线性组合; （2）设AT 是角A 的平分线(它与BC 交于T 点),将AT 分解为21,e e 的线性组合 解：（1）()12123131,e e e e -==-=-=Θ， 2111231323131e e e e e +=-+=+=，同理123132e e +=（2）因为||||TC ＝||11e e , 且 BT 与方向相同，所以 BT ||21e . 由上题结论有||||1||22211e e e e e e +||||212112e e +5．在四面体OABC 中，设点G 是ABC ∆的重心（三中线之交点），求矢量OG 对于矢量,,,的分解式。

解：G Θ是ABC ∆的重心。

∴连接并延长与BC 交于P()()()AC AB AC AB AP AG AC AB AP +=+•==+=31213232,21Θ 同理()()+=+=31,31 C O()++=+=∴31（1） G P()++=+=31（2） A B()CB CA OC CG OC OG ++=+=31（3） （图1）由（1）（2）（3）得()()++++++++=31313++= 即()OC OB OA OG ++=316．用矢量法证明以下各题 （1）三角形三中线共点证明：设BC ，CA ，AB 中，点分别为L ，M ，N 。

AL 与BM 交于1P ，AL 于CN 交于2P BM 于CN 交于3P ，取空间任一点O ，则 A()BC BA OB BM OB BP OB OP ++=+=+=313211 ()()OC OB OA OB OC OB OA OB ++=-+-+=3131 A同理()OP ++=312 N M()OP ++=313 B L C321,,P P P ∴三点重合 O ∴三角形三中线共点 （图2） （第3页）7．已知矢量,不共线，问-=2与23-=是否线性相关？ 证明：设存在不全为0的μλ,，使得0=+μλ 即()()()()0232022=--+-⇒=--+-μλμλμλλ故由已知,不共线得{{0003202===-=--⇒μλμλμλ与假设矛盾， 故不存在不全为0的μλ,，使得0=+μλ成立。