理论力学(机械工业出版社)第十章动量定理习题解答
- 格式：doc
- 大小：246.00 KB
- 文档页数：10
下载文档原格式
合集下载
理论力学课后答案10
课
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
w.
kh
da
w.
co
我在沙滩上写上你的名字，却被浪花带走了；我在云上写上你的名字，却被风儿带走了；于是我在理论力 学的习题答案上写上我的名字.
10.9 质量为 m1 和 m2 的两重物，分别挂在两条绳子上，绳又分别绕在半径为 r1 和 r2 并装在同一轴的鼓轮上，已知鼓轮对转轴 O 的转动惯量为 J ，系统在重力作用 下发生运动，求鼓轮的角加速度。
kh
da
1 (a)： mr 2 2 1 (b)： m(r 2 2e 2 ) 2
w.
co
解：
我在沙滩上写上你的名字，却被浪花带走了；我在云上写上你的名字，却被风儿带走了；于是我在理论力 学的习题答案上写上我的名字.
10.2 如图所示，质量为 m 的偏心轮在水平地面上作平面运动。轮子轴心为 A ， 质心为 C ， AC e ，轮子半径为 R ，对轴心 A 的转动惯量为 J A ； C 、 A 、 B 三 点在同一铅直线上。 (1)当轮子只滚不滑时，若 v A 已知，求轮子的动量和对地面上 B 点的动量矩。 (2)当轮子又滚又滑时，若 v A 、 已知，求轮子的动量和对地面上 B 点的动量矩。
魏 魏
泳 泳
涛 涛 涛
m
系统对 z 轴动量矩守恒。设圆盘角速度为 。则圆盘和人对轴 z 的动量矩分 别为 1 hz1 MR 2 2 ds hz 2 rm(r ) mr 2 mrat dt 初始时刻动量矩为零： hz1 hz 2 0 2mrat MR 2 2mr 2 2mra MR 2 2mr 2
魏 魏 魏
后
泳 泳 泳
理论力学 第十章 动量定理
惯性运动。
——质点动量守恒定律
22
第十章 动量定理
二、质点系的动量定理
对质点系内任一质点i
：
d dt
(mivi )
=
Fi
=
F (e) i
+
F (i) i
∑ ∑ ∑ 对整个质点系：
d dt
(mivi
)
=
F (e) i
+
F (i) i
∑ Q Fi(i) = 0
∑ ∑ d dt
(mivi
)
=
d dt
(mivi
)
=
dp dt
∑ d p =
dt
F (e) i
——质点系的动量定理
即：质点系的动量对时间的一阶导数等于作用于质点系 所有外力的矢量和（外力系的主矢）。
23
第十章 动量定理
∑ 结论：只有外力才能改变质点系的动 d p =
量，内力不能改变整个质点系的动量。 d t
F (e) i
微分形式
∑ ∑ d p =
Oω
vC
vC
ω
C
C
C
(a)
(b)
(c)
解：(a) 长为 l、质量m的均质细杆，角速度为ω 。
则其动量为
p=
mvC
= m⋅ l ω
2
=
ml ω
2
方向与质心速度方向相同。
12
第十章 动量定理
Oω
vC
vC
C
C
vC = 0
ω
C
(a)
(b)
(c)
(b) 质量为m的均质滚轮，质心的速度为vC 。
p = mvC
2. 与质点动力学基本方程的比较
——质点动量守恒定律
22
第十章 动量定理
二、质点系的动量定理
对质点系内任一质点i
：
d dt
(mivi )
=
Fi
=
F (e) i
+
F (i) i
∑ ∑ ∑ 对整个质点系：
d dt
(mivi
)
=
F (e) i
+
F (i) i
∑ Q Fi(i) = 0
∑ ∑ d dt
(mivi
)
=
d dt
(mivi
)
=
dp dt
∑ d p =
dt
F (e) i
——质点系的动量定理
即：质点系的动量对时间的一阶导数等于作用于质点系 所有外力的矢量和（外力系的主矢）。
23
第十章 动量定理
∑ 结论：只有外力才能改变质点系的动 d p =
量，内力不能改变整个质点系的动量。 d t
F (e) i
微分形式
∑ ∑ d p =
Oω
vC
vC
ω
C
C
C
(a)
(b)
(c)
解：(a) 长为 l、质量m的均质细杆，角速度为ω 。
则其动量为
p=
mvC
= m⋅ l ω
2
=
ml ω
2
方向与质心速度方向相同。
12
第十章 动量定理
Oω
vC
vC
C
C
vC = 0
ω
C
(a)
(b)
(c)
(b) 质量为m的均质滚轮，质心的速度为vC 。
p = mvC
2. 与质点动力学基本方程的比较
《理论力学》第十章--动量矩定理试题及答案
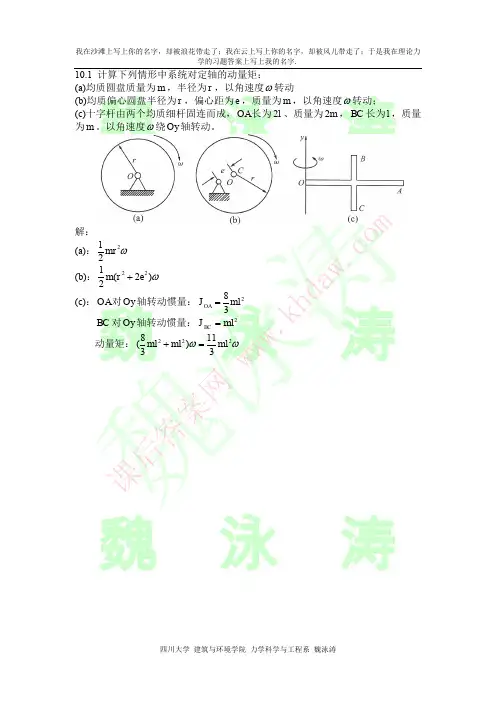
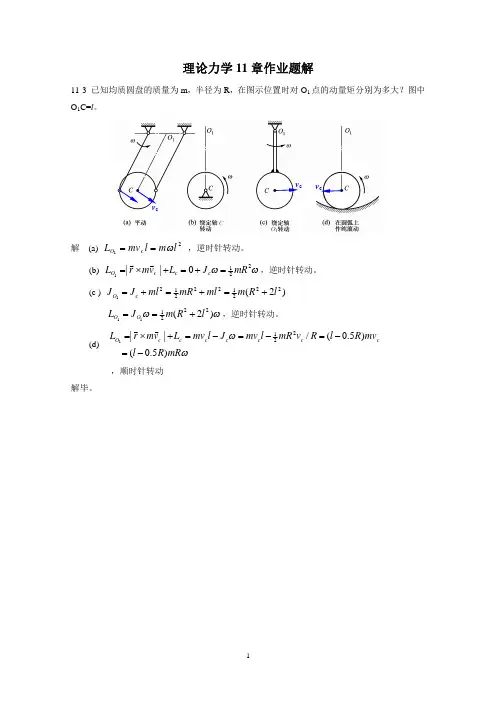
理论力学11章作业题解11-3 已知均质圆盘的质量为m ，半径为R ，在图示位置时对O 1点的动量矩分别为多大？图中O 1C=l 。
解 (a) 21l m l mv L c O w == ，逆时针转动。
(b) w w 2210||1mR J L v m r L c c c O =+=+´=rr ，逆时针转动。
(c ) )2(2221222121l R m ml mR ml J J c O +=+=+=w w )2(222111l R m J L O O +==，逆时针转动。
(d)ww mR R l mv R l R v mR l mv J l mv L v m r L c c c c c c c O )5.0()5.0(/||2211-=-=-=-=+´= r r，顺时针转动解毕。
v cv cv c11-5 均质杆AB 长l 、重为G 1，B 端刚连一重G 2的小球，弹簧系数为k ，使杆在水平位置保持平衡。
设给小球B 一微小初位移0d 后无初速度释放，试求AB 杆的运动规律。
解 以平衡位置（水平）为0=j ，顺时针转为正。
平衡时弹簧受力为：)5.0(312G G F s +=弹簧初始变形量：k G G k F s st /)5.0(3/12+==d在j 角时弹簧的拉力为（小位移）：3/)5.0(3)3/(12l k G G l k F st s j j d ++=+=¢系统对A 点的动量矩：j j j&&&221233l gG G l l g G J L A A +=×+= 对点的动量矩定理)(/å=Ei A A F M dt dL r ：j j 93/5.033221221kl l F lG lG l g G G s -=¢-+=+&& 0)3(321=++j jG G gk &&，令)3(3212G G gkp +=则有02=+j jp &&，其解为： )cos()sin(pt B pt A +=j由初始条件0| ,/|000====t t l jd j &得l B A / ,00d ==。
理论力学
1、运动分析。----说明机构中主要构件的运动形式。 2、作速度分析，需要画出相关速度，求一点速度或图形角
速度。（若要分析加速度，一般需要求图形的角速度）
画速度 （1）沿点的运动轨迹切线，与相关的角速度方向协调。
（2）要符合速度投影定理。
3、作加速度分析，需要画出相关加速度，求一点加速度 或图形角加速度。 画加速度
例8-10
如图所示，在椭圆规的机构中，曲柄OD以匀角速度ω绕O 轴转动。
OD＝AD＝BD＝l。求：当 60 时，尺AB的角加速度和点A的加速度。
B ABC AB D
O O
O
A A
vD
O
aA
n a BA
a A B
aD
v A
aD
n a AD y’ a AD
n a AD l 2
n x’ a A cos aD cos 2 a AD
y’ n a A 0 aD sin aAD cos a AD sin
x’
若OD变速转动，有什么变化？
a A l
2
a 0 AD AD
a AD 0 AD
解：
（1）动点：OA上的A点
动系：摇杆O1B
（2）运动分析： 绝对运动： 圆周运动。 相对运动： 直线运动。 牵连运动： 摇杆转动。
（3）速度分析与计算
v a r
ve
O ω
va
B vr
A ω1
vr va cos
ve va sin
r 2 O1 1 2 2 O1 A l r ve
理论力学课后的习题及答案解析...doc
第一章习题4-1．求图示平面力系的合成结果，长度单位为m。
解：(1) 取O点为简化中心，求平面力系的主矢：求平面力系对O点的主矩：(2) 合成结果：平面力系的主矢为零，主矩不为零，力系的合成结果是一个合力偶，大小是260Nm，转向是逆时针。
习题4－3．求下列各图中平行分布力的合力和对于A点之矩。
解：(1) 平行力系对A点的矩是：取B点为简化中心，平行力系的主矢是：平行力系对B点的主矩是：向B点简化的结果是一个力R B和一个力偶M B，且：如图所示；将R B向下平移一段距离d，使满足：最后简化为一个力R，大小等于R B。
其几何意义是：R的大小等于载荷分布的矩形面积，作用点通过矩形的形心。
(2) 取A点为简化中心，平行力系的主矢是：平行力系对A点的主矩是：向A点简化的结果是一个力R A和一个力偶M A，且：如图所示；将R A向右平移一段距离d，使满足：最后简化为一个力R，大小等于R A。
其几何意义是：R的大小等于载荷分布的三角形面积，作用点通过三角形的形心。
习题4-4．求下列各梁和刚架的支座反力，长度单位为m。
解：(1) 研究AB杆，受力分析，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
(2) 研究AB杆，受力分析，将线性分布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
(3) 研究ABC，受力分析，将均布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
习题4-5．重物悬挂如图，已知G=1.8kN，其他重量不计；求铰链A的约束反力和杆BC所受的力。
解：(1) 研究整体，受力分析（BC是二力杆），画受力图：列平衡方程：解方程组：反力的实际方向如图示。
习题4-8．图示钻井架，G=177kN，铅垂荷载P=1350kN，风荷载q=1.5kN/m，水平力F=50kN；求支座A的约束反力和撑杆CD所受的力。
《理论力学》第10章 质心运动定理
第10章 质心运动定理
26
3、求质心加速度
aC
aB
aCt B
aCnB
4、质心运动定理求约束力，受力分析
ma Cx FixE FA sin450 maCy FiyE FB mg FA cos 450
O
450
1m
A
C
vB
aB
450
B
FA
A
mg
x
FB
C
450
B
★理论力学电子教案
0
px const
★理论力学电子教案
第10章 质心运动定理
18
例题 图示机构，均质杆OA长l，质量为m1，滑块A的质量为m2， 滑道CD的质量为m3。OA杆在一力偶（图中未画出）作用下作 匀角度ω转动。试求O处的水平约束反力（机构位于铅直平面
内，各处摩擦不计）。 C
A
O
E
D
★理论力学电子教案
第10章 质心运动定理
第10章 质心运动定理
27
ma A
第10章 质心运动定理
14
M
C aC mg
FN
F
★理论力学电子教案
第10章 质心运动定理
§2 质点系动量、冲量
质点动量： 质点系动量：
p mv
P mivi mvC
问：刚体系动量？
元冲量：
dI F dt
冲量：
t2 t2
I dI F dt
t1
t1
15
p mv
★理论力学电子教案
第10章 质心运动定理
1
第十章 质心运动定理&动量定理
★理论力学电子教案
第10章 质心运动定理
理论力学课后习题答案 第10章 动能定理及其应用 )
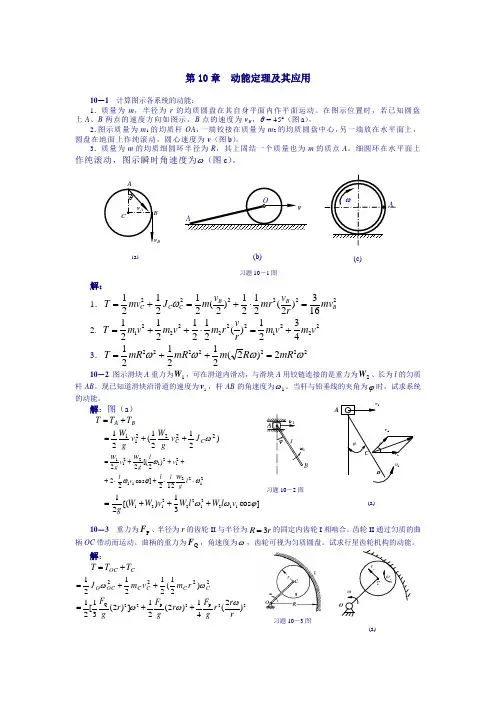
(a)A(a)O第10章 动能定理及其应用10－1 计算图示各系统的动能：1．质量为m ，半径为r 的均质圆盘在其自身平面内作平面运动。
在图示位置时，若已知圆盘上A 、B 两点的速度方向如图示，B 点的速度为v B ，θ = 45º（图a ）。
2．图示质量为m 1的均质杆OA ，一端铰接在质量为m 2的均质圆盘中心，另一端放在水平面上，圆盘在地面上作纯滚动，圆心速度为v（图b ）。
3．质量为m 的均质细圆环半径为R ，其上固结一个质量也为m 的质点A 。
细圆环在水平面上作纯滚动，图示瞬时角速度为ω（图c ）。
解：1．222222163)2(2121)2(212121BB BC C C mv r v mr v m J mv T =⋅+=+=ω 2．222122222214321)(21212121v m v m r v r m v m v m T +=⋅++=3．22222222)2(212121ωωωωmR R m mR mR T =++=10－2 图示滑块A 重力为1W ，可在滑道内滑动，与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。
现已知道滑块沿滑道的速度为1v ，杆AB 的角速度为1ω。
当杆与铅垂线的夹角为ϕ时，试求系统的动能。
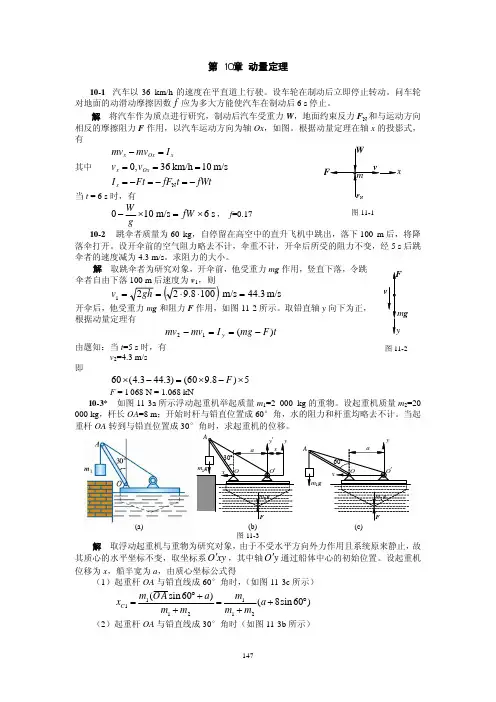
解：图（a ）B A T T T +=)2121(21222211ωC C J v g W v g W ++=21221121212211122]cos 22)2[(22ωϕωω⋅⋅+⋅++++=l gW l l v l v l g W v g W]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10－3 重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。
齿轮II 通过匀质的曲柄OC 带动而运动。
曲柄的重力为Q F ，角速度为ω，齿轮可视为匀质圆盘。
试求行星齿轮机构的动能。
华中科技大学理论力学习题答案
量为P3 ; 轮A上作用常力矩M1 。
求 物体C上升的加速度。
解:
取轮A为研究对象12
P1 g
r12
1
M1
Tr1
(1)
取轮B连同物体C为研究对象
d dt
(
1 2
P2 g
r2 2
2
P3 g
v r2
)T
'r2
P3
r2
(2)
补充运动学条件 r22 v, r22 a r11
化简(2)
得：P2
2 2g
F
左边可写成
r
d
(mv dt
)
d dt
(r
mv
)
dr dt
mv
而dr dt
mv
v
mv
0
,
r F mO (F ) ,
故：
d dt
(r
mv
)r
F
,
ddt[mO (mv )]mO (F )
质点对任一固定点的动量矩对时间的导数，等于作用在质 点上的力对同一点之矩。这就是质点对固定点的动量矩定理。
5
将上式在通过固定点O的三个直角坐标轴上投影，得
，得
19
（2）由质心运动定理
FN (m m1 m2 )g (m m1 m2 )aCy
aCy
yC
mi yi mi
m1a1 m2a2 m m1 m2
(m1r1 m2r2 )
m m1 m2
FN (m m1 m2 )g (m1r1 m2r2 )
（3） 研究 m1
222111rvmrvmjloo????120cynammmgmmmf2121??????212211212211mmmrmrmmmmamammymyaiiiccy????????????????????111111rmamfgmt???111?rgmft??221121rmrmgmmmfn???????2由质心运动定理3研究1m?222222rmamgmft???222?rgmft??2m4研究21一动力学方程对于一个定轴转动刚体代入质点系动量矩定理有?zzjl?ezzmjdtd??22ezzezzmdtdjmj?????或刚体定轴转动微分方程解决两类问题
理论力学练习册及答案
8-7.四杆机构中，曲柄OA以匀角速度ω0=25 rad/s绕O轴转动，OA=50 cm，AB=100 cm，O1B= cm。求∠OAB=900时，B点的加速度，摇臂O1B的角速度和角加速度。
8-8.图示机构中，设当OA与水平线成450角的瞬时，曲柄OA有反时针方向的匀角速度ω＝25 rad/s，连杆AB水平，扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。
解：将力系向A点简化，并过A点建立如图所示坐标系。
由矢量式可得力系简化的最终结果为力螺旋，
作用点为：
3-2.已知A（1，0，1），B（0，1，2）（长度单位为米），F= kN。求力F对x、y、z轴的矩？
解：
3-3.如图所示，长方体边长为a、b、c，力F沿BD，试计算力F对AC轴之矩MAC(F)
解：力F对C点的矩为：
4-3.置于铅垂面内的均质正方形簿板重P= 100kN，与地面间的摩擦系数f= 0.5，欲使簿板静止不动，求作用在点A的力F的最大值？
4-4.折梯放在水平地面上，其两脚与地面的摩擦系数分别为fA= 0.2，fB= 0.6，折梯一边AC的中点D上有一重为P= 500N的重物，折梯重量不计，问折梯能否平衡？如果折梯平衡。试求出两脚与地面间的摩擦力。
第六章 刚体基本运动
6-1．在如图所示中，已知ω、。在图上标示出A、B两的速度、加速度。
6-2．在如图所示的平面机构中，半径为r的半圆盘在A和B处与杆铰接，已知 ， ,曲柄O1A以匀角速度ω转动。求图示瞬时圆盘上M点的速度和加速度。
6-3．在如图所示的平面机构中，齿轮1紧固在杆AC上， ,齿轮1与半径为r2的齿轮2啮合，齿轮2可绕O2轴转动，。设 ， ，试确定 时，轮2的角速度和角加速度。
解：动点取曲柄OA上A点，
8-8.图示机构中，设当OA与水平线成450角的瞬时，曲柄OA有反时针方向的匀角速度ω＝25 rad/s，连杆AB水平，扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。
解：将力系向A点简化，并过A点建立如图所示坐标系。
由矢量式可得力系简化的最终结果为力螺旋，
作用点为：
3-2.已知A（1，0，1），B（0，1，2）（长度单位为米），F= kN。求力F对x、y、z轴的矩？
解：
3-3.如图所示，长方体边长为a、b、c，力F沿BD，试计算力F对AC轴之矩MAC(F)
解：力F对C点的矩为：
4-3.置于铅垂面内的均质正方形簿板重P= 100kN，与地面间的摩擦系数f= 0.5，欲使簿板静止不动，求作用在点A的力F的最大值？
4-4.折梯放在水平地面上，其两脚与地面的摩擦系数分别为fA= 0.2，fB= 0.6，折梯一边AC的中点D上有一重为P= 500N的重物，折梯重量不计，问折梯能否平衡？如果折梯平衡。试求出两脚与地面间的摩擦力。
第六章 刚体基本运动
6-1．在如图所示中，已知ω、。在图上标示出A、B两的速度、加速度。
6-2．在如图所示的平面机构中，半径为r的半圆盘在A和B处与杆铰接，已知 ， ,曲柄O1A以匀角速度ω转动。求图示瞬时圆盘上M点的速度和加速度。
6-3．在如图所示的平面机构中，齿轮1紧固在杆AC上， ,齿轮1与半径为r2的齿轮2啮合，齿轮2可绕O2轴转动，。设 ， ，试确定 时，轮2的角速度和角加速度。
解：动点取曲柄OA上A点，
理论力学 第六版部分习题答案 第十章
上式代入式（4）得
FN = 4mB g − mB
10-6 如图 11-10a 所示，质量为 m 的滑块 A，可以在水平光滑槽中运动，具有刚性系 数为 k 的弹簧 1 端与滑块相连接，另 1 端固定。杆 AB 长度为 l，质量忽略不计，A 端与滑 块 A 铰接，B 端装有质量 m1，在铅直平面内可绕点 A 旋转。设在力偶 M 作用下转动角速度 ω 为常数。求滑块 A 的运动微分方程。
F = 1 068 N = 1.068 kN 10-3* 如图 11-3a 所示浮动起重机举起质量 m1=2 000 kg 的重物。设起重机质量 m2=20 000 kg，杆长 OA=8 m；开始时杆与铅直位置成 60°角，水的阻力和杆重均略去不计。当起 重杆 OA 转到与铅直位置成 30°角时，求起重机的位移。
vC = 2vC1 = lω
代入式(1)，得
149
p=
lω (5m1 + 4m2 ) （方向如图 11-7b 所示） 2
A
p
vC
C
vC1
ω
O
ωt
C1
B
(a) 图 11-7
(b)
10-5
质量为 m1 的平台 AB，放于水平面上，平台与水平面间的动滑动摩擦因数为 f。
质量为 m2 的小车 D，由绞车拖动，相对于平台的运动规律为 s = 不计绞车的质量，求平台的加速度。
棱柱 B 接触水平面时系统质心坐标
a b ⎤ ⎡ m A (l − ) + m B ⎢l − (a − )⎥ 3 3 ⎦ 3(m A + m B )l − a(m A + 3m B ) + m B b ⎣ ′ = = xC m A + mB 3(m A + m B )
理论力学第十章作业答案
v A O A B C D 300w 0
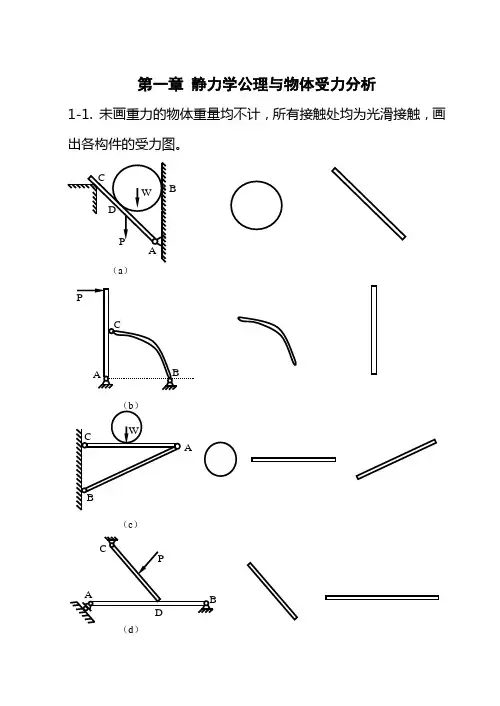
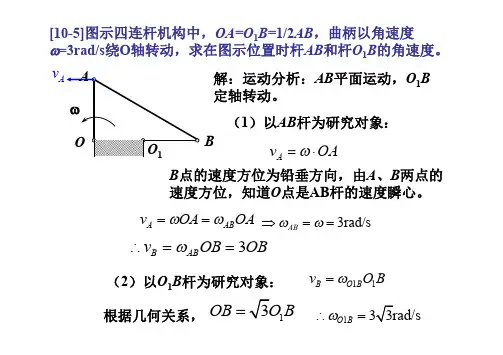
v A v AB v B [10-6]图示曲柄摇块机构中，曲柄OA 以角速度 0绕O 轴转动，带动连杆AC 在摇块B 内滑动,摇块及其刚连的BD 杆则绕B 铰转动，杆BD 长l,求在图示位置时摇块的角速度及D 点的速度.
解：运动分析：OA 、摇块B 定轴转动，AC 平面运动0A v OA ω=⋅以A 点为基点分析B 点的速度
-以摇块上的B 点为动点，以AC 为动系统，通过分析B 点的速度，得知
AC 杆上B 点的速度沿AC 方向。
1/2AB A v v =AB AB v AC
ω=⋅ 又01/4AB ωω⇒=01/4B AB ωωω∴==0
/4D B v l l ωω=⋅=以AC 杆为研究对象：
O A
B C D
300w 0
速度瞬心法：I v A 0A AB v OA IA ωω==由几何关系得：4IA OA
=0
1/4AB ωω⇒=0
1/4B AB ωωω∴==0
/4D B v l l ωω=⋅=
v A A AB v ω= 又01/4AB ωω⇒==
v A v B （3）再研究齿轮D v =v D
（1）取轮为研究对象：v B
（2）取销钉v Br v Be 0cos 60Be B v v =⋅ωO1A
AD 作平面运动。
（1v D
（2）取滑块D 为动点，v Dr v De 0cos30De D v v =1O D ω∴=ωO1D。
理论力学@10动量定理
第10章 动量定理主要内容10.1.1 质点系动量及冲量的计算质点的动量为v K m =质点系的动量为C i i m m v v K ∑=∑=式中m 为整个质点系的质量；对于刚体系常用i C i i m v k K ∑=∑=计算质点系的动量，式中v Ci 为第i 个刚体质心的速度。
常力的冲量t ⋅=F S力系的冲量⎰∑=∑=21d )(t t i i t t F S S或⎰⎰=∑=2121d )(d )(R t t t t i t t t t F F S10.1.2 质点系动量定理质点系动量定理建立了质点系动量对于时间的变化率与外力系的主矢量之间的关系，即)(d de i tF K ∑= （1）质点系动量的变化只决定于外力的主矢量而与内力无关。
（2）质点系动量守恒定律：当作用于质点系的外力系的主矢量0)(=∑e iF ，质点系动量守恒，即K =常矢量。
或外力系的主矢量在某一轴上的投影为零，则质点系的动量在此轴上的投影守恒，如0=∑x F ，则x K =常量。
10.1.3 质心运动定理质点系的质量与质心加速度的乘积等于外力系的主矢量。
即()())(d d d de i i i c m tM t F v v ∑=∑= 对于刚体系可表示为)(1Cie i ni m F a∑=∑=式中a Ci 表示第i 个刚体质心的加速度。
10.1.4 定常流体流经弯管时的动约束力定常流体流经弯管时，v C =常矢量，流出的质量与流入的质量相等。
若流体的流量为Q ，密度为ρ。
流体流经弯管时的附加动约束力为)(12Nv v F -=''Q ρ 式中v 2,v 1分别为出口处和入口处流体的速度矢量。
基本要求1． 能理解并熟练计算动量、冲量等基本物理量。
2． 会应用动量定理解决质点系动力学两类问题，特别是已知运动求未知约束力的情形。
当外力主矢量为零时，会应用动量守恒定理求运动的问题。
3． 会求解定常流体流经弯管时的附加动反力。
理论力学课后习题答案-第10章--动能定理及其应用-)
理论力学课后习题答案-第10章--动能定理及其应用-)(a)v ϕABC rv 1v 1v 1ωϕ(a)CCωCvωO第10章 动能定理及其应用10－1 计算图示各系统的动能：1．质量为m ，半径为r 的均质圆盘在其自身平面内作平面运动。
在图示位置时，若已知圆盘上A 、B 两点的速度方向如图示，B 点的速度为v B ，θ = 45º（图a ）。
2．图示质量为m 1的均质杆OA ，一端铰接在质量为m 2的均质圆盘中心，另一端放在水平面上，圆盘在地面上作纯滚动，圆心速度为v （图b ）。
3．质量为m 的均质细圆环半径为R ，其上固结一个质量也为m 的质点A 。
细圆环在水平面上作纯滚动，图示瞬时角速度为ω（图c ）。
解：1．222222163)2(2121)2(212121BBB CCCmv r v mr v m J mv T =⋅+=+=ω 2．222122222214321)(21212121v m v m r v r m v m vm T +=⋅++= 3．22222222)2(212121ωωωωmR R m mR mR T =++=10－2 图示滑块A 重力为1W ，可在滑道内滑动，与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。
现已知道滑块沿滑道的速度为1v ，杆AB 的角速度为1ω。
当杆与铅垂线的夹角为ϕ时，试求系统的动能。
解：图（a ） B AT T T +=)2121(21222211ωC CJ vgWv g W ++=21221121212211122]cos 22)2[(22ωϕωω⋅⋅+⋅++++=l gW l l v l v l g W v g W]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10－3 重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。
齿轮II 通过匀质的曲柄OC 带动而运动。
理论力学参考答案 第十章
·115·第10章 动量定理一、是非题(正确的在括号内打“√”、错误的打“×”)1．内力虽不能改变质点系的动量，但可以改变质点系中各质点的动量。
( √ ) 2．内力虽不影响质点系质心的运动，但质点系内各质点的运动，却与内力有关。
( √ ) 3．质点系的动量守恒时，质点系内各质点的动量不一定保持不变。
( √ ) 4．若质点系所受的外力的主矢等于零，则其质心坐标保持不变。
( × ) 5．若质点系所受的外力的主矢等于零，则其质心运动的速度保持不变。
( √ ) 二、填空题1．质点的质量与其在某瞬时的速度乘积，称为质点在该瞬时的动量。
2．力与作用时间的乘积，称为力的冲量。
3．质点系的质量与质心速度的乘积称为质点系的动量。
4．质点系的动量随时间的变化规律只与系统所受的外力有关，而与系统的内力无关。
5．质点系动量守恒的条件是质点系所受外力的主矢等于零，质点系在x 轴方向动量守恒的条件是质点系所受外力沿x 轴方向投影的代数和等于零。
6．若质点系所受外力的矢量和等于零，则质点系的动量和质心速度保持不变。
三、选择题1．如图10.12所示的均质圆盘质量为m ，半径为R ，初始角速度为0ω，不计阻力，若不再施加主动力，问轮子以后的运动状态是( C )运动。
(A) 减速(B) 加速(C) 匀速 (D) 不能确定2．如图10.13所示的均质圆盘质量为m ，半径为R ，可绕O 轴转动，某瞬时圆盘的角速度为ω，则此时圆盘的动量大小是( A )。
(A) 0P = (B) P m R =ω (C) 2P m R =ω(D) 2P m R /=ω图10.12 图10.133．均质等腰直角三角板，开始时直立于光滑的水平面上，如图10.14所示。
给它一个微小扰动让其无初速度倒下，问其重心的运动轨迹是( C )。
(A) 椭圆 (B) 水平直线 (C) 铅垂直线(D) 抛物线ABC图10.14·116·4．质点系的质心位置保持不变的必要与充分条件是( D )。
《理论力学》第十章 质心运动定理 动量定理 习题共7页
第十章 质心运动定理 动量定理 习题解[习题10-1] 船A 、B 的重量分别为kN 4.2及kN 3.1，两船原处于静止间距m 6。
设船B 上有一人，重N 500，用力拉动船A ，使两船靠拢。
若不计水的阻力，求当两船靠拢在一起时，船B 移动的距离。
解：以船A 、B 及人组成的物体系统为质点 系。
因为质点系在水平方向不受力。
即：设B 船向左移动了S 米， 则A 船向右移动了6－S 米。
由质点系的动量定理得：[习题10-2] 电动机重1P ，放置在光滑的水平面上，另有一匀质杆，长L 2，重2P ，一端与电动机机轴固结，并与机轴的轴线垂直，另一端则刚连一重3P 的物体，设机轴的角速度为ω（ω为常量），开始时杆处于铅垂位置并且系统静止。
试求电动机的水平运动。
解：以电动机、匀质杆和球构成的质点系为研究对象。
其受力与运动分析如图所示。
匀质杆作平面运动。
因为质点系在水平方向上不受力，所以 由动量定理得：这就是电动机的水平运动方程。
[习题10-3] 浮动起重机起吊重kN P 201=的重物，起重机重kN P 2002=，杆长m OA 8=，开始时杆与铅垂位置成060角，忽略水的阻力，杆重不计，当起重杆OA 转到与铅垂位置成030角时，求起重机的位移。
解：以重物和起重机构成的物体系统为质系。
因为质点系在水平方向不受力，所以0=x Fconst x C ＝。
即OA 运动前后，质点系的质心保持不变。
也就是质心守恒。
当OA 杆转到与铅垂位置成030角时，质点系质心的横坐标为： 当OA 杆转到与铅垂位置成030角时， 质点系质心的横坐标为： 因为质心守恒，所以21C C x x =，即：故，当起重杆OA 转到与铅垂位置成030角时，起重机向左移动了0.2662米。
[习题10-4] 匀质圆盘绕偏心轴O 以匀角速度ω转动。
重P 的夹板借右端弹簧推压面顶在圆盘上，当圆盘转动时，夹板作住复运动。
设圆盘重W ，半径为r ，偏心距为e ，求任一瞬时作用于基础和别螺栓的动反力。
【精】理论力学经典例题
m2vB
(m1
vr 2ve 20 cm/s
vr C
O
M
w
ve va A
B
小环M的加速度分析如图所示 ：
aa ae ar aC
O
aC 2wvr 2 0.5 20 w
B
20 cm/s2
aen M ar C
ac
a aA
y
aen w 2 OM
a 向y方向投影,有: a
0.52
cos
20
aen
5 cm/s2
2w
4ew
3
1
8ew 2
3
B h
aC aa
art
A
aen q
arn
C
O
w
aa cosq aen cosq arn aC
aa
2 (2ew2
3
3 16ew2 8ew2 ) 2 ew2
2 33
3
9
例13 图示曲杆OBC绕O轴转动，使套在其上的小环M沿固定直 杆OA滑动。已知OB＝10 cm，OB与BC垂直，曲杆的角速度为 0.5rad/s，求当φ=60°时小环M的速度和加速度。
va ve vr
va
vr
A
ve
ve w OA
q
va ve tanq w OA
32 3
3ew
3
C O w
vr
ve
cosq
2ew
3
4
3ew
3
2
加速度分析如图
aa ae ar aC
aen OA w 2 2ew 2
arn
vr 2 R
16ew 2
33
aC
2wvr
理论力学课后习题答案1-13章
解：设孔心位置与x轴夹角θ，半径r1
则有
即
联立求解得
2－24一悬臂圈梁，其轴线为 ＝４ｍ的 圆弧。梁上作用着垂直匀布荷载， ＝２ｋＮ／ｍ。求该匀布荷载的合力及其作用线位置。
解：合力大小 ，铅直向下。
作用线位置在圆弧的形心处即平分轴上距离圆心
处
3－１作下列指定物体的示力图。物体重量除图上已注明者外，均略去不计。假设接触处都是光滑的。
解：整体：
先判断零杆如图。
取Ⅰ-Ⅰ截面右半部分
5-5 (b)试用最简捷的方法求图示桁架指定杆件的内力。
解：取Ⅰ-Ⅰ截面上半部分
取Ⅱ-Ⅱ截面右半部分
，
5-8杆系铰接如图所示，沿杆３与杆５分别作用着力FP1与FP2，试求各杆内力。
解：先判断零杆如图。 ，则
5－21板 长 ， 、 两端分别搁在倾角 ＝50°， ＝30°的两斜面上。已知板端与斜面之间的摩擦角 ＝25°。欲使物块Ｍ放在板上而板保持水平不动，试求物块放置的范围。板重不计。
2.绕A点滚动，B点达到极限状态
，
3.绕B点滚动，A点达到极限状态
，
故，FT的最小值为 。
5－29一个半径为300ｍｍ、重为3ｋＮ的滚子放在水平面上。在过滚子重心 而垂直于滚子轴线的平面内加一力 ，恰足以使滚子滚动。若滚动摩擦因数δ＝5mm，求 的大小。
解：滚子受力如图
6-5半圆形凸轮以匀速v=10mm/s沿水平方向向左运动,活塞杆AB长l，沿铅直方向运动。当运动开始时,活塞杆A端在凸轮的最高点上。如凸轮的半径R=80mm，求活塞B的运动方程和速度方程。
解：OA杆力偶系平衡（由于A滑块，FA垂直O1A）
整体力偶系平衡
4—14求下列面积的形心。图中长度单位是m。
则有
即
联立求解得
2－24一悬臂圈梁，其轴线为 ＝４ｍ的 圆弧。梁上作用着垂直匀布荷载， ＝２ｋＮ／ｍ。求该匀布荷载的合力及其作用线位置。
解：合力大小 ，铅直向下。
作用线位置在圆弧的形心处即平分轴上距离圆心
处
3－１作下列指定物体的示力图。物体重量除图上已注明者外，均略去不计。假设接触处都是光滑的。
解：整体：
先判断零杆如图。
取Ⅰ-Ⅰ截面右半部分
5-5 (b)试用最简捷的方法求图示桁架指定杆件的内力。
解：取Ⅰ-Ⅰ截面上半部分
取Ⅱ-Ⅱ截面右半部分
，
5-8杆系铰接如图所示，沿杆３与杆５分别作用着力FP1与FP2，试求各杆内力。
解：先判断零杆如图。 ，则
5－21板 长 ， 、 两端分别搁在倾角 ＝50°， ＝30°的两斜面上。已知板端与斜面之间的摩擦角 ＝25°。欲使物块Ｍ放在板上而板保持水平不动，试求物块放置的范围。板重不计。
2.绕A点滚动，B点达到极限状态
，
3.绕B点滚动，A点达到极限状态
，
故，FT的最小值为 。
5－29一个半径为300ｍｍ、重为3ｋＮ的滚子放在水平面上。在过滚子重心 而垂直于滚子轴线的平面内加一力 ，恰足以使滚子滚动。若滚动摩擦因数δ＝5mm，求 的大小。
解：滚子受力如图
6-5半圆形凸轮以匀速v=10mm/s沿水平方向向左运动,活塞杆AB长l，沿铅直方向运动。当运动开始时,活塞杆A端在凸轮的最高点上。如凸轮的半径R=80mm，求活塞B的运动方程和速度方程。
解：OA杆力偶系平衡（由于A滑块，FA垂直O1A）
整体力偶系平衡
4—14求下列面积的形心。图中长度单位是m。
理论力学(机械工业出版社)第十章动量定理习题解答
习 题10-1 计算图10-7所示各种情况下系统的动量。
(1) 如图10-7a 所示，质量为m 的匀质圆盘沿水平面滚动，圆心O 的速度为0v ；(2) 如图10-7b 所示，非匀质圆盘以角速度ω绕O 轴转动，圆盘质量为m ，质心为C ，偏心距OC=a ；(3) 如图10-7c 所示，胶带轮传动，大轮以角速度ω转动。
设胶带及两胶带轮为匀质的；(4) 如图10-7d 所示，质量为m 的匀质杆，长度为l ，绕铰O 以角速度ω转动。
图10-7(a) 0v p m =； (b) ωma p =（方向与C 点速度方向相同）；(c) 0=p ；(d) 2ωml p = （方向与C点速度方向相同）。
10-2 如图10-8所示，椭圆规尺AB 的质量为2m 1，曲柄OC 的质量为m 1，而滑块A 和B 的质量均为m 2。
已知：OC =AC =CB = l ；曲柄和尺的质心分别在其中点上；曲柄绕O 轴转动的角速度ω为常量。
当开始时，曲柄水平向右，试求此时质点系的动量。
图10-8方法一CAB COC B B A A m m m m v v v v p +++=2CC B A m m m m v v v v 112222+++=C B A m m v v v 1225)(++=因)c o s s i n (j i v ϕϕω+-=l Cj v ϕωcos 2l A = i v ϕωs i n 2l B -=故)cos sin (25)sin 2cos 2(12j i i j p ϕϕωϕωϕω+-+-=l m l l m)cos sin (24521j i ϕϕω+-+=l m m (与v C 方向相同)方法二规尺AB 、滑块A 和B 质心C 处，质量为2(m 1+m 2) 因此系统质心在OC 上，离O 轴距离mlm m ml m m l m 245)(2221211+=++⨯=ξ质心速度ωξωξl m m m m 24521+===v p (方向垂直于OC )10-3 跳伞者质量为60kg ，自停留在高空中的直升飞机中跳出，落下100m 后，将降落伞打开。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习 题10-1 计算图10-7所示各种情况下系统的动量。
(1) 如图10-7a 所示，质量为m 的匀质圆盘沿水平面滚动，圆心O 的速度为0v ；(2) 如图10-7b 所示，非匀质圆盘以角速度ω绕O 轴转动，圆盘质量为m ，质心为C ，偏心距OC=a ；(3) 如图10-7c 所示，胶带轮传动，大轮以角速度ω转动。
设胶带及两胶带轮为匀质的；(4) 如图10-7d 所示，质量为m 的匀质杆，长度为l ，绕铰O 以角速度ω转动。
图10-7(a) 0v p m =； (b) ωma p =（方向与C 点速度方向相同）；(c) 0=p ；(d) 2ωml p = （方向与C点速度方向相同）。
10-2 如图10-8所示，椭圆规尺AB 的质量为2m 1，曲柄OC 的质量为m 1，而滑块A 和B 的质量均为m 2。
已知：OC =AC =CB = l ；曲柄和尺的质心分别在其中点上；曲柄绕O 轴转动的角速度ω为常量。
当开始时，曲柄水平向右，试求此时质点系的动量。
图10-8方法一CAB COC B B A A m m m m v v v v p +++=2CC B A m m m m v v v v 112222+++=C B A m m v v v 1225)(++=因)c o s s i n (j i v ϕϕω+-=l Cj v ϕωcos 2l A = i v ϕωs i n 2l B -=故)cos sin (25)sin 2cos 2(12j i i j p ϕϕωϕωϕω+-+-=l m l l m)cos sin (24521j i ϕϕω+-+=l m m (与v C 方向相同)方法二规尺AB 、滑块A 和B 质心C 处，质量为2(m 1+m 2) 因此系统质心在OC 上，离O 轴距离mlm m ml m m l m 245)(2221211+=++⨯=ξ质心速度ωξωξl m m m m 24521+===v p (方向垂直于OC )10-3 跳伞者质量为60kg ，自停留在高空中的直升飞机中跳出，落下100m 后，将降落伞打开。
设开伞前的空气阻力略去不计，伞重不计。
开伞后阻力不变，经5s 后跳伞者的速度减为4.3m/s 。
试求阻力的大小。
gh v 21=222122t ghv t v v a -=-=22)2(t gh v m ma F mg -==-)2(22t gh v g m F --=N7.1067)9944.78.9(60)51008.923.48.9(60=+=⨯⨯--=10-4 图10-9所示浮动起重机举起质量为m 1=2000kg 的重物。
设起重机质量为m 2=20000kg ，杆长OA =8m ；开始时与铅直位置成60°角。
水的阻力与杆重均略去不计。
当起重杆OA 转到与铅直位置成30°角时，试求起重机的位移。
图10-9设起重机向左移动s ，则重物向右移动)30sin 60(sin s OA -︒-︒质心运动守恒x C =常量0])30sin 60(sin [21=--︒-︒s m s OA m 211)30sin 60(sin m m OA m s +︒-︒=m2662.0220002/)13(82000=-⨯⨯=10-5 如图10-10所示，两小车A 和B 的质量分别为600kg 和800kg ，在水平轨道上分别以匀速v A =1m/s ，v B =0.4m/s 运动。
一质量为40kg 的重物C 以俯角30°，速度v C =2m/s 落入A 车内，A 车与B 车相碰后紧接在一起运动。
试求两车共同的速度。
摩擦忽略不计。
图10-10动量守恒︒++=30cos 1C C B B A A x v m v m v m p v m m m p C B A x )(2++=v m m m v m v m v m C B A C C B B A A )(30cos ++=︒++CB AC C B B A A m m m v m v m v m v ++︒++=30cosm/s6870.0144034092040800600232404.08001600=+=++⨯⨯+⨯+⨯=10-6 平台车质量m 1=500kg ，可沿水平轨道运动。
平台车上站有一人，质量m 2=70kg ，车与人以共同速度v 0向右方运动。
如人相对平台车以速度v r =2m/s 向左方跳出，不计平台车水平方向的阻力及摩擦，试问平台车增加的速度为多少? 动量守恒0211)(v m m p x +=)()(r 02012v v v m v v m p x -+++=∆∆021r 0201)()()(v m m v v v m v v m +=-+++∆∆m/s2456.05701407050027021r 2==+⨯=+=m m v m v ∆10-7 如图10-11所示，质量为m 1的平台AB 放于水平面上，平台与水平面间的动滑动摩擦因数为 。
质量为m 2的小车D ，由绞车拖动，相对于平台的运动规律为s=0.5bt 2，其中b 为常数。
不计绞车的质量，试求平台的加速度。
图10-11设平台向左运动的速度为v ，则小车D 向右运动的速度为v r - v)(r 21v v m v m p x -+-= gm m F F ex )(21N +==∑μμ由动量定理eixx F tp ∑=d d得gm m a a m a m )()(21r 21+=-+-μ212122121r 2)()(m m gm m b m m m gm m a m a ++-=++-=μμ10-8 图10-12所示机构中，鼓轮A 质量为m 1。
转轴O 为其质心。
重物B 的质量为m 2，重物C 的质量为m 3。
斜面光滑，倾角为θ。
已知重物B 的加速度为a ，试求轴承O 处的约束反力。
图10-12由质心运动定理e yCy e x Cx Fma F ma ∑=∑=得θθsin cos N 3F F a rR m Ox -=θθθθθsin cos cos sin cos 3N 3mg a rR m F a rR m F Ox +=+=θθcos )(sin N 32123F g m m m F a m a rR m Oy +++-=- θθcos )(sin N 32123F g m m m a m a rR m F Oy -+++-=θθ232123cos )(sin mg g m m m a m a rR m -+++-=10-9 如图10-13所示，质量为m 的滑块A ，可以在水平光滑槽中运动，具有刚性系数为k 的弹簧一端与滑块相连，另一端固定。
杆长度为l ，质量可忽略不计，A 端与滑块铰接，B 端装有质量为m 1的小球，在铅垂面内绕A 点转动。
设在力偶M 作用下转动角速度w 为常数。
试求滑块A 的运动微分方程。
图10-131111sin )sin (m m t l m x m m t l x m mx x C ++=+++=ωω质心运动定理e x C F xm m ∑=+ )(1 kx t l m x m m -=-+ωωsin )(211t l m kx xm m ωωsin )(211=++tm m l m x m m k xωωsin 1211+=++10-10 如图10-14所示，均质杆OA 长2l ，质量为m ，绕着通过O 端的水平轴在铅直面内转动，转到与水平线成f 角时，角速度与角加速度分别为w 及a 。
试求此时O 端的反力。
图10-14由质心运动定理e yCy e x Cx Fma F ma ∑=∑=得OxC C F a a m =--)sin cos (τnϕϕ)sin cos ()sin cos (2τnϕαϕωϕϕ+-=+-=ml a a m F C C OxmgF a a m Oy C C -=-)cos sin (τn ϕϕmgml mg a a m F C C Oy +-=+-=)cos sin ()cos sin (2τnϕαϕωϕϕ10-11 在图10-15所示曲柄滑杆机构中，曲柄以等角速度 绕O 轴转动，开始时，曲柄OA 水平向右。
已知曲柄质量为m 1，滑块A 的质量为m 2，滑杆的质量为m 3，曲柄的质心在OA 的中点，OA = l ；滑杆的质心在C 点，而2/l BC=。
试求：（1）机构质心的运动方程；（2）作用在O 点的最大水平力。
图10-15ml t l m t l m t l m x C )2cos (cos cos 2321+++=ωωω)(2c o s )22()(23213213213m m m tl m m m m m m lm +++++++=ωmtl m t l m y C ωωs i n s i n 221+=)(2s i n )2(32121m m m t l m m +++=ω质心运动定理ex C F xm ∑=OxF tl m m m =++-2cos )22(2321ωω 2cos )22(2321tl m m m F Ox ωω++-=2)22(2321max ωl m m m F Ox ++=10-12 如图10-16所示，均质杆AB 长l ，直立在光滑的水平面上，试求它从铅直位置无速地倒下时，端点A 相对图示坐标系的轨迹．图10-16任意位置时0=∑exF ，初始速度为零，故质心运动守恒0=C x ，质心沿铅垂方向向下运动θco s2l x A =θs i n l y A =故1)()2(22=+ly lx A A2224ly x A A =+10-13 图10-17所示水平面上放一均质三棱柱A ，在其斜面上又放一均质三棱柱B ，两三棱柱的横截面均为直角三角形。
三棱柱A 的质量m A 为三棱柱B 质量m B 的三倍，其尺寸如图示，若各处摩擦不计，初始时系统静止。
试求当三棱柱B 沿三棱柱A 滑下接触到水平面时，三棱柱A 移动的距离。
图10-17任意位置时0=∑e xF，初始系统静止，故质心运动守恒x C =常量3231b m a m x B A C ⨯+⨯=设三棱柱A 向左移动s ，则三棱柱B 向右移动s b a --)32()3(2s b a b m s a m x B A C --+⨯+-⨯=12C C x x =0)(=--+-s b a m s m B A4)(b a m m b a m s BA B -=+-=10-14 试求题10-13中三棱柱A 运动的加速度及地面的支持力。
任意位置时0=∑exF ，0=Cx a设三棱柱A 向左运动的加速度为a A ，三棱柱B 沿斜面运动的相对加速度为a r0)c o s (r =-+-A B A A a a m a m θ θcos )(r B AB A m a m m a +=三棱柱Bθθsin )cos (r g m a a m B A B =-θθθsin ]cos cos )([g m a m a m m m B A B AB A B =-+θθθsin cos cos )(2g m a m m m B A B B A =-+gm m g m a B A B A θθθθθθ22sin 3cos sin sin cos sin +=+=ga θθ2r sin 3sin 4+=系统eyCy F ma ∑=gm m F a m B A B )()sin (N r +-=-θθθθ22r N sin 3sin 4)(sin )(+-+=-+=gm g m m a m g m m F B B A B B A)sin 3(sin 4422θθ+-=gm g m B Bgm B θ2sin 312+=。