浙江省2020高考数学总复习第8单元第7节抛物线文新人教A版

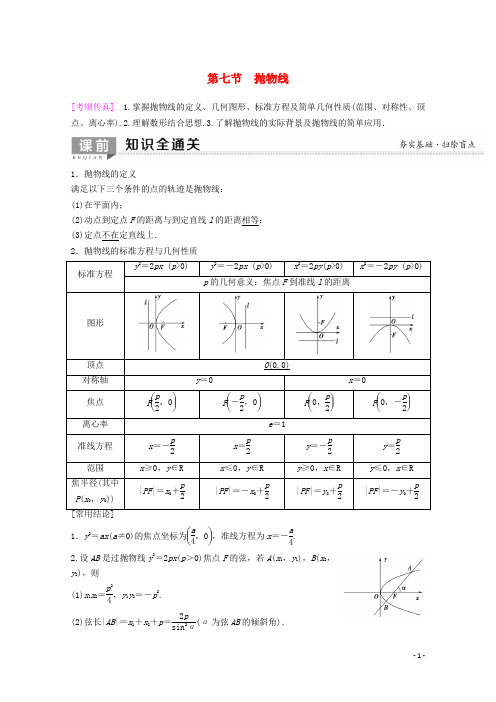
第七节 抛物线[考纲传真] 1.掌握抛物线的定义、几何图形、标准方程及简单几何性质(范围、对称性、顶点、离心率).2.理解数形结合思想.3.了解抛物线的实际背景及抛物线的简单应用．1．抛物线的定义满足以下三个条件的点的轨迹是抛物线： (1)在平面内；(2)动点到定点F 的距离与到定直线l 的距离相等； (3)定点不在定直线上． 2．抛物线的标准方程与几何性质 标准方程y 2＝2px (p >0) y 2＝－2px (p >0) x 2＝2py (p >0) x 2＝－2py (p >0)p 的几何意义：焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 y ＝0x ＝0焦点 F ⎝⎛⎭⎪⎫p 2，0 F ⎝ ⎛⎭⎪⎫－p 2，0 F ⎝⎛⎭⎪⎫0，p 2 F ⎝ ⎛⎭⎪⎫0，－p 2离心率 e ＝1准线方程 x ＝－p 2x ＝p 2y ＝－p 2y ＝p 2范围 x ≥0，y ∈Rx ≤0，y ∈Ry ≥0，x ∈Ry ≤0，x ∈R焦半径(其中P (x 0，y 0))|PF |＝x 0＋p 2|PF |＝－x 0＋p 2|PF |＝y 0＋p 2|PF |＝－y 0＋p21．y 2＝ax (a ≠0)的焦点坐标为⎝ ⎛⎭⎪⎫a 4，0，准线方程为x ＝－a4.2.设AB 是过抛物线y 2＝2px (p ＞0)焦点F 的弦，若A (x 1，y 1)，B (x 2，y 2)，则(1)x 1x 2＝p 24，y 1y 2＝－p 2.(2)弦长|AB |＝x 1＋x 2＋p ＝2psin 2α(α为弦AB 的倾斜角)．(3)以弦AB 为直径的圆与准线相切．(4)通径：过焦点垂直于对称轴的弦，长度等于2p ，通径是过焦点最短的弦．[基础自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹一定是抛物线．( ) (2)若直线与抛物线只有一个交点，则直线与抛物线一定相切．( ) (3)若一抛物线过点P (－2,3)，则其标准方程可写为y 2＝2px (p ＞0)．( ) (4)抛物线既是中心对称图形，又是轴对称图形．( ) [答案] (1)× (2)× (3)× (4)× 2．抛物线y ＝14x 2的准线方程是( )A ．y ＝－1B ．y ＝－2C ．x ＝－1D ．x ＝－2A [∵y ＝14x 2，∴x 2＝4y ，∴准线方程为y ＝－1.]3．(教材改编)顶点在原点，对称轴为坐标轴，且过点P (－4，－2)的抛物线的标准方程是( ) A ．y 2＝－xB ．x 2＝－8yC ．y 2＝－8x 或x 2＝－yD ．y 2＝－x 或x 2＝－8yD [若焦点在y 轴上，设抛物线方程为x 2＝my ，由题意可知16＝－2m ，∴m ＝－8，即x 2＝－8y .若焦点在x 轴上，设抛物线方程为y 2＝nx ，由题意，得4＝－4n ，∴n ＝－1， ∴y 2＝－x .综上知，y 2＝－x 或x 2＝－8y .故选D.]4．(教材改编)若抛物线y ＝4x 2上的一点M 到焦点的距离为1，则点M 的纵坐标是( ) A.1716 B.1516C.78D ．0B [M 到准线的距离等于M 到焦点的距离，又准线方程为y ＝－116，设M (x ，y )，则y ＋116＝1，∴y ＝1516.]5．(教材改编)过抛物线y 2＝4x 的焦点的直线l 交抛物线于P (x 1，y 1)，Q (x 2，y 2)两点，如果x 1＋x 2＝6，则|PQ |等于________．8 [|PQ |＝x 1＋x 2＋p ＝6＋2＝8.]抛物线的定义及应用【例1】 (1)已知F 是抛物线y 2＝x 的焦点，A ，B 是该抛物线上的两点，且|AF |＋|BF |＝3，则线段AB 的中点到y 轴的距离为( ) A.34 B ．1 C.54D.74(2)已知抛物线y 2＝2x 的焦点是F ，点P 是抛物线上的动点，A (3,2)，则|PA |＋|PF |的最小值为________，取最小值时点P 的坐标为________．(1)C (2)72 (2,2) [(1)如图所示，设抛物线的准线为l ，AB 的中点为M ，作AA 1⊥l 于A 1，BB 1⊥l 于B 1，MM 1⊥l 于M 1，由抛物线的定义知p ＝12，|AA 1|＋|BB 1|＝|AF |＋|BF |＝3，则点M 到y 轴的距离为|MM 1|－p 2＝12(|AA 1|＋|BB 1|)－14＝54.故选C. (2)将x ＝3代入抛物线方程y 2＝2x ，得y ＝± 6.因为6＞2，所以点A 在抛物线内部，如图所示．过点P 作PQ ⊥l 于点Q ，则|PA |＋|PF |＝|PA |＋|PQ |， 当PA ⊥l ，即A ，P ，Q 三点共线时，|PA |＋|PQ |最小，最小值为72，即|PA |＋|PF |的最小值为72，此时点P 的纵坐标为2，代入y 2＝2x ，得x ＝2，所以所求点P 的坐标为(2,2)．] [规律方法] 应用抛物线定义的两个关键点1由抛物线定义，把抛物线上点到焦点距离与到准线距离相互转化.2注意灵活运用抛物线上一点P x 0，y 0到焦点F 的距离|PF |＝|x 0|＋p 2或|PF |＝|y 0|＋p2.(1)动圆过点(1,0)，且与直线x ＝－1相切，则动圆的圆心的轨迹方程为________．(2)(2017· 全国卷Ⅱ)已知F 是抛物线C ：y 2＝8x 的焦点，M 是C 上一点，FM 的延长线交y 轴于点N .若M 为FN 的中点，则|FN |＝________.(1)y 2＝4x (2)6 [(1)设动圆的圆心坐标为(x ，y )，则圆心到点(1,0)的距离与到直线x ＝－1的距离相等，根据抛物线的定义易知动圆的圆心的轨迹方程为y 2＝4x . (2)如图，不妨设点M 位于第一象限内，抛物线C 的准线交x 轴于点A ，过点M 作准线的垂线，垂足为点B ，交y 轴于点P ，∴PM ∥OF . 由题意知，F (2,0)，|FO |＝|AO |＝2. ∵点M 为FN 的中点，PM ∥OF ，∴|MP |＝12|FO |＝1.又|BP |＝|AO |＝2， ∴|MB |＝|MP |＋|BP |＝3.由抛物线的定义知|MF |＝|MB |＝3，故|FN |＝2|MF |＝6.]抛物线的标准方程及其性质【例2】 (1)如图所示，过抛物线y 2＝2px (p ＞0)的焦点F 的直线依次交抛物线及准线于点A ，B ，C ，若|BC |＝2|BF |，且|AF |＝4，则抛物线的方程为( ) A ．y 2＝8x B ．y 2＝4x C ．y 2＝2x D ．y 2＝x(2)在平面直角坐标系xOy 中，设抛物线y 2＝4x 的焦点为F ，准线为l ，P 为抛物线上一点，PA ⊥l ，A 为垂足．如果直线AF 的倾斜角为120°，那么|PF |＝_______.(1)B (2)4 [(1)如图，分别过点A ，B 作准线的垂线，交准线于点E ，D ，设准线与x 轴交于点G ，设|BF |＝a ，则由已知得|BC |＝2a ，由定义得|BD |＝a ，故∠BCD ＝30° ，则在Rt△ACE 中，2|AE |＝|AC |，又|AF |＝4，∴|AC |＝4＋3a ，|AE |＝4，∴4＋3a ＝8，从而得a ＝43，∵AE ∥FG ，∴FG AE ＝CF AC ，即p 4＝48，p ＝2.∴抛物线的方程为y 2＝4x .故选B. (2)法一：抛物线y 2＝4x 的焦点为F (1,0)，准线方程为x ＝－1.因为直线AF 的倾斜角为120°，所以∠AFO ＝60°.又tan 60°＝y A1－－1，所以y A ＝2 3.因为PA ⊥l ，所以y P ＝y A ＝2 3.将其代入y 2＝4x ，得x P ＝3，所以|PF |＝|PA |＝3－(－1)＝4.法二：抛物线y 2＝4x 的焦点为F (1,0)，准线方程为x ＝－1.因为PA ⊥l ，所以|PA |＝|PF |.又因为直线AF 的倾斜角为120°，所以∠AFO ＝60°，所以∠PAF ＝60°，所以△PAF 为等边三角形，所以|PF |＝|AF |＝1－－1cos∠AFO＝4.][规律方法] 1.求抛物线标准方程的常用方法是待定系数法，其关键是判断焦点位置、开口方向，在方程的类型已经确定的前提下，由于标准方程只有一个参数p ，只需一个条件就可以确定抛物线的标准方程.2.在解决与抛物线的性质有关的问题时，要注意利用几何图形的形象、直观的特点来解题，特别是涉及焦点、顶点、准线的问题更是如此.△POF的面积为( )A. 2B. 3C．2 D．3(2)设抛物线C：y2＝2px (p＞0)的焦点为F，点M在C上，|MF|＝5，若以MF为直径的圆过点(0,2)，则抛物线C的方程为( )A．y2＝4x或y2＝8x B．y2＝2x或y2＝8xC．y2＝4x或y2＝16x D．y2＝2x或y2＝16x(1)B (2)C [(1)抛物线y2＝4x的焦点为F(1,0)，准线为直线x＝－1.设点P(x，y)，由抛物线的定义，得|PF|＝x＋1＝4，所以x＝3.把x＝3代入y2＝4x，得y＝±23，故△POF的面积S＝12×|OF|×|y|＝12×1×23＝ 3.故选B.(2)如图所示，抛物线y2＝2px的焦点F坐标为⎝⎛⎭⎪⎫p2，0，准线方程为l：x＝－p2.由|MF|＝5，可得点M到准线的距离为5，则点M的横坐标为5－p2，可设M⎝⎛⎭⎪⎫5－p2，m，则MF中点B的坐标为B⎝⎛⎭⎪⎫52，m2，∵以MF为直径的圆过点A(0,2)，∴|AB|＝12|MF|＝52，则有⎝⎛⎭⎪⎫522＋⎝⎛⎭⎪⎫m2－22＝⎝⎛⎭⎪⎫522，解得m＝4，由点M在抛物线上可得m2＝42＝2p⎝⎛⎭⎪⎫5－p2，解得p＝2或p＝8，∴所求抛物线方程为y2＝4x或y2＝16x，故选C.]直线与抛物线的位置关系【例3】(2018·全国卷Ⅰ)设抛物线C：y2＝2x，点A(2,0)，B(－2,0)，过点A的直线l与C交于M，N两点．(1)当l与x轴垂直时，求直线BM的方程；(2)证明：∠ABM＝∠ABN.[解](1)当l与x轴垂直时，l的方程为x＝2，可得点M的坐标为(2,2)或(2，－2)．所以直线BM的方程为y＝12x＋1或y＝－12x－1.(2)证明：当l与x轴垂直时，AB为MN的垂直平分线，所以∠ABM＝∠ABN.当l与x轴不垂直时，设l的方程为y＝k(x－2)(k≠0)，M(x1，y1)，N(x2，y2)，则x1>0，x2>0.由⎩⎪⎨⎪⎧y ＝k x －2，y 2＝2x 得ky 2－2y －4k ＝0，可知y 1＋y 2＝2k，y 1y 2＝－4.直线BM ，BN 的斜率之和为k BM ＋k BN ＝y 1x 1＋2＋y 2x 2＋2＝x 2y 1＋x 1y 2＋2y 1＋y 2x 1＋2x 2＋2.①将x 1＝y 1k ＋2，x 2＝y 2k＋2及y 1＋y 2，y 1y 2的表达式代入①式分子，可得x 2y 1＋x 1y 2＋2(y 1＋y 2)＝2y 1y 2＋4k y 1＋y 2k＝－8＋8k＝0.所以k BM ＋k BN ＝0，可知BM ，BN 的倾斜角互补，所以∠ABM ＝∠ABN . 综上，∠ABM ＝∠ABN .[规律方法] 解决直线与抛物线位置关系问题的三种常用方法1直线与抛物线的位置关系和直线与椭圆的位置关系类似，一般要用到根与系数的关系. 2有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB |＝x 1＋x 2＋p ，若不过焦点，则必须用弦长公式.3涉及抛物线的弦长、弦中点等相关问题时，一般采用“设而不求，整体代入”的解法. 提醒：涉及弦的中点、弦所在直线的斜率时一般用“点差法”求解.(1)过点(0,1)作直线，使它与抛物线y 2＝4x 仅有一个公共点，这样的直线有________条．(2)(2019·临沂模拟)已知点A (m,4)(m ＞0)在抛物线x 2＝4y 上，过点A 作倾斜角互补的两条直线l 1和l 2，且l 1，l 2与抛物线的另一个交点分别为B ，C . ①求证：直线BC 的斜率为定值；②若抛物线上存在两点关于BC 对称，求|BC |的取值范围．(1)3 [结合图形分析可知(图略)，满足题意的直线共有3条：直线x ＝0，过点(0,1)且平行于x 轴的直线以及过点(0,1)且与抛物线相切的直线(非直线x ＝0)．] (2)[解] ①证明：∵点A (m,4)在抛物线上， ∴16＝m 2，∴m ＝±4，又m ＞0，∴m ＝4. 设B (x 1，y 1)，C (x 2，y 2)， 则k AB ＋k AC ＝x 1＋44＋x 2＋44＝x 1＋x 2＋84＝0，∴x 1＋x 2＝－8.∴k BC ＝y 2－y 1x 2－x 1＝x 22－x 214x 2－x 1＝x 1＋x 24＝－2，∴直线BC 的斜率为定值－2.②设直线BC 的方程为y ＝－2x ＋b ，P (x 3，y 3)，Q (x 4，y 4) 关于直线BC 对称，设PQ 的中点为M (x 0，y 0)，则k PQ ＝y 4－y 3x 4－x 3＝x 3＋x 44＝x 02＝12，∴x 0＝1.∴M (1，－2＋b )．又点M 在抛物线内部，∴－2＋b ＞14，即b ＞94.由⎩⎪⎨⎪⎧y ＝－2x ＋b ，x 2＝4y ，得x 2＋8x －4b ＝0，∴x 3＋x 4＝－8，x 3x 4＝－4b . ∴|BC |＝1＋4|x 3－x 4|＝5·x 3＋x 42－4x 3x 4＝5×64＋16b . 又b ＞94，∴|BC |＞10 5.∴|BC |的取值范围为(105，＋∞)．1.(2018·全国卷Ⅰ)设抛物线C ：y 2＝4x 的焦点为F ，过点(－2,0)且斜率为23的直线与C 交于M ，N 两点，则FM →·FN →＝( ) A ．5 B ．6 C ．7D ．8D [过点(－2,0)且斜率为23的直线的方程为y ＝23(x ＋2)，由⎩⎪⎨⎪⎧y ＝23x ＋2，y 2＝4x ，得x2－5x ＋4＝0，解得x ＝1或x ＝4，所以⎩⎪⎨⎪⎧x ＝1，y ＝2，或⎩⎪⎨⎪⎧x ＝4，y ＝4，不妨设M (1,2)，N (4,4)，易知F (1,0)，所以FM →＝(0,2)，FN →＝(3,4)，所以FM →·FN →＝8.故选D.]2．(2016·全国卷Ⅰ)以抛物线C 的顶点为圆心的圆交C 于A ，B 两点，交C 的准线于D ，E 两点．已知|AB |＝42，|DE |＝25，则C 的焦点到准线的距离为( ) A ．2 B ．4 C ．6D ．8B [设抛物线的方程为y 2＝2px (p ＞0)，圆的方程为x 2＋y 2＝r 2. ∵|AB |＝42，|DE |＝25， 抛物线的准线方程为x ＝－p2，∴不妨设A ⎝ ⎛⎭⎪⎫4p ，22，D ⎝ ⎛⎭⎪⎫－p 2，5.∵点A ⎝ ⎛⎭⎪⎫4p ，22，D ⎝ ⎛⎭⎪⎫－p 2，5在圆x 2＋y 2＝r 2上，∴⎩⎪⎨⎪⎧16p 2＋8＝r 2，p 24＋5＝r 2，∴16p 2＋8＝p24＋5， ∴p ＝4(负值舍去)．∴C 的焦点到准线的距离为4.]3.(2018·全国卷Ⅲ)已知点M (－1,1)和抛物线C ：y 2＝4x ，过C 的焦点且斜率为k 的直线与C 交于A ，B 两点．若∠AMB ＝90°，则k ＝________.2 [由题意知抛物线的焦点为(1,0)，则过C 的焦点且斜率为k 的直线方程为y ＝k (x －1)(k ≠0)，由⎩⎪⎨⎪⎧y ＝k x －1，y 2＝4x ，消去y ，得k 2(x －1)2＝4x ，即k 2x 2－(2k 2＋4)x ＋k 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝2k 2＋4k 2，x 1x 2＝1.由⎩⎪⎨⎪⎧y ＝k x －1，y 2＝4x 消去x 得y 2＝4⎝ ⎛⎭⎪⎫1ky ＋1，即y 2－4ky －4＝0，则y 1＋y 2＝4k，y 1y 2＝－4.由∠AMB ＝90°，得MA →·MB →＝(x 1＋1，y 1－1)·(x 2＋1，y 2－1)＝x 1x 2＋x 1＋x 2＋1＋y 1y 2－(y 1＋y 2)＋1＝0，将x 1＋x 2＝2k 2＋4k 2，x 1x 2＝1与y 1＋y 2＝4k，y 1y 2＝－4代入，得k ＝2.]4.(2018·全国卷Ⅱ)设抛物线C ：y 2＝4x 的焦点为F ，过F 且斜率为k (k ＞0)的直线l 与C 交于A ，B 两点，|AB |＝8. (1)求l 的方程；(2)求过点A ，B 且与C 的准线相切的圆的方程．[解] (1)由题意得F (1,0)，l 的方程为y ＝k (x －1)(k ＞0)． 设A (x 1，y 1)，B (x 2，y 2)．由⎩⎪⎨⎪⎧y ＝k x －1，y 2＝4x 得k 2x 2－(2k 2＋4)x ＋k 2＝0.Δ＝16k 2＋16＞0，故x 1＋x 2＝2k 2＋4k2.所以|AB |＝|AF |＋|BF |＝(x 1＋1)＋(x 2＋1)＝4k 2＋4k2.由题设知4k 2＋4k2＝8，解得k ＝－1(舍去)或k ＝1.因此l 的方程为y ＝x －1.(2)由(1)得AB 的中点坐标为(3,2)，所以AB 的垂直平分线方程为y －2＝－(x －3)，即y ＝－x ＋5.设所求圆的圆心坐标为(x 0，y 0)，则⎩⎪⎨⎪⎧y 0＝－x 0＋5，x 0＋12＝y 0－x 0＋122＋16，解得⎩⎪⎨⎪⎧x 0＝3，y 0＝2或⎩⎪⎨⎪⎧x 0＝11，y 0＝－6.因此所求圆的方程为(x －3)2＋(y －2)2＝16或(x －11)2＋(y ＋6)2＝144.。