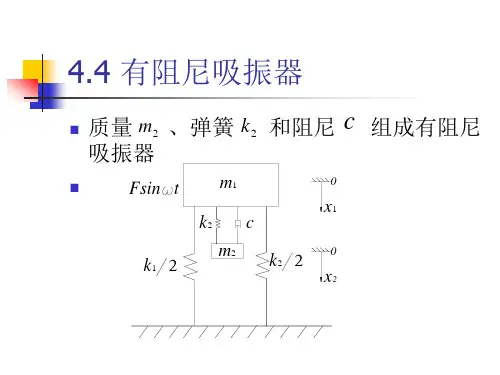
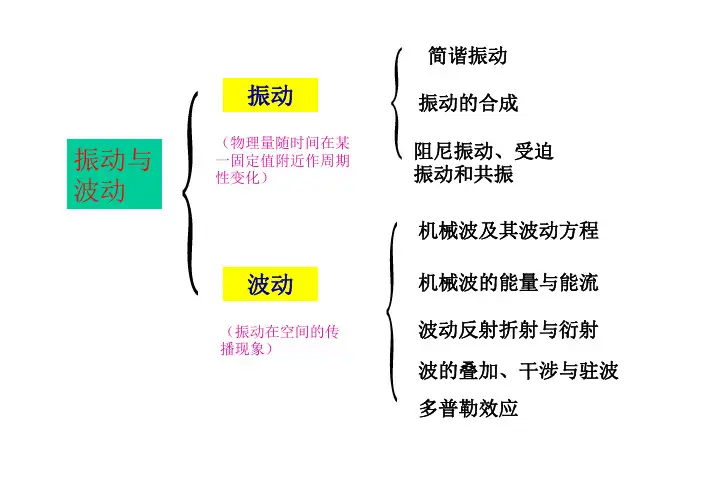
X
k=mg/ l
令向下有位移 x, 则 f=mg-k(l +x)=-kx
作谐振动 设振动方程为 xA cos t (0)
k m
gl
9.8 1r0a/d s 0.098
由初条件得
1r0a/d s
A x02(v0)2 0.09m 8 0 arc(tgvx00 )0,
m
O
x
由x0=Acos0=-0.098<0 cos0<0, 取0=
解:由初始条件:
A
x02
v02
2
0.3 2 9.42 2
4 2
0.42(m 4)
A
0.2 2
x
A
4
0
tg1( v0
x0
由旋转矢量
)tg1(1)
4
质点运动方程:
x0.42c4o2s(t)0.42c4o1s0(t)m ( )
0.2 4
4
(2)由旋转矢量可知:
从t=0到第一次返回x=x0处,相位角的改
对同一谐振动取不同的计时起点不同,但、A不变
例:如图所示,振动系统由一倔强系数为k的 轻弹簧、 一半径为R、转动惯量为I的 定滑轮和一质量为m的 物体所组成。使物体略偏离平衡位置后放手,任其振 动,试证物体作简谐振动,并求其周期T.
解:取位移轴ox,m在平 衡位置时,设弹簧伸长量
为l,则
m gkl0
0 是t =0时刻的位相—初位相
t0时x0A co 0s
v0Asin0
tan0
v0
x0
位相差 两振动位相之差。
21
当=2k ,k=0,±1,±2…,两振动步调相同,称同相 当=(2k+1) , k=0,±1,±2...