《运筹学》 第八章图与网络分析习题及 答案

运筹学教程
第八章习题解答
8.6 分别用深探法、广探法、破圈法找出图852所示图的一个生成树。
page 8 7/14/2020
8
School of Management
运筹学教程
第八章习题解答
page 9 7/14/2020
9
School of Management
运筹学教程
第八章习题解答
page 10 7/14/2020
20 0 36 14 32
D (4)
0
20
18
0
32
12
48
9
0
V1 V2 V3 V4 V5
V1 0 5 16 19 12
V2 20 0 36 14 32
D (5)
V3
50
20
0
20
18
V4 0
V5
32
12
48
9
0
page 23 7/14/2020
23
解：能贮存在同一室内的两种药品之间作一条
连线。贮存在同一室内的药品应该构成一个完全图。 ABG，CFH，DE构成完全图。故，存放这些药品 最少需要3间储藏室。
page 3 7/14/2020
3
School of Management
运筹学教程
第八章习题解答
8.3 6个人围成圆圈就座，每个人恰好只与相 邻者不相识，是否可以重新就座，使每 个人都与邻 座认识?
年。或先使用三年，更新后再使用两年。最小总支 出20。
5
School of Management
运筹学教程
第八章习题解答
8.5 求解如图8-51所示的中国邮路问题，A点 是邮局。

V = {v1 ,v 2 , v 3 , v 4 , v 5 , v 6 }
v1 e1 e2 e5 e8 v5 e6 e7 v3 v2 e3 e v4 4
e 5 = { v1 , v 3 }
e9 = {v 6 , v 6 }
E = {e1 ，2 , e3 , e4 , e5 , e6 , e7 , e8 , e9 , e10 } e e1 = {v1 , v 2 } e 2 = { v1 , v 2 } e10 e 3 = {v 2 , v 3 } e = {v , v }
引
C
言
B A
D
图的基本概念与基本定理
在实际的生产和生活中，人们为了 反映事物之间的关系，常常在纸上用点 点 和线来画出各式各样的示意图。 和线 是我国北京、上海、重庆等十四个城 市之间的铁路交通图，这里用点表示城 市，用点与点之间的线表示城市之间的 铁路线。诸如此类还有城市中的市政管 道图，民用航空线图等等。
例
v6
v1 3 6
4 7 3
v2 2 v3 5
3
4 2
权矩阵
v1 0 v 2 4 v 3 0 A= v4 6 v5 4 v6 3 v1
v5
v4
邻接矩阵
v1 0 v 2 1 v 3 0 B= v 4 1 v 5 1 v 6 1 v1 1 0 1 1 1 0 1 1 0 0 1 0 1 0 1 1 1 0 1 0 0 0 1 0 1 0 1 0 1 0 v 2 v 3 v4 v5 v6
4 3 4
e6 = {v 3 , v 5 }
e8 = {v 5 , v 6 } e10 = {v1 , v6 }
v6
e 7 = {v 3 , v 5 }

进 入 夏 天 ，少 不了一 个热字 当头， 电扇空 调陆续 登场， 每逢此 时，总 会想起 那 一 把 蒲 扇 。蒲扇 ，是记 忆中的 农村， 夏季经 常用的 一件物 品。 记 忆 中 的故 乡 ， 每 逢 进 入夏天 ，集市 上最常 见的便 是蒲扇 、凉席 ，不论 男女老 少，个 个手持 一 把 ， 忽 闪 忽闪个 不停， 嘴里叨 叨着“ 怎么这 么热” ，于是 三五成 群，聚 在大树 下 ， 或 站 着 ，或随 即坐在 石头上 ，手持 那把扇 子，边 唠嗑边 乘凉。 孩子们 却在周 围 跑 跑 跳 跳 ，热得 满头大 汗，不 时听到 “强子 ，别跑 了，快 来我给 你扇扇 ”。孩 子 们 才 不 听 这一套 ，跑个 没完， 直到累 气喘吁 吁，这 才一跑 一踮地 围过了 ，这时 母 亲总是 ，好似 生气的 样子， 边扇边 训，“ 你看热 的，跑 什么？ ”此时 这把蒲 扇， 是 那 么 凉 快 ，那么 的温馨 幸福， 有母亲 的味道 ！ 蒲 扇 是 中 国传 统工艺 品，在 我 国 已 有 三 千年多 年的历 史。取 材于棕 榈树， 制作简 单，方 便携带 ，且蒲 扇的表 面 光 滑 ， 因 而，古 人常会 在上面 作画。 古有棕 扇、葵 扇、蒲 扇、蕉 扇诸名 ，实即 今 日 的 蒲 扇 ，江浙 称之为 芭蕉扇 。六七 十年代 ，人们 最常用 的就是 这种， 似圆非 圆 ， 轻 巧 又 便宜的 蒲扇。 蒲 扇 流 传 至今， 我的记 忆中， 它跨越 了半个 世纪， 也 走 过 了 我 们的半 个人生 的轨迹 ，携带 着特有 的念想 ，一年 年，一 天天， 流向长
page 4 08.01.2021
School of Management
运筹学教程
page 5 08.01.2021
School of Management

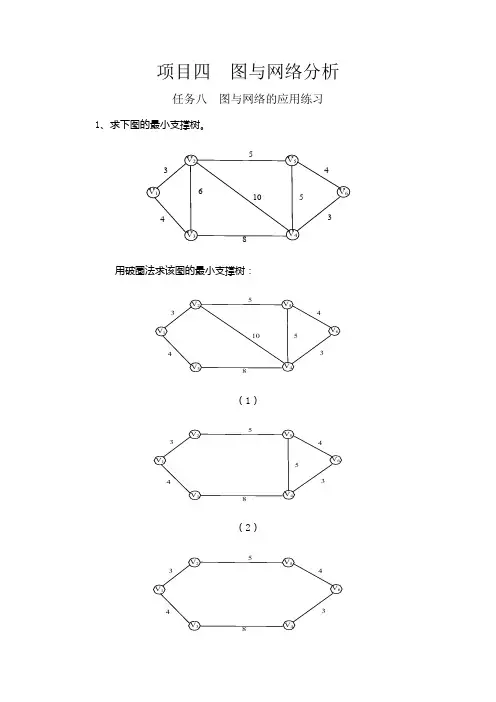
项目四图与网络分析任务八图与网络的应用练习1、求下图的最小支撑树。

用破圈法求该图的最小支撑树：（1）（2）（3）（4）2、分别用破圈法和避圈法求下列各个图的最小支撑树。

a-1：用破圈法求图a的最小支撑树：a-2：用避圈法求图a的最小支撑树：b-1：用破圈法求图b 的最小支撑树：b-2：用避圈法求图b 的最小支撑树：3、用标号法求下图中1v 至7v 的最短路。

1）标号过程（1）初始化；令起点v 1的标号为P ，记做P(1) =0；令其余各点的标号为T ，记做T(i)=∞；（2）计算T标号：刚得到P标号的点为v1，考虑所有与v1相邻的T标号点v 2、v3、v5，修改v2、v3、v5的T标号为：T(2)=min[T(2)，P(1)+d12]=min[+∞，0+4]=4T(3)=min[T(3)，P(1)+d13]=min[+∞，0+3]=3T(5)=min[T(5)，P(1)+d15]=min[+∞，0+5]=5 （3）确定P标号：在所有的T标号点中，找出标号值最小的点标上P标号。

T(2)= 4 T(3) =3 T(4) =+∞T(5)=5 T(6)= +∞ T(7)= +∞令P(3)=3。

（4）计算T标号：刚得到P标号的点为v3，考虑所有与v3相邻的T标号点v 6，修改v6的T标号为：T(6)=min[T(6)，P(3)+d36]=min[+∞，3+2]=5 （5）确定P标号：在所有的T标号点中，找出标号值最小的点标上P标号。

T(2)= 4 T(4) =+∞ T(5)=5 T(6)= 5 T(7)= +∞令P(2)=4。

（6）计算T标号：刚得到P标号的点为v2，考虑所有与v2相邻的T标号点v 5，修改v5的T标号为：T(5)=min[T(5)，P(2)+d25]=min[5，4+1]=5（7）确定P标号：在所有的T标号点中，找出标号值最小的点标上P标号。

T(4) =+∞ T(5)=5 T(6)= 5 T(7)= +∞令P(5)=5。

运筹学
赵明霞山西大学经济与管理学院
2
第八章 图与网络分析
图与网络的基本概念 树 最短路问题 最大流问题 最小费用最大流问题
3
柯尼斯堡七桥问题
欧拉回路：经过每边且仅一次 厄尼斯堡七桥问题、邮路问题哈密尔顿回路：经过每点且仅一次 货郎担问题、快递送货问题
例8-9
28
基本步骤标号T(j)→P(j)

29
2017/10/26
30
最长路问题例8-10（7-9）设某台新设备的年效益及年均维修费、更新净费用如表。试确定今后5年内的更新策略，使总收益最大。
役龄项目
0
1
2
3
4
5
效益vk(t)
5
4.5
4
3.75
3
2.5
14
15
柯尼斯堡七桥问题
欧拉回路：经过每边且仅一次 厄尼斯堡七桥问题、邮路问题 充要条件：无向图中无奇点，有向图每个顶点出次等于入次
16
第二节 树
树是图论中的重要概念，所谓树就是一个无圈的连通图。
图8-4中，(a)就是一个树，而(b)因为图中有圈所以就不是树， (c)因为不连通所以也不是树。
7
G=(V,E)关联边(m)：ei端（顶）点(n)：vi, vj点相邻(同一条边)： v1, v3边相邻(同一个端点)：e2, e3环：e1多重边： e4, e5
8
简单图：无环无多重边
多重图：多重边
9
完全图：每一对顶点间都有边（弧）相连的简单图
10
次（d）：结点的关联边数目d(v3)=4，偶点d(v2)=3，奇点d(v1)=4d(v4)=1，悬挂点e6, 悬挂边d(v5)=0，孤立点
（一）线性(整数)规划法

定义7：子图、生成子图（支撑子图）
图G1={V1、E1}和图G2={V2，E2}如果 V1 V2和E1 E2 称G1是G2的一个子图。
若有 V1＝V2，E1 E2 则称 G1是G2的一 个支撑子图（部分图）。
图8-2（a）是图 6-1的一个子图，图8-2 （b）是图 8-1的支撑子图，注意支撑子图 也是子图,子图不一定是支撑子图。 e1
v2 ▲如果链中所有的顶点v0，v1，…，vk也不相
e1 e2 e4 v1 e3
v3 e5
同，这样的链称初等链（或路）。
e6
▲如果链中各边e1,e2…,ek互不相同称为简单链。
e7
e8
▲当v0与vk重合时称为回路（或圈），如果边不 v4
v5
重复称为简单回路，如果边不重复点也不重复
则称为初等回路。
图8－1中， μ1={v5,e8,v3,e3,v1,e2,v2,e4,v3,e7,v5}是一条链，μ1中因顶 点v3重复出现，不能称作路。
e1
e2 e4 v1 e3
v2
v3
e5
e6
e7
e8
v4
v5
定理1 任何图中，顶点次数的总和等于边数的2倍。
v1
v3
v2
定理2 任何图中，次为奇数的顶点必为偶数个。
e1
e2 e4 v1 e3
v2
v3
e5
e6
e7
e8
v4
v5
定义4 有向图： 如果图的每条边都有一个方向则称为有向图
定义5 混合图： 如何图G中部分边有方向则称为混合图 ② ⑤ ④
定理4 有向连通图G是欧拉图，当且仅当G中每个顶点的出 次等于入次。
② 15
9 10

School of Management
运筹学教程
第八章习题解答
8.11 求图 求图8-56中v1到各点的最短路。 中 到各点的最短路。
page 20 5 April 2012
School of Management
运筹学教程
第八章习题解答
page 21 5 April 2012
School of Management
D (0)
D (1)
5 16 0 20 0 36 =∞ ∞ 0 ∞ ∞ ∞ ∞ 12 ∞ 5 0 20 0 =∞ ∞ ∞ ∞ 32 12 16
12 14 32 20 18 0 ∞ 9 0 19
∞
D (2)
5 0 20 0 =∞ ∞ ∞ ∞ 32 12
page 28 5 April 2012
School of Management
运筹学教程
第八章习题解答
解：最大流量为21。 最大流量为 。
page 29 5 April 2012
School of Management
运筹学教程
第八章习题解答
8.16 如图8-60，从v0派车到v8，中间可经过 如图8 60， 派车到v v1，…，v7各站，若各站间道路旁的数字表示单位时 各站， 间内此路上所能通过的最多车辆数， 间内此路上所能通过的最多车辆数，问应如何派车才 能使单位时间到达v 的车辆最多? 能使单位时间到达v8的车辆最多?
School of Management
运筹学教程
第八章习题解答
8.7 设计如图 设计如图5-53所示的锅炉房到各座楼铺设暖气 所示的锅炉房到各座楼铺设暖气 管道的路线，使管道总长度最(单位 单位： 。 管道的路线，使管道总长度最 单位：m)。

第一章 线性规划及单纯形法（作业）1.4 分别用图解法和单纯型法求解下列线性规划问题，并对照指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。

（1）Max z=2x 1+x 2St.⎪⎩⎪⎨⎧≥≤+≤+0,24261553212121x x x x x x 解：①图解法：由作图知，目标函数等值线越往右上移动，目标函数越大，故c 点为对应的最优解，最优解为直线⎩⎨⎧=+=+242615532121x x x x 的交点，解之得X=(15/4,3/4)T 。

Max z =33/4. ② 单纯形法：将上述问题化成标准形式有： Max z=2x 1+x 2+0x 3+0x 4St. ⎪⎩⎪⎨⎧≥≤++≤++0,,,242615535421421321x x x x x x x x x x其约束条件系数矩阵增广矩阵为：P 1 P 2 P 3 P 4⎥⎦⎤⎢⎣⎡241026150153 P 3,P 4为单位矩阵，构成一个基，对应变量向，x 3,x 4为基变量，令非基变量x 1,x 2为零，找到T 优解，代入目标函数得Max z=33/4.1.7 分别用单纯形法中的大M 法和两阶段法求解下列线性规划问题，并指出属哪一类。

（3）Min z=4x 1+x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 解：这种情况化为标准形式： Max z ＇=-4x 1-x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 添加人工变量y1,y2Max z ＇=-4x 1-x 2+0x 3+0x 4-My 1-My 2⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x(2) 两阶段法： Min ω=y 1+y 2St.⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x第二阶段，将表中y 1,y 2去掉，目标函数回归到Max z ＇=-4x 1-x 2+0x 3+0x 4第二章 线性规划的对偶理论与灵敏度分析（作业）2.7给出线性规划问题：Max z=2x 1+4x 2+x 3+x 4⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤++≤++≤+≤++)4,3,2,1(096628332143221421j x x x x x x x x x x x x j要求：（1）写出其对偶问题；（2）已知原问题最优解为X *=(2,2,4,0),试根据对偶理论，直接求出对偶问题的最优解。

（8）考察V8点，只有一个T标号，T(V8)=15，令P(V8)=15)，记录路 径（V7，V8），计算结束。
反推得最V1至V8的最短路为V1→V2 →V5 →V7 →V8,路长15。
8.2 最短路问题
一、Dijkstra算法：求无负权网络最短路问题。
计算步骤：
（1）给Vs以P标号，P（Vs）=0，其余各点给T标号， T（Vi）=+∞；
且仅得一个圈。
4）图中边数为：p-1（p为顶点数）
8.1 图与网络基本知识
例8-4：一个班级的学生共计选修A、B、C、D、 E、F六门课程，其中一部分人同时选修D、C、A， 一部分人同时选修B、C、F，一部分人同时选修 B、E，还有一部分人同时选修A、B，期终考试 要求每天考一门课，六天内考完，为了减轻学生 负担，要求每人都不会连续参加考试，试设计一 个考试日程表。
（2）若Vi点为刚得到P标号的点，考虑点Vj: (Vi,Vj) 属于E，且Vj为T标号。则修改T(Vj)
T(Vj)=min[T(Vj),P(Vi)+lij]；
（3）比较所有T标号的点，把最小者改为P标号，即： P（Vi）=min[T(Vi)] 当存在两个以上最小者时，可同时改为P标号。
8.2 最短路问题
8.1 图与网络基本知识
三、有向图的有关概念:
有向图：
由点和弧组成。表示为：D=（V，A）
V--点集合 A--弧集合
始点和终点： 对弧a=(u，v)， u为a的始点，v为a的
终点。
链（道路）：
点弧交错序列。
圈（回路）：
如一条链中起点和终点重合。
初等链（道路）： 链中无重复的点和弧。
（3） 考察V5V6和V5V7两边： T(V6)=min[T(V6),P(V5)+l56]=min[+∞,8+5] =13 T(V7)=min[T(V7),P(V5)+l57]=min[+∞,8+6] =14

错误
正确
网络图中不能出现循环回路
错误
节点编号时，按照矢线箭头的指向，升序 排号，保证节点序号先后关系保持一致。
应将各作业的工时数据标注在表示该作业 的矢线的下面。
正确使用虚工序（不消耗资源，一般表示 平行工作关系）
三、PERT图的绘制步骤
先画草图，再修改后变成规范图，步骤如下： @ 根据活动清单中规定的关系，将活动代号栏所有的 活动逐次地画在网络图上，从左到右 @ 理顺活动的紧前、紧后关系，没有紧后活动的活动 所对应的箭线汇集在终止结点上 @ 草图绘制完成后，将序号标在结点上，将活动代号 和时间标在箭 线上 @ 检查无误后，将草图绘制成规范图 •
工作（1，7）有自由时差13，若把它拖至13周开工， 对它后面的工作的最早开工时间及时差等都没有影响， 对整个工期也没有影响。而只有总时差没有自由时差 的工作则不然，若工作（7，8），总时差为1，自由时 差为0，如果让它推迟1周开工，虽然总工期不受影响， 但其后面的工作最早时间及时差都要受影响。所以使 用时差来调整工作时，应尽量先用自由时差。
5、虚箭线：不占用时间和空间，不消耗任何资 源。只是为了明 确活动的相互之间的逻辑关系。
i
A：作业活动代号
j
4A 5 A
3 10 4
结点（表示事件）： 网络图中两条或两条以上的箭线的交接
点就是结点，结点代表的作业开始和结 束。用圆圈加上数字表示。
路线： 从网络图的始点事件开始到终点事
件为止，由一系列首尾相连的箭线和结 点所代表的作业和事件所组成的通道。 网络图一般有多条路线。其中最长的我 们称之为关键路线，关键路线上的工序 为关键工序。
客来沏茶
本问题的几道“工序”有次序时,间:
洗杯盖 2

《运筹学》第八章图与网络分析习题1.思考题(１)解释下列名词，并说明相互之间的区别与联系：①顶点，相邻，关联边；②环，多重边，简单图；③链，初等链；④圈，初等圈，简单拳；⑤ 回 路，初等路；⑥节点的次，悬挂点，孤立点；⑦）连通图，连同分图， 支 撑子图；⑧有向图，基础图，赋权图。

⑨子图，部分图，真子图．(２)通常用记号Ｇ＝（Ｖ，Ｅ）表示一个图，解释Ｖ及Ｅ的涵义及这个表达式 的涵义．(３)通常用记号Ｄ＝（Ｖ，Ａ）表示一个有向图，解释Ｖ及Ａ的涵义及这个表 达式的涵义．(４) 图论中的图与一般几何图形的主要区别是什么？ (５) 试述树与图的区别与联系．(６) 试述 求最短路问题的Ｄijkstra 算法的基本思想及其计算步骤． (７) 试述寻求最大流的标号法的步骤与方法．(８) 简述最小费用最大流的概念及其求解的基本思想和方法．(９) 通常用记号Ｎ＝（Ｖ，Ａ，Ｃ）表示一个网络，试解释这个表达式的涵义． (10) 在最大流问题中，为什么当存在增广链时，可行流不是最大流？ (11) 试叙述最小支撑树、最大流、最短路等问题能解决那些实际问题。

2.判断下列说法是否正确(1) 图论中的图是为了研究问题中有哪些对象及对象之间的关系，它与图的几何形状无关。

(2) 一个图G 是树的充分必要条件是边数最少的无孤立点的图。

(3) 如果一个图G 从V 1到各点的最短路是唯一的，则连接V 1到各点的最短路，再去掉重复边，得到的图即为最小支撑树。

(4 )图G 的最小支撑树中从V 1到V n 的通路一定是图G 从V 1到V n 的最短路。

(5) {f ij =0}总是最大流问题的一个可行流。

(6 )无孤立点的图一定是连通图。

(7) 图中任意两点之间都有一条简单链，则该图是一棵树。

(8) 求网络最大流的问题总可以归结为求解一个线性规划问题。

(9)在图中求一点Ｖ１到另一点Ｖn 的最短路问题总可以归结为一个整数规划问题 (10) 图G 中的一个点V 1总可以看成是G 的一个子图。

X={1}
P1=0
T2=2
2
6
1
2
3
1
10
5
9
3 T4=1 4
7
5
6
5
2
3
4
6
7
4
T6=3
min {T2, T4, T6}=min {2,1,3}=1
X={1,4}, P4=1
8 8
X={1,4}
P1=0
T2=2
2
6
1
2
3
1
10
P4=1
5
9
3
4
7
5
6
5
2
3
4
6
7
8
4
8
T6=3
T7=3
min {T2,T6, T7}=min {2,3,3}=2
■悬挂点： d(v)=1 对应的边为悬挂边
■孤立点： d(v) =0
e1
v5
v4
■奇点： d(v)为奇数 ■偶点： d(v)为偶数
v2
有向图：
e2
v1
e4
e3
e6
e5
v3
■出次 d+(v)：以v为始点的边数 d (v) d (v)
■入次 d-(v)：以v为终点的边数 vV
vV
次的定理1
定理1：任何图中，顶点次数的总和为边数的2倍。 证明思路：每条边必与两个顶点关联
d(v) 2m
vV
次的定理2
定理2：任何图中，奇点必为偶数个
证明思路：
d(v) d(v) 2m
vV1
vV2
Euler图的充要条件
定理3：无向连通图G是Euler图的充要条件是： G中无奇点

向图。记之为G(D)。
链：设(vi1,ai1,vi2,ai2,…,vik-1,aik-1,vik)是D中的一个点弧交错序列，如果这个序
列在基础图G(D)中所对应的点边序列是一条链，则称这个点弧交错序列是D的 一条链。 1，均有ait=(vit,vit+1)，称之为从vi1到vik的一条路。
路：如果(vi1,ai1,vi2,ai2,…,vik-1,aik-1,vik)是D中的一条链，并且对t=1,2,…,k回路：若路的第一个点和最后一点相同，则称之为回路。
3)E中任意两条线之间除端点之外无公共点.
则由V、E构成的二元组合G=(V， E)就是图。 子图：已知图G1（V1，E1）若V1 ﹤V， E1 ﹤ E ; 图G=(V， E)的子图 则称图G1（V1，E1）是
若在图G中，某个边的两个端点相同，则称e是环。 多重边：图中某两点之间有多余一条的边，称之为多重边。 多重图：含有多重边的图。 简单图：无环、无多重边的图。
步骤 v1
例9：（图8－31）
v2 v3 v4 v5 v6 v7
v8
最短 前向 路 结点
1
2 3
0*
∞
4*
∞
6 6*
∞
∞ 9 9 9*
∞
∞ 8 8*
∞
∞ ∞ ∞ 13 13 *
∞
∞ ∞ ∞ 14 14 14*
∞
∞ ∞ ∞ ∞ ∞ 17
0
4 6 8 9 13 14 15 v1 v1 v2 v2 v5 v5
V7 6 4 V8 2 V9 4
6
V4 4 2 V5 3 V2
2
V6 4 V3
4
V1
一、最短路算法
1、情况一： wij≥0(Dijkstra算法) 原理：Bellman最优性定理 方法：图上作业法（标号法）；双标号法（表的形式） 标号：对于点V,若已求出V1到Vi的最短值，标号（αi,βi) αi ：表示V1到Vi的最短路值 βi:表示最短路中最后经过的点

运筹学教程
v2
v6
e3
v3 e7
v5
运筹学教程
V= （ v1， v2，…... v6） E= （ e1， e2，…... e8） （e1）= （v1， v2） （e2）= （v1， v2） （e7）= （v3， v5） （e8）= （v4， v4） (e8)= (v4， v4),称为自回路(环)； v6是孤立点，v5为悬挂点，e7为悬挂边，顶点v3的次为 4，顶点v4的次为4。
2l23+ 2l36+ l69+ l98+ l23+ 2l87+ 2l74+ l41+ l12=51
运筹学教程
第二步：调整可行方案，使重复边最多为一次
重复边 的总长：
v3
l69+ l98+ l41+ l12=21
5
v2
第三步：检查每个初等圈是否 5
v1
定理条件2，如果不满足，进行
2 v6 4 v9
例：求解网络的中国邮路问题
运筹学教程
v3
5
v2
5
v1
2 v6 4 v9
3
3
6 v5 4 v8
4
4
9
v4 4 v7
v3
5
v2
5
v1
2 v6 4 v9
3
3
6
v5 4 v8
4
4
9
v4 4 v7
第一步：确定初始可行方案
先检查图中是否有奇点，如果无奇点，为欧拉图；如果
有奇点，图中的奇点的个数比为偶数个，所以可以两两 配对，构造二重边。图中有4个奇点，v2,v4,v6,v8,配对 v2-v4,v6-v8，构造二重边。重复边 的总长：

（a）
（b）
（c）
图 8-9 图、子图、支撑子图
（4）图的同构 设 G1 与 G2 是两个同阶图，若顶点集合 V1 和 V2 以及边集 E1 和 E2 之间在保持关联性
质条件下的一一对应，则称图 G1 和图 G2 同构。 例如：图 8-10（a）和图 8-10（b）就为同构。
（a）
(b)
图 8-10 同构图
（10）定理 8.1 对于图 G=(V ,E) ，其中 V = n , E = m ,则有：
∑d (v) = 2m
（8-2）
v∈V
证明：每条边都有两个端点，在计算顶点的次时，每个端点都要计算对应边次，故共有
2m 次。
通俗地讲，就是线有两头，共有 2m 个线头的意思。
（11）定理 8.2 奇次顶的总数是偶数。
第八章 图与网络分析
8.1 图与网络的基本知识
8.1.1 图与网络的基本概念 8.1.1.1 图的定义 自然界和人类社会中，大量的事物以及事物之间的关系，常可以用图形来描述。例如： 图 8-4 所示的我国北京、上海等十个城市间的交通图反映了这十个城市间铁路
分布情况。这里用点代表城市，用点和点之间的连线代表这两个城市之间有直通铁路。
图 8-7 一个无向图
G = (V, E) V= {v1, v2 ,v3 , v4} E={e1, e2 ,e3 , e4 ,e5 , e6 , e7}
其中
e1 = [v1 ,v2 ] , e2 = [v1 ,v2 ] , e3 = [v2 ,v3 ] , e4 = [v3 ,v4 ] ,
图 8-8 是一个有向图。该图可以表示为：
图 8-4 十个城市间铁路分布图
又如某单位储存五种化学药品，其中，某些药品是不能放在同一库房里的，为了反映这 种情况，可以用点 v1 、 v2 、 v3 、 v4 、 v5 分别代表这五种药品，若药品 vi 和药品 v j 是不能存 放在同一库房的，则在 vi 和 v j 之间连一条线，如图 8-5 所示。如果问题归结为寻求存放这种 化学药品的最少库房个数，则该问题就是染色问题。事实上，至少需要三个库房来存放这些 药品，即 v1 和 v5 、 v2 和 v4 、 v3 各存放在一个库房里。

School of Management
运筹学教程
第八章习题解答
8.10 如图 如图8-55，v0是一仓库，v9是商店，求一条 ， 是一仓库， 是商店， 的最短路。 从v0到v9的最短路。
page 16 22 May 2012
School of Management
运筹学教程
第八章习题解答
page 17 22 May 2012
D (0)
D (1)
5 16 0 20 0 36 =∞ ∞ 0 ∞ ∞ ∞ ∞ 12 ∞ 5 0 20 0 =∞ ∞ ∞ ∞ 32 12 16
12 14 32 20 18 0 ∞ 9 0 19
∞
D (2)
5 0 20 0 =∞ ∞ ∞ ∞ 32 12
D (5)
page 22 22 May 2012
School of Management
运筹学教程
第八章习题解答
8.13 某设备今后五年的价格预测分别是 ，5，6， 某设备今后五年的价格预测分别是(5， ， ， 7，8)，若该设备连续使用，其第 年的维修费分别为 ， ，若该设备连续使用，其第j年的维修费分别为 (1，2，3，5，6)，某单位今年购进一台，问如何确定 ， ， ， ， ，某单位今年购进一台， 更新方案可使5年里总支出最小 年里总支出最小(不管设备使用了多少 更新方案可使5年里总支出最小(不管设备使用了多少 其残值为0)。 年，其残值为 。 最优解为：先使用两年，更新后再使用三年。 解：最优解为：先使用两年，更新后再使用三年。 或先使用三年，更新后再使用两年。最小总支出20。 或先使用三年，更新后再使用两年。最小总支出 。
page 1 22 May 2012

v6
07
含有奇点的连通图中不含欧拉圈，此时，最优的邮递路线是什么呢？
08
求解中国邮路问题的奇偶点图上作业法
奇偶点表上作业法
奇偶点表上作业法 (1)找出奇点(一定为偶数个)，在每两个奇点之间找一条链，在这些链经过的所有边上增加一条边，这样所有的奇点变为偶点，一定存在欧拉圈，但是不一定是路线最短的，所以需要检验和调整。 (2)检验增加的边的权值是否是最小的。 定理3 假设M是使得图G中不含奇点的所有增加边，则M是权值总和为最小的增加边的充分必要条件是： 1)图G中每条边上最多增加一条边； 2)在图G的每个圈上，增加的边的总权值不超过该圈总权值的一半。 如果上述两个条件都满足则已经找到权值最小的欧拉圈 否则转入3) 3)调整增加边。如果1)不满足，则从该条边的增加边中去掉偶数条； 如果2)不满足，则将这个圈上的增加边去掉，将该圈的其余边上添加增 加边，转入(2)
v1
v2
v3
v4
v5
v1
v2
v3
v4
v5
图2
图3
如果在比赛中： A胜E， B胜C， A胜D， C胜A， E胜D， A胜B，
v1
v2
v3
v4
v5
注：本章所研究的图与平面几何中的图不 同，这里我们只关心图有几个点，点与点 之间有无连线，两条线有无公共顶点，点 与线是否有关联，至于连线的方式是直线 还是曲线，点与点的相对位置如何都是无 关紧要的。
求从v1到v8的最短路
(0)
(1,1)
(1,3)
(3,5)
(2,6)
(5,10)
(5,9)
(5,12)
注：在给顶点编号时，如果在多个为标号点均取得最小值Llk则对这多个点同时标号，这些点的第二个标号相同，但是第一个标号不一定相同。