2021年材料力学(金忠谋)第六版答案第06章
- 格式:doc
- 大小:330.01 KB
- 文档页数:10

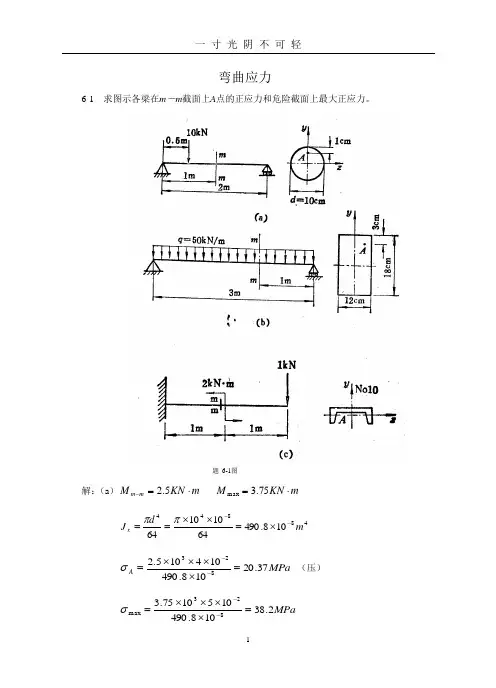
弯曲应力6-1 求图示各梁在m-m截面上A点的正应力和危险截面上最大正应力。
题6-1图解:(a)mKNMmm⋅=-5.2mKNM⋅=75.3max48844108.49064101064mdJx--⨯=⨯⨯==ππMPaA37.20108.490104105.2823=⨯⨯⨯⨯=--σ(压)MPa2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ(b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4,h 1=9.65cm ,h 2=15.35cm 。


第6章 应力状态分析一、选择题1、对于图示各点应力状态,属于单向应力状态的是(A )。
(A )a 点;(B )b 点;(C )c 点;(D )d 点 。
2、在平面应力状态下,对于任意两斜截面上的正应力αβσσ=成立的充分必要条件,有下列四种答案,正确答案是( B )。
(A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。
3、已知单元体AB 、BC 面上只作用有切应力τ,现关于AC 面上应力有下列四种答案,正确答案是( C )。
(A )AC AC /2,0ττσ==; (B)AC AC /2,/2ττσ=; (C)AC AC /2,/2ττσ==;(D)AC AC /2,/2ττσ=-。
4、矩形截面简支梁受力如图(a )所示,横截面上各点的应力状态如图(b )所示。
关于它们的正确性,现有四种答案,正确答案是( D )。
(A )点1、2的应力状态是正确的;(B )点2、3的应力状态是正确的; (C )点3、4的应力状态是正确的;(D )点1、5的应力状态是正确的。
5、对于图示三种应力状态(a )、(b )、(c )之间的关系,有下列四种答案,正确答案是( D )。
(A )三种应力状态均相同;(B )三种应力状态均不同; (C )(b )和(c )相同; (D )(a )和(c )相同;6、关于图示主应力单元体的最大切应力作用面有下列四种答案,正确答案是( B )。
解答:max τ发生在1σ成45的斜截面上7、广义胡克定律适用范围,有下列四种答案,正确答案是( C )。
(A )脆性材料;(B )塑性材料;(C )材料为各向同性,且处于线弹性范围内;(D )任何材料; 8、三个弹性常数之间的关系:/[2(1)]G E v =+ 适用于( C )。
(A )任何材料在任何变形阶级; (B )各向同性材料在任何变形阶级; (C )各向同性材料应力在比例极限范围内;(D )任何材料在弹性变形范围内。

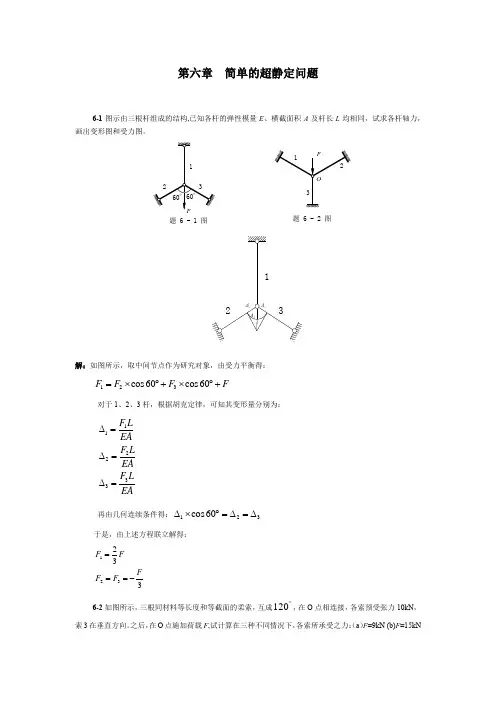
第六章 简单的超静定问题6-1图示由三根杆组成的结构,已知各杆的弹性模量E 、横截面积A 及杆长L 均相同,试求各杆轴力,画出变形图和受力图。
123Δ2Δ3Δ1解:如图所示,取中间节点作为研究对象,由受力平衡得:123cos60cos60F F F F =⨯︒+⨯︒+对于1、2、3杆,根据胡克定律,可知其变形量分别为:112233F L EA F L EA F L EA ∆=∆=∆=再由几何连续条件得:123cos60∆⨯︒=∆=∆于是,由上述方程联立解得:123233F F FF F ===-6-2如图所示,三根同材料等长度和等截面的柔索,互成︒120,在O 点相连接,各索预受张力10kN ,索3在垂直方向。
之后,在O 点施加荷载F ,试计算在三种不同情况下,各索所承受之力:(a )F =9kN (b)F =15kN题 6 - 1 图题 6 - 2 图(c)F =21kN 。
答:(a )F =9kN 时,12313,4N N kN N kN ===(b )F =15kN 时,12315,0N N kN N ===(c )F =21kN 时,12321,0N N kN N === 解:首先计算当绳索3刚好无拉力时荷载F 的值。
如图所示,取节点O 作为研究对象。
由于绳索上实现施加了10KN 的拉力,因此由节点的竖向平衡可知:12cos60cos60F F F =⨯︒+⨯︒则F=10KN(1)由于F=9KN<10KN (不太明白怎么做)于是绳索3中仍然有拉力。
……(2)由于F=15KN>10KN 于是绳索3中没有拉力。
因此由节点的竖向平衡可知:12cos60cos60F F F =⨯︒+⨯︒则123150F F KN F KN===(3)由于F=21KN>10KN 于是绳索3中没有拉力。
因此由节点的竖向平衡可知:12cos60cos60F F F =⨯︒+⨯︒则123210F F KN F KN===6-3图示对称结构中,杆BC 为刚性杆,其余四根杆的EA 均相同,试求荷载F 作用下四根杆的轴力。


金属材料与热处理习题册答案绪论一、填空题1、成分、组织、热处理、性能之间。
2、石器时代、青铜器时代、铁器时代、钢铁时代、人工合成材料时代。
3、成分、热处理、性能、性能。
二、选择题:1、A2、B3、C三、简答题1、掌握金属材料与热处理的相关知识对机械加工有什么现实意义?答:机械工人所使用的工具、刀夹、量具以及加工的零件大都是金属材料,所以了解金属材料与热处理后相关知识,对我们工作中正确合理地使用这些工具,根据材料特点正确合理地选择和刃磨刀具几何参数;选择适当的切削用量;正确选择改善零件工艺必能的方法都具有非常的现实意义。
2、如何学好《金属材料与热热处理》这门课程?答:在学习过程中,只要认真掌握重要的概念和基本理论,按照材料的成分和热处理决定组织,组织决定其性能,性能又决定其用途这一内在关系进行学习和记忆;注意理论联系实际,认真完成作业和实验等教学环节,是完全可以学好这门课程的。
第一章金属的结构和结晶1-1金属的晶体结构一、填空题1、非晶体晶体晶体2、体心立方面心立方密排立方体心立方面心立方密排立方3、晶体缺陷点缺陷面缺陷二、判断题1、√2、√3、×4、√三、选择题1、A2、C3、C四、名词解释1、晶格与晶胞:P5答:将原子简化为一个质点,再用假想的线将它们连接起来,这样就形成了一个能反映原子排列规律的空间格架,称为晶格;晶胞是能够完整地反映晶体晶格特征的最小几何单元。
3、单晶体与多晶体答:只由一个晶粒组成称为单晶格,多晶格是由很多大小,外形和晶格排列方向均不相同的小晶格组成的。
五、简答题书P6□1-2纯金属的结晶一、填空题1、液体状态固体状态2、过冷度3、冷却速度冷却速度4、晶核的产生长大5、强度硬度塑性二、判断题1、×2、×3、×4、×5、√6、√三、选择题1、C、B、A2、B3、A4、A四、名词解释1、结晶与结晶潜热 (P8)答:(1)结晶:是金属从高温液体状态,冷却凝固为原子有序排列的固体状态的过程。

第六版材料力学知识点总结第一章引言本章主要介绍了力学在材料科学与工程中的地位和作用。
力学是分析物体受力情况和相应变形的学科,这在材料科学与工程中具有重要意义。
本章的内容对整本教材的学习打下了基础。
第二章应力在本章中,主要介绍了材料在受到外力作用时所产生的应力的概念。
力的作用有拉伸作用、压缩作用和剪切作用三种,这些力对应的应力分别是拉应力、压应力和剪应力。
材料受力会导致应力在材料内部的分布,通过一些基本方程来描述材料受力的情况。
第三章应变这一章主要介绍了材料在受到外力作用时所产生的应变的概念。
应变是指材料在外部力作用下所产生的形变。
介绍了应变的三种基本形式:线性应变、剪切应变和体积变形。
第四章弹性模量本章介绍了材料的弹性行为及其数学描述。
材料在受力时会发生形变,而且形变是可逆的,这种性质称为弹性。
对材料的弹性行为进行了分析,并引入了弹性模量这一概念,分别是杨氏模量、剪切模量和泊松比。
这些弹性模量对于描述材料的弹性行为有着重要的意义。
第五章弯曲这一章介绍了材料在受力时进行弯曲变形的物理过程和数学描述。
利用梁的理论分析了材料受弯曲力时的受力和应变情况。
并引入了一些相关参数,并给出了一些实际应用问题的数学解析。
第六章扭转这一章详细介绍了材料在受扭转力作用下的受力和应变情况。
对材料进行了基本的力学分析,并引入了剪切弹性模量,这对于描述材料的扭转弹性行为具有重要意义。
第七章变形与尺寸稳定性本章主要介绍了材料在受力后的变形与尺寸稳定性。
材料在受力时会发生变形,而变形又分为弹性变形和塑性变形,并且介绍了材料的屈曲现象和相应的数学分析,这在实际工程中具有重要的意义。
第八章断裂这一章详细介绍了材料在受到过大外力作用时的断裂过程。
材料的断裂可以分为塑性断裂和脆性断裂,分析了断裂的过程及其影响因素,并引入了一些与断裂相关的参数。
第九章强度理论这一章主要介绍了材料的强度理论。
介绍了强度概念以及与强度相关的一些理论模型,如最大正应力理论、最大剪应力理论等。
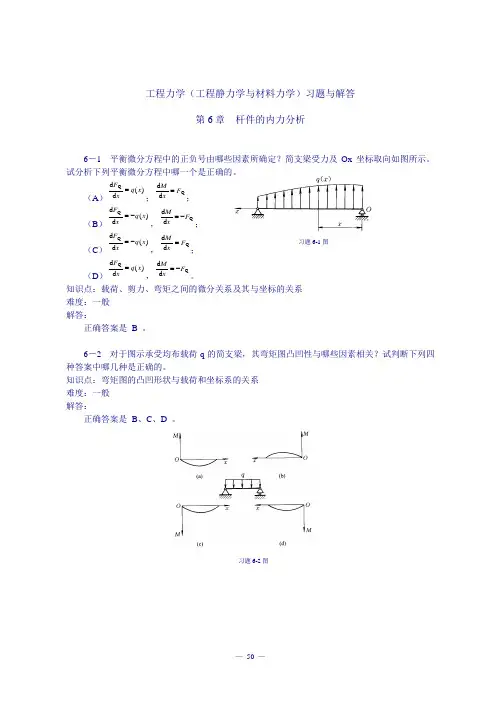
习题时间:2021.03.03 创作:欧阳学8-1 构件受力如图所示。
(1)确定危险点的位置;(2)用单元体表示危险点的应力状态。
解:(a) 在任意横截面上,任意一点24P d σπ=3316M dτπ= τσ (c)A 截面的最上面一点8-2 图示悬臂粱受载荷P=20kN 作用,试绘单元体A 、B 、C 的应力图,并确定主应力的大小及方位。
解:8-3主应力单元体各面上的应力如图所示,试用解析法或图解法计算指定斜截面上的正应力ασ和剪应力ατ,并找出最大剪应力值及方位(应力单位:MPa )。
解:(a) ()()1212205205cos 2cos 6013.752222MPaασσσσσα+---+-=+=+= 45α= (与120σ=方向夹角)(b)()()()121220102010cos 2cos 135 5.6062222M ασσσσσα+---+-=+=+-=-()()122010sin 2sin 13510.60622MPa ασστα---==-=- 45α= (与1σ方向夹角)或135(与水平方向交角)(c)45α= (与140σ=方向夹角)(d)8-4单元体各面的应力如图示(应力单位为MPa ),试用解析法和图解法计算主应力的大小及所在截面的方位,并在单元体内注明。
解:(a)(b)(c)(d)8-5作出图示单元体的三向应力图,并求出主应力和最大剪应力,画出主单元体。
解:(a) (b) (c ) (d)(e)8-6 已知矩形截面梁某截面上的弯矩和剪力分别为M =10kN·m ,FS =120kN ,试绘出截面上1、2、3、4各点单元体的应力状态,并求其主应力。
解:8-7在棱柱形单元体的AB 面上以及与ABC 面平行的前后面上(与纸平面平行的面),均无应力作用。
在AC 面和BC 面上的正应力均为-15MPa ,试求AC 和BC 面上的剪应力与此单元体主应力的大小和方向。
习题欧阳歌谷(2021.02.01)8-1 构件受力如图所示。
(1)确定危险点的位置;(2)用单元体表示危险点的应力状态。
解:(a) 在任意横截面上,任意一点24P d σπ=3316M dτπ= τσ (c)A 截面的最上面一点8-2 图示悬臂粱受载荷P =20kN 作用,试绘单元体A 、B 、C 的应力图,并确定主应力的大小及方位。
解:8-3主应力单元体各面上的应力如图所示,试用解析法或图解法计算指定斜截面上的正应力ασ和剪应力ατ,并找出最大剪应力值及方位(应力单位:MPa )。
解:(a) ()()1212205205cos 2cos 6013.752222MPa ασσσσσα+---+-=+=+= 45α= (与120σ=方向夹角)(b)()()()121220102010cos 2cos 135 5.6062222MP ασσσσσα+---+-=+=+-=-()()122010sin 2sin 13510.60622MPa ασστα---==-=-45α= (与1σ方向夹角)或135(与水平方向交角)(c)45α= (与140σ=方向夹角)(d)8-4单元体各面的应力如图示(应力单位为MPa),试用解析法和图解法计算主应力的大小及所在截面的方位,并在单元体内注明。
解:(a)(b)(c)(d)8-5作出图示单元体的三向应力图,并求出主应力和最大剪应力,画出主单元体。
解:(a) (b)(c ) (d)(e)8-6 已知矩形截面梁某截面上的弯矩和剪力分别为M=10kN·m,F S=120kN,试绘出截面上1、2、3、4各点单元体的应力状态,并求其主应力。
解:8-7在棱柱形单元体的AB面上以及与ABC面平行的前后面上(与纸平面平行的面),均无应力作用。
在AC 面和BC 面上的正应力均为-15MPa ,试求AC 和BC 面上的剪应力与此单元体主应力的大小和方向。
解:015x MPa τ==∑1230;30MPa σσσ∴===- (方向平行于AB )8-8某点的应力状态如图所示,已知αατσ、与y σ,试参考如何根据已知数据直接作出应力图。
第六弯曲应力第六章答案6.1钢丝直径d=0.4mm, 弹性模量E=200GPa, 若将钢丝弯成直径D=400mm 的圆弧时,试求钢丝横截面上的最大弯曲正应力。
(200MPa ) 解:钢丝的弯矩和中性层曲率半径之间的关系为:EIM =ρ1则: ρEIM =,由弯曲正应力公式得ρσmaxmax My ==ρmaxEy ,钢丝弯成圆弧后,产生的弯曲变形,其中性层的曲率半径22Dd D ≈+=ρ 2)2(maxD dE =σ==D Ed MPa 2004004.0102003=⨯⨯6.2 矩形截面梁如图所示。
b = 8cm, h =12cm, 试求危险截面上a 、c 、d 三点的弯曲正应力。
(20.8MPa, 10.4MPa, 0) 解:由平衡方程0)(=∑F M A得到: KN F F B A 44221=⨯⨯== 危险截面在梁的中点处:KNm ql M 442818122max =⨯⨯==I z =1212h b ⨯⨯=44310115212080121mm ⨯=⨯⨯MP a I My MPa I MyI My z d d z c c za a 83.201011526010442.101011523010404646=⨯⨯⨯===⨯⨯⨯====σσσA F BF s F MM机械土木6.3 从直径为d 的圆木中截取一矩形截面梁,试根据强度观点求出所截取的矩形截面的最合理的高h 和宽b 。
(h=d 36, b=d 33) 解:最大弯曲正应力:zz W My I M m a x m a x m a x m a x ==σ h/b 的最佳值应应使梁的抗弯截面系数为最大。
抗弯截面系数: )(61)(616132222b b d b d b bh W -=-==为b 为自变量的函数。
由 06322=-=b d dt dW 36 333222db d h d d b =-===6.4 图示两根简支梁,其跨度、荷载及截面面积都相同。
弯曲应力欧阳光明(2021.03.07)6-1 求图示各梁在m -m 截面上A 点的正应力和危险截面上最大正应力。
题 6-1图解:(a )m KN M m m ⋅=-5.2m KN M ⋅=75.3maxMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ (压) (b )m KN M m m ⋅=-60m KN M ⋅=5.67maxMPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) (c )m KN M m m ⋅=-1m KN M ⋅=1maxMPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x6-3T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知Iz=10170cm4,h1=9.65cm ,h2=15.35cm 。
解:A 截面:Mpa 95.371065.9101017010402831max =⨯⨯⨯⨯=--σ (拉) Mpa 37.501035.15101017010402831min -=⨯⨯⨯⨯-=--σ(压) E 截面Mpa 19.301035.15101017010202832max =⨯⨯⨯⨯=--σ (拉) Mpa 98.181065.9101017010202832min -=⨯⨯⨯⨯-=--σ (压) 6-4 一根直径为d 的钢丝绕于直径为D 的圆轴上。
(1) 求钢丝由于弯曲而产生的最大弯曲正应力(设钢丝处于弹性状态)(2) 若d =lmm ,材料的屈服极限s σ=700MPa ,弹性模量E=210GPa ,求不使钢丝产生残余变形的轴径D 。
解:EJM =ρ16-5 矩形悬臂梁如图示.已知l= 4 m ,32=h b ,q=10kN/m ,许用应力[σ]=10Mpa 。
试确定此梁横截面尺寸。
解:m KN ql M ⋅=⨯⨯==80410212122max6-6 20a 工字钢梁的支承和受力情况如图所示。
若[σ]=160MPa ,试求许用载荷P 。
解:3237cm W =P 32 [][]P W M 32102371016066=⨯⨯⨯=⋅=-σ (M 图) P 326-7压板的尺寸和载荷情况如图所示。
材料为 45钢,s σ=380 MPa ,取安全系数5.1=n 。
试校核压板强度。
解:2331568)121230122030(101mm W =⨯-⨯⨯= 6-8由两个槽钢组成的梁受力如图示。
已知材料的许用应力[σ]=150 MPa ,试选择槽钢号码。
解:m KN M ⋅=60max查表:(22a , 332006.217cm cm W x >=)( M 图)6-9割刀在切割工件时,受到P =1kN 的切销力的作用。
割刀尺寸如图所示。
试求割刀内最大弯曲应力。
解:m N p M ⋅=⨯⨯=-I 810836-10 图示圆木,直径为D ,需要从中切取一矩形截面梁。
试问(1)如要使所切矩形截面的抗弯强度最高,h 、b 分别为何值?(2)如要使所切矩形截面的抗弯刚度最高,h 、b 又分别为何值?解:6)(6222b D b bh W -== ∴从强度讲:D b 57735.0=∴从刚度讲D b 50.0=6-11T 字形截面的铸铁梁受纯弯曲如图示,欲使其最大压应力为最大拉应力的3倍,巳知h= 12cm ,t=3cm ,试确定其翼板宽度b 之值。
解:3max max =下上拉压y y =σσ 6-12 图示简支梁,由No.18工字钢制成,在外载荷作用下,测得横截面A 处梁底面的纵向正应变4100.3-⨯=ε,试计算梁的最大弯曲正应力σmax 。
已知钢的弹性模量E=200GPa, a=1m 。
解:MPa E A 60100.31020049=⨯⨯⨯==-εσ(M 图)6-13 试计算图示矩形截面简支梁的1-1面上a 点和b 点的正应力和剪应力。
解:1-1截面6-14 计算在均布载荷q =10 kN /m 作用下,圆截面简支梁的最大正应力和最大剪应力,并指出它们发生在何处。
解:232max 110108181⨯⨯⨯==ql MMPa 86.101= 在跨中点上、下边缘MPa 46.25= 在梁端,中性轴上 6-15试计算6-12题工字钢简支梁在图示载荷下梁内的最大剪应力。
解: MPa Wqa 60832=qa 41 KN qa Q 2.2216.294343max =⨯⨯== (Q 图)6-16 矩形截面木梁所受载荷如图示,材料的许用应力[σ]=10Mpa 。
试选择该梁的截面尺寸,设1:2:=b h(Q 图) ( M 图)解:KN R A 19=KN R B 29=6-17 试为图示外伸梁选择一工字形截面,材料的许用应力[σ]= 160MPa ,[τ]=80Mpa 。
解:[]3612510160100020cm MW =⨯⨯==σ 取16I , 3141cm W =故 取No16工字钢(Q 图) (M 图)6-18 图示起重机安装在两根工字形钢梁上,试求起重机在移动时的最危险位置及所采用工字型钢的号码。
已知 l =10 m ,a =4 m ,d=2 m 。
起重机的重量W =50 kN ,起重机的吊重P=10 kN ,钢梁材料的许用应力[σ]=160 MPa ,[τ]= 100Mpa 。
解:轻压:KN 10 ,KN 50取 a 2833215.508W cm W z =>=6-19等腰梯形截面梁,其截面高度为h 。
用应变仪测得其上边的纵向线应变611042-⨯-=ε,下边的纵向线应变621014-⨯=ε。
试求此截面形心的位置。
解:11M εσ⋅=⋅E J y b=上 6-20 简支梁承受均布载荷q ,截面为矩形h b ⨯,材料弹性模量E ,试求梁最底层纤维的总伸长。
解:22)(2qx x ql x M -= 6-21矩形截面悬臂梁受力如图(a )所示,若假想沿中性层把梁分开为上下两部分:(1)试求中性层截面上剪应力沿x 轴向的变化规律,参见图(b );(2)试说明梁被截下的部分是怎样平衡的?解:(1)bhqx A Q x 2323==τ (2)由τ产生的合力为T由弯曲产生的轴间力为Nbdy h b y ql dy b J M dy b N h h h ⎰⎰⎰=⋅=⋅⋅=2/02/02/032max 122σ(自证) 6-22 正方形截面边长为a ,设水平对角线为中性轴。
试求(1)证明切去边长为9a 的上下两棱角后,截面的抗弯模量最大;(2)若截面上的弯矩不变,新截面的最大正应力是原截面的几倍?(提示:计算Iz 时可按图中虚线分三块来处理)。
解:原来正方形:削去x 后:6-23 悬臂梁AB 受均布载荷q 及集中力P 作用如图示。
横截面为正方形a a ⨯,中性轴即正方形的对角线。
试计算最大剪应力τmax 值及其所在位置。
解:)(Q ql P +=6-24试绘出图中所示各截面的剪应力流方向,并指出弯曲中心的大致位置。
解:6-25确定开口薄壁圆环截面弯曲中心的位置。
设环的平均半径R0,壁厚t ,设壁厚t 与半径0R 相比很小。
解:ϕϕsin 00⋅⋅⋅=R t d R dS6-26试导出图示不对称工字形截面的弯曲中心位置(当在垂直于对称轴的平面内弯曲时)。
假设厚度t 与其他尺寸相比很小。
解:z J t h b e 4)2(221= 6-27 在均布载荷作用下的等强度悬臂梁,其横截面为矩形,并宽度b=常量,试求截面高度沿梁轴线的变化规律解:2022023621bh ql bh ql W M l ===σ6-28 图示变截面梁,自由端受铅垂载荷P 作用,梁的尺寸l 、b 、h 均为已知。
试计算梁内的最大弯曲正应力。
解:x P x M ⋅=)(6-29当载荷P 直接作用在跨长为l =6m 的简支梁AB 的中点时,梁内最大正应力超过容许值30%。
为了消除此过载现象,配置如图所示的辅助梁CD ,试求此梁的最小跨长a 。
解:x P Pl 270.04=⨯ 6-30 图示外伸梁由25a 号工字钢制成,跨长l=6 rn ,在全梁上受集度为q 的均布载荷作用。
当支座截面A 、B 处及跨度中央截面C 的最大正应力σ均为140MPa 时,试问外伸部分的长度及载荷集度q 等于多少?解:lqa qa ql R A 2832++= 查表:(M 图)6-31 图示悬臂梁跨长L=40cm ,集中力P =250N ,作用在弯曲中心上,梁的截面为等肢角形,尺寸如图,试绘剪应力流分布图,并计算了m ax σ和m ax τ之值。
解:444999.3957112381240mm J z =-= 6-32 圆锥形变截面悬臂梁其两端直径之比db:da =3:1,在自由端承受集中力P 作用,试求梁内的最大弯曲正应力,并将此应力与支承处的最大应力比较。
解:Px x M =)(6-33工字形截面的简支钢梁,跨度l =4m ,跨度中央受集中载荷P 作用。
如材料屈服点s σ=240MPa ,安全系数n=1.6,试按极限载荷法计算此梁的许可载荷。
解:[]2550)300(5010025)50(5020011⨯--+⨯=⨯-+⨯y y6-34 矩形截面简支梁,在跨度中央承受集中力P 。
论确定塑性区域的长度和塑性区城边界方程式()x f a =。
解:261bh W z =故 5.1=sjxM M Pl M jx 41= 故 l e 61=将s σ及a M 代入上方程:。