第四节 透镜成像公式

透镜成像原理u是物体到透镜的距离f是透镜本身的焦距(焦点到透镜中间(也就是光心)的距离)1f<u＜2f时成放大实像u=2f时是等大实象物在焦点不成像,二倍焦距倒同样.大于二焦倒立小,焦外二内幻灯放.物体放在焦点内,对侧看见大虚像.像若能够呈屏上,一定倒立是实像.1．u＞f时成实像，u＜f成虚像，焦点是实像和虚像的分界点。

2．U＞2f时成缩小实像，u＜2f时成放大实像，二倍焦距点是成放大实像与缩小虚像的分界点。

3．成实像时，当物距减小，像距变大，像变大；物距增大时，像距变小，像变小。

4．成实像时，像与物在凸透镜异侧，成虚像时，像与物在凸透镜同侧。

5．实像是实际光线会聚而成的，可显示在光屏上，虚像是实际光线的反向延长线的交点，不显示在光屏上。

关于CCD/CMOS的成像原理-|videofans 发表于2005-8-26 12:51:28编者按：这几天在论坛上看到有些人的帖子，希望能够有人讲一讲关于DC和D V的基础知识，哈哈~~~正对我的口味（某家比较懒，所以拍的PP也不多，不过敲键盘还算勤快）。

我绝不是专家，不过也愿把我所知道的写出来，让大家看看（拍砖的时候希望能够轻点儿，怕疼~~~）这篇帖子是准备介绍一下CCD的，其中也会简单说说CMOS。

不过在开始这些内容之前，考虑到有很多人对DC所知不多（绝无轻视之意~~），我就先简要地说一下DC的成像原理。

DC的成像原理：DC基本上都是由镜头、影像传感器（使用CCD/CMOS）、模拟/数字信号转换器（A/D）、微处理器（MPU）、内置存储器、液晶显示器（LCD）、电子取景器（EVF）、可移动存储器（基本上是各种存储卡）和接口（和PC相连的USB 以及和电视相连的AV等）等部分组成。

它的工作原理大致如下：打开DC的电源开关，主控程序芯片开始检查DC的各个部件是否处于可工作状态。

如果有一个部分出现故障，LCD上就会给出一个错误信息，并使DC停止工作。

如果一切正常，DC则处于待命状态。

凸透镜凹透镜成像原理与公式凸透镜和凹透镜都是常见的光学元件，用于聚焦光线或调节光线的传播方向。

理解凸透镜和凹透镜的成像原理和公式对于理解光学现象和应用非常重要。

首先，我们来看凸透镜的成像原理和公式。

凸透镜是凸面向外的透镜，通过使光线接近光轴的中心线来使其聚焦。

当平行于光轴射入的光线通过凸透镜时，会收敛为一个焦点。

凸透镜的成像公式可以表示为：1/f=1/v-1/u其中，f为透镜的焦距，v为像距（图像与透镜之间的距离），u为物距（物体与透镜之间的距离）。

这个公式被称为薄透镜成像公式，适用于光线通过的区域较窄的透镜。

当物体放置在凸透镜的前焦点的位置时，成像是无穷远的，也就是说图像和透镜之间的距离v无限大。

根据薄透镜成像公式，1/v将接近于0，因此成像公式可简化为：1/f=1/u。

当物体放置在凸透镜的后焦点的位置时，成像是无穷远的。

从薄透镜成像公式可知，1/v-1/u=0，因此v将等于f。

当物体放置在凸透镜的焦点之间时，图像将在凸透镜的另一侧形成。

根据薄透镜成像公式，我们可以计算出图像的位置和大小。

下面，我们来看凹透镜的成像原理和公式。

凹透镜是凹面向外的透镜，通过使光线远离光轴的中心线来使其发散。

当平行于光轴射入的光线通过凹透镜时，会发散为一束。

凹透镜的成像公式与凸透镜的成像公式相同：1/f=1/v-1/u其中，f为透镜的焦距，v为像距，u为物距。

与凸透镜相比，凹透镜的成像具有不同的特点。

当物体放置在凹透镜的前焦点的位置时，成像是虚拟的。

虚像的特点是它们不能投射到屏幕上，只能通过透镜本身观察到。

当物体放置在凹透镜的后焦点的位置时，成像是无穷远的。

根据薄透镜成像公式，我们可以得到1/v-1/u=0，因此v将等于f。

当物体放置在凹透镜的焦点之间时，图像将在凹透镜的同一侧形成。

使用薄透镜成像公式，我们可以计算出图像的位置和大小。

凸透镜和凹透镜是光学实验和仪器中常见的元件，它们广泛应用于望远镜、显微镜、摄像机、眼镜等。

角的变化
分类：正球差和负 球差
对成像质量的影响： 降低图像清晰度和
对比度
添加标题
添加标题
添加标题
添加标题
彗形像差
定义：像点在透镜 像面上呈现的形状 与实际物体形状的 偏差
产生原因：透镜的 球面像差和色散
彗形像差的大小与 透镜的焦距、孔径 大小和波长有关
彗形像差的校正方 法：使用透镜组合 、加装校正器等
望远镜：透镜组合用于放大 远处物体，便于观察天体等。
眼镜：透镜用于矫正视力， 使光线正确聚焦在视网膜上。
投影仪：透镜用于调整图像， 使光线正确投射在屏幕上。
像质优化在摄影镜头中的应用
像质优化技术：通过改进 镜头设计和制造工艺，提 高摄影镜头的成像质量， 减少畸变和失真。
0 1
像质优化在摄影镜头中 的应用案例：如佳能在 EF系列镜头中采用了IS 技术，通过内置光学防 抖机制，有效抑制手抖 导致的图像模糊；蔡司 的Batis镜头系列则通过 采用新的镜头镀膜技术 和材料，提高了镜头的 抗眩光和抗色散性能。
观察物品：镜子可 以反射光线，使人 们能够观察物品的 另一面。
安全监控：在家庭 和商业场所，镜子 常常被用来做安全 监控，观察周围的 环境。
艺术创作：艺术家 可以利用镜子的反 射和折射原理，创 造出独特的艺术作 品。
透镜在光学仪器中的应用
显微镜：透镜组合用于放大 微小物体，便于观察细胞、 细菌等。
透镜焦距的调节：通过旋转透镜或移动透镜的位置，可以调节焦距，从而改变成像的大小和清晰度。
透镜材料对成像的影响
材料折射率对成像 位置的影响
材料色散对成像质 量的影响
不同透镜材料的优 缺点
材料对透镜设计和镜球 面形状导致的像点

一、凸面镜成像规律：物体放在焦点之外，在凸面镜另一侧成倒立的实像，实像有减小、等大、放大三种。

物距越小，像距越大，实像越大。

物体放在焦点之内，在凸面镜同一侧成正立放大的虚像。

物距越大，像距越大，虚像越大。

一）凸面镜成像规律顺口溜：1.二倍焦距之外，倒立减小实像；一倍焦距到二倍焦距，倒立放大实像；一倍焦距之内，正立放大虚像；成实像物和像在凸面镜异侧，成虚像在凸面镜同侧2.一倍焦距分虚实两倍焦距分大小物近像远像变大物远像近像变小二）详见下表：物体到透镜的距离像的大像的正像的虚像的位像到透镜的距离应用实u小倒实置v例u>2f减小倒立实像与物异 2f>v>f照相机侧u=2f等大倒立实像与物异 v=2f侧2f>u>f放大倒立实像与物异 v>2f幻灯机侧u=f————————————u<f放大正立虚像与物同——放大镜侧三）为了研究各种猜想，人们经常用光具座进行试验。

蜡烛，凸面镜，光屏应尽量保持在同一条直线上。

利用透镜的特别光辉作透镜成像光路：（1）、物体处于 2 倍焦距之外（2）、物体处于 2 倍焦距和 1 倍焦距之间（3）、物体处于焦点之内（4）、凹面镜成像光路四）实验研究凸面镜的成像规律是：当物距在一倍焦距之内时，获取正立、放大的虚像；在一倍焦距到二倍焦距之间时获取倒立、放大的实像；在二倍焦距之外时，获取倒立、减小的实像。

透镜成像满足透镜成像公式：1/u(物距)+1/v（像距）=1/f（透镜焦距）二、凹面镜成像规律：只能生成减小的正立的虚像。

成虚像时，若是放大定是凸面镜生成的，减小的必然是凹面镜生成的。

无论是什么透镜生成的虚像必然是正立的，生成的实像必然是倒立的。

一）凹面镜成像规律公式1/u+1/v=1/f(u为物距，v为相距，f为焦距，与凸面镜同样）凹面镜成的像与物体、焦距的关系二）对于薄凹面镜：当物体为实物时，成正立、减小的虚像，像和物在透镜的同侧；当物体为虚物，凹面镜到虚物的距离为一倍焦距之内时，成正立、放大的实像，像与物在透镜的同侧；当物体为虚物，凹面镜到虚物的距离为一倍焦距时，成像于无量远；当物体为虚物，凹面镜到虚物的距离为一倍焦距之外两倍焦距之内时，成倒立、放大的虚像，像与物在透镜的异侧；当物体为虚物，凹面镜到虚物的距离为两倍焦距时，成与物体同样大小的虚像，像与物在透镜的异侧；当物体为虚物，凹面镜到虚物的距离为两倍焦距之外时，成倒立、减小的虚像，像与物在透镜的异侧。

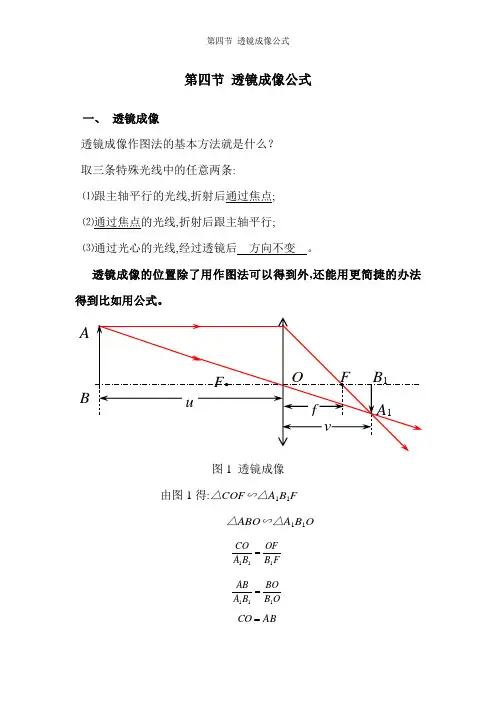
第四节 透镜成像公式一、 透镜成像透镜成像作图法的基本方法就是什么？取三条特殊光线中的任意两条:⑴跟主轴平行的光线,折射后通过焦点;⑵通过焦点的光线,折射后跟主轴平行;⑶通过光心的光线,经过透镜后 方向不变 。

透镜成像的位置除了用作图法可以得到外,还能用更简捷的办法得到比如用公式。

图1 透镜成像由图1得:△COF ∽△A 1B 1F △ABO ∽△A 1B 1OFB OF B A CO 111= OB BO B A AB 111= AB CO =OF=f , B 1F = v －f , BO=u , B 1O=v由 OB BO F B OF 11=得:即:整理得: ——此公式为透镜成像公式⏹ 凸透镜:u , f 总取正值;⏹ u>f 时,v 为正值,像物异侧,实像⏹ u<f 时,v 为负值,像物同侧,虚像二、凹透镜公式⏹ 可以证明,以上公式完全适用于凹透镜,但需注意,焦距应取负值(虚焦点)。

⏹ 由 可知v 为负,这表示凹透镜总成虚像。

注意:其它均为负,在计算题中往往被忽视。

三、放大率定义:像长跟物长的比ABB A 11叫做像的放大率。

因为△ABO ∽△A 1B 1O:所以u v AB B A m ==11 m>1,表示成放大的像,m<1,表示成缩小的像。

注意:实像v 取正,虚像v 取负。

根据 得: vu f v f =-uv fu fv =+f v u 111=+fv u 111=+fv u 111=+⏹ 当u →∞时,u －f ≈ u , v ≈ f 、意义:太阳射来的平行光经凸透镜折射后再焦点会聚。

⏹ 当u >2f 时, u －f > f , v<u , m= u v <1、 意义:成倒立、缩小的实像,如照相机。

⏹ 当u =2f 时, u-f= f , v=u , m=uv =1、意义:成倒立的与物体等大小的实像。

⏹ 当f<u<2f 时,u －f< f , v>u , m=u v >1、意义:成倒立、 放大的实像,如幻灯机。

凸透镜与凹透镜的成像规律与计算方法一、凸透镜成像规律1.物距与像距的关系：凸透镜成像时，物距（u）与像距（v）之间存在以下关系：1/f = 1/v - 1/u，其中f为凸透镜的焦距。

2.成像情况：根据物距与焦距的关系，凸透镜成像分为以下几种情况：（1）当u > 2f时，成倒立、缩小的实像，应用于照相机、摄像机等。

（2）当2f > u > f时，成倒立、放大的实像，应用于幻灯机、投影仪等。

（3）当u < f时，成正立、放大的虚像，应用于放大镜等。

二、凹透镜成像规律1.成像情况：凹透镜成像时，物距（u）与像距（v）之间存在以下关系：1/f = 1/v - 1/u，其中f为凹透镜的焦距。

根据物距与焦距的关系，凹透镜成像分为以下几种情况：（1）当u > f时，成倒立、缩小的实像。

（2）当u < f时，成正立、放大的虚像。

2.发散作用：凹透镜对光线具有发散作用，使通过透镜的光线推迟会聚。

三、凸透镜与凹透镜的计算方法1.凸透镜焦距的计算：当已知凸透镜成像时的物距（u）和像距（v）时，可以通过以下公式计算凸透镜的焦距（f）：1/f = 1/v - 1/u2.凹透镜焦距的计算：当已知凹透镜成像时的物距（u）和像距（v）时，可以通过以下公式计算凹透镜的焦距（f）：1/f = 1/v - 1/u四、凸透镜与凹透镜的应用1.凸透镜的应用：照相机、摄像机、幻灯机、投影仪、放大镜等。

2.凹透镜的应用：近视眼镜、防盗报警器、激光准直等。

综上所述，凸透镜与凹透镜的成像规律与计算方法是光学中的重要知识点。

掌握这些知识，有助于我们更好地理解和应用光学设备。

习题及方法：1.习题：一个凸透镜的焦距是10cm，一物体放在凸透镜前20cm处，求：a)成像情况b)像的大小c)由凸透镜成像规律可知，物距大于2f时，成倒立、缩小的实像。

d)物距为20cm，焦距为10cm，物距是焦距的二倍，所以成倒立、缩小的实像。

本节前言第四节透镜成像公式公元前3世纪，我国晋代《博物志》记有：“削冰令圆，举以向日，以艾于后成其影，则得火。

”那时还未发明玻璃，我们的祖先就知道用冰做成凸透镜来会聚太阳光再用艾草取火了。

从古到今，透镜一直有着广泛的应用，就连现在高科技的光纤通信设备中也离不开透镜。

为了把一路光信号输进极细的光导纤维中，必须用凸透镜使光线会聚才行。

象显微镜、望远镜及照相机中的重要部件就是透镜。

本节中运用动画演示蜡烛经透镜的成像过程，总结透镜成像规律，重在透镜成像公式理解和应用，透镜成像放大率。

大家在学习过程中要循序渐进，逐步掌握。

§1.4 透镜成像公式透镜是利用光的折射定律控制光路和成像的光学器件，透镜分为凸透镜和凹透镜两种，透镜的两个面为球面，中间厚边缘薄的透镜为凸透镜，中间薄边缘厚的透镜为凹透镜，两个面所在球面的球心的连线称为透镜的主轴，凸透镜对光线有汇聚作用，凹透镜对光线有发散作用。

所以我们通常称凸透镜为会聚透镜，称凹透镜为发散透镜。

薄透镜薄透镜是物理上建立的一个理想化的实体模型，在研究问题时，将透镜的厚度忽略不计。

透镜的光轴、光心、焦点、焦距通过透镜两球面球心的直线叫透镜的主光轴。

主光轴与透镜两球面的交点，对薄透镜而言，可看成是重合在一起的，该点称为光心。

通过光心的光线叫光轴，除主光轴而外，其它光轴叫副光轴。

平行于主光轴的光线，经凸透镜后会聚于一点，这个点叫焦点，用F表示，它是由实光线会聚而成的，又叫实焦点。

平行于主光轴的光线经凹透镜后被发散，发散光线的反向延长线也交于主光轴的一点，这个点也叫焦点，因为不是光线的实际会聚点，所以又叫虚焦点。

透镜的焦点与光心的距离叫焦距，用f表示。

透镜成像现在我们通过实验来研究透镜成像的规律。

如图：把蜡烛、透镜、光屏安装在光具座上，蜡烛和光屏距透镜的距离都可以从光具座导轨刻度尺上读出。

大家可通过做透镜的成像实验来掌握其成像规律。

下面的动画是模拟透镜成像的情况。

（1）先做凸透镜成像，拖动左边的蜡烛，仔细观察成像情况。

透镜成像公式的推导与应用一、透镜成像公式透镜成像公式是描述透镜成像规律的重要公式，其表达式为：[ = - ]其中，( f )表示透镜的焦距，( v )表示像距，( u )表示物距。

二、透镜成像规律1.物距与像距的关系根据透镜成像公式，物距与像距的关系可以分为以下三种情况：（1）物距大于二倍焦距：( u > 2f )，成倒立、缩小的实像，应用于照相机和摄像头。

（2）物距等于二倍焦距：( u = 2f )，成倒立、等大的实像，此时像距( v = 2f )。

（3）物距小于二倍焦距：( u < 2f )，成倒立、放大的实像，应用于投影仪和幻灯机。

2.焦距与成像性质的关系（1）焦距越大：成像距离越远，成像越大。

（2）焦距越小：成像距离越近，成像越小。

三、透镜成像应用1.照相机和摄像头：利用物距大于二倍焦距的原理，成倒立、缩小的实像，广泛应用于摄影和监控领域。

2.投影仪和幻灯机：利用物距小于二倍焦距的原理，成倒立、放大的实像，用于教学演示和商务汇报。

3.放大镜：利用物距小于焦距的原理，成正立、放大的虚像，用于观察细小物体。

4.望远镜和显微镜：利用透镜组的设计，实现对远处或微小物体的放大观察。

5.眼睛的成像原理：人眼相当于一个复杂的透镜系统，通过调整晶状体的焦距，使物体在视网膜上形成清晰的倒立实像。

透镜成像公式是光学基础知识的重要组成部分，掌握透镜成像规律和应用，有助于我们更好地理解光学现象，并广泛应用于日常生活和科技领域。

习题及方法：1.习题：一个凸透镜的焦距是20cm，物体放在距凸透镜30cm处，求像的性质和大小。

方法：由题意知，物距( u = 30cm )，焦距( f = 20cm )，因为( u > 2f )，所以成倒立、缩小的实像。

根据透镜成像公式，可以求出像距( v )：[ = - ][ = - ][ = + ][ v = 60cm ]因为像距( v )大于二倍焦距，所以像的大小小于物体的大小。

A
C
A
F B1
F
B1
B
F
O
A1
BF
O
p
p'
A1
解：由透镜成像公式 1 1 1 ，可得 f p p
1 1 1 p 0.18 0.75 p
解之得 p1 = 0.45 m ， p2 = 0.30 m 。
像的放大率为
k
p' p

L p pΒιβλιοθήκη 当p1 = 0.45 m 时，
k1

0.75 0.45 0.45
3. 如果要得到一个放大的实像，应把物体放在一倍焦 距与 二倍焦距 之间； 如果要得到一个放大的虚像，应把 物体放在 一倍焦距之内 之内。
4.已知 凸 透 镜的焦距是 8cm, 物体到透镜的距离是 12cm，光屏应当放在离透镜多远处才能得到清晰的像？放 大还是缩小？
解：由透镜成像公式得 A
F
B1
1 8

0.67
当p2 = 0.30 m 时，
k2

0.75 0.30 0.30
1.5
练习 1. 已知 f = 10 cm，如果把物体放在距凸透镜25 cm 的 地方，则在光屏上会得到一个 倒立 ， 缩小 的 实像 像。 2. 放大镜的工作原理是，当物体到透镜的距离 一倍焦距之内 时，成正立的、放大的、虚像。

1 12

1 p'
BF
O
解之得 p´= 24 cm 。
A1
像的放大率为
k
p p

24 8
3
光屏应当放在离透镜24 cm处才能得到放大、清晰的像。
1. 4 透镜成像公式

物理知识点透镜成像的公式与物像距离的计算透镜成像是物理学中一个重要的概念，它描述了透过透镜后光线的聚焦与成像过程。

理解透镜成像的公式以及物像距离的计算方法对于解决光学问题至关重要。

本文将详细介绍透镜成像的公式以及计算物像距离的方法，以帮助读者更好地掌握这一知识。

1. 透镜成像公式透镜成像公式是描述物体成像的数学关系，由透镜的焦距和物体的位置决定。

对于薄透镜而言，成像公式可分为凸透镜和凹透镜两种情况。

1.1 凸透镜成像公式对于凸透镜而言，成像公式可表示为：1/f = 1/v - 1/u其中，f为透镜的焦距，v为像距(即物体到透镜的距离)，u为物距(即像到透镜的距离)。

1.2 凹透镜成像公式对于凹透镜而言，成像公式同样可表示为：1/f = 1/v + 1/u其中，f为透镜的焦距，v为像距，u为物距。

透镜成像公式的推导基于几何光学的原理，根据光的折射和几何关系可以得出以上公式。

在实际应用中，通过已知物距或者像距，可以计算出另外一个未知量，实现对透镜成像的定量描述。

2. 物像距离的计算方法计算物像距离是解决光学问题的基本步骤之一，通过已知条件可以应用透镜成像公式来求解。

下面将分别介绍物距和像距的计算方法。

2.1 物距的计算方法物距指的是物体到透镜之间的距离，记为u。

具体计算物距的方法取决于物体的位置和朝向。

- 当物体位于透镜同一侧时，物距为正值。

- 当物体位于透镜的焦点处时，物距为正无穷大。

- 当物体位于透镜的背面时，物距为负值。

根据以上规则，我们可以通过测量物体到透镜的距离来确定物距的数值。

在使用透镜成像公式时，需要根据具体问题来合理选择物距的正负值。

2.2 像距的计算方法像距指的是像到透镜之间的距离，记为v。

计算像距时同样需要根据特定的情境来确定正负值。

- 当成像在透镜同一侧时，像距为正值。

- 当成像在透镜的焦点处时，像距为正无穷大。

- 当成像在透镜的背面时，像距为负值。

通过实际测量或者几何推导可以得到像距的数值。

凸透镜与凹透镜的成像特点与公式凸透镜和凹透镜是光学学科中重要的两种透镜类型，它们在成像过程中具有不同的特点和应用。

本文将介绍凸透镜和凹透镜的成像特点，以及相关的公式和用途。

一、凸透镜的成像特点凸透镜是一种中间厚，边缘薄的透镜，其透镜面弧度较大。

凸透镜能够将入射光线聚焦到透镜的对称中心，成像过程中产生实像或虚像。

以下是凸透镜的成像特点：1.1 实像的产生凸透镜当物体距离透镜的距离大于其焦距时，产生的成像是实像。

实像位于凸透镜的焦点之外，并且与物体位置呈现正立关系。

实像的特点是可以在屏幕上观察到，并且可以被眼睛或摄影机所捕捉。

1.2 虚像的产生凸透镜当物体距离透镜的距离小于焦距时，产生的成像是虚像。

虚像位于凸透镜的焦点之内，并且与物体位置呈现倒立关系。

虚像的特点是不能在屏幕上观察到，只能通过透镜产生的透光现象来间接观察。

二、凸透镜的成像公式凸透镜的成像公式描述了物体、像距、焦距和透镜之间的关系。

根据呈现的实像或虚像，可以使用以下公式来计算物体和像距之间的关系：1. 物体距离凸透镜的距离：u2. 像距：v3. 焦距：f1.3 公式一：1/v + 1/u = 1/f其中，v和u分别代表像距和物体距离透镜的距离，f代表透镜的焦距。

当焦距为正值时，凸透镜为凸透镜；当焦距为负值时，凸透镜为凹透镜。

该公式也被称为透镜公式。

1.4 公式二：v/u = -f/v该公式也是描述凸透镜成像的公式，通过计算物体距离透镜和像距之间的比例，可以得到透镜的焦距。

三、凹透镜的成像特点凹透镜是一种中间薄，边缘厚的透镜，其透镜面弧度较小。

凹透镜能够使入射光线发散，成像过程中产生只能看到虚像。

以下是凹透镜的成像特点：3.1 虚像的产生凹透镜无论物体与透镜的距离是多少，都只能产生虚像。

虚像位于凹透镜的背面，并且与物体位置呈现倒立关系。

虚像的特点与凸透镜相似，不能在屏幕上观察到，只能通过透镜产生的透光现象来间接观察。

四、凹透镜的成像公式凹透镜的成像公式与凸透镜的成像公式略有不同，可以使用以下公式来计算物体和像距之间的关系：4.1 公式一：1/v - 1/u = 1/f其中，v和u分别代表像距和物体距离透镜的距离，f代表透镜的焦距。

光的成像与光学仪器知识点总结在我们的日常生活中，光学现象和光学仪器无处不在。

无论是我们所使用的眼镜、望远镜，还是我们常见的相机、显微镜等等，都离不开光学的基本原理和知识。

本文将对光的成像和光学仪器的相关知识进行总结和概述。

一、凸透镜的成像原理及公式凸透镜是常见的光学仪器，它的成像原理可由薄透镜公式表示。

薄透镜公式是描述凸透镜成像的基本方程，它可以将物体和像的距离、物的高度和像的高度联系起来。

薄透镜公式为：1/f = 1/v - 1/u其中，f是凸透镜的焦距，v是像的距离，u是物的距离。

凸透镜成像的规律可以通过一些实例来说明。

例如，当物距u大于2f时，像总是倒立、缩小、实像；当物距u等于2f时，像位于焦点处，无限大；当物距u小于2f但大于f时，像仍然是倒立的，但变成放大、实像；当物距u等于f时，像位于无穷远处，无放大率。

这些规律可以帮助我们更好地理解凸透镜成像的原理。

二、光的折射定律光的折射是指光线从一种介质射入另一种介质时发生偏折的现象。

光的折射定律是描述光在折射过程中的行为的基本规律，它可以用一个简洁的公式表示：n1 * sinθ1 = n2 * sinθ2其中，n1和n2分别表示两种介质的折射率，θ1和θ2表示光线和法线的夹角。

通过光的折射定律，我们可以解释很多光学现象，例如光的弯曲、光的色散、棱镜的工作原理等等。

三、光学仪器：显微镜显微镜是一种重要的光学仪器，它用于放大微小的物体，以便我们能够观察更加细微的结构和细节。

显微镜的主要组成部分包括物镜、目镜和光源。

在显微镜中，物镜起到放大物体的作用，它具有较短的焦距和较高的放大率；目镜则起到放大物镜像的作用，提供给我们一个放大后的视觉。

物镜像和目镜像的放大率可以相乘，从而得到总的放大率。

此外，显微镜还有调焦装置、光源、聚光系统等等，这些组件共同作用确保显微镜的工作正常。

四、光学仪器：望远镜望远镜是另一种重要的光学仪器，它主要用于观测远处的物体和天体。

透镜成像的公式推导物理教案一、前置知识1.光学基本定律：1.光线沿着直线传播；2.光的传播方向和波垂直；3.入射角等于反射角；4.折射定律（即斯涅尔定律）2.光的折射问题：当光从一种介质向另一种介质传播时，会出现折射现象。

入射光线从一个介质进入另一个介质时，入射角(θ1)、折射角(θ2)和光的速度之间的关系由斯涅尔定律给出：n1 sin θ1 = n2 sin θ2其中，n1和n2分别代表两种介质的折射率。

3.光的成像问题：光学成像是光学中的基础问题之一，是指把一个物体上的点或像，通过某种光学系（例如透镜）联合光的传播规律，成像到另一个位置上，使得像的质量和大小与原物相似。

二、透镜成像公式的推导1.透镜的性质：透镜有两个焦点，是一个具有两个球面并由光学材料包裹的透明物体。

我们称作凸透镜和凹透镜。

凸透镜能够将平行于主光轴的光线聚或者发散，其需要的作用力正好等于光线在透镜两面产生的总反弹力的和。

透镜的两个焦点之间的距离称作焦距f，代表光线从平行于主光轴的方向聚焦于该点或者从该点发散成平行于主光轴的方向所需的距离。

凸透镜的两边都能形成凸面，其中一面的曲率半径小于另一面的曲率半径。

凹透镜是曲面向内的透镜，凸面向外。

2.透镜成像：我们考虑一个透镜将一束光线从物体成像到像上的情况。

设此透镜如图1所示，其中左端被视为物体，右端被视为像。

1.png图1物距为u，像距为v。

从物体上任意一点出发的光线（如直线1）与透镜相遇，会被透镜折射，并相交于虚像（如直线2）。

从物体上任意一点出发的光线（如直线3）直接穿过透镜，不偏折，在右侧形成一点像（如直线4）。

从物体上任意一点出发的光线（如直线5）与透镜相交并折射，在右侧形成一点像（如直线6）。

当透镜成像是，满足下列物理关系式：1/u + 1/v = 1/f (1)其中，f是透镜的焦距。

实际上这里的公式是一个著名的透镜方程，可以用于透镜成像物体与像的距离关系。

我们同样能考虑透镜成像时的放大率，物体高度为h1，像高度为h2可得到：h2/h1 = v/u (2)(2)式即为透镜成像的放大率。

像差，提高成像质量
透镜成像的基本概念
透镜的种类和结 构
透镜成像的原理 和特点
透镜焦距的计算 方法
透镜成像的应用 场景
02
透镜成像公式的推导
薄透镜成像公式推导
光线通过透镜的路径：入射光线、折射光线和焦平面 透镜成像的几何关系：物距、像距和焦距之间的关系 透镜成像的公式推导：利用光线传播的几何关系和斯涅尔定律推导 薄透镜成像公式的简化：忽略透镜厚度的影响，得到薄透镜成像公式
透镜成像公式推导
投影仪的工作原理
投影仪的应用场景
投影仪的发展趋势
04
透镜成像公式的扩展
透镜组合成像
透镜组合的定义：由两个或多个透镜组成的成像系统。
透镜组合成像的原理：通过透镜的组合，利用透镜的折射和反射特 性，实现光线的汇聚和扩散，从而形成清晰的像。
透镜组合成像的应用：在光学仪器、摄影镜头、显微镜等领域有广泛 应用。
薄透镜焦距的计算
定义：薄透镜的焦距是指平行于主轴的光线通过透镜后汇聚的点到透 镜中心的距离
公式：f=1/n×(1/v+1/u)
推导过程：通过几何光学和波动光学的原理，结合透镜的几何形状和 折射率，推导出薄透镜的焦距公式
应用：薄透镜焦距的计算是光学设计中的基础，对于透镜成像系统、 望远镜、显微镜等光学仪器的设计和使用具有重要意义
随着科技的发展， 透镜材料、设计 和加工技术也在 不断进步，为光 学仪器的发展提 供了有力支持
感谢观看
汇报人：XX
变焦透镜成像
透镜的变焦原理
变焦透镜成像公式推导
透镜焦距与物距的关系 变焦透镜的应用实例
光学仪器中的透镜应用
透镜在光学仪器 中的应用广泛， 如显微镜、望远 镜、照相机等

凸透镜成像大小计算公式
凸透镜成像大小的计算公式可以通过物距（u）、像距（v）和
焦距（f）来表示。

根据公式可以得到：
物体高/物体距离 = 图像高/图像距离 = 高/距离 = 1/f.
这个公式称为镜公式，其中物距（u）是物体到透镜的距离，像
距（v）是图像到透镜的距离，焦距（f）是透镜的焦距。

这个公式
适用于凸透镜的成像大小计算。

另外，成像的放大率也可以用以下公式表示：
放大率 = 图像高/物体高 = v/u.
这个公式表示了图像的高度与物体高度之间的比率，也可以用
来计算成像的大小。

需要注意的是，这些公式适用于薄透镜近似条件下的成像计算，在实际应用中可能还需要考虑透镜的厚度和形状对成像的影响。

同时，根据正负号的不同，可以确定成像是实际的还是虚拟的，以及
是正立的还是倒立的。

综合考虑这些因素，可以全面准确地计算凸透镜的成像大小。

0.75 0.45 K1 0.67 0.45
B1
当p2 = 0.30 m 时，
0.75 0.30 K2 1.5 0.30
上一页
A1
下一页
目 录
退 出
§1.4
一、透镜成像
透镜成像公式
由光的折射定律知道，空气中的光线透过凸透镜后，向 光主轴方向偏折,这就是凸透镜的会聚作用。透镜对光线的会 聚作用可以得到发光体的像。 我们研究的是薄透镜。 1. 凸透镜成像的三根特殊光线 （1）跟主轴平行的光线，折射后通过焦点； （2）通过焦点的光线，折射后跟主轴平行； （3）通过光心的光线经过透镜后方向不变。
上一页
下一页
目 录
退 出
三、透镜成像放大率 像的长度跟物的长度 AB 之比 1 1 , 叫做像的放大 AB 率，通常用K 表示。
A C F B1
B
F
O
A1
p
p'
由于△ABO 和△A1B1O 相似，所以
A1 B1 p' K AB p 若K>1, 则表示是放大的像;若K<1, 则表示是缩小的像; 若K =1，则表示像与物等大。
上一页 下一页 目 录
退 出
2. 凸透镜成像规律 物体位置
p > 2f p=2f
像的位置
像、物异侧 f < p´ < 2 f 像、物异侧 p′ = 2 f
像的性质
倒立缩小实像 倒立等大实像 倒立放大实像
应用举例
照相机
f<p<2f
p< f
像、物异侧 p′ > 2 f 像、物同侧
幻灯机
正立放大虚像
放大镜
上一页
下ห้องสมุดไป่ตู้页

球面镜成像公式
球面镜成像公式是指在球面镜中，光线经过反射后所形成的像的位置与物体的位置之间的关系式。

球面镜成像的特点是像的大小、位置、方向与物体的大小、位置、方向有关。

球面镜成像公式可以用以下公式表示：
1/f=1/v+1/u
其中，f表示球面镜的焦距，v表示像距，u表示物距。

根据这个公式，我们可以计算出球面镜中物体的像的大小和位置。

需要注意的是，球面镜成像公式只适用于球面镜成像的情况，而不适用于其他类型的成像情况。

此外，球面镜成像公式也有其局限性，例如当物体离镜面过近或过远时，成像可能会失真，需要进行特殊处理。

- 1 -。