动网格计算方法

Fluent中的动网格动网格是目前求解计算域变化问题的常用方法。

参考Fluent帮助，可以知道动网格技术与一般流动计算设置的主要区别在于网格更新方法和更新域设置。

这里就这两方面问题的一点体会作一简单记录。

一、网格更新方法弹簧近似光滑法将任意两网格节点之间的连线理想地看成一条弹簧，并通过近似弹簧的压缩或拉伸实现网格和计算域的改变。

该方法网格拓扑不变，无需网格的插值处理，对结构化（四边形、六面体）和非结构化（三角形、四面体）网格同样适用。

但不适合于大变形情况，当计算区域变形较大时，变形后的网格质量变差，严重影响计算精度。

动态分层法在运动边界相邻处根据运动规律动态增加或减少网格层数，以此来更新变形区域的网格。

该方法适用于结构化网格，通过设置适当的分层和缩减系数，更新后的网格依然为较为均匀的结构化网格，对计算精度影响较小。

对于运动域具有多自由度和任意变形情况，该方法处理起来非常困难。

网格重生方法在整个网格更新区域内依据设定的最大和最小网格尺寸判断需要进行网格重生的网格，并依据设置的更新频率进行网格重生处理。

该方法适用于非结构化网格，能够较好的应用于任意变形的计算区域处理。

二、更新域设置更新域设置是动网格设置中的一项重要工作，最常用的设置是刚体运动域和变形域，这里针对这两种域的设置注意事项和技巧作一简单介绍。

1、域动网格一般来讲，设置为刚体运动域的区域一般为壁面类边界，通过设置固壁的运动，模拟计算域内物体的运动。

由于固壁边界有时形状较为复杂，壁面附近网格尺度与周围网格尺度存在较大差别，网格更新时变形较大。

在这种情况下，可以设置一个包含固壁运动边界的计算域，通过该计算域的整体运动模拟域内物体的运动，在有的地方将这种方法称为域动网格法。

在域动网格法中，需要设置包含运动物体的内部计算域、内部计算域界面均为刚体运动域。

如下图所示。

2、动态分层法中的分界面在应用动态分层网格更新方法时，当分层界面在计算域内部时，需要采用Split interface（这里称分界面）将运动域运动范围与固定计算域区分开来，以保证动态分层网格处理（如果运动域网格与固定域网格没有分界面，动态分层无法执行）。

滑移网格法滑移网格法作为众多网格方法中的一种，在CFD 计算方面应用十分广泛，特别是在处理有旋转域的相关问题上。

但是“滑移”在中文的传统意义上是属于“动”的一种，使得很多人将滑移网格法错误的认为是动网格方法的一种。

以下将具体介绍动网格的三种实现-方法，以及滑移网格和滑移网格方法的具体实现步骤。

1 动网格方法动网格可以用来模拟流场形状由于边界运动而随时间改变的问题。

其在商用软件中的应用十分广泛。

-动网格可以分为以下三种：弹簧近似光顺法、动态分层法、局部网格分层法。

1.1 弹簧近似光顺法弹簧近似光顺法近似将网格节点间通过弹簧相连，任意一个网格节点的位移均会打破网格系统的力的平衡，通过反复迭代，得到一个新的网格系统，变化过程中网格总量不变。

但在处理计算域较大变形问题时，误差较大。

1.2 动态分层法动态分层法是根据移动边界的运动规律，在变形区域实时增加或减少网格。

局部网格发生增减。

相对弹簧近似光顺法，可以处理计算域变形较大的问题。

1.3 局部网格分层法局部网格分层法是在弹性光顺法的基础上发展得到的。

在弹性光顺法得到新的网格系统的基础上，删除部分网格并从新生成。

该方法有一个网格拉伸度尺寸标准，弹性光顺法得到的网格满足标准则继续使用原网格，不满足则从新生成。

由上可见，动网格方法在数值模拟计算域形状发生变化的相关问题上具有较好的效果。

但在处理计算域旋转但形状不变的问题上有所不足。

而滑移网格方法可以很好的弥补这一不足。

2 滑移网格法滑移网方法是在计算过程中，移动单元区域沿网格分界面滑动，移动网格区域内部网格保持不变。

这一特点使得其在数值模拟带有旋转区域相关问题时，具有较大的优势。

2.1 滑移网格法实现步骤（1）读取各计算计算域网格，识别转/静交接面；（2）对转/静交界面上的网格节点进行外延，构造滑移边界；（3）找到每个滑移点的宿主单元，并计算对应的插值型函数；（4）进行流场的定常数值计算，达到收敛标准；（5）开始非定常计算，第一个物理时刻t=0；（6）对旋转域进行相应旋转，重新构造滑移边界、宿主单元搜索和插值函数计算；（7）进行第t 个物理时刻计算，直到满足内迭代收敛标准；判断非定常计算是否完成，完成则终止计算；否则开始下一物理时刻t=t+1时刻的计算，返回（6）。

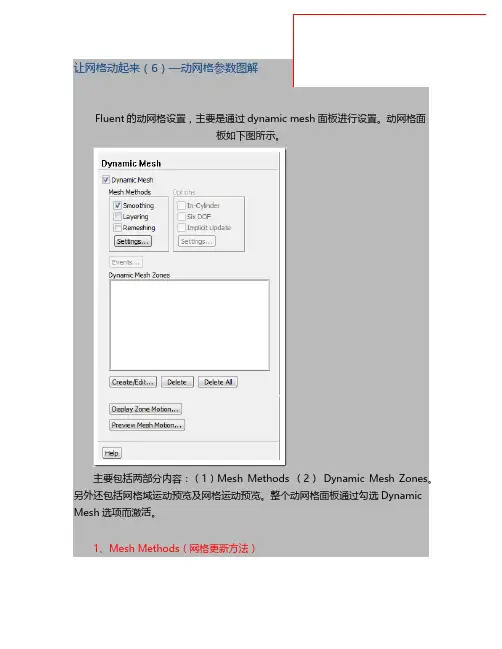
主要包括两部分内容：（1）Mesh Methods （2）Dynamic Mesh Zones。

该部分主要用于网格或网格域在运动过程中，设置计算域中网格节点位置更新方法。

fluent中有三种主要网格更新方法：（1）网格光顺方法（2）动态层方法（3）网格重构。

对于3D模型，还包括in-cylinder、six-dof、Implicit Update
三种选项。

其中in-cyliner用于发动机气缸模拟，six-dof主要用于流体作用于刚体，预测刚体运动。

implicit update用于设定网格更新方式。

默认采用显式方式，勾选此选项可设定网格以隐式方式更新。

2、动态网格域
用于定义网格运动的区域及运动类型。

FLUENT中网格运动类型主要有：静止、刚体运动、变形区域、用户自定义域、耦合域。

静止域在网格运动过程中，区域内节点位置保持不变。

虽然说默认情况下不设定区域运动，则该区域为静止，但是一些情况下还是需要显式设定某些区域为静止域，尤其是在一些与刚体域相连的区域处理上。

刚体运动域：这是fluent动网格中最常见的运动类型。

通过规定刚体的速度或位移来控制运动。

变形域：由于边界运动导致节点变形。

变形域通常与刚体域是相连的。

自定义域：用户可以使用UDF定义自己需要的域
耦合域：节点位移由耦合求解器计算，在流固耦合计算中，耦合面上通常设定为耦合域类型。

Fluent动网格的应用过程一、简介动网格模型可以用来模拟流场形状由于边界运动而随时间改变的问题。

网格的更新过程由FLUENT根据每个迭代步中边界的变化情况自动完成。

FLUENT要求将运动的描述定义在网格面或网格区域上。

如果流场中包含运动与不运动两种区域，则需要将它们组合在初始网格中以对它们进行识别。

二、动网格更新方法动网格计算中网格的动态变化过程可以用三种模型进行计算，即弹簧近似光滑模型、动态分层模型和局部重划模型。

1、弹簧近似光滑模型在弹簧近似光滑模型中，网格的边被理想化为节点间相互连接的弹簧。

移动前的网格间距相当于边界移动前由弹簧组成的系统处于平衡状态。

在网格边界节点发生位移后，会产生与位移成比例的力，力量的大小根据胡克定律计算。

边界节点位移形成的力虽然破坏了弹簧系统原有的平衡，但是在外力作用下，弹簧系统经过调整将达到新的平衡，也就是说由弹簧连接在一起的节点，将在新的位置上重新获得力的平衡。

从网格划分的角度说，从边界节点的位移出发，采用虎克定律，经过迭代计算，最终可以得到使各节点上的合力等于零的、新的网格节点位置，这就是弹簧光顺法的核心思想。

2、动态分层模型对于棱柱型网格区域（六面体和或者楔形），可以应用动态层模型。

动态层模型的中心思想是根据紧邻运动边界网格层高度的变化，添加或者减少动态层，即在边界发生运动时，如果紧邻边界的网格层高度增大到一定程度，就将其划分为两个网格层；如果网格层高度降低到一定程度，就将紧邻边界的两个网格层合并为一个层。

3、局部重划模型在使用非结构网格的区域上一般采用弹簧光顺模型进行动网格划分，但是如果运动边界的位移远远大于网格尺寸，则采用弹簧光顺模型可能导致网格质量下降，甚至出现体积为负值的网格，或因网格畸变过大导致计算不收敛。

为了解决这个问题，FLUENT 在计算过程中将畸变率过大，或尺寸变化过于剧烈的网格集中在一起进行局部网格的重新划分，如果重新划分后的网格可以满足畸变率要求和尺寸要求，则用新的网格代替原来的网格，如果新的网格仍然无法满足要求，则放弃重新划分的结果。

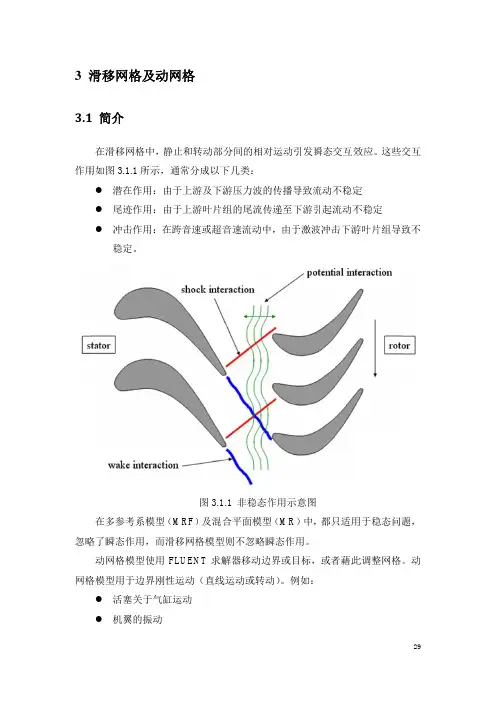
第３０卷第２４期中国机械工程V o l ．３０㊀N o ．２４２０１９年１２月C H I N A M E C HA N I C A LE N G I N E E R I N Gp p．２９６１Ｇ２９６７一种滑动轴承油膜性能计算的动网格方法吴㊀超１㊀尹雪梅２㊀李蒙蒙１㊀李奕君１㊀王㊀文３１．郑州轻工业大学机电工程学院,郑州,４５０００２２．郑州轻工业大学能源与动力工程学院,郑州,４５０００２３．上海大学机电工程与自动化学院,上海,２０００７２摘要:针对应用动网格方法计算油膜轴承性能时出现网格扭曲而导致累计误差过大的现象,提出了一种基于计算流体动力学(C F D )的滑动轴承油膜性能计算的动网格更新方法.该方法保证了网格更新过程中膜厚方向的网格线沿圆周方向上等均分布,且始终垂直于轴颈表面,网格不发生扭曲变形,减小了计算累计误差,提高了轴承性能计算的准确性.通过与典型算例和实验结果对比,验证了所提方法在轴承的油膜力和转子静平衡位置计算中的有效性㊁可行性和稳定性,并利用该方法分析了进油压力和载荷对油膜轴承所支撑转子静平衡位置的影响.该方法可为准确计算油膜轴承转子系统的性能提供参考.关键词:油膜轴承;动网格;静平衡;轴心轨迹;计算流体动力学中图分类号:T H １３３．３D O I :１０．３９６９/j．i s s n ．１００４ １３２X．２０１９．２４．００９开放科学(资源服务)标识码(O S I D ):AD yn a m i cM e s h M e t h o dU s e d t oC a l c u l a t eO i l F i l m P e r f o r m a n c e o f J o u r n a l B e a r i n gs WU C h a o １㊀Y I N X u e m e i ２㊀L IM e n g m e n g １㊀L IY i ju n １㊀WA N G W e n ３１．S c h o o l o fM e c h a n i c a l a n dE l e c t r i c a l E n g i n e e r i n g ,Z h e n g z h o uU n i v e r s i t y o fL i g h t I n d u s t r y ,Z h e n gz h o u ,４５０００２２．S c h o o l o f E n e r g y a n dP o w e rE n g i n e e r i n g ,Z h e n g z h o uU n i v e r s i t y o f L i g h t I n d u s t r y ,Z h e n gz h o u ,４５０００２３．S c h o o l o fM e c h a t r o n i cE n g i n e e r i n g a n dA u t o m a t i o n ,S h a n g h a iU n i v e r s i t y ,S h a n gh a i ,２０００７２A b s t r a c t :I no r d e r t o a v o i d t h e p h e n o m e n o no fm e s hd i s t o r t i o n a n d r e d u c e t h e e r r o r s i n t h e a p pl i Ｇc a t i o n s o f d y n a m i cm e s hm e t h o d t oc a l c u l a t eo i l Ｇf i l m b e a r i n gp e r f o r m a n c e ,ad y n a m i cm e s hu p d a t i n gm e t h o dw a s p r o p o s e db a s e do nC F D．T h i sm e t h o d e n s u r e d t h a t a l l o f t h e u pd a te d r a d i a lm e s h l i n e s a Ｇl o n g o i l Ｇf i l mc l e a r a n c ew e r ew e l l Ｇd i s t r i b u t e d a l o ng th e ci r c u m f e r e n t i a l d i r e c t i o n ．D u r i n g t h em e s hu pＧd a t i n gp r o c e s s e s ,t h e r a d i a lm e s h l i n e s i n t h e d i r e c t i o no f f i l mt h i c k n e s sw e r e a l w a y s p e r pe n d i c u l a r t o t h e j o u r n a l s u rf a c e s ,w h i c hc o u l de n s u r eo i l Ｇf i l m m e s hn o t d i s t o r t i o n s a n d i m p r o v e a c c u r a c y ofm e s h c o m p u t a t i o n ．T h en e wd y n a m i cm e s hu p d a t i n g me t h o dw a s u s e d t o c a l c u l a t e t h e o i l Ｇf i l mf o r c e s o f t h e j o u r n a l b e a r i ng s a n d th e s t a ti c b a l a n c e p o s i t i o n s o f t h e r o t o r s ．T h e r e s u l t sw e r e c o m pa r e dw i t h t h e c a l Ｇc u l a t i n g o n e s a n d t h e e x p e r i m e n t a l o n e s o f t y p i c a l e x a m p l e s ,t h e e f f e c t i v e n e s s ,f e a s ib i l i t y a n d s t a b i l i t yo f t h e d y n a m i cm e s hu p d a t i n g m e t h o d p r o p o s e dm a y b e v e r i f i e d ．B y u s i n g th em e t h o d ,e f f e c t s o f d i f Ｇf e r e n t i n l e t o i l p r e s s u r e s a n d l o a d s o n s t a t i c b a l a n c e p o s i t i o n s o f t h e r o t o r s s u p p o r t e db y oi l Ｇf i l mb e a r Ｇi n g sw e r ea n a l y z e d ．T h e p r o p o s e d m e t h o d m a yp r o v i d er e f e r e n c e f o ra c c u r a t e l y c a l c u l a t i n g t h e p e r Ｇf o r m a n c e o f t h e o i l Ｇf i l mb e a r i n g Ｇr o t o r s ys t e m s ．K e y w o r d s :o i l Ｇf i l m b e a r i n g ;d y n a m i c m e s h ;s t a t i cb a l a n c e ;a x i s l o c u s ;c o m p u t a t i o n a l f l u i dd y Ｇn a m i c s (C F D )收稿日期:２０１８１０１１基金项目:国家自然科学基金资助项目(５１７０６２０９,U １４０４５１５);河南省高校青年骨干教师培养计划资助项目(２０１７G G J S ０９４);河南省科技攻关项目(１９２１０２２１０２１３);河南省教育厅重点项目(２０A ４６００２８)０㊀引言计算油膜轴承性能的关键问题就是求解动态流体润滑方程,得到油膜的压力分布[１Ｇ４].通常情况下,采用动态雷诺方程计算轴承的性能１６９２ 中国机械工程h tt p://ww w.cm em o.or g.cn公众号：t ra ns -c me sCopyright©博看网 . All Rights Reserved.时,难以精确反映转速所引起的油流周向惯性效应㊁动态挤压效应和静压效应之间的线性耦合关系及其对油膜三维压力场㊁温度场和速度场的影响,因此,有必要直接求解N a v i e r ＧS t o k e s方程,精确研究轴承参数对油膜性能的影响[５].文献[６Ｇ８]采用计算流体动力学(c o m pu t a t i o n a l f l u i dd yn a m i c s ,C F D )开展了静压轴承承载特性的研究,证实了在表征复杂求解域流体流动形态方面N a v i e r ＧS t o k e s 方程可弥补雷诺方程的不足.文献[９Ｇ１０]利用F l u e n t 软件,采用静网格方法,研究了气穴现象对滑动轴承性能的影响,但静网格方法不能计算变载荷下轴心的轨迹.文献[１１Ｇ１２]将轴颈的旋转动边界转换为静边界,并利用S m o o t h i n g 动网格模型,成功计算了油膜轴承的动特性系数.文献[１３Ｇ１５]自定义动网格更新程序,提出了基于弹性变形的动网格调整法,能用来求解瞬态轴心轨迹,并利用弱耦合算法研究了轴承刚度随方向的变化以及涡动中心与载荷㊁不平衡量的关系.文献[１６]针对求解复杂转子Ｇ轴承系统非线性动力学特性的问题,基于S m o o t h i n g 动网格技术,提出了一种计算流体力学和计算转子动力学的流固耦合新方法,计算结果表明,该方法能够得到精确的轴心轨迹,并能准确分析复杂转子Ｇ轴承系统非线性动力学特性.文献[１７]利用非定常动网格技术建立了考虑轴颈涡动频率与涡动轨迹的滑动轴承动力特性求解模型,研究了不同的轨迹下轴颈涡动频率和偏心率对滑动轴承动力特性的影响.以上在油膜轴承性能计算中运用的动网格方法是基于S m o o t h i n g 模型或其变形模型基础上进行的,能够方便地求解出油膜轴承的特性参数,分析轴承Ｇ转子系统的动力学性能.S m o o t h i n g 动网格模型[１８]的特点是不改变网格节点间的拓扑关系,只进行网格形状的改变,能够计算变载荷下轴承的轴心轨迹,但S m o o t Ｇh i n g 模型网格位移的更新方法容易造成网格畸变,当偏心率过大时,垂直于轴颈的网格线就会出现严重倾斜,甚至出现负网格的情况,导致计算发散.鉴于F l u e n t 软件在表征流体流动形态方面的优势及其计算油膜轴承动态性能方面的不足,本文提出了一种基于F l u e n t 方法的滑动轴承油膜性能计算的动网格更新方法.在它的每一时间步内,所有网格节点更新方式是依据轴颈中心坐标确定的,使径向网格线始终垂直于轴颈表面,保证了移动前后膜厚方向的网格线沿圆周方向上等均分布,网格不发生扭曲变形,避免了网格节点更新产生的累计误差.通过与典型算例和实验结果对比分析来验证该方法的有效性,并考察了进油压力和载荷对转子静平衡位置的影响.１㊀动网格更新算法原理１．１㊀已有动网格方法动网格模型可以用来模拟由于边界运动而引起的流域随时间的变化.边界运动可以是主动的规定动作(例如,用户可以定义刚体中心的速度和角速度),也可以是被动的待求解的动作(例如,六自由度模型中,已知运动状态的刚体边界,受合力后确定下一时刻的速度和加速度).根据每一个时间步的运动边界的位置,F l u e n t 软件自动对动网格更新处理.对于动网格模型,用户需要确定初始网格和运动区域.３种常用的动网格更新算法[１８]分别是S m o o t h i n g ㊁L a y e r i n g 和Re m e s h Ｇi n g .S m o o t h i n g 方法是不改变网格节点间的拓扑关系,只进行网格形状的改变,但当网格出现畸变时计算容易发散.L a y e r i n g 方法是随着动边界的移动,在边界处发生网格的增加或合并.R e m e s h i n g 方法是将控制区内的所有网格重新划分,一般适用于非结构化网格.理论上,考虑到油膜几何尺寸的特点,应当选择S m o o t h i n g 动网格更新方式,但在轴承性能计算过程中也出现了网格畸变,显然S m o o t h i n g 方法也不能很好地解决轴承油膜的瞬态计算问题.文献[１３]提出的基于S m o o t h i n g 的网格更新模型示意图见图１.网格节点位移按公式Δx i ＝n i Δx /n 和Δy i ＝n i Δy/n 进行计算(n 为膜厚方向网格的层数,n i 为网格节点所在的层数,Δx ㊁Δy 为轴颈中心在该时间步的位移).利用该方法,垂直于轴颈表面的网格线就会出现倾斜,导致计算结果误差较大,特别是多步计算后的位置累计误差.图１㊀文献[１３]网格更新方式F i g ．１㊀M e s hu p d a t i n g me t h o d i n r ef e r e n c e s １．２㊀自定义动网格更新算法原理为解决上述难点,本文提出了一种新的网格更新算法,在网格更新前后,膜厚方向的网格线始２６９２ 中国机械工程第３０卷第２４期２０１９年１２月下半月中国机械工程h tt p://ww w.cm em o.or g.cn公众号：t ra ns -c me sCopyright©博看网 . All Rights Reserved.终指向轴颈的中心,从而避免了出现网格倾斜.本文网格结构更新算法的示意图见图２,网格节点位置计算原理见图３.图２㊀本文提出的新的网格更新方式F i g ．２㊀N e w m e s hu p d a t i n g m e t h o d i n t h i s p a pe r 图３㊀网格节点更新原理图F i g ．３㊀S c h e m a t i c d i a g r a mo fm e s hn o d e u p d a t i n g为使网格不发生扭曲变形,就需要指向轴颈中心的网格线方向始终不改变,即始终垂直于轴颈表面,同时要保证在移动前后膜厚方向的网格线沿圆周方向上等均分布(膜厚网格线的夹角相等),即更新前后网格线平行,也就是图３中的向量O １N １与O ２N ２共线.具体方法如下.记轴承的中心为O ,移动前后的轴颈的中心分别为O １和O ２,油膜网格在膜厚方向上分成k 层网格,假设N １为t １时刻网格上任意一个待更新节点,节点N １以及与其相对应的更新后的节点N ２均在第k i 层网格上,根据此刻轴颈所受的油膜力㊁轴颈坐标㊁轴颈中心位移速度㊁轴颈质量可以得到下一时刻t ２的轴颈中心坐标,根据时刻t ２的轴颈中心坐标和该节点相对轴心的单位向量(与向量O １N １平行或者共线),作射线分别交轴颈圆和轴承圆于点A ２㊁B ２.又知待求点N ２所在的层数为k i ,即已知L A ２N ２＝(k i/k )L A ２B ２,L O B ２为轴承半径,L O ２A ２为轴颈半径.N ２坐标求解算法步骤如下.(１)求出L O O ２;(２)已知向量O １N １的单位法向量e ,由于向量O １N １与向量O ２N ２共线,故可得到向量O ２N ２的单位法向量e ;(３)求解向量O ２O 与向量O ２B ２的夹角余弦c o s α;(４)利用三角形关系式求解L O ２B ２:L O ２B ２＝L O O ２c o s α＋(L O O ２c o s α)２－L ２O O ２＋L ２O B ２(５)求出L A ２B ２＝L O ２B ２－L O ２A ２;(６)O ２N ２＝e (k i kL A ２B ２＋L O ２A ２).已知轴颈中心移动后的坐标O ２,根据上述算法可求出节点位置N １移动到新位置的坐标N ２.２㊀轴心静平衡位置的求解方法２．１㊀数学模型根据牛顿第二定律,运动方程[１３]为mS ＝G ＋F(１)式中,m 为转子质量的一半;S 为转子中心距原点的位移,G ＝m g ;F 为转子受的油膜合力.已知时间步Δt ,上一时间步对应的速度v ０,根据牛顿第二定律求解每一个时间点轴颈中心的相对位移和速度计算公式如下:ΔS ＝１２G ＋F mΔt ２＋v ０Δt(２)v ＝v ０＋(G ＋F )Δt /m(３)求解油膜力F 的分量F x 和F y 的公式如下:F x ＝ʏl /２－l /２ʏ２π０p A co s θd θd z(４)F y＝ʏl /２－l /２ʏ２π０p A si n θd θd z (５)式中,F x ㊁F y 分别为x 轴和y 轴方向的油膜力;A 为某一网格单元的面积;p 为根据N ＧS 方程计算出的轴承油膜各点的压力.２．２㊀求解轴心静平衡位置流程及宏函数的选用基于F l u e n t 软件,利用该方法计算油膜轴承所支撑轴颈静平衡位置的流程如图４所示,首先设定轴颈初始速度和初始位移,通过u d f 宏D E F I N E _G R I D _MO T I O N 计算出油膜力F x 和F y ,再根据式(２)和式(３)计算出轴心坐标和速度.同时按照新提出的算法原理进行网格更新,在该时间步内迭代完后进入下一个时间步.下一个时间步用到上一时间步的轴心坐标和速度(读取储存于文件２和文件３最后一次更新的数值).一直循环下去,直到轴颈中心趋近于一定点,即可停止计算,该定点即稳态下径向油膜轴承所支撑轴颈中心的静平衡位置.一般来说,动网格节点的位移由坐标确定,但滑动轴承油膜是一种长径比很大的网格,用坐标３６９２ 一种滑动轴承油膜性能计算的动网格方法吴㊀超㊀尹雪梅㊀李蒙蒙等中国机械工程h tt p://ww w.cm em o.or g.cn公众号：t ra ns -c me sCopyright©博看网 . All Rights Reserved.图４㊀轴心静平衡位置计算流程图F i g ．４㊀C o m p u t a t i o n a l f l o wc h a r t a b o u t s t a t i c b a l a n c e p o s i t i o no f t h e r o t o r判断节点位置容易出现错误,可采用节点全局编号判定节点的位置,强制精确控制每一个节点的位移变化.利用D E F I N E _G R I D _MO T I O N 宏对网格节点位置进行强制性精确定义,可有效降低网格畸变的可能性,由于轴颈表面各点的速度不一样,可通过编写D E F I N E _P R O F I L E 宏程序控制轴颈表面各点的速度.按照以上步骤,可以利用动网格方法实现对滑动轴承油膜状态的仿真.３㊀算法的正确性和有效性验证本文提出的网格更新方法与文献[１３]所使用的网格更新方法的主要区别就是更新后油膜厚度方向的网格线是否垂直于轴颈表面.要验证所提动网格算法的正确性和有效性,需要进行两方面的验证:用于静态油膜力计算的精度验证;用于轴颈中心静平衡位置求解的累积误差验证.３．１㊀算例１:用于静态油膜力计算的精度验证(单次油膜力计算)利用所提出的网格结构和文献[１３Ｇ１５]的网格结构,分别计算轴颈转动角速度为５００r a d /s㊁偏心率为０．５和０．９的圆柱轴承的油膜力,来对比这两种网格在静态油膜力计算(用于静网格计算时,单次网格计算)的精度.算例选取的轴承几何参数和润滑油物性参数见表１.轴承供油方式采用两侧双向进油并且设置轴向油槽.由于油膜厚度尺寸很小,故油膜厚度方向的网格划分对计算结果影响最大,需要先进行网格独立性验证.网格独立性计算时选择多项流混合模型,气穴模型选用S i n g h a l 全空化模型,连续性方程㊁动量方程和气穴方程均选用一阶迎风格式进行求解,速度耦合格式选择S I M P I L E 格式.轴表１㊀轴承和润滑油物性参数T a b ．１㊀P a r a m e t e r s o f b e a r i n g a n d l u b r i c a t i n g oi l 轴承直径(mm )３２轴承宽度(mm )１６半径间隙(mm )０．０３２油槽包角(ʎ)３０进油边界压力(k P a )２００(表压)出口边界压力(P a)０(表压)环境压力０(大气压)气化压力(P a )２９１８５(绝对压力)角速度(r a d /s)５００润滑油密度(k g/m ３)８５０润滑油黏度(k g /(m s ))０．０１２５气相密度(k g/m ３)１．２２５气相黏度(k g/(m s ))１．７８９４ˑ１０－５承油膜网格初始划分的网格数(膜厚方向ˑ周向ˑ轴向)为５ˑ６００ˑ８０,通过改变膜厚方向的网格层数,并以净流量小于进口和出口流量两者之间的最小值的１％作为判断收敛的标准.膜厚方向上设置不同的网格层数,以承载力作为观测量,网格独立性验证结果见表２.结果表明,本文所用的网格密度计算结果的最大偏差均小于４％.表２㊀网格独立性验证结果T a b ．２㊀G r i d i n d e pe n d e n c e v e r if i c a t i o n r e s u l t s 膜厚方向网格层数承载力(N )相对偏差(％)５２５９．１０３．９７１０２６６．３２１．２９１５２６９．５００．１１２０２６９．８０㊀㊀综合考虑计算效率和计算精度,把油膜膜厚方向网格划分为６层(６ˑ６００ˑ８０),见图５.算例中压力速度耦合格式分别选S I M P I L E ㊁S I M ＧP I L E C ㊁P I S O 方式,其他设置同上.采用瞬态计算方法,利用文献中的网格方法和本文的网格方法计算得到的承载力结果和圆周方向的压力分布结果(取轴承宽度中间L /２处,偏心率为０ ９)分别见表３和图６.图５㊀油膜网格F i g．５㊀O i l f i l m m e s h４６９２ 中国机械工程第３０卷第２４期２０１９年１２月下半月中国机械工程h tt p://ww w.cm em o.or g.cn公众号：t ra ns -c me sCopyright©博看网 . All Rights Reserved.表３㊀两种静网格结构计算的承载力对比T a b ．３㊀C o m p a r i s o no f b e a r i n g c a p a c i t y of t w ok i n d s o f s t a t i cm e s h s t r u c t u r e s偏心率压力速度耦合格式承载力(N )文献[１３Ｇ１５]方法本文方法文献[１９]方法０．５S I M P I L E ２６１．５２２６１．５７S I M P I L E C ２６１．５２２６１．５７P I S O计算发散２６１．５８２３９．７６０．９S I M P I L E ３８６６．５３３９８０．３９S I M P I L E C ３８６６．２９３９８０．３９P I S O计算发散计算发散４０３２(a )文献[１３Ｇ１５]方法的计算结果(b)本文方法的计算结果图６㊀油膜周向压力分布F i g ．６㊀C i r c u m f e r e n t i a l pr e s s u r e d i s t r i b u t i o no f o i l f i l m 由表３和图６可以看出,基于两种网格方法得到的轴承承载力和瓦块圆周方向的压力计算结果相同,均与文献[１９]结果相接近,表明两种网格(油膜厚度方向的网格线垂直于或者不垂直于轴颈表面)用于轴承油膜稳态油膜力计算时,均能满足精度要求(＜９％).由于在计算过程中网格不更新(静网格法),无论油膜厚度方向的网格线是否倾斜,累计计算误差都不存在,故两种网格的计算结果基本无差别.这就证明了S m o o t h i n g 网格方法和本文提出的网格方法来计算轴承稳态油膜力(静网格法)的精度是满足要求的.３．２㊀算例２:用于静平衡位置求解的累计误差验证(多次油膜力计算)根据文献[１３]的算例,选取轴颈角速度为５００r a d /s ,转子质量为１７．５２７k g (１７１．７６N ),轴承㊁润滑油的参数和油膜网格划分同算例１,对轴颈中心轨迹的收敛过程及静平衡位置进行了仿真,结果见图７,计算得到其偏心率为０．２２１.根据文献[１９](未给出进油压力,其他条件完全一样),在相同轴承参数下,据此载荷计算出轴承偏心率为０．２６７,与本文计算结果相比,相对误差是１７．２％.文献[１３]和本文在计算时考虑了气穴的影响,而文献[１９]没有考虑气穴的影响.(a)二维图(b)三维图图７㊀本文方法计算的轴心轨迹F i g ．７㊀C a l c u l a t i o n r e s u l t o f a x i a l c o n v e r g e n c e t r a j e c t o r yi n t h i s p a pe r 文献[１３]的静平衡位置所对应的偏心率为０ ０４６.将文献[１３]结果和本文的计算结果分别与文献[１８]相比较,文献[１３]的计算结果差别更大,偏心率明显不在同一数量级,表明文献[１３]的网格经多次更新后,出现了较大的累计误差.这与文献[１３]在网格更新时沿膜厚方向的网格线与轴颈表面不垂直有关,也与其网格节点坐标更新的计算方式与轴颈表面的位置有关,从而导致多次迭代后求解轴颈中心静平衡位置时出现了较大的误差.为验证所编制程序的稳定性,从３个不同起始位置开始分别计算相同条件下的轴心静平衡位置,轴心轨迹收敛曲线如图８所示.可以看出,３条曲线最终收敛于一点,表明计算的起始位置对轴颈的静平衡位置并无影响,验证了所编制的网格更新程序的稳定性.３．３㊀算例３:进油压力对轴心静平衡位置的影响为了分析进油压力对轴承所支撑转子轴心静５６９２ 一种滑动轴承油膜性能计算的动网格方法吴㊀超㊀尹雪梅㊀李蒙蒙等中国机械工程h tt p://ww w.c m e m o .o r g.cn公众号：t ra ns -c me sCopyright©博看网 . All Rights Reserved.图８㊀不同起点位置的轴心收敛轨迹F i g ．８㊀A x i a l c o n v e r g e n c e t r a j e c t o r y of d i f f e r e n t s t a r t i n gpo s i t i o n s 平衡位置的影响,在给定气化压力２９１８５P a㊁转子质量１７．５２７k g㊁角速度５００r a d /s 和０００r a d /s 的条件下,计算了供油压力在０．１~０．５M P a 之间时转子轴心的静平衡位置.轴承的偏心率和偏位角随进油压力的变化关系如图９所示.算例的其他计算参数见表１.(a)偏心率(b)偏位角图９㊀进油压力对偏心率和偏位角的影响F i g ．９㊀T h e e f f e c t o f i n l e t p r e s s u r e o n e c c e n t r i c i t y a n dd e f l e c t i o na n gl e 由图９可以看出,随着进油压力的增大,偏心率减小(＜７％),偏位角增大(＜９％).这是因为在载荷和转速不变的前提下,随着进油压力的增大,轴承油膜的最大压力增大,承载能力增强,偏心率减小.同时由于进油口在水平方向上,故随着进油压力增大,偏位角增大.计算结果表明进油压力对轴承的承载性能有影响,但影响率小于１０％.结合算例２的结果,进一步证明了所提出的动网格更新方法用于轴心轨迹计算时累计误差相对较小.通过以上算例验证了所提出的动网格方法在油膜性能计算的有效性㊁可行性和稳定性.４㊀结论(１)本文提出了一种用于滑动轴承油膜性能计算的动网格更新方法,验证了其正确性.本文方法能够保证在网格移动前后膜厚方向的网格线沿圆周方向上等均分布,并使指向轴颈中心的网格线方向始终垂直于轴颈表面,网格不发生倾斜.(２)本文方法应用于求解滑动轴承所支撑转子的静平衡位置时,能够减少网格计算的累计误差,提高计算的精度;同时发现利用F l u e n t 软件动网格方法计算油膜轴承流场时,膜厚方向网格倾斜会对计算结果产生较大的累计误差.(３)在相同的条件下,随着进油压力增大,轴承偏心率减小,偏位角增大,但进油压力对轴承的承载性能的影响率一般小于１０％.参考文献:[１]㊀李锋,刘占生,李明海,等．非零压差边界下间隙流动雷诺方程近似解析解[J ]．航空动力学报,２０１８,３３(１):１５６Ｇ１６４．L IF e n g ,L I U Z h a n s h e n g ,L I M i n g h a i ,e ta l ．A pＧp r o x i m a t e A n a l y t i c a l S o l u t i o n o f t h e R e y n o l d s E qu a t i o nf o rC l e a r a n c eF l o w w i t h P r e s s u r eD i f f e r Ｇe n c eB o u n d a r y C o n d i t i o n s [J ]．J o u r n a lo fA e r o s p a c e P o w e r ,２０１８,３３(１):１５６Ｇ１６４．[２]㊀康召辉,任兴民,何尚文,等．浮环涡动对浮动环轴承油膜压力分布影响的研究[J ]．航空动力学报,２０１０,２５(５):１１９７Ｇ１２０２．K A N GZ h a o h u i ,R E N X i n g m i n ,H ES h a n gw e n ,e t a l ．S t u d y o nt h eE f f e c t so f W h i r l i n g M o t i o no f t h e F l o a t i n g R i n g on t h eD i s t r i b u t i o no fO i l P r e s s u r e i n aF l o a t i n g R i n g B e a r i n g [J ]．J o u r n a lo f A e r o s p a c e P o w e r ,２０１０,２５(５):１１９７Ｇ１２０２．[３]㊀S H ID Y ,S H IXJ ,S H IXB ．N u m e r i c a l C o m pu t a Ｇt i o no f D yn a m i c C h a r a c t e r C o e f f i c i e n to fJ o u r n a l B e a r i n g [J ]．K e y E n g i n e e r i n g M a t e r i a l s ,２０１１,４８６(７):４５Ｇ４８．[４]㊀吕延军,张永芳,季丽芳,等．固定瓦可倾瓦滑动轴承转子非线性系统的动力特性分析[J ]．中国电机工程学报,２０１０,３０(２０):７９Ｇ８７．L Y U Y a n j u n ,Z HA N G Y o n g f a n g ,J IL i f a n g,e t a l ．６６９２ 中国机械工程第３０卷第２４期２０１９年１２月下半月中国机械工程h tt p://ww w.c m e m o.or g.cn公众号：t ra ns -c me sCopyright©博看网 . All Rights Reserved.A n a l y s i s o fD yn a m i cC h a r a c t e r i s t i c so fR o t o rN o n Ｇl i n e a rS y s t e m S u p p o r t e db y F i x e d Ｇt i l t i n g P a dJ o u r Ｇn a lB e a r i n g [J ]．P r o c e e d i n g so f t h eC S E E ,２０１０,３０(２０):７９Ｇ８７．[５]㊀MO R IA ,MA K I N O T ,MO R IH．E n t r y Fl o wa n d P r e s s u r eJ u m p i n S u b m e r g e d M u l t i Ｇp a d B e a r i n g s a n d G r o o v e d B e a r i n g s [J ]．J o u r n a lo f T r i b o l o g y ,１９９２,１１４(２):３７０Ｇ３７７．[６]㊀T U C K E RPG ,K E O G H P S ．O n t h e D yn a m i c T h e r m a lS t a t ei na H y d r o d y n a m i cB e a r i n g w i t ha W h i r l i n g J o u r n a lU s i n g C F DT e c h n i q u e s [J ]．J o u r n a l o fT r i b o l o g y,１９９６,１１８(２):３５６Ｇ３６３．[７]㊀S A H L I N F ,G L A V A T S K I H SB ,A L MQ U I S T ,e t a l ．T w oD i m e n s i o n a l C F D A n a l y s i s o fM i c r o Ｇpa t Ｇt e r n e dS u r f a c e si n H y d r o d y n a m i c L ub r ic a t i o n [J ]．J o u r n a l o fT r i b o l o g y,２００５,１２７(１):９６Ｇ１２７．[８]㊀G E R T Z O S K P ,N I K O L A K O P O U L O SP G ,P A P ＧA D O P O U L O SC A ．C F D A n a l y s i so f J o u r n a lB e a r i n gH y d r o d y n a m i cL u b r i c a t i o nb y B i n gh a m L u b r i c a n t [J ]．T r i b o l o g y In t e r n a t i o n a l ,２００８,４１(１２):１１９０Ｇ１２０４．[９]㊀孟凡明,陈原培,杨涛．C F X 和F l u e n t 在径向滑动轴承润滑计算中的异同探讨[J ]．重庆大学学报,２０１３,３６(１):７Ｇ１４．M E N G F a n m i n g ,C H E N Y u a n pe i ,Y A N G T a o ．D i s c u s s i o no nS i m i l a r i t i e sa n d D if f e r e n c e sb e t w e e nC F X a n d F l u e n t S o f t w a r ei n C a l c u l a t i n g Jo u r n a l B e a r i n g L u b r i c a t i o n [J ]．J o u r n a l o fC h o n g q i n g Un i Ｇv e r s i t y,２０１３,３６(１):７Ｇ１４．[１０]㊀黄首峰,郭红,张绍林,等．基于F L U E N T 的径向滑动轴承油膜压力仿真[J ]．机械设计与制造,２０１２(１０):２４８Ｇ２５０．H U A N GS h o u f e n g ,G U O H o n g,Z H A N GS h a o l i n ,e ta l ．S t a t i cC h a r a c t e r i s t i c sS i m u l a t i o no fJ o u r n a l S l i d i n g B e a r i n g B a s e do nF L U E N T [J ]．M a c h i n e r yD e s i gn &M a n u f a c t u r e ,２０１２(１０):２４８Ｇ２５０．[１１]㊀熊万里,侯志泉,吕浪,等．基于动网格模型的液体动静压轴承刚度阻尼计算方法[J ]．机械工程学报,２０１２,４８(２３):１１８Ｇ１２６．X I O N G W a n l i ,HO U Z h i q u a n ,L Y U L a n g,e t a l ．M e t h o d f o rC a l c u l a t i n g S t i f f n e s s a n dD a m p i n g Co Ｇe f f i c i e n t so f H y b r i d B e a r i n g s B a s e d o n D yn a m i c M e s h M o d e l [J ]．J o u r n a lo f M e c h a n i c a lE n gi n e e r Ｇi n g,２０１２,４８(２３):１１８Ｇ１２６．[１２]㊀王少力,熊万里,桂林,等．偏载液体静压转台旋转工况下承载力及倾覆力矩动网格计算方法[J ]．机械工程学报,２０１４,５０(２３):６６Ｇ７４．WA N G S h a o l i ,X I O N G W a n l i ,G U I L i n ,e ta l ．D y n a m i cM e s hM e t h o d f o rC a l c u l a t i n g B e a r i n g C a Ｇp a c i t y a n dO v e r t u r n i n g Mo m e n to fP a r t i a lL o a d e d H y d r o s t a t i cR o t a r y T a b l e su n d e rR o t a t i n g Co n d i Ｇt i o n [J ]．J o u r n a l o fM e c h a n i c a lE n g i n e e r i n g,２０１４,５０(２３):６６Ｇ７４．[１３]㊀李强,许伟伟,赵月,等．基于瞬态流场计算的滑动轴承静平衡位置求解[J ]．中国石油大学学报,２０１５,３９(２):１０４Ｇ１１０．L IQ i a n g,X U W e i w e i ,Z HA O Y u e ,e t a l ．S o l u t i o n o fS t a t i c E q u i l i b r i u m P o s i t i o no fJ o u r n a lB e a r i n gB a s e do nT r a n s i e n tF l o wC a l c u l a t i o n [J ]．J o u r n a l o f C h i n aU n i v e r s i t y ofP e t r o l e u m ,２０１５,３９(２):１０４Ｇ１１０．[１４]㊀L IQ i a n g ,Y U G u i c h a n g ,L I U S h u l i a n ,e t a l ．A pＧp l i c a t i o n o f C o m p u t a t i o n a l F l u i d D yn a m i c s a n d F l u i dS t r u c t u r eI n t e r a c t i o n T e c h n i qu e sf o rC a l c u Ｇl a t i n g t h e３D T r a n s i e n tF l o w o fJ o u r n a lB e a r i n gs C o u p l e dw i t hR o t o rS ys t e m s [J ]．C h i n e s eJ o u r n a l o fM e c h a n i c a l E n g i n e e r i n g,２０１２,２５(５):９２６Ｇ９３２．[１５]㊀L IM e n g x u a n ,G U C h a o h u a ,P A N X i a o h o n g,e t a l ．A N e w D y n a m i c M e s hA l g o r i t h mf o rS t u d y i n gt h e ３DT r a n s i e n t F l o wF i e l d o fT i l t i n g Pa d J o u r n a l B e a r i n g s [J ]．J o u r n a lo f E n g i n e e r i n g T r ib o l o g y,２０１６,２３０(１２):１４７０Ｇ１４８２．[１６]㊀林禄生,刘桂萍,陈园．复杂转子Ｇ轴承系统非线性动力学特性分析[J ]．机械强度,２０１５,３７(３):３８１Ｇ３８６．L I N L u s h e n g ,L I U G u i p i n g,C H E N Y u a n ．N o n l i n Ｇe a rD y n a m i cB e h a v i o r s A n a l y s i so fC o m pl e x R o t o r Ｇb e a r i n g S y s t e m [J ]．J o u r n a lo f M e c h a n i c a lS t r e n gt h ,２０１５,３７(３):３８１Ｇ３８６．[１７]㊀孙丹,李胜远,白伟钢,等．考虑轴颈涡动的滑动轴承动力特性数值研究[J ]．航空动力学,２０１８,３３(１):１３７Ｇ１４６．S U N D a n ,L I S h e n g y u a n ,B A IW e i g a n g ,e t a l ．N u Ｇm e r i c a l S t u d y o nD y n a m i cC h a r a c t e r i s t i c so f J o u r Ｇn a lB e a r i n g C o n s i d e r i n g J o u r n a l W h i r l i n g M o t i o n [J ]．J o u r n a l o fA e r o s pa c eP o w e r ,２０１８,３３(１):１３７Ｇ１４６．[１８]㊀周俊杰,徐国权,张华俊．F L U E N T 工程技术与实例分析[M ]．北京:中国水利水电出版社,２０１０:４１Ｇ６６．Z H O U J u n j i e ,X U G u o q u a n ,Z H A N G H u a j u n ．F L U E N T E n g i n e e r i n g T e c h n o l o g y a n d C a s e S t u d y [M ]．B e i j i n g :C h i n aW a t e r P o w e r P r e s s ,２０１０:４１Ｇ６６．[１９]㊀张直明．滑动轴承的流体动力润滑理论[M ]．北京:高等教育出版社,１９８６:２１１Ｇ２２２,２７６．Z HA N G Z h i m i n g ．H y d r o d y n a m i c L u b r i c a t i o n T h e o r y o f S l i d i n g B e a r i n g s [M ]．B e i j i n g :H i gh e r E d Ｇu c a t i o nP r e s s ,１９８６:２１１Ｇ２２２,２７６．(编辑㊀陈㊀勇)作者简介:吴㊀超,男,１９７８年生,副教授㊁博士.研究方向为滑动轴承Ｇ转子系统动力学.发表论文２０篇.E Ｇm a i l :w u c h a o ７３７９＠１６３．c o m .尹雪梅(通信作者),女,１９７９年生,副教授.研究方向为辐射传热及流体性能计算等.E Ｇm a i l :yi n x u e m e i h i t ＠１２６．c o m .７６９２ 一种滑动轴承油膜性能计算的动网格方法吴㊀超㊀尹雪梅㊀李蒙蒙等中国机械工程h tt p://ww w.cm em o.or g.cn公众号：t ra ns -c me sCopyright©博看网 . All Rights Reserved.。

①进行动网格演示时，首先设置为transient;②动网格预览：display zone motion---preview mesh motion;预览之后不保存，重新打开才能恢复原样；③问题:出现负体积：如果有error前有warning,仔细查看；第一章理论基础1.1 网格生成方法比较1）铺层layering计算区域进行扩张和收缩时，网格进行合并或删除；特点：①网格的增加或删除是一层一层进行的；②适用于四边形、六面体和三棱柱网格，不适用于三角形、四面体网格；③常适用于边界线线性运动；2）弹性光顺spring smoothing计算区域进行扩张和收缩时，网格和节点像弹簧一样被拉伸和压缩（接近运动的地方压缩严重）；特点：①节点数量和链接关系不发生变化；②如果变形幅度过大，网格会高度扭曲；③适用于三角形、四面体网格，也适用于四边形、六面体和三棱柱网格；3）局部重构local remeshing计算区域进行扩张和收缩时，会自动重构扭曲或尺寸过大的网格，以满足要求；①节点的数量和链接关系会发生变化；②适合大变形、大位移；仅使用与三角形网格和四面体网格；③常和spring smoothing联合使用；1.2 边界运动1.2.1 in-cylinder对于类活塞运动，fluent集成了气缸（in-cylinder）模型；dynamic mesh---option---in cylinder;1)常用参数Crank radius:曲柄半径；connecting rod length:连杆半径；(1)通过设置起始、终止角度、曲柄、连杆半径，调整指定边界运动范围；设置crank angle step size,调整边界运动速度；设置起始、终止角度、piston axis方向，调整边界运动的方向；2）指定运动区域Dynamic mesh zones---creat/edit;Zone name---选择gambit中指定的运动边界；Type---rigid body；Motion attributes---选择piston-full(motion udf/profile)---指定活塞轴方向(piston axis);设置h_ideal(meshing option---cell hight);1.2.2 profile对于预先指定的运动，可用profile来描述；1）define---profile---read;后缀名为prof;1.2.3 六自由度模型对于物体运动和流体作用力耦合的计算问题，可以使用六自由度模型；1.2.4 udf1.3 变形的指定1.3.1 deforming1)边界上的节点，默认情况下是静止的（既不弹性光顺也不局部重构）；在smoothing时，如果将边界设置为deforming，则边界上的节点会做类似内部节点的运动和生成；2)deforming的变形形式(1)面板中只能定义cylinder和plane类型的变形；如果边界复杂，则需要用DEFINE_GEOM来定义形状；①cylinder：2d：轴不能是z轴，其实成了一个矩形，定义的边界沿着两条直线变形；(2)对于边界沿直线变化，用layering时不需要定义deforming;但是沿曲线变化则需要用deforming的udf（如扇形网格中的圆弧）；3）变形原理第二章铺层2.1 参数设置Hight based:铺层形成的网格在同一层内高度相同；Ratio based:同一层网格高度可能不同，但是不同位置处不同层网格高度比相同（移动边界为斜直线或曲线时常常出现）；Split factor:相邻网格的高度为h_ideal,当网格高度h > (1 + split factor) * h_ideal 时，一层网格被分成两层网格；Collapse fator:当网格高度h < collapse factor * h_ideal时，该层网格与相邻网格层合并；2.2 运动形式1）静止stationary2)刚体运动rigid body motion3)变形deforming4)用户自定义user-defined2.3 区域优先级1）运动优先级静止区域:高；面区域：中；单元区域：低；2）以活塞向上运动为例活塞边界（wall_down）为面区域，fluid为单元区域；如果指定wall_down为rigid body，则网格在wall_down运动的地方进行铺层；如果指定fluid(或者interior和其他边界)为rigid body,指定wall_up为stationary,则网格在顶部进行铺层；2.4 边界条件的继承性第三章弹性光顺3.1 参数3.1.1 convergence tolerance（收敛容差）1）收敛容差和迭代步数，默认值在一般情况下都比较适用；2）在迭代过程中，节点当前一次迭代位移与第一次迭代位移之比作为收敛控制参数，当其小于设定的收敛容差时，迭代停止；在一定迭代步内不能达到规定的收敛容差，也需要停止迭代，防止死循环；3.1.2 spring constant factor弹性常数主要控制内部节点相对于运动边界的位移变形；范围0-1；默认为1，此时网格在活塞（运动边界）变形明显，远离活塞变形不明显，网格仅局部变化，插值过程少，但是网格拉伸扭曲大时，也会影响计算精度；为0时，运动边界几乎影响到所有边界，网格全局变化，需要全局插值，影响计算精度；3.1.3 laplace node relaxation节点松弛因子：内部节点位移对变形边界（deforming）节点位移的影响程度；范围0-1；默认1；先在dynamic mesh zones---meshing option---smoothing methord---laplace,然后在smoothing设置该参数才会起作用；为1，内部节点充分影响到变形边界节点运动；为0，不影响，相当于没有设置deforming变形；3.2 smoothing用于其它类型网格Smoothing一般用于三角形和四面体网格，但也可以用于其他类型的网格；设置：mesh method---setting---smoothing---parameters---element---all;第四章局部重构4.1 remeshing基本特点1）当网格的扭曲率或者尺寸超过用户规定范围时，网格被重构；2）适用于三角形和四面体网格，网格节点和数量都发生改变；3）remeshing一般和smoothing结合使用；4）适用于大位移大变形，比如转动和平动结合的运动；4.2 remeshing算法4.2.1 remeshing算法流程1）标记网格参数：Minimum length scale,maxmum length scale，maxmum cell skewness;标记出尺寸超出最小最大范围的网格，以及扭曲率超过给定值的网格；Size remeshing interval:每几个时间步进行一次网格重构；Mesh cell info可以查看当前网格的信息；2）标记的网格被删除形成空穴；3）求解器使用一系列重构方法，进行区域填充；4）将物理量在重构的网格上进行插值；4.2.2 算法1）面网格重构：(1)Region face remeshing:区域面网格重构；一般定义最小网格尺度是平均尺度的0.4倍，最大尺度是平均尺度的1.4倍；(2)local face remeshing:局部面网格重构；完全基于网格的扭曲率；不能重构那些同时属于多个变形区域的面网格；设置：首先mesh moethods---setting---选中local face---设置face skewness;然后dynamic mesh zones---meshing option---remeshing method---勾选local;(3)2.5Dface remeshing:2.5维度面网格重构；见例9，虽然是三维网格，但是重构仅仅涉及一对表面，故为2.5d；设置：Remeshing---2.5d---设置参数即可；对于2.5为cell hight没什么用；4.2.3 remeshing参数1）Size remeshing interval(SRI):通过网格尺寸控制网格重构的频率；每一个时间步，fluent都会根据扭曲率进行标记网格，并决定是否重构:如果扭曲率超标，进行重构；如果扭曲率不超标，且达到SRI的间隔，且最小最大尺寸超标，则也进行重构；网格扭曲率对计算的影响大于网格尺寸；SRI较大时，网格重构主要受扭曲率控制，SRI较小时，网格重构受扭曲率和尺寸共同控制；2）maxmum cell skewness二维:0.6-0.7；三维：0.85；4.3 其它4.3.1 时间步长动网格预览时的时间步长的选取：1）基于网格尺寸和运动速度：Deta_t < min_scale / max_velocity;4.3.2 算法技巧动网格的时间步长要足够小，每一次移动网格应该小于最小网格尺寸的一半；光顺方法的结合可以适当增加时间步长；如果移动幅度已知，最好将区域划分，减少计算；4.4 sizing function尺寸函数4.4.1 说明1）功能:尺寸函数用于控制重构过程中网格的分布，使网格变化更加均匀；尺寸函数在运动边界处约束网格，使其维持在一个较小的尺度，在远离运动边界处，逐步将其增大；运用尺寸函数时，fluent自动标记出网格尺度大于当地尺寸函数值的网格；尺寸函数仅用于网格标识，并不在重构过程中控制网格尺寸；2）fluen重构网格步骤（1）标记扭曲率大于maximum cell skewness的网格；(2)如果time = SRI * deta_t,标记出长度尺度小于minmum scale length和大于maxmum scale length的网格；(3)如果打开了sizing function，标记出不满足当地尺寸函数的网格；(4)对标记网格进行重构；(5)如果打开了smoothing(推荐打开),进行光顺；4.4.2 参数1）resolution：分辨率，控制背景网格的密度；variation：变化量，最大允许网格尺度的量度；Rate:变化率，网格成长率的量度；rate=0,意味着线性增长，rate越大，表明边界处网格生长越慢，内部网格生长越快；2）设置fluent会自动生成variation和rate,默认参数就行；4.4.3 技巧1）以等高线显示尺寸函数分布：初始化流场---输入：/solve/set/expert---keep temporary memory be freed?[no]yes(这一个打开，其它全为no)---graphics and animation---countours---adaption---background size function;4.4.4 原理1）[me]fluent将当前网格边长代入尺寸函数进行计算，如果大于标准值，则标记出来；标准值：由标准网格尺寸代入求解；标准尺寸deta_s：二维，与网格等面积的三角形网格边长；三维，等体积的四面体边长；第五章其它5.1 耦合运动6DOF5.1.1 概念用in-cylinder或者profile定义的运动一般是预知的；而6DOF求解器可以计算运动与流场耦合的运动5.2.2 设置1)原理6DOF是将每一个时间步的速度角速度进行积分得到当前位置和角度的；2）设置首先：在dynamic mesh中勾选6DOF---setting设置重力加速度；然后：rigid body---motion attributes---six DOF option勾中on；第十章网格实例10.1 油缸1）设置底边为rigid body:网格在底边生成和销毁；10.2 箱体移动1）设置fluid和箱体为rigid body，左右边界为stationary:网格在左右边界生成和销毁；10.3 子弹移动设置下面流域和子弹体为rigid body；最左右侧边界设为stationary;网格在左右侧产生和销毁；设置子弹体为rigid body:网格在子弹体左右产生和销毁（不利于计算）；10.4 扇形网格扇形网格铺层：定义右下边界为rigid body,用profile文件定义其转动角速度；定义内外圆弧为deforming，用udf中define_geom定义其上节点在圆上进行节点位置更新；①udf：sector.c: DEFINE_GEOM();10.5 油缸弹性Smoothing网格光顺；左右边界设置为deforming;下边界设置为rigid body;10.6 箱体振动Smoothing其他类型网格；Box设置为rigid body;10.7 投弹Remeshing + smoothing;设置边界层为regid body（边界层自动包含弹体边界）;之前出现负网格，是因为指定单体边界运动，而周围边界层网格为四边形不能remeshing;①如果用6DOF:弹体和fluid_bondary_layer都设置为rigid body,并且在fulid_bondary_layer打开6DOF时，选中passive;②udf：6DOF_missile_drop.c:DEFINE_SDOF_PROPERTIES()10.8 活塞Remeshing---region face + smoothing;底面设置rigid body,圆柱侧面设置为deforming---cylinder;10.9 2.5D设置内外表面为rigid body;用profil文件定义旋转，方向相反（设置一个转动即可）；设置上下表面为deforming---plane,上表面的meshing method中勾选remeshing，下表面的不勾选remeshing，因为下表面是由上表面拉伸过去的。

非结构动网格分区并行计算方法程兴华;刘巍;张理论【摘要】针对包含运动边界的非定常流动问题,基于弹簧近似法设计了一套非结构动网格分区并行计算流程,引入了METIS软件进行非结构网格二次剖分,研究了对接边界通信类型及其处理方法,基于消息传递并行编程模式实现了非结构动网格求解器的并行化.测试结果表明:该求解器具有较高的并行效率,网格变形模块对非结构动网格并行计算性能具有重要影响.%For parallel simulation of the unsteady flow field with moving boundary, a domain-decomposed computation procedure was designed based on the spring analogy method, and the METIS software was introduced to repartition the original grids.With the research of 1-to-1 interface communication styles and realization, the unstructured dynamic mesh solver was parallelized based on the message passing interface.The test shows that the solver has high parallel efficiency, and the module of mesh deforming has significant effect on the parallel performance.【期刊名称】《国防科技大学学报》【年(卷),期】2017(039)001【总页数】5页(P81-85)【关键词】非结构网格;动网格;区域分解;并行计算【作者】程兴华;刘巍;张理论【作者单位】国防科技大学海洋科学与工程研究院, 湖南长沙 410073;国防科技大学海洋科学与工程研究院, 湖南长沙 410073;国防科技大学海洋科学与工程研究院, 湖南长沙 410073【正文语种】中文【中图分类】O35动网格技术是解决多体分离、流固耦合、可变形飞行器、机翼气动弹性振动和生物仿生流等包含运动边界的非定常流动问题的关键技术[1-3]。

滑移网格模型和动网格模型计算比较对于涉及运动边界的仿真问题，在现有的的CFD软件平台中出现了诸如多参考系、混合平面、滑移网格、动网格技术，在这些技术中只有滑移网格和动网格是真正进行动态模拟可以给出运动边界的实时运动状况下的的瞬态流场。

本文主要介绍两种模型在计算时的一些差别。

1、数学模型上的区别滑移网格和动网格两者均采用守恒方程进行计算，但区别在于每步的体积计算，动网格第n+1步的体积Vn+1=Vn+dV/dt△t。

就是说：下一步的运动情况是由当前时间步的计算结果确定的，各个时间步的体网格更新是基于边界条件新的位置由Fluent自动来完成的。

而滑移网格模型的网格是刚性的第n+1步的体积n f i g，I .Ai；而滑移网格Vn+1=Vn 。

另外，动网格模型的控制体的体积导数为∑uu模型的控制体的体积导数为0。

在数据传递方面，滑移网格模型是通过滑移面（交界面）传递区域计算数据，而动网格模型直接通过变形网格（增加或减少网格）传递数据。

2、建模处理的区别滑移网格的计算模型比较复杂，要专门建一个滑移的区域和滑移相交面。

动网格技术的网格模型相对比较简单，不需要构建滑动区域与交界面，但动网格的运动需要profile文件或UDF函数驱动，网格在计算过程达到一定限度后自动进行重划分。

另外滑移网格模型对于对于网格的设置有许多限定条件，完全考虑需要花费很多时间。

动网格运用profile文件或UDF函数驱动的话运动形式可以更加的多样。

3、计算速度的比较采用同一计算机对同一问题的滑移网格模型和动网格模型进行模拟计算时，动网格模型在计算初期计算比较快，但随着计算步的增大，计算速度下降，主要是因为动网格模型在计算时不断对网格重新检查，当变形超过限定时会对网格重划分，占用了一部分时间，计算速度收网格重划分的影响，时有波动。

而滑移网格依靠滑移面交换数据，计算初期慢于动网格模型，在计算过程中计算速度比较稳定。

在滑移网格模型规模稍大于动网格的情况下，滑移网格模型表现较好的稳定性和较快的计算速度。

FLUENT动网格教程摘自/dvbbs/dispbbs.asp?boardid=61&id=1396 题记：在学习使用Fluent的时候，有不少朋友需要使用动网格模型(Dynamic Me sh Model)，因此，本版推出这个专题，进行大讨论，使大家在使用动网格时尽量少走弯路，更快更好地掌握；也欢迎使用过的版友积极参与讨论指导，谢谢！。

该专题主要包括以下的主要内容：§一、动网格的相关知识介绍；§二、以NACA0012翼型俯仰振荡实例进行讲解动网格的应用过程；§三、与动网格应用有关的参考文献；§四、使用动网格进行计算的一些例子。

§一、动网格的相关知识介绍有关动网格基础方面的东西，请具体参考FLUENT User’s Guide或FLUENT全攻略的相关章节，这里只给出一些提要性的知识要点。

1、简介动网格模型可以用来模拟流场形状由于边界运动而随时间改变的问题。

边界的运动形式可以是预先定义的运动，即可以在计算前指定其速度或角速度；也可以是预先未做定义的运动，即边界的运动要由前一步的计算结果决定。

网格的更新过程由FLUE NT 根据每个迭代步中边界的变化情况自动完成。

在使用动网格模型时，必须首先定义初始网格、边界运动的方式并指定参予运动的区域。

可以用边界型函数或者UDF定义边界的运动方式。

FLUENT 要求将运动的描述定义在网格面或网格区域上。

如果流场中包含运动与不运动两种区域，则需要将它们组合在初始网格中以对它们进行识别。

那些由于周围区域运动而发生变形的区域必须被组合到各自的初始网格区域中。

不同区域之间的网格不必是正则的，可以在模型设置中用FLUENT软件提供的非正则或者滑动界面功能将各区域连接起来。

注：一般来讲，在Fluent中使用动网格，基本上都要使用到UDF，所以你最好具备一定的C语言编程基础。

2、动网格更新方法动网格计算中网格的动态变化过程可以用三种模型进行计算，即弹簧近似光滑模型(spring-based smoothing)、动态分层模型（dynamic layering）局部重划模型（local remeshing）1）弹簧近似光滑模型原则上弹簧光顺模型可以用于任何一种网格体系，但是在非四面体网格区域（二维非三角形），最好在满足下列条件时使用弹簧光顺方法：（1）移动为单方向。

CAE联盟论坛精品讲座系列FLUENT中被动型动网格问题求解方案：6DOF主讲人：流沙 CAE联盟论坛—总版主利用CFD软件解决动网格问题，通常可分为以下两类：（1）主动型动网格主动型动网格问题通常指的是边界运动规律及运动状态已知，通常可由软件使用者通过函数或程序进行描述。

在程序计算过程中，求解器调用边界运动轨迹描述程序实现边界运动。

这类动网格例子很多，如各类泵、风扇等。

（2）被动型动网格还有一类动网格问题，其边界运动规律往往是未知的，常常需要通过计算边界上的力或力矩，以此来求取边界的运动。

在这类动网格计算设置中，网格变化规律难以预料，导致网格参数经常需要进行多次调整才能达到目的。

这类例子在现实中其实也很多，比如风力发电机的叶轮、水轮机等。

解决主动型动网格问题比较容易，利用CFD软件提供的动网格模拟能力很容易解决。

需要关注的地方是边界运动后，网格节点如何重新布置和生成。

如在FLUENT软件中，其动网格主要包括三种网格功能：弹簧光顺、动态层及网格重构。

利用网格重构功能几乎可以解决所有主动型动网格问题。

那被动型动网格问题怎么处理呢？一般来说，这类边界的运动都是由于内部流体对其压力所造成的，那么就涉及到力和力矩计算的问题。

对于这类问题，在FLUENT软件中可以采用6DOF 模型进行计算。

需要注意的是，以上所有类型动网格计算均建立在边界为刚性的情况下。

即不会计算由于流动产生的力的作用导致的边界变形。

若要计算边界变形，则需要采用流固耦合方法，利用固体求解器计算。

被动型动网格中的力和力矩均是压力对面的积分计算而来。

1、6DOF UDF宏在FLUENT中利用6DOF是需要定义UDF宏的。

该宏的定义形式如下：DEFINE_SDOF_PROPERTIES(name, properties, dt ,time ,dtime)函数中：Name：宏名称Real *properties：存储6DOF属性的数组Dynamic_Thread *dt：存储制定的动网格属性Real time：当前时间Real dtime：时间步长该UDF宏没有返回值。

Fluent UDF计算动网格区域的形心、转动惯量在使用动网格和重叠网格计算刚体的运动时，可能需要用到刚体的形心和三个轴的转动惯量。

一般来说，三维建模软件如Creo、SW、Spacecliam都可以直接计算出上述变量，但如果你拿到的只有一个fluent的case，阁下又该如何应对呢？1、形心（重心）对于密度均匀的物体，质心就是重心。

我们来看看质心的计算公式:\bar{x}_i=\iiint x_i\rm{d} v\\ 在fluent里， x_i 是网格三个方向的坐标，dv是网格体积。

用该公式，通过遍历网格可以很轻松地求出流体域的形心，但动网格区域都是没有网格的，所以无法直接应用上式。

观察到，虽然动网格区域没有网格，但它的边界我们是可以得到的，根据三维有界闭区域的高斯公式：\iiint\nabla\cdot \vec{F} \text{dv}=\oint \vec{F}\cdot \text d\vec{\text {S}}\\ 通过构造合适的向量场函数，形心公式可以转化为：\iiint\frac{\partial 0.5x_i^2}{\partialx_i}\text{dv}=\sum0.5x_i^2\cdot\text{d}\vec{\text{S}}\\ 应用上述环路积分可以通过遍历动网格区域的壁面就可以得到形心。

2. 转动惯量与上述思路相同，将转动惯量的体积分转化为环路积分，以Ixx为例：Ixx=\rho\iiint(y^2+z^2)\text{dv}=\text{fabs}\left(\fra c{1}{3}\rho\sum (y^3A[1]+z^3A[2])\right)\\ 其中 \rho 为你固体的材料密度，A为网格面的面积向量，可由以下宏得到：最后得到值是负的，因此需要加个fabs()求绝对值。

扣1送源代码。

Remeshing方法中的一些参数设定：Remeshing中的参数Minimum length scale和Maximum Length Scale，这两个参数你可以参考mesh scale info中的值，仅是参考,因为mesh scale info中的值是整个网格的评价值，设置的时候看一下动网格附近的网格和整个网格区域的大小比较，然后确定这两个参数，一般来讲，动网格附近的网格较密，这些值都比整体的小，所以在设置时通常设置为比mesh scale info中的Minimum length scale大一点，比Maximum Length Scale小一点。

以上是一般来讲的设置思路。

下面是我在NACA0012翼型动网格例子中的设置：Remeshing中的参数设定：为了得到较好的网格更新，本例在使用局部网格重新划分方法时,使用尺寸函数,也就是Remeshing+Must Improve Skewness+Size Function的策略。

将Minimum Length Scale及Maximum Length Scale均设置为0，为了使所有的区域都被标记重新划分；Maximum Cell Skewness（最大单元畸变)，参考Mesh Scale Info…中的参考值0.51，将其设定为0。

4,以保证更新后的单元质量；Size Remesh Interval（依照尺寸标准重新划分的间隔），将这个值设定为1，在FLUENT,不满足最大网格畸变的网格在每个时间步都会被标记,而后重新划分，而不满足最小，最大及尺寸函数的网格，只有在Current Time=（Size Remesh Interval）＊delta t的时候，才根据这些尺寸的标准标记不合格的单元进行重新划分,为了保证每步的更新质量，将其修改为1，就是每个时间都根据尺寸的标准标记及更新网格.Size Function Resolution(尺寸函数分辨率)，保持默认的3;Size Function Variation（尺寸函数变量）：建议使用一个小值，在0.1到0。

动网格模型（Dynamic Mesh ）一个简单的例子。

水在通道中流动如图所示，有一个入口(ab)，一个出口(cd)，一个可移动的挡板(fg)，挡板有一定的移动范围(ef,gh)。

本例研究简单动网格的应用，将会涉及到：（1） UDF 函数的读入以及要注意的问题 （2） 动网格参数的设定 （3） 动网格动画的设定一、 利用Gambit 建立计算模型1、 创建各控制点2、 由点连成直线3、 由线段创建面——流域4、 设定边界类型ab--速度入口（inlet ）；cd--压力出流（outlet ）； ef —可变形边界（form1）；hg —可变形边界（form2）； fg —移动边界（valve ） 5、 输出网格文件二、 利用fluent-2d 进行计算1、 读入mesh 文件File → Read → Case …2、 网格检查（注意最大长度和最小长度）3、 长度单位设定（cm ），并显示网格fg4、设置非定常求解器保持Unstready Formulation 的1st－Order Implict注意：目前动态网格计算只能用first－Order5、选择紊流模型6、材料设置为水7、边界条件：设置速度入口条件8、编译程序（1）读入和编辑udf函数Define→ User－Defined→ Functions→ Compiled…（a）在Source Files下，点击 Add…Select File 面板将会打开，选择valve.c（b）在Compiles UDF 面板下，点击Build注意：将会在FLUENT目录下产生一个缺省libudf文件夹。

如果工作目录下已有这个文件夹，请将删掉。

（c）点击Load注意：如果出现“找不到系统文件之类的提示”，则需要在计算机里装一个c语言的程序。

Valve.c的内容如下:#include <stdio.h>#include "udf.h"DEFINE_CG_MOTION(valve,dt,cg_vel,cg_omega,time,dtime){if(time<=0.5)cg_vel[0]= - 0.2;elsecg_vel[0]=0.0;}这是一个UDF文件，即用户自定义函数，可用来确定阀门的运动规律。

动网格技术题记：在学习使用Fluent的时候，有不少朋友需要使用动网格模型(Dynamic Mesh Model)，因此，本版推出这个专题，进行大讨论，使大家在使用动网格时尽量少走弯路，更快更好地掌握；也欢迎使用过的版友积极参与讨论指导，谢谢！该专题主要包括以下的主要内容：##1.动网格的相关知识介绍；##2.以NACA0012翼型俯仰振荡实例进行讲解动网格的应用过程；##3. 与动网格应用有关的参考文献；##4. 使用动网格进行计算的一些例子。

##1.动网格的相关知识介绍有关动网格基础方面的东西，请具体参考FLUENT User’s Guide 或FLUENT全攻略的相关章节，这里只给出一些提要性的知识要点。

1、简介动网格模型可以用来模拟流场形状由于边界运动而随时间改变的问题。

边界的运动形式可以是预先定义的运动，即可以在计算前指定其速度或角速度；也可以是预先未做定义的运动，即边界的运动要由前一步的计算结果决定。

网格的更新过程由FLUENT 根据每个迭代步中边界的变化情况自动完成。

在使用动网格模型时，必须首先定义初始网格、边界运动的方式并指定参予运动的区域。

可以用边界型函数或者UDF 定义边界的运动方式。

FLUENT 要求将运动的描述定义在网格面或网格区域上。

如果流场中包含运动与不运动两种区域，则需要将它们组合在初始网格中以对它们进行识别。

那些由于周围区域运动而发生变形的区域必须被组合到各自的初始网格区域中。

不同区域之间的网格不必是正则的，可以在模型设置中用FLUENT软件提供的非正则或者滑动界面功能将各区域连接起来。

注：一般来讲，在Fluent中使用动网格，基本上都要使用到UDF，所以你最好具备一定的C 语言编程基础。

2、动网格更新方法动网格计算中网格的动态变化过程可以用三种模型进行计算，即弹簧近似光滑模型(spring-based smoothing)、动态分层模型（dynamic layering）和局部重划模型（local remeshing）。