旋转知识点总结33641教学提纲

教案教学内容图形的旋转1、旋转：把一个图形绕某一点O转动一个角度的图形变换叫做旋转，其中点O叫做旋转中心，转动的角叫做旋转角。

对应点：如果图形上一点P经过旋转后，变为P’，那么这两个点叫做对应点。

旋转的三要素：旋转中心、旋转方向、旋转角2、旋转的性质：（1）对应点到旋转中心的距离相等。

（2）对应点与旋转中心所连线段的夹角等于旋转角。

（3）旋转后的两个图形全等。

例：如图，在边长为1的小正方形组成的网格中，△AOB的三个顶点均在格点上，点A、B的坐标分别为A（﹣2，3）、B（﹣3，1）．（1）画出坐标轴，画出△AOB绕点O顺时针旋转90°后的△A1OB1；（2）点A1的坐标为_________；（3）四边形AOA1B1的面积为_________．想一想：在第（1）题中，旋转中心与旋转角分别是什么？并且，你能得出哪些线段相等？哪些角相等呢？3、中心对称：把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形互相重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心。

推论：两个图形同时绕某一点旋转180°，旋转后的图形不变，那么这两个图形成中心对称。

4、中心对称的性质：（1）关于中心对称的两个图形是全等形；（2）关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分；（3）关于中心对称的两个图形，对应线段平行（或在同一直线上）且相等。

5、中心对称图形的判定：如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称。

6、坐标系中对称点的特征：（1）关于原点对称的点的特征：两个点关于原点对称时，它们的坐标的符号相反，即点P（X，Y）关于原点的对称点为点Q（-X，-Y）（2）关于X轴对称的点的特征：两个点关于X轴对称时，它们的坐标中X相等、Y符号相反，即点P（X，Y）关于原点的对称点为点Q（X，-Y）（3）关于Y轴对称的点的特征：两个点关于Y轴对称时，它们的坐标中Y相等、X符号相反，即点P（X，Y）关于原点的对称点为点Q（-X，Y）1。

旋转知识点总结旋转是一种常见的几何变换，它改变了物体的方向、位置和角度。

在计算机图形学、几何学、物理学和工程学等领域都有广泛的应用。

下面是对旋转相关知识点的一些总结：1. 旋转的定义：旋转是一种刚体运动，它将物体绕着特定的轴线转动一定的角度。

旋转由旋转中心、旋转轴和旋转角度三个要素来描述。

2. 旋转的方向：旋转可以是顺时针方向或逆时针方向。

在三维空间中，右手法则可以确定旋转的方向。

3. 旋转角度的表示：旋转角度可以用弧度制或角度制来表示。

弧度制是使用弧长与半径的比值来表示角度，角度制则是使用度数来表示。

4. 旋转矩阵：旋转可以用旋转矩阵来表示。

旋转矩阵是一个二维矩阵，其中每个元素表示旋转后的坐标与旋转前的坐标之间的关系。

5. 旋转轴的表示：旋转轴可以用向量来表示，向量的方向和大小决定了旋转轴的方向和旋转角度的大小。

6. 旋转的基本性质：旋转具有一些基本的性质，包括不变性、可逆性、可叠加性等。

这些性质对于旋转的应用非常重要。

7. 旋转的合成：旋转可以进行合成，即先进行一个旋转，再进行另一个旋转。

合成旋转可以通过旋转矩阵的乘法来实现。

8. 旋转的变换：旋转可以用来进行物体的变换，包括位置的变换、形状的变换和姿态的变换等。

旋转变换可以通过矩阵乘法来实现。

9. 欧拉角和四元数：欧拉角和四元数是常用的旋转表示方法。

欧拉角使用三个独立的角度来表示旋转，而四元数使用一个四维向量来表示旋转。

10. 旋转的应用：旋转在计算机图形学中有广泛的应用，包括三维建模、动画、物理模拟等。

旋转也被广泛应用于机器人学、飞行控制、游戏开发等领域。

11. 旋转的误差：由于测量误差和计算误差等原因，旋转变换可能会引入一定的误差。

为了减少误差，可以使用数值方法和优化算法等技术来进行旋转估计和校正。

12. 旋转的性能优化：旋转的计算通常比较复杂，对于大规模的数据和复杂的模型，旋转计算可能会成为性能瓶颈。

为了提高性能，可以使用并行计算、SIMD指令、快速算法等技术来加速旋转计算。

旋转是数学中的一个重要概念，初中数学九年级的旋转知识点主要涉及到平面上的图形的旋转。

下面是对旋转知识点的详细总结。

一、旋转的基本概念旋转是指将一个平面上的图形绕着一个圆心旋转一定角度后得到的新图形。

旋转可以分为顺时针旋转和逆时针旋转两种。

二、旋转的基本要素1.旋转中心：旋转时固定不动的点，通常用O表示。

2.旋转角度：图形绕旋转中心旋转的角度，通常用θ表示。

3.旋转方向：图形绕旋转中心旋转的方向，可为顺时针或逆时针。

三、旋转的基本性质1.旋转前后的对应关系：旋转前后，图形上的各个点在对应的位置。

2.旋转角度的正负性：顺时针旋转时，旋转角度为负值；逆时针旋转时，旋转角度为正值。

3.旋转的复合性：对一个图形连续旋转两次，相当于对这个图形进行一次旋转，旋转角度为两次旋转角度的和。

四、旋转的具体操作1.给定旋转中心和旋转角度，旋转一个点：将给定点与旋转中心连接，然后以旋转角度为自由度，将连接线旋转相应角度，确定旋转点的新位置。

2.给定旋转中心和旋转角度，旋转一条线段：将给定线段上的两个端点分别旋转，得到旋转线段的两个端点，然后连接这两个点得到旋转线段。

3.给定旋转中心和旋转角度，旋转一个多边形：将多边形上的各个顶点依次旋转，得到旋转多边形的各个顶点，然后连接这些点得到旋转多边形。

五、旋转的性质与判定1.旋转过程中的不变性：旋转前后，图形的形状、大小和角度不变。

2.图形的旋转对称性：图形相对于旋转中心旋转一定角度后，与原图形完全重合。

3.旋转角度的关系：相交的两个线段，经过旋转后的线段之间的夹角等于它们旋转前的夹角。

4.旋转中心判定：判断一个点关于一个给定点旋转一定角度后的位置。

六、旋转的运用1.添加旋转对称部分：先将一个图形旋转一定角度，然后与旋转前的图形拼接，可以得到一个具有旋转对称性的图形。

2.图形的旋转判定：给定一个图形，根据旋转的要素和性质，判断该图形能否通过旋转得到另一个图形。

3.旋转变换的应用：在解决实际问题时，可以运用旋转变换来简化问题的处理过程，比如地球绕太阳的自转等。

旋转知识点总结旋转知识点归纳知识点1：旋转的定义及其有关概念在平面内，将一个图形绕一个定点O沿某个方向转动一个角度，这样的图形运动称为旋转。

定点O称为旋转中心，转动的角称为旋转角。

如果图形上的点P经过旋转到点P'，那么这两个点叫做这个旋转的对应点。

如图1，线段AB绕点O顺时针转动90度得到AB'，这就是旋转，点O就是旋转中心，∠BOB'和∠AOA'都是旋转角。

说明：旋转的范围是在平面内旋转，否则有可能旋转为立体图形，因此“在平面内”这一条件不可忽略。

决定旋转的因素有三个：一是旋转中心；二是旋转角；三是旋转方向。

知识点2：旋转的性质由旋转的定义可知，旋转不改变图形的大小和形状，这说明旋转前后的两个图形是全等的。

由此得到如下性质：⑴经过旋转，图形上的每一点都绕旋转中心沿相同方向转动了相同的角度，对应点的排列次序相同。

⑵任意一对对应点与旋转中心的连线所成的角都是旋转角。

⑶对应点到旋转中心的距离相等。

⑷对应线段相等，对应角相等。

例1：如图2，D是等腰Rt△ABC内一点，BC是斜边，如果将△ADB绕点A逆时针方向旋转到△ADC的位置，则∠ADD'的度数是（）。

分析：抓住旋转前后两个三角形的对应边相等、对应角相等等性质，本题就很容易解决。

由△ADC是由△ADB旋转所得，可知△ADB≌△ADC，∴AD=AD'，∠DAB=∠D'AC，∵∠DAB+∠___，∴∠D'AC+∠___，∴∠ADD'=45，故选D。

评注：旋转不改变图形的大小与形状，旋转前后的两个图形是全等的，紧紧抓住旋转前后图形之间的全等关系，是解决与旋转有关问题的关键。

知识点3：旋转作图1.明确作图的条件：（1）已知旋转中心；（2）已知旋转方向与旋转角。

2.理解作图的依据：（1）旋转的定义：在平面内，将一个图形绕一个定点O沿某个方向转动一个角度的图形变换叫做旋转；（2）旋转的性质：经过旋转，图形上的每一点都绕旋转中心沿相同的方向转动了相同的角度，任意一对对应点与旋转中心的连线所组成的角都是旋转角，对应点到旋转中心的距离相等。

旋转现象知识点总结1. 旋转现象的基本原理旋转现象基本原理是物体围绕自身中心轴进行旋转运动。

这种运动形式是刚体运动的一种，而刚体的旋转运动是以固定点为轴心，刚体的各点都做圆周运动的运动形式。

在旋转中，刚体上所有点都作圆周运动，而且速度和加速度都不相同。

这种运动可以通过角位移、角速度和角加速度来描述。

角位移表示旋转的角度大小，角速度表示旋转的快慢，而角加速度则表示旋转的加速或减速程度。

在物理学中，旋转现象的基本原理受到角动量守恒定律的影响。

根据角动量守恒定律，如果没有外力矩作用，旋转态的角动量守恒，即角动量大小和方向保持不变。

这就意味着在旋转过程中，如果没有外力矩的作用，物体的角速度和角动量会保持不变。

除了角动量守恒，旋转现象还受到转动惯量的影响。

转动惯量是描述物体抵抗转动的能力，它和物体的形状、质量分布有关。

转动惯量的大小和形状、质量分布都有关系，例如，长杆的转动惯量要比球体的小。

转动惯量的大小影响着物体旋转的难易程度，而且其大小还决定了物体在旋转中的动能大小。

2. 旋转现象的应用旋转现象在工程学、医学、航天航空等领域都有着广泛的应用。

在工程学领域，旋转现象被广泛应用于机械系统中，例如发动机、泵、风力发电机等设备。

这些设备都是通过旋转来实现能量转换和传递的。

旋转还在制造业中用于车床、铣床等机床设备，加工工件时通过旋转实现切削加工。

此外，旋转还在交通运输行业中应用广泛，例如汽车、飞机、船舶等交通工具都需要通过发动机和车轮的旋转来实现运动。

在医学方面，旋转现象也有着重要的应用。

例如，MRI（核磁共振成像）技术就是基于旋转原理的一种诊断技术，它通过物质原子核的旋转运动产生信号，来获取人体组织的影像。

此外，旋转还在手术器械、假肢等医疗器械中有着广泛的应用。

在航天航空领域，旋转现象也被广泛应用于飞行器的姿态控制、推进系统等方面。

例如，飞行器通过调整旋转状态来实现姿态控制，通过发动机旋转来产生推进力。

此外，还有卫星、航天飞行器等载具通过旋转来调整轨道、实现定位和导航等任务。

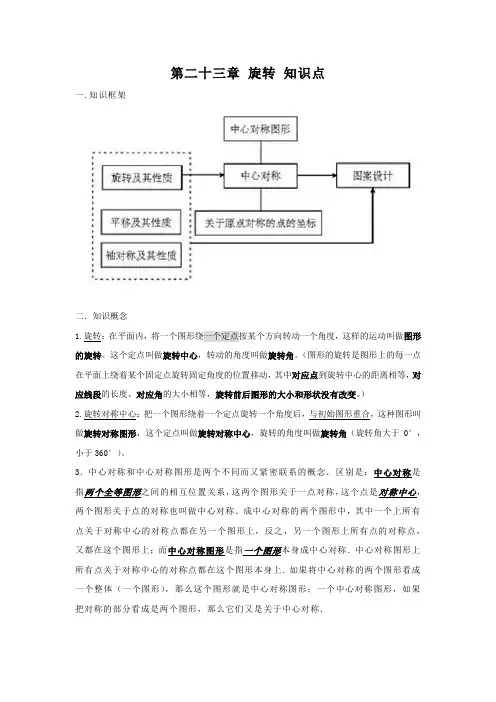
第二十三章旋转知识点一.知识框架二．知识概念1.旋转：在平面内，将一个图形绕一个定点按某个方向转动一个角度，这样的运动叫做图形的旋转。

这个定点叫做旋转中心，转动的角度叫做旋转角。

（图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，对应线段的长度、对应角的大小相等，旋转前后图形的大小和形状没有改变。

）2.旋转对称中心：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角（旋转角大于0°，小于360°）。

3．中心对称和中心对称图形是两个不同而又紧密联系的概念．区别是：中心对称是指两个全等图形之间的相互位置关系，这两个图形关于一点对称，这个点是对称中心，两个图形关于点的对称也叫做中心对称．成中心对称的两个图形中，其中一个上所有点关于对称中心的对称点都在另一个图形上，反之，另一个图形上所有点的对称点，又都在这个图形上；而中心对称图形是指一个图形本身成中心对称．中心对称图形上所有点关于对称中心的对称点都在这个图形本身上．如果将中心对称的两个图形看成一个整体（一个图形），那么这个图形就是中心对称图形；一个中心对称图形，如果把对称的部分看成是两个图形，那么它们又是关于中心对称．4.中心对称图形与中心对称：中心对称图形：如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形。

中心对称：如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称。

5.把一个图形绕着某一点旋转180°，如果它能与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心，这两个图形的对应点叫做关于中心的对称点。

6.中心对称的性质：关于中心对称的两个图形是全等形。

关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。

旋转图形知识点总结一、旋转的基本概念1. 旋转的定义：旋转是指把一个图形绕着一个固定的点旋转一定的角度，使得原图形和旋转后的图形具有相同的形状和大小。

2. 旋转的中心：旋转的中心是一个固定的点，图形绕着这个点进行旋转。

3. 旋转角度：旋转角度是指图形经过旋转后，原始图形和旋转后的图形之间的角度差。

通常用度数来表示旋转角度。

4. 旋转方向：旋转方向是指图形在旋转过程中的运动方向，可以是顺时针方向或者逆时针方向。

二、旋转图形的特点1. 旋转图形的不变性：当一个图形绕着一个固定的点进行旋转时，它的形状和大小不会发生改变，只是方向和位置发生了变化。

2. 旋转图形的对称性：旋转图形和原始图形之间具有一定的对称性，通过旋转可以得到图形的对称图形。

三、旋转的基本操作1. 如何进行旋转：要进行图形的旋转操作，首先需要确定旋转的中心点和旋转的角度，然后按照旋转规则进行操作。

2. 旋转后的图形：根据旋转的角度和方向，可以得到旋转后的图形，通常可以通过计算或者直接作图的方式来得到旋转后的图形。

四、旋转图形的相关性质和定理1. 判断旋转对称图形：通过观察图形的对称性，可以判断出一个图形是否具有旋转对称性。

2. 旋转对称图形的性质：旋转对称图形具有一些特殊的性质，比如对称轴上的点经过旋转后还是对称轴上的点。

3. 旋转变换的相关定理：旋转变换有一些相关的定理，比如旋转变换是一种保持长度和角度不变的变换。

五、常见的旋转图形1. 旋转正多边形：正多边形是一种常见的图形，在进行旋转操作时，可以通过旋转规则来得到旋转后的正多边形。

2. 旋转圆形：圆形是一种特殊的图形，通过旋转操作可以得到不同位置和方向的圆形。

3. 旋转长方形和正方形：长方形和正方形在进行旋转操作时，可以根据旋转的规则来得到旋转后的图形。

六、应用举例1. 旋转图形的应用：旋转图形不仅在几何学中有应用，还可以在实际生活中得到应用，比如在工程设计、建筑设计等领域中可以通过旋转图形来实现设计需求。

旋转的知识点总结一、旋转的基本概念1. 旋转的定义旋转是物体绕着某一点或某一条轴心进行的运动。

在旋转运动中，物体的各个部分绕着轴心或转动中心做圆周运动，同时保持相对位置不变。

2. 旋转的基本术语（1）轴心：旋转的固定点或固定轴。

（2）转动中心：物体绕轴心旋转时，轴心在物体外部的点称为转动中心。

（3）转动轴：绕着轴心旋转的直线称为转动轴。

（4）转动惯量：物体绕轴心旋转时所具有的惯性度量。

（5）角速度：描述物体旋转的速度大小和方向的物理量。

（6）角加速度：描述物体旋转的加速度大小和方向的物理量。

二、旋转的数学描述1. 转动角度旋转的大小通常用角度或弧度来描述。

角度是一种常用的角度单位，表示一个圆心角所占的平面角度为360度。

弧度是一种物理角度单位，表示一个圆心角所对应的圆弧长度等于半径的长度。

2. 旋转的向量描述在物理学中，旋转通常被描述为一个向量。

这个向量被称为“角速度向量”，它表示物体垂直于转动平面的旋转方向和速度大小。

3. 旋转的运动方程旋转的运动方程描述了物体在旋转运动中的运动规律。

通常包括角速度、转动半径、转动角度、角加速度等物理量之间的关系。

三、旋转的力学原理1. 物体的转动惯量转动惯量是描述物体绕轴心旋转时所具有的惯性度量。

转动惯量取决于物体的形状和质量分布。

通常用符号I表示，单位是千克·米平方。

2. 物体的角动量物体的角动量是描述物体旋转运动状态的物理量。

它与物体的转动惯量和角速度有关。

通常用符号L表示，单位是千克·米平方/秒。

3. 牛顿第二定律在旋转运动中的应用牛顿第二定律（F=ma）在旋转运动中的形式为τ=Iα，其中τ表示力矩，I表示物体的转动惯量，α表示角加速度。

这个公式描述了物体在受力作用下的转动运动规律。

四、旋转的应用1. 刚体旋转刚体旋转是刚体围绕轴心或转动中心进行的旋转运动。

刚体旋转的应用广泛，包括汽车的转向、水泵的旋转、风车的旋转等。

2. 陀螺运动陀螺是一种常见的旋转运动装置，可以应用于导航、稳定、测量等领域。

旋转知识点总结一、旋转1.旋转的概念：在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转.这个定点叫做旋转中心，转动的角叫做旋转角.2.旋转三要素：①旋转中心；②旋转方向；③旋转角度3.旋转的性质：（1）对应点到旋转中心的距离相等；（2）对应点与旋转中心所连线段的夹角等于旋转角（3）旋转前后的图形全等.4.网格中的旋转：①确定旋转中心、旋转方向及旋转角；②找原图形的关键点；③连接关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到各关键点的对应点；④按原图形依次连接各关键点的对应点,得到旋转后的图形.二、中心对称1.中心对称：中心对称是指把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称.2.中心对称图形：把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形.三、尺规作图（旋转）1.作图方法：以旋转点为中心找出各点旋转对应角度后得到的对应点，再顺次连接得到旋转后的图形.四、关于原点对称的点的坐标1.关于原点对称后点的坐标：若对称前的点坐标为（x，y），那么对称后的点坐标为（－x，－y）.五、旋转90°的点的坐标1.绕原点旋转90°后的点的坐标：（1）顺时针旋转：若对称前的点坐标为（x，y），那么对称后的点坐标为（y，－x）.（2）逆时针旋转：若对称前的点坐标为（x，y），那么对称后的点坐标为（－y，x）.六、常见全等模型（手拉手模型）1.手拉手模型：两个等腰三角形共顶点时，就有全等三角形.结论：（1）△ABE≌△DBC（2）AE=DC（3）AE交DC于点H，∠AHD＝∠ABD（4）HB平分∠AHC七、常见全等模型（半角模型）1.半角模型：共顶点的两个角度，当一个角等于另一个角的一半时，可以将三角形旋转，得到全等三角形.结论：（1）△AEF≌△AGF（2）EF=BF+DEDA CB八、常见全等模型（对角互补四边形旋转模型）1.对角互补四边形旋转模型：四边形对角互补且有一组邻边相等时，可以将三角形旋转，得到等腰三角形或正方形.。

旋转的知识点归纳总结旋转的知识点主要包括旋转的基本概念、旋转的运动规律、旋转的动力学和静力学分析、以及旋转在工程技术中的应用等方面。

本文将对这些知识点进行系统归纳总结，希望能够帮助读者更全面地理解旋转的相关概念和原理。

一、旋转的基本概念1. 旋转的定义旋转是物体在围绕某一点或轴线上旋转的运动形式。

在旋转过程中，每一个点都有一个不同的速度和加速度，这是与直线运动的显著区别。

在旋转过程中，我们通常用角度来描述物体的位置和方向。

2. 旋转的基本量在描述旋转运动时，我们通常会涉及到一些基本量，比如角度、角速度和角加速度。

角度用来描述物体在旋转过程中沿着轴线或者绕着某一点旋转的程度，通常用弧度或者度来表示。

角速度用来描述物体在旋转过程中单位时间内转过的角度，通常用弧度/秒或者度/秒来表示。

角加速度用来描述物体在旋转过程中单位时间内角速度的变化，通常用弧度/秒^2或者度/秒^2来表示。

3. 旋转的方向在旋转过程中，我们通常也会关注物体旋转的方向。

旋转的方向通常可以用飞轮定则来描述，即如果按照顺时针方向旋转，则对应的角速度和角加速度都为正值，如果按照逆时针方向旋转，则对应的角速度和角加速度都为负值。

二、旋转的运动规律1. 旋转平衡在旋转过程中，物体可能存在平衡和不平衡的情况。

当物体的旋转力矩和惯性矩平衡时，物体就处于旋转平衡状态；否则，物体就处于旋转不平衡状态。

旋转平衡是旋转运动稳定进行的前提，因此对于旋转平衡的分析和判断是非常重要的。

2. 旋转的动力学在旋转运动中，我们通常会涉及到力矩、惯性矩和角加速度等概念。

力矩用来描述物体在旋转过程中受到的力的作用，通常用力和力臂的乘积来表示。

惯性矩用来描述物体在旋转过程中惯性对旋转运动的阻碍程度，通常用质量和半径的平方的乘积来表示。

角加速度用来描述物体在旋转过程中单位时间内角速度的变化，通常用力矩和惯性矩的比值来表示。

根据牛顿第二定律，力矩等于惯性矩乘以角加速度，即力矩=惯性矩*角加速度。