近代数学小波计算题答案

现代数学基础习题解答1 集合与映射-51 证明R ~)1,1(-，其中R 为实数集。

证明 ： 设R 11x x f ⨯-∈⊆)},(|{，()f y x ∈,当且仅当21x xy -=，容易验证，f 是双射。

所以R ~)1,1(-。

2 证明：如果M 是无限集，A 是可数集合，则A M M ⋃~。

证明： 不失一般性，设Φ=⋂A M 。

由于M 是无限集，故M 存在可数子集，设M '是M 的可数子集，则()M M M M '⋃'-=，()()A M M M A M ⋃'⋃'-=⋃，且()Φ='⋂'-M M M ，()()Φ=⋃'⋂'-A M M M ，于是A M ⋃'是可数集合，记{} ,,,,21n m m m M ='，{},,,,21n a a a A M =⋃'， 令A M M f ⋃→:为：若Φ='-M M ，()n n a m f =；若Φ≠'-M M ()⎩⎨⎧'-∈==M M x xm x a x f nn,,，易知f 为双射，故A M M ⋃~。

3 记区间[]1,0中全体无理数所构成集合为D ，证明：[]1,0~D 。

证明： 由于D 是无限集，故D 存在可数无线集，记为D '。

令[]Q Q ⋂='1,0，于是()D D D D '⋃'-=，[]()()Q D D D Q D '⋃'⋃'-='⋃=1,0，且()Φ='⋂'-D D D ，()()Φ='⋃'⋂'-Q D D D ，而且Q D '⋃'为可数集，记{} ,,,,21n d d d D ='，{},,,,21n q q q Q D ='⋃'， 令[]1,0:→D f 为：()⎩⎨⎧'-∈==D D x xd x q x f nn,,，易知f 为双射，故[]1,0~D 。

似，因此系数c 可以反映这种波形的相关程度；步骤3: 把小波向右移，距离为 ，得到的小波函数为 ，然后重复步骤1和2。

再把小波向右移，得到小波 ，重复步骤1和2。

按上述步骤一直进行下去，直到信号 结束；步骤4: 扩展小波 ，例如扩展一倍，得到的小波函数为 ；步骤5: 重复步骤1~4。

五、阐述多分辨分析的思想并给出MALLAT 算法的表达式。

（10分）答：Meyer 于1986年创造性地构造出具有一定衰减性的光滑函数，其二进制伸缩与平移构成L2 (R )的规范正交基，才使小波得到真正的发展。

1988年S.Mallat 在构造正交小波基时提出了多分辨分析（Multi-Resolution Analysis ）的概念，从空间的概念上形象地说明了小波的多分辨率特性， 将此之前的所有正交小波基的 构造法统一起来，给出了正交小波的构造方法以及正交小波变化的快速算法，即Mallat 算法。

Mallat 算法在小波分析中的地位相当于快速傅立叶变换算法在经典傅立叶分析中的地位。

定义：空间 L2 ( R) 中的多分辨分析是指 L2 ( R) 满足如下性质的一个空间序列Z ∈j j }{V ：（1）单调性：ΛΛ⊂⊂⊂⊂-101V V V ；（2）逼近性：)(},0{2R L V V j Zj j Zj ==∈∈Y I ；（3）伸缩性：1)2()(+∈⇔∈j j V t f V t f ；（4）平移不变性：j j V t f V t f ∈-⇒∈)1()(，Z k ∈∀；（5）存在函数0)(V t g ∈，使得Z k k)}-{g(t ∈构成0V 的Riesz 基。

满足上述个条件的函数空间集合成为一个多分辨分析， 如果)(t g 生成一个多 分辨分析，那么称)(t g 为一个尺度函数。

关于多分辨分析的理解，我们在这里以一个三层的分解进行说明，其小波分解树如图所示。

从图可以明显看出，多分辨分析只是对低频部分进行进一步分解，而高 频部分则不予以考虑。

小波变换的数学基础及原理解析小波变换是一种信号分析方法，可以将信号分解成不同频率的小波成分，从而揭示信号的局部特征。

它在信号处理、图像处理、数据压缩等领域有着广泛的应用。

本文将从数学基础和原理解析两个方面来介绍小波变换。

一、数学基础小波变换的数学基础主要包括信号的时频分析和小波函数的定义。

在时频分析中，我们希望能够同时观察到信号的时域特征和频域特征。

然而，传统的傅里叶变换只能提供信号的频域信息，无法提供时域信息。

小波变换通过引入尺度参数，可以在时频域上同时进行分析。

小波函数是小波变换的基础，它是一种特殊的函数形式。

与傅里叶变换中的正弦函数和余弦函数不同，小波函数具有局部化的特点，即在时域上具有有限长度。

这种局部化的特性使得小波函数能够更好地描述信号的局部特征。

二、原理解析小波变换的原理可以通过连续小波变换和离散小波变换来解析。

连续小波变换是将信号与小波函数进行内积运算，得到信号在不同尺度和位置上的小波系数。

离散小波变换是连续小波变换的离散形式，通过对信号进行采样和离散化，得到离散的小波系数。

在连续小波变换中，小波函数是一个连续的函数，可以用于对连续信号的分析。

而在离散小波变换中，小波函数是一个离散的序列，可以用于对离散信号的分析。

离散小波变换通过多级滤波和下采样的方式来实现信号的分解和重构。

小波变换的核心思想是多尺度分析，即对信号进行多次分解，每次分解都将信号分解成低频部分和高频部分。

低频部分包含信号的整体特征，高频部分包含信号的细节特征。

通过不断分解和重构，可以得到信号在不同尺度上的小波系数，从而揭示信号的局部特征。

小波变换还具有一些重要的性质，如平移不变性、尺度不变性和能量守恒性。

平移不变性表示信号的平移对小波系数没有影响；尺度不变性表示信号的尺度变化对小波系数的影响是可逆的；能量守恒性表示信号的能量在小波分解和重构过程中是守恒的。

三、应用领域小波变换在信号处理、图像处理、数据压缩等领域有着广泛的应用。

一年级数学金钱练习题及答案
1. 小波有10元，他花了4元买了一个玩具车，剩下多少钱？
答案：6元
2. 丽丽有5元，她想买一本故事书，需要花费3元，还剩下多少钱？
答案：2元
3. 小明去超市买水果，他买了2个苹果，每个苹果价格是2元，还
买了3个橙子，每个橙子价格是1元，他一共花了多少钱？
答案：(2元/个 × 2个) + (1元/个 × 3个) = 4元
4. 小张有3枚1元硬币，他想买一个冰淇淋，需要支付多少钱？
答案：3元
5. 妈妈给小明零钱一共10元，他去买了一本绘本，需要支付8元，还剩下多少钱？
答案：10元 - 8元 = 2元
6. 小红家有一张5元的纸币，她想买一个小笔记本，需要支付多少钱？
答案：5元
7. 小李去超市购物，他买了一盒饼干，价格是2元，还买了一瓶果汁，价格是3元，他一共花了多少钱？
答案：2元 + 3元 = 5元
8. 小王有一张10元的纸币，他买了一包糖果，价格是6元，还剩
下多少钱？
答案：10元 - 6元 = 4元
9. 小燕家有10元和5元的纸币各一张，她想买一本漫画书，需要
支付多少钱？
答案：10元 + 5元 = 15元
10. 小刚有10元，他买了一支铅笔，价格是3元，买了一个橡皮擦，价格是1元，还剩下多少钱？
答案：10元 - 3元 - 1元 = 6元。

一、叙述小波分析理论发展的历史和研究现状答：傅立叶变换能够将信号的时域和特征和频域特征联系起来,能分别从信号的时域和频域观察,但不能把二者有机的结合起来;这是因为信号的时域波形中不包含任何频域信息,而其傅立叶谱是信号的统计特性,从其表达式中也可以看出,它是整个时间域内的积分,没有局部化分析信号的功能,完全不具备时域信息,也就是说,对于傅立叶谱中的某一频率,不能够知道这个频率是在什么时候产生的;这样在信号分析中就面临一对最基本的矛盾——时域和频域的局部化矛盾;在实际的信号处理过程中,尤其是对非常平稳信号的处理中,信号在任一时刻附近的频域特征很重要;如柴油机缸盖表明的振动信号就是由撞击或冲击产生的,是一瞬变信号,单从时域或频域上来分析是不够的;这就促使人们去寻找一种新方法,能将时域和频域结合起来描述观察信号的时频联合特征,构成信号的时频谱,这就是所谓的时频分析,亦称为时频局部化方法;为了分析和处理非平稳信号,人们对傅立叶分析进行了推广乃至根本性的革命,提出并开发了一系列新的信号分析理论：短时傅立叶变换、时频分析、Gabor 变换、小波变换Randon-Wigner变换、分数阶傅立叶变换、线形调频小波变换、循环统计量理论和调幅—调频信号分析等;其中,短时傅立叶变换和小波变换也是因传统的傅立叶变换不能够满足信号处理的要求而产生的;短时傅立叶变换分析的基本思想是：假定非平稳信号在不同的有限时间宽度内是平稳信号,从而计算出各个不同时刻的功率谱;但从本质上讲,短时傅立叶变换是一种单一分辨率的信号分析方法,因为它使用一个固定的短时窗函数,因而短时傅立叶变换在信号分析上还是存在着不可逾越的缺陷;小波变换是一种信号的时间—尺度时间—频率分析方法,具有多分辨率分析Multi-resolution的特点,而且在时频两域都具有表征信号局部特征的能力,使一种窗口大小固定不变,但其形状可改变,时间窗和频率窗都可以改变的时频局部化分析方法;小波变换在低频部分具有较高的频率分辨率和较低的时间分辨率;在高频部分具有较高的时间分辨率和较低的频率分辨率,很适合于探测正常信号中夹带的瞬态反常现象并展示其成分,所以被誉为分析信号的显微镜;小波分析最早应用在地震数据压缩中, 以后在图像处理、故障诊断等方面取得了传统方法根本无法达到的效果. 现在小波分析已经渗透到了自然科学、应用科学等方面, 小波分析已成为国际研究热点. 无论是傅里叶分析还是小波分析均以线性变换为基础, 按非线性傅立叶分析提出了非线性小波变换, 这种非线性小波变换处理非线性问题更为有效.二、分析小波的基本定义答：小波Wavelet 这一术语,顾名思义,“小波”就是小的波形;所谓“小”是指它具有衰减性；而称之为“波”则是指它的波动性,其振幅正负相间的震荡形式;与Fourier 变换相比,小波变换是时间空间频率的局部化分析,它通过伸缩平移运算对信号逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节,解决了Fourier 变换的困难问题,成为继Fourier 变换以来在上的重大突破;有人把小波变换称为“数学显微镜”;小波分析方法是一种窗口大小即窗口面积固定但其形状可改变,时间窗和频率窗都可改变的时频局部化分析方法,即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率;正是这种特性,是小波变换具有对信号的自适应性;小波分析被看成调和分析这一数学领域半个世纪以来的工作结晶,已经和必将广泛地应用于信号处理、图像处理、量子场论、地震勘探、语音识别与合成、音乐、雷达、CT 成像、彩色复印、流体湍流、天体识别、机器视觉、机械故障诊断与监控、分形以及数字电视等科技领域;原则上讲,传统上使用傅立叶分析的地方,都可以用小波分析取代;小波分析优于傅立叶变换的地方是,它在时域和频域同时具有良好的局部化性质;设()()R L t 2∈ψ()R L 2表示平方可积的实数空间,即能量有限的信号空间,其傅立叶变换为()ωψ∧;()ωψ∧满足允许条件Admissible Condition ：时,我们称()t ψ为一个基本小波或母小波Mother Wavelet;将母函数()t ψ经伸缩和平移后,就可以得到一个小波序列;对于连续的情况,小波序列为其中,a 为伸缩因子,b 为平移因子;对于离散的情况,小波序列为对于任意的函数()()R L t f 2∈的连续小波变换为其逆变换为小波变换的时频窗口特性与短时傅立叶的时频窗口不一样;其窗口形状为两个矩形[]⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∆+±⎪⎭⎫ ⎝⎛∆-±⨯∆+∆-∧∧a a a b a b /,/,00ψωψωψψ,窗口中心为()a b /,0ω±,时窗宽和频窗宽分别为ψ∆a 和a /∧∆ψ;其中b 仅仅影响窗口在相平面时间轴上的位置,而a 不仅影响窗口在频率轴上的位置,也影响窗口的形状;这样小波变换对不同的频率在时域上的取样步长是调节性的：在低频时小波变换的时间分辨率较差,而频率分辨率较高；在高频时小波变换的时间分辨率较高,而频率分辨率较低,这正符合低频信号变化缓慢而高频信号变换迅速的特点;这便是它优于经典的傅立叶变换与短时傅立叶变换的地方;从总体上来说,小波变换比短时傅立叶变换具有更好的时频窗口特性;三、小波分析是傅立叶分析思想方法的发展与延拓,二者相辅相成,试对小波分析和傅立叶变换进行比较答：小波分析是傅立叶分析思想的发展与延拓,它自产生以来,就一直与傅立叶分析密切相关,他的存在性证明,小波基的构造以及结果分析都依赖于傅立叶分析,二者是相辅相成的,两者主要的不同点：1、傅立叶变换实质是把能量有限信号ft 分解到以{expjωt}为正交基的空间上去；小波变换的实质是把能量有限信号ft 分解到W-j 和V-j 所构成的空间上去的;2、傅立叶变换用到的基本函数只有sinωt,cosωt,expjωt,具有唯一性；小波分析用到的函数即小波函数则具有多样性,同一个工程问题用不同的小波函数进行分析有时结果相差甚远;小波函数的选用是小波分析运用到实际中的一个难点问题也是小波分析研究的一个热点问题,目前往往是通过经验或不断地试验对结果进行对照分析来选择小波函数;3、在频域分析中,傅立叶变换具有良好的局部化能力,特别是对于那些频率成分比较简单的确定性信号,傅立叶变换很容易把信号表示成各频率成分的叠加和的形式,如sinω1t+ω2t+ω3t,但在时域中傅立叶变换没有局部化能力,即无法从ft 的傅立叶变换中看出ft 在任一时间点附近的性态;事实上,Fwdw 是关于频率为w 的谐波分量的振幅,在傅立叶展开式中,它是由ft 的整体性态所决定的;4、在小波分析中,尺度a 的值越大相当于傅立叶变换中w 的值越小;5、在短时傅立叶变换中,变换系数Sω,τ主要依赖于信号在τ-δ,τ+δ片段中的情况,时间宽度是2δ因为δ是由窗函数gt 唯一确定的,所以2δ是一个定值;在小波变换中,变换系数Wfa,b 主要依赖于信号在b-aΔφ,b+aΔφ片断中的情况,时-间宽度是2aΔφ,该时间的宽度是随尺度a 变化而变化的,所以小波变换具有时间局部分析能力;6、若用信号通过滤波器来解释,小波变换与短时傅立叶变换不容之处在于：对短时傅立叶变换来说,带通滤波器的带宽Δf 与中心频率f 无关；相反小波变换带通滤波器的带宽Δf 则正比于中心频率f;四、阐述多分辨分析的思想并给出MALLAT 算法的表达式答：Meyer 于1986年创造性地构造出具有一定衰减性的光滑函数,其二进制伸缩与平移构成()R L 2的规范正交基,才使小波得到真正的发展;1988年在构造正交小波基时提出了多分辨分析Multi-Resolution Analysis 的概念,从空间的概念上形象地说明了小波的多分辨率特性,将此之前的所有正交小波基的构造法统一起来,给出了正交小波的构造方法以及正交小波变化的快速算法,即Mallat 算法;Mallat 算法在小波分析中的地位相当于快速傅立叶变换算法在经典傅立叶分析中的地位; 定义：空间)(2R L 中的多分辨分析是指)(2R L 满足如下性质的一个空间序列{}Z j j V ∈：1调一致性：1+⊂j j V V ,对任意Z j ∈2渐进完全性：Φ=∈j Z j V I ,{})(2R L V U close j Z j =∈ 3伸缩完全性：1)2()(+∈⇔∈j j V t f V t f4平移不变性：j j j j j V k t V t Z k ∈-⇒∈∈∀--)2()2(,2/2/φφ5Riesz 基存在性：存在0)(V t ∈φ,使得{}Z k k t j j ∈--|)2(2/φ构成j V 的Risez 基;关于Riesz 的具体说明如下：若)(t φ是0V 的Risez 基,则存在常数A,B,且,使得：对所有双无限可平方和序列{}k c ,即 {}∞<=∑∈222Z k k k c c 成立; 满足上述个条件的函数空间集合成为一个多分辨分析,如果)(t φ生成一个多分辨分析,那么称)(t φ为一个尺度函数;关于多分辨分析的理解,我们在这里以一个三层的分解进行说明,其小波分解树如图所示;从图可以明显看出,多分辨分析只是对低频部分进行进一步分解,而高频部分则不予以考虑;分解的关系为1231D D D A S +++=;另外强调一点这里只是以一个层分解进行说明,如果要进行进一步的分解,则可以把低频部分3A 分解成低频部分4A 和高频部分4D ,以下再分解以此类推;在理解多分解分析时,我们必须牢牢把握一点：其分解的最终目的是力求构造一个在频率上高度逼近()R L 2空间的正交小波基,这些频率分辨率不同的正交小波基相当于带宽各异的带通滤波器;从上面的多分辨分析树型结构图可以看出,多分辨分析只对低频空间进行进一步的分解,使频率的分辨率变得越来越高;MALLAT 算法中包括两个主要的过程,这就是分解过程和重构过程; 对于一个多分辨分析Z j j V ∈}{,以及信号021V f g g g f n n ∈++++= ,其中1、分解算法⏹ 由于()10-∈∈V V t ϕ以及()10-∈∈V W t ψ,故有：⏹ 信号分析和处理是,常常需要知道它在各个闭子空间的小波系数;首先由其采样值,经计算得其中的系数,同时：⏹ 其中1-j k c 和1-j k d 都是j c 使用分解序列在偶整数点的抽样,这称为向下抽样;小波分解2、重构算法⏹ 空间1-V 是空间0V 和0W 的值和,故有：则数列Z k j k c ∈}{、Z k j k d ∈}{、Z k j k c ∈-}{1具有如下公式：小波重构五、基于MATLAB,请自行选择一个一维信号,采用DB3小波函数,进行3尺度分…………解与重构;要求：1附上源程序；2绘出原始信号以及分解、重构的结果图;答：load leleccum;S=leleccum1:1000;w=’db3’;Subplot621;plots;Title‘原始信号’；Dwtmode;cazpd,cdzpd=dwts,w;Lxtzpd=2lengthcazpdXzpd=idwtcazpd,cazpd,w,lx;Subplot622;plotxzpd;Title‘zpd模式重构图’；Dwtmode‘sym’;casym,cdsym=dwts,w;Lxtzpd=2lengthcaspdXsym=idwtcasym,cdsym,w,lx;Subplot625;plotxsym;Title‘sym模式重构图’；Dwtmode‘spd’;casym,cdsym=dwts,w;Lxtzpd=2lengthcaspdXsym=idwtcaspd,cdspd,w,lx;Subplot626;plotxspd;Title‘spd模式重构图’；六、给出一个小波分析的应用实例对于一给定的信号信号序列文件名为,利用小波分析对深夜时段信号分析答：源程序如下：Load leleccum;s=leleccum;w=’db3’;c,1=wavedecs,5,w;For i=1:5DI,:=wrcoeef‘d’,c,l,w,i;Endtt=1+100:lengths -100;subplot6,1,1;plottt,stt,’r’;title‘Electrical Signal and Details’;for i=1:5,subplot6,1,i+1;plottt,D5-i+1,tt,’g’; end。

现代数值计算习题答案现代数值计算习题答案数值计算是现代科学和工程领域中的重要组成部分，它涉及到使用数值方法和计算机技术来解决实际问题。

在学习数值计算的过程中，习题是不可或缺的一部分，通过解答习题可以帮助学生巩固所学的知识，并提高解决实际问题的能力。

本文将为读者提供一些现代数值计算习题的答案，帮助读者更好地理解和掌握这一领域的知识。

一、数值线性代数1. 解释什么是线性方程组的LU分解？答：线性方程组的LU分解是将一个矩阵分解为一个下三角矩阵L和一个上三角矩阵U的乘积的过程。

其中，L矩阵的对角线元素为1，U矩阵的对角线元素与原矩阵相同。

通过LU分解，可以简化线性方程组的求解过程，提高计算效率。

2. 什么是矩阵的条件数？答：矩阵的条件数是衡量矩阵相对于其逆矩阵的敏感程度的一个指标。

条件数越大，矩阵的求逆过程越不稳定，误差积累的可能性越大。

条件数可以用来评估数值解的稳定性和精确性。

二、插值和拟合1. 什么是插值？答：插值是指通过已知数据点来构造一个函数，使得该函数在这些数据点上的取值与已知数据完全一致。

插值可以用于估计数据点之间的未知值，常用的插值方法包括拉格朗日插值和牛顿插值。

2. 什么是最小二乘拟合？答：最小二乘拟合是一种通过最小化残差平方和来拟合数据的方法。

在最小二乘拟合中，通过选择合适的函数形式和参数，使得拟合函数与实际数据之间的误差最小化。

最小二乘拟合广泛应用于数据分析和曲线拟合领域。

三、数值微积分1. 什么是数值积分？答：数值积分是一种通过数值方法来近似计算定积分的方法。

数值积分可以通过将定积分区间划分为若干小区间，然后在每个小区间上使用数值方法来估计积分值。

常用的数值积分方法包括梯形法则和辛普森法则。

2. 什么是数值微分？答：数值微分是一种通过数值方法来近似计算导数的方法。

数值微分可以通过使用有限差分公式来估计导数值。

常用的数值微分方法包括前向差分、后向差分和中心差分。

四、常微分方程数值解1. 什么是常微分方程？答：常微分方程是描述自变量和未知函数之间关系的方程，其中未知函数的导数出现。

一，证明：低通滤波器0h 与高通滤波器1h 的关系： )1()1()(01k h k h k --=证明： 0)()()()(1010=+++πωπωH H w H w H （1） ∴一定存在一个以π2为周期的函数)(ωλ使)()()(01πωωλ+=H w H （2） )()()2()()(001ωπωλπωπωλH H w H +=++= （3） 将（2）,（3）带入（1）中有0)]()()[()(00=+++πωλωλπωωH H （4） 若（4）式成立则)()(πωλωλ++=0 有一个特解为：)2()(ωωλωg e i = （5）其中，)(ωg 为周期为π2的函数 将（5）代入（2）中有)()2()(01πωωωω+=H g e H i 取 ωωim eg =)(对所有的ω都成立，则有)()(0)12(1ωω+=+-H e H m i （6） 当 0=m 时，)()(01πωωω+=-H e H i 显然（6）是（1）的解， 由ki ke k h ωω-∑=H )(21)(00ki ke k h ωω-∑=H )(21)(11则 （6） 式左右两边分别为 ki ke k h ωω-∑=H )(21)(11 (7)∑∑-+----==+H kik kkki i i e k h e k h e e ωπωωωπω)1(21)1( )(21)(0)(00 (8)比较（7）（8）两式有)1()1()(01k h k h k --= 证毕一、证明因子a /1的作用是保证不同尺度下，函数)(,t b a ψ与母小波)(t ψ的能量相同。

证明：由)(/1)(,at a t b a τψψ-=，可知其能量为 dt at a dt t E b a 22,|)(/1||)(|⎰⎰+∞∞-+∞∞--==τψψ 令at x τ-=则有adx dt = ⎰⎰⎰+∞∞-+∞∞-+∞∞-===∴dx x dx x a a ax d x a E 222|)(||)(/1|)(|)(/1|ψψψ)(t ψ的能量E dt t E =='⎰+∞∞-2|)(|ψ由此可见因子a /1的作用是保证不同尺度下，函数)(,t b a ψ与母小波)(t ψ的能量相同。

从傅里叶(Fourie‎r)变换到伽柏(Gabor)变换再到小波‎(Wavele‎t)变换题目：从傅里叶(Fourie‎r)变换到伽柏(Gabor)变换再到小波‎(Wavele‎t)变换本文是边学习‎边总结和摘抄‎各参考文献内‎容而成的，是一篇综述性‎入门文档，重点在于梳理‎傅里叶变换到‎伽柏变换再到‎小波变换的前‎因后果，对于一些概念‎但求多而全，所以可能会有‎些理解的不准‎确，后续计划分别‎再展开学习研‎究。

通过本文可以‎了解到：1）傅里叶变换的‎缺点；2）Gabor变‎换的概念及优‎缺点；3）什么是小波；4）小波变换的概‎念及优点。

一、前言首先，我必须说一下‎，在此之前，虽然我听说过‎小波变换（具体是前几年‎听一位博士毕‎业答辩里提到‎了小波降噪）但就再也没什‎么了，虽然近一年来‎零零散散地在‎接触语音信号‎处理过程中用‎过短时傅里叶‎变换(Short Time Fourie‎r Trans‎f orm, STFT)，但也就如此了‎，之于Gabo‎r变换听都没‎有听过。

这些天看稀疏‎基，其实也就是看‎各种变换了，前面看了离散‎余弦变换(Discre‎t e Cosine‎T ransf‎o rm, DCT)、离散正弦变换‎(Discre‎t e Sine Transf‎o rm, DST)、离散W 变换(Discre‎t eW Transf‎o rm, DWT)、离散哈特莱变‎换(Discre‎t e Hartle‎y Transf‎o rm, DHT)，总体来说理解‎个表皮还是比‎较容易的，于是打算继续‎学习，随便挑了一个‎C urvel‎e t基打算学‎习一下，搜了一下资料‎才发现不能从‎这个开始学习‎，必须Gabo‎r、Wavele‎t、Ridgel‎e t、Curvel‎e t、Wedgel‎e t、Bandel‎e t、Beamle‎t、Contou‎r let等慢‎慢开始学起，我知道我又陷‎入了一片沼泽‎，但或许是一片‎幸福的沼泽，一个做信号处‎理的人对这些‎是应该有一个‎基本的概念级‎了解的。

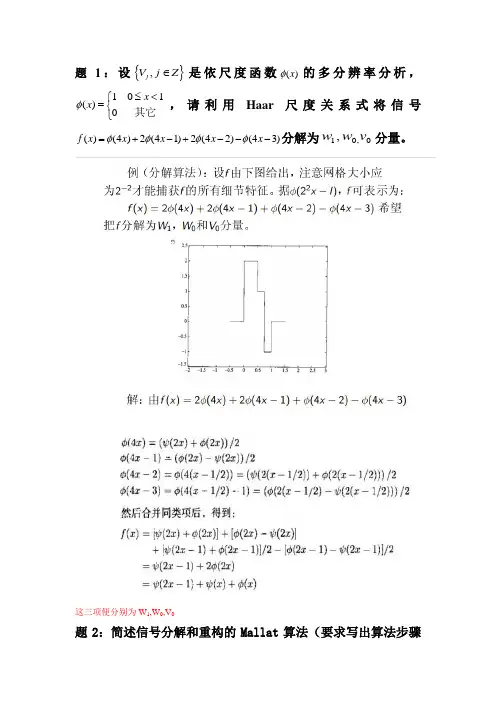
题1：设{},j V j Z ∈是依尺度函数()x φ的多分辨率分析，101()0x x φ≤<⎧=⎨⎩其它，请利用Haar 尺度关系式将信号()(4)2(41)2(42)(43)f x x x x x φφφφ=+-+---分解为10,0,w w v 分量。

这三项便分别为W 1,W 0,V 0题2：简述信号分解和重构的Mallat 算法（要求写出算法步骤并列出分解重构公式。

）分解初始化：选择适当的f j，用来逼近f迭代：由f j分解为f j-1和W j-1，……，以此类推，最后得到f0和W0终止：j=0，并生成下面那两个系数重构：差不多就是倒着说回去。

下面那个系数就是重构出来的f的系数（k(2)j jka x k φ-∑，好像是这个玩意）题3：设{},,,φφψψ构成双正交多分辨分析：（1）写出双正交条件；,,,,,,,,()()()()()()()()()()()(),,l n m n j k j l k nj k j m k nx x x x x x x x x k x k x k x k ϕϕψψϕψϕψϕϕψψϕϕδδψψδδ----<>=<>=⊂⊂⊂⊂⊂-2-1012设存在尺度函数、和小波函数和构成双正交多分辨率分析，则、、、应满足基本条件：（1）平移系{}、{}、{}、{}无关但不正交；（2）满足双正交条件：（3）两种空间嵌套序列：V V V V V ,,,{}{}j j k j j k V span V span ϕ⊂⊂⊂⊂⊂==-2-1012V V V V V 其中,,1111{}{}()(2)()(2)()(2)()(2)j j kj j k j j j j j j j j j j k k k Z k Z k k k Zk ZW span W span V W V W V V W V V W x x k x x k x x k x x k ψφφφφψφψφ----∈∈∈∈==⊥⊥=+=+=-=-=-=-（4）正交补关系：设（5）双尺度方程变为：（2） 写出4个双尺度方程（尺度系数分别为,,,k k k k h h g g ）；()(2)()2(2)k k k kt h t k t h t k φφφφ⎧=-⎪⎪⎨⎪=-⎪⎩∑ ()(2)()2(2)k k k k t g t k t g t k ψφψφ⎧=-⎪⎪⎨⎪=-⎪⎩∑ （3） 写出尺度系数间的对应关系。

第3章小波与小波变换(征求意见稿)清华大学计算机科学与技术系智能技术与系统国家重点实验室林福宗，2001-9-25小波是近十几年才发展起来并迅速应用到图像处理和语音分析等众多领域的一种数学工具，是继110多年前的傅立叶(Joseph Fourier)分析之后的一个重大突破，无论是对古老的自然学科还是对新兴的高新技术应用学科都产生了强烈冲击。

小波理论是应用数学的一个新领域。

要深入理解小波理论需要用到比较多的数学知识。

本章企图从工程应用角度出发，用比较直观的方法来介绍小波变换和它的应用，为读者深入研究小波理论和应用提供一些背景材料。

3.1 小波介绍3.1.1 小波简史傅立叶理论指出，一个信号可表示成一系列正弦和余弦函数之和，叫做傅立叶展开式。

用傅立叶表示一个信号时，只有频率分辨率而没有时间分辨率，这就意味我们可以确定信号中包含的所有频率，但不能确定具有这些频率的信号出现在什么时候。

为了继承傅立叶分析的优点，同时又克服它的缺点，人们一直在寻找新的方法。

20世纪初，哈尔(Alfred Haar)对在函数空间中寻找一个与傅立叶类似的基非常感兴趣。

1909年他发现了小波，并被命名为哈尔小波(Haar wavelets)，他最早发现和使用了小波。

20世纪70年代，当时在法国石油公司工作的年轻的地球物理学家Jean Morlet提出了小波变换WT(wavelet transform)的概念。

进入20世纪80年代，法国的科学家Y.Meyer和他的同事开始为此开发系统的小波分析方法。

Meyer于1986年创造性地构造出具有一定衰减性的光滑函数，他用缩放(dilations)与平移(translations)均为j2(j≥0的整数)的倍数构造了2L(R)空间的规范正交基，使小波得到真正的发展。

小波变换的主要算法则是由法国的科学家Stephane Mallat在1988年提出[1]。

他在构造正交小波基时提出了多分辨率的概念，从空间上形象地说明了小波的多分辨率的特性，提出了正交小波的构造方法和快速算法，叫做Mallat算法[1]。

1. 从Fourier 变换到小波变换的三个阶段： *）信号加窗；**）基加窗；***）小波基；⑴ Fourier 变换是一个强有力的数学工具，它具有重要的物理意义，即信号()f x 的Fourier 变换()()⎰+∞∞-ω-=ωx x f F x d e i表示信号的频谱。

正是Fourier 变换的这种重要的物理意义，决定了Fourier 变换在信号分析和信号处理中的独特地位，特别是作为平稳信号分析的最重要的工具。

但是，在实际应用中，所遇到的信号大多数并不是平稳的。

所以，随着应用范围的逐步扩大和理论分析的不断深入，Fourier 变换的局限性就渐渐展示出来了：首先，从理论上说，为了由Fourier 变换研究一个时域信号()f x 的频谱特性，必须获得信号在时域中的全部信息，以致于包括将来的信息；其次，Fourier 变换对信号的局部畸变没有标定和度量能力。

但是，在许多实际应用中，畸变正是我们所关心的信号在局部范围内的特征；再次，Fourier 变换不能反映信号在局部时间范围内和局部频带上的谱信息分析，或称为局部化时-频分析，而这正是许多实际应用最感兴趣的问题之一；最后，因为一个信号的频率与它的周期长度成反比，因而要给进行分析的一个灵活多变的时间和频率的“窗口”，使其在“中心频率(或称为平均频率、主频)”高的地方，时间窗自动变窄，而在“中心频率”低的地方，时间窗应自动变宽。

⑵ 时间加窗：Gabor 在1946年的论文中，为了提取信号的局部信息，这包括时间和频率两方面的局部信息，引入了一个时间局部化的“窗口函数”()g t b -，其中参数b 用于平行移动窗口，以便于覆盖整个时域。

Gabor 变换继承了Fourier 变换所具有的“信号频谱”这样的物理解释，同时，它克服了Fourier 变换只能反映信号的整体特征而对信号的局部特征没有任何分析能力的缺陷，大大地改进了Fourier 变换的分析能力，为信号处理提供了一种新的分析和处理工具，即信号的时-频分析。

01()2()(2)()2()(2)n Z n Zt g n t n t g n t n ϕϕψϕ∈∈⎨=-⎪⎪=-∑∑小波函数：()(2)nt h t n φφ=-∑ 5、Mallat 算法答： 1989年，Mallat 在小波变换多分辨率分析理论与图像处理的应用研究中受到塔式算法的启发，提出了信号的塔式多分辨率分析与重构的快速算法称为马拉特（Mallat ）算法。

Mallat分解算法：,1,2(1)j k n j n k n Zc h c ++∈=∑，,1,2(2)j k n j n k n Z d g c ++∈=∑ Mallat 重构算法：1,2,2,(3)j n n k j k n k j k n Z n Zc h c gd +--∈∈=+∑ 6、双尺度方程答：双尺度方程，本质就是将j V 的基函数表示成1j V +的基函数的线性和。

因为0101(),()t V V t W V ϕψ∈⊂∈⊂，所以()t ϕ和()t ψ都可以用1V 空间的一个基(2)n Z t n φ∈-线性表示： ()(2)()(2)n n t h t n t g t n φφϕφ⎧=-⎪⎨=-⎪⎩∑∑，即为双尺度方程。

一、简述小波的定义及其主要性质。

（10分）答：小波(Wavelet)这一术语，顾名思义，“小波”就是小的波形。

所谓“小”是指它 具有衰减性；而称之为“波”则是指它的波动性，其振幅正负相间的震荡形式。

与傅里叶 变换相比，小波变换是时间(空间)频率的局部化分析，它通过伸缩平移运 算对信号(函数)逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了傅里叶变换的困难问题，成为继傅里叶变换以来在科学方法上的重大突破。

小波性能除了正交性以外还有光滑性、紧支性、衰减性、对称性以及消失矩和时频窗面积。

二、阐述Fourier 变换和小波变换的各自的特点，并比较它们之间的优缺点。

近代概率论基础题库（计算证明题部分）一、某人写好n 封信，又写好n 个信封，然后在黑暗中随机地把n 封信放入n 个信封中（一个信封中只能放一封信），试求至少有一封信放对的概率。

（10分） 一、解：若以i A 记第i 封信与信封符合，则所求的事件为：12n A A A 。

不难求得：(1)!1()!i n P A n n-== ， (2)!1()!(1)i j n P A A n n n -==-， (3)!1()!(1)(2)i j k n P A A A n n n n -==--，121()!n P A A A n =故12()n P A A A11111(1)123(1)(1)(2)!n n n n n n n n n n n -⎛⎫⎛⎫⎛⎫=-+++- ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭ 11111(1)2!3!!n n -=-+-+-二、从数字1,2,,9中（可重复地）任取n 次，试求所取的n 个数的乘积能被10整除的概率。

（10分）二、解：n 个数的乘积要能被10整除，则这n 个数中至少有一个是偶数，也至少有一个为5。

因取数是放回抽样，显然样本空间中有基本事件9n个。

设A ={所取的n 个数的乘积能被10整除}，B ={所取的n 个数中至少有一个是偶数}，={所取的n 个数中至少有一个为5}， 则为所取的n 个数全为奇数，故B 所含基本事件数为5n；C 为所取的n 个数无5，故C 所含基本事件数为8n ；BC 为所取的n 个数全为奇数且不含5，故BC 所含基本事件数为4n ，且,A BC A B C ==所以由计算公式得：()1()1()1[()()()]P A P A P B C P B P C P BC =-=-=-+-5845841()1.999999n n n n n nn n n n n n =-+-=--+三、一质点从平面上某点出发，等可能的向上、下、左及右方向移动，每次移动的距离为1，求经过2n 次移动后回到出发点的概率。

2016级博士生数学复习题1.设(X)=IlA^11是实Hilb e rt空间H上的泛函，证明,当XHo, /U)在点X处沿着“方向的GateaUX微分。

P81证明：Iim /(χ+ 〃?)-/(X) = IinI卜+ 〃?卜何=Iim (|卜+呦-闵1)(卜+呦+制)z→0t /TO t7 r(∣∣x + rΛ∣∣ + ∣∣Λ∙∣∣)Iirn卜 + 呦2-卜If =Iim◎ +心 + 呦_心〉=Iiln 2(儿巾〉-仲M)“ r(∣∣x÷∕A∣∣÷ IA-Il) ^ -O /(∣χ÷rA∣∣÷∣∣χ∣∣)_ “，(卜+ 呦+ 卜||)-(^Z o于是，当XHO时，f在X处沿着Ii方向的GateauX微分为：砒(M) = ¥半IkIl处不是FreChet微分。

P84证明：由于X4 + y1≤^∣x∣,V.r,yX3 yG χ÷y+ J . /Uθ,) = S ' X +y- 2.设泛函〔°(x,y)H(0,0)(XJy)=(O,O),证明/(兀刃在点(°,°)所以f在点(0,0)处连续，令" = (■〃)，则有lim∕(O÷r∕Q-/(O)=Iiln∕→<) f t→0tξ + tη +(fξ)3f∏(/鉀+(S’= ξ + fj因此,f 在点（Oe ）处沿方向h 的GateaUX 微分为Zy （（0、0）,（歹,〃）） = § + 〃，但是,如果令ξ = η∖则有Il 州=(孕+〃2)"2=(孕+0严于是=∣∣⅛⅛≠θ所以，f 在点（0,0）处不是FreChet 可微的。

3.设"，$）为10,l ］χ［0,l ］上的二元连续函数，定义以"⑶为积分核的积分算子^ιΔ2（［0,l ］）→Δ2（［0,l ］）为 (/(/)(∕) = ∫∖(r,5)∕(5)√5,∀f ∈Δ2([0,l])V JL证明：对于任意的/,g∈Δ2（［0,l ］）,有㈣,g> = (伽，s)f($)ds,g(f» =』lw ，s)/(s)d$ g{t}dt = =打(S)^k(TS)g(t)dt ds∕ = (∕,f ",s)g(s)"s 则有(∕√)(r) = ∫7(r,5)∕(5M5,V∕'∈L 2([θ,l])4 求证.(K 了)(/)= [殆可G)ds,WeW[°,ll)∙ blH（孑+缈= ∫j ,∕(0 ^k(JTS) g(S ) d ST(K,∙∙∙) = (討∣χ3,∙∙∙,乎和…)^Il r lLP41证明：对于任意的x = (x∖x2√-∙)∈/2,有II rV Il=Z I r(Xl‘ 疋‘…)iHG 吃,彳兀3,X n‘ ∙∙∙)∣∣「1,2、H ■>"|,/2F产)-+(严)÷ -÷(-χw)-÷- )≤ [(吃)2 + (-Vj)2+••■ + (A H)2+∙∙ )]'2≤ [(^1)2 + (AS)2 + (A3)2 + ∙ +(⅞)2+∙ O]'2 =M于是I∣7'∣∣≤ 1,另外，对于5 = (O,∙∙∙,OJ,O,∙∙-),则有其中ci, C2为任意常数，作变化 1［厂y-广→ 1(〃→ S)所以IlrlI = I5.判断下面方程的类型并把它化成标准型:4%+5g+q+/+匕+ 2 = 0.证明：因为判别式△ = 〃2_4必=9〉0,故方程为双曲型。

数学正比例和反比例试题答案及解析1.（2013•华亭县模拟）=单价（一定），和成比例．【答案】总价，数量，正．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：=单价（一定），总价和数量成正比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．2.（2013•黄冈模拟）如果xy=100，x 和y成比例；如果8x=y，x和y成比例．【答案】反，正．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为xy=100（一定），所以x和y成反比例；如果8x=y，则：y÷x=8（一定），所以x和y成正比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．3. b﹣a=17.25，则a和b不成比例．【答案】正确．【解析】判断a和b成不成比例，成什么比例，就看a和b是对应的比值一定，还是对应的乘积一定，如果是比值一定，就成正比例，如果是乘积一定，就成反比例，如果是其它的量一定或乘积、比值不一定，就不成比例．解：因为b﹣a=17.25（一定），是a和b对应的差一定，所以a和b不成比例；点评：此题属于根据正、反比例的意义，辨识两种相关联的量成不成比例，成什么比例，就看这两种量是对应的比值一定，还是对应的乘积一定，还是对应的其它量一定，再做出判断．4.判断变化的量是否成正比例，说明理由．圆柱的高一定，体积和底面积．【答案】不成反比例．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为圆柱的体积=底面积×高，所以圆柱的体积÷底面积=高（一定），符合正比例的意义，所以圆柱的高一定，底面积与体积不成反比例．点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．5.判断两个量是否成正比例或反比例，说明理由：看一本书，每天看的页数和所看的天数．【答案】成反比例．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为，每天看到页数×看的天数=一本书的总页数（一定），所以，每天看的页数和需要看的天数成反比例．点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．6.判断题中的两种量是不是成比例，成什么比例，并说明理由．圆的半径和它的面积．【答案】不成比例．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为S÷r=πr，r变化，πr就变化，所以圆的面积和它的半径不成比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．7.判断题中两种量是否成比例：三角形的面积一定，高与底．理由：．【答案】反比例【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为三角形的底×高=面积×2（一定），是乘积一定，它的底和高成反比例．反比例，三角形的底×高=面积×2（一定）．点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．8.判断题中的两种量是不是成比例，成什么比例，并说明理由．路程一定，速度和时间；时间一定，速度和路程；速度一定，路程和时间．【答案】反比例，正比例，正比例．【解析】判断两种相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：（1）因为速度×时间=路程（一定），是乘积一定，符合反比例的意义，所以路程一定，速度和时间成反比例；（2）因为路程÷速度=时间（一定），是比值一定，符合正比例的意义，所以时间一定，路程和速度成正比例；（3）因为路程÷时间=速度（一定），是比值一定，符合正比例的意义，所以速度一定，路程和时间成正比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．9.小波打字的个数与所用的时间如下表．）打字的个数与用的时间成比例．（2）根据表中数据，把打字个数与时间所对应的点，按顺序连起来的图形描出来．（3）估一估，小波5分钟打字个，打450个字用分钟．【答案】正；250；9．【解析】（1）判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．（2）成正比例的图象是一条直线，由此描点，即可画出；（3）先利用工作效率=工作总量÷工作时间，求出1分钟能打多少个字，即可解决问题．解：（1）100：2=200：4=300：6…=600：12，是打字个数与所用时间的比值相等，所以打字的个数与用的时间成正比例．（2）根据题干中的数据可以描出打字个数与时间所对应的点，按顺序连起来的图形描出来，如图所示（3）100÷2=50（字），50×5=250（字），450÷50=9（分钟），答：5分钟能打250字，450字需要9分钟．点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断；成正比例关系的图象是一条直线．10.在同一时间、同一地点测得的不同树的高度与影长如下表：树高/m12578（1）在下边描出树高和对应影长的点，然后把它们连起来，图象有什么特点？（2）根据表中的数据树高和影长是否成正比例或反比例？为什么？（3）如果一棵树高为4.8m，影长约为多少米？（用比例知识解）【答案】都在一条直线上成正比例关系；影长2.88米．【解析】（1）先依据所给数据描出对应点，进而可以连接各点，再观察图象的特点即可；（2）通过图象特点，即可发现规律；（3）依据树高和影长的比例关系，即可判断树高4.8米时，影子的长度．解：（1）所作图象如下图，观察发现：表示树高和对应影长的点，都在一条直线上；（2）连线以后，发现表示树高和对应影长的点，都在一条直线上，这说明树高和影长成正比例关系，因为随着树的高度的增加，影长也在增加，且树高与影长的商是一定的，所以树高和影长成正比例关系；（3）设树高4.8m时，影长为x米，则有1：0.6=4.8：x，x=4.8×0.6，x=2.88；答：树高4.8m时，影长2.88米．点评：解答此题的关键是明白：如果两个量的商一定，则说明这两个量成正比，据此即可逐步求解．11.表中是普通客车硬座票价表．车票价格和所行里程成不成比例？为什么？【答案】不成比例．【解析】判断两种相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：根据表格中的数据可以看出：车票价格和所行里程之间，既不是对应的乘积一定，它们的比值也不是定值，所以车票价格和所行里程不成比例．答：车票价格和所行里程不成比例．点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，如果对应的比值和乘积都不一定时，这两个量不成比例．12.如果=，那么X和Y成关系；如果14X=Y ，那么X 和Y成关系．【答案】反，正．【解析】根据判断两种量成正比例还是成反比例的方法：关键是看这两种相关联的量中相对应的两个数的商一定还是积一定，如果商一定，就成正比例关系；如果积一定，就成反比例关系；据此判断即可．解：因为=，则有xy=4，X与Y的积一定，则X与Y反比例关系；因为14X=Y，则=14，Y与X的商一定，则Y与X正比例关系；点评：此题主要考查正比例和反比例的意义．13.在一个长4.5米，宽3.5米的房间地面上铺同一种规格的正方形地砖，每块砖的面积和用砖的块数成比例．现在有四种规格的地砖，它们的连长分别是40厘米、30厘米、50厘米、60厘米．要想铺满房间，且一块地砖也不锯破，应该选择边长是厘米的地砖，需要块．【答案】反，50，63．【解析】（1）根据题意知道房间的面积一定，每块砖的面积×用砖的块数=房间的面积（一定），所以每块砖的面积和用砖的块数成反比例；（2）先算出房间的面积，再分别算出边长是40厘米、30厘米、50厘米、60厘米的方砖的面积，观察方砖的面积与房间的面积的数的特点，得出要选择方砖的长度．解：（1）因为每块砖的面积×用砖的块数=房间的面积（一定），符合反比例的意义，所以每块砖的面积和用砖的块数成反比例；（2）4.5米=450厘米，3.5米=350厘米，房间的面积：450×350=157500（平方厘米），方砖的面积分别是：40×40=1600（平方厘米），30×30=900（平方厘米），50×50=2500（平方厘米），60×60=3600（平方厘米），观察方砖的面积数与房间的面积数，把方砖的面积数与房间的面积数都缩小100倍，只有1575是25的倍数，所以157500能够被2500整除，需要方砖的块数：157500÷2500=63（块）；点评：关键是判断出每块砖的面积和用砖的块数成反比例，再根据基本的数量关系解决问题．14.有一批稻谷，碾出的大米数量和出米率成反比例．．【答案】×．【解析】判断两种相关联的量是否成反比例，就看这两种量是否是对应的乘积一定，如果是乘积一定，就成反比例，如果不是乘积一定或乘积不一定，就不成反比例．解：因为×100%=出米率，所以大米的重量÷出米率=稻谷的重量（一定），不符合反比例的意义，所以有一批稻谷，碾出的大米数量和出米率不成反比例；点评：此题属于辨识成反比例的量，就看这两种量是否是乘积一定，再做出判断．15.圆柱的体积一定，它的高和成反比例．【答案】底面积．【解析】判断路程和速度之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为圆柱的底面积×高=体积（一定），符合反比例的意义，所以圆柱的体积一定，它的高和底面积成反比例．；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断；也考查了圆柱的体积=底面积×高，这一公式的运用．16.如果A×B﹣5=12.3，那么A与B成反比例．．【答案】正确．【解析】判断A与B是否成反比例，就看这两种量是否是对应的乘积一定，如果是乘积一定，就成反比例，如果是乘积不一定，就不成反比例．解：A×B﹣5=12.3，A×B=17.3（一定），是乘积一定，A与B就成反比例．点评：此题属于辨识成反比例的量，就看这两种量是否是对应的乘积一定，再做出判断．17.完成一项工程，每天完成的量和所需天数成比例．【答案】反．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为：每天完成的量×所需天数=这项工程的工作总量（一定），所以每天完成的量和所需天数成反比例．点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．18.李玲的体重与她的身高．【答案】不成比例．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例；如果不是乘积或比值一定，就不成比例．解：一个人的身高和体重虽是两种相关联的量，但是它们的乘积或比值都不一定，所以李玲的体重与她的身高不成比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．19.判断题中的两个量是否成正比例，并说明理由订阅《少年报》的份数和钱数．．【答案】成正比例．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为钱数÷份数=单价（一定），所以订阅《少年报》的份数与钱数成正比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．20.400ml水，分的杯数与每杯水的体积．．（判断成什么比例关系）【答案】成反比例．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为每杯水的体积×分得杯数=水的总体积（一定），所以400ml水，分的杯数与每杯水的体积成反比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．21.一袋大米，吃去的千克数与剩下的千克数成比例．（在横线里写上“正”“反”“不成”）【答案】不成．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：吃去的千克数+剩下的千克数=一袋大米的总质量（不变），是和一定，故吃去的千克数与剩下的千克数不成比例．点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．22.小明要做了12到数学题，做完的题和没做的题．．【答案】不成比例．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为做完的题+没做的题=题的总数（一定），因为是“和”一定，所以小明要做了12到数学题，做完的题和没做的题不成比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．23.一堆货物的总重量一定，每辆车的载重量和汽车辆数比例．【答案】反．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为每辆车的载重量×汽车辆数=一堆货物的总重量（一定），所以每辆车的载重量和汽车辆数反比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．24.出米率一定，稻谷的重量和大米的重量成比例．【答案】正．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为：×100%=出米率（一定），所以出米率一定，稻谷的重量和大米的重量成正比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．25.圆柱的体积和底面积成正比例．．（判断对错）【答案】×．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为圆柱的体积=底面积×高，所以圆柱的体积÷底面积=高，因为高不一定，所以圆柱底面积与体积不成正比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．26.工作效率一定，工作总量和工作时间比例工作时间一定，工作效率和工作总量比例工作总量一定，工作效率和工作时间比例．【答案】正，正，反．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：①因为工作总量÷工作时间=工作效率，如果工作效率一定，工作总量和工作时间成正比例；②因为工作总量÷工作效率=工作时间，如果工作时间一定，工作总量和工作效率成正比例；③因为工作效率×工作时间=工作总量，如果工作总量一定，工作效率和工作时间成反比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．27.圆锥的高一定，体积和底面积．（是否成正比例）理由：．【答案】正比例，=×高（一定）．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为圆锥的体积=×底面积×高，且圆锥的高一定，则=×高（一定），所以底面积和体积成正比例．点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．28.一房间铺地面积和用砖数如下表，根据要求填空．铺地面积（平方米）12345（1）表中和是相关联的量，随着的变化而变化．（2）表中第三组这两种量相对应的两个数的比是，比值是；第五组这两种量相对应的两个数的比是，比值是．（3）上面所求出的比值所表示的意义是，铺地面积和砖的块数的是一定的，所以铺地面积和砖的块数．【答案】铺地面积，用砖块数，用砖块数，铺地面积，75：3，25，125：5，25，每平方米用砖的块数，比值，成正比例．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：（1）表中铺地面积和用砖块数是相关联的量，用砖块数随着铺地面积的变化而变化．（2）表中第三组这两种量相对应的两个数的比是75：3，比值是25；第五组这两种量相对应的两个数的比是125：5，比值是25．（3）上面所求出的比值所表示的意义是每平方米用砖的块数，铺地面积和砖的块数的比值是一定的，所以铺地面积和砖的块数成正比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．29.正方体一个面的面积和它的表面积．．【答案】正比例．【解析】判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例．解：因为正方体的表面积÷一个面的面积=6（一定），是比值一定，符合正比例的意义，所以正方体一个面的面积和它的表面积成正比例；点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．30.因为=工效（一定），所以和成比例．【答案】工作量、工作时间、工作量、工作时间、正．【解析】判断工作量与工作时间之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为=工效（一定），符合正比例的意义，所以工作量与工作时间成正比例．点评：此题主要考查了工作量、工作时间与工效的关系，及辨识成正、反比例的量．31.购买《学习报》的钱数和数量成比例．（在横线里写上“正”“反”“不成”）【答案】正．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为购买《学习报》的钱数÷数量=《学校报》的单价（一定），所以购买《学习报》的钱数和数量成正比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．32.判断下面每题中的两种量是不是成正比例，并说明理由．（1）小新跳高的高度和他的身高．（2）长方形的宽一定，它的面积和长．（3）小麦每公顷产量一定，小麦的公顷数和总产量．【答案】不成正比例；成正比例；成正比例．【解析】判定两种量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定，就成反比例．解：（1）因为小新跳高的高度和他的身高的比值不是一定的，所以小新跳高的高度和他的身高不成正比例；（2）因为长方形的面积=长×宽，所以长方形的面积÷长=宽（一定），即长方形的面积与长的比值一定，符合正比例的意义，所以一个长方形的宽一定，它的面积和长成正比例；（3）种小麦的面积和总产量是两种相关联的量，它们与每公顷小麦产量有下面的关系：总产量：小麦的公顷数=每公顷小麦产量（一定）；点评：此题属于根据正、反比例的意义，判断两种相关联的成正比例还是成反比例，就看是对应的比值一定，还是对应的乘积一定，再做出解答．33.判断是否成比例，成什么比例：种子的总量一定，每公顷的播种量和播种的公顷数．．【答案】反比例．【解析】判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例．解：每公顷的播种量×播种的公顷数=种子的总量（一定），是乘积一定，符合反比例的意义，所以种子的总量一定，每公顷的播种量和播种的公顷数成反比例；点评：此题属于根据正、反比例的意义，判断两种相关联的量是成正比例还是成反比例，就看两种量是对应的比值一定，还是对应的乘积一定，再做出解答．34.三（1）班的出勤率一定，全班人数和出勤人数．÷=因为和的一定，所以和正比例．【答案】正比例，出勤人数，全班人数，出勤率，出勤人数，全班人数，比值，出勤人数，全班人数．【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为出勤人数÷全班人数=出勤率（一定），即出勤人数和全班人数的比值一定，所以全班人数和出勤人数成正比例；点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．35.根据规律判断比例关系，并填空．Y．A．成正比例B．成反比例．【答案】B．X与Y成反比例；【解析】判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解：因为3×4=5×2.4=12，即y和x的乘积一定，所以x和y成反比例；12÷2=6，12÷12=1，12÷10=1.2；X 2 3 5 1 10 …Y 6 4 2.4 12 1.2 …点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．。

北师大版初中数学八年级（下）第五章数据的收集与处理5．4数据的波动课后练习（二）试题一、基础训练1、选择题（1）已知一组数据－1，x，0，1，－2的平均数是0，那么这组数据的方差是___________．A．2 B．2C．4 D．10（2）若甲组数据的方差比乙组数据的方差大，那么下列说法正确的是___________．A．甲组数据的平均数比乙组数据的平均数大B．甲组数据比乙组数据稳定C．乙组数据比甲组数据稳定D．甲、乙组的稳定性不能确定（3）已知一组数据的方差是4，则这组数据的标准差是___________．A．2 B．4C．8 D．16（4）从A、B两班分别任抽10名学生进行英语口语测试，其测试成绩的方差是S A2=13．2，S B2=26．36，则___________．A．A班10名学生的成绩比B班10名学生的成绩整齐B．B班10名学生的成绩比A班10名学生的成绩整齐C．A、B两班10名学生的成绩一样整齐D．不能比较A、B两班学生成绩的整齐程度2、填空题（5）一组数据7，8，9，10，11，12，13的方差是________．（6）已知一组数据1，2，3，5，x的平均数是3，则这组数据的标准差是________．（7）已知数据7，9，19，a，17，15的中位数为13，则这组数的平均数为________，方差为________．（8）在一次知识竞赛中，学生甲和乙的各科总平均分相等，但甲的标准差比乙的标准差小，这说明__________________________________．二、拓展训练1．计算下列各组数据的方差和标准差(结果保留到小数点后第二位)(1)8 9 10 10 11 12(2)78 80 80 81 82 83 83 852．为了从甲、乙两名同学中选拔一人参加射击比赛，对他们的射击水平进行了测试，两人在相同条件下各射靶10次，每次命中的环数如下：甲：7 8 6 8 6 5 9 10 7 4乙：9 5 7 8 7 6 8 6 7 7(1)分别计算甲、乙两组数据的方差．(2)你认为应选拔哪位同学参加射击比赛？为什么？3．甲、乙两台机床同时加工直径为100毫米的零件，为了检验产品质量，质量检查员从两台机床的产品中各随机抽出6件进行测量，测得数据如下(单位：毫米)：机床甲：99 100 98 100 100 103机床乙：99 100 102 99 100 100(1)分别计算上述两组数据的平均数及方差；(2)如果你是质量检查员，在收集到上述数据后，你将说明哪一台机床加工的零件更符合要求．4．甲、乙两台包装机同时包装质量为500克的糖果，从中各抽出10袋，测得其实际质量分别如下(单位：克)：甲 501 500 508 506 510 509 500 493 494 494 乙 503 504 502 496 499 501 505 497 502 499哪台包装机包装的10袋糖果的质量比较稳定？参考答案一、基础训练1、选择题（1）B （2）C （3）A （4）A2、填空题（5）4 （6）2 （7）13 18.67 （8）学生甲的各科成绩差异较小二、拓展训练1．(1)S 2 ≈1．67 S ≈1.29 (2)S 2≈4.25 S ≈2.062．(1)甲、乙两组数据的方差分别为3和1.2(2)因为甲、乙二学生的平均数相同，甲的方差比乙的方差大，所以乙学生的成绩比较稳定，应选乙学生参加射击比赛．3．(1)机床甲、乙两组数据的平均数分别为100和100，方差分别为37和1 (2)通过数据分析：甲、乙的平均数相同，甲机床的方差大于乙机床的方差，所以乙机床加工的零件更符合要求．4．甲、乙两组数据的方差分别为38.05和7.96，所以乙包装机包装的10袋糖果的质量比较稳定．希望以上资料对你有所帮助，附励志名言3条：1、上帝说：你要什么便取什么，但是要付出相当的代价。

机械波点点清专题4 波传播的周期性和多解性问题1.波动问题多解的主要因素(1)周期性①时间周期性：时间间隔Δt与周期T的关系不明确.每经过nT，质点完成n次全振动回到原来的状态，在时间上形成多解，多解通式为t ＝nT＋Δt.②空间周期性：波传播的距离Δx与波长λ的关系不明确.在波形图上，相距nλ的质点振动状态完全一致，在空间上形成多解，多解通式为x＝n λ＋Δx.(2)双向性①传播方向双向性：波的传播方向不确定.只告诉波速不指明波的传播方向，应考虑沿两个方向传播的可能，即沿x轴正方向或沿x轴负方向传播。

②振动方向双向性：质点位移、速度方向不确定.质点达到最大位移处，则有正向和负向最大位移两种可能，质点在某一确定位置，振动速度方向有向上、向下(或向左、向右)两种可能；(3)波形的不确定：在波动问题中，往往只给出完整波形的一部分，或给出几个特殊点，波形就有多种情况，形成波动问题的多解性。

2.求解波的多解问题一般思路(1)根据题设条件结合多解的主要因素判断是唯一解还是多解(2)根据周期性、双向性、波形的隐含性，采用从特殊到一般的思维方法，即找出一个周期内满足条件的关系Δt或Δx，确定时间t和距离x的关系通式。

若此关系为时间，则t ＝nT＋Δt(n＝0,1,2，…)；若此关系为距离，则x＝nλ＋Δx(n＝0,1,2，…).(3)根据波速公式v ＝Δx Δt 或v ＝λT ＝λf 求波速。

题型1 波形的不确定性形成多解【典例1】（2013年重庆卷）（多选）一列简谐横波沿直线传播，某时刻该列波上正好经过平衡位置的两质点相距6 m ，且这两质点之间的波峰只有一个，则该简谐波可能的波长为（ ）A.4 m 、6 m 和8 mB.6 m 、8 m 和12 mC.4 m 、6 m 和12 mD.4 m 、8 m 和12 m 【解析】 根据题意，有以下三种情况符合要求：ab ＝6 m ，即λ12＝6 m ， λ1＝12 m.cd ＝6 m ，即λ2＝6 m.ef ＝6 m ，即32λ3＝6 m ，λ3＝4 m ，故C 正确，A 、B 、D 错误.【答案】 C 题型2 双向性形成多解【典例2】（双向性）一列简谐横波在t ＝0时刻的波形如图中的实线所示，t ＝0.02 s 时刻的波形如图中虚线所示。