高中数学 第三章 二倍角例题讲解素材 北师大版必修4(1)

§3 二倍角的三角函数1．掌握倍角公式与半角公式及公式的推导方法．(重点)2．能利用倍角公式与半角公式进行三角函数的求值、化简、证明．(重点)3．能利用倍角公式与半角公式解决一些简单的实际问题．(难点)[基础·初探]教材整理 二倍角公式与半角公式阅读教材P 124～P 127练习2以上部分，完成下列问题．1．二倍角公式2．半角公式(1)sin α2＝± 1－cos α2； (2)cos α2＝± 1＋cos α2； (3)tan α2＝± 1－cos α1＋cos α＝sin α1＋cos α＝1－cos αsin α.判断(正确的打“√”，错误的打“×”)(1)对任意α∈R ，总有sin 2α＝2sin α.( )(2)对任意α∈R ，总有cos 2α＝1－2cos 2α.( )(3)对任意α∈R ，总有tan 2α＝2tan α1－tan 2α.( ) (4)sin 22°30′cos 22°30′＝24.( )(5)sin 2 α＝1－cos 2α2.( ) 【解析】 (1)sin 2α＝2sin αcos α，所以(1)错．(2)cos 2α＝2cos 2α－1，所以(2)错．(3)α≠π4＋k π2(k ∈Z )时，有tan 2α＝2tan α1－tan 2α，所以(3)错． (4)sin 22°30′cos 22°30′＝12×2sin 22°30′cos 22°30′＝12sin 45°＝24，所以(4)对．(5)对．【答案】 (1)× (2)× (3)× (4)√ (5)√[小组合作型]【精彩点拨】 根据条件求出sin α，然后求出cos α，利用半角公式求tan α2.【自主解答】 ∵α为第四象限的角，cos α＝33，∴sin α＝－1－cos 2α＝－63.∴tan α＝sin αcos α＝－ 2.∵α为第四象限角，∴α2是第二或第四象限的角，。

二倍角解方攻略二倍角的三角函数是和、差角的三角函数的特例，其求值，化简，证明的出发点是统一角，统一函数和降低次数。

在变形过程中，要注意角与角之间的和、差、倍关系和特殊角之间的关系等。

同时还要观察式子的特征，适当选用公式进行化简。

这里对几种常用方法举例解析，供同学们参考。

一、逆用公式法： 例1 求sin10°sin30°sin50°sin70°的值。

分析：注意到sin10°sin50°sin70°=cos80°cos40°cos20°,分子分母可同时乘以2sin20°,逆用正弦的二倍角公式求解，也可用变形式作商相消。

解法1 (连续逆用法)sin10°sin30°sin50°sin70°= 12 cos80°cos40°cos20°=14sin20° ·cos80°cos40°·(2sin20°cos20°) =18sin20°·cos80°·(2sin40°cos40°) = 116sin20° ·(2sin80°cos80°) = sin160°16sin20° = 116解法2 (作商法)sin10°sin30°sin50°sin70°= 12cos80°cos40°cos20°= 12 · sin160°2sin80° · sin80°2sin40° · sin40°2sin20° = sin160°16sin20° = 116 评注：①解法1是根据其特点采用同乘同除一个三角函数式，使其构成使用二倍角公式sin2α=2sin αcos α的形式，从而达到求值的目的。

二倍角的三角函数一.教学目标：1.知识与技能（1）能够由和角公式而导出倍角公式；（2）能较熟练地运用公式进行化简、求值、证明，增强学生灵活运用数学知识和逻辑推理能力；（3）能推导和理解半角公式；（4）揭示知识背景，引发学生学习兴趣，激发学生分析、探求的学习态度，强化学生的参与意识. 并培养学生综合分析能力.2.过程与方法让学生自己由和角公式而导出倍角公式和半角公式，领会从一般化归为特殊的数学思想，体会公式所蕴涵的和谐美，激发学生学数学的兴趣；通过例题讲解，总结方法.通过做练习,巩固所学知识.3.情感态度价值观通过本节的学习，使同学们对三角函数各个公式之间有一个全新的认识；理解掌握三角函数各个公式的各种变形，增强学生灵活运用数学知识、逻辑推理能力和综合分析能力.提高逆用思维的能力. 二.教学重、难点重点:倍角公式的应用. 难点:公式的推导. 三.学法与教法教法与学法：(1)自主+探究性学习：让学生自己由和角公式导出倍角公式，领会从一般化归为特殊的数学思想，体会公式所蕴涵的和谐美，激发学生学数学的兴趣。

(2)反馈练习法：以练习来检验知识的应用情况，找出未掌握的内容及其存在的差距. 四.教学过程 （一）探究新知1、复习两角和与差的正弦、余弦、正切公式：2、提出问题：公式中如果β=α，公式会变得如何？3、让学生板演得下述二倍角公式：α-=-α=α-α=ααα=α2222sin 211cos 2sin cos 2cos cos sin 22sinααα2tan 1tan 22tan -=[展示投影]这组公式有何特点？应注意些什么？注意：1．每个公式的特点，嘱记：尤其是“倍角”的意义是相对的，如：4α是8α的倍角. 2．熟悉“倍角”与“二次”的关系（升角——降次，降角——升次） 3．特别注意公式的三角表达形式，且要善于变形：22cos 1sin ,22cos 1cos 22α-=αα+=α 这两个形式今后常用. （二）[展示投影]例题讲评（学生先做，学生讲，教师提示或适当补充） 例1.（公式巩固性练习）求值： ①．sin22︒30’cos22︒30’=4245sin 21=②．=-π18cos22224cos =π ③．=π-π8cos 8sin22224cos -=π- ④．=ππππ12cos 24cos 48cos 48sin8216sin 12cos 12sin 212cos 24cos 24sin 4=π=ππ=πππ 例2.化简 ①．=π-ππ+π)125cos 125)(sin 125cos 125(sin2365cos 125cos 125sin 22=π-=π-π ②．=α-α2sin 2cos44α=α-αα+αcos )2sin 2)(cos 2sin 2(cos 2222 ③．=α+-α-tan 11tan 11α=α-α2tan tan 1tan 22④．=θ-θ+2cos cos 21221cos 2cos 2122=+θ-θ+例3、已知),2(,135sin ππ∈α=α，求sin2α，cos2α，tan2α的值。

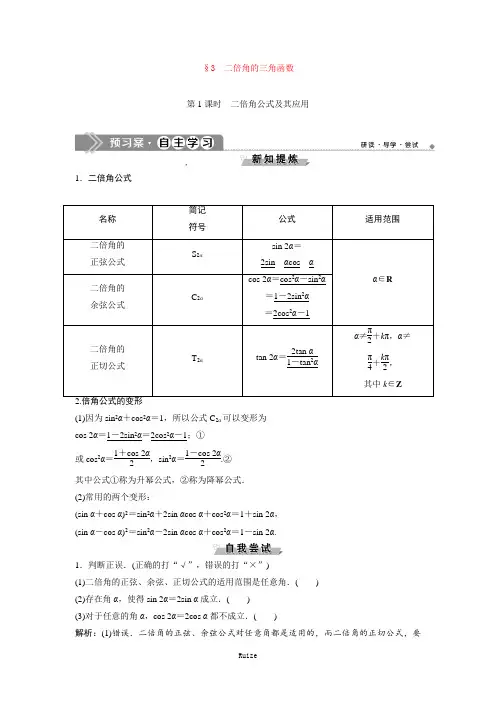
§3二倍角的三角函数第1课时二倍角公式及其应用,1．二倍角公式名称简记符号公式适用范围二倍角的正弦公式S2αsin 2α＝2sin__αcos__αα∈R 二倍角的余弦公式C2αcos 2α＝cos2α－sin2α＝1－2sin2α＝2cos2α－1二倍角的正切公式T2αtan 2α＝2tan α1－tan2αα≠π2＋kπ，α≠π4＋kπ2，其中k∈Z(1)因为sin2α＋cos2α＝1，所以公式C2α可以变形为cos 2α＝1－2sin2α＝2cos2α－1；①或cos2α＝1＋cos 2α2，sin2α＝1－cos 2α2.②其中公式①称为升幂公式，②称为降幂公式．(2)常用的两个变形：(sin α＋cos α)2＝sin2α＋2sin αcos α＋cos2α＝1＋sin 2α，(sin α－cos α)2＝sin2α－2sin αcos α＋cos2α＝1－sin 2α.1．判断正误．(正确的打“√”，错误的打“×”)(1)二倍角的正弦、余弦、正切公式的适用范围是任意角．()(2)存在角α，使得sin 2α＝2sin α成立．()(3)对于任意的角α，cos 2α＝2cos α都不成立．()解析：(1)错误．二倍角的正弦、余弦公式对任意角都是适用的，而二倍角的正切公式，要求α≠π2＋k π(k ∈Z )且α≠π4＋k π(k∈Z )，故此说法错误．(2)正确．当α＝k π(k ∈Z )时，sin 2α＝2sin α. (3)错误．当cos α＝1－32时，cos 2α＝2cos α.★答案★：(1)× (2)√ (3)× 2.sin 110°sin 20°cos 2155°－sin 2155°的值为( )A ．－12B.12C.32D ．－32解析：选B.原式＝cos 20°sin 20°cos 225°－sin 225°＝12sin 40°cos 50°＝12sin 40°sin 40°＝12. 3.tan 15°1－tan 215°＝________．解析：原式＝12×2tan 15°1－tan 215°＝12tan 30°＝36.★答案★：364．若sin α＝55，则cos 4α－sin 4α＝________. 解析：cos 4α－sin 4α＝(cos 2α＋sin 2α)(cos 2α－sin 2α) ＝cos 2α－sin 2α＝1－2sin 2α＝1－2×⎝⎛⎭⎫552＝35. ★答案★：351．对倍角公式的三点说明 (1)前提：所含各三角函数有意义．(2)联系：公式S 2α，C 2α，T 2α是在公式S α＋β，C α＋β，T α＋β中，分别令β＝α时，得到的一组公式，即倍角公式是和角公式的特例．(3)倍角公式中的“倍角”的相对性：对于两个角的比值等于2的情况都成立，如6α是3α的2倍，3α是3α2的2倍．这就是说，“倍”是相对而言的，是描述两个数量之间的关系的．2．二倍角的余弦公式的运用在二倍角公式中，二倍角的余弦公式最为灵活多样，应用广泛．常用形式：①1＋cos 2α＝2cos 2α，②cos 2α＝1＋cos 2α2，③1－cos 2α＝2sin 2α，④sin 2α＝1－cos 2α2.化简求值求下列各式的值：(1)cos π5cos 2π5；(2)12－cos 2π8；(3)tan π12－1tan π12.【解】 (1)原式＝2sin π5cos π5cos2π52sinπ5＝sin 2π5cos 2π52sin π5＝sin 4π54sin π5＝sin π54sinπ5＝14.(2)原式＝1－2cos 2π82＝－2cos 2π8－12＝－12cos π4＝－24.(3)原式＝tan 2π12－1tan π12＝－2·1－tan 2π122tan π12＝－2×1tanπ6＝－233＝－2 3.应用二倍角公式化简(求值)的策略(1)化简求值关注四个方向：分别从“角”“函数名”“幂”“形”着手分析，消除差异． (2)公式逆用：主要形式有2sin αcos α＝sin 2α，sin αcos α＝12sin 2α，cos α＝sin 2α2sin α，cos 2α－sin 2α＝cos 2α，2tan α1－tan 2 α＝tan 2α.1.(1)计算：cos 10°＋3sin 10°1－cos 80°＝________.(2)求sin 6°sin 42°sin 66°sin 78°的值．解：(1)原式＝2⎝⎛⎭⎫12cos 10°＋32sin 10°2sin 240°＝2sin 40°2sin 40°＝ 2.故填 2.(2)原式＝sin 6°cos 48°cos 24°cos 12° ＝24sin 6°cos 6°cos 12°cos 24°cos 48°24cos 6° ＝23sin 12°cos 12°cos 24°cos 48°16cos 6°＝22sin 24°cos 24°cos 48°16cos 6°＝2sin 48°cos 48°16cos 6°＝sin 96°16cos 6°＝cos 6°16cos 6° ＝116.给值求值(1)若sin α＝13，则cos 2α＝( )A.89 B.79 C ．－79D ．－89(2)已知sin ⎝⎛⎭⎫π4＋αsin ⎝⎛⎭⎫π4－α＝16，且α∈⎝⎛⎭⎫π2，π，求tan 4α的值． 【解】 (1)选B.cos 2α＝1－2sin 2α＝1－2×⎝⎛⎭⎫132＝79.故选B. (2)因为sin ⎝⎛⎭⎫π4－α＝ sin ⎣⎡⎦⎤π2－⎝⎛⎭⎫π4＋α＝cos ⎝⎛⎭⎫π4＋α， 则已知条件可化为sin ⎝⎛⎭⎫π4＋αcos ⎝⎛⎭⎫π4＋α ＝16， 即12sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4＋α＝16， 所以sin ⎝⎛⎭⎫π2＋2α＝13， 所以cos 2α＝13.因为α∈⎝⎛⎭⎫π2，π， 所以2α∈(π，2π)，从而sin 2α＝－1－cos 22α＝－223，所以tan 2α＝sin 2αcos 2α＝－22， 故tan 4α＝2tan 2α1－tan 22α＝－421－（－22）2＝427.把本例(1)中的条件“sin α＝55”改为“sin α＋cos α＝55”，求sin 2α，cos 2α，tan 2α的值． 解：因为sin α＋cos α＝55， 所以(sin α＋cos α)2＝15，即1＋2sin αcos α＝15，sin 2α＝2sin αcos α＝－45.因为α∈⎝⎛⎭⎫π2，π，所以cos α<0， 所以sin α－cos α>0，所以sin α－cos α＝（sin α－cos α）2＝1－sin 2α＝355，所以cos 2α＝cos 2α－sin 2α＝(cos α＋sin α)(cos α－sin α) ＝55×⎝⎛⎭⎫－355＝－35， 所以tan 2α＝sin 2αcos 2α＝43.(1)三角函数求值问题的一般思路一是对题设条件变形，将题设条件中的角、函数名向结论中的角、函数名靠拢；另一种是对结论变形，将结论中的角、函数名向题设条件中的角、函数名靠拢，以便将题设条件代入结论． (2)另外，注意几种诱导公式的应用，如： ①sin 2x ＝cos ⎝⎛⎭⎫π2－2x ＝cos ⎣⎡⎦⎤2⎝⎛⎭⎫π4－x ＝2cos 2⎝⎛⎭⎫π4－x －1＝1－2sin 2⎝⎛⎭⎫π4－x ； ②cos 2x ＝sin ⎝⎛⎭⎫π2－2x ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4－x ＝2sin ⎝⎛⎭⎫π4－x cos ⎝⎛⎭⎫π4－x ；③cos 2x ＝sin ⎝⎛⎭⎫π2＋2x ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4＋x ＝2sin ⎝⎛⎭⎫π4＋x cos ⎝⎛⎭⎫π4＋x .2.已知cos α＝－34，sin β＝23，α是第三象限角，β∈⎝⎛⎭⎫π2，π. (1)求sin 2α的值； (2)求cos(2α＋β)的值．解：(1)因为α是第三象限角，cos α＝－34，所以sin α＝－1－cos 2α＝－74， 所以sin 2α＝2sin αcos α＝2×⎝⎛⎭⎫－74×⎝⎛⎭⎫－34＝378.(2)因为β∈⎝⎛⎭⎫π2，π，sin β＝23，所以cos β＝－1－sin 2β＝－53， cos 2α＝2cos 2α－1＝2×916－1＝18，所以cos(2α＋β)＝cos 2αcos β－sin 2αsin β ＝18×⎝⎛⎭⎫－53－378×23＝－5＋6724. 二倍角公式在实际中的应用焊接工王师傅遇到了一个难题：如图所示，有一块扇形钢板，半径为1米，圆心角θ＝π3，施工要求按图中所画的那样，在钢板OPQ 上裁下一块平行四边形钢板ABOC ，要求使裁下的钢板面积最大．试问王师傅如何确定A 的位置，才能使裁下的钢板符合要求？最大面积为多少？ 【解】 连接OA ，设∠AOP ＝α，过A 作AH ⊥OP ，垂足为H ，在Rt △AOH 中，OH ＝cos α，AH ＝sin α，所以BH ＝AH tan 60°＝33sin α，所以OB ＝OH－BH ＝cos α－33sin α，设平行四边形ABOC 的面积为S ，则S ＝OB ·AH ＝⎝⎛⎭⎫cos α－33sin α·sin α＝sin αcos α－33sin 2α＝12sin 2α－36(1－cos 2α)＝12sin 2α＋36cos 2α－36＝13⎝⎛⎭⎫32sin 2α＋12cos 2α－36＝13sin ⎝⎛⎭⎫2α＋π6－36. 由于0<α<π3，所以π6<2α＋π6<56π，当2α＋π6＝π2，即α＝π6时，S max ＝13－36＝36，所以当A 是PQ ︵的中点时，所裁钢板的面积最大，最大面积为36平方米．解决此类实际问题，应首先确定主变量角α以及相关的常量与变量，建立关于角α的三角函数式，再利用和(差)角公式或二倍角公式求解．对于求三角函数最值的问题，一般利用三角函数的有界性来解决．3.如图，在某点B 处测得建筑物AE 的顶端A 的仰角为θ，由B 点到E 点的方向前进30 m 至点C 处，测得顶端A 的仰角为2θ，再沿刚才的方向继续前进10 3 m 到D 点，测得顶点A 的仰角为4θ，求θ的大小和建筑物AE 的高．解：因为∠ACD ＝θ＋∠BAC ， 所以∠BAC ＝θ，所以AC ＝BC ＝30 m.又因为∠ADE ＝2θ＋∠CAD ，所以∠CAD ＝2θ， 所以AD ＝CD ＝10 3 m. 在Rt △ADE 中，AE ＝AD ·sin 4θ ＝103sin 4θ，在Rt △ACE 中，AE ＝AC ·sin 2θ＝30sin 2θ， 所以103sin 4θ＝30sin 2θ，即203sin 2θcos 2θ＝30sin 2θ，所以cos 2θ＝32. 又因为2θ∈⎝⎛⎭⎫0，π2，所以2θ＝π6，所以θ＝π12. 所以AE ＝30sin π6＝15(m)．所以θ＝π12，建筑物AE 的高为15 m.规范解答关于三角函数性质的综合问题(本题满分12分)已知函数f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π4(ω>0)的最小正周期为π. (1)求ω的值；(2)讨论f (x )在区间⎣⎡⎦⎤0，π2上的单调性． [解] (1)f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π4 ＝22sin ωx ·cos ωx ＋22cos 2ωx ＝2(sin 2ωx ＋cos 2ωx )＋ 2 ＝2sin ⎝⎛⎭⎫2ωx ＋π4＋ 2.(4分)因为f (x )的最小正周期为π，且ω>0， 从而有2π2ω＝π，故ω＝1.(6分)(2)由(1)知，f (x )＝2sin ⎝⎛⎭⎫2x ＋π4＋ 2. 若0≤x ≤π2，则π4≤2x ＋π4≤5π4.(7分)当π4≤2x ＋π4≤π2，即0≤x ≤π8时，f (x )是递增的； (9分)当π2<2x ＋π4≤5π4，即π8<x ≤π2时，f (x )是递减的． (11分)综上可知，f (x )在区间⎣⎡⎦⎤0，π8上是递增的，在区间⎝⎛⎦⎤π8，π2上是递减的．(12分)(1)对于倍角公式、两角和与差的三角公式、辅助角公式，不仅要熟练正用，还要逆用，变形应用．如本例中两个关键步骤：即处由2(sin 2ωx ＋cos 2ωx )＋2到2sin(2ωx ＋π4)＋2的变化．在处，对2x ＋π4的范围进行判断．(2)在判定函数单调性和求单调区间时，应在给定区间内求解，如本例中⎣⎡⎦⎤0，π2.1．sin π12cos 5π12的值等于( )A ．－12＋34B.12－34 C ．－12－34D.12＋34解析：选B.sin π12cos 5π12＝sin π12sin ⎝⎛π2⎭⎫－5π12＝sin 2π12＝1－cos π62＝1－322＝12－34. 2．如果等腰三角形的周长是底边长的5倍，那么它的顶角的余弦值为( ) A.518 B.34 C.32D.78解析：选D.由题设易知，等腰三角形的腰长是底边长的2倍，如图所示，在△ABC 中，AB ＝AC ，D 为BC 边的中点，设∠BAD ＝θ， 因为AB ＝4BD ，所以sin θ＝14，故cos ∠BAC ＝cos 2θ＝1－2sin 2θ＝1－2×⎝⎛⎭⎫142＝78.3．已知α是第二象限的角，tan(π＋2α)＝－43，则tan α＝________.解析：由tan(π＋2α)＝－43，得tan 2α＝－43，所以2tan α1－tan 2α＝－43.因为α是第二象限的角，所以tan α<0，所以tan α＝－12.★答案★：－124．锐角三角形ABC 中，若B ＝2A ，则sin Bsin A 的取值范围是________．解析：因为B 为锐角，所以0<A <π4.又C 为锐角，且C ＝π－B －A ＝π－3A ， 所以0<π－3A <π2.所以－π2<3A －π<0.所以π2<3A <π，π6<A <π4.所以2<2cos A < 3.所以sin B sin A ＝sin 2A sin A ＝2cos A ∈(2，3)．★答案★：(2，3)[A 基础达标]1．已知cos α＝13，则cos(π－2α)的值等于( )A ．－79B.79C.23D ．－23解析：选B.cos(π－2α)＝－cos 2α＝－2cos 2α＋1 ＝－2×⎝⎛⎭⎫132＋1＝79，故选B. 2．在△ABC 中，若sin B sin C ＝cos 2A2，则△ABC 是( )A ．等边三角形B ．等腰三角形C ．直角三角形D ．等腰直角三角形解析：选B.由sin B sin C ＝1＋cos A2⇒2sin B sin C ＝1－cos(B ＋C )⇒2sin B sin C ＝1－cos B cos C ＋sin B sin C ⇒cos B cos C ＋sin B sin C ＝1⇒cos(B －C )＝1，又－180°<B －C <180°，所以B －C ＝0°⇒B ＝C ⇒△ABC 是等腰三角形． 3．若tan α＝2，则sin 2α－cos 2α1＋cos 2α的值是( )A.76B.32C.16D ．－16解析：选A.原式＝2sin αcos α－cos 2α＋sin 2αsin 2α＋2cos 2α＝2tan α－1＋tan 2αtan 2α＋2＝2×2－1＋2222＋2＝76.4．tan 67°30′－1tan 67°30′的值为( )A ．1 B. 2 C ．2D ．4解析：选C.tan 67°30′－1tan 67°30′＝tan 267°30′－1tan 67°30′＝－22tan 67°30′1－tan 267°30′＝－2tan 135°＝2.5．已知0<α<β<π4，sin α＋cos α＝m ，sin β＋cos β＝n ，则( )A ．m <nB ．m >nC ．mn <1D ．mn >1解析：选A.m 2＝(sin α＋cos α)2＝1＋sin 2α， n 2＝(sin β＋cos β)2＝1＋sin 2β， 因为0<α<β<π4，所以0<2α<2β<π2，因为y ＝sin x 在⎝⎛⎭⎫0，π2上为增函数，所以sin 2α<sin 2β，即m 2<n 2，又m >0，n >0，所以m <n ，故选A.6．化简：sin 2αcos α－sin αcos 2α＝________．解析：sin 2αcos α－sin αcos 2α＝2sin αcos 2α－sin α2cos 2α－1＝sin α（2cos 2α－1）2cos 2α－1＝sin α.★答案★：sin α7．已知tan x ＝2，则tan 2⎝⎛⎭⎫x －π4＝________． 解析：因为tan x ＝2，所以tan 2x ＝2tan x 1－tan 2x＝－43.tan 2⎝⎛⎭⎫x －π4＝tan ⎝⎛⎭⎫2x －π2＝sin ⎝⎛⎭⎫2x －π2cos ⎝⎛⎭⎫2x －π2 ＝－cos 2x sin 2x ＝－1tan 2x ＝34.★答案★：348．函数y ＝12sin 2x ＋sin 2x ，x ∈R 的值域是________．解析：y ＝12sin 2x ＋sin 2x ＝12sin 2x ＋1－cos 2x 2＝12sin 2x －12cos 2x ＋12 ＝22sin ⎝⎛⎭⎫2x －π4＋12， 所以函数的值域为⎣⎡⎦⎤－22＋12，22＋12. ★答案★：⎣⎡⎦⎤－22＋12，22＋12 9．已知π2＜α＜π，cos α＝－45.(1)求tan α的值；(2)求sin 2α＋cos 2α的值．解：(1)因为cos α＝－45，π2＜α＜π，所以sin α＝35，所以tan α＝sin αcos α＝－34.(2)sin 2α＝2sin αcos α＝－2425. cos 2α＝2cos 2α－1＝725，所以sin 2α＋cos 2α＝－2425＋725＝－1725.10．如图，有一块以点O 为圆心的半圆形空地，要在这块空地上划出一个内接矩形ABCD 开辟为绿地，使其一边AD 落在半圆的直径上，另两点B ，C 落在半圆的圆周上．已知半圆的半径长为20 m ，如何选择关于点O 对称的点A ，D 的位置，可以使矩形ABCD 的面积最大？解：连接OB ，设∠AOB ＝θ，则AB ＝OB sin θ＝20sin θ，OA ＝OB cos θ＝20cos θ，且θ∈(0，π2)．因为A ，D 关于点O 对称， 所以AD ＝2OA ＝40cos θ. 设矩形ABCD 的面积为S ，则 S ＝AD ·AB ＝40cos θ·20sin θ ＝400sin 2θ.因为θ∈⎝⎛⎭⎫0，π2， 所以当sin 2θ＝1， 即θ＝π4时，S max ＝400(m 2)．此时AO ＝DO ＝102(m)．故当A 、D 距离圆心O 为10 2 m 时，矩形ABCD 的面积最大，其最大面积是400 m 2.[B 能力提升]11．已知α∈R ，sin α＋2cos α＝102，则tan 2α＝( ) A.43 B.34 C ．－34D ．－43解析：选C.把条件中的式子两边平方，得sin 2α＋4sin αcos α＋4cos 2α＝52，即3cos 2α＋4sin αcosα＝32，所以3cos 2α＋4sin αcos αcos 2α＋sin 2α＝32，所以3＋4tan α1＋tan 2α＝32，即3tan 2α－8tan α－3＝0，解得tan α＝3或tan α＝－13，所以tan 2α＝2tan α1－tan 2α＝－34.12．已知角α，β均为锐角，且1－cos 2α＝sin αcos α，tan(β－α)＝13，则β＝________．解析：由1－cos 2α＝sin αcos α，得1－(1－2sin 2α)＝sin αcos α，即2sin 2α＝sin αcos α. 因为α为锐角，所以sin α≠0，所以2sin α＝cos α，即tan α＝12.法一：由tan(β－α)＝tan β－tan α1＋tan βtan α＝tan β－121＋12tan β＝13，得tan β＝1.因为β为锐角，所以β＝π4.法二：tan β＝tan(β－α＋α)＝tan （β－α）＋tan α1－tan （β－α）tan α＝13＋121－13×12＝1，因为β为锐角，所以β＝π4.★答案★：π413．已知向量a ＝(cos ωx －sin ωx ，sin ωx )，b ＝(－cos ωx －sin ωx ，23cos ωx )，设函数f (x )＝a ·b ＋λ(x ∈R )的图像关于直线x ＝π对称，其中ω，λ为常数，且ω∈⎝⎛⎭⎫12，1. (1)求函数f (x )的最小正周期；(2)若y ＝f (x )的图像经过点⎝⎛⎭⎫π4，0，求函数f (x )在区间⎣⎡⎦⎤0，3π5上的取值范围． 解：(1)f (x )＝a ·b ＋λ＝sin 2ωx －cos 2ωx ＋ 23sin ωx cos ωx ＋λ＝3sin 2ωx －cos 2ωx ＋λ ＝2sin ⎝⎛⎭⎫2ωx －π6＋λ， 且直线x ＝π是f (x )的图像的一条对称轴， 所以2ωπ－π6＝k π＋π2(k ∈Z )，所以ω＝k 2＋13(k ∈Z )．又因为ω∈⎝⎛⎭⎫12，1，所以ω＝56， 所以f (x )的最小正周期为6π5.(2)y ＝f (x )的图像经过点⎝⎛⎭⎫π4，0， 所以f ⎝⎛⎭⎫π4＝0，即λ＝－2sin ⎝⎛⎭⎫2×56×π4－π6＝－2sin π4＝－2， 则f (x )＝2sin ⎝⎛⎭⎫53x －π6－2，又x ∈⎣⎡⎦⎤0，3π5， 则53x －π6∈⎣⎡⎦⎤－π6，5π6，所以函数f (x )在区间⎣⎡⎦⎤0，3π5上的取值范围为[－1－2，2－2]． 14．(选做题)某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数： ①sin 213°＋cos 217°－sin 13°cos 17°； ②sin 215°＋cos 215°－sin 15°cos 15°； ③sin 218°＋cos 212°－sin 18°cos 12°； ④sin 2(－18°)＋cos 248°－sin(－18°)cos 48°； ⑤sin 2(－25°)＋cos 255°－sin(－25°)cos 55°. (1)请根据②式求出这个常数；(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论． 解：(1)计算如下：sin 215°＋cos 215°－sin 15°cos 15° ＝1－12sin 30°＝34.(2)三角恒等式为sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝34.证明如下：法一：sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝sin 2α＋(cos 30°cos α＋sin 30°sin α)2－sin α·(cos 30°cos α＋sin 30°·sin α)＝sin 2α＋34·cos 2α＋32sin αcos α＋14sin 2α－32sin αcos α－12sin 2α＝34sin 2α＋34cos 2α＝34. 法二：sin 2α＋cos 2(30°－α)－sin αcos(30°－α)＝1－cos 2α2＋1＋cos （60°－2α）2－sin α(cos 30°·cos α＋sin 30°sin α)＝12－12cos 2α＋12＋12(cos 60°cos 2α＋sin 60°sin 2α)－32sin α·cos α－12sin 2α＝12－12cos 2α＋12＋14cos 2α＋34sin 2α－34sin 2α－14·(1－cos 2α)＝34.。

学习目标1.会从两角和的正弦、余弦、正切公式推导出二倍角的正弦、余弦、正切公式.2.能熟练运用二倍角的公式进行简单的恒等变换并能灵活地将公式变形运用．知识点一二倍角公式思考1二倍角的正弦、余弦、正切公式就是用α的三角函数表示2α的三角函数的公式．根据前面学过的两角和与差的正弦、余弦、正切公式，你能推导出二倍角的正弦、余弦、正切公式吗？思考2根据同角三角函数的基本关系式sin2α＋cos2α＝1，你能否只用sin α或cos α表示cos 2α？梳理二倍角的正弦、余弦、正切公式sin 2α＝2sin αcos α，(S2α)(3.9)cos 2α＝cos2α－sin2α(C2α)(3.10)＝1－2sin2α (3.11)＝2cos2α－1，(3.12)tan 2α＝2tan α1－tan2α. (T2α)(3.13)知识点二二倍角公式的变形1．公式的逆用2sin αcos α＝sin 2α，sin αcos α＝____________，cos2α－sin2α＝________，2tan α1－tan2α＝tan 2α.2．二倍角公式的重要变形——升幂公式和降幂公式升幂公式1＋cos 2α＝________，1－cos 2α＝________，1＋cos α＝________________，1－cos α＝________________________ .降幂公式cos 2α＝1＋cos 2α2，sin 2α＝1－cos 2α2.类型一 给角求值例1 求下列各式的值：(1)cos 72°cos 36°；(2)13－23cos 215°； (3)1－tan 275°tan 75°；(4)1sin 10°－3cos 10°.反思与感悟 对于给角求值问题，一般有两类：(1)直接正用、逆用二倍角公式，结合诱导公式和同角三角函数的基本关系对已知式子进行转化，一般可以化为特殊角．(2)若形式为几个非特殊角的三角函数式相乘，则一般逆用二倍角的正弦公式，在求解过程中，需利用互余关系配凑出应用二倍角公式的条件，使得问题出现可以连用二倍角的正弦公式的形式．跟踪训练1求下列各式的值： (1)cos 2π7cos 4π7cos 6π7； (2)1sin 50°＋3cos 50°.类型二 给值求值例2(1)若sin α－cos α＝13，则sin 2α＝________. (2)若tan α＝34，则cos 2α＋2sin 2α等于() A.6425B.4825C ．1 D.1625引申探究在本例(1)中，若改为sin α＋cos α＝13，求sin 2α. 反思与感悟 (1)条件求值问题常有两种解题途径：①对题设条件变形，把条件中的角、函数名向结论中的角、函数名靠拢；②对结论变形，将结论中的角、函数名向题设条件中的角、函数名靠拢，以便将题设条件代入结论．(2)一个重要结论：(sin θ±cos θ)2＝1±sin 2θ.跟踪训练2 已知tan α＝2.(1)求tan ⎝⎛⎭⎫α＋π4的值； (2)求sin 2αsin 2α＋sin αcos α－cos 2α－1的值．类型三 利用倍角公式化简例3 化简2cos 2α－12tan ⎝⎛⎭⎫π4－αsin 2⎝⎛⎭⎫π4＋α.反思与感悟 (1)对于三角函数式的化简有下面的要求：①能求出值的应求出值；②使三角函数种数尽量少；③使三角函数式中的项数尽量少；④尽量使分母不含有三角函数；⑤尽量使被开方数不含三角函数．(2)化简的方法：①弦切互化，异名化同名，异角化同角．②降幂或升幂．③一个重要结论：(sin θ±cos θ)2＝1±sin 2θ.跟踪训练3化简下列各式：(1)π4＜α＜π2，则1－sin 2α＝________； (2)α为第三象限角，则1＋cos 2αcos α－1－cos 2αsin α＝________.1.12sin π12cos π12的值等于() A.14 B.18 C.116 D.12 2．sin 4π12－cos 4π12等于() A ．－12 B ．－32 C.12 D.323.tan 7.5°1－tan 27.5°＝________. 4．设sin 2α＝－sin α，α∈⎝⎛⎭⎫π2，π，则tan 2α＝________.5．已知sin ⎝⎛⎭⎫π4－x ＝513，0<x <π4，求cos 2x cos ⎝⎛⎭⎫π4＋x 的值．1．对于“二倍角”应该有广义上的理解，如：8α是4α的二倍；6α是3α的二倍；4α是2α的二倍；3α是32α的二倍；α2是α4的二倍； α3是α6的二倍；α2n ＝2·α2n ＋1(n ∈N ＋)． 2．二倍角余弦公式的运用在二倍角公式中，二倍角的余弦公式最为灵活多样，应用广泛．二倍角的常用形式：①1＋cos 2α＝2cos 2α；②cos 2α＝1＋cos 2α2； ③1－cos 2α＝2sin 2α；④sin 2α＝1－cos 2α2. 答案精析问题导学知识点一思考1sin 2α＝sin(α＋α)＝sin αcos α＋cos αsin α＝2sin αcos α；cos 2α＝cos(α＋α)＝cos αcos α－sin αsin α＝cos 2α－sin 2α；tan 2α＝tan(α＋α)＝2tan α1－tan 2α. 思考2cos 2α＝cos 2α－sin 2α＝cos 2α－(1－cos 2α)＝2cos 2α－1；或cos 2α＝cos 2α－sin 2α＝(1－sin 2α)－sin 2α＝1－2sin 2α.知识点二1.12sin 2αcos 2α 2．2cos 2α2sin 2α2cos 2α22sin 2α2题型探究例1解 (1)cos 36°cos 72°＝2sin 36°cos 36°cos 72°2sin 36° ＝2sin 72°cos 72°4sin 36°＝sin 144°4sin 36°＝14. (2)13－23cos 215°＝－13(2cos 215°－1)＝－13cos 30° ＝－36. (3)1－tan 275°tan 75°＝2·1－tan 275°2tan 75°＝2·1tan 150°＝－2 3. (4)1sin 10°－3cos 10°＝cos 10°－3sin 10°sin 10°cos 10°＝2⎝⎛⎭⎫12cos 10°－32sin 10°sin 10°cos 10°＝4(sin 30°cos 10°－cos 30°sin 10°)2sin 10° cos 10° ＝4sin 20°sin 20°＝4. 跟踪训练1(1)18(2)4 例2(1)89(2)A 引申探究解 由题意，得(sin α＋cos α)2＝19， ∴1＋2sin αcos α＝19， 即1＋sin 2α＝19， ∴sin 2α＝－89. 跟踪训练2 解 (1)tan ⎝⎛⎭⎫α＋π4 ＝tan α＋tanπ41－tan αtan π4＝2＋11－2×1＝－3. (2)sin 2αsin 2α＋sin αcos α－cos 2α－1＝2sin αcos αsin 2α＋sin αcos α－2cos 2α ＝2tan αtan 2α＋tan α－2＝2×24＋2－2＝1. 例3解 方法一原式＝2cos 2α－12·sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－αsin 2⎝⎛⎭⎫π4＋α ＝2cos 2α－12·sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－αcos 2⎝⎛⎭⎫π4－α ＝2cos 2α－1sin ⎝⎛⎭⎫π2－2α＝cos 2αcos 2α＝1. 方法二 原式＝cos 2α2·1－tan α1＋tan α⎝⎛⎭⎫22sin α＋22cos α2 ＝cos 2αcos α－sin αcos α＋sin α(sin α＋cos α)2＝cos 2α(cos α－sin α)(cos α＋sin α)＝cos 2αcos 2α－sin 2α＝1. 跟踪训练3(1)sin α－cos α(2)0当堂训练1．B2.B3.1－324. 3 5．解 原式＝sin ⎝⎛⎭⎫π2＋2x cos ⎝⎛⎭⎫π4＋x ＝2sin ⎝⎛⎭⎫π4＋x cos ⎝⎛⎭⎫π4＋x cos ⎝⎛⎭⎫π4＋x ＝2sin ⎝⎛⎭⎫π4＋x . ∵sin ⎝⎛⎭⎫π4－x ＝cos ⎝⎛⎭⎫π4＋x ＝513，且0<x <π4， ∴π4＋x ∈⎝⎛⎭⎫π4，π2， ∴sin ⎝⎛⎭⎫π4＋x ＝1－cos 2⎝⎛⎭⎫π4＋x ＝1213，∴原式＝2×1213＝2413.。

第一课时 二倍角公式及其应用预习课本P124～125，思考并完成以下问题 1．二倍角的正弦公式是什么？2．二倍角的余弦公式是什么？3．二倍角的正切公式是什么？[新知初探]二倍角的公式[点睛](1)成立的条件：在公式S 2α，C 2α中，角α可以为任意角，T 2α中则只有当α≠k π＋π2且α≠k π2＋π4(k ∈Z)时才成立． (2)倍角公式不局限于2α是α的二倍形式，其他如4α是2α的二倍、α是α2的二倍、3α是3α2的二倍等都是适用的． [小试身手]1．判断下列命题是否正确．(正确的打“√”，错误的打“×”)(1)存在α使得sin 2α＝2sin α，tan 2α＝2tan α ( ) (2)cos 215°－sin 215°＝2cos 215°－1＝1－2sin 215° ( ) 答案：(1)√ (2)√2．若sin α2＝33，则cos α的值为 ( )A ．－23B ．－13C.13D.23解析：选C 因为sin α2＝33，所以cos α＝1－2sin 2α2＝1－2×⎝⎛⎭⎫332＝13. 3．已知α为第三象限角，且cos α＝－55，则tan 2α的值为 ( ) A ．－43 B.43C ．－34 D ．－2解析：选A ∵α为第三象限角， ∴sin α＝－1－cos 2α＝－255，∴tan α＝2，∴tan 2α＝2tan α1－tan 2α＝41－4＝－43.4．sin 22.5°cos 202.5°＝________.解析：sin 22.5°cos 202.5°＝sin 22.5°·(－cos 22.5°)＝－12sin 45°＝－24.答案：－24给角求值[典例] (1)sinπ12cos π12；(2)1－2sin 2750°； (3)2tan 150°1－tan 2150°；(4)1sin 10°－3cos 10°；(5)cos 20°cos 40°cos 80°.[解] (1)原式＝2sin π12cos π122＝sinπ62＝14.(2)原式＝cos(2×750°)＝cos 1 500° ＝cos(4×360°＋60°) ＝cos 60°＝12.(3)原式＝tan(2×150°)＝tan 300°＝tan(360°－60°) ＝－tan 60°＝－ 3.(4)原式＝cos 10°－3sin 10°sin 10°cos 10°＝2⎝⎛⎭⎫12cos 10°－32sin 10°sin 10°cos 10°＝4(sin 30°cos 10°－cos 30°sin 10°)2sin 10°cos 10°＝4sin 20°sin 20°＝4.(5)原式＝2sin 20°·cos 20°·cos 40°·cos 80°2sin 20°＝2sin 40°·cos 40°·cos 80°4sin 20°＝2sin 80°·cos 80°8sin 20°＝sin 160°8sin 20°＝18.根据三角函数式的特征，经过适当变形，同时变换出特殊角，进而利用公式，获得三角函数式的值，在变形中一定要从整体上考虑式子的特征． [活学活用] 化简tan 14°1－tan 214°·cos 28°的结果为 ( )A.sin 28°2 B ．sin 28°C ．2sin 28°D ．sin 14°cos 28° 解析：选Atan 14°1－tan 214°·cos 28°＝12×2tan 14°1－tan 214°·cos 28°＝12tan 28°·cos 28°＝sin 28°2，故选A.三角函数式的化简[典例] 化简：θ)； (2)11－tan θ－11＋tan θ. [解] (1)原式＝1＋cos (2θ＋30°)2＋1－cos (2θ－30°)2＋cos θsin θ＝1＋12(cos 2θcos 30°－sin 2θsin 30°－cos 2θ· cos 30°－sin 2θsin 30°)＋12sin 2θ＝1－sin 2θsin 30°＋12sin 2θ＝1.(2)原式＝1＋tan θ－(1－tan θ)(1－tan θ)(1＋tan θ)＝tan θ＋tan θ1－tan 2θ＝2tan θ1－tan 2θ＝tan 2θ.三角函数式化简的四个方向三角函数式的化简有四个方向，即分别从“角”“函数名”“幂”“形”着手分析，消除差异． [活学活用]化简：2cos 2α－12tan ⎝⎛⎭⎫π4－αsin 2⎝⎛⎭⎫π4＋α.解：法一：原式 ＝cos 2α－sin 2α2×1－tan α1＋tan α⎝⎛⎭⎫sin π4cos α＋cos π4sin α2＝(cos 2α－sin 2α)(1＋tan α)(1－tan α)(cos α＋sin α)2＝(cos 2α－sin 2α)⎝⎛⎭⎫1＋sin αcos α⎝⎛⎭⎫1－sin αcos α(cos α＋sin α)2＝1.法二：原式＝cos 2α2tan ⎝⎛⎭⎫π4－αcos 2⎝⎛⎭⎫π4－α＝cos 2α2sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－α＝cos 2αsin ⎝⎛⎭⎫π2－2α＝cos 2αcos 2α＝1.给值求值[典例] 已知x ∈⎝⎛⎭⎫π4，π2，sin ⎝⎛⎭⎫π4－x ＝－35，求cos 2x 的值．[解] 法一：(变角求值) cos 2x ＝sin ⎝⎛⎭⎫π2－2x ＝2sin ⎝⎛⎭⎫π4－x cos ⎝⎛⎭⎫π4－x ， ∵sin ⎝⎛⎭⎫π4－x ＝－35，x ∈⎝⎛⎭⎫π4，π2， ∴π4－x ∈⎝⎛⎭⎫－π4，0，cos ⎝⎛⎭⎫π4－x ＝45， ∴cos 2x ＝2×⎝⎛⎭⎫－35×45＝－2425. 法二：(变结构求值)由已知条件得cos x －sin x ＝－325，将此式两边平方得2sin x cos x ＝725， ∴sin 2x ＝725.∵x ∈⎝⎛⎭⎫π4，π2，∴2x ∈⎝⎛⎭⎫π2，π. ∴cos 2x ＝－ 1－sin 22x ＝－1－⎝⎛⎭⎫7252＝－2425.解决上面典例要注意角“2x ”与“π4－x ”的变换方法，即cos 2x ＝sin ⎝⎛⎭⎫π2－2x ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4－x ； 常见的此类变换，还有：(1)sin 2x ＝cos ⎝⎛⎭⎫π2－2x ＝cos ⎣⎡⎦⎤2⎝⎛⎭⎫π4－x ； (2)sin 2x ＝－cos ⎝⎛⎭⎫π2＋2x ＝－cos ⎣⎡⎦⎤2⎝⎛⎭⎫π4＋x ； (3)cos 2x ＝sin ⎝⎛⎭⎫π2＋2x ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4＋x . 已知sin ⎝⎛⎭⎫x ＋π4sin ⎝⎛⎭⎫π4－x ＝16，x ∈⎝⎛⎭⎫π2，π，求sin 4x ，cos 4x ，tan 4x 的值． 解：法一：(变角求值) ∵sin ⎝⎛⎭⎫x ＋π4sin ⎝⎛⎭⎫π4－x＝sin ⎝⎛⎭⎫π4＋x cos ⎣⎡⎦⎤π2－⎝⎛⎭⎫π4－x ＝sin ⎝⎛⎭⎫x ＋π4cos ⎝⎛⎭⎫π4＋x ＝12sin ⎝⎛⎭⎫2x ＋π2＝12cos 2x ＝16， ∴cos 2x ＝13.∵x ∈⎝⎛⎭⎫π2，π，∴2x ∈(π，2π)． ∴sin 2x ＝－223.∴sin 4x ＝2sin 2x cos 2x ＝－429.∴cos 4x ＝2cos 22x －1＝2×19－1＝－79.∴tan 4x ＝sin 4x cos 4x ＝427. 法二：(变结构求值) 由sin ⎝⎛⎭⎫π4＋x sin ⎝⎛⎭⎫π4－x ＝16， 得22(sin x ＋cos x )×22(cos x －sin x )＝16， ∴－sin 2x ＋cos 2x ＝13，即cos 2x ＝13.下同解法一．层级一 学业水平达标1．已知cos x ＝－14，x 为第二象限角，那么sin 2x ＝ ( )A ．－154B ．±158C ．－158 D.158解析：选C 因为cos x ＝－14，x 为第二象限角，所以sin x ＝154，所以sin 2x ＝2sin x cosx ＝2×154×⎝⎛⎭⎫－14＝－158，故选C. 2．若tan α＝3，则sin 2αcos 2α的值等于 ( )A ．2B ．3C ．4D ．6 解析：选D sin 2αcos 2α＝2sin αcos αcos 2α＝2tan α＝2×3＝6，故选D.3．已知sin 2α＝23，则cos 2⎝⎛⎭⎫α＋π4等于( ) A.16 B.13 C.12 D.23 解析：选A ∵sin 2α＝23，∴cos 2⎝⎛⎭⎫α＋π4＝1＋cos ⎝⎛⎭⎫2α＋π22＝1－sin 2α2＝1－232＝16.4．已知α为锐角，且满足cos 2α＝sin α，则α等于 ( )A ．75°B ．45°C ．60°D ．30°解析：选D 因为cos 2α＝1－2sin 2α，故由题意，知2sin 2α＋sin α－1＝0，即(sin α＋1)(2sin α－1)＝0.因为α为锐角，所以sin α＝12，所以α＝30°.故选D.5．若α∈⎝⎛⎭⎫0，π2，且sin 2α＋cos 2α＝14，则tan α的值等于 ( ) A.22 B.33C. 2D. 3 解析：选D 由已知得sin 2α＋1－2sin 2α＝14，所以sin 2α＝34，而α∈⎝⎛⎭⎫0，π2，所以sin α＝32，cos α＝12. 因此，tan α＝ 3.6．(cos 75°－sin 75°)(cos 75°＋sin 75°)＝________.解析：(cos 75 °－sin 75°)(cos 75°＋sin 75°)＝cos 275°－sin 275°＝cos 150°＝－cos 30°＝ －32. 答案：－327．已知α为第二象限角，sin α＝35，则tan 2α＝______.解析：由于α为第二象限角，且sin α＝35，∴cos α＝－45，tan α＝－34，∴tan 2α＝2tan α1－tan 2α＝2×⎝⎛⎭⎫－341－⎝⎛⎭⎫－342＝－321－916＝－247.答案：－2478．计算sin 10°sin 30°sin 50°sin 70°＝________.解析：原式＝12cos 20°cos 40°cos 80°＝23·sin 20°cos 20°cos 40°cos 80°23·2sin 20° ＝sin 160°16sin 20°＝sin 20°16sin 20°＝116. 答案：1169．已知α，β均为锐角，且tan α＝7，cos β＝255，求α＋2β的值．解：∵β为锐角，且cos β＝255，∴sin β＝55. ∴tan β＝12，tan 2β＝2tan β1－tan 2β＝2×121－⎝⎛⎭⎫122＝43.∴0<2β<π2，0<α＋2β<π，又tan(α＋2β)＝tan α＋tan 2β1－tan αtan 2β＝7＋431－7×43＝－1，∴α＋2β＝3π4.10．化简：sin 2α·sin 2β＋cos 2α·cos 2β－12cos 2α·cos 2β.解：法一：(从角入手)原式＝sin 2α·sin 2β＋cos 2α·cos 2β－12·(2cos 2α－1)·(2cos 2β－1)＝sin 2α·sin 2β－cos 2α·cos 2β＋cos 2α＋cos 2β－12＝sin 2α·sin 2β＋cos 2α·sin 2β＋cos 2β－12＝sin 2β＋cos 2β－12＝1－12＝12.法二：(从次数入手)原式＝1－cos 2α2·1－cos 2β2＋1＋cos 2α2·1＋cos 2β2－12cos 2α·cos 2β＝14(1＋cos 2α·cos 2β－cos 2α－cos 2β)＋14(1＋cos 2α·cos 2β＋cos 2α＋cos 2β)－12·cos2α·cos 2β＝14＋14＝12.层级二 应试能力达标1．已知sin ⎝⎛⎭⎫π4－x ＝35，则cos ⎝⎛⎭⎫π2－2x 的值为 ( ) A.1925 B.1625 C.1425 D.725 解析：选D 因为sin ⎝⎛⎭⎫π4－x ＝35， 所以cos ⎝⎛⎭⎫π2－2x ＝cos 2⎝⎛⎭⎫π4－x ＝1－2sin 2⎝⎛⎭⎫π4－x ＝725.2．若f (x )＝2tan x －2sin 2x2－1sin x 2cos x 2，则f ⎝⎛⎭⎫π12的值为 ( )A ．43 B.833C ．4D ．8解析：选D ∵f (x )＝2tan x －2sin 2x 2－1sin x 2cos x 2＝2tan x －－cos x 12sin x ＝2tan x ＋2cos xsin x ＝2⎝⎛⎭⎫sin x cos x ＋cos x sin x ＝2×sin 2x ＋cos 2x sin x cos x ＝4sin 2x ， ∴f ⎝⎛⎭⎫π12＝4sinπ6＝412＝8. 3．函数y ＝2cos 2⎝⎛⎭⎫x －π4－1是 ( ) A ．最小正周期为π的奇函数 B ．最小正周期为π的偶函数 C ．最小正周期为π2的奇函数D ．最小正周期为π2的偶函数 解析：选A y ＝2cos 2⎝⎛⎭⎫x －π4－1＝cos ⎝⎛⎭⎫2x －π2＝sin 2x ，为奇函数，最小正周期T ＝2π2＝π，故选A.4．设向量a ＝(1，cos θ)与b ＝(－1,2cos θ)垂直，则cos 2θ等于 ( ) A.22 B.12C ．0D ．－1解析：选C 由向量互相垂直，得a ·b ＝－1＋2cos 2θ＝cos 2θ＝0.5．设sin 2α＝－sin α，α∈⎝⎛⎭⎫π2，π，则tan 2α的值是________．解析：∵sin 2α＝2sin αcos α＝－sin α，∴cos α＝－12，又α∈⎝⎛⎭⎫π2，π，∴sin α＝32，tan α＝－3，∴tan 2α＝2tan α1－tan 2α＝－231－(－3)2＝ 3.答案： 36．已知sin ⎝⎛⎭⎫π6－α＝13，则cos 2⎝⎛⎭⎫π3＋α的值是________． 解析：∵sin ⎝⎛⎭⎫π6－α＝13， ∴cos ⎝⎛⎭⎫π3－2α＝cos 2⎝⎛⎭⎫π6－α ＝1－2sin 2⎝⎛⎭⎫π6－α＝79， ∴cos 2⎝⎛⎭⎫π3＋α＝cos ⎝⎛⎭⎫2π3＋2α＝cos ⎣⎡⎦⎤π－⎝⎛⎭⎫π3－2α ＝－cos ⎝⎛⎭⎫π3－2α＝－79. 答案：－797．已知sin x 2－2cos x 2＝0. (1)求tan x 的值；(2)求cos 2xcos ⎝⎛⎭⎫5π4＋x sin (π＋x )的值．解：(1)由sin x 2－2cos x 2＝0，知cos x 2≠0，∴tan x 2＝2，∴tan x ＝2tan x 21－tan 2x 2＝2×21－22＝－43. (2)由(1)，知tan x ＝－43， ∴cos 2x cos ⎝⎛⎭⎫5π4＋x sin (π＋x ) ＝cos 2x －cos ⎝⎛⎭⎫π4＋x (－sin x )＝cos 2x －sin 2x ⎝⎛⎭⎫22cos x －22sin x sin x ＝(cos x －sin x )(cos x ＋sin x )22(cos x －sin x )sin x ＝2×cos x ＋sin x sin x＝2×1＋tan x tan x＝24.8．已知函数f (x )＝2cos ⎝⎛⎭⎫x －π6，x ∈R. (1)求f (π)的值；(2)若f ⎝⎛⎭⎫α＋2π3＝65，α∈⎝⎛⎭⎫－π2，0，求f (2α)的值． 解：(1)f (π)＝2cos ⎝⎛⎭⎫π－π6＝－2cos π6＝－2×32＝－ 3.(2)因为f ⎝⎛⎭⎫α＋2π3＝2cos ⎝⎛⎭⎫α＋2π3－π6＝2cos ⎝⎛⎭⎫α＋π2 ＝－2sin α＝65，所以sin α＝－35. 又α∈⎝⎛⎭⎫－π2，0，故cos α＝1－sin 2α＝ 1－⎝⎛⎭⎫－352＝45， 所以sin 2α＝2sin αcos α＝2×⎝⎛⎭⎫－35×45＝－2425，cos 2α＝2cos 2α－1＝2×⎝⎛⎭⎫452－1＝725. 所以f (2α)＝2cos ⎝⎛⎭⎫2α－π6＝2cos 2αcos π6＋2sin 2α sin π6＝2×725×32＋2×⎝⎛⎭⎫－2425×12＝73－2425.。