湖南省怀化市高二上学期期末考试数学试卷含答案

2021-2022学年湖南省高二（上）期末数学试卷一、单选题（本大题共8小题，共40分。

在每小题列出的选项中，选出符合题目的一项）1.已知集合，，则( )A. B.C. D.2.若，则的最小值为( )A. B. C. D. 53.已知向量，，则( )A. B. 10 C. 5 D. 254.已知直线：与：垂直，则m与n的等比中项为( )A. B. C. D.5.已知双曲线的渐近线与圆相切，则( )A. B. 5 C. D.6.若的三个顶点坐标分别为，，，则外接圆的圆心坐标为( )A. B. C. D.7.某公司技术部为了激发员工的工作积极性，准备在年终奖的基础上再增设30个“幸运奖”，投票产生“幸运奖”，按照得票数假设每人的得票数各不相同排名次，发放的奖金数成等差数列．已知前10名共发放2000元，前20名共发放3500元，则前30名共发放( )A. 4000元B. 4500元C. 4800元D. 5000元8.在长方体中，，，O是AC的中点，点P在线段上，若直线OP与平面所成的角为，则的取值范围是( )A. B. C. D.二、多选题（本大题共4小题，共20分。

在每小题有多项符合题目要求）9.下列四个关于圆锥曲线的命题中，为真命题的是( )A. 椭圆与双曲线有相同的焦点B. 设A，B为两个定点，k为非零常数，若，则动点P的轨迹为双曲线C. 方程的两根可分别作为椭圆和双曲线的离心率D. 动圆P过定点且与定直线l：相切，则圆心P的轨迹方程是10.如图，平面平面ABEF，四边形ABCD是正方形，四边形ABEF是矩形，若G是EF的中点，，，则( )A.B. 平面ABCDC.D. 三棱锥外接球的表面积是11.已知为曲线上一动点，则( )A. 的最小值为B. 存在一个定点和一条定直线，使得P到定点的距离等于P到定直线的距离C. P 到直线距离的最小值小于D. 的最小值为612.设和分别为数列和的前n项和．已知，，则( )A. 是等比数列B. 是递减数列C.D.三、填空题（本大题共4小题，共20分）13.若复数z满足，则z的虚部为__________.14.过圆柱的轴作截面，得到一个边长为2的正方形，则该圆柱的表面积是__________.15.已知函数的图象关于直线对称，则m的最大值为__________.16.数列满足，前12项的和为298，则__________.四、解答题（本大题共6小题，共70分。

一、单选题1．已知向量，则它们的位置关系是（ ）()()()1,2,2,3,6,6,2,1,2a b c =-=--=A ．∥，∥B ．，a b a c a b ⊥ a c ⊥ C ．，∥D ．∥，a b ⊥ b c a b b c ⊥ 【答案】D【分析】由向量坐标运算即可判断共线和垂直.【详解】由题可知：得， 3b a =- //a b 2240a c a c ⋅=+-=⇒⊥66120b c b c ⋅=--+=⇒⊥ 故选：D.2．在三棱柱中，是的中点，是的中点，且，则111ABC A B C -D 1CC F 1A B DF AB AC αβ=+A ．B ．1,12αβ==-1,12αβ=-=C ．D ．11,2αβ==-11,2αβ=-=【答案】A【分析】根据向量加法的多边形法则可得，从而可求1111111111=222222DF DC CB BF CC CB BA A A AB AC BA AA AB AC =++=++=+-++-α，β，【详解】根据向量加法的多边形法则以及已知可得，1111111111=222222DF DC CB BF CC CB BA A A AB AC BA AA AB AC =++=++=+-++-∴α=，β=﹣1， 12故选A ．【点睛】本题主要考查了平面向量加法的三角形法则及多边形法则的应用，解题的关键是要善于利用题目中正三棱柱的性质，把所求的向量用基本向量表示．3．已知的三个顶点是，，，则边上的高所在的直线方程为ABC A ()30A -,()6,2B ()0,6C -AC （ ）A ．B ．220x y +-=220x y --=C ．D ．240x y --=2140x y +-=【答案】B【分析】求出边上的高所在的直线的斜率，再利用点斜式方程可得答案. AC 【详解】因为，所以边上的高所在的直线的斜率为， 623==--AC k AC 12k =所以边上的高所在的直线方程为， AC ()1262-=-y x 即. 220x y --=故选：B.4．已知定点，点在圆上运动，则线段的中点的轨迹方程是（ ） (3,0)B A 22(1)4x y ++=AB M A ． B ． 22(1)1x y ++=22(2)4x y -+=C ． D ．22(1)1x y -+=22(2)4x y ++=【答案】C【分析】设再表达出的坐标代入圆方程化简即可. (,)M x y A 22(1)4x y ++=【详解】设，则满足.故 .故.(,)M x y (),A A Ax y 3,(,)22A A x y x y +⎛⎫=⎪⎝⎭232A Ax x y y =-⎧⎨=⎩23(2),A x y -又点在圆上.故. A 22(1)4x y ++=2222(231)(2)4(1)1x y x y -++=⇒-+=故选:C【点睛】本题主要考查了轨迹方程的求法，属于基础题型.5．已知，是椭圆：的两个焦点，点在上，则的最大值为（ ）1F 2F C 22194x y +=M C 12MF MF ⋅A ．13 B ．12C ．9D ．6【答案】C【分析】本题通过利用椭圆定义得到，借助基本不等式1226MF MF a +==即可得到答案．212122MF MF MF MF ⎛+⎫⋅≤ ⎪⎝⎭【详解】由题，，则，229,4a b ==1226MF MF a +==所以（当且仅当时，等号成立）． 2121292MF MF MF MF ⎛+⎫⋅≤= ⎪⎝⎭123MF MF ==故选：C ．【点睛】6．已知双曲线C ：，，分别是双曲线的左､右焦点，是双()222210,0x y a b a b -=>>1F 2F M 曲线右支上一点连接交双曲线左支于点，若是以为直角顶点的等腰直角三角1MF C N 2MNF A 2F 形，则双曲线的离心率为（ ）A B C ． D2【答案】B【分析】利用双曲线的定义结合余弦定理可以建立关于，的齐次方程，即可求出离心率 a c【详解】设，则，，，，因为2MF m =2NF m =MN =12NF m a =-12MF m a =-，所以，故，122MF MF a -=22a a -=m =在中，由余弦定理可知，整理得12NF F △()()22242822c a a a ⎛=-+--⋅⋅ ⎝，即，所以22412c a =23e =e =故选：B7．设数列的通项公式为，则（ ） {}n a 27n a n =-1215a a a +++= A ．153 B ．210C ．135D ．120【答案】A【分析】根据数列的通项公式，判断数列为等差数列，并求得数列的前3项均小于，从第4{}n a 0项起均大于，对所求式子去掉绝对值，利用等差数列前项和，求得式子值.0n 【详解】因为，所以数列是均小于，均大于的等差270 3.5n a n n =-≥⇒≥{}n a 123,,a a a 045,,a a 0数列，所以1215152413a a a a a a a a --++++=-++ 121341253())2(a a a a a a a a ++=++++-+ .选A.15(523)2(531)2⋅-+=----153=【点睛】本题考查数列中的基本量法求数列的前项和，解题的关键在于判断各项的正负.n 8．已知等比数列的首项为2，公比为，其前项和记为，若对任意的，均有{}n a 13-n n S *n ∈N 恒成立，则的最小值为（ ）13n nA SB S ≤-≤B A -A ．B ．C ．D ．7294114136【答案】B 【分析】Sn •，①n 为奇数时，Sn •，根据单调性可得：Sn ≤2；②n 为3322=-1(3n -3322=+1()3n 32＜偶数时，Sn •，根据单调性可得：≤Sn ．可得Sn 的最大值与最小值分别为：2，3322=-1()3n 4332＜43．考虑到函数y ＝3t 在（0，+∞）上单调递增，即可得出．1t-【详解】Sn •， 12[1)33312213n ⎛⎤-- ⎥⎝⎦==-⎛⎫-- ⎪⎝⎭1()3n-①n 为奇数时，Sn •，可知：Sn 单调递减，且•，∴Sn ≤S 1＝2；3322=+1()3n 3322+13()32n >32＜②n 为偶数时，Sn •，可知：Sn 单调递增，且•，∴S 2≤Sn ．3322=-1()3n 3322-13()32n <43=32＜∴Sn 的最大值与最小值分别为：2，． 43考虑到函数y ＝3t 在（0，+∞）上单调递增，1t-∴A．14113(3)34343n min n S S ≤-=⨯-=B ． 1111(3)3222n max n S S ≥-=⨯-=∴B ﹣A 的最小值． 11139244=-=故选B ．【点睛】本题考查了等比数列的求和公式及数列单调性的判断和应用问题，考查了恒成立问题的转化，考查了推理能力与计算能力，属于中档题．9．已知P 是平行四边形ABCD 所在平面外一点，如果，，()2,1,4AB =--()4,2,0AD = ，则下列结论中错误的是（ ） ()1,2,1AP =--A ．B ．AP AB ⊥ ⊥ AP AD C ．是平面ABCD 的法向量D ．APAP//BD 【答案】D【分析】根据题意，结合线面位置关系的向量判断方法，一一判断即可.【详解】因为，所以，故A 正确；2240AB AP ⋅=--+=AB AP ⊥ 因为，所以，故B 正确； 4400AP AD ⋅=-++= ⊥AP AD 由A ，B 知，C 正确；与不平行，故D 错误． ()2,3,4BD AD AB =-= ()1,2,1AP =--故选：D.二、多选题10．若直线过点，且在两坐标轴上截距的绝对值相等，则直线方程可能为（ ） ()1,2A l A ． B ． 10x y -+=30x y +-=C ． D ．20x y -=10x y --=【答案】ABC【分析】讨论直线过原点时和直线不过原点时，分别求出对应的直线方程即可． 【详解】当直线经过原点时，斜率为，所求的直线方程为y =2x ，即； 20210k -==-20x y -=当直线不过原点时，设所求的直线方程为x ±y =k ，把点A （1，2）代入可得1-2=k ，或1+2=k ， 求得k =-1，或k =3，故所求的直线方程为，或； 10x y -+=30x y +-=综上知，所求的直线方程为、，或． 20x y -=10x y -+=30x y +-=故选：ABC ．【点睛】本题考查了利用分类讨论思想求直线方程的问题，是基础题．11．已知双曲线，以为圆心，为半径作圆2222:1(0,0)x y C a b a b -=>>A A b ，圆与双曲线的一条渐近线交于，两点，则有A A C M NA ．渐近线方程为B ．渐近线方程为 y =y x =C ．D ．60MAN ∠=︒120MAN ∠=︒【答案】BC【分析】由离心率公式化简可得渐近线方程，通过求圆心A 到渐近线的距离结合直角22222c a b a a +=三角形可得到的值.MAN ∠【详解】双曲线离心率为 2222:1y ,x y b C x a b a -==±的渐近线方程为c a = 222222222411,33c a b bb b a a a a a 则则，+==+===故渐近线方程为， y x =取MN 的中点P,连接AP,利用点到直线的距离公式可得, d AP ab c==则， cos ab AP a c PAN AN b c∠===所以则221cos cos 2212a MAN PAN c ∠=∠=⨯-=60MAN ∠=︒故选BC【点睛】本题考查双曲线的简单的几何性质，考查双曲线的渐近线和离心率的应用，考查圆的有关性质，属于中档题.12．已知等比数列的公比为，其前项的积为，且满足，，，{}n a q n n T 11a >9910010a a ->99100101a a -<-则（ ） A ．B ．01q <<9910110a a -<C ．的值是中最大的 D ．使成立的最大正整数数的值为198100T n T 1n T >n 【答案】ABD【分析】根据题目所给已知条件，结合等比数列的性质对选项逐一分析，由此确定正确选项. 【详解】∵，∴，∴. 9910010a a ->199000a a >0q >∵，∴， 99100101a a -<-()()99100110a a --<又，∴.故A 正确.11a >01q <<由A 选项的分析可知，，∴，∴，，故991a >10001a <<2991011001a a a =<9910110a a -<1009910099T T a T =<B 正确，C 不正确.∴，()()()()99198121981198219799100991001T a a a a a a a a a a a ===> ，()()()1991991219819911992198991011001001T a a a a a a a a a a a a ===< ∴使成立的最大正整数数的值为198，故D 正确. 1n T >n 故选：ABD三、填空题13．如图，在空间四边形中，若，，，则____.ABCD AB a = BD b = AC c = CD =【答案】a b c +- 【分析】由向量的运算法则即得【详解】因为，，，AB a =BD b = AC c = 所以，CD CB BD CA AB BD AC AB BD a b c =+=++=-++=+- 故答案为：a b c +-14．已知圆C:，当m 变化时，圆C 上的点与原点的最短距离是_________. 22(2)(4)1x y m -++-=【答案】1【详解】解：圆C ：（x ﹣2）2+（y +m ﹣4）2＝1表示圆心为C （﹣2，﹣m +4），半径R ＝1的圆，求得|OC |， ∴m ＝4时，|OC |的最小值为2故当m 变化时，圆C 上的点与原点的最短距离是﹣R ＝2﹣1＝1， ()OC 的最小值故答案为1．15．抛物线的焦点为，其准线与相交于A ，两点，若为等边()220x py p =>F 22133y x -=B ABF △三角形，则___________. p =【答案】6【分析】求出抛物线的焦点和准线方程，求出AB 的长，根据为等边三角形，得到关于p 的ABF △方程，即可求得答案.【详解】抛物线的焦点为，其准线为，()220x py p =>(0,)2p F 2p y =-将与联立，得，解得 2py =-22133y x -=221312x p -=x =则， ||AB =由于， ABF △|AB p =，解得 ，p =6p =故答案为：616．如图所示：正方形上连接着等腰直角三角形，等腰直角三角形腰上再连接正方形，…，如此继续下去得到一个树形图形，称为“勾股树”．若某勾股树含有个正方形，且其最大的正方形的边1023，则其最小正方形的边长为________．【答案】132【详解】由题意，正方形的边长构成以为首项，以1023个正方形，则有，∴，∴，故答案11221023n -++⋯+=10n =9132=为. 132四、解答题17．设是各项均为正数的等比数列，且，．{}n a 124a a +=39a =Ⅰ求的通项公式； (){}n a Ⅱ．(31323)log log log n a a a ++⋯⋯+【答案】（Ⅰ）（Ⅱ）13n n a -=()12n n -【分析】Ⅰ首项利用已知条件求出数列的通项公式;Ⅱ利用Ⅰ的结论，进一步对数关系式的变()()()换求出数列的和．【详解】Ⅰ设首项为，公比为q 的各项均为正数的等比等列， ()1a 且，．124a a +=39a =则：，112149a a q a q +=⎧⎨=⎩解得：，负值舍去， 334q =-或()所以：，11a =则：．11133n n n a --=⋅=（Ⅱ）由于：，13n n a -=所以：．31323log log log n a a a ++⋯⋯+， ()312log n a a a =⋅⋯，()121n =++⋯+-，()()1112n n -+-=．()12n n -=【点睛】本题考查的知识要点：数列的通项公式的求法及应用，对数关系式的应用，等差数列的前n 项和的应用，主要考查学生的运算能力和转化能力，属于基础题型．18．设公比为正数的等比数列 的前 项和为 ，已知 ， ，数列 满{}n a n n S 38a =248S ={}n b 足 .24log n n b a =(1)求数列 和 的通项公式；{}n a {}n b (2)是否存在，使得 是数列 中的项？若存在，求出 的值；若不存在，请*N m ∈12m m m b b b ++⋅{}n b m 说明理由.【答案】(1)，.62nn a -=424n b n =-+(2)存在， 或 56【分析】（1）设的公比为 ，利用等比数列的通项公式以及前n 项和公式，列方程组，{}n a ,0q q >求得公比和首项，即得；根据即可求得；62nn a -=24log n n b a =424n b n =-+（2）结合（1）可得的表达式，进行变形化简为，由题意设 是数列 12m m m b b b ++⋅243t t ⎛⎫++ ⎪⎝⎭12m m m b b b ++⋅中的第项，则 ，分类讨论t 的取值，可求得答案. {}n b 0m ()024346t m t ⎛⎫++=- ⎪⎝⎭【详解】（1）设的公比为 ，又 ,，{}n a ,0q q >38a =248S =则 ，解得 或 （舍），2111848a q a a q ⎧=⎨+=⎩12q =A 13q =-所以 ， ，12832a q ==1613222n n n a --⎛⎫=⨯= ⎪⎝⎭，()6224log 4log 246424n n n b a n n -===⨯-=-+即数列 的通项公式为 ，{}n a 62nn a -=数列 的通项公式为.{}n b 424n b n =-+（2）， ()()()()122442044651644m m m m m m m b b b m m++----⋅==--由于，令 ，， ， *N m ∈4t m =-3,0t t ≤≠Z t ∈所以， ()()12421243m m m t t b b t b t t ++++⋅⎛⎫==++ ⎪⎝⎭设是数列 中的第项，则 ， 12m m m b b b ++⋅{}n b 0m ()024346t m t ⎛⎫++=- ⎪⎝⎭则 为小于等于的整数，t 为2的约数，所以 ， 23t t++5{}2,1,1,2t ∈--当或时， ，不合题意； 1t =2236t t++=当 或 时， ，与题意相符. 1t =-2t =-230t t++=所以当 或 时， 1t =-2t =-即或 时，是数列 中的项. 5m =6m =12m m m b b b ++⋅{}n b19．如图，在三棱柱 中，底面，，，111ABC A B C -1AA ⊥ABC 90CAB ∠= 2AB AC ==1AA =， 为的中点， 为侧棱 上的动点．M BC P 1BB(1)求证：平面平面；APM ⊥11BB C C (2)试判断直线 与是否能够垂直．若能垂直，求的长；若不能垂直，请说明理由．1BC AP PB 【答案】(1)证明见解析(2)不能垂直，理由见解析【分析】（1）利用，推出平面，即可证明面面垂直； AM BC ⊥1AM BB ⊥AM ⊥11BB C C（2）建系，写出的坐标，设，利用直线与能垂直，数量积为零，1,,B C A (0BP t t =≤≤1BC AP求出，，不能垂直. t =1t BB =>【详解】（1）因为在三棱柱 中，底面，，，111ABC A B C -1BB ⊥ABC 90CAB ∠= 2AB AC ==为的中点， 为侧棱 上的动点．1AA =M BC P 1BB 所以 ，，AM BC ⊥1AM BB ⊥因为，平面1BC BB B = 1,BC BB ⊂11BB C C 所以平面，AM ⊥11BB C C 因为平面，AM ⊂APM 所以平面平面．APM ⊥11BB C C （2）以为原点，为轴，为轴，为轴，建立空间直角坐标系，A AC x AB y 1AA z，，， ()020B ，，(1C ()000A ，，设， (0BP t t =≤≤则， ()(()10,2,,2,,0,2,P t BC AP t =-=若直线与能垂直，则，1BC AP 1040BC AP ⋅=-=解得， t =因为， 1t BB =>=所以直线与不能垂直．1BC AP 20．已知圆心坐标为（2，1）的圆C 与y 轴相切.(1)求圆C 的方程；(2)设直线与圆C 交于A ，B 两点，从条件①，条件②中选择一个作为已知，求m 0l x y m -+=：的值.条件①②：.AB =120ACB ∠= 【答案】(1)()()22214x y -+-=(2)1-【分析】（1）根据题意得出圆心和半径，即可得圆的方程；（2）对于①②均可根据垂径定理分析得圆心到直线的距离为1，结合点到直线的距离公式运算求解.【详解】（1）由题意可得：圆C 的圆心坐标为，半径为，()2,1C 2r =故圆C 的方程为. ()()22214x y -+-=（2）若选①：圆心C 到直线的距离， 0l x y m -+=：1d ==，解得1m =-若选②：圆心C 到直线的距离，0l x y m -+=：cos 601d r =︒=，解得1m =-21．已知椭圆经过点，动点. ()222210x y a b a b +=>>12P ⎫⎪⎪⎭()()2,0M t t >(1)求椭圆的标准方程；(2)求以为直径且被直线截得的弦长为的圆的方程；OM 3450x y --=2(3)设是椭圆的右焦点，过点作的垂线与以为直径的圆交于点，证明线段的长为F F OM OM N ON 定值，并求出这个定值.【答案】(1) 2212x y +=(2)()()22125x y -+-=(3)【分析】（1）根据已知条件可得出关于、、的方程组，解出这三个量，可得出椭圆的方程； a b c （2）确定所求圆的圆心坐标与半径，利用勾股定理求出圆心到直线的距离，结合点3450x y --=到直线的距离公式可得出关于的方程，由求出的值，即可得出所求圆的方程； t 0t >t （3）设，由可得出，再由可求得的值，再利()00,N x y 0FN OM⋅= 0022x ty +=0MN ON ⋅= 2200x y +用平面内两点间的距离公式可求得的值，即可证得结论成立.ON 【详解】（1）解：由题意得，① c a =因为椭圆经过点，② 12P ⎫⎪⎪⎭22121b ⎛⎫ ⎪⎝⎭+=又，③ 222a b c =+由①②③解得，，所以椭圆方程为. 22a =221b c ==2212x y +=（2）解：以为直径的圆的圆心为，半径 OM 1,2t ⎛⎫ ⎪⎝⎭r =故以为直径的圆的方程为， OM ()2221124t t x y ⎛⎫-+-=+ ⎪⎝⎭因为以为直径的圆被直线截得的弦长为 ，OM 3450x y --=2所以圆心到直线的距离. 3450x y --=2t d ==由点到直线的距离公式可得，，解得， 32522552t t t d --+===0t > 4t =因此，所求圆的方程为 .()()22125x y -+-=（3）证明：设，则，，，，()00,N x y ()001,FN x y =- ()2,OM t = ()002,MN x y t =-- ()00,ON x y = 因为，则，所以，， FN OM ⊥ ()00210FN OM x ty ⋅=-+= 0022x ty +=又因为，则，MN ON ⊥()()000020MN ON x x y y t ⋅=-+-=所以，.22000022x y x ty +=+==【点睛】方法点睛：求定值问题常见的方法有两种：（1）从特殊入手，求出定值，再证明这个值与变量无关；（2）直接推理、计算，并在计算推理的过程中消去变量，从而得到定值．22．已知椭圆 的离心率为 为椭圆的右焦点. ()2222:10x y C a b a b +=>>F (1)求椭圆 的方程；C (2)已知点 ， 是椭圆上的点，求 的最小值；()3,0A P PA PF ⋅ (3)点 是以长轴为直径的圆 上一点，圆 在点 处的切线交直线 于点 ，求M O O M 3x =N 证：过点 且垂直于 的直线 过定点.M ON l 【答案】(1) 22132x y +=(2)6-(3)证明见解析【分析】（1）由长轴长得，再由离心率得，然后求出得椭圆方程；a c b（2）用三角换元法，设，，由数量积的坐标运算把数量积表示为)P θθ[]()0,2πθ∈θ的三角函数形式，利用三角函数的性质、二次函数性质可得最小值；（3）设 ，，则 ，由圆切线性质得出，按和()3,N t ()00,M x y 22003x y +=00330x y t +-=0=t 0t ≠分类讨论得出直线的方程，根据刚才和关系式可得直线所过定点坐标．MN 【详解】（1）由题意得 解得， 2a c a⎧=⎪⎨=⎪⎩a =1c =所以 ，则椭圆 的方程为 . 2222b a c =-=C 22132x y +=（2）由 是椭圆 上的动点， P 22132x y +=可设 ，，)P θθ[]()0,2πθ∈则，， ()3,PA θθ=()1,PF θθ= 所以 ()()()()31PA PF θθθθ⋅=+⋅2233cos 2sin θθθ=-++ ,2cos 5θθ=-+因为，[]cos 1,1∈-θ所以当 时， 取得最小值，最小值为 ，cos 1θ=PA PF ⋅ 6-（3）由题意知，圆 的方程为 ，O 223x y +=设 ，，则 ，()3,N t ()00,M x y 22003x y +=由 ，得 ，223ON MN =+()()222200333t x y t +=+-+-即 ， 2222000093692t x x y ty t +=+-++-+即 ，2200003620x x y ty +-+-=因为 ，所以 ，22003x y +=00330x y t +-=当 时，，直线 的方程为 ，直线 过椭圆的右焦点 ，0=t 01x =l 1x =l ()1,0F 当 时，直线 的方程为 ， 0t ≠MN ()003y y x x t-=--即 ，即 ，0033ty ty x x -=-+()31ty x =--直线 过椭圆的右焦点 ， l ()1,0F综上所述，直线 过椭圆 的右焦点 .l C ()1,0F 【点睛】方法点睛：直线过定点问题，一般设出动点坐标（或其他参数），由动点坐标（参数）表示出动直线方程，再结合动点坐标（参数）满足的性质观察直线方程得出定点坐标．。

湖南省怀化市2012-2013年高二期末考试数学（理）试题本试卷分第一部分（选择题）和第二部分（非选择题）两部分，共150分.时量：120分钟.第一部分（选择题）一．选择题（本大题共8个小题，每小题5分，共计40分，在每小题给出的四个选项中，只有一项符合题目要求） 1．数列4,3,2,1,的通项公式可以是A ．5n a n =-B ．62n a n =-C ．3n a n =+D ．22n a n =+ 2．下列不等式恒成立的是A ．22a b a b >⇒> B ．||||a b a b >⇒>C ．11a b a b>⇒< D ．,a b c d a c b d ><⇒->- 3．不等式230x y +-≤表示的平面区域（用阴影表示）是4． 在数列{}n a 中，13a =，且12n n a a +-=（n ∈N *），则10a 为A ．17B ．19C ．21D ．235．已知双曲线2218x y a -=的一条渐近线为2y x =，则实数a 的值为 A ．16 B ．8 C ．4 D ．26．如图，已知平行六面体1111OABC O A B C -，点G 是上底面1111O A B C 的中心，且a OA =， b OC =，=1，则用a ，b ，c 表示向量OG 为A ．)2(21c b a ++B ．)2(21c b a ++C ．)2(21c b a ++ D ．)(21c b a ++ 7． 已知0x >，则函数234x x y x++=的最小值是GAC B 1O 1C 1A 1OA ．8 B． C．1 D．18．设变量,x y 满足约束条件10302x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩，，，则目标函数2z x y =-的最小值是A ．5-B ．4-C ．3-D ．0第二部分（非选择题）二、填空题：(本大题共7个小题，每小题5分，共35分，把正确答案填在题中横线上)9．命题“若2x >，则24x >”的逆否命题是 ．10．不等式2310x x ≥+的解集是 ． 11．等比数列{}n a 的前n 项和为n S ，若632827S S =，则公比q = ． 12．已知)3,1,2(-=，)2,4(，y -=，且)(+⊥，则y 的值为 ．13．椭圆2213616x y +=上一点M 到左焦点1F 的距离为2，N 是线段1MF 的中点(O 为坐标原点)，则||ON = ．14．已知0x >，则函数y =的最大值是 ．15．设抛物线2:2(0)C y px p =>的焦点为F ，准线为l ，A 为C 上一点，已知以F 为圆心，FA 为半径的圆F 交l 于,B D 两点，若BDF ∆为等边三角形，ABD ∆的面积为6，则p 的值为 ，圆F 的方程为 ．三、解答题：(本大题共6个小题，共75分，解答应写出文字说明、证明过程或演算步骤) 16．（本小题满分12分）求双曲线221169y x -=的实轴和虚轴的长、顶点和焦点的坐标、离心率．17．（本小题满分12分）如图，某军舰艇位于岛屿A 的正西方C 处， 且与岛屿A 相距120海里．经过侦察发现，国 际海盗艇以100海里/小时的速度从岛屿A 出发 沿东偏北60︒方向逃窜，同时，该军舰艇从C 处出发沿东偏北α的方向匀速追赶国际海盗船， 恰好用2小时追上． （1）求该军舰艇的速度； （2）求sin α的值．18．（本小题满分12分）已知2()4f x x x =-，2()1g x m x =-(m ∈R )． （1）求当[]0,3x ∈时()f x 的最大值和最小值；（2）对[]11,1x ∀∈-，[]00,3x ∃∈，使10()()g x f x =，求m 的取值范围．19．（本小题满分13分）在四棱锥P OABC -中，PO ⊥底面OABC ，60OCB ∠=︒，90AOC ABC ∠=∠=︒, 且2OP OC BC ===.(1)若D 是PC 的中点，求证：//BD 平面AOP ; (2)求二面角P AB O --的余弦值．20．（本小题满分13分）已知{}n a 是等差数列，其前n 项和为n S ，{}n b 是等比数列，且112a b ==，3424a b +=，5424S b -=．（1）求数列{}n a 与{}n b 的通项公式；（2）对任意n ∈N *，是否存在正实数λ，使不等式9n n a b λ-≤恒成立，若存在，求出λ 的最小值，若不存在，说明理由．21．（本小题满分13分）DOCAB P已知椭圆2222:1(0)x y C a b a b+=>>的右焦点(1,0)F ，离心率为12．过点F 的直线l 交椭圆C 于,A B 两点，且27||||311FA FB ≤⋅≤． （1）求椭圆C 的方程；（2）求直线l 的斜率的取值范围怀化市2012年下学期期末教学质量统一检测试卷高二数学（理）参考答案与评分标准一、选择题：题号 1 2 3 4 5 6 7 8 答案 AD B C D A C B二、填空题：9．若24x ≤，则2x ≤；10．(][),25,-∞-+∞； 11．13； 12．12； 13．5； 14．34； 15．3，223122x y ⎛⎫-+= ⎪⎝⎭（前者记3分，后者记2分）．三、解答题：16解：由题意，得双曲线的焦点在y 轴上，4,3a b ==，………2分则5c = ……………4分 所以双曲线的实轴、虚轴的长分别为8,6， ………………6分 顶点坐标为()0,4,(0,4)-， ………………8分 焦点坐标为()()0,5,0,5-， ………………10分 离心率为54c e a == ………………12分17解：（1）依题意知，120,1002200CAB AB ∠=︒=⨯=,120AC =，ACB α∠=， 在ABC ∆中，由余弦定理得2222cos BC AB AC AB AC CAB =+-⋅∠222001202200120cos120=+-⨯⨯︒ 78400=，解得280BC =………………4分所以该军舰艇的速度为1402BC=海里/小时 ……………6分 （2）在ABC ∆中，由正弦定理，得 sin sin120AB BCα=︒…………8分即200sin1202sin 280AB BC α︒=== ……………12分 18解：（1）因为()2()24f x x =--在[]0,2上递减，在[]2,3上递增，所以max ()(0)0f x f ==，min ()(2)4f x f ==-…………6分（2）记[]4,0A =-，2()1g x m x =-在[]1,1-上的值域为B ．因为20m ≥，所以221,1B m m ⎡⎤=---⎣⎦，依题意得B A ⊆……………10分即221410m m ⎧--≥-⎨-≤⎩，解得11m -≤≤…………12分 19 解：（1）如图，建立空间直角坐标系O xyz -．连接OB ,易知OBC ∆为等边三角形，(0,0,2),(0,2,0),,0)P C B ，则(0,1,1),D (3,0,1)BD =-．又易知平面AOP 的法向量为 (0,2,0)OC =,由3002100BD OC ⋅=-+⨯+⨯=,得 BD OC ⊥,所以//BD 平面AOP ………………………6分(2)在OAB ∆中，2,30OB AOB ABO =∠=∠=︒,则120OAB ∠=︒,由正弦定理,得OA =,即A ，所以3(,1,0)AB =，(3,1,2)PB =-． 设平面PAB 的法向量为(,,)m x y z =，由30320m AB m AB x y m PB m PB x y z ⎧⎧⊥⋅=+=⎪⎪⇒⎨⎨⊥⎪⎪⎩⋅=+-=⎩， 令x =1,1y z =-=，即(3,1,1)m =-…………………10分yxzDO CA B P又平面OABC 的法向量为(0,0,2)n OP ==,所以，||cos ,5||||5m n m n mn ⋅<>===⨯． 即二面角P AB O --13分 20解：设数列{}n a 的公差为d ，数列{}n b 的公比为q ，则334354124322224242510224a b d d q S b q a d q -==⎧++=⎧⎧⇒⇒⎨⎨⎨-==+-=⎩⎩⎩……………4分 所以31,2n n n a n b =-=……………6分（2）存在正实数λ，使不等式9n n a b λ-≤恒成立，即3102nn λ-≥对任意n ∈N *恒成立． 设3102n n n c -=，则1113(1)10310133222n nn n n n n nc c ++++----=-=…………8分 当5n ≥时，1n n c c +<，{}n c 为单调递减数列；当15n ≤<时，1n n c c +>，{}n c 为单调递增数列。

湖南省怀化市2017-2018学年高二上学期期末考试数学（理）试题一、选择题 本大题共12道小题。

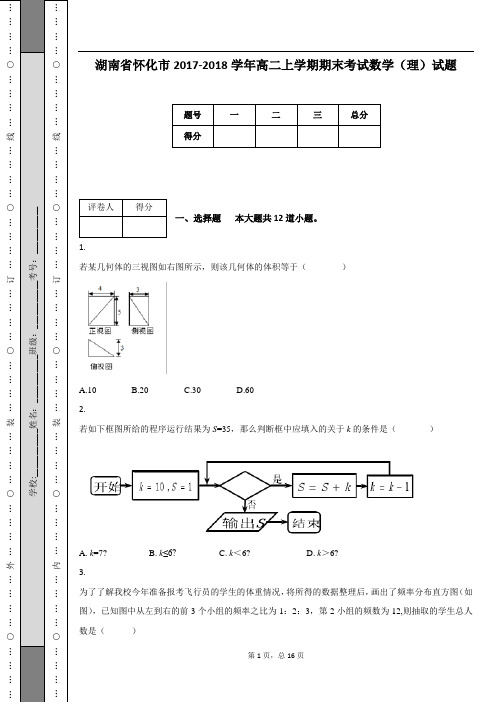
1.若某几何体的三视图如右图所示，则该几何体的体积等于（）A.10B.20C.30D.602.若如下框图所给的程序运行结果为S =35，那么判断框中应填入的关于k 的条件是（）A. k =7?B. k ≤6?C. k ＜6?D. k ＞6?3.为了了解我校今年准备报考飞行员的学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为12,则抽取的学生总人数是（）A.12B.24C.48D.564.河南洛阳的龙门石窟是中国石刻艺术宝库之一，现为世界文化遗产，龙门石窟与莫高窟、云冈石窟、麦积山石窟并称中国四大石窟.现有一石窟的某处“浮雕像”共7层，每上层的数量是下层的2倍，总共有1016个“浮雕像”，这些“浮雕像”构成一幅优美的图案，若从最下层往上“浮雕像”的数量构成一个数列{a n }，则log 2(a 3·a 5)的值为（ ） A.16B.12C.10D.85.以A (1,3)，B (－5,2)为端点的线段的垂直平分线方程是（）A.380x y -+=B.340x y ++=C.360x y -+=D.330x y ++=6.已知函数(1),0()(m 1)1,0ln x m x f x ax b x ++≥⎧<-⎨-+<⎩，对于任意s R ∈，且0s ≠，均存在唯一实数t ，使得()()f s f t =，且s ≠t ，若关于x 的方程()2m f x f ⎛⎫= ⎪⎝⎭有4个不相等的实数根，则a 的取值范围是（）A.(－4,－2)B.(－1,0)C.(－2,－1)D.(－4,－1)∪(－1,0)7.将函数sin cos 22y x x ϕϕ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭的图象沿x 轴向右平移8π个单位后，得到一个偶函数的图象，则φ的取值不可能是（）A.54π-B.4π-C.4π D.34π 8.下列函数中，既是偶函数又在(0,+∞)上单调递增的函数是（ ） A.3y x =B.21y x =-+C.2y x =D.1y x =+9.设集合{}2230A x x x =--<，{}ln B x y x ==,则A B 等于（）A.(0,3)B.(0,2)C.(0,1)D.(1,2)10.函数1()22xf x x ⎛⎫=-+ ⎪⎝⎭的零点所在的一个区间是（） A.(2,3)B.(0,1)C.(－1,0)D.(1,2)11.设m ，n 是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（ ）A.若m α∥，n α∥，则m n ∥B.若αβ∥，m α⊂，n β⊂，则m n ∥C. 若αβ⊥，m αβ=，n α⊂则n β⊥D.若m α⊥，m n ∥，n β⊂则αβ⊥12.已知直线x y a +=与圆224x y +=交于A ,B 两点，且OA OB OA OB +=-uu r uu u r uu r uu u r（其中O 为坐标原点），则实数a 的值为（ ）A.2C.2或－2或一、填空题 本大题共4道小题。

湖南高二年级期末联合考试数学（答案在最后）注意事项：1．答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上．2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．3．考试结束后，将本试卷和答题卡一并交回．4．本试卷主要考试内容：人教A 版选择性必修第一册，第二册至5.2一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.某物体运动s t 后，其位移（单位：m ）为2122y t t=+．在24t ≤≤这段时间里，该物体的平均速度为（）A.5m/sB.6m/sC.8m/sD.10m/s【答案】A 【解析】【分析】根据平均速度的含义，进行计算即可求得答案.【详解】当2t =时，位移为2122262⨯+⨯=，当4t =时，位移为21424162⨯+⨯=，在24t ≤≤这段时间里，该物体的平均速度为：1665m/s 42-=-．故选：A.2.直线:10l -=的倾斜角为（）A.45︒B.60︒C.120︒D.135︒【答案】D 【解析】【分析】根据直线方程求斜率，进而可得倾斜角.【详解】设l 的倾斜角为α，则0180α︒≤<︒，由题可知l 的斜率为tan 1k α==-，所以l 的倾斜角为135︒．故选：D.3.在数列{}n a 中，已知11a =，112n n n a a a +=+，若17m a =，则m =（）A.2B.3C.4D.5【答案】C 【解析】【分析】通过取倒数的方法，证得数列1{}n a 是等差数列，求得121n n a =-，进而求出121n a n =-，解决问题即可.【详解】由112n n n a a a +=+，11a =，取倒数得：1112n na a +=+，则1{}n a 是以111a =为首项，2为公差的等差数列．所以11(1)221n n n a =+-⨯=-，所以121n a n =-；由于11217m a m ==-，故4m =．故选：C.4.在三棱锥-P ABC 中，M 为AC 的中点，则PM =（）A.1122BA BC BP ++B.1122BA BC BP +-C.111222BA BC BP +-D.111222BA BC BP ++【答案】B 【解析】【分析】连接BM ，根据空间向量的运算法则，准确化简，即可求解.【详解】连接BM ，根据向量的运算法则，可得1122PM BM BP BA BC BP =-=+-.故选：B.5.过抛物线2:2(0)C y px p =>的焦点的直线与抛物线C 相交于A ，B 两点，若线段AB中点的坐标为(4,，则p =（）A.4 B.3C.2D.1【答案】A 【解析】【分析】利用点差法及中点与焦点坐标分别表示直线AB 的斜率，可建立关于p 的方程，求解可得.【详解】设11(,)A x y ，22(,)B x y ，则2112222,2,y px y px ⎧=⎨=⎩，两式作差得，2212121212()()2()y y y y y y p x x -=+-=-，当12x x =时，则AB 中点坐标为焦点,02p F ⎛⎫⎪⎝⎭，不满足题意；当12x x ≠时，得1212122y y px x y y -=-+．设线段AB 中点M ，因为M坐标(4,，且过焦点F ，所以12y y +=则AB的斜率42AB FM k k p -===-，解得4p =．故选：A.6.若三条不同的直线1:20l ax y ++=，2:10l x y +-=，3:30l x y -+=不能围成一个三角形，则a 的取值集合为（）A.{1,1}-B.{4,1}C.1,12⎧⎫-⎨⎬⎩⎭D.{4,1,1}-【答案】D 【解析】【分析】分线线平行和三线共点讨论即可.【详解】若12//l l ，则1a -=-，解得1a =．若13//l l ，则1a -=，解得1a =-．若1l ，2l ，3l 交于一点，联立方程组1030x y x y +-=⎧⎨-+=⎩，解得得12x y =-⎧⎨=⎩，代入20ax y ++=，得220a -++=，解得4a =，故a 的取值集合为{4,1,1}-．故选：D .7.如图，三角形蜘蛛网是由一些正三角形环绕而成的图形，每个正三角形的顶点都是其外接正三角形各边的中点．现有17米长的铁丝材料用来制作一个网格数最多的三角形蜘蛛网，若该三角形蜘蛛网中最大的正三角形的边长为3米，则最小的正三角形的边长为（）A.34米 B.38米 C.316米 D.332米【答案】B 【解析】【分析】根据题意，构造正三角形周长满足的等比数列，结合等比数列前n 项和公式及指数不等式进行求解.【详解】由题可知，该三角形蜘蛛网中三角形的周长从大到小是以9为首项，12为公比的等比数列.设最小的正三角形的边长为1132n -⎛⎫⨯ ⎪⎝⎭米，则191217112n ⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦≤-，则11218n⎛⎫≥ ⎪⎝⎭，即218n ≤，得4n ≤，故最小的正三角形的边长为313328⎛⎫⨯= ⎪⎝⎭米.故选：B.8.已知双曲线C ：221x y -=的左、右焦点分别为1F ，2F ，直线l ：2y x m =-与C 相交于A ，B 两点，若1F AB 的面积是2F AB 面积的3倍，则m =（）A.B.C.或D.或【答案】B 【解析】【分析】设1F 到直线AB 的距离为1d ，2F 到直线AB 的距离为2d ，根据题意得到123d d =，列出方程求得m ，结合0∆>，即可求解.【详解】依题意，双曲线C ：221x y -=的左、右焦点分别为()1F，)2F ，设1F 到直线AB 的距离为1d ，2F 到直线AB 的距离为2d ，则1d =2d =，因为1F AB 的面积是2F AB 面积的3倍，所以123d d =，即3m m -=，解得m =，联立方程组2221y x m x y =-⎧⎨-=⎩，整理得223410x mx m -++=，则()22Δ161210m m =-+>，解得23m >，所以m =．故选：B.【点睛】关键点睛：本题解决的关键是将面积比转化为距离的比，从而得解.二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9.等差数列{}n a 的前n 项和为n S ，若79a =，443S a =，则（）A.{}n a 的公差为1B.{}n a 的公差为2C.418S =D.20232025a =【答案】ACD 【解析】【分析】列出方程组，求出等差数列的公差和首项，判断A ，B ；根据等差数列通项公式以及前n 项和公式即可判断C ，D.【详解】设{}n a 的公差为d ，由79a =，443S a =，得111694639a d a d a d+=⎧⎨+=+⎩，解得131a d =⎧⎨=⎩，故A 正确，B 错误；414618S a d =+=，2023120222025a a d =+=，C ，D 正确.故选：ACD10.下列结论正确的是（）A.若sin 2y x x =-，则cos 2y x '=--B.若(1)ln y x x =+，则1ln 1y x x'=++C.若23ex xy -=，则23(23)ex xy x -'=- D.若21e x x y +=，则2(1)e xx y --'=【答案】BCD 【解析】【分析】由导数的四则运算和复合函数的导数公式计算.【详解】对A ,若sin 2y x x =-，则()()sin 2cos 2y x x x ''=='--，A 选项不正确；对B ,若(1)ln y x x =+，则()1(1)ln (1)ln ln 1y x x x x x x'=+++=+'+'，B 选项正确；对C ,若23e xxy -=，则()222333e (23)e xxxxy x x x '--=-'=-，C 选项正确．对D ,若21exx y +=，则()()()()22221e 1e (1)ee x xxx x x x y ''+-+--='=，D 选项正确．故选：BCD11.在棱长为2的正方体1111ABCD A B C D -中，,E E 分别为棱1,AD DD 的中点，G 为线段1B C 上的一个动点，则（）A.三棱锥D EFG -的体积为定值B.存在点G ，使得平面//EFG 平面11AB DC.当113CG CB = 时，直线EG 与1BC 所成角的余弦值为20D.当G 为1B C 的中点时，三棱锥1A EFG -的外接球的表面积为22π3【答案】ABD 【解析】【分析】对于A 项，由等体积法D EFG G DEF V V --=即可判断，对于B 项，运用空间向量坐标法计算两个平面法向量平行求解即可，对于C 项，运用空间向量坐标公式计算异面直线所成角余弦值即可，对于D 项，由1||||||||OA OE OF OG ===列方程求解即可.【详解】对于A 项，因为平面11BCC B //平面DEF ，1B C ⊂平面11BCC B ，所以1B C //平面DEF ，所以点G 到平面DEF 的距离h 为定值，又13D EFG G DEF DEF V V S h --==⋅△，DEF 的面积为定值，所以三棱锥D EFG -的体积为定值，故A 项正确；建立如图1所示的空间直角坐标系，则(2,0,0)A ，1(0,0,2)D ，()()()()()()112,0,2,0,2,0,1,0,0,0,0,1,2,2,2,2,2,0,A C E F B B ()10,2,2C ，对于B 项，()10,2,2AB =，()12,0,2AD =- ，()()()12,0,2,1,0,1,1,2,0CB EF EC ==-=- ，设()12,0,2,01CG tCB t t t ==≤≤ ，则()21,2,2EG EC CG t t =+=-．设平面EFG 的法向量为()111,,n x y z =，由()11111021220n EF x z n EG t x y tz ⎧⋅=-+=⎪⎨⋅=-++=⎪⎩ ，令12x =，可得()2,14,2n t =- ．设平面11AB D 的法向量为()222,,m x y z =，由122122220220m AB y z m AD x z ⎧⋅=+=⎪⎨⋅=-+=⎪⎩ ，令21x =，可得()1,1,1m =- ．若平面EFG ∥平面11AB D ，则2142111t -==-，解得3t 4=，故B 项正确；对于C 项，建立如图1所示的空间直角坐标系，当1122,0,333CG CB ⎛⎫== ⎪⎝⎭ 时，()()122121,2,0,0,,2,,2,0,23333EG BC ⎛⎫⎛⎫=-+=-=- ⎪ ⎪⎝⎭⎝⎭．设直线EG 与1BC 所成的角为θ，则1182cos 8241229EG BC EG BC θ⋅==⋅⨯ ，即直线EG 与1BC 所成角的余弦值为38282，故C 项错误；对于D 项，如下图，当G 为1B C 的中点时，()()()()12,0,2,1,0,0,0,0,1,1,2,1A E F G ．设三棱锥1A EFG -的外接球的球心为(),,O x y z ，半径为r ，则2222222222222222(2)(2)(1)(1)(1)(2)(1)r x y z r x y z r x y z rx y z ⎧=-++-⎪=-++⎪⎨=++-⎪⎪=-+-+-⎩，解得2762376116x y z r ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩，所以三棱锥1A EFG -的外接球的表面积为2224π3r π=，故D 项正确．故选：ABD.12.已知F 是椭圆2222:1(0)x y C a b a b+=>>的右焦点，直线y kx =与椭圆C 交于A ，B 两点，M ，N 分别为AF ，BF 的中点，O 为坐标原点，若60MON ∠=︒，则椭圆C 的离心率可能为（）A.32B.910C.12D.134【答案】BD 【解析】【分析】根据题意，先画出图象，然后判断四边形1AF BF 为平行四边形，由60MON ∠=︒可得1120FAF ∠=︒，进而结合椭圆的定义与基本不等式可得有关,a c 的不等式，解不等式得到离心率的取值范围，从而逐项判断四个选项即可得到答案.【详解】根据题意，图象如图所示：设1F 为椭圆C 的左焦点，因为直线y kx =与椭圆C 交于A ，B 两点，所以由椭圆的对称性得OA OB =，又1OF OF =，于是四边形1AF BF 为平行四边形.因为M ，N 分别为AF ，BF 的中点，O 是1F F 中点，所以1//AF OM ，1//BF ON ，平行四边1AF BF 中160AF B MON ∠=∠=︒,1120FAF ∠=︒，在1AF F 中，2221112cos 120F FAF AF AF AF =+-∠()()()()222211111344AF AF AF AFAF AF AF AF AF AF ++=+-≥+-=.因为直线y kx =斜率存在，所以A ，B 两点不在y 轴上，即1AF AF ≠，又在2222:1(0)x y C a b a b+=>>中，112,2AF AF a FF c +==，所以，()221134AF AFF F +>，即2243c a ≥，又a c >，所以22314c a <<，即3e <12<.综上所述，3,12e ⎛⎫∈ ⎪ ⎪⎝⎭；因为313,,1222⎛⎫∉ ⎪ ⎪⎝⎭，故A ，C 错误；223758191210010010⎛⎫⎛⎫=<=< ⎪ ⎪ ⎪⎝⎭⎝⎭，即9,1102⎛⎫∈ ⎪ ⎪⎝⎭，故B 正确；1244=<<，即,142⎛⎫∈ ⎪ ⎪⎝⎭，故D 正确.故选：BD ．三、填空题：本题共4小题，每小题5分，共20分．13.已知点A '是点(2,1,2)A -在坐标平面Oxy 内的射影，则OA '=__________．【答案】【解析】【分析】根据给定条件，求出点A '的坐标，再利用向量模的坐标表示即得.【详解】由点A '是点(2,1,2)A -在坐标平面Oxy 内的射影，得(2,1,0)A '-，即(2,1,0)OA '=-，所以OA '=故答案为14.已知()f x '是函数()f x 的导函数，且0()3f x '=，则000()(2)lim x f x x f x x x∆→-∆-+∆=∆__________．【答案】9-【解析】【分析】根据题意结合导数的定义运算求解.【详解】由题意可得：0000000()(2)()(2)lim 3lim 3()93x x f x x f x x f x x f x x f x x x∆→∆→-∆-+∆-∆-+∆'=-=-=-∆-∆．故答案为：9-.15.若直线310x y +-=是圆22280x y ax +--=的一条对称轴，则点P 与该圆上任意一点的距离的最小值为__________．【答案】1【解析】【分析】利用圆关于直线对称可知该直线过圆心(,0)a ，可得1a =，再利用定点到圆上点距离的最值的求法即可求得结果.【详解】由题可知，该圆的圆心为(,0)a ，直线310x y +-=过圆心，则10a -=，解得1a =，则该圆的方程转化为22(1)9x y -+=，该圆圆心为()1,0，半径为3，易知圆心与P 的距离为2=，故点P 与该圆上任意一点的距离的最小值为321-=．故答案为：116.在数列{}n a 中，11a =，1e n n n a a ++=，其中e 是自然对数的底数，令1232111e e1e n n n S a a a a -=++++ ，则()1lne e n nS n a +-=____________．【答案】1n -【解析】【分析】根据题意，得到123211e e e en n n S a a a a -=++++ ，两式相加，结合等比数列的求和公式和对数的运算法则，即可求解.【详解】由1232111e e 1e n n n S a a a a -=++++ ，得123211e e e en n n S a a a a -=++++ ，则()()()()112231211111e e e e en n n n n n S a a a a a a a a ---+=++++++++ ，则()111e e en nn S n a -+=+，故()1e eln 1n nS n n a +-=-．故答案为：1n -.四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17.已知数列{}n a 满足14a =，且对于任意m ，*n ∈N ，都有m n m n a a a +=．（1）证明{}n a 为等比数列，并求{}n a 的通项公式；（2）若21log n nb a =，求数列1{}n n b b +的前n 项和n S ．【答案】（1）证明见解析，4nn a =（2）44nn +【解析】【分析】（1）取1m =，得到14n n a a +=，得到{}n a 是4为公比的等比数列，求出通项公式；（2）裂项相消得到111141n n b b n n +⎛⎫=- ⎪+⎝⎭，再进行求和即可.【小问1详解】取1m =，则由m n m n a a a +=，得11n n a a a +=．因为14a =，所以14n n a a +=，所以{}n a 是以4为首项，4为公比的等比数列，故114n n n a a q-==．【小问2详解】由（1）可知22111log log 42n n n b a n===，则111114(1)41n n b b n n n n +⎛⎫==- ⎪++⎝⎭，故11111114223144n n S n n n ⎛⎫=-+-+⋅⋅⋅+-= ⎪++⎝⎭．18.已知四边形ABCD 的三个顶点(1,0)A ，(3,2)B -，(4,1)C -．（1）求过A ，B ，C 三点的圆的方程．（2）设线段AB 上靠近点A 的三等分点为E ，过E 的直线l 平分四边形ABCD 的面积．若四边形ABCD 为平行四边形，求直线l 的方程．【答案】（1）22515222x y ⎛⎫⎛⎫-++=⎪ ⎪⎝⎭⎝⎭（2）550x y --=【解析】【分析】（1）方法一：根据斜率分析可知AB BC ⊥，结合直角三角形的外接圆的性质分析求解；方法二：设圆的一般方程，代入A ，B ，C 三点运算求解即可；（2）利用向量关系求得52,33E ⎛⎫-⎪⎝⎭.方法一：根据题意可知直线l 过线段AC 的中点51,22M ⎛⎫- ⎪⎝⎭，再利用直线的两点式方程运算求解；方法二：设l 与CD 相交于点()22,F x y ，可知13CF DC =-uu u r uuur ，利用向量关系求得点101,33F ⎛⎫-⎪⎝⎭，再利用直线的两点式方程运算求解.【小问1详解】方法一：因为(1,0)A ，(3,2)B -，(4,1)C -，则20131AB k --==--，1(2)143BC k ---==-，由1AB BC k k ⋅=-，得AB BC ⊥，则过A ，B ，C 三点的圆的圆心为线段AC 的中点51,22M ⎛⎫-⎪⎝⎭，半径122r AC ===，所以过A ，B ，C 三点的圆的方程为22515222x y ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭；方法二：设过A ，B ，C 三点的圆的方程为220x y Dx Ey F ++++=，则10133201740D F D E F D E F ++=⎧⎪+-+=⎨⎪+-+=⎩，解得514D E F =-⎧⎪=⎨⎪=⎩，故过A ，B ，C 三点的圆的方程为22540x y x y +-++=，即22515222x y ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭.【小问2详解】设()11,E x y ，由题意可得：(2,2)DC AB ==-uuu r uu u r，()111,AE x y =- ，因为线段AB 上靠近点A 的三等分点为E ，则122,333AE AB ⎛⎫==- ⎪⎝⎭ ，则1121323x y ⎧-=⎪⎪⎨⎪=-⎪⎩，解得115323x y ⎧=⎪⎪⎨⎪=-⎪⎩，即52,33E ⎛⎫- ⎪⎝⎭．方法一：直线l 平分四边形ABCD 的面积，可知直线l 过线段AC 的中点51,22M ⎛⎫-⎪⎝⎭，所以直线l 的方程为253312552323y x +-=-+-，整理得550x y --=；方法二：设l 与CD 相交于点()22,F x y ，则()224,1CF x y =-+，由直线l 平分四边形ABCD 的面积，可得122,333CF DC ⎛⎫=-=- ⎪⎝⎭ ，则22243213x y ⎧-=-⎪⎪⎨⎪+=⎪⎩，解得2210313x y ⎧=⎪⎪⎨⎪=-⎪⎩，即101,33F ⎛⎫- ⎪⎝⎭，所以直线l 的方程为2533121053333y x +-=-+-，整理得550x y --=.19.已知函数32()f x x ax bx =++的图象经过点(1,1)A ，且在点A 处的切线与直线:0l x y +=垂直．（1）求a ，b 的值；（2）求经过点(2,4)且与曲线()y f x =相切的切线方程．【答案】（1）22a b =-⎧⎨=⎩（2）20x y -=或680x y --=【解析】【分析】（1）求导，根据题意结合导数的几何意义分析列式求解；（2）设切点320000(,22)x x x x -+，切线斜率()2000342k f x x x =-'=+，求直线方程并代入点(2,4)运算求解即可.【小问1详解】由32()f x x ax bx =++，则2()32f x x ax b '=++，因为()f x 的图象在点(1,1)A 处的切线与直线:0l x y +=垂直，则()()1111321f a b f a b ⎧=++=⎪⎨=++='⎪⎩，解得22a b =-⎧⎨=⎩.【小问2详解】由（1）可设切线与曲线()y f x =相切于点320000(,22)x x x x -+，则切线斜率()2000342k f x x x =-'=+，则切线的方程为322000000(22)(342)()y x x x x x x x --+=-+-，将点(2,4)代入方程整理得3220000044(2)0x x x x x -+=-=，解得00x =或02x =．当00x =时，切线方程为20x y -=．当02x =时，切线方程为680x y --=．故经过点(2,4)且与曲线()y f x =相切的切线方程为20x y -=或680x y --=．20.如图，在三棱锥-P ABC 中，PA ⊥平面ABC ，AB BC ⊥，24AC BC ==，F 是PC 的中点，且⊥AF PB ．（1）求AP 的长;（2）求二面角B AF C --的正弦值.【答案】（1）AP =（2）4【解析】【分析】（1）结合垂直关系，以B 为坐标原点建立空间直角坐标系，利用⊥AF PB 计算出AP 的长度即可；（2）利用向量法求出平面ABF 的法向量与平面AFC 的法向量，进而求出二面角B AF C --的正弦值即可.【小问1详解】因为PA ⊥平面ABC ，AB BC ⊥，故以B 为坐标原点，建立如下图所示的空间直角坐标系．设AP a =，由24AC BC ==，得(0,0,0)B ，(0,3,0)A ，(0,3,)P a ，(2,0,0)C ．因为F 是PC 的中点，所以3,2a F ⎛⎫ ⎪⎝⎭，则1,3,2a AF ⎛⎫=- ⎪⎝⎭ ，(0,23,)BP a = ．又⊥AF PB ，所以2602a AF BP ⋅=-+= ，解得3a =，故3AP =．【小问2详解】由（1）可知，3,3)F ，则(1,3,3)AF = ，(0,23,0)AB =- ，(2,23,0)AC =-．设平面ABF 的法向量为111(,,)m x y z =，则111133030x z ⎧+=⎪⎨-=⎪⎩，令11z =，得(3,0,1)m = ．设平面AFC 的法向量为222(,,)n x y z =，则222223302230x z x ⎧+=⎪⎨-=⎪⎩，令21y =，得(3,1,0)n = ．所以3cos ,4m n m n m n ⋅〈〉==-，故二面角B AF C --237144⎛⎫--= ⎪⎝⎭．21.已知{}n a 是首项为1的等差数列，{}n b 是公比为2的等比数列，且12b a =，24b a =．（1）求{}n a 和{}n b 的通项公式；（2）在{}n a 中，对每个正整数k ，在k a 和1k a +之间插入k 个k b ，得到一个新数列{}n c ，设n T 是数列{}n c 的前n 项和，比较66T 与20000的大小关系．【答案】（1）n a n =，2nn b =（2）6620000T <【解析】【分析】（1）根据题意结合等差、等比数列的通项公式运算求解；（2）根据题意分析可知6612111210()(210)T a a a b b b =++⋅⋅⋅++++⋅⋅⋅+，利用分组求和法结合等差、等比数列求和公式以及错位相减法运算求解.【小问1详解】设数列{}n a 的公差为d ，因为1224b a b a =⎧⎨=⎩，则111213b d b d =+⎧⎨=+⎩，解得112d b =⎧⎨=⎩，所以11n a n n =+-=，1222n nn b -=⨯=．【小问2详解】因为(1)1232k k k ++++⋅⋅⋅+=，当10k =时，(1)552k k +=，可知6612111210()(210)T a a a b b b =++⋅⋅⋅++++⋅⋅⋅+，且1211(111)11662a a a +⨯++⋅⋅⋅+==，令{}n nb 的前n 项和为n S ，则234122232422nn S n =⨯+⨯+⨯+⨯+⋅⋅⋅+⨯，可得234512122232422n n S n +=⨯+⨯+⨯+⨯+⋅⋅⋅+⨯，两式相减得()231112(21)22222212221n nn n n n S n n n +++--=+++⋅⋅⋅+-⨯=-⨯=-⨯--，即1(1)22n n S n +=-⨯+，可得111210210922b b b ++⋅⋅⋅+=⨯+，所以1166922661850020000T =⨯++=<．22.已知椭圆22122:1(0)x y C a b a b +=>>与双曲线22222:1(0)x y C a b a b-=>>的焦距之比为12．（1）求椭圆1C 和双曲线2C 的离心率；（2）设双曲线2C 的右焦点为F ，过F 作FP x ⊥轴交双曲线2C 于点P （P 在第一象限），A ，B 分别为椭圆1C的左、右顶点，AP 与椭圆1C 交于另一点Q ，O 为坐标原点，证明：BP OP OQ OP k k k k ⋅=+．【答案】（1）椭圆1C的离心率5，双曲线2C的离心率5（2）证明见解析【解析】【分析】（1）根据题意结合椭圆、双曲线的方程与性质运算求解；（2）由（1）可知3,55P a a ⎛⎫ ⎪ ⎪⎝⎭，联立方程求点Q 的坐标，结合斜率公式分析证明.【小问1详解】椭圆1C的焦距12c =，双曲线2C的焦距22c =12=，整理得2235b a =，从而2222125c a b a =-=，2222285c a b a =+=，故椭圆1C 的离心率11105c e a ==，双曲线2C 的离心率222105c e a ==．【小问2详解】由（1）可知2103,55P a a ⎛⎫ ⎪ ⎪⎝⎭，椭圆22122:135x y C a a +=，因为(,0)A a -，所以直线AP的方程为5()5y x a =+．联立方程组22225()5135y x a x y a a ⎧-=+⎪⎪⎨+=⎪⎪⎩，整理得22(8(13(50x ax a -+-+-=，则2Q ax -=，则Q x =，可得5()5Q Q y x a =+=，即Q ⎛⎫⎪⎪⎭，因为35BPa k ==，35OP a k ==，35Q OQQ y k x ==，则1231020BP OP k k +⋅==，312310520OQ OP k k ++==，故BP OP OQ OP k k k k ⋅=+．【点睛】方法点睛：与弦端点相关问题的解法。

2019-2020学年湖南省怀化市高二上学期期末数学试题一、单选题1．已知i 为虚数单位，则复数1z ii=+在复平面内对应的点位于（ ） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限【答案】A【解析】分析：利用复数的除法运算法则：分子、分母同乘以分母的共轭复数，化简复数z ，从而可得结果.详解：：由于复数，1i z i =+()()()i 1i 1+i 11i 1i 1i 222-===++-， 在复平面的对应点坐标为11,22⎛⎫⎪⎝⎭， ∴在第一象限，故选A.点睛：复数是高考中的必考知识，主要考查复数的概念及复数的运算．要注意对实部、虚部的理解，掌握纯虚数、共轭复数这些重要概念，复数的运算主要考查除法运算，通过分母实数化转化为复数的乘法，运算时特别要注意多项式相乘后的化简，防止简单问题出错，造成不必要的失分.2．抛物线2x y =的焦点坐标是（ ）A ．104⎛⎫ ⎪⎝⎭，B ．102⎛⎫ ⎪⎝⎭，C ．102⎛⎫ ⎪⎝⎭，D ．104⎛⎫ ⎪⎝⎭，【答案】D【解析】对比抛物线的焦点在y 轴正半轴的标准方程22x py =，求解出焦点坐标为0,2p ⎛⎫⎪⎝⎭即可. 【详解】因为2x y =，所以2122x y =⋅⋅， 所以12p =，所以焦点坐标为10,4⎛⎫ ⎪⎝⎭. 故选：D.本题考查根据抛物线的标准方程求解抛物线的焦点坐标，难度较易.形如22x py =的抛物线方程的焦点坐标为0,2p ⎛⎫ ⎪⎝⎭，准线方程为2p y =-；形如22y px =的抛物线方程的焦点坐标为,02p ⎛⎫⎪⎝⎭，准线方程为2p x =-.3．已知命题sin 1p x R x ∀∈≥-:，，则（ ） A ．00sin 1p x R x ⌝∃∈<-:， B ．sin 1p x R x ⌝∀∈>-:， C ．sin 1p x R x ⌝∀∈≥-:， D ．00sin 1p x R x ⌝∃∈≤-:， 【答案】A【解析】根据含一个量词的命题的否定方法：“修改量词，否定结论”，即可得到相应结果. 【详解】原命题是全称命题，所以其否定为特称命题，x R ∀∈的否定为0x R ∃∈，sin 1x ≥-的否定为0sin 1x <-，所以原命题的否定为：00sin 1x R x ∃∈<-，. 故选：A. 【点睛】本题考查含一个量词的命题的否定，难度较易.注意在修改量词的同时否定结论.4．已知数列{}n a 的前n 项和为n S ，且满足*1111N n a a n +==∈，，，则2a 的值为（ ） A ． B ．2C ．3D ．4【答案】C【解析】利用11n a +=+，将1n =代入原式，即可得到关于2a 的等式，并代入相关值即可计算出2a 的值. 【详解】因为11n a +=+，所以当1n =时有21a =且111S a ==，所以21213a ==+=.本题考查根据数列的递推公式求值，难度较易.对任意数列{}n a 以及前n 项和n S 总有()111,2,*n n n a S S S a n n N -=-=≥∈.5．设椭圆方程为()22220x y a b a b+>>，左右焦点分别为12F F ，，上顶点为B ，若12F BF V 为等边三角形，则椭圆的离心率为（ ） A ．13B ．12C ．3 D ．22【答案】B【解析】根据题意作出示意图，根据12F BF V 为等边三角形求解出,b c 之间的关系式，从而求解出椭圆的离心率. 【详解】 如图所示：因为12F BF V 13FO BO =，所以3b c =， 所以22223b c a c ==-，所以224a c =，所以12e =. 故选：B. 【点睛】本题考查根据几何图形的性质求解椭圆的离心率，难度一般.求解椭圆或者双曲线的离心率时，若涉及到规则几何图形，注意借助几何图形的性质求解问题：如长度、角度之间的关系.6．两个正数a b 、的等差中项是72，一个等比中项是23a b <，则双曲线22221x y a b-=的渐近线方程为（ ） 5543【解析】根据等差、等比中项求解出,a b 的值，再根据双曲线的渐近线方程为by x a=±即可求解出渐近线的方程. 【详解】因为a b 、的等差中项是72且一个等比中项是 所以712a b ab +=⎧⎨=⎩且a b <，所以34a b =⎧⎨=⎩，所以43b a =，所以渐近线方程为：43y x =±. 故选：C. 【点睛】本题考查根据数列与双曲线的综合应用求解渐近线方程，难度一般.求解双曲线22221x y a b-=的渐近线方程时，如果不记得对应的渐近线方程可通过令22220x y a b -=得到渐近线方程.7．若a b c R ∈，，，则以下命题为真的是（ ） A ．若a b >，则11a b< B ．若a b >，则22ac bc > C ．若a b >，则22a b > D ．若a b >，则22a b >【答案】D【解析】A ．举例：取0,0a b ><的值，检验；B ．举例：0c =，检验；C ．举例：取0,0a b ><的值(注意大小)，检验；D ．考虑两边同时平方来证明.【详解】A ．取1,1a b ==-，所以11a b>，故错误； B ．取0c =，所以22ac bc =，故错误； C ．取1,2a b ==-，所以22a b <，故错误；D ．因为0a b >≥，所以22a b >，所以22a b >，故正确. 故选：D. 【点睛】本题考查利用不等式的性质判断命题的真假，难度一般.(1)不等号两边同时乘以一个正8．“33a b ＞”是“77log log a b ＞”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】B【解析】将33a b ＞及77log log a b ＞都化成最简形式，分别是a b ＞及0a b >＞，从而能得出结论. 【详解】若33a b ＞，则a b ＞，当0b a ≤＜，或0a b ≥＞时，由a b ＞推不出77log log a b ＞；反之，若77log log a b ＞，则有a b ＞，所以，“33a b ＞”是“77log log a b ＞”的必要不充分条件，故选B. 【点睛】判断充分条件必要条件考题，可以通过将两命题都化成最简形式，再利用“小范围可以推出大范围”的特点，可以得出结论.9．已知数列{}n a 为各项均为正数的等比数列，n S 是它的前n 项和，若174a a =，且47522a a +=，则5S =（ ） A ．32 B ．31C ．30D ．29【答案】B【解析】根据已知求出4712,4a a ==，再求出公比和首项，最后求5S . 【详解】 因为174a a =，所以2444,0,2n a a a =>∴=Q . 因为47522a a +=， 所以714a =. 所以3111,16.82q q a =∴==，，所以55116[1()]2=311S -=.故选B【点睛】本题主要考查等比数列的通项的基本量的计算，考查等比中项的应用，考查等比数列的前n项和的求法，意在考查学生对这些知识的理解掌握水平和分析推理能力.10．如图，在平行六面体中，底面是边长为1的正方形，若，且，则的长为A．B．C．D．【答案】A【解析】由几何图形可得，然后两边平方，根据向量的数量积可得，进而得到的长度．【详解】因为，所以||2=()2=||2+||2+||2)．故A1C的长为．故选A．【点睛】本题考查向量数量积的应用，利用数量积可解决垂直、长度、夹角等问题，用向量求长度时，可将向量用基底或坐标表示出来，然后根据数量积的运算或坐标运算求解即可，体现了向量具有数形二重性的特点．11．若两个正实数x、y满足211x y+=，且222x y m m+>+恒成立，则实数m的取A ．()[)0,24,--+∞UB ．(][),42,-∞-+∞UC ．()4,2-D ．()2,4-【答案】C【解析】将代数式2x y +与21x y+相乘，展开后利用基本不等式求出2x y +的最小值，然后解二次不等式()2min 22m m x y +<+即可.【详解】x Q 、0y >，且211x y+=，由基本不等式得()214224y x x y x y x y x y⎛⎫+=++=++ ⎪⎝⎭48≥=，当且仅当2x y =时，等号成立，所以2x y +的最小值为8，由题意可得()2min 228m m x y +<+=，即2280m m +-<，解得42m -<<.因此，实数m 的取值范围是()4,2-，故选：C. 【点睛】本题考查基本不等式恒成立问题，同时也考查了一元二次不等式的解法，在利用基本不等式求最值时，要注意对代数式进行配凑，考查运算求解能力，属于中等题.12．已知函数f （x ）=2x x 1x 1--+，g （x ）=-e x-1-lnx+a 对任意的x 1∈[1，3]，x 2∈[1，3]恒有f （x 1）≥g （x 2）成立，则a 的范围是（ ） A ．1a 2≤B ．1a 2≥C ．10a 2<≤D ．11a 22-≤≤ 【答案】A【解析】先利用导数求出min max ()()f x g x 、，再解不等式min max ()()f x g x >即得解. 【详解】由题得222()0,()(1)x xf x f x x +'=>∴+在[1，3]上单调递增， 所以min 1()(1).2f x f ==-由题得11()()0x g x e -'=-+<，所以函数g （x ）在[1,3]上单调递减，所以max ()(1)1g x g a ==-， 由题得min max 1()(),1,2f xg x a >∴-≥- 所以12a ≤. 故选A 【点睛】本题主要考查利用导数求函数的最值，考查利用导数研究不等式的恒成立问题，意在考查学生对这些知识的理解掌握水平和分析推理能力.二、填空题13．曲线3ln y x x =+在点()11，处的切线方程为____________________________．【答案】430x y --=.【解析】先求解出曲线对应函数的导函数，然后计算出切点处导数值即为切线的斜率，根据直线的点斜式方程求解出切线方程. 【详解】因为()3ln y f x x x ==+，所以()31y f x x''==+， 所以()31141f '=+=，所以切线方程为：()411y x =-+， 即为430x y --=.故答案为：430x y --=. 【点睛】本题考查曲线上某点处切线方程的求解，难度较易.求解曲线上某点处的切线方程的方法：(1)先求解出函数的导函数并求解出对应切点处的导数值即为切线斜率；(2)根据直线的点斜式方程写出直线的切线方程并化简整理.14．若z C ∈，且234z z i +=+，则z =_____________．【解析】设z a bi =+，并计算出z ，根据234z z i +=+以及复数相等的原则计算出,a b的值，再根据z =z .【详解】又因为234z z i +=+，所以334a bi i -=+，所以14a b =⎧⎨=-⎩，所以z ==【点睛】本题考查复数的共轭复数、模长以及根据复数相等求解参数，难度一般.已知复数a bi +与复数i c d +相等，则有a cb d =⎧⎨=⎩. 15．函数()()()1f x ax x b =-+，如果不等式()0f x >的解集为()1,3-，那么a b +=______.【答案】4-【解析】先求解()0f x =的根,分别讨论0a >,0a =,0a <的情况,根据解集与方程根的关系求解即可 【详解】由题,令()0f x =,则()()10ax x b -+=,当0a =时,x b =-,若()0f x >,则x b <-,舍去；当0a ≠时,即11,x a =2x b =-,当0a >时,若()0f x >,则1x a>或x b <-；或x b >-或1x a <,舍去；当0a <时,若()0f x <,由于解集为()1,3-,则11a=-,3b -=,则1,3a b =-=-,所以134a b +=--=-故答案为：4- 【点睛】本题考查由不等式解集求参问题,考查分类讨论思想,考查运算能力 16．已知正数a b ，满足：1910a b a b+++=，则+a b 的最小值是_____________． 【答案】2.【解析】将等式两边同时乘以()a b +，然后利用基本求解出()min a b +，同时分析取()min a b +的条件是否满足.【详解】因为1910a b a b +++=，所以()()()2910a b a b a b a b a b+++++=+， 所以()()291010b a a b a b a b ++++=+，所以()()291010b a a b a b a b++=+-+， 所以()()2101016a b a b +-+≥+=，取等号时3b a =， 所以()()280a b a b +-+-≤⎡⎤⎡⎤⎣⎦⎣⎦，所以28a b ≤+≤，当2a b +=时，1232a b ⎧=⎪⎪⎨⎪=⎪⎩符合条件，所以()min 2a b +=.故答案为：2. 【点睛】本题考查基本不等式的综合应用，对于转化和计算的能力要求较高，难度较难.利用基本不等式求解最值时，注意分析取等号时对应的条件是否满足.三、解答题17．已知数列{}n a 为正项等比数列，满足34a =，且546,3,a a a 构成等差数列，数列{}n b 满足221log log n n n b a a +=+． （I ）求数列{}n a 的通项公式； （II ）求数列{}n b 的前n 项和n S ．【答案】（I ）12n n a -=；（II ）2n S n =．【解析】（I ）根据34a =以及546,3,a a a 构成等差数列，求解出等比数列的公比q ，由此求解出{}n a 的通项公式；（II ）根据221log log n n n b a a +=+先计算出{}n b 的通项公式，判断出{}n b 为特殊数列并利用对应求和公式完成求解. 【详解】（I ）设等比数列{}n a 的公比为()0q q >，由题意，得256466a a a q q +=⇒+=，解得2q =或3q =-（舍）所以1112n n n a a q --==．（II ）221log log 121n n n b a a n n n +=+=-+=-， 所以数列{}n b 是以1为首项2为公差的等差数列．()()1212122n n n n n b b S n ⎡⎤+-+⎣⎦===． 【点睛】本题考查等差数列、等比数列的综合应用，难度一般.(1)已知等比数列中的某几项成等差数列，可通过将其中项改写成首项和公比的形式，从而计算出等比数列的基本量；(2)等差数列常见求和公式：()()11122n n a a n n n S a n d +-==+.18．已知函数()31f x ax bx =++的图象经过点(1)3-，且在1x =处，()f x 取得极值．求：（1）函数()f x 的解析式； （2）()f x 的单调递增区间．【答案】（1）()3261f x x x =-+；（2）()f x 的单调递增区间为()()11-∞-+∞，，，． 【解析】（1）代入点的坐标，求出导函数，解方程组可得a 、b ； （2）求出导函数，令导函数大于0得出函数的单调递增区间. 【详解】（1）由()31f x ax bx =++的图象过点(1)3-，得13a b ++=-， ∵()23f x ax b '=+，又(1)30f a b '=+=，∴由430a b a b +=-⎧⎨+=⎩得26a b =⎧⎨=-⎩，∴()3261f x x x =-+． （2）∵()266f x x '=-，∴由()0f x '>得1x >或1x <-，∴()f x 的单调递增区间为(1)-∞-，和(1)+∞，．【点睛】本题是一道关于利用函数求导函数的题目，关键掌握利用导数研究函数的单调性的方法.19．如图所示，在三棱锥P ABC -中，PC ⊥平面ABC ，32PC ACB π=∠=，，D E，分别为线段AB BC ，上的点，且32222CD DE AC CE EB =====，，．（I ）证明：ED ⊥平面PCD ； （II ）求二面角A PD C --的余弦值． 【答案】（I ）证明见解析；（II ）36．【解析】（I ）根据PC ⊥平面ABC 并结合CDE △的形状，利用线面垂直的判定定理进行证明；（II ）建立空间直角坐标系，求解出平面APD 的一个法向量，写出平面PDC 的一个法向量，计算出法向量夹角的余弦并结合图形判断二面角A PD C --是钝角还是锐角，从而计算出二面角A PD C --的余弦值. 【详解】 （I ）证明：因为PC ⊥平面ABC ，DE ⊂平面ABC ， 所以PC DE ⊥． 由22CE CD DE ===，CDE △为等腰直角三角形，故CD DE ⊥，又PC CD C =I ，且PC ⊂面PCD ，CD ⊂面PCD ， 故DE ⊥平面PCD ． （II ）如图，以点C 为原点，分别以CA CB CP u u u r u u u r u u u r，，的方向分别为x 轴，y 轴，z 轴的正方向，建立直角坐标系()()()()3000003000201102C P A E D ⎛⎫ ⎪⎝⎭，，，，，，，，，，，，，，， ()()1110113102ED DP DA ⎛⎫=-=--=- ⎪⎝⎭u u u r u u u r u u u r ，，，，，，，，，设平面PAD 的法向量为()1111n x y z =u r ，，，则0n DP ⋅=r u u u r，即1111130102x y z x y --+=⎧⎪⎨-=⎪⎩，令12x =，则1111y z ==，，故可取()1211n =u r，，．由（I ）可知DE ⊥平面PCD ，故平面PCD 的法向量2n u u r 可取为ED u u u r， 即()2110n =-u u r，，， 则1212123cos 626n n n n n n ⋅<>===⨯u r u u ru r u u r u u r u u r ，， 又二面角A PD C --为锐二面角， 所以二面角A PD C --的余弦值为36． 【点睛】本题考查线面垂直的证明以及利用空间向量求解二面角的余弦值，难度一般.利用空间向量求解二面角的余弦值时，可通过平面法向量夹角的余弦值结合图形中二面角的实际情况完成求解.20．已知数列{}n a 满足：()2*1231111nn n N a a a a ++++=∈…，令1n n n b a a +=． （I ）求n a 和n b ；（II ）n S 为数列{}n b 的前n 项和，对任意的正整数n ，不等式12n S λ>-恒成立，求实数λ的取值范围． 【答案】（I ）11122121n b n n ⎛⎫=- ⎪-+⎝⎭；（II ）56⎛⎫-∞ ⎪⎝⎭，． 【解析】（I ）将原等式变形为1n -时对应的等式，两式相减得到{}n a 的通项公式注意验证1n =是否成立，从而可求{}n b 的通项公式；（II ）利用裂项相消法求解出n S 的表达式，再根据恒成立思想计算出()min n S ，根据()min 12n S λ>-即可求解出λ的取值范围. 【详解】 （I ）∵()2*1231111nn n N a a a a ++++=∈…①， ∴当2n ≥时，()2123111111n n a a a a -++++=-…② ①-②得：()1212nn n a =-≥， 又111a =，满足上式，∴()*121n n N a n =-∈，()()1111212122121n b n n n n ⎛⎫==- ⎪-+-+⎝⎭．（II ）11111112335212121n nS n n n ⎛⎫=-+-++-= ⎪-++⎝⎭…， ∵1121242n n S n n ==-++，所以n S 是递增的， 又因为1111263S =-=，所以1132n S ⎡⎫∈⎪⎢⎣⎭，， 所以原不等式等价于1132λ>-， ∴56λ<．∴实数λ的取值范围为56⎛⎫-∞ ⎪⎝⎭，． 【点睛】本题考查利用递推公式求解数列的通项公式以及用裂项相消法求和并完成恒成立问题的求解，难度一般.(1)利用递推公式求解通项公式时，若出现了下标为1n -的情况，在最后要注意验证1n =是否满足条件；(2)常见适用裂项相消法求和的数列的通项形式：()11111n n n n =-++，()()()()1111212122121n n n n ⎡⎤=-⎢⎥-+-+⎣⎦，1=-21．已知椭圆()2222x y D 1a b 0a b +=：＞＞的离心率为e 2=，点)1-在椭圆D 上．（1）求椭圆D 的标准方程；（2）过y 轴上一点E （0，t ）且斜率为k 的直线l 与椭圆交于A ，B 两点，设直线OA ，OB （O 为坐标原点）的斜率分别为k OA ，k OB ，若对任意实数k ，存在λ∈[2，4]，使得k OA +k OB =λk ，求实数t 的取值范围．【答案】（1）22142x y +=；（2）[]1,1t ∈- 【解析】（1）根据条件列方程组，解得a ，b （2）利用坐标表示OA OB k k +，设直线l 的方程，并与椭圆方程联立，由韦达定理代入化简可得242t λ-=-，最后根据[]2,4λ∈，解得t 的取值范围 【详解】（1）椭圆D的离心率e ==，a ∴=，又点)1-在椭圆上，22211a b ∴+=，得2a =，b =∴椭圆D 的标准方程为22142x y +=. （2）由题意得，直线l 的方程为y kx t =+，由22142x y y kx t ⎧+=⎪⎨⎪=+⎩，消元可得 ()222214240kx ktx t +++-=，设()11,A x y ，()22,B x y ，则122421kt x x k -+=+，21222421t x x k -=+， 1212OA OB y y k k x x +=+ 1212kx t kx t x x ++=+= ()12122t x x k x x ++= 22242122124kt k k t k k -++⋅⋅+- 242k t -=-， 由OA OB k k k λ+=，得242t λ-=-，即242t λ=-，又[]2,4λ∈，[]20,1t ∴∈，[]1,1t ∴∈-.【点睛】直线和圆锥曲线的位置关系，一般转化为直线方程与圆锥曲线方程组成的方程组，利用韦达定理或求根公式进行转化，通常抓住函数关系，将目标量表示为一个(或者多个)变量的函数，然后借助于函数性质的探求来使问题得以解决. 22．已知函数()()()1sin cos 2f x a x x x x a R =--∈，()()'g x f x =（()'f x 是()f x 的导函数），()g x 在0,2π⎡⎤⎢⎥⎣⎦上的最大值为12π-. （1）求实数a 的值；（2）判断函数()f x 在()0,π内的极值点个数，并加以证明. 【答案】（1）1a =（2）()f x 在()0,π上共有两个极值点，详见解析 【解析】（1）先求得()()1'sin 2g x f x ax x ==-，再求得()()'sin cos g x a x x x =+，再讨论a 的符号，判断函数()g x 的单调性，再求最值即可得解； （2）利用（1）的结论，结合()1002g =-<，10222g ππ⎛⎫=-> ⎪⎝⎭，由零点定理可()g x 在0,2π⎛⎤⎥⎝⎦上有且仅有一个变号零点；再当,2x ππ⎛⎫∈⎪⎝⎭时，由导数的应用可0,2x ππ⎛⎫∃∈ ⎪⎝⎭使()0'0g x =，即()g x 在0,2x π⎛⎫⎪⎝⎭上单调递增，在()0,x π上单调递减，再结合特殊变量所对应的函数值的符号可得()g x 在,2ππ⎛⎫⎪⎝⎭上有且仅有一个变号零点，综合即可得解. 【详解】解：（1）由()()()1sin cos 2f x a x x x x a R =--∈ 则()()1'sin 2g x f x ax x ==-， 则()()'sin cos g x a x x x =+， ①当0a =时()12g x =-，不合题意，舍去. ②当0a <时()'0g x <，∴()g x 在0,2π⎡⎤⎢⎥⎣⎦上单调递减，∴()()max 11022g x g π-==-≠，不合题意，舍去. ③当0a >时()'0g x >，∴()g x 在0,2π⎡⎤⎢⎥⎣⎦上单调递增，∴()max 112222a g x g πππ-⎛⎫==-= ⎪⎝⎭，解得1a =， ∴综上：1a =.（2）由（Ⅰ）知()1sin 2g x x x =-，()'sin cos g x x x x =+， 当0,2x π⎛⎤∈ ⎥⎝⎦时，()g x 在0,2π⎛⎤⎥⎝⎦上单调递增，()1002g =-<，10222g ππ⎛⎫=-> ⎪⎝⎭，∴()g x 在0,2π⎛⎤⎥⎝⎦上有且仅有一个变号零点；当,2x ππ⎛⎫∈⎪⎝⎭时，()''2cos sin 0g x x x x =-<，∴()'g x 在,2ππ⎛⎫⎪⎝⎭上单调递减.又'102g π⎛⎫=>⎪⎝⎭，()'0g ππ=-<， ∴0,2x ππ⎛⎫∃∈⎪⎝⎭使()0'0g x =且当0,2x x π⎛⎫∈ ⎪⎝⎭时()'0g x >，当()0,x x π∈时()'0g x <，∴()g x 在0,2x π⎛⎫⎪⎝⎭上单调递增，在()0,x π上单调递减. 又10222g ππ⎛⎫=->⎪⎝⎭，()002g x g π⎛⎫>> ⎪⎝⎭，()102g π=-<，∴()g x 在,2ππ⎛⎫ ⎪⎝⎭上有且仅有一个变号零点.∴()g x 在0,2π⎛⎤⎥⎝⎦和,2ππ⎛⎫⎪⎝⎭上各有一个变号零点，∴()f x 在()0,π上共有两个极值点. 【点睛】本题考查了利用导数研究函数的单调性及最值，主要考查了零点定理，重点考查了函数的思想及运算能力，属综合性较强的题型.。

2019-2020学年湖南省怀化市高二（上）期末数学试卷、选择题：本大题共 12小题，每小题5分，满分60分•在每小题给出的四个选项中, 只有一项是符合题目要求的.1. （ 5分）设i 是虚数单位，则复数 L 在复平面内所对应的点位于 （ ）A .第一象限 1 iB .第二象限 C. 第三象限 D .第四象限22. （ 5分）抛物线x y 的焦点坐标为（ )1A .匕,0)41B . (0,)4C . (0，；) 4D .（打 43. （ 5分）已知命题 p: x R , sinx …1 , 则P（)A . x 0R , sin x^ 1B . X 。

R , sin 人 1C . x R , sinx, 1D .x R ,sin x14.（ 5分）已知数列 ®｝的前n 项和为&，且满足d 1 , a . 1 2 S ? 1,n N *，则a ?的值为（）C . 3、 、、x 2 y5. （5分）设椭圆方程为 —2（a ba b为等边三角形，则椭圆的离心率为（2話1的渐近线方程为（5 y -x0）,左右焦点分别为R ,F 2,上顶点为6. （5分）两个正数 b 的等差中项是，一个等比中项是2 .3，且b ，则双曲线(5 分)"a 3 b 3 ”是 “ log ? a log 7 b ”的()B .必要不充分条件 D .既不充分也不必要条件3C . y7.(5 分)若 a , b , e R ,则以下命题为真的是 （B .若b ，则 2ae2beD .若|b|，则 a 2 A .充分不必要条件 C .充要条件9. （ 5分）已知数列｛寻｝为各项为正数的等比数列， S n 是它的前n 项和，若 叩？ 4，且a 4 2a 7 5，则 S 5 () 210. （ 5分）如图，在平行六面体ABCD ABQD I 中，底面是边长为1的正方形，若AAB AAD 60，且 AA 3，则 AC 的长为（ ）C . .142 1 211 . （5分）若两个正实数x , y 满足1,且x 2y m 2m 恒成立，则实数 m 的取 x y值范围是（）14 . (5 分)若 z C ，且 z 2z 3 4i ，则 |z| 为 ____ .1 916 . （5分）已知正数a , b 满足：a b10 ,则a b 的最小值是a b三、解答题：共70分，解答应写出文字说明、证明过程和演算步骤 17 . （10分）已知数列｛a n ｝为正项等比数列，满足 a 3 4，且a 5, 3a 。

2020-2021学年湖南省怀化市高二（上）期末数学试卷一、单选题（本大题共8小题，共40.0分）1.复数2i1−i的虚部为()A. iB. −iC. 1D. −12.关于x的不等式x2−ax+1>0的解集是R，则实数a的取值范围为()A. (−∞,−2)∪(2,+∞)B. (−∞,−2]∪[2,+∞)C. (−2,2)D. [−2,2]3.在△ABC中，已知2sinAcosB=sinC，那么△ABC一定是()A. 直角三角形B. 等腰三角形C. 等腰直角三角形D. 正三角形4.在等差数列{a n}中，a2、a6是方程x2−3x+2=0的两根，则a4的值为()A. 2B. 3C. ±2D. 325.(理科做)设f(x)为可导函数，且满足limx→0f(1)−f(1−2x)2x=−1，则过曲线y=f(x)上点(1,f(1))处的切线率为()A. 2B. −1C. 1D. −26.已知动圆M与圆C1：(x+4)2+y2=2外切，与圆C2：(x−4)2+y2=2内切，则动圆圆心M的轨迹方程为()A. x22−y216=1(x≤−√2) B. x22−y214=1(x≥√2)C. x22−y216=1 D. x22−y214=17.在△ABC中，sin2A≤sin2B+sin2C−sinBsinC，则A的取值范围是()A. (0,π6] B. [π6,π) C. (0,π3] D. [π3,π)8.历史上数列的发展，折射出许多有价值的数学思想方法，对时代的进步起了重要的作用，比如意大利数学家列昂纳多⋅斐波那契以兔子繁殖为例，引入“兔子数列”：1，1，2，3，5，8，13，21，34，55，89，….即F(1)=F(2)=1，F(n)=F(n−1)+ F(n−2)(n≥3,n∈N∗)，此数列在现代物理、准晶体结构及化学等领域有着广泛的应用，若此数列被4整除后的余数构成一个新的数列{b n}，又记数列{c n}满足c1= b1，c2=b2，c n=b n−b n−1(n≥3,n∈N∗)，则c1+c2+c3+⋅⋅⋅+c2021的值为()A. 4B. −728C. 2D. 3二、多选题（本大题共4小题，共20.0分）9.已知函数y=f(x)的导函数的图象如图所示，下列结论中正确的是()A. −1是函数f(x)的极小值点B. −3是函数f(x)的极小值点C. 函数f(x)在区间(−3,1)上单调递增D. 函数f(x)在x=0处切线的斜率小于零10.下面命题正确的是()<1”的充分不必要条件A. “a>1”是“1aB. 命题p：∃x∈[−1,1]，x2+2x−1≥0，则命题p的否定为：∀x∈[−1,1]，x2+2x−1<0C. “(a−b)⋅a2<0”是“a<b”的必要不充分条件D. 设a，b∈R，则“a≠0”是“ab≠0”的必要不充分条件11.如图，在正四棱锥S−ABCD中，E，M，N分别是BC，CD，SC的中点，动点P在线段MN上运动时，下列四个结论中恒成立的为()A. EP⊥ACB. EP//BDC. EP//面SBDD. EP⊥面SAC12.如图，已知椭圆C1：x2+y2=1，过抛物线C2：x2=4y焦点F的直线交抛物线于4M，N两点，连接NO，MO并延长分别交C1于A，B两点，连接AB，△OMN与△OAB 的面积分别记为S△OMN，S△OAB.则下列命题：A.若记直线NO，MO的斜率分别为k1，k2，则k1k2的大小是定值−14B.△OAB的面积S△OAB是定值1C.线段OA，OB长度的平方和|OA|2+|OB|2是定值5D.设λ=S△OMN，则λ≥√5S△OAB其中正确的命题有()A. AB. BC. CD. D三、单空题（本大题共4小题，共20.0分）13.已知向量a⃗=(1,2,3)，b⃗ =(2,1,k)，若a⃗⊥(a⃗+b⃗ )，则k的值为．+ 14.已知直线ax+by+c−1=0(bc>0)，经过圆x2+y2−2y−5=0的圆心，则4b1的最小值是______．c15.如图，圆O与椭圆相切，已知F1，F2是椭圆的左、右焦点，点P在椭圆上，线段PF2与圆O相切于点Q，且点Q为线段PF2的中点，则椭圆的离心率为______ ．,e]上有两个不同的交点，16.已知函数ℎ(x)=xlnx与函数g(x)=kx−1的图象在区间[1e则实数k的取值范围是______ ．四、解答题（本大题共6小题，共70.0分）)sinB+(c−17.已知在△ABC中，角A，B，C所对的边分别为a，b，c，并且满足(b−c2b)sinC−asinA=0．2(1)求角A的大小；(2)若a=√3，b+c=3，求△ABC的面积．18. 已知数列{a n }的前n 项和为S n ，且满足S n =43(a n −1)，n ∈N +．(1)求数列{a n }的通项公式； (2)令b n =log 4a n ，记数列{1b n b n+1}的前n 项和为T n ，求T 2021．19. 如图1，在边长为5的菱形ABCD 中，AC =6，现沿对角线AC 把△ADC 翻折到△APC的位置得到四面体P −ABC ，如图2所示，已知PB =4√2． (1)求证：平面PAC ⊥平面ABC ；(2)若Q 是线段AP 上的点，且PQ ⃗⃗⃗⃗⃗ =2QA ⃗⃗⃗⃗⃗ ，求二面角Q −BC −A 的余弦值．20. 第二届中国国际进口博览会于2019年11月5日至10日在上海国家会展中心举行，来自151个国家和地区的3617家企业参展，规模和品质均超过首届．更多新产品、新技术、新服务“全球首发，中国首展”，专(业)精(品)尖(端)特(色)产品精华荟萃．某跨国公司带来了高端空调模型参展，通过展会调研，中国甲企业计划在2020年与该跨国公司合资生产此款空调．生产此款空调预计全年需投入固定成本260万元，每生产x千台空调，需另投入资金R(x)万元，且R(x)={10x2+ax,0<x<40901x2−9450x+10000x,x≥40.经测算生产10千台空调需另投入的资金为4000万元．由调研知，每台空调售价为0.9万元时，当年内生产的空调当年能全部销售完．(1)求2020年的企业年利润W(x)(万元)关于年产量x(千台)的函数关系式；(2)2020年产量为多少(千台)时，企业所获年利润最大？最大年利润是多少？注：利润=销售额−成本21.已知抛物线C：x2=2py(p>0)的焦点为F，点P(x0,3)为抛物线C上一点，且|PF|=4，过点A(a,0)作抛物线C的切线AN(斜率不为0)，设切点为N．(1)求抛物线C的标准方程；(2)求证：以FN为直径的圆过点A．22.设函数f(x)=e x−ax−2．(1)求f(x)的单调区间；(2)若a=1，k为整数，且当x>0时，(x−k)f′(x)+x+1>0，求k的最大值．答案和解析1.【答案】C【解析】解：∵2i1−i =2i(1+i)(1−i)(1+i)=−1+i，∴复数2i1−i的虚部为1．故选：C．直接利用复数代数形式的乘除运算化简得答案．本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．2.【答案】C【解析】解：由已知可得不等式x2−ax+1>0在R上恒成立，则只需△=a2−4<0，解得−2<a<2，所以实数a的范围为(−2,2)，故选：C．利用一元二次不等式恒成立问题即可求解．本题考查了一元二次不等式恒成立问题，考查了学生的运算能力，属于基础题．3.【答案】B【解析】解：由2sinAcosB=sinC知2sinAcosB=sin(A+B)，∴2sinAcosB=sinAcosB+cosAsinB．∴cosAsinB−sinAcosB=0．∴sin(B−A)=0，∵A和B是三角形的内角，∴B=A．故选：B．根据三角形三个内角和为180°，把角C变化为A+B，用两角和的正弦公式展开移项合并，公式逆用，得sin(B−A)=0，因为角是三角形的内角，所以两角相等，得到三角形是等腰三角形．在三角形内会有一大部分题目出现，应用时要抓住三角形内角和是180°，就有一部分题目用诱导公式变形，对于题目中正用、逆用两角和的正弦和余弦公式，必须在复杂的式子中学会辨认公式应用公式．4.【答案】D【解析】解：∵等差数列{a n}中，a2、a6是方程x2−3x+4=0的两根，∴a2+a6=2a4=3，∴a4=32，故选：D．由题意利用等差数列的性质、韦达定理，求出a4的值．本题主要考查等差数列的性质、韦达定理，属于基础题．5.【答案】B【解析】解：∵limx→0f(1)−f(1−2x)2x=limx→0f(1)−f(1−2x)1−(1−2x)=−1，即y′|x=1=−1，∴y═f(x)在点(1,f(1))处的切线斜率为−1，故选B．由导数的几何意义，求出在曲线y=f(x)上点(1,f(1))处的导数，即求得在此点处切线的斜率．本题考查导数及其运算，求解问题的关键，是对所给的极限极限表达式进行变形，利用导数的几何意义求出曲线y=f(x)上点(1,f(1))处的切线率．6.【答案】B【解析】解：设动圆M的半径为r，又圆C1与圆C2的半径均为√2，则由已知得MC1=r+√2,MC2=r−√2，所以MC1−MC2=2√2．又点C1(−4,0)，C2(4,0)，则C1C2=8，所以2√2<C1C2，根据双曲线的定义可知，点M的轨迹是以C1(−4,0)，C2(4,0)为焦点的双曲线的右支．因为a=√2,c=4，所以b2=c2−a2=14，于是点M的轨迹方程为x22−y214=1(x≥√2)．故选：B．设动圆M的半径为r，又圆C1与圆C2的半径均为√2，判断点M的轨迹是以C1(−4,0)，C2(4,0)为焦点的双曲线的右支．求出双曲线方程即可．本题考查轨迹方程的求法，双曲线的定义的应用，是基本知识的考查．7.【答案】C【解析】解：由正弦定理可知a=2RsinA，b=2RsinB，c=2RsinC，∵sin2A≤sin2B+sin2C−sinBsinC，∴a2≤b2+c2−bc，∴bc≤b2+c2−a2∴cosA=b2+c2−a22bc≥12∴A≤π3∵A>0∴A的取值范围是(0,π3]故选：C．先利用正弦定理把不等式中正弦的值转化成边，进而代入到余弦定理公式中求得cos A 的范围，进而求得A的范围．本题主要考查了正弦定理和余弦定理的应用．作为解三角形中常用的两个定理，考生应能熟练记忆．8.【答案】C【解析】解：由题意可得，数列{b n}中的项为：1，1，2，3，1，0，1，1，2，3，1，0，1，1，…，故数列{b n}是周期为6的数列，数列{c n}中的项为：1，1，1，1，−2，−1，1，0，1，1，−2，−1，1，0，…，故数列{c n}是从第三项起周期为6的数列，所以c1+c2+c3+⋅⋅⋅+c2021=(c1+c2)+(c3+c4+⋯+c8)+⋯+(c2019+c2020+c2021)=1+1+0+1+1+(−2)=2．故选：C．利用题中给出的信息，得到数列{b n}中的项，然后得到数列{c n}中的项，再观察归纳，得到两个数列的周期性，利用周期性求和即可．本题考查了归纳推理的应用，涉及了数列知识的应用，解题的关键是正确理解题中给出的信息，发现数列的规律性，属于中档题．9.【答案】BC【解析】解：由图象得x<−3时，f′(x)<0，x>−3时，f′(x)≥0，故f(x)在(−∞,−3)递减，在(−3,+∞)递增，故−3是函数f(x)的极小值点，故选：BC．结合图象求出函数的单调区间，求出函数的极值点，判断选项即可．本题考查了函数的单调性，极值点问题，考查数形结合思想，是一道常规题．10.【答案】ABD【解析】解：“a>1”推出“1a <1”，反之不成立，所以“a>1”是“1a<1”的充分不必要条件，所以A正确；命题p：∃x∈[−1,1]，x2+2x−1≥0，则命题p的否定为：∀x∈[−1,1]，x2+2x−1<0，满足命题的否定形式，所以B正确；“(a−b)⋅a2<0”是“a<b”的充分不必要条件，所以C不正确；设a，b∈R，则“a≠0”推不出“ab≠0”反之成立，所以设a，b∈R，则“a≠0”是“ab≠0”的必要不充分条件，所以D正确；故选：ABD．利用充要条件判断A、C、D，命题的否定形式判断B即可．本题考查命题的真假的判断与应用，考查充要条件的判断，命题否定的判断，是基础题．11.【答案】AC【解析】解：如图所示，连接AC 、BD 相交于点O ，连接EM ，EN ．由正四棱锥S −ABCD ，可得SO ⊥底面ABCD ，AC ⊥BD ，∴SO ⊥AC ．∵SO ∩BD =O ，∴AC ⊥平面SBD ，∵E ，M ，N 分别是BC ，CD ，SC 的中点，∴EM//BD ，MN//SD ，而EM ∩MN =N ，∴平面EMN//平面SBD ，∴AC ⊥平面EMN ，∴AC ⊥EP.故A 正确．由异面直线的定义可知：EP 与BD 是异面直线，不可能EP//BD ，因此B 不正确； 平面EMN//平面SBD ，∴EP//平面SBD ，因此C 正确．EM ⊥平面SAC ，若EP ⊥平面SAC ，则EP//EM ，与EP ∩EM =E 相矛盾，因此当P 与M 不重合时，EP 与平面SAC 不垂直．即D 不正确． 故选：AC ．如图所示，连接AC 、BD 相交于点O ，连接EM ，EN ．由正四棱锥S −ABCD ，可得SO ⊥底面ABCD ，AC ⊥BD ，进而得到SO ⊥AC.可得AC ⊥平面SBD.由已知E ，M ，N 分别是BC ，CD ，SC 的中点，利用三角形的中位线可得EM//BD ，MN//SD ，于是平面EMN//平面SBD ，进而得到AC ⊥平面EMN ，AC ⊥EP ． 由异面直线的定义可知：EP 与BD 是异面直线，因此不可能EP//BD ； 平面EMN//平面SBD ，可得EP//平面SBD ；EM ⊥平面SAC ，可用反证法证明：当P 与M 不重合时，EP 与平面SAC 不垂直． 本题考查了空间线面、面面的位置关系判定，属于中档题．12.【答案】ABC【解析】解：F(0,1)，设直线MN 方程为y =k +1，代入抛物线方程得：x 2−4kx −4=0，设M(x 1,y 1)，N(x 2,y 2)，则x 1+x 2=4k ，x 1x 2=−4，k 1k 2=y 1y 2x 1x 2=116x 1x 2=−14，A正确．设直线OA 的方程为：y =k 1x ，由对称性令k 1>0，代入椭圆的方程得：A(−2√1+4k 12,−2k1√1+4k 12)，同理可得，B(√1+4k 22√1+4k 2)，|OA|=2√1+k 12√1+4k 1，点B 到直线OA 的距离d =12√1+4k 2√1+k 1，S △OAB =12|OA|d =√4(k 1−k 2)2(1+4k 12)(1+4k 12)=√4(k 1−k 2)24(k 12−2k1k 2+k 12)=1，B 正确．|OA|2+|OB|2=4+4k 121+4k 12+4+4k 221+4k 22 =4×(1+k 12)(1+4k 22)+(1+k 22)(1+4k 12)(1+4k 12)(1+4k 22)=4×52+5k 12+5k 222+4k 12+4k 22=5，C 正确． λ=|OM|⋅|ON||OA|⋅|OB|=|x 1x 2||x A x B |=√(1+4k 12)(1+4k 22)=√2+4(k 12+k 22)≥√2+4×2√k 12⋅k 22=2，当且仅当k 1=−k 2时等号成立．D 不正确． 故选：ABC ．设直线MN 方程为y =k +1，代入抛物线方程得：x 2−4kx −4=0，设M(x 1,y 1)，N(x 2,y 2)，利用韦达定理，结合斜率，转化求解判断A ；设直线OA 的方程为：y =k 1x ，由对称性令k 1>0，代入椭圆的方程得A 的坐标，同理可得B 的坐标，然后求解三角形的面积，判断B ；利用距离的平方和，判断C ；求解λ判断D ．本题考查直线与椭圆的位置关系的应用，直线与抛物线的位置关系的应用，命题的真假的判断，是中档题．13.【答案】−6【解析】 【分析】本题考查了空间向量的坐标运算，涉及了向量加法、数量积的坐标运算、向量垂直的充要条件，解题的关键是熟练掌握空间向量的坐标运算，属于基础题．先利用向量加法的坐标运算求出a ⃗ +b ⃗ 的坐标，然后利用向量垂直的充要条件结合数量积的坐标运算，列出关于k 的方程，求解即可． 【解答】解：因为向量a ⃗ =(1,2,3)，b ⃗ =(2,1,k)， 所以a ⃗ +b ⃗ =(3,3,k +3)，又因为a ⃗ ⊥(a ⃗ +b ⃗ )，所以a ⃗ ⋅(a ⃗ +b ⃗ )=3+6+3(k +3)=0， 解得k =−6． 故答案为：−6．14.【答案】9【解析】解：圆x 2+y 2−2y −5=0化成标准方程，得x 2+(y −1)2=6， ∴圆x 2+y 2−2y −5=0的圆心为C(0,1)，半径r =√6．∵直线ax +by +c −1=0经过圆心C ，∴a ×0+b ×1+c −1=0，即b +c =1， 因此4b+1c=(4b+1c)(b +c)=5+4c b+b c ≥5+2√4c b×bc=9；当且仅当4c b =bc 时等号成立． 由此可得当b =2c ，即b =23且c =13时，4b +1c 的最小值为9． 故答案为：9．将圆化成标准方程可得圆心为C(0,1)，代入题中的直线方程算出b +c =1，从而化简得4b+1c =(4b +1c )(b +c)=5+4c b+b c ；再根据基本不等式加以计算，可得当b =23且c =13时，所求最小值为9．本题给出已知圆的圆心在直线ax +by +c −1=0上，在b 、c >0的情况下求4b +1c 的最小值．着重考查了直线与圆的位置关系、圆的标准方程和基本不等式等知识，属于中档题．15.【答案】√53【解析】解：连接PF 1，OQ ，由题意知PF 1//OQ ，|PF 1|=2|OQ|=2b ， ∴|PF 2|=2a −2b ，PF 1⊥PF 2，∴由勾股定理可得：4b 2+4(a −b)2=4c 2=4a 2−4b 2， 整理得3b =2a ，所以ba =23，则椭圆的离心率为e =ca =√1−(ba )2=√1−49=√53，故答案为：√53．连接PF 1，OQ ，由题意知PF 1//OQ ，|PF 1|=2|OQ|=2b ，∴|PF 2|=2a −2b ，PF 1⊥PF 2，利用勾股定理以及离心率公式即可求解．本题考查了椭圆的几何性质以及直角三角形的性质，考查了学生的运算能力，属于基础题．16.【答案】(1,1+1e ]【解析】解：令xlnx −kx +1=0，即k =lnx +1x ，则函数ℎ(x)=xlnx 与函数g(x)=kx −1的图象在区间[1e ,e]上有两个不同的交点，等价于k =lnx +1x 在[1e ,e]上有两个根， 等价于y =k 与y =lnx +1x 有两个不同的交点，令f(x)=lnx +1x ，则f′(x)=1x −1x 2=1x (1−1x )，令f′(x)>0，可得1<x <e ，令f′(x)<0，可得1e <x <1，可得f(x)在[1e ,1)上单调递减，在[1,e)单调递增，函数的最小值为f(1)=1， 又f(1e )=−1+e ，f(e)=1+1e ，故函数的最大值为e −1， 故1<k ≤1+1e ， 故答案为：(1,1+1e ]，先将两个函数有两个交点转化为相应的方程xlnx −kx +1=0有两个根，再分离参数转化为k =lnx +1x 在[1e ,e]上有两个根，等价于y =k 与y =lnx +1x 有两个不同的交点，然后求导研究出函数y =lnx +1x 的极值与端点值，从而得出实数k 的取值范围． 本题考查函数图象交点个数问题，此类题通常转化为对应方程根的个数问题，熟练掌握根的个数与函数图象交点个数的对应关系是解答此类题的关键，此类题难度一般较高，本题是中档题．17.【答案】解：(1)由题意利用正弦定理可得(b −c2)b +(c −b2)c −a 2=0，化简可得b 2+c 2−a 2=bc ， 利用余弦定理可得cosA =b 2+c 2−a 22bc=12，又A ∈(0,π)，所以A =π3．(2)由(1)及题意知，A =π3，a =√3，b +c =3，由余弦定理知a2=b2+c2−2bccosA=(b+c)2−3bc，所以3=9−3bc，解得bc=2，所以S△ABC=12bcsinA=12×2×√32=√32．【解析】(1)由已知利用正弦定理得b2+c2−a2=bc，利用余弦定理可得cos A的值，结合A∈(0,π)，可求A的值．(2)由(1)及余弦定理可求bc的值，再根据三角形的面积公式，即可得到△ABC的面积．本题主要考查了正弦定理，余弦定理，三角形的面积公式在解三角形中的综合应用，考查了计算能力和转化思想，属于基础题．18.【答案】解：(1)∵S n=43(a n−1)，n∈N∗，当n=1时，S1=43(a1−1)，∴a1=4．当n≥2时，a n=S n−S n−1=43(a n−1)−43(a n−1−1)=43(a n−a n−1)．∴a n=4a n−1，又a1=4．∴{a n}是以4为首项，4为公比的等比数列，∴a n=a1q n−1=4n(n∈N∗)．(2)b n=log4a n=n，1b n b n+1=1n(n+1)=1n−1n+1，T n=b1+b2+⋅⋅⋅+b n=(1−12)+(12−13)+⋅⋅⋅+(1n−1n+1)=1−1n+1=nn+1．∴T2021=20212022．【解析】(1)利用递推关系式推出{a n}是以4为首项，4为公比的等比数列，然后求解通项公式．(2)化简1b n b n+1=1n(n+1)=1n−1n+1，利用裂项消项法求解数列的和即可．本题考查数列的递推关系式的应用，数列求和的方法，考查转化思想以及计算能力，是中档题．19.【答案】解：(1)证明：取AC的中点为O，连接PO，BO得到△PBO，∵ABCD是菱形，∴PA=PC，PO⊥AC，∵DC=5，AC=6，∴OC=3，OP=OB=4，∵PB =4√2，∴OP 2+OB 2=PB 2，∴PO ⊥OB ， ∴BO ∩AC =O ，BO ⊂平面BAC ，AC ⊂平面BAC ， ∴PO ⊥平面ABC ．∵PO ⊂平面PAC ，∴平面ABC ⊥平面PAC ．(2)∵AB =BC ，∴BO ⊥AC.易知OB ，OC ，OP 两两垂直，以O 为坐标原点OB ，OC ，OP 所在的直线分别为x 轴，y 轴，z 轴建立空间直角坐标系O −xyz ．则B(4,0，0)，C(0,3，0)，P(0,0，4)，A(0,−3,0).设Q(x,y ，z)．由PQ ⃗⃗⃗⃗⃗ =2QA ⃗⃗⃗⃗⃗ ，得Q(0,−2,43)．BC ⃗⃗⃗⃗⃗ =(−4,3,0)，BQ ⃗⃗⃗⃗⃗⃗ =(−4,−2,43)． 设n 1⃗⃗⃗⃗ =(x 1,y 1,z 1)为平面BCQ 的一个法向量．由{n 1⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =−4x 1+3y 1=0n 1⃗⃗⃗⃗ ⋅BQ ⃗⃗⃗⃗⃗⃗ =−4x 1−2y 1+43z 1=0，取z 1=15，则n 1⃗⃗⃗⃗ =(3,4,15)． 取平面ABC 的一个法向量n 2⃗⃗⃗⃗ =(0,0,1)，cos〈n ⃗ 1,n ⃗ 2〉=n 1⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗⃗|n 1⃗⃗⃗⃗⃗ ||n 2⃗⃗⃗⃗⃗ |=3√1010． ∴二面角Q −BC −A 的余弦值为3√1010．【解析】(1)取AC 的中点为O ，连接PO ，BO ，证明PO ⊥AC ，PO ⊥OB ，推出PO ⊥平面ABC ，然后证明平面ABC ⊥平面PAC ．(2)OB ，OC ，OP 两两垂直，以O 为坐标原点OB ，OC ，OP 所在的直线分别为x 轴，y 轴，z 轴建立空间直角坐标系O −xyz.求出平面BCQ 的一个法向量，平面ABC 的一个法向量，利用空间向量的数量积求二面角Q −BC −A 的余弦值即可．本题考查直线与平面垂直的判断定理，平面与平面垂直的判断定理，二面角的平面角的求法，考查空间想象能力，转化思想以及计算能力，是中档题．20.【答案】解：(1)由题意R(10)=10×102+10a =4000，所以a =300，当0<x <40时，W(x)=900x −(10x 2+300x)−260=−10x 2+600x −260； 当x ≥40时，W(x)=900x −901x 2−9450x+10000x−260=−x 2+9190x−10000x，所以W(x)={−10x 2+600x −260,0<x <40−x 2+9190x−10000x ,x ≥40．(2)当0<x <40，W(x)=−10(x −30)2+8740 当x =30时，W(x)max =8740…当x ≥40，W(x)=−x 2+9190x−10000x=−x −10000x+9190=−(x +10000x)+9190，因为x >0，所以x +10000x≥2√10000=200，当且仅当x =10000x时，即x =100时等号成立，此时W(x)≤−200+9190=8990， 所以W(x)max =8990万元， 因为8740<8990，所以2020年产量为100(千台)时，企业所获利润最大，最大利润是8990万元．【解析】(1)根据条件将x =10代入可求出a ，进而分段表示出W(x)即可； (2)利用二次函数最值、基本不等式求出分段函数W(x)的最值即可．本题考查函数模型的实际应用，考查二次函数最值，基本不等式求最值等知识点，属于中档题．21.【答案】(1)解：由题意知：|PF|=y P +p2=3+p2=4，∴p =2，所以抛物线C 的标准方程为：x 2=4y ．(2)证明：设切线AN 的方程为：y =k(x −a)，k ≠0，联立直线与抛物线方程得{x 2=4yy =k(x −a)，消去y 可得x 2−4kx +4ka =0，由直线与抛物线相切，∴△=16ka 2−16ka =0，解得a =k ． 所以切点N(2a,a 2)，F(0,1)，A(a,0)，∴AF ⃗⃗⃗⃗⃗ =(−a,1)，AN ⃗⃗⃗⃗⃗⃗ =(a,a 2)，∴AF ⃗⃗⃗⃗⃗ ⋅AN ⃗⃗⃗⃗⃗⃗ =−a 2+a 2=0． ∴∠FAN =90°，以FN 为直径的圆过点A ．【解析】(1)通过|PF|=4，结合抛物线的性质，求解p ，然后求解抛物线方程． (2)设切线AN 的方程为：y =k(x −a)，k ≠0，联立直线与抛物线方程得{x 2=4y y =k(x −a)，消去y 可得x 2−4kx +4ka =0，由直线与抛物线相切，得a =k.然后通过向量的数量积的计算，证明即可．本题考查抛物线的简单性质，抛物线方程的求法，直线与抛物线的位置关系的综合应用，是中档题．22.【答案】解：(1)f(x)的定义域为R，f′(x)=e x−a，若a≤0，则f′(x)>0，f(x)在R上单调递增；若a>0，则f′(x)=0解得x=lna．当x变化时，f′(x)，f(x)变化如下表：所以，f(x)的单调减区间是：(−∞,lna)，增区间是：(lna,+∞)．(2)由于a=1，所以(x−k)f′(x)+x+1=(x−k)(e x−1)+x+1．故当x>0时，(x−k)f′(x)+x+1>0等价于k<x+1e x−1+x(x>0)①，令g(x)=x+1e x−1+x，则g′(x)=e x(e x−x−2)(e x−1)2，而函数f(x)=e x−x−2在(0,+∞)上单调递增，f(1)<0，f(2)>0，所以f(x)在(0,+∞)存在唯一的零点．故g′(x)在(0,+∞)存在唯一的零点．设此零点为a，则a∈(1,2)．当x∈(0,a)时，g′(x)<0；当x∈(a,+∞)时，g′(x)>0．所以g(x)在(0,+∞)的最小值为g(a)．又由g′(a)=0，可得e a=a+2，所以g(a)=a+1∈(2,3)．由于①式等价于k<g(a)，故整数k的最大值为2．【解析】(1)分类讨论，利用导数的正负，可求f(x)的单调区间；(2)当x>0时，(x−k)f′(x)+x+1>0等价于k<x+1e x−1+x(x>0)，令g(x)=x+1e x−1+x，求最值，即可求k的最大值．本题考查利用导数研究曲线上某点切线方程，考查函数的单调性，考查函数的最值，正确求导、确定函数的单调性是关键．。