近似数

二年级关于近似数的说明1、两位数取近似数[四舍五入]其实我到是觉得.四舍五入也不难理解.讲明白了反而有助于孩子估数。

两位数取近似数.原则上按四舍五入.如.36≈40,42≈40,35≈40。

但是.估算时.仍可以具体情况具体分析.如.45+36≈？按四舍五入法.是90.但孩子们可能觉得.如果把45中的5舍去.结果“80”更接近准确数“81”.这样更好。

2、三位数取近似数[取整百或整百整十的数]分为以下几种情况；a、十位上是8、9或0、1.不管个位上是几.都可以取整百的数.如.382≈400,991≈1000,209≈200,318≈300。

[这种情况实际上是从十位向百位的四舍五入.鼓励用此方法.方便估算]。

有些同学觉得.如果取整百整十的数其结果会更接近近似数.于是把个位向十位四舍五入.变成；382≈380,991≈990..209≈210,318≈320.这样也很好。

但是.如果要取整百整十的数.就取最接近准确数的那个.比如.382不要估成390.要按四舍五入法去取。

特别说明的是.像九百九十几这样的数.干脆直接约成1000。

b、十位上是3——7的数.取整百整十的数.严格按照四舍五入.如.371 ≈370,567 ≈570。

3、四位数取近似数[取整千或整千整百的数]同理.百位上是0、1或8、9.则可以取整千的数.如；3098≈3000,2156≈2000.3849≈4000,3912≈4000。

根据具体情况取整千整百也行.如3098≈其他情况要严格按照从十位向百位四舍五入.如.3789≈3800,2643≈2600.[实际上.像2643这种情况.估成2700也可以.几十个数对于上千的数来说.舍掉或进上去.都无所谓。

但为了让孩子们不迷惑.所以我就这样规定了。

] 需要说明的是.四位数不要估成整千整百整十的数.比如.8952不能估成8950.没意义.可以估成8900.也可以直接估成9000.像9992.直接估成10000。

（2）某人一天饮水1 890mL（精确到1000mL）；
（3）人的眼睛可以看见的红光的波长为0.000 077cm （精确到0.000 01 cm）
1.下列由四舍五入得到的近 似数，各精确到哪一位？ （1）1.02×105精确到___千__位 （2）3.2×10-3精确到_万__分__位 （3） 2.56万精确到___百__位
近似数
1.你今年几岁了？ 2.你身高是多少㎝？
3.你体重是多少㎏？ 4.你家有几口人？
你觉得生活中出现的这些数 有什么不同吗？
生活中不仅需要准确数， 同时也需要近似数!
试举出生活中你熟悉的近似数 与准确数的例子
近似数常见的情况
1.实际生活中有许多数据都是近似数，如：用度量工具 测量出来的长度、质量、时间、速度等数据都是近似数
四舍五入.
问题1：
小亮用天平称得一个罐头的质量为2.026kg，试按下列 要求取近似值：
（1）精确到0.01kg (2)精确到0.1kg (3)精确到1kg
2.03kg
2.0kg
2kg
近似数2.0与2有区别吗？
问题2：
用四舍五入法，按要求对下列各数取近似值，并用科学 记数法表示.
（1）地球上七大洲的面积约为149 480 000km2 （精确到10 000 000 km2）；
2.由于客观原因不容易或不可能得到准确数时，只能得 到近似数。如：人口普查的结果。
下列数据中，哪些准确数？哪些是近似数？ （1）某词典有1752页； （2）量杯里有水50ml （3）女子短跑100m世界纪录为10.49s； （4）世界人口为61亿
我们学过哪些取近似数的方法？
“四舍五入”是我们常用的取近似数的方法．
3.太空探测器“先驱者10号”从发射到2003年2月人们 收到它最后一次发回的信号时，它已飞离地球12 200 000 000km（精确到1000 000 000km )，用科学记数 法表示_________万__位

近似数一个数与准确数相近(比准确数略多或者略少些),这一个数称之为近似数，如:我国的人口无法计算准确数目，但是可以说出一个近似数.比如说我国人口有13亿,13亿就是一个近似数.一个近似数四舍五入到哪一位，那么就说这个近似数精确到哪一位，从左边第一个不是0的数字起到精确的数位止的所有数止。

如:我国的人口无法计算准确数目，但是可以说出一个近似数.比如说我国人口有15亿,15亿就是一个近似数.近似数的四则计算加法和减法在通常情况下，近似数相加减，精确度最低的一个已知数精确到哪一位，和或者差也至多只能精确到这一位。

示例例如，一个同学去年体重30.4千克，今年体重比去年增加了3.18千克。

求今年体重时要把这两个近似数加起来。

因为30.4只精确到十分位，比3.18的精确度（精确到百分位）低，所以加得的和最多也只能精确到十分位。

为了容易看出计算结果的可靠程度，我们在竖式中每一个加数末尾添上一个“？”，用来表示被截去的数字。

30.4？+ 3.18 33.5？可以看到，因为第一个加数从百分位起的数就不能确定，所以加得的和从百分位起数字也不能确定。

近似数的加减一般可按下列法则进行：（1）确定计算结果能精确到哪一个数位。

（2）把已知数中超过这个数位的尾数“四舍五入”到这个数位的下一位。

（3）进行计算，并且把算得的数的末一位“四舍五入”。

例1 求近似数2.37与5.4258的和。

先把5.4258“四舍五入”到千分位，得5.426，再做加法。

2.37 +5.426 7.796 把7.796“四舍五入”到百分位，得7.80。

例2 求近似数0.075与0.001263的差。

先把0.001263“四舍五入”到万分位。

0.075 －0.0013 0.0737 把0.0737“四舍五入”到千分位，得0.074。

例3 求近似数25.3、0.4126、2.726的和。

25.3 0.41 + 2.73 28.44 把28.44“四舍五入”到十分位，得28.4。

3202 1872
1960
2000
2000
最高位的下一位的数比5小，最高位上的数不变。 最高位的下一位的数比5大，最高位上的数加1。
最高位是百，近似数常常是整百。
说出下列数的近似数： 588 120 600 100 400 230 709 391 613 906 200 700 400 600 900
407 897
680
900
700
最高位的下一位的数比5小，最高位上的数不变。 最。
说出下列数的近似数： 2781 3089 3000 3000 6000 哪种近似数更容易记住？ 2800 3100 6200 4800 8900 2780 只有一个数不 3090 是“0”的近似 数最容易记住 4810 8930
6203 4809
8928
5000
9000
最高位的下一位的数比5小，最高位上的数不变。 最高位的下一位的数比5大，最高位上的数加1。
近似数 整百 、 整十 来表示。 可以用整千、
30 3000 700 4000 90 200 8003
4900 4050 1100
6500 5000 760 706
整千的数有：
整百的数有：
整十的数有：
最高位是千，近似数常常是整千。
说出下列数的近似数： 4008 1002 4000 1000 3000 6200 7098 6870 4005 9753 6000 7000 7000 4000 10000

近似数及其计算方法江苏省泗阳县李口中学沈正中一、求近似数的三种方法1.四舍五入法这是一种最常用的求近似数的方法，就是看确定保留数位的下一位数字，比5小的（即0、1、2、3、4），就把这个数字以及后面的所有数字舍去；如果这个数字比4大（即5、6、7、8、9），就把这个数字以及后面的所有数字舍去后，向前一位进一。

如64.96283，保留到万分位写为64.9628，即64.96283≈64.9628（以下类推），保留到千分位写作64.963，保留到百分位写作68.96，保留到十分位写作64.0，保留到整数写作64。

由此可以看出：“四舍”时，近似数比准确值小，“五入”时，近似数比准确值大。

在实际生活中，有时把一个数的留存数位确认后，只要下一位数字或后面的数字存有不以0的（即1、2、3、……、9），都必须向前一位入一。

例如：同学们同时回去独木舟，每只船上最多可载7个同学，17个同学至少须要几只船？17÷7≈2.4，就是说17个同学须要2只船还余3人，这3人还须要一只船，所以一共须要3只船。

即17÷7＝≈3(只)。

由此可知：用进一法获得的对数数总比精确值大。

在实际生活中，有时把一个数的保留数位确定后，不管下一位数字或后面的数字是几（即0、1、2、3、……、9），都不要向前一位进一。

例如：用一根5m米短水管制成一批27cm长相同规格的水管，可以制成多少根？500÷27＝≈18（根）由此可知：Weinreb尾法获得的对数数总比精确数大。

二、近似数的四则混合运算1.对数数的加减法在一般情况下，近似数相加减的和或差精确到哪一位，与已知数中精确度最低的一个相同，计算法则：（1）确认结果准确至哪一个数位（与已知数中精确度最高那个数准确数位相同）；（2）把已知数中的其它数，四舍五入到已知数中精确度最低那个数数位的下一位；（3）展开排序，并且把配得的数的末位数字四舍五入。

【例1】求近似数25.4、0.456、8.738和56的和。

近似数、近似值
同实际数相接近的一个数，称为近似数．例如，某省有3800万人，“3800万”就是该省人口数的近似数．因为一个省的人口，有出生、有死亡，经常有变动，很难得到一个准确的实际数．
近似等于精确值的值，称为近似值．例如，除法运算的商，求至某位上四舍五入，所得到的值，都是这个商的近似值，如果是四舍，则所得的值称为过剩近似值．
不足近似值﹤精确值﹤过剩近似值
由此可知，近似数指的是根据实际情况，不可能得到或很难得到的一个不甚准确的数．而近似值是对精确值而言的，这个精确值是可能得到的．。

近似数导学案学习目标：1、了解近似数与有效数字的概念，能按精确度的要求取近似数，能根据近似数的不同形式确定其精确度和有效数字。

2、体会近似数在生活中实际应用。

重点：近似数的求法，精确度有效数的确定难点：精确度及有效数字的确定一、自主学习：1、回顾四舍五入法取近似值如：π≈3 （精确到个位）π≈3.1 （精确到0.1或精确到十分位）π≈3.14 （精确到或精确到）π≈（精确到万分位或精确到）2、近似数（1）生活中有的量很难或没有必要用准确数表示，而是用一个有理数近似地表示出来，我们称这个有理数为这个量的近似数。

如长江的长约为6300㎞，这里的6300㎞就是近似数。

因此，我们把接近准确数而不等于准确数的数，叫做这个数的近似数或近似值。

（2）304.35精确到个位的近似数为。

（3）精确度是指近似数与准确数的。

一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位，保留两位小数，精确到0.01，精确到百分位等说法的含义相同。

按括号要求取近似数①12341000（精确到万位）②2.715万（精确到百位）（4）有效数字：在四舍五入后的近似数中，从一个数的左边起，到末位数字止，所有的数字都是这个数的。

例1：近似数0.03050，最前面的两个0不是有效数字，而3后面的0和5后面的0都是这个数的有效数字。

用科学记数法表示的近似数a×10n，有效数字只与a有关，如3.12×510的有效数字为3，1，2。

当近似数后面有单位时，有效数字与单位无关，只与单位前面的数有关，如2.35万，有三个有效数字为2，3，5。

所以按照有效数字个数的要求对一个数取近似数，如：1.804（保留两个有效数字）的近似值为1.8。

例2：下列由四舍五入得到的近似数，它们精确到哪一位，有几个有效数字？①0.01020 ②1.20 ③1.50万④-2.30×410例3：用四舍五入法，按括号要求取近似值①607500 （保留两个有效数字）②0.030549 （保留三个有效数字）注意例2中③和④的精确度的确定：对于a×10n精确度由还原后的数字a的末位数字所在的数位决定；对于含有文字单位的近似值，精确度也是由还原后的数字中近似数的末位数字所在的位数决定的。

近似数
1、我们班级的人数是 中女生有 ，男生有
，其 。
2、量一量数学课本的长度约 是 ，宽度约 是 。
1、准确数和近似数：
观察上面两题中的数字，它们之 间有什么区别？
• 与实际完全符合的数是准确数. • 与实际非常接近的数是近似数. • 测量的结果，往往是近似数。除了测量， 还常常会遇到或用到近似数，如，我国 的陆地面积约为960万平方公里，小明 的年龄为12岁，这里的960、12都是近 似数。
【说明】 进一法：不论精确位后的数 如何，只要比0大，就进一；去尾法:不 论精确位后的数如何，一律舍去。
【方法点拨】
一般地，一个近似数四舍五入到某一 位，就说这个近似数精确到那一位。 例如，小明的身高为1.70米，1.70这 个近似数精确到百分位。
下列由四舍五入法得到的近似数 ，各精确到哪一位？
(1) 132.4
(2) 0.0572
十分位
万分位 百位
(3) 2.40 万
王平与李明测量一根钢管的长，王平测 得长是0.80米，李明测得长是0.8米。两人 测量的结果是否相同？为什么？
（3）130542 （精确到千位）
注意：精确到十位及其以上位数时， 首先用科学计数法表示，再1.50与近似数 1.5相同吗？近似数1.50末尾 的0能否去掉不写？
某校学生 320 人外出参观，已 有65名学生坐校车出发，现还需要 几辆45座的大巴？ 要把一根100cm长的圆柱形 钢材截成6cm的一段一段做零件 。最多可以截得几段？
2、关于精确度问题：
近似数的近似程度是精确度。 我们都知道：Л= 3.1415926…… 计算中我们需对Л取近似数。 如果结果只取整数，那么按四舍五入的法则应为 3，就叫做精确到个位（或精确1）； 如果结果取1位小数，那么应为3.1，就叫做精确 到0.1（或精确到十分位）； 如果结果取2位小数，那么应为3.14，就叫做精 确到0.01（或精确到百分位）； ……

≈
≈
3501002万
350亿
6201239648
≈
≈
620124万
62亿

求近似数的方法： 1、用“万”作单位的近似数，找到“万”位，应看 千位上的数是几，再决定是“四舍”还是“五入”. 2、用“亿”作单位的近似数，找到“亿”位，应看 千万位上的数是几，再决定是“四舍”还是“五入”. 3、不管是用“万”还是“亿”作单位，写近似数时 都要用“ ”连接，末尾还要写上“万”字或“亿”字。

生活中一些事物的数量，有时不需要准确 地表示出来，用近似数表示更方便。
近似数 近
似 数
学习目标

知道近似数的含义，并会根 据要求用“四舍五入”的方法省略 一个数的尾数求近似数，会用“万” 或“亿”做单位求一个数的近似数。
11030大约是几万？ 178680000大约是几亿？ 11030 ≈ 1万 ┆ ┆ 约等号
下面是2003年我国部分主要工业产品的产量， 求出它们的近似数
产品名称 水泥 钢材 原煤
产
量
四舍五入到亿位 （ ）亿吨 （ ）亿吨
862000000吨
222336000吨
1667000000吨 （ ）亿吨
将下面各数按从小到大的顺序排列。

3400760 980968
11203400 3400670
人口数/万人 1674万 9079万 4677万 6440万 4489万 我国每十年 进行一次人 口普查。
山 东
浙 江 湖 南 广 西 云 南
42879000
4288万
先省略万位后面的尾数求近似数，在 省略亿位后面的尾数求近似数
5624589634 ≈ ≈ 35010023647 562459万 56亿

(5)84960（精确到百位，并用科学记数法表示）
1. 本节课你学到了一些什么知识? 2. 在学习中你得了一些什么结论?
解：(1) 0.0158≈0.016; (2)1.8935 ≈1.89; (3)1.804 ≈1.8; (4) 1.804 ≈1.80; （5）603400＝6.034×105 ≈ 6.0×105; (6) 61235 ＝6.1235×104 ≈ 6.1×104
问题与思考
1. 6.0×106 精确到哪一位？
2. 3.9万 精确到哪一位？
注：判断一个用科学记数法表示的数精确到 哪一位，一定要先将这个数还原成一般的完 整的形式，再去数它精确到的位数．
2. 用四舍五入法按括号的要求对下列各数取近似 值。 (1)0.6779 (精确到百分位)
0.68 29.8 8.06×104 3.145
(2)29.756
1、下列由四舍五入法得到的近似数各精确到哪一 位？ (1)11亿 (2)36.8 (3)1.2万 (4)1.20万 2、用四舍五入法，按括号内的要求对下列各数取 近似值： (1)0.33448（精确到千分位）(2)64.8（精确到个位）
(3)1.5952（精确到0.01）(4)0.05069（精确到0.001）
1.什么叫准确数?
与实际完全符合的数称为准确数。
2.什么叫近似数?
与实际接近的数称为近似数。
▲注意：通过测量或估计得到的都是近似数
小调查
问题①：我们班有
男生有 人, 女生有
位同学，其中
人。 厘米
问题②：你的身高是
大家想一想，上述两个问 题中的几个数据有什么不同。
p57做一做：
下列叙述的各数中哪些是准确数？哪些是近似数？ （1）教室里有24张课桌； （2）小明的身高是1.57米； （3）某本书的定价是4.50元; （4）月球与地球之间的平均距离大约是38万千米; （5）据美国一家猫粮制作公司调查：“在美国共有8500万只 猫咪，22%的猫主人都选择猫咪爱看得频道。”

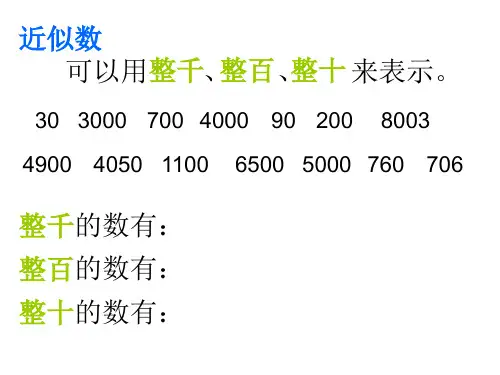
求近似数有哪几种方法？
求近似数有哪几种方法？一般有3种：
1.四舍五入法这是最常用的求近似数的方法。

当省略的尾数的最高位上的数是4或比4小的时候，就把尾数舍去；当省略的尾数最高位上的数是5或比5大时，把尾数去掉后，要向前一位进1。

举例（45000≈5万，612000≈61万）
2.进一法在实际生活中，有时把一个数的尾数省略后，不管尾数最高位上的数是几，都要向它的前一位进一。

用进一法得到的近似数总比准确值大。

举例（45000≈5万，612000≈62万）
3.去尾法在实际生活中，有时把一个数的尾数省略后，不管尾数最高位上的数字是几，都不要向它的前一位进一。

用去尾法得到的近似数总比准确值小。

举例（45000≈4万，612000≈61万）。

近似数（精选7篇）（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如总结报告、合同协议、规章制度、条据文书、策划方案、心得体会、演讲致辞、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays, such as summary reports, contract agreements, rules and regulations, doctrinal documents, planning plans, insights, speeches, teaching materials, complete essays, and other sample essays. If you want to learn about different sample formats and writing methods, please pay attention!近似数（精选7篇）近似数篇一课题：教学目标1.使学生理解并掌握近似数的概念。

近似数都有以下特点：1、取的近似数要方便计算。

2、近似数要取整千、整百、整十的数。

3、近似数不唯一。

现在最难理解的是第三点。

举例说明：1、两位数取近似数（四舍五入）其实我到是觉得，四舍五入也不难理解，讲明白了反而有助于孩子估数。

两位数取近似数，原则上按四舍五入，如，36≈40,42≈40,35≈40。

但是，估算时，仍可以具体情况具体分析，如，45+36≈？按四舍五入法，是90，但孩子们可能觉得，如果把45中的5舍去，结果“80”更接近准确数“81”，这样更好。

2、三位数取近似数（取整百或整百整十的数）分为以下几种情况：?a、十位上是8、9或0、1，不管个位上是几，都可以取整百的数，如，382≈400,991≈1000,209≈200,318≈300。

（这种情况实际上是从十位向百位的四舍五入，鼓励用此方法，方便估算）。

有些同学觉得，如果取整百整十的数其结果会更接近近似数，于是把个位向十位四舍五入，变成：382≈380,991≈990，，209≈210,318≈320，这样也很好。

但是，如果要取整百整十的数，就取最接近准确数的那个，比如，382不要估成390，要按四舍五入法去取。

特别说明的是，像九百九十几这样的数，干脆直接约成1000。

b、十位上是3——7的数，取整百整十的数，严格按照四舍五入，如，371?≈?370,567??≈570。

3、四位数取近似数（取整千或整千整百的数）同理，百位上是0、1或8、9，则可以取整千的数，如：3098≈3000,2156≈2000，3849≈4000,3912≈4000。

根据具体情况取整千整百也行，如3098≈其他情况要严格按照从十位向百位四舍五入，如，3789≈3800,2643≈2600.（实际上，像2643这种情况，估成2700也可以，几十个数对于上千的数来说，舍掉或进上去，都无所谓。

但为了让孩子们不迷惑，所以我就这样规定了。

）需要说明的是，四位数不要估成整千整百整十的数，比如，8952不能估成8950，没意义，可以估成8900，也可以直接估成9000.像9992，直接估成10000。

五、拓展练习 7 7 5 6 5 6 4 4 4 4 4 4 ≈ 7000 ≈ 8000 ≈ 5700 ≈ 58用式子表示出（10分） 8700是8660的近似数 9320是9317的近似数 2、判断句子中的数是不是近似数，是近似数在（）打√，不是 近似数的在（）打×。（20分） 我国有大约3600只熊猫（） 蜻蜓大概每分钟吃50只蚊子（） 丫丫每天走600米路（） 中国有近14亿人口（） 3、写出下面各数的近似数（20分） 980≈ 1079≈ 97≈ 7932≈ 3496≈ 4、在方格中填入一个数，使得等式成立。（20分） 7 8 8 ≈ 5800 3 6 4 ≈ 4000
近似数知识小结
一、近似数的定义
与准确数比较接近的整十、整百、整千叫做准确数的 近似数。
二、近似数的特征
1、与准确数接近 2、整十、整百、整千
三、近似数的表示方式
5000是4982的近似数 表示为： 4982≈5000 四千九百八十二约等 读作: 于五千
四、近似数的求法
4867≈ 4870 4867≈ 4900 4867≈ 5000
5、用4,6,0,8这四个数字组成的千位上是8且只读一个零的数有 （ ）；一个零也不读的四位数有（ ） 。（有几个写几个） （30分）

四年级数学近似数知识点
一、近似数的概念
近似数是指与准确数相近的一个数。

准确数：即这个数的最原始数据，没有经过约分、化简、或者四
舍五入等任何运算之前的表达方法。

近似数：经过四舍五入、进一法或者去尾法等方法得到的一个与
原始数据相差不大的一个数。

二、四舍五入法
1. 如果尾数的最高位数字是 4 或者比 4 小，就把尾数去掉。

例如：54321 近似到万位，因为千位是 4，所以54321 ≈ 50000
2. 如果尾数的最高位数是 5 或者比 5 大，就把尾数舍去并且在它的前一位进 1。

例如：65890 近似到万位，因为千位是 5，所以65890 ≈ 70000
三、进一法
进一法是去掉多余部分的数字后，在保留部分的一个数字上加
1。

例如：一堆货物需要装 3.2 个箱子，实际需要 4 个箱子才能装完。

四、去尾法
去尾法是去掉数字的小数部分，取其整数部分。

例如：用一匹布做衣服，每件衣服用布 2.5 米，这匹布可以做 8 件衣服。

五、求近似数的应用
在实际生活中，经常会用到近似数来描述一些数量。

比如：描述城市的人口数量、统计商品的销售额等。

在计算时，要根据具体情况选择合适的方法求近似数。

精确的程度． 【知识拓展】 取某数近似数常见的方法：
（1）精确到某位或精确到小数点后某位，一个近似数四舍五入到哪一位，就说这个近似数精确到哪一位．如：近似 数0.25 精确到百分位或精确到0.01 ． （2）对较大的数取近似数时，结果一般要用科学记数法表示．如：8903000（精确到万位）的近似数为8.90 × 10 ．
5
18
/0Leabharlann 三、精确度．6/
12
6
1
3.14159
（精确到0.001 ）
爱
智
康
近似数与准确数的接近程度可以用精确度表示，一个近似数四舍五入到哪一位就称这个数精确到哪一位，精确度是
20
2
下列说法正确的是（ ）． A. 2.46 万精确到万位，有三个有效数字 B. 近似数6百和600精确度是相同的 C. 317500精确到千位可以表示为31.8 万，也可表示为3.18 × 10 D. 0.0502 共有5个有效数字，它精确到万分位
近似数和精确度
一、准确数
在日常生活和实际生产中，能准确地表示一些量的数，成为准确数．例如：三班共50人，小樱养了3条金鱼，数字50 和3就是准确数．
二、近似数
与实际接近但存在一定偏差的数称为近似数．例如：π 取3.14 ，体重约54kg ，这里3.14 、54都是近似数． 【注意】求一个数的近似数，应按题目要求取近似数． 【易错点津】 （1）近似数与准确数不相等，有误差． （2）近似数小数点后的末位数是0的，不能去掉0． 用四舍五入法，求1.549 的近似值（保留两个有效数字）是 ．

近似数及其计算方法集团文件版本号：（M928-T898-M248-WU2669-I2896-DQ586-M1988）近似数及其计算方法江苏省泗阳县李口中学沈正中一、求近似数的三种方法1. 四舍五入法这是一种最常用的求近似数的方法，就是看确定保留数位的下一位数字，比5小的（即0、1、2、3、4），就把这个数字以及后面的所有数字舍去；如果这个数字比4大（即5、6、7、8、9），就把这个数字以及后面的所有数字舍去后，向前一位进一。

如64.96283，保留到万分位写为64.9628，即64.96283≈64.9628（以下类推），保留到千分位写作64.963，保留到百分位写作68.96，保留到十分位写作64.0，保留到整数写作64。

由此可以看出：“四舍”时，近似数比准确值小，“五入”时，近似数比准确值大。

2. 进一法在实际生活中，有时把一个数的保留数位确定后，只要下一位数字或后面的数字有不为0的（即1、2、3、……、9），都要向前一位进一。

如：同学们同时去划船，每只船上最多能载7个同学，17个同学至少需几只船？17÷7≈2.4，就是说17个同学需要2只船还余3人，这3人还需一只船，所以一共需要3只船。

即17÷7＝≈3 (只)。

由此可知：用进一法得到的近似数总比准确值大。

3. 去尾法在实际生活中，有时把一个数的保留数位确定后，不管下一位数字或后面的数字是几（即0、1、2、3、……、9），都不要向前一位进一。

如：用一根5m米长水管做成一批27cm长相同规格的水管，可以做成多少根？500÷27＝≈18（根）由此可知：用去尾法得到的近似数总比准确数小。

二、近似数的四则混合运算1. 近似数的加减法在一般情况下，近似数相加减的和或差精确到哪一位，与已知数中精确度最低的一个相同，计算法则：（1）确定结果精确到哪一个数位（与已知数中精确度最低那个数精确数位相同）；（2）把已知数中的其它数，四舍五入到已知数中精确度最低那个数数位的下一位；（3）进行计算，并且把算得的数的末位数字四舍五入。