例 如图,在△ABC内任取一点D,连接AD和 BD.点E在△ABC外,∠EBC=∠ABD, ∠ECB=∠DAB.求证: △DBE∽△ABC.
分析: 好容易得出∠ABC=∠DBE BE BC 只需要再证明 BD AB BE BD 即证
BC AB
A D
只要证明△ABD∽△CBE
B
E
C
判定定理3
三条平行线截两条直线,所得 的 对应线段成比例. 平行于三角形一边的直线截其他两边 (或
两边的延长线)所得的对应线段成比例.
反比、合分比的性质 P7
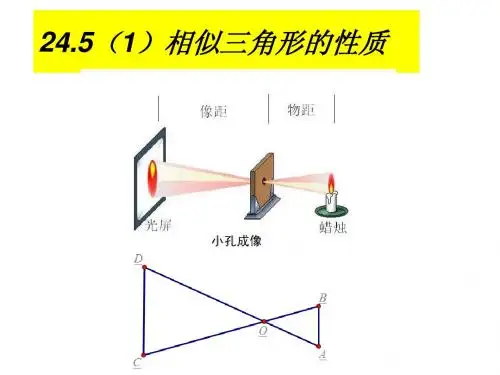
三 相似三角形的判定及性质
1.相似三角形的定义
对应角相等,对应边成比例的两个三 角形叫做相似三角形.相似三角形对应 边的比值叫做相似比(或相似的系数).
(1)相似三角形对应高的比、对应中 线 的比和对应角平分线的比都等于 相似比;
(2)相似三角形周长的比等于相似比; (3)相似三角形面积的比等于相似比的 平方;
已知:梯形ABCD中 AD∥BC,AD=36cm, BC=60cm,延长两腰 BA,CD交于点 O,OF⊥BC,交AD于 E,EF=32cm,则 OF=_______. 80cm
判定定理2 对于任意两个三角形,如果一个三 角形的两边和另一个三角形的两边对 应成比例,并且夹角相等,那么这两个 三角形相似.
简述:两边对应成比例且夹角相等,两三角形相似
已知:如图,在△ABC和△ABC中,∠A=∠A, A' B ' A' C ' 求证: △ABC∽△ABC
AB AC
E
∴△ABC∽△ABC
C
例 如图,已知D、E、F分别是△ABC三边、 BC、CA、AB的中点. 求证:△DEF∽△ABC