2021年中考数学九年级复习微专题专项课时练：三角形的面积(选择题)(一)

14、 (2020长春.中考模拟) 如图是用8块A型瓷砖（白色四边形）和8块B型瓷砖（黑色三角形）不重叠，无空隙拼接而成的 一个正方形图案，图案中A型瓷砖的总面积与B型瓷砖的总面积之比为________。
15、
(2020自贡.中考真卷) 如图，在矩形
中，E是 上的一点，连接
的中点F处，在 上取一点O，以点O为圆心， 的长为半径作半圆与
17、
(2020青岛.中考真卷) 如图，在正方形
中，对角线 与 交于点O，点 在 的延长线上，连接 ，点
F是 的中点，连接 交 于点G．若
，
，则点A到 的距离为________．
18、
(2020抚顺.中考真卷) 如图，四边形
是矩形，延长 到点 ，使
，连接 ，点 是 的中点
，连接 ， ，得到
；点 是 的中点，连接 ， ，得到
备 考 2021中 考 数 学 复 习 专 题 ： 图 形 的 性 质 _三 角 形 _三 角 形 的 面 积 ， 填 空 题 答 案
1.答案： 2.答案： 3.答案： 4.答案： 5.答案： 6.答案： 7.答案：
8.答案： 9.答案： 10.答案： 11.答案： 12.答案： 13.答案： 14.答案： 15.答案： 16.答案：
13、 (2019顺城.中考模拟) 如图所示，n+1个边长为1的等边三角形，其中点A，C1 ， C2 ， C3 ， …∁n在同一条直线上，若 记△B1C1D1的面积为S1 ， △B2C2D2的面积为S2 ， △B3C3D3的面积为S3 ， …，△Bn∁nDn的面积为Sn ， 则Sn＝_____ ___.
备考2021年中考数学复习专题：图形的性质_三角形_三角形的面积，填空题专
训及答案

28.答案：
A . 1个 B . 2个 C . 3个 D . 4个 8、 (2019宁波.中考模拟) 如图，ABCDEF为⊙O的内接正六边形，AB＝m，则图中阴影部分的面积是（ ）
A . m2 B . m2 C .
m2 D .
m2
9、 (2019.中考模拟) 如图，点C为线段AB上一点，且AC=2CB，以AC、CB为边在AB的同侧作等边△ADC和等边△EBC ，连接DB、AE交于点F，连接FC，若FC=3，设DF=a、EF=b，则a、b满足（ ）
点F，已知S△AEF＝3，则下列结论：①
；②S△BCE＝30；③S△ABE＝9；④△AEF∽△ACD，其中一定正确的是（
）
A . ①②③④ B . ①③ C . ②③④ D . ①②③ 22、 (2019张掖.中考模拟) 如图，矩形ABCD中，AB＝4，AD＝6，E为AD中点，分别以B、E为圆心，以AB、AE为半径画 弧，两弧交于点F，连接AF、BE，则AF的长为（ ）
A. B. C. D.5 23、 (2019张掖.中考模拟) 如图，在Rt△ABC中，∠BAC＝90°，且AB＝3，BC＝5，⊙A与BC相切于点D，交AB于点E， 交AC于点F，则图中阴影部分的面积为（ ）
A . 12﹣ π B . 12﹣ π C . 6﹣
24、
(2019新乡.中考模拟) 如图，菱形
9.答 案 ： D 10.答 案 ： C 11.答 案 ： C 12.答 案 ： B 13.答 案 ： C 14.答 案 ： B 15.答 案 ： C 16.答 案 ： C 17.答 案 ： C 18.答 案 ： D 19.答 案 ： D 20.答 案 ： B 21.答 案 ： B 22.答 案 ： C 23.答 案 ： C 24.答 案 ： A 25.答 案 ： A 26.答 案 ： C 27.答案：

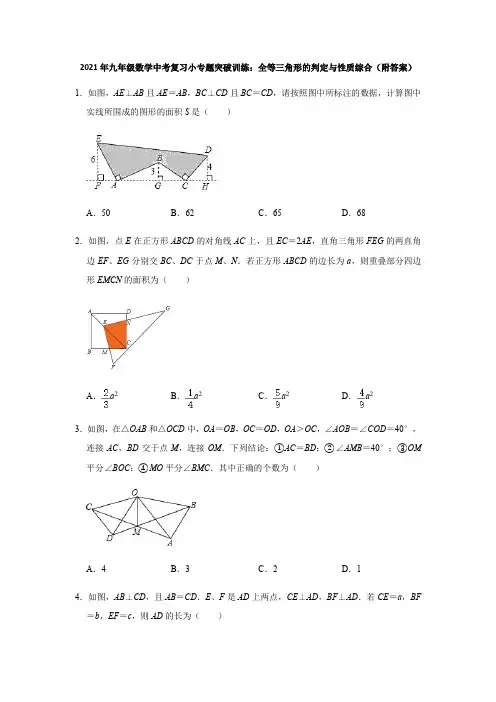
2021年九年级数学中考复习小专题突破训练：全等三角形的判定与性质综合（附答案）1．如图，AE⊥AB且AE＝AB，BC⊥CD且BC＝CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（）A．50B．62C．65D．682．如图，点E在正方形ABCD的对角线AC上，且EC＝2AE，直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N．若正方形ABCD的边长为a，则重叠部分四边形EMCN的面积为（）A．a2B．a2C．a2D．a23．如图，在△OAB和△OCD中，OA＝OB，OC＝OD，OA＞OC，∠AOB＝∠COD＝40°，连接AC，BD交于点M，连接OM．下列结论：①AC＝BD；②∠AMB＝40°；③OM 平分∠BOC；④MO平分∠BMC．其中正确的个数为（）A．4B．3C．2D．14．如图，AB⊥CD，且AB＝CD．E、F是AD上两点，CE⊥AD，BF⊥AD．若CE＝a，BF ＝b，EF＝c，则AD的长为（）A．a+c B．b+c C．a﹣b+c D．a+b﹣c5．如图，在△ABC中，AD是∠A的外角平分线，P是AD上异于A的任意一点，设PB＝m，PC＝n，AB＝c，AC＝b，则（m+n）与（b+c）的大小关系是（）A．m+n＞b+c B．m+n＜b+c C．m+n＝b+c D．无法确定6．如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA＝60°；③△BPQ为等边三角形；④MB平分∠AMC，其中结论正确的有（）A．1个B．2个C．3个D．4个7．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE＝2BF．给出下列四个结论：①DE＝DF；②DB＝DC；③AD ⊥BC；④AC＝3BF，其中正确的结论共有（）A．4个B．3个C．2个D．1个8．如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE、下列说法：①CE＝BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF ≌△CDE．其中正确的有（）A．1个B．2个C．3个D．4个9．如图，在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别为R、S，若AQ＝PQ，PR＝PS，则这四个结论中正确的有（）①P A平分∠BAC；②AS＝AR；③QP∥AR；④△BRP≌△CSP．A．4个B．3个C．2个D．1个10．两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD ＝CD，AB＝CB，詹姆斯在探究筝形的性质时，得到如下结论：①AC⊥BD；②AO＝CO＝AC；③△ABD≌△CBD，其中正确的结论有（）A．0个B．1个C．2个D．3个11．如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN 在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM＝PN恒成立；（2）OM+ON的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（）A．4B．3C．2D．112．如图，点E，F在AC上，AD＝BC，DF＝BE，要使△ADF≌△CBE，还需要添加的一个条件是（）A．∠A＝∠C B．∠D＝∠B C．AD∥BC D．DF∥BE13．如图，正方形ABCD的边长为6，点E、F分别在AB，AD上，若CE＝3，且∠ECF ＝45°，则CF的长为（）A．2B．3C．D．14．如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝．15．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3＝°．16．如图，在△ABC中，已知∠1＝∠2，BE＝CD，AB＝5，AE＝2，则CE＝．17．如图，在四边形ABCD中，AB＝AD，∠BAD＝∠BCD＝90°，连接AC．若AC＝6，则四边形ABCD的面积为．18．如图，四边形ABCD的对角线AC、BD相交于点O，△ABO≌△ADO．下列结论：①AC⊥BD；②CB＝CD；③△ABC≌△ADC；④DA＝DC．其中所有正确结论的序号是．19．如图，在△ABC中，∠A＝90°，AB＝AC，∠ABC的平分线BD交AC于点D，CE⊥BD，交BD的延长线于点E，若BD＝8，则CE＝．20．如图，在四边形ABCD中，AD＝4，CD＝3，∠ABC＝∠ACB＝∠ADC＝45°，则BD 的长为．21．已知：如图，BD为△ABC的角平分线，且BD＝BC，E为BD延长线上的一点，BE＝BA，过E作EF⊥AB，F为垂足，下列结论：①△ABD≌△EBC；②∠BCE+∠BCD＝180°；③AD＝EF＝EC；④AE＝EC，其中正确的是（填序号）22．如图，四边形ABCD中，∠BAD＝∠BCD＝90°，AB＝AD，若四边形ABCD的面积为24cm2，则AC长是cm．23．如图，四边形ACDF是正方形，∠CEA和∠ABF都是直角且点E，A，B三点共线，AB ＝4，则三角形ABC的面积是．24．如图，AE⊥AB，且AE＝AB，BC⊥CD，且BC＝CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是．25．如图，△ABC的内角∠ABC和外角∠ACD的平分线相交于点E，BE交AC于点F，过点E作EG∥BD交AB于点G，交AC于点H，连接AE，有以下结论：①∠BEC＝∠BAC；②△HEF≌△CBF；③BG＝CH+GH；④∠AEB+∠ACE＝90°，其中正确的结论有（将所有正确答案的序号填写在横线上）．26．如图，已知△ABC三个内角的平分线交于点O，点D在CA的延长线上，且DC＝BC，AD＝AO，若∠BAC＝80°，则∠BCA的度数为．27．如图，在△ABC中，AB＝AC＝2，∠BAC＝120°，点D、E都在边BC上，∠DAE ＝60°．若BD＝2CE，则DE的长为．28．（1）如图1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD 上的点，且∠EAF＝∠BAD．求证：EF＝BE+FD；（2）如图2，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD 上的点，且∠EAF＝∠BAD，（1）中的结论是否仍然成立？（3）如图3，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF＝∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．29．如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C＝90°，∠B ＝∠E＝30°．（1）操作发现如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是．（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想．（3）拓展探究已知∠ABC＝60°，点D是角平分线上一点，BD＝CD＝4，DE∥AB交BC于点E（如图4）．若在射线BA上存在点F，使S△DCF＝S△BDE，请直接写出相应的BF的长．30．已知：如图，在△ABC、△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，点C、D、E三点在同一直线上，连接BD．（1）求证：△BAD≌△CAE；（2）试猜想BD、CE有何特殊位置关系，并证明．31．如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，AF⊥CB，垂足为F．（1）求证：△ABC≌△ADE；（2）求∠F AE的度数；（3）求证：CD＝2BF+DE．32．已知△ABN和△ACM位置如图所示，AB＝AC，AD＝AE，∠1＝∠2．（1）求证：BD＝CE；（2）求证：∠M＝∠N．33．将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB＝∠DEB＝90°，∠A＝∠D＝30°，点E落在AB上，DE所在直线交AC所在直线于点F．（1）求证：AF+EF＝DE；（2）若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°＜α＜60°，其它条件不变，请在图②中画出变换后的图形，并直接写出你在（1）中猜想的结论是否仍然成立；（3）若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°＜β＜180°，其它条件不变，如图③．你认为（1）中猜想的结论还成立吗？若成立，写出证明过程；若不成立，请写出AF、EF与DE之间的关系，并说明理由．34．已知：在△ABC中，AC＝BC，∠ACB＝90°，点D是AB的中点，点E是AB边上一点．（1）直线BF垂直于直线CE于点F，交CD于点G（如图1），求证：AE＝CG；（2）直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M（如图2），找出图中与BE相等的线段，并证明．35．如图，已知在四边形ABCD中，点E在AD上，∠BCE＝∠ACD＝90°，∠BAC＝∠D，BC＝CE．（1）求证：AC＝CD；（2）若AC＝AE，求∠DEC的度数．参考答案1．解：∵AE⊥AB且AE＝AB，EF⊥FH，BG⊥FH⇒∠EAB＝∠EF A＝∠BGA＝90°，∠EAF+∠BAG＝90°，∠ABG+∠BAG＝90°⇒∠EAF＝∠ABG，∴AE＝AB，∠EF A＝∠AGB，∠EAF＝∠ABG⇒△EF A≌△AGB，∴AF＝BG，AG＝EF．同理证得△BGC≌△CHD得GC＝DH，CH＝BG．故FH＝F A+AG+GC+CH＝3+6+4+3＝16故S＝（6+4）×16﹣3×4﹣6×3＝50．故选：A．2．解：过E作EP⊥BC于点P，EQ⊥CD于点Q，∵四边形ABCD是正方形，∴∠BCD＝90°，又∵∠EPM＝∠EQN＝90°，∴∠PEQ＝90°，∴∠PEM+∠MEQ＝90°，∵三角形FEG是直角三角形，∴∠NEF＝∠NEQ+∠MEQ＝90°，∴∠PEM＝∠NEQ，∵AC是∠BCD的角平分线，∠EPC＝∠EQC＝90°，∴EP＝EQ，四边形PCQE是正方形，在△EPM和△EQN中，，∴△EPM≌△EQN（ASA）∴S△EQN＝S△EPM，∴四边形EMCN的面积等于正方形PCQE的面积，∵正方形ABCD的边长为a，∴AC＝a，∵EC＝2AE，∴EC＝a，∴EP＝PC＝a，∴正方形PCQE的面积＝a×a＝a2，∴四边形EMCN的面积＝a2，故选：D．3．解：∵∠AOB＝∠COD＝40°，∴∠AOB+∠AOD＝∠COD+∠AOD，即∠AOC＝∠BOD，在△AOC和△BOD中，，∴△AOC≌△BOD（SAS），∴∠OCA＝∠ODB，AC＝BD，①正确；∴∠OAC＝∠OBD，由三角形的外角性质得：∠AMB+∠OAC＝∠AOB+∠OBD，∴∠AMB＝∠AOB＝40°，②正确；作OG⊥MC于G，OH⊥MB于H，如图2所示：则∠OGC＝∠OHD＝90°，在△OCG和△ODH中，，∴△OCG≌△ODH（AAS），∴OG＝OH，∴MO平分∠BMC，④正确；∵∠AOB＝∠COD，∴当∠DOM＝∠AOM时，OM才平分∠BOC，假设∠DOM＝∠AOM∵△AOC≌△BOD，∴∠COM＝∠BOM，∵MO平分∠BMC，∴∠CMO＝∠BMO，在△COM和△BOM中，，∴△COM≌△BOM（ASA），∴OB＝OC，∵OA＝OB∴OA＝OC与OA＞OC矛盾，∴③错误；正确的个数有3个；故选：B．4．解：∵AB⊥CD，CE⊥AD，BF⊥AD，∴∠AFB＝∠CED＝90°，∠A+∠D＝90°，∠C+∠D＝90°，∴∠A＝∠C，∵AB＝CD，∴△ABF≌△CDE，∴AF＝CE＝a，BF＝DE＝b，∵EF＝c，∴AD＝AF+DF＝a+（b﹣c）＝a+b﹣c，故选：D．5．解：在BA的延长线上取点E，使AE＝AC，连接EP，∵AD是∠BAC的外角平分线，∴∠CAD＝∠EAD，在△ACP和△AEP中，，∴△ACP≌△AEP（SAS），∴PE＝PC，在△PBE中，PB+PE＞AB+AE，∵PB＝m，PC＝n，AB＝c，AC＝b，∴m+n＞b+c．故选：A．6．解：∵△ABD、△BCE为等边三角形，∴AB＝DB，∠ABD＝∠CBE＝60°，BE＝BC，∴∠ABE＝∠DBC，∠PBQ＝60°，在△ABE和△DBC中，，∴△ABE≌△DBC（SAS），∴①正确；∵△ABE≌△DBC，∴∠BAE＝∠BDC，∵∠BDC+∠BCD＝180°﹣60°﹣60°＝60°，∴∠DMA＝∠BAE+∠BCD＝∠BDC+∠BCD＝60°，∴②正确；在△ABP和△DBQ中，，∴△ABP≌△DBQ（ASA），∴BP＝BQ，∴△BPQ为等边三角形，∴③正确；∵∠DMA＝60°，∴∠AMC＝120°，∴∠AMC+∠PBQ＝180°，∴P、B、Q、M四点共圆，∵BP＝BQ，∴，∴∠BMP＝∠BMQ，即MB平分∠AMC；∴④正确；综上所述：正确的结论有4个；故选：D．7．解：∵BF∥AC，∴∠C＝∠CBF，∵BC平分∠ABF，∴∠ABC＝∠CBF，∴∠C＝∠ABC，∴AB＝AC，∵AD是△ABC的角平分线，∴BD＝CD，AD⊥BC，故②③正确，在△CDE和△BDF中，，∴△CDE≌△BDF（ASA），∴DE＝DF，CE＝BF，故①正确；∵AE＝2BF，∴AC＝3BF，故④正确．故选：A．8．解：∵AD是△ABC的中线，∴BD＝CD，又∠CDE＝∠BDF，DE＝DF，∴△BDF≌△CDE，故④正确；由△BDF≌△CDE，可知CE＝BF，故①正确；∵AD是△ABC的中线，∴△ABD和△ACD等底等高，∴△ABD和△ACD面积相等，故②正确；由△BDF≌△CDE，可知∠FBD＝∠ECD∴BF∥CE，故③正确．故选：D．9．解：（1）P A平分∠BAC．∵PR⊥AB，PS⊥AC，PR＝PS，AP＝AP，∴△APR≌△APS，∴∠P AR＝∠P AS，∴P A平分∠BAC；（2）由（1）中的全等也可得AS＝AR；（3）∵AQ＝PR，∴∠1＝∠APQ，∴∠PQS＝∠1+∠APQ＝2∠1，又∵P A平分∠BAC，∴∠BAC＝2∠1，∴∠PQS＝∠BAC，∴PQ∥AR；（4）∵PR⊥AB，PS⊥AC，∴∠BRP＝∠CSP，∵PR＝PS，∴△BRP不一定全等与△CSP（只具备一角一边的两三角形不一定全等）．故选：B．10．解：在△ABD与△CBD中，，∴△ABD≌△CBD（SSS），故③正确；∴∠ADB＝∠CDB，在△AOD与△COD中，，∴△AOD≌△COD（SAS），∴∠AOD＝∠COD＝90°，AO＝OC，∴AC⊥DB，故①②正确；故选：D．11．解：如图作PE⊥OA于E，PF⊥OB于F．∵∠PEO＝∠PFO＝90°，∴∠EPF+∠AOB＝180°，∵∠MPN+∠AOB＝180°，∴∠EPF＝∠MPN，∴∠EPM＝∠FPN，∵OP平分∠AOB，PE⊥OA于E，PF⊥OB于F，∴PE＝PF，在△POE和△POF中，，∴△POE≌△POF，∴OE＝OF，在△PEM和△PFN中，，∴△PEM≌△PFN，∴EM＝NF，PM＝PN，故（1）正确，∴S△PEM＝S△PNF，∴S四边形PMON＝S四边形PEOF＝定值，故（3）正确，∵OM+ON＝OE+ME+OF﹣NF＝2OE＝定值，故（2）正确，在旋转过程中，△PMN是等腰三角形，形状是相似的，因为PM的长度是变化的，所以MN的长度是变化的，故（4）错误，故选：B．12．解：当∠D＝∠B时，在△ADF和△CBE中∵，∴△ADF≌△CBE（SAS），13．解：如图，延长FD到G，使DG＝BE；连接CG、EF；∵四边形ABCD为正方形，在△BCE与△DCG中，，∴△BCE≌△DCG（SAS），∴CG＝CE，∠DCG＝∠BCE，∴∠GCF＝45°，在△GCF与△ECF中，，∴△GCF≌△ECF（SAS），∴GF＝EF，∵CE＝3，CB＝6，∴BE＝＝＝3，∴AE＝3，设AF＝x，则DF＝6﹣x，GF＝3+（6﹣x）＝9﹣x，∴EF＝＝，∴（9﹣x）2＝9+x2，即AF＝4，∴GF＝5，∴DF＝2，∴CF＝＝＝2，故选：A．14．解：∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，∴∠1＝∠EAC，在△BAD和△CAE中，∴△BAD≌△CAE（SAS），∴∠2＝∠ABD＝30°，∵∠1＝25°，∴∠3＝∠1+∠ABD＝25°+30°＝55°，故答案为：55°．15．解：观察图形可知：△ABC≌△BDE，∴∠1＝∠DBE，又∵∠DBE+∠3＝90°，∴∠1+∠3＝90°．∵∠2＝45°，∴∠1+∠2+∠3＝∠1+∠3+∠2＝90°+45°＝135°．故答案为：135．16．解：△ABE和△ACD中，，∴△ABE≌△ACD（AAS），∴AD＝AE＝2，AC＝AB＝5，∴CE＝BD＝AB﹣AD＝3，故答案为3．17．解：如图，作AM⊥BC、AN⊥CD，交CD的延长线于点N；∵∠BAD＝∠BCD＝90°∴四边形AMCN为矩形，∠MAN＝90°；∵∠BAD＝90°，∴∠BAM＝∠DAN；在△ABM与△ADN中，，∴△ABM≌△ADN（AAS），∴AM＝AN（设为λ）；△ABM与△ADN的面积相等；∴四边形ABCD的面积＝正方形AMCN的面积；由勾股定理得：AC2＝AM2+MC2，而AC＝6；∴2λ2＝36，λ2＝18，故答案为：18．18．解：∵△ABO≌△ADO，∴AB＝AD，∠BAO＝∠DAO，∠AOB＝∠AOD＝90°，OB＝OD，∴AC⊥BD，故①正确；∵四边形ABCD的对角线AC、BD相交于点O，∴∠COB＝∠COD＝90°，在△ABC和△ADC中，，∴△ABC≌△ADC（SAS），故③正确；∴BC＝DC，故②正确．故答案为：①②③．19．解：如图，延长BA、CE相交于点F，∵BD平分∠ABC，∴∠ABD＝∠CBD，在△BCE和△BFE中，，∴△BCE≌△BFE（ASA），∴CE＝EF，∵∠BAC＝90°，CE⊥BD，∴∠ACF+∠F＝90°，∠ABD+∠F＝90°，∴∠ABD＝∠ACF，在△ABD和△ACF中，，∴△ABD≌△ACF（ASA），∴BD＝CF，∵CF＝CE+EF＝2CE，∴BD＝2CE＝8，∴CE＝4．故答案为：4．20．解：在AD的上方过点A作AD′⊥AD，使得AD′＝AD，连接CD′，DD′，如图：∵∠BAC+∠CAD＝∠DAD′+∠CAD，即∠BAD＝∠CAD′，在△BAD与△CAD′中，，∴△BAD≌△CAD′（SAS），∴BD＝CD′．∠DAD′＝90°由勾股定理得DD′＝，∠D′DA+∠ADC＝90°由勾股定理得CD′＝，∴BD＝CD′＝，故答案为：．21．解：①∵BD为△ABC的角平分线，∴∠ABD＝∠CBD，在△ABD和△EBC中，，∴△ABD≌△EBC（SAS），∴①正确；②∵BD为△ABC的角平分线，BD＝BC，BE＝BA，∴∠BCD＝∠BDC＝∠BAE＝∠BEA，∵△ABD≌△EBC，∴∠BCE＝∠BDA，∴∠BCE+∠BCD＝∠BDA+∠BDC＝180°，∴②正确；③∵∠BCE＝∠BDA，∠BCE＝∠BCD+∠DCE，∠BDA＝∠DAE+∠BEA，∠BCD＝∠BEA，∴∠DCE＝∠DAE，∴△ACE为等腰三角形，∴AE＝EC，∵△ABD≌△EBC，∴AD＝EC，∴AD＝AE＝EC，∵BD为△ABC的角平分线，EF⊥AB，而EC不垂直与BC，∴EF≠EC，∴③错误；④由③知AD＝AE＝EC，∴④正确；综上所述，正确的结论是①②④．故答案是：①②④．22．解：延长CD至点E，使DE＝BC，连接AE，∵∠BAD＝∠BCD＝90°，∴∠2+∠B＝180°，∵∠1+∠2＝180°，∠2+∠B＝180°，∴∠1＝∠B，在△ABC与△ADE中，∵，∴△ABC≌△ADE（SAS），∴∠EAD＝∠BAC，AC＝AE，S△AEC＝S四边形ABCD ∵∠BAD＝90°，∴∠EAC＝90°，∴△ACE是等腰直角三角形，∵四边形ABCD的面积为24cm2，∴AC2＝24，解得AC＝4或﹣4，∵AC为正数，∴AC＝4．故答案为：4．23．解：∵四边形ACDF是正方形，∴AC＝AF，∠CAF＝90°，∴∠EAC+∠F AB＝90°，∵∠ABF＝90°，∴∠AFB+∠F AB＝90°，∴∠EAC＝∠AFB，在△CAE和△AFB中，，∴△CAE≌△AFB，∴EC＝AB＝4，∴阴影部分的面积＝×AB×CE＝8，故答案为：8．24．解：∵AE⊥AB且AE＝AB，EF⊥FH，BG⊥FH⇒∠FED＝∠EF A＝∠BGA＝90°，∠EAF+∠BAG＝90°，∠ABG+∠BAG＝90°⇒∠EAF＝∠ABG，∴AE＝AB，∠EF A＝∠AGB，∠EAF＝∠ABG⇒△EF A≌△ABG同理证得△BGC≌△DHC得GC＝DH，CH＝BG．故FH＝F A+AG+GC+CH＝3+6+4+3＝16故S＝（6+4）×16﹣3×4﹣6×3＝50．故答案为50．25．解：①BE平分∠ABC，∴∠EBC＝∠ABC，∵CE平分∠ACD，∴∠DCE＝ACD，∵∠ACD＝∠BAC+∠ABC，∠DCE＝∠CBE+∠BEC，∴∠EBC+∠BEC＝（∠BAC+∠ABC）＝∠EBC+BAC，∴∠BEC＝∠BAC，故①正确；∵②△HEF与△CBF只有两个角是相等的，能得出相似，但不含相等的边，所有不能得出全等的结论，故②错误．③BE平分∠ABC，∴∠ABE＝∠CBE，∵GE∥BC，∴∠CBE＝∠GEB，∴BG＝GE，同理CH＝HE，∴BG﹣CH＝GE﹣EH＝GH，故③正确．④过点E作EN⊥AC于N，ED⊥BC于D，EM⊥BA于M，如图，∵BE平分∠ABC，∴EM＝ED，∵CE平分∠ACD，∴EN＝ED，∴EN＝EM，∴AE平分∠CAM，设∠ACE＝∠DCE＝x，∠ABE＝∠CBE＝y，∠MAE＝∠CAE＝z，如图，则∠BAC＝180°﹣2z，∠ACB＝180﹣2x，∵∠ABC+∠ACB+∠BAC＝180°，∴2y+180°﹣2z+180°﹣2x＝180°，∴x+z＝y+90°，∵z＝y+∠AEB，∴x+y+∠AEB＝y+90°，∴x+∠AEB＝90°，即∠ACE+∠AEB＝90°，故④正确；故答案为：①③④．26．解：∵△ABC三个内角的平分线交于点O，∴∠ACO＝∠BCO，在△COD和△COB中，，∴△COD≌△COB，∴∠D＝∠CBO，∵∠BAC＝80°，∴∠BAD＝100°，∴∠BAO＝40°，∴∠DAO＝140°，∵AD＝AO，∴∠D＝20°，∴∠CBO＝20°，∴∠ABC＝40°，∴∠BCA＝60°，故答案为：60°．27．解：（方法一）将△ABD绕点A逆时针旋转120°得到△ACF，连接EF，过点E作EM ⊥CF于点M，过点A作AN⊥BC于点N，如图所示．∵AB＝AC＝2，∠BAC＝120°，∴BN＝CN，∠B＝∠ACB＝30°．在Rt△BAN中，∠B＝30°，AB＝2，∴AN＝AB＝，BN＝＝3，∴BC＝6．∵∠BAC＝120°，∠DAE＝60°，∴∠BAD+∠CAE＝60°，∴∠F AE＝∠F AC+∠CAE＝∠BAD+∠CAE＝60°．在△ADE和△AFE中，，∴△ADE≌△AFE（SAS），∴DE＝FE．∵BD＝2CE，BD＝CF，∠ACF＝∠B＝30°，∴设CE＝2x，则CM＝x，EM＝x，FM＝4x﹣x＝3x，EF＝ED＝6﹣6x．在Rt△EFM中，FE＝6﹣6x，FM＝3x，EM＝x，∴EF2＝FM2+EM2，即（6﹣6x）2＝（3x）2+（x）2，解得：x1＝，x2＝（不合题意，舍去），∴DE＝6﹣6x＝3﹣3．故答案为：3﹣3．（方法二）：将△ABD绕点A逆时针旋转120°得到△ACF，取CF的中点G，连接EF、EG，如图所示．∵AB＝AC＝2，∠BAC＝120°，∴∠ACB＝∠B＝∠ACF＝30°，∴∠ECG＝60°．∵CF＝BD＝2CE，∴CG＝CE，∴△CEG为等边三角形，∴EG＝CG＝FG，∴∠EFG＝∠FEG＝∠CGE＝30°，∴△CEF为直角三角形．∵∠BAC＝120°，∠DAE＝60°，∴∠BAD+∠CAE＝60°，∴∠F AE＝∠F AC+∠CAE＝∠BAD+∠CAE＝60°．在△ADE和△AFE中，，∴△ADE≌△AFE（SAS），∴DE＝FE．设EC＝x，则BD＝CF＝2x，DE＝FE＝6﹣3x，在Rt△CEF中，∠CEF＝90°，CF＝2x，EC＝x，EF＝＝x，∴6﹣3x＝x，x＝3﹣，∴DE＝x＝3﹣3．故答案为：3﹣3．28．证明：（1）延长EB到G，使BG＝DF，连接AG．∵∠ABG＝∠ABC＝∠D＝90°，AB＝AD，∴△ABG≌△ADF．∴AG＝AF，∠1＝∠2．∴∠1+∠3＝∠2+∠3＝∠EAF＝∠BAD．∴∠GAE＝∠EAF．又∵AE＝AE，∴△AEG≌△AEF．∴EG＝EF．∵EG＝BE+BG．∴EF＝BE+FD（2）（1）中的结论EF＝BE+FD仍然成立．（3）结论EF＝BE+FD不成立，应当是EF＝BE﹣FD．证明：在BE上截取BG，使BG＝DF，连接AG．∵∠B+∠ADC＝180°，∠ADF+∠ADC＝180°，∴∠B＝∠ADF．∵AB＝AD，∴△ABG≌△ADF．∴∠BAG＝∠DAF，AG＝AF．∴∠BAG+∠EAD＝∠DAF+∠EAD＝∠EAF＝∠BAD．∴∠GAE＝∠EAF．∵AE＝AE，∴△AEG≌△AEF．∴EG＝EF∵EG＝BE﹣BG∴EF＝BE﹣FD．29．解：（1）①∵△DEC绕点C旋转点D恰好落在AB边上，∴AC＝CD，∵∠BAC＝90°﹣∠B＝90°﹣30°＝60°，∴△ACD是等边三角形，∴∠ACD＝60°，又∵∠CDE＝∠BAC＝60°，∴∠ACD＝∠CDE，∴DE∥AC；②∵∠B＝30°，∠C＝90°，∴CD＝AC＝AB，∴BD＝AD＝AC，根据等边三角形的性质，△ACD的边AC、AD上的高相等，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1＝S2；故答案为：DE∥AC；S1＝S2；（2）如图，∵△DEC是由△ABC绕点C旋转得到，∴BC＝CE，AC＝CD，∵∠ACN+∠BCN＝90°，∠DCM+∠BCN＝180°﹣90°＝90°，∴∠ACN＝∠DCM，∵在△ACN和△DCM中，，∴△ACN≌△DCM（AAS），∴AN＝DM，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1＝S2；（3）如图，过点D作DF1∥BE，易求四边形BEDF1是菱形，所以BE＝DF1，且BE、DF1上的高相等，此时S△DCF1＝S△BDE；过点D作DF2⊥BD，∵∠ABC＝60°，F1D∥BE，∴∠F2F1D＝∠ABC＝60°，∵BF1＝DF1，∠F1BD＝∠ABC＝30°，∠F2DB＝90°，∴∠F1DF2＝∠ABC＝60°，∴△DF1F2是等边三角形，∴DF1＝DF2，∵BD＝CD，∠ABC＝60°，点D是角平分线上一点，∴∠DBC＝∠DCB＝×60°＝30°，∴∠CDF1＝180°﹣∠BCD＝180°﹣30°＝150°，∠CDF2＝360°﹣150°﹣60°＝150°，∴∠CDF1＝∠CDF2，∵在△CDF1和△CDF2中，，∴△CDF1≌△CDF2（SAS），∴点F2也是所求的点，∵∠ABC＝60°，点D是角平分线上一点，DE∥AB，∴∠DBC＝∠BDE＝∠ABD＝×60°＝30°，又∵BD＝4，∴BE＝×4÷cos30°＝2÷＝，∴BF1＝，BF2＝BF1+F1F2＝+＝，故BF的长为或．30．（1）证明：∵∠BAC＝∠DAE＝90°∴∠BAC+∠CAD＝∠DAE+∠CAD即∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS）．（2）BD、CE特殊位置关系为BD⊥CE．证明如下：由（1）知△BAD≌△CAE，∴∠ADB＝∠E．∵∠DAE＝90°，∴∠E+∠ADE＝90°．∴∠ADB+∠ADE＝90°．即∠BDE＝90°．∴BD、CE特殊位置关系为BD⊥CE．31．证明：（1）∵∠BAD＝∠CAE＝90°，∴∠BAC+∠CAD＝90°，∠CAD+∠DAE＝90°，∴∠BAC＝∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS）；（2）∵∠CAE＝90°，AC＝AE，∴∠E＝45°，由（1）知△BAC≌△DAE，∴∠BCA＝∠E＝45°，∵AF⊥BC，∴∠CF A＝90°，∴∠CAF＝45°，∴∠F AE＝∠F AC+∠CAE＝45°+90°＝135°；（3）延长BF到G，使得FG＝FB，∵AF⊥BG，∴∠AFG＝∠AFB＝90°，在△AFB和△AFG中，，∴△AFB≌△AFG（SAS），∴AB＝AG，∠ABF＝∠G，∵△BAC≌△DAE，∴AB＝AD，∠CBA＝∠EDA，CB＝ED，∴AG＝AD，∠ABF＝∠CDA，∴∠G＝∠CDA，∵∠GCA＝∠DCA＝45°，在△CGA和△CDA中，，∴△CGA≌△CDA（AAS），∴CG＝CD，∵CG＝CB+BF+FG＝CB+2BF＝DE+2BF，∴CD＝2BF+DE．32．（1）证明：在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴BD＝CE；（2）证明：∵∠1＝∠2，∴∠1+∠DAE＝∠2+∠DAE，即∠BAN＝∠CAM，由（1）得：△ABD≌△ACE，∴∠B＝∠C，在△ACM和△ABN中，，∴△ACM≌△ABN（ASA），∴∠M＝∠N．33．（1）证明：连接BF（如图①），∵△ABC≌△DBE（已知），∴BC＝BE，AC＝DE．∵∠ACB＝∠DEB＝90°，∴∠BCF＝∠BEF＝90°．在Rt△BFC和Rt△BFE中，∴Rt△BFC≌Rt△BFE（HL）．∴CF＝EF．又∵AF+CF＝AC，∴AF+EF＝DE．（2）解：画出正确图形如图②∴（1）中的结论AF+EF＝DE仍然成立；（3）成立．证明：连接BF，∵△ABC≌△DBE，∴BC＝BE，∵∠ACB＝∠DEB＝90°，∴△BCF和△BEF是直角三角形，在Rt△BCF和Rt△BEF中，，∴△BCF≌△BEF（HL），∴CF＝EF；∵△ABC≌△DBE，∴AC＝DE，∴AF＝AC+FC＝DE+EF．34．（1）证明：∵点D是AB中点，AC＝BC，∠ACB＝90°，∴CD⊥AB，∠ACD＝∠BCD＝45°，∴∠CAD＝∠CBD＝45°，∴∠CAE＝∠BCG，又∵BF⊥CE，∴∠CBG+∠BCF＝90°，又∵∠ACE+∠BCF＝90°，∴∠ACE＝∠CBG，在△AEC和△CGB中，∴△AEC≌△CGB（ASA），∴AE＝CG，（2）解：BE＝CM．证明：∵CH⊥HM，CD⊥ED，∴∠CMA+∠MCH＝90°，∠BEC+∠MCH＝90°，∴∠CMA＝∠BEC，又∵∠ACM＝∠CBE＝45°，在△BCE和△CAM中，，∴△BCE≌△CAM（AAS），∴BE＝CM．35．解：∵∠BCE＝∠ACD＝90°，∴∠3+∠4＝∠4+∠5，∴∠3＝∠5，在△ABC和△DEC中，，∴△ABC≌△DEC（AAS），。

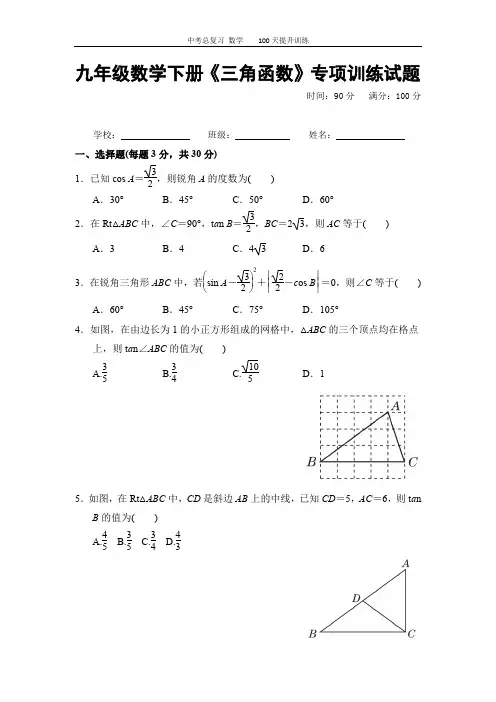
九年级数学下册《三角函数》专项训练试题时间：90分 满分：100分学校： 班级： 姓名：一、选择题(每题3分，共30分)1．已知cos A ＝32，则锐角A 的度数为( )A ．30°B ．45°C ．50°D ．60°2．在Rt △ABC 中，∠C ＝90°，t a n B ＝32，BC ＝23，则AC 等于( )A ．3B ．4C ．4 3D ．6 3．在锐角三角形ABC 中，若⎝ ⎛⎭⎪⎫sin A －322＋⎪⎪⎪⎪⎪⎪22－c os B ＝0，则∠C 等于( ) A ．60° B ．45° C ．75° D ．105°4．如图，在由边长为1的小正方形组成的网格中，△ABC 的三个顶点均在格点上，则t a n ∠ABC 的值为( )A.35B.34C.105 D ．15．如图，在Rt △ABC 中，CD 是斜边AB 上的中线，已知CD ＝5，AC ＝6，则t a n B 的值为( )A.45B.35C.34D.436．为了测量被池塘隔开的A，B两点之间的距离，根据实际情况，作出如图所示的图形，其中AB⊥BE，EF⊥BE，AF交BE于点D，C在BD上．有四名同学分别测量出以下4组数据：①BC，∠ACB；②CD，∠ACB，∠ADB；③EF，DE，BD；④DE，DC，BC.能根据所测数据，求出A，B两点之间距离的有()A．1组B．2组C．3组D．4组7．如图，沿AE折叠矩形纸片ABCD，使点D落在BC边上的点F处．已知AB ＝4，BC＝5，则cos∠EFC的值为()A.34 B.43 C.35 D.458．如图所示，从热气球C处测得地面A，B两点的俯角分别为30°，45°，如果此时热气球的高度CD为100 m，点A，D，B在同一直线上，则A，B两点之间的距离是()A．200 m B．200 3 m C．220 3 m D．100(3＋1)m9．如图，若△ABC和△DEF的面积分别为S1，S2，则()A．S1＝12S2B．S1＝72S2C．S1＝85S2D．S1＝S210．已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示)，点B1在y轴上，点C1，E1，E2，C2，E3，E4，C3在x轴上．若正方形A1B1C1D1的边长为1，∠B1C1O＝60°，B1C1∥B2C2∥B3C3，则点A3到x轴的距离是()A.3＋318 B.3＋118 C.3＋36 D.3＋16二、填空题(每题3分，共24分)11．计算：cos245°＋tan 30°·sin 60°＝________。

专练03三角形中的面积和周长问题1.已知 ΔABC 的面积是 120 ，请完成下列问题：（1）如图1所示，若 AD 是 ΔABC 的 BC 边上的中线，则 ΔABD 的面积________ ΔACD 的面积．（填“ > ”“ < ”或“ = ”）（2）如图2所示，若 CD ， BE 分别是 ΔABC 的 AB ， AC 边上的中线，求四边形 ADOE 的面积可以用如下方法：连接 AO ，由 AD =DB 得： S ΔADO =S ΔBDO ，同理： S ΔCEO =S ΔAEO ，设 S ΔADO =x ， S ΔCEO =y 则 S ΔBDO =x ， S ΔAEO =y ．由题意得： S ΔABE =12S ΔABC =60 ， S ΔADC =12S ΔABC =60 ，可列方程组为 {2x +y =60x +2y =60 ，解得________，通过解这个方程组可得四边形 ADOE 的面积为________． （3）如图3所示， AD:DB =1:3 ， CE:AE =1:2 ，请你计算四边形 ADOE 的面积，并说明理由． 【答案】（1）如图1，过A 作 AH ⊥BC 于H ，∵AD 是 △ABC 的 BC 边上的中线， ∴BD =CD ，∴ S △ABD =12BD ·AH ， S △ACD =12CD ·AH ， ∴ S △ABD =S △ACD ， （2）解方程组得 {x =20y =20 ， ∴S △AOD =S △BOD =20 ，∴S 四边形ADOB =S △AOD +S △AOE =20+20=40 ， 故答案为： {x =20y =20 ，40； （3）解：如图3，连结 AO ，∵AD:DB =1:3 ， ∴ S △ADO =13S △BDO ，∵CE:AE =1:2 ， ∴ S △CEO =12S △AEO ，设 S △ADO =x ， S △CEO =y ，则 S △BDO =3x ， S △AEO =2y ， 由题意得： S △ABE =23S △ABC =80 ， S △ADC =14S △ABC =30 ， 可列方程组为： {x +3y =304x +2y =80 ， 解得： {x =18y =4， ∴S 四边形ADOE =S △ADO +S △AEO =x +2y =36 ．2.如图1，Rt △ABC 中，∠ACB=Rt ∠，AC=8，BC=6，点D 为AB 的中点，动点P 从点A 出发，沿AC 方向以每秒1个单位的速度向终点C 运动，同时动点Q 从点C 出发，以每秒2个单位的速度先沿CB 方向运动到点B ，再沿BA 方向向终点A 运动，以DP ，DQ 为邻边构造▱PEQD ，设点P 运动的时间为t 秒．（1）当t=2时，求PD 的长；（2）如图2，当点Q 运动至点B 时，连结DE ，求证：DE ∥AP. （3）如图3，连结CD ．①当点E 恰好落在△ACD 的边上时，求所有满足要求的t 值；②记运动过程中▱PEQD 的面积为S ，▱PEQD 与△ACD 的重叠部分面积为S 1 ， 当 S 1S＜ 13 时，请直接写出t 的取值范围．【答案】 （1）解：如图1中，作DF ⊥CA 于F ，=3，当t=2时，AP=2，DF=AD•sinA=5× 35=4，∵AF=AD•cosA=5× 45∴PF=4-2=2，∴PD= √DF2+PF2= √32+22= √13．（2）证明：如图2中，在平行四边形PEQD中，∵PE∥DQ，∴PE∥AD，∵AD=DQ．PE=DQ，∴PE=AD，∴四边形APED是平行四边形，∴DE∥AP．（3）解：①分三种情况讨论：Ⅰ．当点E在CA上时，DQ⊥CB（如图3所示），∵∠ACB=Rt∠，CD是中线，∴CD=BD，∴CQ= 12CB=3即：t= 32Ⅱ．当点E在CD上，且点Q在CB上时（如图4所示），过点E作EG⊥CA于点G，过点D作DH⊥CB于点H，易证Rt△PGE≌Rt△PHQ，∴PG=DH=4，∴CG=4-t，GE=HQ=CQ-CH=2t-3，∵CD=AD，∴∠DCA=∠DAC∴在Rt△CEG中，tan∠ECG= GECG = 2t−34−t= 34，∴t= 2411Ⅲ．当点E在CD上，且点Q在AB上时（如图5所示），过点E作EF⊥CA于点F，∵CD=AD，∴∠CAD=∠ACD．∵PE∥AD，∴∠CPE=∠CAD=∠ACD，∴PE=CE，∴PF= 12PC= 8−t2，PE=DQ=11-2t，∴在Rt△PEF中，cos∠EPF= PFPE =8−T211−2t= 45∴t= 4811综上所述，满足要求的t的值为32或2411或4811；7225＜t＜5617②如图6中，PE交CD于E′，作E′G′⊥AC于G′，EG⊥AC于G．当△PDE′的面积等于平行四边形PEDQD的面积的13时，PE′：EE′=2：1，由（Ⅱ）可知CG=4-t ，GE=2t-3，∴PG=8-t-（4-t）=4，∵E′G′∥EG，∴PG′PG = E′G′EG= PE′PE= 23，∴PG′= 83，E′G′= 23（2t-3），CG′=8-t- 83= 163-t ，∵tan∠ECG= E′G′CG′=23(2t−3)163−t=34，解得t= 7225．如图7中，当点Q在AB上时，PE交CD于E′，作E′G′⊥AC于G′．∵△PDE′的面积等于平行四边形PEDQD的面积的13，∴PE′：EE′=2：1，由Ⅲ可知，PG′= 12PC=4- 12t ，PE′= 23DQ= 23（11-2t），∵cos∠E′PG′= PG′PE′= 45，∴4−12t23(11−2t)=45，解得t= 5617，综上所述，当S1S ＜13时，请直接写出t的取值范围是7225＜t＜5617．3.如图，在平面直角坐标系中，点O为原点，△OAB为等边三角形，P、Q分别为AO、AB边上的动点，点P、点Q同时从点A出发，且当其中一点停止运动时，另一点也立即停止运动；若P以2个单位长度每秒的速度从点A向终点O运动，点Q以3个单位长度每秒的速度从点A向终点B运动，设运动时间为t ，已知点A坐标为（a ，b），且满足（a﹣6）2+| √3a﹣b|=0．（1）求A点坐标；（2）如图1，连接BP、OQ交于点C ，请问当t为何值时，∠OCP=60°；（3）如图2，D为OB边上的中点，P ，Q在运动过程中，D ，P ，Q三点是否能构成使∠PDQ=120°的等腰三角形，若能，求运动时间t并直接写出四边形APDQ的面积：若不能，请说明理由．【答案】（1）解：∵（a﹣6）2+| √3a﹣b|=0，又∵(a﹣6)2≥0，| √3a﹣b|≥0，∴a=6，b=6 √3∴点A（6，6 √3）；（2）解：如图1中，∵△AOB是等边三角形，点A（6，6 √3）∴AO=BO=AB=12，∠AOB=∠ABO=60°=∠A，∵∠OCP=60°=∠AOB，∴∠AOB=∠QOB+∠AOQ=∠QOB+∠PBO=∠PCO=60°，∴∠AOQ=∠PBO，且AO=BO，∠A=∠AOB=60°，∴△AOQ≌△OBP（ASA），∴OP=AQ，∴12﹣2t=3t，∴t=2.4，∴当t=2.4时，∠OCP=60°；（3）解：如图2中，过点D作DF⊥AO，DE⊥AB，连接AD，∵△ABO是等边三角形，D是OB中点，点A（6，6 √3）∴OD=BD=6，∠AOB=∠ABO=60°，AD=6 √3，又∵∠DFO=∠DEB=90°，∴△ODF≌△BDE（AAS）∴OF=BE，DF=DE，∵AO=AB，∴AO﹣OF=AB﹣BE∴AF=AE，∵DF=DE，PD=DQ，∴Rt△DFP≌Rt△DEQ（HL）∴PF=EQ，∵OD=6，∠AOD=60°，∠DFO=90°，∴∠ODF=30°，∴OF=3，DF= √3OF=3 √3，∴AF=AO﹣OF=9=AE，BE=OF=3，∵AP+AQ=AP+AE+EQ=AP+PF+AE=AF+AE=2AF=18，∴2t+3t=18，∴t=3.6，∴当t=3.6时，D，P，Q三点是能构成使∠PDQ=120°的等腰三角形，∵Rt△DFP≌Rt△DEQ，∴S△DFP=S△DEQ ，∴S四边形APDQ=S四边形AFDQ=S△AOB﹣2S△OFD= 12×12×6 √3﹣2×12×3×3 √3=27 √3．4.如图，△ABC为等边三角形，边长为6，P ，Q分别为AB ，AC边上的动点，点P ，点Q同时个单位每秒的速度从点A向点B运动，点Q以2个单位每秒的速度从点A向点C 从点A出发，若P以32运动，设运动时间为t ．（1）如图1，①当t＝________时，P是线段AB的中点，此时线段AQ与AC的数量关系是AQ＝________AC ．②在点P、Q运动过程中，△APQ是否能构成等腰三角形？________；A ．有可能B ．不可能C ．无法确定（2）如图2，连接CP、BQ交于点M ，请问当t为何值时，∠BMP＝60°；（3）如图3，D为BC边上的中点，P ，Q在运动过程中，D ，P ，Q三点是否能构成使∠PDQ＝120°的等腰三角形？若能，试求：①运动时间t；②设四边形APDQ的面积为S1，△ABC的面积为S2．请直接写出S1与S2的关系式；若不能，请说明理由．＝2，【答案】（1）①当P是AB中点时，AP＝3，故t＝3÷32AC ，此时AQ＝2×2＝4，故AQ＝23；②假设△APQ可以成为等腰三角形，故答案为2，23∵△ABC为等边三角形，即∠A＝60°，则△APQ为等边三角形，而AP≠AQ ，故△APQ不可能为等腰三角形，故答案为B；（2）解：∵△ABC为等边三角形且边长为6，∴AB＝BC＝AB＝6，∠ABC＝∠ACB＝60°＝∠A，∵∠PMB＝60°＝∠ABC，∴∠ABC＝∠QBC+∠ABQ＝∠QBC+∠PCB＝∠PBC，∴∠ABQ＝∠PCB，且AB＝BC，∠A＝∠ABC，∴△ABQ≌△BCP（ASA），∴AQ＝BP，∴6﹣32t＝2t，∴t＝127，∴当t＝127时，∠BMP＝60°；（3）解：①如图，过点D作DF⊥AC，DE⊥AB，连接AD，∵△ABC是等边三角形，D是CB中点，∴CD＝BD＝3，∠ABC＝∠ACB＝60°，AD＝3 √3，又∵∠DFB＝∠DEC＝90°，∴△BDF≌△CDE（AAS），∴BF＝CE，DF＝DE，∵AB＝AC，∴AB﹣BF＝AC﹣CE，∴AF＝AE，∵DF＝DE，PD＝DQ，∴Rt△DFP≌Rt△DEQ（HL），∴PF＝EQ，∵BD＝3，∠ABD＝60°，∠DFB＝90°，∴∠BDF＝30°，∴BF＝32，DF＝√3BF＝3√32，∴AF＝AB﹣BF＝92＝AE，CE＝BF＝32，∵AP+AQ＝AP+AE+EQ＝AP+PF+AE＝AF+AE＝2AF，∴32t+2t＝9，∴t＝187，∴当t＝187时，D，P，Q三点是能构成使∠PDQ＝120°的等腰三角形；②∵Rt△DFP≌Rt△DEQ，∴S△DFP＝S△DEQ ，而S△AOB＝6×3√32，∴S四边形APDQ＝S四边形AFDQ＝S△AOB﹣2S△OFD＝6×3√32﹣2×12×3√32×32＝27√34，故S1=34S2．5.（感知）如图①，△ABC是等边三角形，点D、E分别在AB、BC边上，且AD=BE，易知：△ADC≌△BEA．（1）（探究）如图②，△ABC是等边三角形，点D、E分别在边BA、CB的延长线上，且AD=BE，△ADC 与△BEA还全等吗？如果全等，请证明：如果不全等，请说明理由．（2）（拓展）如图③，在△ABC中，AB=AC，∠1=∠2，点D、E分别在BA、FB的延长线上，且AD=BE，若AF= 32CF=2BE，S△ABF=6，则S△BCD的大小为________．【答案】（1）解：△ADC与△BEA全等，理由：在等边三角形ABC中，AB=AC，∠BAC=∠ABC=60°，∴∠DAC=180°﹣∠BAC=120°，∠EBA=180°﹣∠ABC=120°，∴∠DAC=∠EBA，∵AD=BE，∴△ADC≌△BEA；（2）拓展：∵∠1=∠2，∴AF=BF，∠DAC=∠EBA，∵AD=BE，AC=AB，∴△ADC≌△BEA（SAS），∴S△ADC=S△BEA ，∵AF=2BE，AF=BF，∴BF=2BE，∴S△ABE= 12S△ABF=3（同高的两三角形的面积比是底的比），∴S△ADC=3，∵AF= 32CF，∴S△BFC= 23S△ABF=4（同高的两三角形的面积比是底的比），∴S△BCD=S△BCF+S△ABF+S△ADC=13，故答案为13． 6.（1）如图1，在△ABC 中，D 是BC 的中点，过D 点画直线EF 与AC 相交于E ， 与AB 的延长线相交于F ， 使BF ＝CE ．①已知△CDE 的面积为1，AE ＝kCE ， 用含k 的代数式表示△ABD 的面积为多少； ②求证：△AEF 是等腰三角形；（2）如图2，在△ABC 中，若∠1＝2∠2，G 是△ABC 外一点，使∠3＝∠1，AH ∥BG 交CG 于H ， 且∠4＝∠BCG ﹣∠2，设∠G ＝x ， ∠BAC ＝y ， 试探究x 与y 之间的数量关系，并说明理由； （3）如图3，在（1）、（2）的条件下，△AFD 是锐角三角形，当∠G ＝100°，AD ＝a 时，在AD 上找一点P ， AF 上找一点Q ， FD 上找一点M ， 使△PQM 的周长最小，试用含a 、k 的代数式表示△PQM 周长的最小值________．（只需直接写出结果） 【答案】 （1）解： ①∵AE ＝kCE ， ∴S △DAE ＝kS △DEC ， ∵S △DEC ＝1， ∴S △DAE ＝k ，∴S △ADC ＝S △DAE+S △DEC ＝k+1， ∵D 为BC 中点，∴S △ABD ＝S △ADC ＝k+1．②如图1，过B 点作BG ∥AC 交EF 于G ．∴ ∠BGD =∠CED ， ∠BGF =∠AED 在△BGD 和△CED 中， {∠BGD =∠CED BD =CD ∠BDG =∠CDE，∴△BGD≅△CED（ASA），∴BG＝CE，又∵BF＝CE，∴BF＝BG，∴∠BGF=∠F，∴∠F=∠AED∴AF＝AE，即△AEF是等腰三角形．（2）解：如图2，设AH与BC交与点N，∠2＝α．则∠3＝∠1＝2∠2＝2α，∵AH∥BG，∴∠CNH＝∠ANB＝∠3＝2α，∵∠CNH＝∠2+∠4，∴2α＝α+∠4，∴∠4＝α，∵∠4＝∠BCG﹣∠2，∴∠BCG＝∠2+∠4＝2α，在△BGC中，∠3+∠BCG+∠G=180°，即：4α+x=180°，在△ABC中，∠1+∠2+∠BAC=180°，即：3α+y=180°，x+45°．联立消去α得：y＝34（3）如图3，作P点关于FA、FD的对称点P'、P''，连接P'Q、P'F、PF、P''M、P''F、P'P''，则FP'＝FP＝FP''，PQ＝P'Q ，PM＝P''M ，∠P'FQ＝∠PFQ ，∠P''FM＝∠PFM ，∴∠P'FP''＝2∠AFD ，∵∠G＝100°，∴∠BAC＝34∠G+45°＝120°，∵AE＝AF ，∴∠AFD＝30°，∴∠P'FP''＝2∠AFD＝60°，∴△FP'P''是等边三角形，∴P'P''＝FP'＝FP ，∴PQ+QM+PM＝P'Q+QM+MP''≥P'P''＝FP ，当且仅当P'、Q、M、P''四点共线，且FP⊥AD时，△PQM的周长取得最小值．∵AE=kCE，AF=AE，BF=CE，∴ABAF =k−1k，∴S△ADF=kk−1S△ABD=k(k+1)k−1，∴当FP⊥AD时，FP=2S△ADFAD =2k(k+1)(k−1)a，∴△PQM的周长最小值为2k(k+1)(k−1)a．7.如图，在ΔABC中，AC=BC，∠ACB=120°，AB=6，点D是射线AM上一点（不与A、B两点重合），点D从点A出发，沿射线AM的方向运动，以CD为一边在CD的右侧作ΔCDE，使CE=CD，∠DCE=∠ACB，连结BE．（1）求∠ABE的度数；（2）是否存在以D、E、B为顶点的三角形是直角三角形？若存在，求出线段BD的长；若不存在，请说明理由；（3）ΔBDE的周长是否存在最小值？若存在，求出ΔBDE的最小周长；若不存在，请说明理由．【答案】（1）解：∵AC=BC，∠ACB=120°，∴∠A=∠ABC=30°．∵∠DCE=∠ACB，∴∠DCE－∠DCB=∠ACB－∠DCB，即∠ACD=∠BCE．在ΔACD 与ΔBCE 中，{AC=BC∠ACD=∠BCECD=CE，∴ΔACD≌ΔBCE(SAS)，∴∠A=∠CBE=30°，∴∠ABE=∠ABC+∠CBE=60°（2）解：当点D在线段AB上时，由（1）得∠DBE=60°恒成立，∴∠DBE≠90°，∴ΔDBE为直角三角形分两种情况讨论．①当∠DEB=90°时，∵∠DBE=60°，∴DB=2BE，∵ΔACD≌ΔBCE（已证），∴AD=BE．∵AD+DB=6，∴BE+DB=6，即3BE=6，∴BE=2，∴BD=4；②当∠EDB=90°时，∵∠DBE=60°，∴BE=2BD，∵ΔACD≌ΔBCE（已证），∴AD=BE，∵AD+DB=6，BE=6，∴BE+DB=6，即32∴BE=4，∴BD=2；当点D在AB的延长线上时，∵ΔACD≌ΔBCE（已证），∴∠A=∠CBE=30°，∴∠ABC+∠CBE=30°+30°=60°，∴∠DBE=120°，∴不存在直角三角形，综上所述：当ΔDBE为直角三角形时，BD的长为4或2．（3）解：∵ΔACD≌ΔBCE（已证），∴AD=BE，∴ΔBDE的周长=DB+BE+DE=DB+AD+DE=AB+DE=6+DE，∵CE=CD，∠DCE=∠ACB=120°，∴ DE = √3CD，∴ΔBDE的周长= 6+√3CD，当CD⊥AB时，CD取得最小值为√3，ΔBDE的周长取最小值为9 8.据图回答问题：（1）感知：如图①．AB=AD ，AB ⊥AD ，BF ⊥AF 于点F ，DG ⊥AF 于点G ．求证：△ADG ≌△BAF ； （2）拓展：如图②，点B ，C 在∠MAN 的边AM ，AN 上，点E ，F 在∠MAN 在内部的射线AD 上，∠1，∠2分别是△ABE ，△CAF 的外角，已知AB=AC ，∠1=∠2=∠BAC ．求证：△ABE ≌△CAF ； （3）应用：如图③，在△ABC 中，AB=AC ，AB ＞BC ，点在D 边BC 上，CD=2BD ，点E ，F 在线段AD 上，∠1=∠2=∠BAC ．若△ABC 的面积为12，则△ABE 与△CDF 的面积之和为________． 【答案】 （1）证明：∵AB ⊥AD ，BF ⊥AF ， ∴∠DAG+∠BAF=90°，∠B+∠BAF=90°， ∴∠DAG=∠B ， 在△ADG 和△BAF 中， {∠DAG =∠B∠AGD =∠BFA =90∘AD =AB ，∴△ADG ≌△BAF （AAS ）； （2）证明：∵∠1=∠2， ∴∠AEB=∠CFA ，∠1=∠ABE+∠BAE ，∠BAC=∠CAF+∠BAE ，∠1=∠BAC ， ∴∠ABE=∠CAF ， 在△ABE 和△CAF 中， {∠AEB =∠CFA ∠ABE =∠CAF AB =AC，∴△ABE ≌△CAF （AAS ）； （3）∵CD=2BD ， ∴S △ADC= 23 S △ABC=8， 由（2）得，△ABE ≌△CAF ，∴△ABE 与△CDF 的面积之和=△CAF 与△CDF 的面积之和=S △ADC=8， 故答案为8．9.在△ABC 中，AB=AC ，P 为平面内一点（1）如图1，若∠BAP=∠CAP求证：BP=CP（2）如图2，若∠APB=∠APC求证：BP=CP（3）如图3，BD为AC边上的高，BE平分∠ABD交AC于点E，EF ⊥BC于F，EF与BD交于点G，若ED= a，CD= b，求△BGC的面积（用含a，b的代数式表示）.【答案】（1）证明：如图1∵AB=AC、∠BAP=∠CAP、AP=AP∴△ABP≌△ACP（SAS）∴BP=CP.（2）解：如下图2过A分别作CP、BP的垂线，交它们的延长线于M、N∴∠AMP=∠ANP=90°∵∠APB=∠APC∴∠APM=∠APN又∵AP=AP∴△APM≌△APN∴AM=AN、PM=PN又∵AB=AC∴△ACM≌△ABN（HL）∴CM=BN∴BP=CP.（3）解：如下图3∵BD⊥CD∴∠DBC=90°-∠ACB又∵AB=AC∴∠ABC=∠ACB∴∠ABD=∠ABC-∠DBC=∠ABC-(90°-∠ACB)=2∠ABC-90°∵BE平分∠ABD∴∠EBD=∠ABC-45°∴∠EBF=∠EBD+∠DBC=∠ABC-45°+90°-∠ACB=45°又∵EF ⊥ BC于F∴∠BEF=45°∴∠BEF=∠EBF∴EF=BF∵∠BDE=∠EFB=90°、∠BGF=∠EGD∴∠GBF=∠FEC∴△BGF≌△ECF∴BG=EC=ED+DC=a+b∴△BGC的面积为: BG⋅CD2= b(a+b)2=12ab+12b2 .10.已知：如图1，RtΔABC中，∠ACB=90°，CA=CB，等边ΔCDE的边CE在CB上，点D在AB上.（1）求证：∠ACD=2∠BDE（2）如图2，将ΔADC沿着CD翻折，得到ΔCDF.连接EF，求证：AD=EF（3）如图3，在（2）的条件下，过点D作DG⊥CD交CB延长线于点G，若BE=m，DG=4+2m.求ΔFDE的面积.【答案】（1）证明：∵CA=CB，∠ACB=90°，ΔCDE是等边三角形，∴∠B=45°，∠CED=∠DCE=60°，∴∠BDE=∠DEC−∠B=60∘−45∘=15∘，∠ACD=90∘−∠DCE=90∘−60∘=30∘，∴∠ACD=2∠BDE（2）证明：如图示：由折叠可知，∠DFC=∠A=45°，∠ACD=∠FCD=30∘，∴∠FCB=90∘−∠ACD−∠FCD=90∘−30∘−30∘=30∘，在ΔDFG和ΔCGB中，∠DFG=∠B=45°，∠DGF=∠CGB，∴∠FDG=∠FCB=30∘，∴∠FDO=∠FDG+∠GDO=30∘+15∘=45∘，即有：∠FDO=∠FDO=45∘∴ΔDFO是等腰直角三角形，∴OD=OF∵ΔCDE是等边三角形，∠FCB=∠FCD=30∘，∴OD=OE=OF，∴ΔFOE是等腰直角三角形，并ΔFOE≅ΔFOD则ΔDFE是等腰直角三角形，∴DF=FE∴AD=FE；（3）解：如图3所示，∵∠DCG=60∘，DG⊥CD，∴∠DGC=30∘，∴CDDG =CD4+2m=√3，∴CD=√3(4+2m)3，∴DE=CD=√3(4+2m)3，由（2）可知，ΔDFE是等腰直角三角形，∴DFDE=√3(4+2m)3=√2，∴DF=√6(2+m)3，∴SΔFDE=12DF2=12×[√6(2+m)3]2=(2+m)23.11.如图,在△ABC中，∠ACB=90∘，AC=BC，点D为AB的中点，AE=CF.求证：（1）DE=DF；（2）DE⊥DF；（3）若AC=3，求四边形CFDE的面积.【答案】（1）证明：如图，连接CD.∵BC=AC，∠BCA=90°，∴△ABC是等腰直角三角形，∵D为AB中点，∴BD=CD，CD平分∠BCA，CD⊥AB.∵∠A+∠ACD=∠ACD+∠FCD=90°，∴∠A=∠FCD，在△ADE和△CFD中，{AE=CF∠A=∠FCDAD=CD，∴△ADE≌△CFD（SAS），∴DE=DF（2）证明：由（1）知，△ADE≌△CFD（SAS），∴∠ADE=∠CDF.∵∠ADE+∠EDC=90°，∴∠CDF+∠EDC=∠EDF=90°，即DE⊥DF（3）证明：∵△ADE≌△CFD，∴S△AED=S△CFD ，∴S四边形CEDF=S△ADC ，∵D是AB的中点，∴S△ACD= 12S△ACB= 12×3×3=4.5.∴S四边形CEDF=4.5.12.在RtΔABC中，∠C=90°,AC=8,BC=6，P、Q分别为边AB、AC的动点.（1）若AP=a，则当AQ=________时，ΔAPQ与ΔABC相似（用含a的式子表示）；（2）若点P从点A处出发，沿线段AB以每秒钟5个单位的速度向点B运动，同时点Q从点C处出发，沿线段CA以每秒钟4个单位的速度向点A运动：①当运动到第几秒时，BQ⊥CP?②令线段PQ的中点为M，则运动过程中，ΔMBC的周长的最小值是多少?【答案】（1）∵∠C=90°,AC=8,BC=6∴AB= √AC2+BC2=√82+62=10当ΔAPQ∼ΔACB时，可知APAB =AQAC，即a10=AQ8解得AQ=45a同理，当ΔAPQ∼ΔABC时，可知APAC =AQAB，即a8=AQ10解得AQ=54a故答案为：45a或54a；（2）解：①如图，过点P做PD⊥AC于点D设两点运动时间为t，则AP=5t，CQ=4t∵DP∥CB∴ADAC =DPCB=APAB∴AD=4t，DP=3t∴DC=8-4t∵∠ACB=90°, BQ⊥CP ∴∠DCP=∠CBQ∵∠ACB=∠PDC=90°∴ΔDCP∼ΔCBQ∴CBDC =CQDP，即68−4t=4t3t解得t= 78，t=0（舍去）②如图，分别取AC、AB中点E、F，接EF，交EF于点M 过点P做PN⊥EF与点N由已知，PF=5-5t∵EF∥CB ，PN∥AC∴ΔPNF∼ΔACB∴PN=4-4t∴PN=QE∵∠QEM=∠PNM=90°∠EMQ=∠NMP∴ΔEMQ≅ΔNMP∴M为PQ中点，故在P、Q运动过程中，PQ中点M在EF上运动. ∵EF为RtΔABC中位线∴点C与点A关于直线EF对称∴当点M与点F重合时，MB+MC最小此时MB+MC=AB=10则ΔMBC的周长的最小值是10+6=16.。

得起点 B 的仰角为 40°.斜坡 CD 的坡度为 i＝1∶2.4，底端点 C 与顶端
点 D 的距离为 26 m．参赛运动员们将从点 A 出发乘车沿水平方向行驶 100
m 到达点 C 处，再沿斜坡 CD 行驶至点 D 处，最后乘垂直于水平方向的电
梯到达点 B 处，则电梯 BD 的高度约为(参考数据：sin 40°≈0.64，cos
结
BD＝AB
CD＝EA，BD＋DA＝BA AD＋CE＋FB＝AB
1．(2021·南岸区校级期中)如图，某大楼 AB 正前方有一栋小楼 ED，小
明从大楼顶端 A 测得小楼顶端 E 的俯角为 45°，从大楼底端 B 测得小楼
顶端 E 的仰角为 24°，小楼底端 D 到大楼前梯坎 BC 的底端 C 有 90 m，
在坡比为 5∶12 的山坡上走了 1 300 m，此时小明看山顶的角度为 60°，
则山高为
( B)
A．(600－250 5)m
B．(600 3－250)m
C．(350＋350 3)m
D．500 3 m
6．(2021·重庆一中三模)如图，小欢同学为了测量建筑物 AB 的高度，
从建筑物底端点 B 出发，经过一段坡度 i＝1∶2.4 的斜坡，到达 C 点，
则高楼 AB 的高度为(参考数据：sin 22°≈0.37，cos 22°≈0.93，tan
22°≈0.40)
(D)
A．60 m
B．70 m
C．80 m
D．90 m
4．如图，斜坡 AB 长 20 m，其坡度 i＝1∶0.75，BC⊥AC，斜坡 AB 正前
方一座建筑物 ME 上悬挂了一幅巨型广告，小明在点 B 测得广告顶部 M 点
梯坎 BC 长 65 m，梯坎 BC 的坡度 i＝1∶2.4，则大楼 AB 的高度为(结果

2021中考数学复习专题之三角形03【三角形的面积】基础训练一．选择题1．△ABC中，BC＝10，AC﹣AB＝4．过C作∠BAC的角平分线的垂线，垂足为D，连结BD，CD，则S的最大值为（）△BDCA．10B．15C．12D．142．如图，在四边形ABCD中，对角线AC，BD交于点O，∠CBD＝90°，BC＝4，OB＝OD＝3，AC＝10，则四边形ABCD的面积为（）A．48B．36C．24D．123．在平面直角坐标系中，由点A（a，3），B（a+4，3），C（b，﹣3）组成的△ABC的面积是（）A．6B．12C．24D．不确定4．如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8，四边形DHOG面积为（）A．6B．7C．8D．95．如图，在△ABC中，AG＝BG，BD＝DE＝EC，CF＝4AF，若四边形DEFG的面积为14，则△ABC的面积为（）A．24B．28C．35D．306．如图，点P在直线m上移动，A，B是直线n上的两个定点，且直线m∥n．对于下列各值：①点P到直线n的距离；②△PAB的周长：③△PAB的面积：④∠APB的大小．其中不会随点p 的移动而变化的是（）A．①②B．①③C．②④D．③④7．如图，△ABC中，AD是BC上的中线，BE是△ABD中AD边上的中线，若△ABC的面积是20，则△ABE的面积是（）A ．10B ．6C ．5D ．48．活动课上，小华将两张直角三角形纸片如图放置，已知AC ＝8，O 是AC 的中点，△ABO 与△CDO 的面积之比为4：3，则两纸片重叠部分即△OBC 的面积为（ ）A ．4B ．6C ．2D ．29．如图，已知△ABC 中，CN ＝3BN ，AM ＝CM ，AN 交BM 于O ．若S △ABC ＝40，则下列正确的是（ ）①S △ABO ＝2；②BO ：MO ＝2：3；③AO ：NO ＝4；④S △AMO ＝12：⑤S △CMO ＝13．A ．①②④B ．②③④C ．②③④⑤D ．①②③④10．已知点A （1，2a +1），B （﹣a ，a ﹣3），若线段AB ∥x 轴，则三角形AOB 的面积为（ ） A ．21B ．28C ．14D ．10.5二．填空题11．如图，点E 、F 都在线段AB 上，分别过点A 、B 作AB 的垂线AD 、BC ，连接DE 、DF 、CE 、CF ，DF 交CE 于点G ，已知AD ＝BE ＝7.5，AE ＝BF ＝CB ＝2.5．如果△DEG 的面积为S 1，△CFG 的面积为S 2，则S 1﹣S 2＝ ．12．如图，在△ABC 中，∠BAC ＝90°，AD 是高，BE 是中线，CF 是角平分线，CF 交AD 于点G ，交BE 于点H ，下面说法中正确的序号是 ．①△ABE 的面积等于△BCE 的面积；②∠AFG ＝∠AGF ；③∠FAG ＝2∠ACF ；④BH ＝CH ．13．如图，△ABC 中，D 是AB 的中点，且AE ：CE ＝3：1，S △CEP ＝1，则S △BPC ＝ ．14．如图，已知△ABC 中，∠BAC ＝120°，点D 在边BC 上，且AD ＝4．BD ：CD ＝3：2．当△ABD 面积最大时，AB 的长为 ．15．如图，AD 是△ABC 的中线，G 是AD 上的一点，且AG ＝2GD ，连结BG ，若S △ABC ＝12，则S △ABG 为 ．三．解答题16．在平面直角坐标系中，已知点A，B，C的坐标分别为A（﹣1，0），B（3，﹣2），C（a，b），且+|a+2b﹣7|＝0．（1）求点C的坐标；（2）画出△ABC并求△ABC的面积；（3）若BC与x轴交点为点M，求点M坐标．17．如图，长方形ABCD中，AB＝10cm，BC＝8cm，点E是CD的中点，动点P从A点出发，以每秒2cm的速度沿A→B→C→E运动，最终到达点E．若点P运动的时间为x秒，那么当x为何值时，△APE的面积等于32cm2？（提醒：同学们，要分类讨论哦！）18．如图，在△ABC中，AD是BC边上的中线，AE是BC边上的高线，已知AE＝4，△ABD的面积是6，求BC的长．19．在平面直角坐标系中，已知以A（﹣1，0）或以B（3，0）为直角顶点的直角三角形ABC的面积为6，求顶点C的坐标．20．已知A（0，2），B（4，0），C（6，6）（1）在图中的直角坐标系中画出△ABC；（2）求△ABC的面积．参考答案一．选择题1．解：如图：延长AB ，CD 交点于E ，∵AD 平分∠BAC ，∴∠CAD ＝∠EAD ，∵CD ⊥AD ，∴∠ADC ＝∠ADE ＝90°，在△ADE 和△ADC 中，，∴△ADE ≌△ADC （ASA ），∴AC ＝AE ，DE ＝CD ；∵AC ﹣AB ＝4，∴AE ﹣AB ＝4，即BE ＝4；∵DE ＝DC ，∴S △BDC ＝S △BEC ，∴当BE ⊥BC 时，S △BDC 面积最大，即S △BDC 最大面积＝××10×4＝10．故选：A ．2．解：在Rt△OBC中，由勾股定理，得CO＝＝＝5．∵AC＝10，∴AO＝5，∴OA＝OC，∵OB＝OD＝3，∴四边形ABCD是平行四边形．四边形ABCD的面积为BC•BD＝4×（3+3）＝24，故选：C．3．解：∵点A（a，3），B（a+4，3），∴AB＝4，∵C（b，﹣3），∴点C在直线y＝﹣3上，∵AB ：y ＝3与直线y ＝﹣3平行，且平行线间的距离为6，∴S ＝×4×6＝12，故选：B ．4．解：连接OC ，OB ，OA ，OD ，∵E 、F 、G 、H 依次是各边中点，∴△AOE 和△BOE 等底等高，所以S △OAE ＝S △OBE ，同理可证，S △OBF ＝S △OCF ，S △ODG ＝S △OCG ，S △ODH ＝S △OAH ，∴S 四边形AEOH +S 四边形CGOF ＝S 四边形DHOG +S 四边形BFOE ，∵S 四边形AEOH ＝6，S 四边形BFOE ＝7，S 四边形CGOF ＝8，∴6+8＝7+S 四边形DHOG ，解得S 四边形DHOG ＝7．故选：B ．5．解：连接EG ，CG ，∵BD ＝DE ＝EC ，∴BD ＝BC ，∵AG ＝BG ＝AB ，∴S △BDG ＝S △BCG ＝S △ABC ＝S △ABC ，同理S △ECF ＝S △ABC ＝S △ABC ，S △AFG ＝×S △ABC ＝S △ABC ，∴S 四边形DEFG ＝S △ABC ﹣S BDG ﹣S △CEF ﹣S △AGF ＝S △ABC ＝14，∴S △ABC ＝30．故选：D ．6．解：①∵直线m ∥n ，∴点P 到直线n 的距离不变；②∵PA 、PB 的长度随点P 的移动而变化，∴△PAB 的周长会随点P 的移动而变化；③∵点P 到直线n 的距离不变，AB 的大小，∴△PAB 的面积不变；④直线m 、n 之间的距离不随点P 的移动而变化，∠APB 的大小随点P 的移动而变化； 故不会随点p 的移动而变化的是①③，故选：B ．7．解：∵AD 是BC 上的中线，∴S △ABD ＝S △ACD ＝S △ABC ，∵BE 是△ABD 中AD 边上的中线，∴S △ABE ＝S △BED ＝S △ABD ，∴S △ABE ＝S △ABC ， ∵△ABC 的面积是20，∴S △ABE ＝＝5． 故选：C ．8．解：∵点O 是直角△ABC 斜边AC 的中点，∴S △ABO ＝S △CBO ，OB ＝OA ＝OC ，∵△ABO 与△CDO 的面积之比为4：3，∴△CBO 与△CDO 的面积之比为4：3，∴OB ：OD ＝4：3，设OB ＝4x ，则OD ＝3x ，∴OA ＝OC ＝4x ，∵AC ＝8，∴4x +4x ＝8，解得x ＝1，在Rt △ODC 中，OD ＝3，OC ＝4，∴CD ＝＝，∴S △ODC ＝×3×＝，而△CBO 与△CDO 的面积之比为4：3，∴S △OBC ＝×＝2．故选：D ．9．解：过M 点作MD ∥BC ，交AN 于点N ，连接OC ，则△DOM ∽△NOB ，∴DM ：BN ＝DO ：ON ＝MO ：BO ，∵AM ＝CM ，∴DM 为△ANC 的中位线，∴AD ＝DN ，BC ＝2DM ，∵CN ＝3BN ，∴DM ：BN ＝3：2，BN ：BC ＝1：4，∴DO ：ON ＝MO ：BO ＝3：2，∴BO ：MO ＝2：3，故②正确；AO ：NO ＝4：1，故③正确；AO ：AN ＝4：5，OM ：BM ＝3：5，∵S △ABC ＝40，AM ＝CM ，BN ：BC ＝1：4，∴S △ABN ＝10，S △ABM ＝20，∵S △ABO ：S △ABN ＝AO ：AN ＝4：5，S △AMO ：S △ABM ＝MO ：BM ＝3：5，∴S △ABO ＝8，故①错误；S △AMO ＝12，故④正确；∵AM ＝CM ，∴S △CMO ＝S △AMO ＝12，故⑤错误．故选：B ．10．解：∵AB ∥x 轴，∴2a +1＝a ﹣3．解得a ＝﹣4．∴A （1，﹣7），B （4，﹣7）．∴AB ＝3．∴△AOB 的面积为：×3×7＝10.5，故选：D ．二．填空题11．解：∵AD ＝BE ＝7.5，AE ＝BF ＝CB ＝2.5．∴AF ＝BE ，∴AD ＝AF ＝7.5，在△ADE 和△BEC 中，，∴△ADE ≌△BEC （SAS ），∴S △DAE ＝S △CBE ，∵S 1＝S △DAF ﹣S △DAE ﹣S △EFG ，S 2＝S △CBE ﹣S △EFG ﹣S △CBF ，∴S 1﹣S 2＝S △DAE +S △CBF ＝+＝．故答案为．12．解：∵BE是中线，∴AE＝CE，∴△ABE的面积＝△BCE的面积（等底等高的三角形的面积相等），故①正确；∵CF是角平分线，∴∠ACF＝∠BCF，∵AD为高，∴∠ADC＝90°，∵∠BAC＝90°，∴∠ABC+∠ACB＝90°，∠ACB+∠CAD＝90°，∴∠ABC＝∠CAD，∵∠AFG＝∠ABC+∠BCF，∠AGF＝∠CAD+∠ACF，∴∠AFG＝∠AGF，故②正确；∵AD为高，∴∠ADB＝90°，∵∠BAC＝90°，∴∠ABC+∠ACB＝90°，∠ABC+∠BAD＝90°，∴∠ACB＝∠BAD，∵CF是∠ACB的平分线，∴∠ACB＝2∠ACF，∴∠BAD＝2∠ACF，即∠FAG ＝2∠ACF ，故③正确；根据已知条件不能推出∠HBC ＝∠HCB ，即不能推出BH ＝CH ，故④错误；故答案为：①②③．13．解：连接PA ，∵D 是AB 的中点，∴S △ADC ＝S △BCD ，S △PAD ＝S △PBD ，∴S △BPC ＝S △APC ，∵AE ：CE ＝3：1，S △CEP ＝1，∴S △AEP ＝3S △CEP ＝3，∴S △APC ＝4，∴S △BPC ＝4，故答案为4．14．解：作DE ⊥AB 于E ，∴S △ABD ＝AB •DE ，∵DE ⊥AB ，∴DE ≤AD ．当DA ⊥AB 时，DE 与DA 重合，此时，DE 取得最大值4，△ABD 面积最大，作CF ⊥AB ，交BA 的延长线于F ，∴DE ∥CF ，∴△BDE ∽△BCF ，∴＝，即＝，∴＝，∴CF ＝，∵∠BAC ＝120°，∴∠CAF ＝60°，∴∠ACF ＝30°∴AF ＝tan30°•CF ＝×＝，∵AD ∥CF ，∴＝＝，∴AB ＝．故答案为．15．解：∵AD 是△ABC 的中线，S △ABC ＝12，∴S △ABD ＝S △ABC ＝×12＝6，∵AG ＝2GD ，∴S △ABG ＝S △ABD ＝×6＝4，故答案为：4．三．解答题16．解：（1）∵+|a +2b ﹣7|＝0，∴， 解得：，∴C （1，3）；（2）如图，△ABC 为所作，如图，分别过点B ，点C 作x 轴的平行线BF ，DE ，过点A ，点B 作y 轴的平行线DF ，EB ， ∴S △ABC ＝S 四边形DFBE ﹣S △ADC ﹣S △BCE ﹣S △ABF ，＝4×5﹣﹣﹣，＝8；（3）设点M 的坐标为（m ，0），∵S△ABC ＝S△AMC+S△ABM，S△ABC＝8，∴，∴AM＝，∴m﹣（﹣1）＝，∴m＝，∴M（，0）．17．解：①如图1，当P在AB上时，∵△APE的面积等于32，∴×2x•8＝32，解得：x＝4；②当P在BC上时，∵△APE的面积等于32，∴S 矩形ABCD ﹣S △CPE ﹣S △ADE ﹣S △ABP ＝32，∴10×8﹣（10+8﹣2x ）×5﹣×8×5﹣×10×（2x ﹣10）＝32，解得：x ＝6.6；③当P 在CE 上时，∴（10+8+5﹣2x ）×8＝32，解得：x ＝7.5＜（10+8+5），x ＝7.5时2x ＝15，P 在BC 边，∴舍去；答：4或6.6．18．解：∵AD 为△ABC 的中线，∴S △ABC ＝2S △ABD ＝2×6＝12，∴×AE •BC ＝12，即4•BC ＝12，∴BC ＝6．19．解：设C 点的纵坐标为t ，∵A （﹣1，0），B （3，0），∴AB ＝4，word 版初中数学 21 / 21 ∵S △ABC ＝×4×|t |＝6，解得|t |＝3，∴点C 的坐标为（﹣1，3）或（3，3）或（﹣1，﹣3）或（3，﹣3）．20．解：（1）在平面直角坐标系中画出△ABC 如图所示：（2）△ABC 的面积＝6×6﹣×4×2﹣﹣＝36﹣4﹣6﹣12＝14．。

2021年九年级数学中考复习分类专题：三角形面积问题综合1．如图，△ABC中，D，E两点分别在AB，BC上，若AD：DB＝CE：EB＝2：3，则△DBE与△ADC的面积比为（）A．3：5 B．4：5 C．9：10 D．15：162．三角形的下列线段中能将三角形的面积分成相等两部分的是（）A．中线B．角平分线C．高D．中位线3．如图，两个三角形的面积分别是9，6，对应阴影部分的面积分别是m，n，则m﹣n等于（）A．2 B．3 C．4 D．无法确定4．如图，在四边形ABCD中，∠ABC＝90°，AB＝BC＝2，E、F分别是AD、CD的中点，连接BE、BF、EF．若四边形ABCD的面积为6，则△BEF的面积为（）A．2 B．C．D．35．如图，△ABC的面积为16，点D是BC边上一点，且BD＝BC，点G是AB上一点，点H 在△ABC内部，且四边形BDHG是平行四边形，则图中阴影部分的面积是（）A ．3B ．4C ．5D ．66．如图，D 为△ABC 内部一点，E 、F 两点分别在AB 、BC 上，且四边形DEBF 为矩形，直线CD 交AB 于G 点．若CF ＝6，BF ＝9，AG ＝8，则△ADC 的面积为何？（ ）A ．16B ．24C ．36D ．547．在平面直角坐标系xOy 中，若A 点坐标为（﹣3，3），B 点坐标为（2，0），则△ABO 的面积为（ ） A ．15B ．7.5C ．6D ．38．如图中，∠ACB ＝90°，AC ＞BC ，分别以△ABC 的边AB 、BC 、CA 为一边向△ABC 外作正方形ABDE 、BCMN 、CAFG ，连接EF 、GM 、ND ，设△AEF 、△CGM 、△BND 的面积分别为S 1、S 2、S 3，则下列结论正确的是（ ）A ．S 1＝S 2＝S 3B ．S 1＝S 2＜S 3C ．S 1＝S 3＜S 2D ．S 2＝S 3＜S 19．如图，在△ABC 中E 是BC 上的一点，EC ＝2BE ，点D 是AC 的中点，设△ABC ，△ADF ，△BEF 的面积分别为S △ABC ，S △ADF ，S △BEF ，且S △ABC ＝12，则S △ADF ﹣S △BEF ＝（ ）A ．1B ．2C ．3D ．410．如图，在长方形网格中，每个小长方形的长为2，宽为1，A 、B 两点在网格格点上，若点C也在网格格点上，以A、B、C为顶点的三角形面积为2，则满足条件的点C个数是（）A．2 B．3 C．4 D．511．如图，把△ABC沿AB边平移到△A1B1C1的位置，图中所示的三角形的面积S1与四边形的面积S2之比为4：5，若AB＝4，则此三角形移动的距离AA1是．12．如图所示的网格是正方形网格，A，B，C，D是网格线交点，则△ABC的面积与△ABD的面积的大小关系为：S△ABC S△ABD（填“＞”，“＝”或“＜”）．13．如图，已知△ABC，通过测量、计算得△ABC的面积约为cm2．（结果保留一位小数）14．如图，在平面直角坐标系xOy中，我们把横、纵坐标都是整数的点为“整点”，已知点A的坐标为（5，0），点B在x轴的上方，△OAB的面积为，则△OAB内部（不含边界）的整点的个数为．15．如图．在Rt△ABC中，AC＝3，∠ABC＝90°，BD是△ABC的角平分线，过点D作DE⊥BD交BC边于点E．若AD＝1，则图中阴影部分的面积为16．如图，△ABC的面积为S．点P1，P2，P3，…，P n﹣1是边BC的n等分点（n≥3，且n为整数），点M，N分别在边AB，AC上，且＝＝，连接MP1，MP2，MP3，…，MP n﹣1，连接NB，NP1，NP2，…，NP n﹣1，线段MP1与NB相交于点D1，线段MP2与NP1相交于点D2，线段MP3与NP2相交于点D3，…，线段MP n﹣1与NP n﹣2相交于点D n﹣1，则△ND1P1，△ND2P2，△ND3P3，…，△ND n﹣1Pn﹣1的面积和是．（用含有S与n的式子表示）17．某课题研究小组就图形面积问题进行专题研究，他们发现如下结论：（1）有一条边对应相等的两个三角形面积之比等于这条边上的对应高之比；（2）有一个角对应相等的两个三角形面积之比等于夹这个角的两边乘积之比；…现请你继续对下面问题进行探究，探究过程可直接应用上述结论．（S表示面积）问题1：如图1，现有一块三角形纸板ABC ，P 1，P 2三等分边AB ，R 1，R 2三等分边AC ．经探究知＝S △ABC ，请证明．问题2：若有另一块三角形纸板，可将其与问题1中的拼合成四边形ABCD ，如图2，Q 1，Q 2三等分边DC ．请探究与S 四边形ABCD 之间的数量关系．问题3：如图3，P 1，P 2，P 3，P 4五等分边AB ，Q 1，Q 2，Q 3，Q 4五等分边DC ．若S 四边形ABCD＝1，求．问题4：如图4，P 1，P 2，P 3四等分边AB ，Q 1，Q 2，Q 3四等分边DC ，P 1Q 1，P 2Q 2，P 3Q 3将四边形ABCD 分成四个部分，面积分别为S 1，S 2，S 3，S 4．请直接写出含有S 1，S 2，S 3，S 4的一个等式．18．探索：在如图1至图3中，△ABC 的面积为a ．（1）如图1，延长△ABC 的边BC 到点D ，使CD ＝BC ，连接DA ．若△ACD 的面积为S 1，则S 1＝ （用含a 的代数式表示）；（2）如图2，延长△ABC 的边BC 到点D ，延长边CA 到点E ，使CD ＝BC ，AE ＝CA ，连接DE ．若△DEC 的面积为S 2，则S 2＝ （用含a 的代数式表示），并写出理由；（3）在图2的基础上延长AB 到点F ，使BF ＝AB ，连接FD 、FE ，得到△DEF （如图3）．若阴影部分的面积为S 3，则S 3＝ （用含a 的代数式表示）． 发现：像上面那样，将△ABC 各边均顺次延长一倍，连接所得端点，得到△DEF （如图3），此时，我们称△ABC 向外扩展了一次．可以发现，扩展一次后得到的△DEF 的面积是原来△ABC 面积的 倍．应用：去年在面积为10m 2的△ABC 空地上栽种了某种花卉．今年准备扩大种植规模，把△ABC 向外进行两次扩展，第一次由△ABC 扩展成△DEF ，第二次由△DEF 扩展成△MGH （如图4）．求这两次扩展的区域（即阴影部分）面积共为多少平方米？参考答案1．解：∵AD ：DB ＝CE ：EB ＝2：3，∴S △BDC ：S △ADC ＝3：2，S △BDE ：S △DCE ＝3：2，∴设S △BDC ＝3x ，则S △ADC ＝2x ，S △BED ＝1.8x ，S △DCE ＝1.2x ， 故△DBE 与△ADC 的面积比为：1.8x ：2x ＝9：10． 故选：C ．2．解：∵三角形的中线把三角形分成两个等底同高的三角形， ∴三角形的中线将三角形的面积分成相等两部分． 故选：A ．3．解：设空白出图形的面积为x ， 根据题意得：m +x ＝9，n +x ＝6， 则m ﹣n ＝9﹣6＝3． 故选：B ．4．解：连接AC ，过B 作EF 的垂线交AC 于点G ，交EF 于点H ， ∵∠ABC ＝90°，AB ＝BC ＝2，∴AC ＝＝＝4，∵△ABC 为等腰三角形，BH ⊥AC ， ∴△ABG ，△BCG 为等腰直角三角形， ∴AG ＝BG ＝2∵S △ABC ＝•AB •BC ＝×2×2＝4，∴S △ADC ＝2， ∵＝2，∵△DEF ∽△DAC ，∴GH ＝BG ＝， ∴BH ＝， 又∵EF ＝AC ＝2，∴S △BEF ＝•EF •BH ＝×2×＝， 故选C ．方法二：S △BEF ＝S 四边形ABCD ﹣S △ABE ﹣S △BCF ﹣S △FED ， 易知S △ABE +S △BCF ＝S 四边形ABCD ＝3，S △EDF ＝，∴S △BEF ＝S 四边形ABCD ﹣S △ABE ﹣S △BCF ﹣S △FED ＝6﹣3﹣＝． 故选：C ．5．解：设△ABC 底边BC 上的高为h ，△AGH 底边GH 上的高为h 1，△CGH 底边GH 上的高为h 2，则有h ＝h 1+h 2．S △ABC ＝BC •h ＝16，S 阴影＝S △AGH +S △CGH ＝GH •h 1+GH •h 2＝GH •（h 1+h 2）＝GH •h ．∵四边形BDHG 是平行四边形，且BD ＝BC ， ∴GH ＝BD ＝BC ，∴S 阴影＝×（BC •h ）＝S △ABC ＝4． 故选：B ．6．解：S △ADC ＝S △AGC ﹣S △ADG ＝×AG ×BC ﹣×AG ×BF＝×8×（6+9）﹣×8×9＝60﹣36＝24．故选：B．7．解：如图，根据题意得，△ABO的底长OB为2，高为3，∴S＝×2×3＝3．△ABO故选：D．8．解：作ER⊥FA交FA的延长线于R，作DH⊥NB交NB的延长线于H，作NT⊥DB交DB的延长线于T，设△ABC的三边长分别为a、b、c，∵分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG，∵AE＝AB，∠ARE＝∠ACB，∠EAR＝∠CAB，∴△AER≌△ABC，∴ER＝BC＝a，FA＝b，＝ab，∴S1S＝ab，2同理可得HD＝AR＝AC，∴S1＝S2＝S3＝．故选：A．9．解：∵S△ABC＝12，EC＝2BE，点D是AC的中点，∴S△ABE＝＝4，S△ABD＝＝6，∴S△ABD ﹣S△ABE，＝S△ADF ﹣S△BEF，＝6﹣4，＝2．故选：B．10．解：C点所有的情况如图所示：故选：C．11．解：∵把△ABC沿AB边平移到△A1B1C1的位置，∴AC∥A1C1，∴△ABC∽△A1BD，∵S△A1BD ：S四边形ACDA1＝4：5，∴S：S△ABC＝4：9，∴A1B：AB＝2：3，∵AB＝4，∴A1B＝，∴AA1＝4﹣＝．故答案为：．12．解：∵S△ABC ＝×2×4＝4，S△ABD＝2×5﹣×5×1﹣×1×3﹣×2×2＝4，∴S△ABC ＝S△ABD，故答案为：＝．13．解：过点C作CD⊥AB的延长线于点D，如图所示．经过测量，AB＝2.2cm，CD＝1.7cm，∴S△ABC＝AB•CD＝×2.2×1.7≈1.9（cm2）．故答案为：1.9．14．解：设B（m，n），∵B在x轴上方，∴n＞0，∵点A的坐标为（5，0），∴OA＝5，∵△OAB的面积＝5•n＝，∴n＝3，∴B（m，3），由图形的对称性，设m≥，①当m＝5时，可得△OAB内部的整数点4个，②当m≥且m≠5时，OB的直线解析式y＝x，AB的直线解析式y＝x﹣设直线y＝2与直线OB与直线AB分别交于点C，D，∴C（，2），D（，2），∴CD＝，∴△OAB内部（不含边界）直线y＝2上的整点的个数为1或2，同理可得，△OAB内部（不含边界）直线y＝1上的整点的个数为3或4，综上所述，△OAB内部（不含边界）的整点的个数为4或5或6．故答案为4或5或6；15．解：如图，作DH⊥BC于H，∵∠ABC＝90°，BD是△ABC的角平分线，∠DBC＝∠ABD＝45°，∵DE⊥BD，∴∠DEB＝45°，∴△BDE是等腰直角三角形，设DH＝BH＝EH＝a，∵DH∥AB∴△CDH∽△CAB，∴，∵AD＝1，AC＝3，∴，∴AB ＝a ，CE ＝a ，∵AB 2+BC 2＝AC 2， ∴，， ∴图中阴影部分的面积＝． 故答案为：1．16．解：连接MN ，设BN 交MP 1于D 1，MP 2交NP 1于D 2，MP 3交NP 2于D 3． ∵＝＝，∴MN ∥BC ， ∴＝＝，∵点P 1，P 2，P 3，…，P n ﹣1是边BC 的n 等分点，∴MN ＝BP 1＝P 1P 2＝P 2P 3，∴四边形MNP 1B ，四边形MNP 2P 1，四边形MNP 3P 2都是平行四边形，易知S △ABN ＝•S ，S △BCN ＝•S ，S △MNB ＝•S ， ∴＝＝＝•S ∴S 阴＝S △NBC ﹣（n ﹣1）•﹣＝•S ﹣（n ﹣1）••S ﹣S ＝•S ，故答案为•S ．17．解：问题1，证明：如图1，连接P 1R 2，R 2B ，在△AP 1R 2中，∵P 1R 1为中线，∴S △AP 1R 1＝S △P 1R 1R 2， 同理S △P 1R 2P 2＝S △P 2R 2B ，∴S △P 1R 1R 2+S △P 1R 2P 2＝S △ABR 2＝S 四边形P 1P 2R 2R 1，由R 1，R 2为AC 的三等分点可知，S △BCR 2＝S △ABR 2，∴S △ABC ＝S △BCR 2+S △ABR 2＝S 四边形P 1P 2R 2R 1+2S 四边形P 1P 2R 2R 1＝3S 四边形P 1P 2R 2R 1，∴S 四边形P 1P 2R 2R 1＝S △ABC ；问题2，S 四边形ABCD ＝3S 四边形P 1Q 1Q 2P 2．理由：如图2，连接AQ 1，Q 1P 2，P 2C ，在△AQ 1P 2中，∵Q 1P 1为中线，∴S △AQ 1P 1＝S △P 1Q 1P 2，同理S △P 2Q 1Q 2＝S △P 2Q 2C ，∴S △P 1Q 1P 2+S △P 2Q 1Q 2＝S 四边形AQ 1CP 2＝S 四边形P 1Q 1Q 2P 2，由Q 1，P 2为CD ，AB 的三等分点可知，S △ADQ 1＝S △AQ 1C ，S △BCP 2＝S △AP 2C ，∴S △ADQ 1+S △BCP 2＝（S △AQ 1C +S △AP 2C ）＝S 四边形AQ 1CP 2，∴S 四边形ABCD ＝S △ADC +S △ABC ＝S 四边形AQ 1CP 2+S △ADQ 1+S △BCP 2＝3S 四边形P 1Q 1Q 2P 2，即S 四边形ABCD ＝3S 四边形P 1Q 1Q 2P 2；问题3，解：如图3，由问题2的结论可知，3S 2＝S 1+S 2+S 3，即2S 2＝S 1+S 3，同理得2S 3＝S 2+S 4，2S 4＝S 3+S 5，三式相加得，S 2+S 4＝S 1+S 5，∴S 1+S 2+S 3+S 4+S 5＝2（S 2+S 4）+S 3＝2×2S 3+S 3＝5S 3，即S 四边形P 2Q 2Q 3P 3＝S 四边形ABCD ＝；问题4，如图4，关系式为：S 2+S 3＝S 1+S 4．18．解：（1）∵BC ＝CD ，∴△ACD 和△ABC 是等底同高的，即S 1＝a ；（2）2a ；理由：连接AD ，∵CD ＝BC ，AE ＝CA ，∴S △DAC ＝S △DAE ＝S △ABC ＝a ，∴S 2＝2a ；（3）结合（2）得：2a ×3＝6a ；发现：扩展一次后得到的△DEF 的面积是6a +a ＝7a ，即是原来三角形的面积的7倍． 应用：拓展区域的面积：（72﹣1）×10＝480（m 2）．。

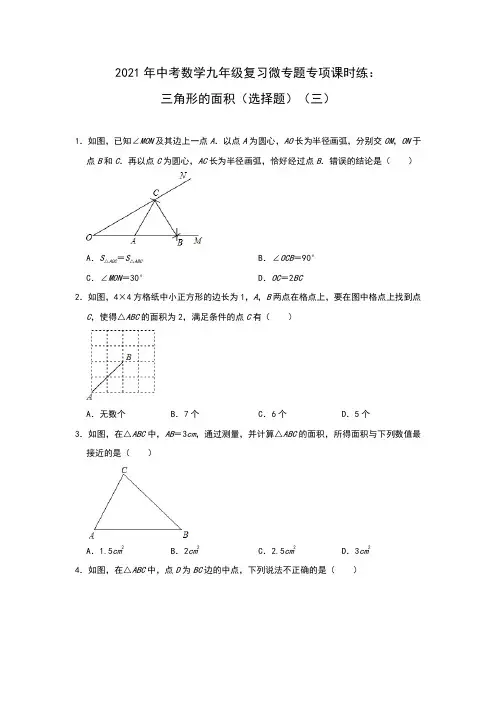
2021年中考数学九年级复习微专题专项课时练：三角形的面积（选择题）（三）1．如图，已知∠MON及其边上一点A．以点A为圆心，AO长为半径画弧，分别交OM，ON于点B和C．再以点C为圆心，AC长为半径画弧，恰好经过点B．错误的结论是（）A．S△AOC ＝S△ABCB．∠OCB＝90°C．∠MON＝30°D．OC＝2BC2．如图，4×4方格纸中小正方形的边长为1，A，B两点在格点上，要在图中格点上找到点C，使得△ABC的面积为2，满足条件的点C有（）A．无数个B．7个C．6个D．5个3．如图，在△ABC中，AB＝3cm，通过测量，并计算△ABC的面积，所得面积与下列数值最接近的是（）A．1.5cm2B．2cm2C．2.5cm2D．3cm24．如图，在△ABC中，点D为BC边的中点，下列说法不正确的是（）A．BD＝DC B．BD＝BCC．∠BAD＝∠CAD D．S△BAD ＝S△CAD5．如图，D、E分别是△ABC边AB、BC上的点，AD＝2BD，BE＝CE，设△ADF的面积为S1，△CEF的面积为S2，若S△ABC＝9，则S1﹣S2＝（）A．B．1 C．D．26．如图，在△ABC中，AB＝2，BC＝4，△ABC的高AD与CE的比为（）A．1：2 B．2：1 C．1：4 D．4：17．如图，在边长为1的小正方形网格中，小正方形的顶点叫格点，以格点为顶点的多边形叫格点多边形．图中①、②、③、④四个格点多边形的面积分别记为S1，S2，S3，S4，下列说法正确的是（）A．S1＝S2B．S2＝S3C．S1+S2＝S4D．S1+S3＝S48．如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若AA'＝1，则AD等于（）A．B．3 C．D．9．如图是边长为1的正方形网格，A、B、C、D均为格点，则四边形的面积为（）A．7 B．10 C．D．810．如图，在△ABC中，点D、E分别在AC、AB上，BD与CE交于点O，若四边形AEOD的面积记为S1，S△BEO＝S2，S△BOC＝S3，S△COD＝S4，则S1•S3与S2•S4的大小关系为（）A．S1•S3＜S2•S4B．S1•S3＝S2•S4C．S1•S3＞S2•S4D．不能确定11．如图，在△ABC中，D、E、F分别为BC、AD、BE的中点，且阴影面积S△CEF＝1，则△ABC 的面积为（）A．2 B．4 C．8 D．1612．如图，点D是△ABC边AC上的中点，连接BD，将△BCD沿BD折叠，使得点C落在点E处，且BE交AC于点F，若S△ABF ＝S△BDF，∠BDC＝130°，则∠A的度数为（）A．50°B．80°C．96°D．100°13．已知：如图△ABC中，点D，E，F分别在三边上，E是AC的中点，AD，BE，CF交于一点G，BD＝2DC，S△BGD ＝8，S△AGE＝3，则△ABE的面积是（）A．11 B．14 C．15 D．3014．如图，D是△ABC的边AB上一点（不与点A、B重合），DE∥BC，交AC于点E，连接BE，已知△ABC的面积为9，则△BDE面积的最大值为（）A．3 B．C．D．15．如图，四边形ABCD中，AD∥BC，点M是AD的中点，若动点N从点B出发沿边BC方向向终点C运动，连结BM，CM，AN，DN，则在整个运动过程中，阴影部分面积和的大小变化情况是（）A．不变B．一直变大C．先减小后增大D．先增大后减小16．在△ABC中，D是BC延长线上一点，且BC＝m•BD，过D点作直线AB，AC的垂线，垂足分别为E、F，若AB＝n•AC．则＝（）A．B．C．D．17．如图所示，AD、BF、CE分别是△ABC的三条高线，则下列△ABC的面积表述正确的是（）A．AB•BF B．AB•CE C．BC•BF D．AC•CE18．在△ABC中，AC＝4，AB＝5，则△ABC面积的最大值为（）A．6 B．10 C．12 D．2019．在直角坐标系xOy中，点O（0，0），动点A（t，t）在第一象限，动点B（0，m）在y 轴上．当AB＝4时，△OAB面积的最大值为（）A．8 B．C．D．20．如图所示，AD，BE，CF分别是△ABC的角平分线，高线和中线，则下列求△ABC的面积正确的公式是（）A．B．＝BE•CEC．D．S△ABC参考答案1．解：由题意可知OA＝AC＝AB＝BC，∴△ABC是等边三角形，∴∠CAB＝60°，∴∠MON＝∠OCA＝30°，∴∠OCB＝30°+60°＝90°．∴S△AOC ＝S△ABC，∴A，B，C，正确．故选：D．2．解：如图，满足条件的点C有6个．故选：C．3．解：过C作CD⊥AB于D，通过测量，CD＝1.7cm，∴S△ABC＝AB•CD＝ 1.7×3＝2.55（cm2），故选：C．4．解：A、在△ABC中，点D为BC边的中点，则BD＝DC，所以A选项的说法正确；B、在△ABC中，点D为BC边的中点，则BD＝BC，所以B选项的说法正确；C、在△ABC中，若∠BAD＝∠CAD，则必须有∠ADB＝∠ADC，则必须有△ADB≌△ADC，得出AD⊥BC，因为AD不垂直于BC，所以C选项的说法不正确；D、在△ABC中，点D为BC边的中点，则BD＝DC，等底同高的三角形面积相等，所以D选项的说法正确．故选：C．5．解：∵BE＝CE，∴BE＝BC，∵S△ABC＝9，∴S△ABE ＝S△ABC＝×9＝4.5．∵AD＝2BD，S△ABC＝9，∴S△BCD ＝S△ABC＝×9＝3，∵S△ABE ﹣S△BCD＝（S△ADF+S四边形BEFD）﹣（S△CEF+SS四边形BEFD）＝S△ADF﹣S△CEF，即S△ADF ﹣S△CEF＝S△ABE﹣S△BCD＝4.5﹣3＝1.5．故选：C．6．解：S△ABC＝AB•CE＝BC•AD，∵AB＝2，BC＝4，∴×2•CE＝×4•AD，∴＝．故选：A．7．解：∵S1＝2.5，S2＝3，S3＝3，S4＝6，∴S2＝S3，S3+S2＝S4，故选：B．8．解：如图，∵S △ABC ＝9、S △A ′EF ＝4，且AD 为BC 边的中线， ∴S △A ′DE ＝S △A ′EF ＝2，S △ABD ＝S △ABC ＝， ∵将△ABC 沿BC 边上的中线AD 平移得到△A 'B 'C '，∴A ′E ∥AB ， ∴△DA ′E ∽△DAB ， 则＝，即（， 解得A ′D ＝2或A ′D ＝﹣（舍）， ∴AD ＝AA '+A 'D ＝1+2＝3 故选：B ．9．解：S 四边形ABCD ＝3×4﹣×2×1×2﹣×1×3×2＝12﹣5＝7， 故选：A ．10．解：如图，连接DE ，设S △DEO ＝S ′1，则＝＝，从而有S 1′S 3＝S 2S 4．因为S 1＞S 1′，所以S 1S 3＞S 2S 4． 故选：C ． 11．解：∵EF ＝FB ， ∴S △EFC ＝S △BFC ＝1， ∴S △BCE ＝2，∴S△BDE ＝S△DCF＝1，∵AE＝ED，∴S△ABE ＝S△AEB＝1，S△AEC＝S△EDC＝1，∴S△ABC＝4，故选：B．12．解：延长ED交BC于G，∵点D是△ABC边AC上的中点，∴S△ABD ＝S△CBD∵将△BCD沿BD折叠，使得点C落在点E处，∴CD＝ED，∠C＝∠E，S△BDC ＝S△BDE，∴S△ABD ＝S△BDE，∵S△ABF ＝S△BDF，∴S△ABF ＝S△EDF＝S△ABD＝S△BDC，在△CDG和△EDF中，，∴△CDG≌△EDF（ASA），∴S△CDG ＝S△EDF，DG＝DF＝AD，∴S△ABF ＝S△CDG＝S△BDC，∴BG＝GC，∵AD＝CD，∴DG∥AB，DG＝AB，∴AB＝AD，∴∠ABD＝∠ADB，∵∠BDC＝130°，∴∠ADB＝180°﹣130°＝50°，∴∠A＝180°﹣2×50°＝80°，13．解：∵BD＝2DC，∴S△CGD ＝S△BGD＝×8＝4；∵E是AC的中点，∴S△CGE ＝S△AGE＝3，∴S△BCE ＝S△BGD+S△CGD+S△CGE＝8+4+3＝15，∵BE是△ABC的中线，∴△ABC的面积是：15×2＝30．∴△ABE的面积＝30＝15，故选：C．14．解：设△BDE面积为y，，则△ADE面积为，∵DE∥BC，∴△ADE∽△ABC，∴，∴，∴y ＝9x （1﹣x ）＝﹣9（x ﹣）2+，∴当x ＝时，y 最大值为．故选：B ．15．解：连接MN ，∵AD ∥BC∴S △ABM ＝S △NMA ，∴△AEB 与△NME 的面积相等，同理△NMF 与△CDF 的面积相等，∴S 阴影＝S 四边形ABCD ﹣2S 四边形MENF ，设AM ＝MD ＝a ，BC ＝b ，BN ＝x ，S △AMN ＝S △DMN ＝k ，k 为常数 ∴所以S △AEM ：S △AMN ＝∴S △AEM ＝同理S △DFM ＝令S ＝S △AEM +S △DFM ＝＝ 令y ＝（a +x ）（a +b ﹣x ）它的对称轴为x ＝当0＜x ＜时，y 随x 的增大而增大，此时S 随着x 的增大而减小所以S 四边形MENF 随x 的增大而增大所以S 空白随x 的增大而增大所以S 阴影随x 的增大而减小 当＜x ＜b 时，y 随x 的增大而减小，此时S 随着x 的增大而增大所以S 阴影随x 的增大而增大故选：C ．16．解：连接AD ，∵BC ＝m •BD ，∴CD ＝（1﹣m ）BD∴S △ACD ＝（1﹣m ）S △ABD ，又∵S △ABD ＝，S △ACD ＝， ∴＝（1﹣m ）， ∵AB ＝n •AC ，∴AC •DF ＝（1﹣m ）n •AC •DE∴DF ＝（1﹣m ）n •DE ∴故选：C ．17．解：∵AD 、BF 、CE 分别是△ABC 的三条高线，∴求△ABC 的面积正确的公式是S △ABC ＝BC •AD ＝AC •BF ＝AB •CE ．故选：B ．18．解：把AB 边作为底边，则AB 边上的高的最大值为AC 的长度，同理把AC 边作为底边，则AC 边上的高的最大值为AB 的长度，即三角形为直角三角形时面积最大；所以，在△ABC 中，AC ＝4，AB ＝5，则△ABC 面积的最大值为×AC ×AB ＝10，故选：B ．19．解：根据条件可知，∠AOB ＝45°，AB ＝4，以AB 为弦，所对圆周角等于45°作一辅助圆，如图所示：当点O 位于优弧中点时，点O 到直线AB 的距离最大，即“高”最大，而底AB 为定值4， 所以此时△OAB 的面积最大，计辅助圆圆心为G ，∠AGB ＝90°，AG ＝BG ＝2， 所以点O 位于优弧中点时，点O 到直线AB 的距离为2+2，所以△OAB面积的最大值×4×（2+2）＝4+4．故选：B．20．解：∵BE是△ABC的高线，∴求△ABC的面积正确的公式是S＝CA•BE．△ABC故选：B．。

2021中考数学复习专题之三角形【三角形的面积】专项训练一．选择题1．如图，在△ABC中，D、E分别是BC、AD的中点，点F在BE上，且EF＝2BF，若S＝2cm2，△BCF 则S为（）△ABCA．4cm2B．8cm2C．12cm2D．16cm22．如图，已知AD是△ABC的边BC上的中线，CE是△ADC的边AD上的中线，若△ABD的面积为16cm2，则△CDE的面积为中（）A．32 cm2B．16cm2C．8cm2D．4cm23．如图，在△ABC中，∠C＝90°，BC＝8cm，AC＝6cm，点E是BC的中点，动点P从A点出发，先以每秒2cm的速度沿A→C运动，然后以1cm/s的速度沿C→B运动．若设点P运动的时间是t秒，那么当t＝（），△APE的面积等于8cm2．A．2秒B．2或秒C．秒D．2或或秒4．如图，将三角形ABC沿直线AB向右平移后得到三角形BDE，连接CD，CE，若三角形ACD的面积为10，则三角形BCE的面积为（）A．4B．5C．6D．105．如图，△ABC的面积为30cm2，AE＝ED，BD＝2DC，则图中四边形EDCF的面积等于（）A．6cm2B．8cm2C．9cm2D．10cm26．如图，在△ABC中，点D、E分别为BC、AD的中点，EF＝2FC，若△ABC的面积为12cm2，则△BEF的面积为（）A．2cm2B．3cm2C．4cm2D．5cm27．如图，在△ABC中，D是BC的中点，E在AC上，且AE：EC＝1：3，连接AD，BE交于点F，若S△ABC ＝40，则S四边形DCEF＝（）A．14B．15C．18D．208．如图，在纸面所在的平面内，一只电子蚂蚁从数轴上表示原点的位置O点出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其移动路线如图所示，第1次移动到A1，第2次移动到A2，第3次移动到A3，……，第n次移动到A n，则△OA2A2019的面积是（）A．504B．C．D．10099．如图，△ABC的三边的中线AD，BE，CF的公共点为G，且AG：GD＝2：1，若S△ABC＝12，则图中阴影部分的面积是（）A．3B．4C．5D．610．如图，在四边形ABCD中，M，N分别是AB，CD的中点，AN，BN，DM，CM划分四边形所成7个区域的面积分别为S1，S2，S3，S4，S5，S6，S7，那么恒成立的关系式是（）A．S2+S6＝S4B．S1+S7＝S4C．S2+S3＝S4D．S1+S6＝S4二．填空题11．如图，△ABC中，AD为BC边上的中线，E、F分别是AD、CD的中点，连接EF、BE，若△BEF的面积为6，则△ABC的面积是．12．如图，△ABC中，∠B＝90°，AB＝8，将△ABC平移至△DEF的位置，若四边形DGCF的面积为35，且DG＝2，则CF的长为．13．如图，EM＝6，EF＝4，EN＝10，且F为MN边上的中点，则△EMN的面积为．14．如图，△ABC的面积是16，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是．15．已知D、E分别是△ABC的边BC和AC的中点，若△ABC的面积＝24cm2，则△DEC的面积为．三．解答题16．如图，在△ABC中AD、AE、AF分别为△ABC的高、角平分线和中线，已知△AFC的面积为10，AD＝4，∠DAE＝20°，∠C＝30°．（1）求BC的长度；（2）求∠B的度数．17．如图所示，在平面直角坐标系中，点A，B的坐标分别为A（a，0），B（b，0），且a，b满足|a+3|+＝0，点C的坐标为（0，3）．（1）求a ，b 的值及S △ABC ；（2）若点M 在x 轴上，且S △ACM ＝S △ABC ，试求点M 的坐标．18．如图，在平面直角坐标系中，已知A （0，a ），B （b ，0），C （6，c ）三点，其中a ，b ，c 满足关系式|a ﹣2|+（b ﹣3）2+＝0，（1）求A ．B ．C 的坐标；（2）求三角形ABC 的面积；（3）在y 轴上是否存在点P ，使三角形APC 的面积与三角形ABC 的面积相等？若存在，求出点P 的坐标；若不存在，请说明理由．19．如图，在△ABC中，AE为边BC上的高，点D为边BC上的一点，连接AD．（1）当AD为边BC上的中线时．若AE＝4，△ABC的面积为24，求CD的长；（2）当AD为∠BAC的角平分线时．①若∠C＝65°，∠B＝35°，求∠DAE的度数；②若∠C﹣∠B＝20°，则∠DAE＝°．20．如图①，在△ABC中，AD是三角形的高，且AD＝6cm，E是一个动点，由B向C移动，其速度与时间的变化关系如图②，已知BC＝8cm．（1）求当E点在运动过程中△ABE的面积y与运动时间x之间的关系式；（2）当E点停止后，求△ABE的面积．参考答案一．选择题1．解：如图，∵EF ＝2BF ，若S △BCF ＝2cm 2，∴S △BEC ＝3S △BCF ＝3×2＝6cm 2，∵D 是BD 的中点，∴S △BDE ＝S △CDE ＝S △BEC ＝3cm 2，∵E 是AD 的中点，∴S △ABD ＝S △ACD ＝2S △BDE ＝6cm 2，∴△ABC 的面积为12cm 2，故选：C ．2．解：∵AD是△ABC的边BC上的中线，△ABD的面积为16cm2，∴△ADC的面积为16cm2，∵CE是△ADC的边AD上的中线，∴△CDE的面积为8cm2，故选：C．3．解：分两种情况：①如图1，当点P在AC上，由题意得：AP＝2t，∵BC＝8，点E是BC的中点，∴CE＝4，∵△APE的面积等于8，∴AP•CE＝AP×4＝8，∵AP＝4，∴t＝2；②如图2，当点P在BC上，∵E是BC的中点，∴BE＝CE＝4，∴EP•AC＝•EP×6＝8，∴EP＝，∴t＝3+4﹣＝，或t＝3+4+＝；综上所述，当t＝2或或时，△APE的面积等于8，故选：D．4．解：∵△ABC沿直线AB向右平移后到达△BDE的位置，∴AB＝BD，BC∥DE，∴S△ABC ＝S△BCD＝S△ACD＝×10＝5，∵DE∥BC，∴S△BCE ＝S△BCD＝5．故选：B．5．解：如图，连接DF，∵AE ＝ED ，BD ＝2DC ，∴△AEF 的面积等于△EFD 的面积，△ABE 的面积等于△BED 的面积，△BDF 的面积等于△FDC 的面积的2倍，△ABD 的面积等于△ADC 面积的2倍．设△AEF 面积为x ，△BDE 面积为y ，则x +x +y +y +（x +y ）＝30；①2y ＝2[2x +②得出x +y ＝12． 解得x ＝2．y ＝10，故四边形CDEF 的面积等于x +（x +y ）＝8cm 2，故选：B ．6．解：∵D 是BC 的中点，∴S △ABD ＝S △ADC （等底等高的三角形面积相等），∵E 是AD 的中点，∴S △ABE ＝S △BDE ，S △ACE ＝S △CDE （等底等高的三角形面积相等），∴S △ABE ＝S △DBE ＝S △DCE ＝S △AEC ，∴S △BEC ＝S △ABC ＝6cm 2．∵EF ＝2FC ，∴S △BEF ＝S △BCE ，∴S △BEF ＝S △BEC ＝4cm 2．故选：C ．7．解：过G 作DG ∥AC ，交BE 于G ，连接DE ，∵D 为BC 的中点，∴DG 为△BCE 的中位线，∴EC ＝2GD ，∴BG ＝EG ，∵AE ：EC ＝1：3，∴AE ：GD ＝2：3，∵DG ∥AC ，∴△DGF ∽△AEF ，∴EF ：FG ＝AE ：DG ＝2：3，∴EF ：BE ＝1：5，∵S △ABC ＝40，∴S △ADC ＝20，S △AEB ＝10，∴S △AEF ＝2，∴S 四边形DCEF ＝S △ADC ﹣S △AEF ＝20﹣2＝18，故选：C ．8．解：观察图形可知：点A 2n 在数轴上，OA 2n ＝n ，∵OA 2016＝1008，∴OA 2019＝1009，点A 2019在数轴上，∴＝×1009×1＝，故选：B ．9．解：∵△ABC 的三条中线AD 、BE ，CF 交于点G ，AG ：GD ＝2：1，∴AE ＝CE ，∴S △CGE ＝S △AGE ＝S △ACF ，S △BGF ＝S △BGD ＝S △BCF ，∵S △ACF ＝S △BCF ＝S △ABC ＝×12＝6，∴S △CGE ＝S △ACF ＝×6＝2，S △BGF ＝S △BCF ＝×6＝2，∴S 阴影＝S △CGE +S △BGF ＝4．故选：B ．10．解：过A 作AE ⊥DC 于E ，过M 作MH ⊥DC 于H ，过B 作BQ ⊥DC 于Q ，则AE ∥MH ∥BQ ，∵M 为AB 中点，∴H 为EQ 中点，即MH 是梯形AEQB 的中位线，∴2MH ＝AE +BQ ，∵S3+S4+S6＝S＝×DC×MH，△MDCS7+S6＝S＝×NC×BQ，△BNCS1+S3＝S＝×DN×AE，△ADN∵N为DC中点，∴DN＝CN，∴S7+S6+S1+S3，＝×NC×BQ+×DN×AE，＝DN×（AE+BQ），＝DN×2MH，＝DN×MH，＝CD×MH，∴S7+S6+S1+S3＝S3+S4+S6，∴S4＝S1+S7；故选：B．二．填空题11．解：连接EC，∵点D是BC的中点，∴△BED的面积＝△CED的面积，∵点F是CD的中点，∴△DEF的面积＝△FEC的面积，∴△BED的面积＝2×△DEF的面积，∵△BEF的面积为6，∴△BDE的面积为4，∵点E是AD的中点，∴△BEA的面积＝△BDE的面积＝4，∴△BDA的面积为8，∵点D是BC的中点，∴△ABC的面积＝2△ABD的面积＝16，故答案为：16．12．解：根据题意得，DE＝AB＝8；设BE＝CF＝x，∵CG∥DF．∴EG＝8﹣2＝6；EG：GD＝EC：CF，即6：2＝EC：x，∴EC＝3x，∴EF＝EC+CF＝4x，∴S＝×4x×8＝16x；△EFDS＝×6×3x＝9x．△ECG∴S＝16x﹣9x＝35．阴影部分解得：x＝5．故答案为：5．13．解：延长EF至A，使AF＝EF＝4，连接AN，如图所示：则AE＝AF+EF＝8，∵F为MN边上的中点，∴FN＝FM，在△ANF和△EMF中，，∴△ANF≌△EMF（SAS），∴∠A＝∠MEF，AN＝EM＝6，∵AN＝6，AE＝8，EN＝10，∴AN2+AE2＝EN2，∴△AEN是直角三角形，∠A＝90°，∴∠MEF＝90°，∴△EMN的面积＝EM×EF＝×6×4＝12，故答案为：12．14．解：∵点D 是BC 的中点，∴AD 是△ABC 的中线，∴△ABD 的面积＝△ADC 的面积＝×△ABC 的面积，同理得：△AEF 的面积＝×△ABE 的面积＝×△ABD 的面积＝×△ABC 的面积＝＝2，△AEG 的面积＝2，△BCE 的面积＝×△ABC 的面积＝8，又∵FG 是△BCE 的中位线，∴△EFG 的面积＝×△BCE 的面积＝＝2，∴△AFG 的面积是2×3＝6，故答案为：6．15．解：∵D 、E 分别是△ABC 的边BC 和AC 的中点，∴S △ABC ＝2S △ADC又∵D 是△ABC 的边BC 的中点，S △ABC ＝24cm 2，∴S △DEC ＝S △ABC ＝6cm 2．故答案为：6cm 2．三．解答题16．解：（1）∵AF是△ABC的中线，∴BC＝2BF＝2CF，BF＝CF，∴△ABF和△ACF的面积相等，∵△AFC的面积为10，∴∠ABF的面积为10，∵AD＝4，∴＝10，∴BF＝5，∴BC＝2BF＝10；（2）∵AD是△ABC的高，∴∠ADC＝90°，∵∠DAE＝20°，∴∠AED＝180°﹣90°﹣20°＝70°，∵∠C＝30°，∴∠CAE＝∠AED﹣∠C＝40°，∵AE是△ABC的角平分线，∴∠BAC＝2∠CAE＝80°，∴∠B＝180°﹣∠BAC﹣∠C＝180°﹣80°﹣30°＝70°．17．解：（1）∵|a+3|+＝0，∴a+3＝0，5﹣b＝0，∴a ＝﹣3，b ＝5，∴点A （﹣3，0），点B （5，0）．又∵点C （0，3），∴AB ＝|﹣3﹣5|＝8，CO ＝3，∴S △ABC ＝AB •CO ＝×8×3＝12；（2）设点M 的坐标为（x ，0），则AM ＝|x ﹣（﹣3）|＝|x +3|， 又∵S △ACM ＝S △ABC ，∴AM •OC ＝×12，∴|x +3|×3＝3，∴|x +3|＝2，即x +3＝±2，解得：x ＝﹣1或﹣5，故点M 的坐标为（﹣1，0）或（﹣5，0）．18．解：（1）∵|a ﹣2|+（b ﹣3）2+＝0， 又∵|a ﹣2|≥0，（b ﹣3）2≥0，≥0，∴a ＝2，b ＝3，c ＝4，∴A （0，2）B （3，0）C （6，4）．（2）S △ABC ＝4×6﹣×2×3﹣×2×6﹣×3×4＝9（3）设P（0，m），由题意：×|m﹣2|×6＝9，∴m＝5或﹣1，P（0，﹣1）或（0，5）19．解：（1）∵AE⊥BC，AE＝4，△ABC的面积为24，∴×BC×AE＝24，∴×BC×4＝24，∴BC＝12，∵AD是△ABC的中线，∴CD＝BC＝6；（2）①∠BAC＝180°﹣∠B﹣∠C＝180°﹣35°﹣65°＝80°∵AD平分∠BAC，∴∠BAD＝∠BAC＝40°，∵AE⊥BC，∴∠AEB＝90°，∴∠BAE＝90°﹣∠B＝55°，∴∠DAE＝∠BAE﹣∠BAD＝55°﹣40°＝15°；②由①可得：∠DAE＝∠BAE﹣∠BAD＝90°﹣∠B﹣（180°﹣∠B﹣∠C）＝（∠C﹣∠B）＝10°，故答案为：10．20．解：（1）有图2可知E点的速度为3，∴y＝×3x×AD＝9x，即y＝9x（0＜x≤2）．（2）当E点停止后，BE＝6，∴x＝，2时，y＝9×2＝18．∴△ABE的面积是18cm2．21/ 21。

第二单元 多边形的面积三角形的面积练习课教学内容：课本第11-13页、教学目标：1、进一步理解和掌握三角形的面积计算方法，并能正确、灵活地运用公式解决有关三角形的面积计算的实际问题，正确率达到80℅以上。

2、通过独立完成、小组合作等多种形式进行练习，注重数据与图形、图形与图形之间的联系，注重解题后的反思和总结。

3、培养学生的对应思想、有序思考、逻辑判断等思维品质。

教学重点：进一步理解和运用三角形面积的计算方法。

教学难点：三角形底与高的对应关系，图形之间的内在联系，基本数量关系的分析。

教学准备：课件教学过程：一、回顾知识，夯实基础。

（预设8分钟）1、计算练习。

（第10题）25×12÷2 122×8÷225×（12÷2） 122×（8÷2）这节课，我们对三角形面积计算进行练习。

计算时采用男女生比赛。

提问：你有什么发现？用自己的语言或字母表示出来。

2．不计算直接列式求下面三角形的面积。

定制别墅施工详细问题了解下！32单位：厘米回忆三角形面积计算公式。

→提醒：第三幅图，你为什么会上当？怎么改就可以了？→点拨：在选择数据时要注意什么？3、量一量、再计算。

（1）量出每个三角形的底和高，算出它们的面积。

（第12题）（2）量出红领巾的底和高，（取整厘米数），算出它的面积。

（第15题）提示：量的时候要量哪些数据？（取整厘米数）导学单：时间3分钟（1）组长分工，1人负责把红领巾的边拉直，1人度量，1人记录。

（2）想一想，可以怎样量出红领巾的高？（3）计算红领巾的面积。

小组围绕导学单展开测量活动，再算出红领巾的面积。

二、变式练习，优化结构（预设11分钟）1、画一画。

（第11题）你能利用方格纸画出面积为9平方厘米的三角形吗？（一个格子的面积是1平方厘米），画完后请把底和高的长度标出来。

2、汇报交流画法。

和同桌说说你是怎么画的？总结写出公式，加以还原：三角形的面积=底×高÷2底×高=三角形的面积×2=9×2=18提醒：分析学生列举的几种方法。

初三求三角形面积的练习题三角形的面积是初中数学中重要的概念之一，也是学生在几何学习中需要掌握的基础内容。

通过解决一些求三角形面积的练习题，能够帮助初三学生巩固和应用所学的知识。

本文将从简单到复杂，逐步介绍几个具体的求三角形面积的练习题。

一、求等边三角形的面积首先，让我们解决一个简单的问题：如何求等边三角形的面积呢？假设等边三角形的边长为a，则根据等边三角形的性质，它的高也是a，将等边三角形分为两个等边直角三角形，很容易得出每个等边直角三角形的面积为：S = (a * a) / 2因此，等边三角形的面积就是两个等边直角三角形的面积之和：S = 2 * [(a * a) / 2] = a^2二、求任意三角形的面积接下来，我们来解决一个稍微复杂一些的问题：如何求任意三角形的面积呢？对于任意三角形，我们可以利用海伦公式来求解。

海伦公式表示为：S = √[p * (p - a) * (p - b) * (p - c)]其中，p表示三角形的半周长，即p = (a + b + c) / 2a、b、c分别表示三角形的三条边的长度。

通过海伦公式，我们可以求得任意三角形的面积。

三、求特殊三角形的面积在解决练习题时，我们可能会遇到特殊的三角形，例如直角三角形、等腰三角形等。

下面，我们就来讨论如何求解这些特殊三角形的面积。

1. 求直角三角形的面积对于直角三角形，我们可以利用直角边的长度来求解面积。

假设直角边分别为a和b，斜边为c，则直角三角形的面积为：S = (a * b) / 22. 求等腰三角形的面积对于等腰三角形，我们可以利用底边和高来求解面积。

假设等腰三角形的底边长度为a，高为h，则等腰三角形的面积为：S = (a * h) / 23. 求等边三角形的面积前面已经介绍了等边三角形的面积计算方法。

练习题一：已知等边三角形的边长为5cm，求其面积。

解：根据前面的解析，我们知道等边三角形的面积就是边长的平方，因此所求面积为：S = 5^2 = 25cm^2练习题二：已知三角形的三边分别为3cm、4cm和5cm，求其面积。

二次函数中三角形面积问题真题训练（解析版）一．解答题（共15小题）1．如图，抛物线y＝a（x﹣2）2﹣2与y轴交于点A（0，2），顶点为B．（1）求该抛物线的解析式；（2）若点P（t，y1），Q（t+3，y2）都在抛物线上，且y1＝y2，求P，Q两点的坐标；（3）在（2）的条件下，若点C是线段QB上一动点，经过点C的直线y＝﹣x+m与y轴交于点D，连接DQ，DB，求△BDQ面积的最大值和最小值．【解答】解：（1）将A（0，2）代入到抛物线解析式中，得，4a﹣2＝2，解得，a＝1，∴抛物线解析式为y＝（x﹣2）2﹣2；（2）∵y1＝y2，∴（t﹣2）2﹣2＝（t+3﹣2）2﹣2，解得，，∴P（），Q；（3）由题可得，顶点B为（2，﹣2），将直线y＝﹣x+m进行平移，当直线经过B点时，﹣2＝2+m，解得m＝0，当直线经过点Q时，，解得m＝，∵经过点C直线y＝﹣x+m与y轴交于点D，∴D为（0，m），∵点C是线段QB上一动点，∴，延长QB交y轴于点E，设直线QB的解析式为y＝kx+b，入点Q、B坐标得，，解得，∴QB的解析式为：，令x＝0，则y＝﹣5，∴E（0，﹣5），由图可得，S△BDQ＝S△DEQ﹣S△DEB，∴＝，∵，∴当m＝0时，S△BDQ最小值为，当m＝时，S△BDQ最大值为．2．如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于A、B两点（点A在点B左侧），交y轴正半轴于点C，M为BC中点，点P为抛物线上一动点，已知点A坐标（﹣1，0），且OB＝2OC＝4OA．（1）求抛物线的解析式；（2）当△PCM≌△POM时，求PM的长；（3）当4S△ABC＝5S△BCP时，求点P的坐标．【解答】解：（1）∵A（﹣1，0），∴OA＝1，又∵OB＝2OC＝4OA，∴OC＝2，OB＝4，∴B（4，0），C（0，2），∵点B，点C，点A在抛物线上，∴解得：，、∴抛物线解析式为：；（2）连接OM，∵M为BC中点，∴M（2，1），∵△PCM≌△POM，∴CM＝OM，PC＝PO，∴MP是OC的垂直平分线，∴PM∥x轴，∴点P的纵坐标为1，当y＝1时，代入，解得：，∴或，∴PM＝或；（3）∵S△ABC＝×AB×OC＝5，4S△ABC＝5S△BCP，∴S△BCP＝4，∵B（4，0），C（0，2），∴直线BC解析式为y＝﹣x+2，当点P在BC上方时，如图2，过点P作PE⊥x轴，交BC于点E，设点P（p，﹣p2+p+2），则点E（p，﹣p+2），∴PE＝﹣p2+2p，∴4＝×4×（﹣p2+2p），∴p＝2，∴点P（2，3）；当点P在BC下方时，如图3，过点P作PE⊥x轴，交BC于点E，∴PE＝p2﹣2p，∴4＝×4×（p2﹣2p），∴p＝2±2，∴点P或；综上，点P的坐标为：（2，3）或或．3．如图1，抛物线y＝﹣x2+bx+c过点A（﹣1，0），点B（3，0），与y轴交于点C．在x轴上有一动点E（m，0）（0＜m＜3），过点E作直线l⊥x轴，交抛物线于点M．（1）求抛物线的解析式及C点坐标；（2）当m＝1时，D是直线l上的点且在第一象限内，若△ACD是以∠DCA为底角的等腰三角形，求点D的坐标；（3）如图2，连接BM并延长交y轴于点N，连接AM，OM，设△AEM的面积为S1，△MON的面积为S2，若S1＝2S2，求m的值．【解答】解：（1）将点A、B的坐标代入抛物线表达式得，解得，故抛物线的表达式为y＝﹣x2+2x+3，当x＝0时，y＝3，故点C（0，3）；（2）当m＝1时，点E（1，0），设点D的坐标为（1，a），由点A、C、D的坐标得，AC＝＝，同理可得：AD＝，CD ＝，①当CD＝AD时，即＝，解得a＝1；②当AC＝AD时，同理可得a＝（舍去负值）；故点D的坐标为（1，1）或（1，）；（3）∵E（m，0），则设点M（m，﹣m2+2m+3），设直线BM的表达式为y＝sx+t，则，解得，故直线BM的表达式为y＝（﹣m﹣1）x+3m+3，当x＝0时，y＝3m+3，故点N（0，3m+3），则ON＝3m+3；S1＝AE×y M＝×（m+1）×（﹣m2+2m+3），2S2＝ON•x M＝（3m+3）×m＝S1＝×（m+1）×（﹣m2+2m+3），解得m＝﹣2±或﹣1（舍去负值），故m＝﹣2．4．如图，抛物线过点A（0，1）和C，顶点为D，直线AC与抛物线的对称轴BD的交点为B（，0），平行于y轴的直线EF与抛物线交于点E，与直线AC交于点F，点F的横坐标为，四边形BDEF为平行四边形．（1）求点F的坐标及抛物线的解析式；（2）若点P为抛物线上的动点，且在直线AC上方，当△P AB面积最大时，求点P的坐标及△P AB面积的最大值；（3）在抛物线的对称轴上取一点Q，同时在抛物线上取一点R，使以AC为一边且以A，C，Q，R为顶点的四边形为平行四边形，求点Q和点R的坐标．【解答】解：（1）设抛物线的解析式为y＝ax2+bx+c（a≠0），∵A（0，1），B（，0），设直线AB的解析式为y＝kx+m，∴，解得，∴直线AB的解析式为y＝﹣x+1，∵点F的横坐标为，∴F点纵坐标为﹣+1＝﹣，∴F点的坐标为（，﹣），又∵点A在抛物线上，∴c＝1，对称轴为：x＝﹣，∴b＝﹣2a，∴解析式化为：y＝ax2﹣2ax+1，∵四边形DBFE为平行四边形．∴BD＝EF，∴﹣3a+1＝a﹣8a+1﹣（﹣），解得a＝﹣1，∴抛物线的解析式为y＝﹣x2+2x+1；（2）设P（n，﹣n2+2n+1），作PP'⊥x轴交AC于点P'，则P'（n，﹣n+1），∴PP'＝﹣n2+n，S△ABP＝OB•PP'＝﹣n＝﹣+，∴当n＝时，△ABP的面积最大为，此时P（，）．（3）∵，∴x＝0或x＝，∴C（，﹣），设Q（，m），①当AQ为对角线时，∴R（﹣），∵R在抛物线y＝+4上，∴m+＝﹣+4，解得m＝﹣，∴Q，R；②当AR为对角线时，∴R（），∵R在抛物线y＝+4上，∴m﹣+4，解得m＝﹣10，∴Q（，﹣10），R（）．综上所述，Q，R；或Q（，﹣10），R（）．5．二次函数y＝ax2+bx+3的图象与x轴交于A（2，0），B（6，0）两点，与y轴交于点C，顶点为E．．（1）求这个二次函数的表达式，并写出点E的坐标；（2）如图①，D是该二次函数图象的对称轴上一个动点，当BD的垂直平分线恰好经过点C时，求点D的坐标；（3）如图②，P是该二次函数图象上的一个动点，连接OP，取OP中点Q，连接QC，QE，CE，当△CEQ的面积为12时，求点P的坐标．【解答】解：（1）将A（2，0），B（6，0）代入y＝ax2+bx+3，得，解得∴二次函数的解析式为y＝﹣2x+3．∵y＝﹣1，∴E（4，﹣1）．（2）如图1，图2，连接CB，CD，由点C在线段BD的垂直平分线CN上，得CB＝CD．设D（4，m），∵C（0，3），由勾股定理可得：42+（m﹣3）2＝62+32．解得m＝3±．∴满足条件的点D的坐标为（4，3+）或．（3）如图3，设CQ交抛物线的对称轴于点M，设P（n，﹣2n+3），则Q（），设直线CQ的解析式为y＝kx+3，则nk+3．解得k＝，于是CQ：y＝（）x+3，当x＝4时，y＝4（）+3＝n﹣5﹣，∴M（4，n﹣5﹣），ME＝n﹣4﹣．∵S△CQE＝S△CEM+S△QEM＝．∴n2﹣4n﹣60＝0，解得n＝10或n＝﹣6，当n＝10时，P（10，8），当n＝﹣6时，P（﹣6，24）．综合以上可得，满足条件的点P的坐标为（10，8）或（﹣6，24）．6．如图，抛物线经过点A（﹣3，0）、B（1，0）、C（0，3）．（1）求抛物线的解析式；（2）点P（m，n）是抛物线上的动点，当﹣3＜m＜0时，试确定m的值，使得△P AC的面积最大；（3）抛物线上是否存在不同于点B的点D，满足DA2﹣DC2＝6，若存在，请求出点D的坐标；若不存在，请说明理由．【解答】解：（1）由题意可以假设抛物线的解析式为y＝a（x+3）（x﹣1），把C（0，3）代入，可得a＝﹣1，∴抛物线的解析式为y＝﹣x2﹣2x+3．（2）设直线AC的解析式为y＝kx+b，将A（﹣3，0），C（0，3）代入得到，解得，∴直线AC的解析式为y＝x+3．当﹣3＜m＜0时，点P（m，n）在直线AC的上方，过点P作x轴的垂线交AC于Q．则P （m，﹣m2﹣2m+3），Q（m，m+3），∴PQ＝﹣m2﹣2m+3﹣（m+3）＝﹣m2﹣3m＝﹣（m+）2+，∵﹣3＜m＜0，∴当m＝﹣时，PQ的值最大，此时S△P AC＝•PQ•AO＝PQ最大，∴m＝﹣．（3）由A（﹣3，0），B（1，0），C（0，3），可得AB＝4，OB＝1，OC＝3，∵BC2＝10，∠CAO＝45°，∴BA2﹣BC2＝6，连接BC，过点B作AC的垂线交抛物线于D，交AC于H，连接AD，DC，则∠AHB＝90°，∠DBA＝∠CAO＝45°，∴DA2﹣DC2＝HA2﹣HC2＝AB2﹣BC2＝6，∵∠CAO＝∠DBA，∴点H在AB的垂直平分线上，即点H在抛物线的对称轴x＝﹣1上，∴点D与点C关于抛物线的对称轴x＝﹣1对称，∵C（0，3），∴点D的坐标为（﹣2，3）．7．如图，在直角坐标系中，四边形OABC是平行四边形，经过A（﹣2，0），B，C三点的抛物线y＝ax2+bx+（a＜0）与x轴的另一个交点为D，其顶点为M，对称轴与x轴交于点E．（1）求这条抛物线对应的函数表达式；（2）已知R是抛物线上的点，使得△ADR的面积是▱OABC的面积的，求点R的坐标；（3）已知P是抛物线对称轴上的点，满足在直线MD上存在唯一的点Q，使得∠PQE＝45°，求点P的坐标．【解答】解：（1）OA＝2＝BC，故函数的对称轴为x＝1，则x＝﹣＝1①，将点A的坐标代入抛物线表达式得：0＝4a﹣2b+②，联立①②并解得，故抛物线的表达式为：y＝﹣x2+x+③；（2）∵y＝﹣x2+x+＝﹣（x﹣1）2+3，∴抛物线的顶点M（1，3）令y＝0，可得x＝﹣2或4，∴点D（4，0）；∵△ADR的面积是▱OABC的面积的，∴×AD×|y R|＝×OA×OB，则×6×|y R|＝×2×，解得：y R＝±④，联立④③并解得或，故点R的坐标为（1+，﹣）或（1，﹣）或（1，）或（1﹣，）；（3）（Ⅰ）当点Q在MD之间时，作△PEQ的外接圆R，∵∠PQE＝45°，故∠PRE＝90°，则△PER为等腰直角三角形，当在直线MD上存在唯一的点Q时，圆R与直线MD相切，∵点M、D的坐标分别为（1，3）、（4，0），则ME＝3，ED＝4﹣1＝3，则MD＝3，过点R作RH⊥ME于点H，设点P（1，2m），则PH＝HE＝HR＝m，则圆R的半径为m，则点R（1+m，m），S△MED＝S△MRD+S△MRE+S△DRE，即×EM•ED＝×MD•RQ×ED•y R+×ME•RH，∴×3×3＝×3×m+×3×m×3×m，解得：m＝，故点P（1，）；（Ⅱ）当点Q与点D重合时，由点M、E、D的坐标知，ME＝ED，即∠MDE＝45°；①当点P在x轴上方时，当点P与点M重合时，此时∠PQE＝45°，此时点P（1，3），②当点P在x轴下方时，同理可得：点P（1，﹣3），综上，点P的坐标为（1，）或（1，3）或（1，﹣3）．8．如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于点A，B，与y轴交于点C．且直线y＝x﹣6过点B，与y轴交于点D，点C与点D关于x轴对称，点P是线段OB 上一动点，过点P作x轴的垂线交抛物线于点M，交直线BD于点N．（1）求抛物线的函数解析式；（2）当△MDB的面积最大时，求点P的坐标；（3）在（2）的条件下，在y轴上是否存在点Q，使得以Q，M，N三点为顶点的三角形是直角三角形？若存在，直接写出点Q的坐标；若不存在，说明理由．【解答】解：（1）令y＝0，得y＝x﹣6＝0，解得x＝6，∴B（6，0），令x＝0，得y＝x﹣6＝﹣6，∴D（0，﹣6），∵点C与点D关于x轴对称，∴C（0，6），把B、C点坐标代入y＝﹣x2+bx+c中，得，解得，，∴抛物线的解析式为：y＝﹣x2+5x+6；（2）设P（m，0），则M（m，﹣m2+5m+6），N（m，m﹣6），则MN＝﹣m2+4m+12，∴△MDB的面积＝＝﹣3m2+12m+36＝﹣3（m﹣2）2+48，∵﹣3＜0，∴当m＝2时，△MDB的面积最大，此时，P点的坐标为（2，0）；（3）由（2）知，M（2，12），N（2，﹣4），当∠QMN＝90°时，QM∥x轴，则Q（0，12）；当∠MNQ＝90°时，NQ∥x轴，则Q（0，﹣4）；当∠MQN＝90°时，设Q（0，n），则QM2+QN2＝MN2，即4+（12﹣n）2+4+（n+4）2＝（12+4）2，解得，n＝4±2，∴Q（0，4+2）或（0，4﹣2）．综上，存在以Q，M，N三点为顶点的三角形是直角三角形．其Q点坐标为（0，12）或（0，﹣4）或（0，4+2）或（0，4﹣2）．9．如图所示，拋物线y＝ax2+bx+c（a≠0）与x轴交于A、B两点，与y轴交于点C，且点A的坐标为A（﹣2，0），点C的坐标为C（0，6），对称轴为直线x＝1．点D是抛物线上一个动点，设点D的横坐标为m（1＜m＜4），连接AC，BC，DC，DB．（1）求抛物线的函数表达式；（2）当△BCD的面积等于△AOC的面积的时，求m的值；（3）在（2）的条件下，若点M是x轴上一动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形．若存在，请直接写出点M的坐标；若不存在，请说明理由．【解答】解：（1）由题意得：，解得：，∴抛物线的函数表达式为：y＝﹣x2+x+6；（2）过点D作DE⊥x轴于E，交BC于G，过点C作CF⊥ED交ED的延长线于F，如图1所示：∵点A的坐标为（﹣2，0），点C的坐标为（0，6），∴OA＝2，OC＝6，∴S△AOC＝OA•OC＝×2×6＝6，∴S△BCD＝S△AOC＝×6＝，当y＝0时，﹣x2+x+6＝0，解得：x1＝﹣2，x2＝4，∴点B的坐标为（4，0），设直线BC的函数表达式为：y＝kx+n，则，解得：，∴直线BC的函数表达式为：y＝﹣x+6，∵点D的横坐标为m（1＜m＜4），∴点D的坐标为：（m，﹣m2+m+6），点G的坐标为：（m，﹣m+6），∴DG＝﹣m2+m+6﹣（﹣m+6）＝﹣m2+3m，CF＝m，BE＝4﹣m，∴S△BCD＝S△CDG+S△BDG＝DG•CF+DG•BE＝DG×（CF+BE）＝×（﹣m2+3m）×（m+4﹣m）＝﹣m2+6m，∴﹣m2+6m＝，解得：m1＝1（不合题意舍去），m2＝3，∴m的值为3；（3）由（2）得：m＝3，﹣m2+m+6＝﹣×32+×3+6＝，∴点D的坐标为：（3，），分三种情况讨论：①当DB为对角线时，如图2所示：∵四边形BDNM是平行四边形，∴DN∥BM，∴DN∥x轴，∴点D与点N关于直线x＝1对称，∴N（﹣1，），∴DN＝3﹣（﹣1）＝4，∴BM＝4，∵B（4，0），∴M（8，0）；②当DM为对角线时，如图3所示：由①得：N（﹣1，），DN＝4，∵四边形BDNM是平行四边形，∴DN＝BM＝4，∵B（4，0），∴M（0，0）；③当DN为对角线时，∵四边形BDNM是平行四边形，∴DM＝BN，DM∥BN，∴∠DMB＝∠MBN，∴点D与点N的纵坐标互为相反数，∵点D（3，），∴点N的纵坐标为：﹣，将y＝﹣代入y＝﹣x2+x+6中，得：﹣x2+x+6＝﹣，解得：x1＝1+，x2＝1﹣，当x＝1+时，如图4所示：则N（1+，﹣），分别过点D、N作x轴的垂线，垂足分别为E、Q，在Rt△DEM和Rt△NQB中，，∴Rt△DEM≌Rt△NQB（HL），∴BQ＝EM，∵BQ＝1+﹣4＝﹣3，∴EM＝﹣3，∵E（3，0），∴M（，0）；当x＝1﹣时，如图5所示：则N（1﹣，﹣），同理得点M（﹣，0）；综上所述，点M的坐标为（8，0）或（0，0）或（，0）或（﹣，0）．10．如图所示，抛物线y＝x2﹣2x﹣3与x轴相交于A、B两点，与y轴相交于点C，点M为抛物线的顶点．（1）求点C及顶点M的坐标．（2）若点N是第四象限内抛物线上的一个动点，连接BN、CN，求△BCN面积的最大值及此时点N的坐标．（3）若点D是抛物线对称轴上的动点，点G是抛物线上的动点，是否存在以点B、C、D、G为顶点的四边形是平行四边形．若存在，求出点G的坐标；若不存在，试说明理由．（4）直线CM交x轴于点E，若点P是线段EM上的一个动点，是否存在以点P、E、O为顶点的三角形与△ABC相似．若存在，求出点P的坐标；若不存在，请说明理由．【解答】解：（1）令y＝x2﹣2x﹣3中x＝0，此时y＝﹣3，故C点坐标为（0，﹣3），又∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴抛物线的顶点M的坐标为（1，﹣4）；（2）过N点作x轴的垂线交直线BC于Q点，连接BN，CN，如图1所示：令y＝x2﹣2x﹣3＝0，解得：x＝3或x＝﹣1，∴B（3，0），A（﹣1，0），设直线BC的解析式为：y＝ax+b，将C（0，﹣3），B（3，0）代入直线BC的解析式得：，解得：，∴直线BC的解析式为：y＝x﹣3，设N点坐标为（n，n2﹣2n﹣3），故Q点坐标为（n，n﹣3），其中0＜n＜3，则＝＝，（其中x Q，x C，x B分别表示Q，C，B三点的横坐标），且QN＝（n﹣3）﹣（n2﹣2n﹣3）＝﹣n2+3n，x B﹣x C＝3，故，其中0＜n＜3，当时，S△BCN有最大值为，此时点N的坐标为（），（3）设D点坐标为（1，t），G点坐标为（m，m2﹣2m﹣3），且B（3，0），C（0，﹣3）分情况讨论：①当DG为对角线时，则另一对角线是BC，由中点坐标公式可知：线段DG的中点坐标为，即，线段BC的中点坐标为，即，此时DG的中点与BC的中点为同一个点，∴，解得，经检验，此时四边形DCGB为平行四边形，此时G坐标为（2，﹣3）；②当DB为对角线时，则另一对角线是GC，由中点坐标公式可知：线段DB的中点坐标为，即，线段GC的中点坐标为，即，此时DB的中点与GC的中点为同一个点，∴，解得，经检验，此时四边形DCBG为平行四边形，此时G坐标为（4，5）；③当DC为对角线时，则另一对角线是GB，由中点坐标公式可知：线段DC的中点坐标为，即，线段GB的中点坐标为，即，此时DC的中点与GB的中点为同一个点，∴，解得，经检验，此时四边形DGCB为平行四边形，此时G坐标为（﹣2，5）；综上所述，G点坐标存在，为（2，﹣3）或（4，5）或（﹣2，5）；（4）连接AC，OP，如图2所示：设MC的解析式为：y＝kx+m，将C（0，﹣3），M（1，﹣4）代入MC的解析式得：，解得：∴MC的解析式为：y＝﹣x﹣3，令y＝0，则x＝﹣3，∴E点坐标为（﹣3，0），∴OE＝OB＝3，且OC⊥BE，∴CE＝CB，∴∠CBE＝∠E，设P（x，﹣x﹣3），又∵P点在线段EC上，∴﹣3＜x＜0，则，，由题意知：△PEO相似于△ABC，分情况讨论：①△PEO∽△CBA，∴，∴，解得，满足﹣3＜x＜0，此时P的坐标为；②△PEO∽△ABC，∴，∴，解得x＝﹣1，满足﹣3＜x＜0，此时P的坐标为（﹣1，﹣2）．综上所述，P点的坐标为或（﹣1，﹣2）．11．如图，直线y＝﹣2x+10分别与x轴，y轴交于A，B两点，点C为OB的中点，抛物线y＝x2+bx+c经过A，C两点．（1）求抛物线的函数表达式；（2）点D是直线AB下方的抛物线上的一点，且△ABD的面积为，求点D的坐标；（3）点P为抛物线上一点，若△APB是以AB为直角边的直角三角形，求点P到抛物线的对称轴的距离．【解答】解：（1）直线y＝﹣2x+10中，令x＝0，则y＝10，令y＝0，则x＝5，∴A（5，0），B（0，10），∵点C是OB中点，∴C（0，5），将A和C代入抛物线y＝x2+bx+c中，，解得：，∴抛物线表达式为：y＝x2﹣6x+5；（2）联立：，解得：或，∴直线AB与抛物线交于点（﹣1，12）和（5，0），∵点D是直线AB下方抛物线上的一点，设D（m，m2﹣6m+5），∴﹣1＜m＜5，过点D作DE⊥x轴，交直线AB于点E，∴E（m，﹣2m+10），∴DE＝﹣2m+10﹣m2+6m﹣5＝﹣m2+4m+5，∴S△ABD＝＝＝，解得：m＝2，∴点D的坐标为（2，﹣3）；（3）抛物线表达式为：y＝x2﹣6x+5，∵△APB是以AB为直角边的直角三角形，设点P（n，n2﹣6n+5），∵A（5，0），B（0，10），∴AP2＝（n﹣5）2+（n2﹣6n+5）2，BP2＝n2+（n2﹣6n+5﹣10）2，AB2＝125，当点A为直角顶点时，BP2＝AB2+AP2，解得：n＝或5（舍），当点B为直角顶点时，AP2＝AB2+BP2，解得：n＝或，而抛物线对称轴为直线x＝3，则3﹣＝，﹣3＝，3﹣＝，综上：点P到抛物线对称轴的距离为：或或．12．如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣2交x轴于A，B两点，交y轴于点C，且OA＝2OC＝8OB．点P是第三象限内抛物线上的一动点．（1）求此抛物线的表达式；（2）若PC∥AB，求点P的坐标；（3）连接AC，求△P AC面积的最大值及此时点P的坐标．【解答】解：（1）抛物线y＝ax2+bx﹣2，则c＝﹣2，故OC＝2，而OA＝2OC＝8OB，则OA＝4，OB＝，故点A、B、C的坐标分别为（﹣4，0）、（，0）、（0，﹣2）；则y＝a（x+4）（x﹣）＝a（x2+x﹣2）＝ax2+bx﹣2，故a＝1，故抛物线的表达式为：y＝x2+x﹣2；（2）抛物线的对称轴为x＝﹣，当PC∥AB时，点P、C的纵坐标相同，根据函数的对称性得点P（﹣，﹣2）；（3）过点P作PH∥y轴交AC于点H，设P（x，x2+﹣2），由点A、C的坐标得，直线AC的表达式为：y＝﹣x﹣2，则△P AC的面积S＝S△PHA+S△PHC＝PH×OA＝×4×（﹣x﹣2﹣x2﹣x+2）＝﹣2（x+2）2+8，∵﹣2＜0，∴S有最大值，当x＝﹣2时，S的最大值为8，此时点P（﹣2，﹣5）．13．已知抛物线y＝ax2+bx+c与x轴交于A（﹣1，0），B（5，0）两点，C为抛物线的顶点，抛物线的对称轴交x轴于点D，连接BC，且tan∠CBD＝，如图所示．（1）求抛物线的解析式；（2）设P是抛物线的对称轴上的一个动点．①过点P作x轴的平行线交线段BC于点E，过点E作EF⊥PE交抛物线于点F，连接FB、FC，求△BCF的面积的最大值；②连接PB，求PC+PB的最小值．【解答】解：（1）根据题意，可设抛物线的解析式为：y＝a（x+1）（x﹣5），∵抛物线的对称轴为直线x＝2，∴D（2，0），又∵＝，∴CD＝BD•tan∠CBD＝4，即C（2，4），代入抛物线的解析式，得4＝a（2+1）（2﹣5），解得，∴二次函数的解析式为＝﹣x2++；（2）①设P（2，t），其中0＜t＜4，设直线BC的解析式为y＝kx+b，∴，解得即直线BC的解析式为，令y＝t，得：，∴点E（5﹣t，t），把代入，得，即，∴，∴△BCF的面积＝×EF×BD＝（t﹣）＝，∴当t＝2时，△BCF的面积最大，且最大值为；②如图，据图形的对称性可知∠ACD＝∠BCD，AC＝BC＝5，∴，过点P作PG⊥AC于G，则在Rt△PCG中，，∴，过点B作BH⊥AC于点H，则PG+PB≥BH，∴线段BH的长就是的最小值，∵，又∵，∴，即，∴的最小值为．14．如图，已知抛物线y＝ax2+bx+6经过两点A（﹣1，0），B（3，0），C是抛物线与y轴的交点．（1）求抛物线的解析式；（2）点P（m，n）在平面直角坐标系第一象限内的抛物线上运动，设△PBC的面积为S，求S关于m的函数表达式（指出自变量m的取值范围）和S的最大值；（3）点M在抛物线上运动，点N在y轴上运动，是否存在点M、点N使得∠CMN＝90°，且△CMN与△OBC相似，如果存在，请求出点M和点N的坐标．【解答】解：（1）将A（﹣1，0）、B（3，0）代入y＝ax2+bx+6，得：，解得：，∴抛物线的解析式为y＝﹣2x2+4x+6．（2）过点P作PF∥y轴，交BC于点F，如图1所示．当x＝0时，y＝﹣2x2+4x+6＝6，∴点C的坐标为（0，6）．设直线BC的解析式为y＝kx+c，将B（3，0）、C（0，6）代入y＝kx+c，得：，解得：，∴直线BC的解析式为y＝﹣2x+6．∵点P（m，n）在平面直角坐标系第一象限内的抛物线上运动，∴点P的坐标为（m，﹣2m2+4m+6），则点F的坐标为（m，﹣2m+6），∴PF＝﹣2m2+4m+6﹣（﹣2m+6）＝﹣2m2+6m，∴S＝PF•OB＝﹣3m2+9m＝﹣3（m﹣）2+，∴当m＝时，△PBC面积取最大值，最大值为．∵点P（m，n）在平面直角坐标系第一象限内的抛物线上运动，∴0＜m＜3．综上所述，S关于m的函数表达式为＝﹣3m2+9m（0＜m＜3），S的最大值为．（3）存在点M、点N使得∠CMN＝90°，且△CMN与△OBC相似．如图2，∠CMN＝90°，当点M位于点C上方，过点M作MD⊥y轴于点D，∵∠CDM＝∠CMN＝90°，∠DCM＝∠NCM，∴△MCD∽△NCM，若△CMN与△OBC相似，则△MCD与△OBC相似，设M（a，﹣2a2+4a+6），C（0，6），∴DC＝﹣2a2+4a，DM＝a，当时，△COB∽△CDM∽△CMN，∴，解得，a＝1，∴M（1，8），此时ND＝DM＝，∴N（0，），当时，△COB∽△MDC∽△NMC，∴，解得a＝，∴M（，），此时N（0，）．如图3，当点M位于点C的下方，过点M作ME⊥y轴于点E，设M（a，﹣2a2+4a+6），C（0，6），∴EC＝2a2﹣4a，EM＝a，同理可得：或＝2，△CMN与△OBC相似，解得a＝或a＝3，∴M（，）或M（3，0），此时N点坐标为（0，）或（0，﹣）．综合以上得，存在M（1，8），N（0，）或M（，），N（0，）或M（，），N（0，）或M（3，0），N（0，﹣），使得∠CMN＝90°，且△CMN与△OBC相似．15．如图，抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），点B（3，0），与y轴交于点C，且过点D（2，﹣3）．点P、Q是抛物线y＝ax2+bx+c上的动点．（1）求抛物线的解析式；（2）当点P在直线OD下方时，求△POD面积的最大值．（3）直线OQ与线段BC相交于点E，当△OBE与△ABC相似时，求点Q的坐标．【解答】解：（1）函数的表达式为：y＝a（x+1）（x﹣3），将点D坐标代入上式并解得：a＝1，故抛物线的表达式为：y＝x2﹣2x﹣3…①；（2）设直线PD与y轴交于点G，设点P（m，m2﹣2m﹣3），将点P、D的坐标代入一次函数表达式：y＝sx+t并解得：直线PD的表达式为：y＝mx﹣3﹣2m，则OG＝3+2m，S△POD＝×OG（x D﹣x P）＝（3+2m）（2﹣m）＝﹣m2+m+3，∵﹣1＜0，故S△POD有最大值，当m＝时，其最大值为；（3）∵OB＝OC＝3，∴∠OCB＝∠OBC＝45°，∵∠ABC＝∠OBE，故△OBE与△ABC相似时，分为两种情况：①当∠ACB＝∠BOQ时，AB＝4，BC＝3，AC＝，过点A作AH⊥BC于点H，S△ABC＝×AH×BC＝AB×OC，解得：AH＝2，则sin∠ACB＝＝，则tan∠ACB＝2，则直线OQ的表达式为：y＝﹣2x…②，联立①②并解得：x＝或﹣，故点Q（，﹣2）或（﹣，2），②∠BAC＝∠BOQ时，tan∠BAC＝＝3＝tan∠BOQ，则点Q（n，﹣3n），则直线OQ的表达式为：y＝﹣3x…③，联立①③并解得：x＝，故点Q（，）或（，）；综上，当△OBE与△ABC相似时，Q的坐标为：（，﹣2）或（，）．（﹣，2），（，）．。

2021年中考复习数学分类专题提分训练：三角形的面积（三）1．如图，△ABC 中，∠C ＝90°，AC ＝12，BC ＝9，AB ＝15，若动点P 从点C 开始，按C →A →B →C 的路径运动，且速度为每秒3个单位，设运动的时间为t 秒．（1）当t ＝ 时，CP 把△ABC 的面积分成相等的两部分；（2）当t ＝5时，CP 把△ABC 分成的两部分面积之比是S △APC ：S △BPC ＝（3）当t ＝ 时，△BPC 的面积为18．2．在直角坐标系中，已知A （2，5），B （4，2）．（1）在直角坐标系中描出上面各点；（2）求△OAB 的面积．3．在平面直角坐标系中，A （a ，0），B （b ，0），C （﹣1，2），且|3a +2b |+＝0（1）求ab的值；（2）在y轴上是否存在一点M，使△COM的面积为△ABC面积的，求出点M的坐标．4．如图，线段AB的长为5，CA⊥AB于点A，DB⊥AB于点B，且AC＝2，DB＝1，点P为线段AB上的一个动点，连结CP，DP．（1）若AP＝a，请用含a的代数式表示BP；（2）当AP＝1时，求△ACP与△BPD的面积之比；（3）若C，D是同一平面内的两点，连结CD，若点P以每秒1个单位的速度从点A向点B运动，设运动时间为t秒，当t为何值时，△PCD的面积等于3．5．如图①，在△ABC中，AD是三角形的高，且AD＝6cm，E是一个动点，由B向C移动，其速度与时间的变化关系如图②，已知BC＝8cm．（1）求当E点在运动过程中△ABE的面积y与运动时间x之间的关系式；（2）当E点停止后，求△ABE的面积．6．如图，有一时钟，时针OA长为6cm，分针OB长为8cm，△OAB随着时间的变化不停地改变形状．求：（1）13点时，△OAB的面积是多少？（2）14点时，△OAB的面积比13点时增大了还是减少了？为什么？（3）问多少整点时，△OAB的面积最大？最大面积是多少？请说明理由．（4）设∠BOA＝α（0°≤α≤180°），试归纳α变化时△OAB的面积有何变化规律（不证明）7．在Rt△ABC中，∠ACB＝90°，△ABC的面积为10，设AC＝x，BC＝y （1）求y与x之间的函数关系式；（2）令x+y＝m，①当m＝12时，求△ABC的周长；②求m的最小值．8．如图，已知：D ，E 分别是△ABC 的边BC 和边AC 的中点，连接DE ，AD ，若S △ABC ＝24cm 2，求△DEC 的面积．9．请阅读材料，并完成相应的任务．已知点D 在△ABC 的边BC 上（点D 不与点B ，C 重合），点P 是AD 上任意一点，连接BP ，CP ．如图1，若＝，显然有S △ABP ＝S △ACP ．如图2，若＝，那么S △ABP 与S △ACP 之间的数量关系又是怎样的呢？下面是小李同学的部分求解过程：如图3，作BM ⊥AD 的延长线于点M ，作CN ⊥AD 于点N ．∴∠BMD ＝∠CND ＝90°．在△BMD 和△CND 中，∵∠BMD ＝∠CND ，∠BDM ＝∠CDN ，∴△BMD ～△CND ．…（1）请把小李同学的求解过程补充完整．（2）猜想：＝，则S △ABP 与S △ACP 之间的数量关系是 ．10．如图，在四边形ABCD中，对角线AC与BD相交于P，请添加一个条件，使四边形ABCD＝AC•BD，并说明理由．的面积为：S四边形ABCD解：添加的条件：理由：。

2021中考复习数学考点专项训练——专题十三：三角形一、填空题1．建高楼常需要塔吊来吊建筑材料，而塔吊的上部是三角形结构，请你说说这样做的依据是____________________．2．已知三角形的两条边长分别为3cm和2cm，如果这个三角形的第三条边长为奇数，则这个三角形的周长为cm．3．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3＝4．如图，在中，，，，则________ ．5．如图，在中，，，，若，连结BM，则BM的长是____________．6．如图，点B，C，E，F在同一直线上，AB∥DC，DE∥GF，∠B＝∠F＝72°，则∠D＝________．7．如图，已知边长为1的正方形ABCD，AC，BD交于点O，过点O任作一条直线分别交AD，BC于点E，F，则阴影部分的面积是________．8．如图，已知四边形ABCD中，AC平分∠BAD，CE⊥AB于点E，且AE＝12(AB＋AD)，若∠D＝115°，则∠B＝________．二、选择题1．如图，△ABC的中线AD、BE相交于点F，若△ABF的面积是4，则四边形FDCE的面积是（）A．4 B．4.5 C．3.5 D．52．在△ABC中，，则△ABC为（）A．等腰直角三角形B．有60°角的直角三角形C．等边三角形D．顶角为120°的等腰三角形3．现有3 cm，4 cm，7 cm，9 cm长的四根木棒，任取其中三根组成一个三角形，那么可以组成的三角形的个数是( )A．1 B．2 C．3 D．44．根据下列已知条件，能画出唯一一个．．．．△ABC的是( )A．AB＝1，BC＝6，AC＝8 B．AB＝4，BC＝3，∠A＝30°C．∠A＝40°，∠B＝45°，AB＝4 D．∠A＝90°，∠B＝30°，∠C＝60°5.如图，已知△ABC中，∠ABC＝45°，F是高AD和BE的交点，CD＝4，则线段DF的长度为（）A．3 B．4 C．5 D．61 6.如图，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，∠EAF＝2∠BAD，若DF＝1，BE＝5，则线段EF的长为（）A．3 B．4 C．5 D．67．下列的正方形网格中，小正方形的边长均为1，如图放置，点，，都在格点上，则的值为（）．A．B．C．D．8．如图，小明为了测量照母山上“览星塔”的高度，先从与塔底中心在同一水平面上的点出发，沿着坡度为的斜坡行走10米至坡顶处，再从处沿水平方向继续前行若干米后至点处，在点测得塔顶的仰角为，塔底的俯角为，与的水平距离为4米（图中、、、、、在同一平面内，、和、、分别在同一水平线上），根据小明的测量数据，计算出“览星塔”的高度约为（计算结果精确到0.1米，参考数据：，，）（）A．17.8米B．23.7米C．31.5米D．37.4米9．如图，在正方形ABCD中．以AD、AB为斜边分别向外和向内作Rt△ADN和Rt△ABM，且满足AN=AM，连接MN交AD于点T．若DC=4，tan∠ABM=，则AT的长为（）A．1 B．C．D．10．如图，AD∥BC，AB∥CD，AC，BD交于O点，过O点的直线EF交AD于E点，交BC于F点，且BF＝DE，则图中的全等三角形共有( )A．6对 B．5对 C．3对 D．2对三、解答题1.已知如图，△ABC≌△ADE，∠B=30°，∠E=20°，∠BAE=105°，求∠BAC、∠DAC的度数.2.已知如图，E、F是AB上的两点，AE=BF，AC∥BD，且AC=DB求证：（1）CF=DE．（2）CF∥DE3.如图，B是CE的中点，AD=BC，AB=D C．DE交AB于F点求证：（1）AD∥BC（2）AF=BF4.如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF（1）求证：BG=CF（2）请你判断BE+CF与EF的大小关系，并说明理由。