推断统计案例

高维数据统计推断方法高维数据统计推断方法是一种处理多维数据的统计学技术，可以从大规模、复杂的数据集中提取有用信息并进行推断分析。

它在许多领域，如机器学习、数据挖掘、模式识别等中都有广泛的应用。

本文将介绍高维数据统计推断方法的基本原理、常用技术和应用案例。

1. 高维数据的特点高维数据是指包含大量维度的数据，每个维度都代表一个变量或特征。

与低维数据相比，高维数据具有以下特点：(1) 维度爆炸：随着维度的增加，数据空间呈指数级增长，导致数据稀疏性的增加。

(2) 维度相关性：高维空间中的数据点之间存在较高的相关性，使得数据处理和分析变得更加复杂。

(3) 噪声问题：高维数据中存在大量的噪声，对于准确的统计推断造成了挑战。

2. 高维数据统计推断方法的原理高维数据统计推断方法通过对数据进行降维、特征选择和模型建立等步骤来实现统计分析。

常用的方法包括：(1) 主成分分析(PCA)：通过线性变换将原始数据映射到低维空间，保留最大方差的主成分，从而实现数据降维。

(2) 奇异值分解(SVD)：将原始数据矩阵分解为三个矩阵的乘积，从而找到数据的最佳近似表示，减小维度的同时保留重要信息。

(3) 稳健统计方法：通过引入鲁棒性测量，对高维数据中的异常值和噪声进行抵抗，提高统计推断的准确性和稳定性。

(4) 压缩感知理论：利用样本稀疏性的特点，对高维数据进行压缩表示，减少数据存储和计算开销。

(5) 高斯图模型：利用图模型描述高维数据中的变量之间的关系，进行概率推断和参数估计。

3. 高维数据统计推断方法的应用案例高维数据统计推断方法在各个领域都有广泛的应用。

以下是几个常见的应用案例：(1) 生物信息学：通过对基因芯片数据、基因组数据等高维数据的统计推断，可以识别基因表达模式、发现基因关联关系等，进而揭示生物学过程的机制。

(2) 健康医疗：利用高维数据统计推断方法，可以从大规模的医疗数据中挖掘患者的疾病风险、预测疾病发展等，为个性化医疗提供支持。

一、概述在统计学中，假设检验是一种常用的推断性统计方法，用于判断样本数据的特征是否符合某种假设条件。

bootstrap假设检验是一种基于重复抽样的非参数检验方法，相较于传统假设检验方法，其具有更广泛的适用范围和更强的鲁棒性。

本文将通过一个具体的案例来介绍bootstrap假设检验的应用和实现方法，并探讨其在实际数据分析中的价值和意义。

二、案例背景假设有一个电商评台A和一个电商评台B，它们分别在同一时间段内进行了一次促销活动，目的是比较两个评台的促销效果是否存在显著差异。

对于这个问题，我们可以使用bootstrap假设检验来进行分析，以确定两个评台的促销效果是否存在统计学上的显著差异。

三、数据收集为了进行bootstrap假设检验，我们首先需要收集来自两个电商评台的促销活动数据，包括参与活动的用户数量、用户下单金额等相关信息。

这些数据可以从两个评台的后台数据库中获取，或者通过统计分析工具来进行数据采集和整理。

四、假设设定在进行假设检验前，我们需要明确研究问题的假设设定。

针对本案例，我们可以进行如下假设设定：- 零假设H0：电商评台A和电商评台B的促销效果没有显著差异。

- 备择假设H1：电商评台A和电商评台B的促销效果存在显著差异。

五、bootstrap抽样在进行bootstrap假设检验时，我们首先需要进行重复抽样。

具体来说，我们可以从两个电商评台的促销活动数据中随机抽取一定数量的样本，然后利用这些样本数据来构建抽样分布。

重复这个过程多次，得到多个抽样分布。

六、统计量计算在得到多个抽样分布之后，我们需要计算统计量以进行假设检验。

对于本案例，可以选择比较两个评台的用户下单金额的平均值作为统计量，计算两个抽样分布的差异。

七、bootstrap假设检验我们可以进行bootstrap假设检验，以判断零假设H0的拒绝与否。

具体来说，可以计算出抽样分布中比真实观测值更特殊的概率，若该概率小于显著性水平（通常设定为0.05），则可以拒绝零假设，认为两个评台的促销效果存在显著差异；反之，则接受零假设。

论文写作中的常见统计分析方法及应用引言统计分析是论文写作中不可缺少的环节。

通过运用统计分析方法，研究人员可以对数据进行整理、解读和预测，从而最终得出可靠的结论。

本文将介绍一些常见的统计分析方法，并讨论它们在论文写作中的应用。

一、描述统计分析描述统计分析是研究人员对数据进行整理、总结和表达的方法。

以下是常见的描述统计分析方法：1. 频数分析：统计数据集中各个取值出现的次数。

通过频数分析，我们可以了解到数据的分布情况以及不同取值的频率。

2. 中心趋势分析：包括均值、中位数和众数等。

均值是指所有数据值的平均数，中位数是将数据从小到大排列后的中间值，众数是出现频率最高的数值。

3. 变异性分析：用来描述数据的离散程度。

常见的指标有标准差、方差和极差。

标准差越大，数据的离散程度越大。

4. 相关性分析：主要用于研究两个或多个变量之间的关系。

常用的方法包括相关系数和散点图。

相关系数可以表示两个变量之间的线性相关程度。

二、推断统计分析推断统计分析是通过对样本数据的分析，得出总体特征或总体参数的估计和推断，从而对研究问题进行回答。

以下是常见的推断统计分析方法：1. 样本检验：用于检验样本与总体之间差异的统计方法。

例如，我们可以使用t检验来判断两个样本的均值是否有显著差异。

2. 方差分析：用于比较不同样本组之间的均值是否存在显著差异。

方差分析常用于多个样本组的比较。

3. 回归分析：通过建立数学模型，研究自变量与因变量之间的关系。

回归分析可以用于预测和解释数据。

4. 生存分析：主要用于研究事件发生的概率和时间。

生存分析常用于医学、生物学和社会科学等领域的研究。

三、应用案例统计分析方法在不同学科领域的论文中都有广泛的应用。

以下是一些实际案例：1. 医学研究：医学研究中经常使用统计分析方法来比较不同药物的疗效、评估治疗方案的有效性等。

2. 社会科学研究：社会学、心理学等社会科学领域的研究中，常用统计分析方法来研究人群特征、社会现象等。

统计学案例分析范文统计学是一门利用数理统计方法研究数据的科学，通过收集、整理、描述和分析数据来推断和判断问题的方法和原理。

统计学在各种领域中都有广泛的应用，包括经济、生物学、医学和社会科学等。

在本文中，我们将以一个统计学案例分析为例，展示统计学在实际问题中的应用。

假设我们要研究一些小镇的居民收入情况，我们希望了解居民的平均收入水平，并通过统计学方法验证我们的假设。

我们采用简单随机抽样的方式，从该小镇的居民中选取一定数量的样本。

首先，我们需要确定抽样大小。

根据统计学原理，较大的样本容量可以提高估计的准确度。

因此，我们决定选择抽取500个样本。

然后，我们使用简单随机抽样方法从抽样框架中选取样本。

简单随机抽样是指每个个体都有相等的机会被选入样本。

在本例中，我们可以使用随机数表来选择样本，或者使用计算机生成随机数。

假设我们使用计算机生成随机数，我们将生成500个随机数，代表样本的编号。

然后，我们从抽样框架中选择对应编号的个体作为样本。

在得到样本后，我们需要进行数据收集。

在本例中，我们需要收集每个样本的收入数据。

为了确保数据的准确性，我们可以要求样本回答一个有关收入的调查问卷，或者使用其他适当的方式进行数据收集。

收集数据后，我们需要进行统计分析。

最常见的统计学描述方法是计算平均值。

在本例中，我们可以计算选取样本的平均收入，作为对整个小镇居民平均收入的估计。

此外，我们还可以计算样本的方差，作为对小镇居民收入的变异程度的估计。

当我们得到估计值后，我们需要进行推论统计分析，以验证我们的假设。

一个常用的方法是进行假设检验。

假设检验允许我们根据样本数据推断总体参数的信息。

在本例中，我们可以假设小镇居民的平均收入为其中一特定值，然后使用统计学方法来确定该假设的接受或拒绝程度。

如果我们拒绝了假设，我们可以得出结论，即小镇居民的平均收入与所假设的值不同。

最后，我们需要对结果进行解释和报告。

我们可以使用图表、表格和文字来展示和解释我们的数据分析结果。

统计学案例总量指标与相对指标案例1：指出下面的统计分析报告摘要错在哪里？并改正：1、本厂按计划规定，第一季度的单位产品成本应比去年同期降低10%，实际执行结果是，单位产品成本较去年同期降低8%，仅完成产品成本计划的80%（即8%÷10%＝80%）。

2、本厂的劳动生产率（按全部职工计算）计划在去年的基础上提高8%，计划执行结果仅提高4%，劳动生产率的计划任务仅实现一半（即4%÷8%＝50%）。

3、该车间今年1月份生产老产品的同时，新产品首次小批投产，出现了2件废品(按计算，车间废品率为1.2%)。

2月份老产品下马，新产品大批投产，全部制品1000件，其中废品8件，废品量是1月份的4倍，因此产品质量下降了。

4、在组织生产中，本厂先进小组向另一组提出高产优质的挑战竞赛。

本月先进小组的产量超过了另一小组的1倍，但是在两组废品总量中该组却占了60%，所以在产品质量方面，先进小组明显地落后了。

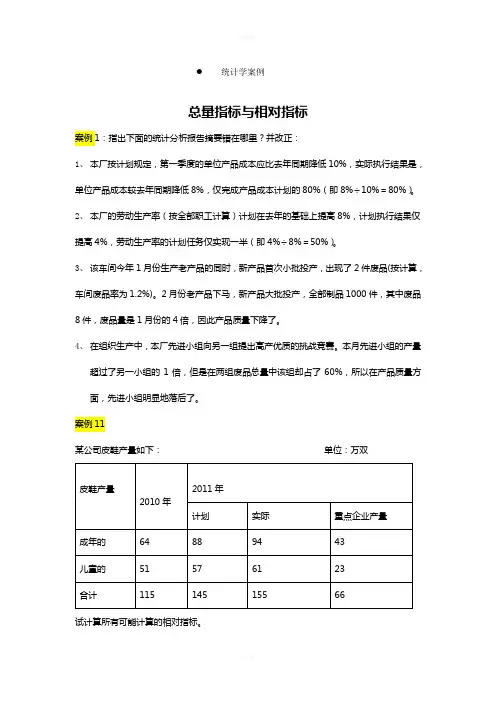
案例11某公司皮鞋产量如下：单位：万双试计算所有可能计算的相对指标。

案例2：根据下表资料分析哪个企业对社会贡献更大？上缴税金情况表平均指标与变异指标根据上表资料分析哪个村成绩更好？为什么？案例4：某单位有10个人，其中1人月工资为10万元，9人每人月工资为1000元。

该单位职工月平均工资为10900元。

即：)(109001091000100000元=⨯+你认为这个平均数有代表性吗？如果缺乏代表性应如何改正？案例5：以下是各单位统计分析报告的摘录1、 本局所属30个工厂，本月完成生产计划的情况是不一致的。

完成计划90%的有3个，完成96%的有5个，完成102%的有10个，完成110%的有8个，完成120%的有4个。

平均全局生产计划完成程度为104.33%。

即：304%1208%11010%1025%963%90⨯+⨯+⨯+⨯+⨯＝104.33％2、 本厂开展增产节约运动以后，产品成本月月下降，取得显著的成绩，根据财务部门的报告，1 月份开支总成本15000元，平均单位产品成本为15元，2月份开支总成本25000元，平均单位产品成本下降为10元，3月份开支总成本45000元，平均单位产品成本仅8元。

统计学研究报告分析案例引言统计学是一门研究数据收集、分析和解释的学科。

在研究领域中，统计方法被广泛应用于数据分析和决策制定。

本文以某研究机构进行的一项关于消费者购买行为的统计学研究报告为案例进行分析。

背景该研究报告旨在了解消费者在购买某电子产品时的决策因素和购买意愿。

研究机构通过在不同地区选择了一定数量的受访者，并设计了一份问卷调查，以收集有关消费者购买行为的数据。

在收集到足够的样本后，研究机构对数据进行了统计学分析，并将结果整理成报告。

方法研究机构使用了随机抽样的方法，选择了来自不同地区的1000名消费者作为受访者。

问卷包括了关于消费者个人信息、购买偏好和购买决策的问题。

在收集到问卷数据后，研究机构对数据进行了整理、清洗和编码。

然后，应用统计学方法对数据进行了描述性统计和推断统计分析。

结果描述性统计分析在对问卷中的个人信息问题进行描述性统计时，发现约占调查对象总数28%的受访者年龄在18-25岁之间，占据了受访者的最大比例。

而男性和女性受访者的比例相对均衡，分别占调查对象总数的52%和48%。

此外，大部分受访者在教育程度上具备大学本科或以上的学历。

在购买行为方面，分析结果显示，大多数受访者的购买决策受到产品质量、价格和品牌声誉等因素的共同影响。

此外，在线评价和媒体广告也对一部分受访者的购买决策产生一定的影响。

在购买偏好方面，统计结果表明，受访者更愿意购买具备先进技术和多功能性的电子产品。

推断统计分析为了对调查结果进行推断统计分析，研究机构使用了卡方检验和回归分析等方法。

卡方检验的结果表明，消费者的购买决策与年龄、性别和教育程度之间存在显著的相关性。

回归分析则进一步揭示了购买决策因素与购买意愿之间的关联。

例如，产品质量、价格和品牌声誉被发现对购买意愿有较大的正向影响。

除了以上的统计分析，研究机构还对调查结果进行了可视化处理，通过绘制柱状图和饼图等图表，使得数据更加直观和易于理解。

结论通过对统计学研究报告的分析，可以得出以下结论：1.统计数据表明，年龄、性别和教育程度是影响消费者购买行为的重要因素。

案例分析—四格表确切概率法【例1-5】为比较中西药治疗急性心肌梗塞的疗效，某医师将27例急性心肌梗塞患者随机分成两组，分别给予中药和西药治疗，结果见表1-4。

经检验，得连续性校正χ2=3.134，P＞0.05，差异无统计学意义，故认为中西药治疗急性心肌梗塞的疗效基本相同。

表1-4 两种药物治疗急性心肌梗塞的疗效比较药物有效无效合计有效率（％）中药12（9.33）2（4.67）1485.7西药 6（8.67）7（4.33）1346.2合计1892766.7【问题1-5】（1）这是什么资料？（2）该资料属于何种设计方案？（3）该医师统计方法是否正确？为什么？【分析】(1) 该资料是按中西药的治疗结果（有效、无效）分类的计数资料。

(2) 27例患者随机分配到中药组和西药组，属于完全随机设计方案。

(3) 患者总例数n=27＜40，该医师用χ2检验是不正确的。

当n＜40或T＜1时，不宜计算χ2值，需采用四格表确切概率法（exact probabilities in 2×2 table）直接计算概率案例分析－卡方检验（一）【例1-1】某医师为比较中药和西药治疗胃炎的疗效，随机抽取140例胃炎患者分成中药组和西药组，结果中药组治疗80例，有效64例，西药组治疗60例，有效35例。

该医师采用成组t检验（有效=1，无效=0）进行假设检验，结果t＝2.848，P＝0.005，差异有统计学意义检验（有效=1，无效=0）进行进行假设检验，结果t＝2.848，P＝0.005，差异有统计学意义，故认为中西药治疗胃炎的疗效有差别，中药疗效高于西药。

【问题1-1】（1）这是什么资料？（2）该资料属于何种设计方案？（3）该医师统计方法是否正确？为什么？（4）该资料应该用何种统计方法？【分析】(1) 该资料是按中西药疗效（有效、无效）分类的二分类资料，即计数资料。

(2) 随机抽取140例胃炎患者分成西药组和中药组，属于完全随机设计方案。

统计推断基本原理与实际案例统计推断是基于已有的样本数据对总体进行推断和判断的一种方法。

它是统计学中非常重要的一个分支，可以通过对样本数据进行分析和计算，得出对总体特征的合理估计和结论。

本文将介绍统计推断的基本原理，并通过实际案例来加深对这一概念的理解。

一、统计推断的基本原理统计推断的基本原理包括抽样、假设检验和置信区间估计。

1. 抽样抽样是指从总体中选取一部分样本来进行数据收集和分析。

通过合理的抽样方法，可以使样本具有代表性，从而基于样本的分析结果可以推广到整个总体。

常见的抽样方法有简单随机抽样、系统抽样和分层抽样等。

2. 假设检验假设检验是统计推断中的一种方法，用于对总体参数的假设进行检验。

假设检验包括设定原假设（H0）和备择假设（Ha），并利用样本数据对两者进行比较和判断。

通过计算得到的统计量与临界值进行比较，来确定是否拒绝原假设。

3. 置信区间估计置信区间估计是一种对总体参数进行估计的方法。

通过计算出一个区间范围，可以使这个区间以一定的概率包含总体参数的真实值。

置信区间的计算方法主要依赖于样本数据的分布和样本容量。

二、统计推断的实际案例下面将通过一个实际案例来说明统计推断的应用。

假设某电商平台在推出新产品后，希望了解用户在使用新产品后的满意度水平。

为此，平台进行了一项调研，并随机抽取了300名用户，并要求他们填写满意度调查问卷，满分为10分。

现在需要利用这300个样本数据来对总体的满意度水平进行统计推断。

首先，根据抽样原理，我们可以认为这300名用户的样本具有代表总体的特征。

接下来，我们可以利用假设检验和置信区间估计来对总体的满意度水平进行推断。

假设检验的步骤如下：1. 建立原假设和备择假设。

原假设H0认为总体的满意度平均值为μ0，备择假设Ha认为总体的满意度平均值不等于μ0。

2. 计算样本的满意度平均值x和标准差s。

3. 计算统计量t，其中t=(x-μ0) / (s/√n)，n为样本容量。

毕业论文写作中的统计分析案例在毕业论文写作中，统计分析案例是一种非常重要的方法，可以帮助研究者得出准确的结论，并支持研究的目的和假设。

本文将以一个虚拟的案例来说明如何运用统计分析方法进行毕业论文写作。

引言在本次研究中，我们将通过统计分析方法探讨某公司员工的工作满意度与其绩效之间的关系。

通过统计分析，我们可以找出是否有相关性存在，以及这种相关性的程度。

这将对公司管理层提供决策方向和参考依据。

数据收集首先，我们需要收集相关数据以进行统计分析。

我们从目标公司的员工数据库中获取了500名员工的工作满意度和其绩效评分。

工作满意度采用1到10的评分进行衡量，绩效评分则使用0到100的评分体系。

这些数据将作为我们进行统计分析的样本。

描述统计分析我们将首先进行描述统计分析，以便更好地理解我们的样本数据。

描述统计分析可以提供样本的中心趋势、离散程度、分布形态等信息。

中心趋势我们计算了工作满意度和绩效评分的均值、中位数和众数，以了解其中的中心趋势。

根据计算结果，工作满意度的均值为7.2，中位数为7，众数为8；而绩效评分的均值为75，中位数为76，众数为80。

这些数值可以帮助我们了解样本中的典型情况。

离散程度通过计算标准差和范围，我们可以了解样本数据的离散程度。

工作满意度的标准差为1.5，范围为1到10；而绩效评分的标准差为15，范围为30到100。

这些数值可以帮助我们判断数据的变化幅度，并了解样本的一致性。

分布形态为了了解数据的分布形态，我们可以画出工作满意度和绩效评分的频率分布直方图。

从直方图中可以判断数据是否呈正态分布或偏态分布。

此外，我们还可以通过绘制箱线图来观察数据是否存在离群值。

推断统计分析在描述统计分析的基础上，我们还需要进行推断统计分析，以便推断出总体的特征并进行显著性检验。

相关性分析我们将使用相关分析方法来探讨工作满意度和绩效评分之间的相关性。

通过计算相关系数（如皮尔逊相关系数），我们可以了解两个变量之间的线性关系强度。

任务八 抽样推断任务描述与分析在A市自来水公司的客户满意度调查中，我们抽样调查了A市自来水公司的700个客户，从前面的调查分析中我们了解到这700户客户对A市自来水公司的产品和服务等方面的评价。

现在你需要思考的是：这700户客户的意见能在多大程度上反映所有客户的意见？误差的可能性有多大？为了保证调查的准确性，我们是否需要再追加调查？任务分析（1）如何判断我们抽样调查的700个客户够不够？（2）根据抽调客户的意见我们如何推断出所有客户的意见？（3）被调查客户的意见与所有客户的意见误差有多少？案例8-1：为了加强与顾客的沟通，深入了解客户需求，以解决客户遇到的问题，并在此基础上持续改进公司的产品质量，进一步优化供水服务，A市自来水公司决定进行客户满意度调查，要求在2个月时间内完成调查报告。

A市共有自来水用户200万户，在短短两个月时间内必须完成客户调查并出具调查报告，你如何完成这项工作？抽样调查抽样推断是按照随机原则从总体中抽取一部分总体单位作为样本单位，组成样本总体，并以样本的数量特征对总体的数量特征做出具有一定可靠程度的估计和推断的统计分析方法。

抽样推断具有以下特点：1．抽样推断是用样本指标值来估计总体指标值 2．抽样的随机原则是抽样推断的前提3．抽样推断的误差是可以事先计算并加以控制节省调查费调查速度快调查结果准确可靠应用范围广抽样调查抽样推断常用概念总体样本从总体中按照随机原则抽选出来的一部分单位称为样本，用n 表示 我们所要调查研究的事物或现象的全体，总体单位数通常用N表示总体指标样本指标总体指标又称参数，是反映总体数量特征的综合指标，总体指标主要有：总体平均数，总体方差σ 2，总体标准差σ、总体成数P 和Q。

样本指标又称统计量，是根据样本各单位的标志值或标志特征计算的、反映样本数量特征的综合指标。

样本指标主要有：样本平均数，样本方差s2，样本标准差s，样本成数p和q。

样本容量样本样本个数又称样本可能数目，是指在一个抽样方案中从总体中所有可能被抽取的样本总数。

参数估计与假设检验案例在统计学中，参数估计是一种通过对样本数据做出合理的推测来估计总体参数的方法。

假设检验则是一种基于样本数据进行统计推断的方法，用于判断对于一个总体的一些假设是否可接受。

为了更好地理解参数估计和假设检验的应用，我们可以考虑以下案例：假设我们是一家电商公司的数据分析师，想要评估一项新推出的增值服务是否对用户购买力有正面影响。

具体而言，我们想知道购买了增值服务的用户相对于没有购买的用户，在订单总金额上是否存在显著差异。

首先，我们需要建立两个假设：1.零假设（H0）：购买增值服务与订单总金额之间不存在显著差异；2.备择假设（H1）：购买增值服务与订单总金额之间存在显著差异。

接下来，我们需要进行参数估计。

假设我们从公司的数据库中随机抽取了两组用户数据：一组是购买了增值服务的用户，另一组是没有购买增值服务的用户。

我们从这两组用户中分别计算出了订单总金额的均值和标准差。

然后，我们可以使用参数估计的方法来估计总体订单总金额的均值差异。

具体而言，我们可以使用两个样本的均值差（例如，购买了增值服务的用户订单总金额的均值减去没有购买增值服务的用户订单总金额的均值）作为总体均值差的估计。

此外，我们还可以使用标准差来估计总体均值差的标准误差。

然后，我们可以进行假设检验。

我们使用一个统计量来评估观察到的样本均值差是否足够大，以至于我们可以拒绝零假设并接受备择假设。

在这种情况下，我们可以使用一个双侧t检验来进行假设检验。

假设我们设置了一个显著性水平（α）为0.05，即我们愿意承担5%的错误接受备择假设的风险。

然后，我们计算出双侧t检验的p值（即观察到的样本均值差在零假设下出现的概率）。

如果p值小于0.05，我们可以拒绝零假设，并得出结论：购买了增值服务的用户与没有购买的用户在订单总金额上存在显著差异。

最后，我们可以汇报我们的研究结果和结论。

我们可以得出结论：购买了增值服务的用户相对于没有购买的用户，在订单总金额上存在显著差异。

概率推断原理概率推断原理是统计学中的一个重要概念，它通过对已有数据的分析和推理，来推断未知的事件或结果的概率。

概率推断原理在各个领域都有着广泛的应用，如医学诊断、金融风险评估、天气预测等。

本文将从概率推断原理的基本概念、应用案例以及优缺点等方面进行探讨。

一、概率推断原理的基本概念概率推断原理是基于统计学的理论和方法，它通过收集和分析已有的数据，来推断未知事件或结果的概率。

在概率推断中，我们首先需要明确一个假设，然后通过已有的数据来判断这个假设的概率。

具体而言，概率推断原理有以下几个基本概念：1.1 似然函数似然函数是概率推断中的重要概念，它用来描述已知数据出现的概率。

通过似然函数，我们可以计算出已有数据出现的概率，从而进一步推断未知事件或结果的概率。

1.2 先验概率先验概率是指在考虑已有数据之前，我们对未知事件或结果的概率的主观估计。

通过先验概率，我们可以将主观估计与已有数据相结合，得出更准确的推断结果。

1.3 后验概率后验概率是指在考虑已有数据之后，我们对未知事件或结果的概率的估计。

通过后验概率，我们可以将已有数据的信息纳入考虑，得出更准确的推断结果。

二、概率推断原理的应用案例2.1 医学诊断概率推断原理在医学诊断中有着广泛的应用。

例如，在癌症检测中，医生可以通过已有的病例数据来推断一个病人是否患有癌症的概率。

通过计算似然函数、先验概率和后验概率，医生可以得出一个准确的诊断结果，并进一步制定治疗方案。

2.2 金融风险评估概率推断原理在金融风险评估中也有着重要的应用。

例如，在股票市场中，投资者可以通过已有的市场数据来推断某只股票的涨跌概率。

通过计算似然函数、先验概率和后验概率，投资者可以得出一个准确的风险评估结果，并做出相应的投资决策。

2.3 天气预测概率推断原理在天气预测中也有着广泛的应用。

例如，在气象预测中，气象学家可以通过已有的气象数据来推断未来几天的天气情况。

通过计算似然函数、先验概率和后验概率，气象学家可以得出一个准确的天气预测结果，并向公众发布相应的天气预警。