理想气体的热力过程
- 格式：ppt
- 大小：796.00 KB
- 文档页数：58
下载文档原格式
合集下载
理想气体的热力学过程
6
dV d p 0 V p
式中
Cp CV
, 在温度变化不很大时，可以看作常量。
将上式积分，得
ln V + ln p = 恒量
pV γ 恒量 或 这个关系称为泊松 (S.D.Poisson)公式。
根据泊松公式和理想气体物态方程, 可以分别得到
TV γ 1 恒量
T γ pγ 1 恒量
Qp = H 气 H水
= (2676.3103 419.06103 ) Jkg1
= 2257.2103 Jkg1
16
17
经绝热过程压缩气体做的功：
CV 20.44J mol K
1
1
m 4 A CV T2 T1 4.70 10 J M
在等压过程中，系统从外界获得的热量，一部分用 以增大内能，一部分用以对外作功。 三、等温过程 (isothermal process) 等温过程 特征: 过程方程: 系统的温度保持恒定的过程。 T=0
p1V1 p2V2
p p1
T=恒量
恒温热源
1(p1,V1,T)
过程曲线:
内能增量：
等温线为等轴双曲线。
=1.40，可得：
p2 T2 T1 p 1
1 /
1 300 50
0.286
98.0K
19
例6 一定质量的理想气体先后经历 P 两个绝热过程即1态到2态，3态到4
态(如图所示)且T1=T3、T2=T4，在 1态与3态，2态与4态之间可分别连 接 两 条 等 温 线 。 求 证 ：
考虑到 T1=T3，T2=T4，
T2 V1 1 2 T1 V2
《热力学》理想气体的热力过程
p2 p1
v1 v2
n
T2 T1
v1 v2
n1
T2 T1
p2 p1
(n1) / n
n lnp2 lnp1 lnv2 ln v1
(2)利用已知或可求的与n有关的能量求解
2020年10月20日
第四章 理想气体的热力过程
28
例4-3（p80） 有一台空气压缩机，压缩前空气的温度为27 ℃、 压力为0.1 MPa，气缸的容积为5 000 cm3；压缩后空气的温度升 高到213 ℃。压缩过程消耗的功为1.166 kJ。试求压缩过程的多变 指数n。
15
（2）图表法 由
ds
cp0
dT T
Rg
dp p
对可逆绝热过程可得
ln
p2 p1
1 Rg
T2
T1
c
p
0
dT T
A:利用热力性质表中的标准状态熵
ln
p2 p1
1 Rg
T1
T0
c
p
0
dT T
c T2
T0
p0
dT T
1 Rg
s0 T2
s0 T1
T2 工质的热力性质表中还提供了u与h的数值。
2020年10月20日
第四章 理想气体的热力过程
19
例4-2 (p76) 一台燃气轮机装置，从大气吸入温度为17 ℃、压 力为0.1 MPa的空气，然后在压气机中进行绝热压缩，使空气 的压力提高到0.9MPa。试求压气机消耗的轴功：(1)按定值比 热容计算；(2)按空气热力性质表计算。
思路：
定值比热容
2020年10月20日
第四章 理想气体的热力过程
14
变比热容分析
工程热力学第四章理想气体热力过程教案
第四章 理想气体的热力过程概 述热能⇔机械能的相互转化是靠工质在热力设备中吸热、膨胀、压缩等状态变化的过程来实现的，这个状态变化的过程就是热力过程，那么，在前面第一章研究的平衡状态，第二章研究理想气体的性质以及第三章研究分析开、闭口系热力状态变化的工具——热力学第一定律都是为这一章打基础。
前面第三章已提到过相同的工质在相同的温度下，不同的热力过程，能量转化的状况是不同的。
P V q q >，00v p w w ==膨技，，因此工程上实际过程多种多样、复杂、多变，不是可逆过程，据传递能量的工质不一不可能一一加以研究，何况逐个研究不总结规律性的知识用途也不大。
因此，我们仍采用热力学常用的方法，对复杂多样的热力过程进行合理化的假设。
认为是理想气体的可逆过程，这就是我们下面要研究的理想气体○V ○P ○T ○S 。
○P ：例如各种环热设备，工质一面流动一面被加热，流动中克服阻力的压力降与其压力相比小很多，故认为压力不变。
○V ：汽油机工作时，火花塞一点火，气缸内已被压缩的可燃混合气即燃烧，在一瞬间烧完，这期间气缸与外界无质量交换，活塞移动极微，可近似定容过程。
○T ：如往复式压气机，气体在气缸中被压缩时温度升高，为了省功气缸周围有冷却水套，若冷却效果好，气缸中温度几乎不变，可近似定温过程。
○S ：例气缸中燃烧产物在气缸中膨胀对外作功过程，由于工质与外界交换的热量很少可略去不计，认为是定熵过程。
上述过程实际上是略去次要因素后的一个等同特征，就是过程中有一个状态参数不变，对理想气体()u f t = ()h f t =这研究起来就方便很多，而且只有实际意义。
4—1 研究热力过程的目的及方法一． 目的1．实现预期的能量转化，合理安排热力过程，从而来提高功力装置的热经济性。
2．对确定的过程，也可预计热→功之多少。
二．解决的问题1．根据过程特点，寻找过程方程式 2．分析状态参数在过程中的变化规律3．确定热功转化的数量关系，及过程中,,u h s ∆∆∆的变化 4．在P —V ，T —S 图上直观地表示。
第四章 理想气体的热力过程
q12 0
w1 2 u1 u 2 cV 0 dT
2 1
ws h1 h2 c p 0 dT
2
1
4-6 多变过程 The Polytropic Process
各种热力过程，其过程方程式通常都可以表示为下述形式：
pv p v 常量
n n 1 1
前述的四种典型过程均为多变过程的一个特例： n=0→pv0=p=常量—定压过程； n=1→pv=常量—定温过程； n=κ→pvκ=常量—绝热过程； n=∞→ p1/nv= p0v= v=常量—定容过程. 多变过程在状态参数坐标图上的表示。
过程中能量转换关系 定温过程系统所作的容积变化功为：
p
Rg T v
p 2 v1 p1 v 2
w1 2
21Leabharlann v2 p1 pdv Rg T1 ln Rg T1 ln v1 p2
稳定流动的开口系统，若其工质的流动动能和重力位能的变 化可以忽略不计，则按定温过程方程式，定温过程中系统所 作的轴功为：
n 1 1
pv n p1 v1n 常量
v p p1 ( 1 ) n v
1 ( p1v1 p 2 v 2 ) n 1 Rg (T1 T2 ) n 1
多变过程的热量： The heat of the polytropic process:
q1 2 u 2 u1 pdv
1 2
cV 0 (T2 T1 )
Rg n 1
(T2 T1 )
即
q12 cV 0
n (T2 T1 ) n 1
按比热与热量之间的关系，上式可写为
q12 c n (T2 T1 )
工程热力学第四章理想气体热力过程
详细描述
03
CHAPTER
等容过程
等容过程是指气体在变化的整个过程中，其容积保持不变的过程。
定义
特点
适用场景
气体在等容过程中，气体温度和压力会发生变化，但容积保持不变。
等容过程常用于高压、高温或低温等极端条件下的气体处理。
03
02
01
等容过程定义
在等容过程中，气体吸收的热量等于气体所做的功和气体温度升高所吸收的热量之和。
多变过程的具体形式取决于气体所经历的压力和温度的变化规律。
多变过程定义热力学第一定律 Nhomakorabea热力学第二定律
理想气体状态方程
热效率
多变过程的热力学计算
01
02
03
04
能量守恒定律，用于计算多变过程中气体吸收或释放的热量。
熵增原理，用于分析多变过程中气体熵的变化。
描述气体压力、体积和温度之间的关系，可用于多变过程的计算。
衡量多变过程能量转换效率的指标，通过比较输入和输出的热量来计算。
提高热效率的方法
优化多变过程参数，如压力和温度的变化规律，以减少不可逆损失和提高能量转换效率。
热效率与熵增的关系
根据熵增原理，不可逆过程会导致熵的增加，从而降低热效率。因此，减少不可逆损失是提高多变过程热效率的关键。
热效率计算公式
$eta = frac{Q_{out}}{Q_{in}}$，其中$Q_{out}$为输出热量，$Q_{in}$为输入热量。
计算公式
通过优化气体的初态和终态，以及选择合适的加热和冷却方式，可以提高等容过程的热效率。同时，也可以通过改进设备结构和操作方式来提高热效率。
提高热效率的方法
等容过程的热效率
04
CHAPTER
03
CHAPTER
等容过程
等容过程是指气体在变化的整个过程中，其容积保持不变的过程。
定义
特点
适用场景
气体在等容过程中，气体温度和压力会发生变化，但容积保持不变。
等容过程常用于高压、高温或低温等极端条件下的气体处理。
03
02
01
等容过程定义
在等容过程中，气体吸收的热量等于气体所做的功和气体温度升高所吸收的热量之和。
多变过程的具体形式取决于气体所经历的压力和温度的变化规律。
多变过程定义热力学第一定律 Nhomakorabea热力学第二定律
理想气体状态方程
热效率
多变过程的热力学计算
01
02
03
04
能量守恒定律，用于计算多变过程中气体吸收或释放的热量。
熵增原理，用于分析多变过程中气体熵的变化。
描述气体压力、体积和温度之间的关系，可用于多变过程的计算。
衡量多变过程能量转换效率的指标，通过比较输入和输出的热量来计算。
提高热效率的方法
优化多变过程参数，如压力和温度的变化规律，以减少不可逆损失和提高能量转换效率。
热效率与熵增的关系
根据熵增原理，不可逆过程会导致熵的增加，从而降低热效率。因此，减少不可逆损失是提高多变过程热效率的关键。
热效率计算公式
$eta = frac{Q_{out}}{Q_{in}}$，其中$Q_{out}$为输出热量，$Q_{in}$为输入热量。
计算公式
通过优化气体的初态和终态，以及选择合适的加热和冷却方式，可以提高等容过程的热效率。同时，也可以通过改进设备结构和操作方式来提高热效率。
提高热效率的方法
等容过程的热效率
04
CHAPTER
第三章__理想气体热力性质及过程
容积成分： i
Vi V
， i
1
摩尔成分： xi
ni n
， xi
1
换算关系：
i xi
i
xi M i xi M i
xi M i M eq
xi Rg,eq Rg ,i
，
xi
i Rg,i
Rg ,e q
分压力的确定：
由
piV=ni RT PVi=ni RT
ppi V Vi i ,
2
u 1 cVdT
如果取定值比热或平均比热，又可简化为
二、焓
ucVT
也可由热Ⅰ导得 d h(cVRg)dT cpdT
同理，有
2
h 1 cpdT
hcpT
结论：理想气体的u、h 均是温度的单值函数。
三、 熵变的计算
由可逆过程
ds du pd
T
ds du
cp
Rg 1
三、 真实比热容、平均比热容和定值比热容
1. 真实比热容（精确，但计算繁琐）
cpa0a 1 Ta2T2a3 T3
c V (a 0 R g) a 1 T a 2 T 2 a 3 T 3
qp
2 1
cpdt
2
q 1 cdt
2. 平均比热容（精确、简便）
cV
ln
T2 T1
Rg
ln
2 1
s
c
p
ln
T2 T1
Rg
ln
p2 p1
s
c
p
ln
2 1
cV
ln
p2 p1
第四章 理想气体的热力过程
k pv RT isentropic (3) 当 n = k pv const s C
p
T
cn cn 0
cn cv
s
v
(4) 当 n = p isochoric v const v C
1 n
理想气体 p 过程的p-v,T-s图
T dT ( )p ? cp ds
T2
已知p1,T1,T2 , 求p2 若是空气，查附表2
p2 p1exp
s s
0 T2
0 T1
R
理想气体 s u, h, s,的计算
状态参数的变化与过程无关 内能变化 焓变化 熵变化
u cv dT
h cp dT
s 0
理想气体 s w,wt ,q的计算
膨胀功 w
h>0 q>0 u> 0 p w>0
q Tds
T
qw
T
h>0 u>0
n0
n 1 wt>0
w>0
n0
wt>0
n
n 1
nk
n
q>0
nk
v
s
u,h,w,wt,q在p-v,T-s图上的变化趋势
u,h↑(T↑) w↑(v↑) wt↑(p↓) q↑(s↑) h>0 q>0 u> 0 T p w>0 w>0 n 0 h>0 u>0
q0
4-6 理想气体热力过程综合分析
一、过程线分布规律
顺时针方向n增大
二、过程特性和过程中能量传递的方向
u在p-v,T-s图上的变化趋势
u = T u> 0 p
p
T
cn cn 0
cn cv
s
v
(4) 当 n = p isochoric v const v C
1 n
理想气体 p 过程的p-v,T-s图
T dT ( )p ? cp ds
T2
已知p1,T1,T2 , 求p2 若是空气，查附表2
p2 p1exp
s s
0 T2
0 T1
R
理想气体 s u, h, s,的计算
状态参数的变化与过程无关 内能变化 焓变化 熵变化
u cv dT
h cp dT
s 0
理想气体 s w,wt ,q的计算
膨胀功 w
h>0 q>0 u> 0 p w>0
q Tds
T
qw
T
h>0 u>0
n0
n 1 wt>0
w>0
n0
wt>0
n
n 1
nk
n
q>0
nk
v
s
u,h,w,wt,q在p-v,T-s图上的变化趋势
u,h↑(T↑) w↑(v↑) wt↑(p↓) q↑(s↑) h>0 q>0 u> 0 T p w>0 w>0 n 0 h>0 u>0
q0
4-6 理想气体热力过程综合分析
一、过程线分布规律
顺时针方向n增大
二、过程特性和过程中能量传递的方向
u在p-v,T-s图上的变化趋势
u = T u> 0 p
3第三章理想气体的热力性质和热力过程详解
t1 0
t1
1.021433271.0045427306.89（kJ/kg）
讨论
利用工程图表时，常会遇到表中不能直接查到的参数 值，此时需要运用插值的方法。常用的最简单的插值为线 性插值。
以平均比热容计算的结果为基准，可求得按定值比热
容计算结果的相对偏差。
306.89 301.35 1.81％
本章难点
1. 比热容的种类较多，理解起来有一定的难度。应 注意各种比热容的区别与联系。在利用比热容计算过程 热量及热力学能和焓的变化量时应注意选取正确的比热 容，不要相互混淆，应结合例题与习题加强练习。
2. 理想气体各种热力过程的初、终态基本状态参数 间的关系式以及过程中热力系与外界交换的热量和功量 的计算式较多，如何记忆和运用是一难点，应结合例题 与习题加强练习。
Rg
R M
例3-1 氧气瓶内装有氧气，其体积为0.025m3，压力表
读数为0.5MPa，若环境温度为20℃，当地的大气压力为0.1 MPa，求：（1）氧气的比体积；（2）氧气的物质的量。
解：（1）瓶中氧气的绝对压力为
p（0.50.1）1060.6106（Pa）
气体的热力学温度为 T273.1520293.15 （ K ）
三、利用比热容计算热量
由比热容的定义式可得 q cdt
因此，温度从t1变到t2所需的热量为
q t2 cdt t2 f tdt
t1
t1
将 c f t 表示在图上。热力过程l-2
吸收的热量 q t2 cdt t1
可用过程曲线与
对应横坐标围成的曲边梯形的面积12t2t11表示。
为简化计算，工程上常使用气体的定值比热容和平
306.89
可见，在温度变化范围不大时，采用平均比热容和采 用定值比热容计算所得结果相差不大，而采用定值比热容 计算较为简单。
08理想气体的基本热力过程(完整版)
pv图和ts图上曲线群的大小变化趋势过程中各能量项正负方向分析热力学能与焓dtdtdudhdhdtdtdudh定温线是确定uh正负的分界线pv图定温线右上方ts图定温线上方dstds定熵线是确定q正负的分界线pv图定熵线右上方ts图定熵线右方dvpdv定容线是确定w正负的分界线pv图定容线右方ts图定容线右下方dpvdp正负的分界线pv图定压线下方ts图定压线右下方1试将满足以下要求的理想气体多变过程在pv图和ts图上表示出来
¾ 多变比热容
q = cn (T2 − T1 )
⎫ n −γ ⎪ cV ⎬ cn = n −γ n −1 q= cV (T2 − T1 ) ⎪ n −1 ⎭
n=0 c p = γ cV
cT → ∞ cs → 0 n =1 n=γ
n取特殊值，可 得四种基本热力 过程的比热容
对理想气体各种可逆热力过程的分析，可以 参考以下内容和步骤进行： 第一步：建立过程方程 第二步：由过程方程和理想气体状态方程， 建立初、终态p，v，T参数之间的关系式。根 据理想气体的计算式，求得热力学能变化、 2 焓变、熵变 v2 dT
Δu = u2 − u1 = ∫ cV (T ) dT
1 2
¾ p-v图和T-s图
pv = const. dp p =− dv T v
¾ 能量转换
dT = 0 d ( pv) = 0 qT = Δu + w = w = Δh + wt = wt w = ∫ pdv = ∫
v1 v2 v2
Rg T v
v1
dv
v2 v2 p2 = Rg T ln = p1v1 ln = − p1v1 ln v1 v1 p1 wt = w
¾ p-v图和T-s图
dT ds p = c p T dT T = ds p c p
¾ 多变比热容
q = cn (T2 − T1 )
⎫ n −γ ⎪ cV ⎬ cn = n −γ n −1 q= cV (T2 − T1 ) ⎪ n −1 ⎭
n=0 c p = γ cV
cT → ∞ cs → 0 n =1 n=γ
n取特殊值，可 得四种基本热力 过程的比热容
对理想气体各种可逆热力过程的分析，可以 参考以下内容和步骤进行： 第一步：建立过程方程 第二步：由过程方程和理想气体状态方程， 建立初、终态p，v，T参数之间的关系式。根 据理想气体的计算式，求得热力学能变化、 2 焓变、熵变 v2 dT
Δu = u2 − u1 = ∫ cV (T ) dT
1 2
¾ p-v图和T-s图
pv = const. dp p =− dv T v
¾ 能量转换
dT = 0 d ( pv) = 0 qT = Δu + w = w = Δh + wt = wt w = ∫ pdv = ∫
v1 v2 v2
Rg T v
v1
dv
v2 v2 p2 = Rg T ln = p1v1 ln = − p1v1 ln v1 v1 p1 wt = w
¾ p-v图和T-s图
dT ds p = c p T dT T = ds p c p
理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
第三节 理想气体的热力学能与焓 理想气体的状态方程及比热容确定后，利用热力学第一定律就可方便地求得理想气体的热力学能和焓的计算式。
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
图7-3 例7-3图
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
图7-7 绝热过程在p-v、T-s图上的表示
Cycle Diagram
Text
Text
Text
Text
Text
Cycle name
Add Your Text
Diagram
Your Slogan here
第七章 理想气体的热力性质及其热力过程
二、四个基本热力过程分析 1.定容过程
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
图7-4 定容过程在p-v、T-s图上的表示
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
2.定压过程
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
热工设备中实际进行的热力过程均是多变过程，且通常要比理论的多变过程更为复杂。例如，制冷压缩机气缸中制冷剂蒸汽的压缩过程，在整个过程中指数n是变化的。压缩开始时，工质温度低于缸壁温度，工质是吸热的，随着对工质不断地压缩，温度升高，高于缸壁温度后开始放热，瞬时多变指数约从1．4左右变化到1．0左右。制冷压缩机压缩过程的多变指数大小还与制冷剂的种类、制冷剂蒸汽与气缸壁的热交换情况、活塞与气缸壁的密封情况等因素有关。通常，制冷压缩机压缩多变指数要小于活塞式空气压缩机压缩多变指数。对多变指数n是变化的实际过程，热工计算中为简便起见常常这样处理：若n的变化范围不大，则用一个不变的平均多变指数近似地代替实际变化的n；如果n的变化较大，可将实际过程分段，每段近似为n值不变，各力性质及其热力过程
第三节 理想气体的热力学能与焓 理想气体的状态方程及比热容确定后，利用热力学第一定律就可方便地求得理想气体的热力学能和焓的计算式。
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
图7-3 例7-3图
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
图7-7 绝热过程在p-v、T-s图上的表示
Cycle Diagram
Text
Text
Text
Text
Text
Cycle name
Add Your Text
Diagram
Your Slogan here
第七章 理想气体的热力性质及其热力过程
二、四个基本热力过程分析 1.定容过程
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
图7-4 定容过程在p-v、T-s图上的表示
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
2.定压过程
第七章 理想气体的热力性质及其热力过程
第七章 理想气体的热力性质及其热力过程
热工设备中实际进行的热力过程均是多变过程，且通常要比理论的多变过程更为复杂。例如，制冷压缩机气缸中制冷剂蒸汽的压缩过程，在整个过程中指数n是变化的。压缩开始时，工质温度低于缸壁温度，工质是吸热的，随着对工质不断地压缩，温度升高，高于缸壁温度后开始放热，瞬时多变指数约从1．4左右变化到1．0左右。制冷压缩机压缩过程的多变指数大小还与制冷剂的种类、制冷剂蒸汽与气缸壁的热交换情况、活塞与气缸壁的密封情况等因素有关。通常，制冷压缩机压缩多变指数要小于活塞式空气压缩机压缩多变指数。对多变指数n是变化的实际过程，热工计算中为简便起见常常这样处理：若n的变化范围不大，则用一个不变的平均多变指数近似地代替实际变化的n；如果n的变化较大，可将实际过程分段，每段近似为n值不变，各力性质及其热力过程
第3章理想气体的性质与热力过程
矩形面积的高度即为平均比热容。
平均比热容图表：
q
t2 cdt
t1
t2 cdt
0
t1 0
cdt
c
|
t2 0
t2
c
|
t1 0
t1
其中：
c
|
t 0
温度自0-t的平均比热容值。
因此气体的平均比热容表示为：
c
|
t2
t1
c
|
tt2
02
t2
c| t1
tt1
01
只要确定了
c
| t1
0
和
c
| t2
0
3-2-1 热容的定义（Heat capacity）：
1. 热容：物体温度升高1K（或1℃）所需要的热量，
用C表示，单位J/K。
C Q Q
2. 根据物质计量单位不同，热容分三类： dT dt
（1）比热容（specific heat）
q
c
单位质量物质的热容量（质量热容）
dT
用c表示 ，单位 J / (kg . K) （2）摩尔热容（molar heat）
q1 2 t2 t1
t2cd t
t1
t2 t1
c c a0 a1T a2T 2 a3T 3 q1-2
热量：
q
c
|
t2 t1
(t2
t1 )
c
|
t2 t1
几何意 义
c |t2 t1
0
t1 dt t2 t
q1-2为过程线下面的面积。如果过程线下面的面 积可以用一个相同宽度的矩形面积来代替，则该
当温度变化趋于零的极限时的比热容。 它表示某瞬间温度的比热容。
3-理想气体的热力过程
（3） 绘出过程曲线； （4） 拟定过程中内能、焓和熵旳变化量：
u cvT ; h cp T
熵旳变化：
s12
2
1 cV
dT T
Rg
ln v2 v1
cV
ln T2 T1
Rg
ln v2 v1
s12
2
1 cp
dT T
Rg
ln
p2 p1
cp
ln T2 T1
Rg
ln
p2 p1
s12
实际上在PV 图上判断旳TS 变化时，可把 PV坐标假设为 TS坐标；
在 TS图上 判断PV旳变化 时，可把TS坐 标假设为PV 坐标。
多边过程旳过程方程
4-6 多变过程
1.过程方程 特例
pvn 定值
( n )
n 0 p 定值
定压过程
n 1 pv 定值
定温过程
nk n
pvk 定值 v 定值
n
ln ln
p2 p1 v1
v2
3.多变过程旳p—v图和T-s图
p
T
n=＋∞ n= —∞
n=1
n=1
n=0
n=0
n= —∞
v
s
4. 功和热量
多变过程中容积功旳计算
内能变化量 u u2 u1 cvT
焓旳变化量 h h2 h1 cpT
容积功
w v2 pdv v2 p vn dv pvn v2 dv
容 积 功 w cV (T1 T2 )
k
1 1
Rg
(T1
T2 )
k
1( 1
p1v1
p2v2 )
技 术 功 wt cp (T1 T2 ) kw
u cvT ; h cp T
熵旳变化：
s12
2
1 cV
dT T
Rg
ln v2 v1
cV
ln T2 T1
Rg
ln v2 v1
s12
2
1 cp
dT T
Rg
ln
p2 p1
cp
ln T2 T1
Rg
ln
p2 p1
s12
实际上在PV 图上判断旳TS 变化时，可把 PV坐标假设为 TS坐标；
在 TS图上 判断PV旳变化 时，可把TS坐 标假设为PV 坐标。
多边过程旳过程方程
4-6 多变过程
1.过程方程 特例
pvn 定值
( n )
n 0 p 定值
定压过程
n 1 pv 定值
定温过程
nk n
pvk 定值 v 定值
n
ln ln
p2 p1 v1
v2
3.多变过程旳p—v图和T-s图
p
T
n=＋∞ n= —∞
n=1
n=1
n=0
n=0
n= —∞
v
s
4. 功和热量
多变过程中容积功旳计算
内能变化量 u u2 u1 cvT
焓旳变化量 h h2 h1 cpT
容积功
w v2 pdv v2 p vn dv pvn v2 dv
容 积 功 w cV (T1 T2 )
k
1 1
Rg
(T1
T2 )
k
1( 1
p1v1
p2v2 )
技 术 功 wt cp (T1 T2 ) kw
工程热力学(理想气体的热力过程)
2.参数关系式
p2 v1 p1 v2
3.功量、热量
膨胀功： w
2
pdv
1
2 dv 1 p1v1 v
p1v1
ln
v2 v1
p1v1 ln
p1 p2
RgT1 ln
p1 p2
2
技术功：
wt
vdp
1
2
= pdv w 1
热量： q u w w
三、定温过程
4.p-v图和T-s图
p-v图
（1）各种过程的方程式： p pv （2）各种过程的基本状态参数间的关系： （3）各种过程的膨胀功w、技术功wt、热量q等能量交换
和转换关系，建立功量和热量计算式：
（4）在p-v图和T-s图上表示出各过程，并进行定性分析。
＊计算公式表
工程热力学 Thermodynamics Ш. 主要公式
理想气体热力过程的主要公式归纳
0.297 (300 571.1)
1.4 1
201.3
kJ
kg
q0
工程热力学 Thermodynamics
在p-v图和T-s图上，从同一初态1出发压缩至相同体积 的 过程, 过程和 过程分别为 1 2T ，1 2n 和 1 2S 。
p
2S 2n 2T
1
O
v
p-v图
T
定 v2线
2S
2n
2T
0
工程热力学 Thermodynamics
第二节 理想气体的多变过程
1.过程方程式
pv n 定值
➢ 当 n=0 时： p=定值，定压过程； ➢ 当 n=1 时： pv=定值，定温过程； ➢ 当 n=κ 时： pvκ=定值，定熵过程； ➢ 当 n=±∞ 时： p1/nv=定值，定容过程。
理想气体的典型热力过程
理想气体的典型热力过程
1. 等压过程：在恒定的压力下，气体的体积增加或减少，热量从气体传给环境或从环境传给气体。
这类过程也称作“伯努利过程”。
2. 等温过程：在恒定的温度下，气体随着压力的变化而膨胀或收缩，此时所吸收或释放的热量与温度成正比例。
这类过程也称作“卡诺过程”。
3. 等体过程：在恒定的体积下，气体的压强增加或减少，需要向气体注入或从气体中抽取热能。
这类过程也称作“热容过程”。
4. 绝热过程：在没有热量交换的情况下，气体的压强、温度和体积都同时变化。
这类过程也称作“奥托过程”。
理想气体基本热力过程
理想气体的基本热力过程热力设备中，热能与机械能的相互转化，通常是通过气态工质的吸热、膨胀、放热、压缩等热力过程来实现的。
实际的热力过程都很复杂，而且几乎都是非平衡、非可逆的过程。
但若仔细观察会发现，某些常见过程非常近似一些简单的可逆过程。
常见的主要有四种简单可逆过程-基本热力过程，指系统某一状态参数保持不变的可逆过程。
包括定容过程、定压过程、定温过程和绝热过程。
我们以1kg理想气体的闭口系统为例来分析这几种基本热力过程，分析方法包括5点：（1）依据过程特点建立过程方程式；（2）由过程方程和理想气体状态方程确定初、终态基本状态参数之间的关系，即P1、v1、T1和P2、v2、T2之间的关系；（3）绘制过程曲线；我们主要绘制两种坐标图P-v图和T-s图，因为P-v图上可以表示过程中做功量的多少，而T-s图上可以表示过程中吸收或放出热量的多少；（4）分析计算△u，△h，△s；（5）分析计算过程的热量q和功w。
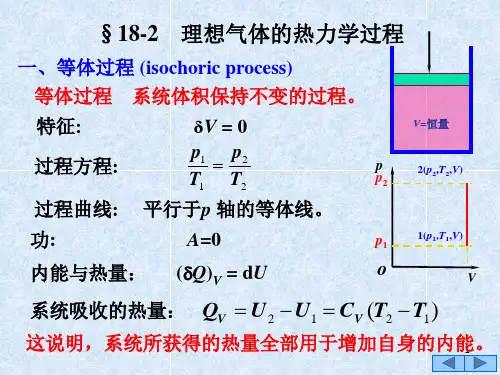
一、定容过程定容过程即工质的容积在整个过程中维持不变，dv=0，通常是一定量的气体在刚性容器中进行定容加热或定容放热。
（1）依据过程特点建立过程方程式定容过程的特点是体积保持不变，所以建立过程方程式：v=常数；或dv=0或v1=v2（2）由过程方程和理想气体状态方程确定初、终态基本状态参数之间的关系过程方程式：v1=v2理想气体状态方程：112212Pv P v T T = 由以上两个方程可以得到初末基本状态参数之间的关系：122211v v P T P T =⎧⎪⎨=⎪⎩ 即定容过程中工质的压力与温度成正比。
（3）绘制过程曲线；定容过程有两种情况：定容加热和定容放热。
（4）分析计算△u ，△h ，△s ；2211v v u u u c dT c T ∆=-==∆⎰ 2211p p h h h c dT c T ∆=-==∆⎰ 222111ln ln ln p v v v P P s c c c v P P ∆=+=或222111ln ln ln v v T v T s c R c T v T ∆=+= （5）分析计算过程的热量q 和功w 。
理想气体的热力过程
对于技术功则有： 对于技术功则有： t w
= − ∫ v dp = v ( p1 − p 2 )
1
2
（4-5） ）
热能工程教研室
理想气体 v 的参数关系
求过程的△ 、 求过程的△U、 △ H、 △ S 、
du = c v dT dh = c p dT
取定值 比热容
∆ u = cv ∆ T ∆h = c p ∆T
显然，过温度相同的同一点的定容线斜率大于定压线斜率。 显然，过温度相同的同一点的定容线斜率大于定压线斜率。 定容线斜率大于定压线斜率
热能工程教研室
理想气体 P 的参数关系
对于定压过程,其初、终态状态参数间的关系： 对于定压过程 其初、终态状态参数间的关系： 其初
du = c v dT dh = c p dT
δwt = −vdP = 0 可逆定压过程的技术功： 10） 可逆定压过程的技术功： （4-10） 它表明：定压过程中系统不对外作技术功。 它表明：定压过程中系统不对外作技术功。 适用于 工质,不限于理想气体 上述式(4 8)、(4-9)和(4-10)适用 任何工质 不限于理想气体。 (4上述式(4-8)、(4-9)和(4-10)适用于任何工质 不限于理想气体。
（4-4） ）
结论：定容过程中工质不输出膨胀功， 结论：定容过程中工质不输出膨胀功，其获得的热量等于工质的 热力学能的增量。它直接由热力学第一定律推出， 热力学能的增量。它直接由热力学第一定律推出，适用于所有气 体。
q v的计算结果为正，是吸热过程，反之是放热过程。 的计算结果为正，是吸热过程，反之是放热过程。
取定值 比热容
∆ u = cv ∆ T ∆h = c p ∆T
dP = 0
dT ds = c p T dv ds = c p v
= − ∫ v dp = v ( p1 − p 2 )
1
2
（4-5） ）
热能工程教研室
理想气体 v 的参数关系
求过程的△ 、 求过程的△U、 △ H、 △ S 、
du = c v dT dh = c p dT
取定值 比热容
∆ u = cv ∆ T ∆h = c p ∆T
显然，过温度相同的同一点的定容线斜率大于定压线斜率。 显然，过温度相同的同一点的定容线斜率大于定压线斜率。 定容线斜率大于定压线斜率
热能工程教研室
理想气体 P 的参数关系
对于定压过程,其初、终态状态参数间的关系： 对于定压过程 其初、终态状态参数间的关系： 其初
du = c v dT dh = c p dT
δwt = −vdP = 0 可逆定压过程的技术功： 10） 可逆定压过程的技术功： （4-10） 它表明：定压过程中系统不对外作技术功。 它表明：定压过程中系统不对外作技术功。 适用于 工质,不限于理想气体 上述式(4 8)、(4-9)和(4-10)适用 任何工质 不限于理想气体。 (4上述式(4-8)、(4-9)和(4-10)适用于任何工质 不限于理想气体。
（4-4） ）
结论：定容过程中工质不输出膨胀功， 结论：定容过程中工质不输出膨胀功，其获得的热量等于工质的 热力学能的增量。它直接由热力学第一定律推出， 热力学能的增量。它直接由热力学第一定律推出，适用于所有气 体。
q v的计算结果为正，是吸热过程，反之是放热过程。 的计算结果为正，是吸热过程，反之是放热过程。
取定值 比热容
∆ u = cv ∆ T ∆h = c p ∆T
dP = 0
dT ds = c p T dv ds = c p v
第六章理想气体的热力过程
曲线斜率
p
p
2'
1
T
T
2
2'
1
v2
(
T s
)
p
T Cp
cp cv
w0
w0
q0
q0
T T
v
s cv cp
在T-s图上，同一v温度下定容线比定s压线的斜率大
p
4、能量转 换u cv (t2 t1) h cp (t2 t1)
2
1）过程功 dp 0 wt,p vdp0
1
2
wp pdv p(v2 v1)
RM 8314J /(kmol K)
2、气体常数与通用气体常数的关系：
pV
nRM T
m M
RM
T
pV mRT
R RM M
或 RM MR
➢M 为气体的摩尔质量（kg/kmol）
➢R单位为J/（kg.K）
3、不同物量下理想气体的状态方程式
pv RT pV mRT
1 kg 理想气体 m kg 理想气体
u cv (t2 t1) h cp (t2 t1)
1）热量
q0
u ws 0
或
u ws
封闭系统对外界做的膨胀功是系统内 能减少的结果
h wt,s 0 或 h wt,s 开口系统对外界做的技术功是工质焓
2）过程功
值减少的结果
ws
u
cv (T1
T2 )
k
R
1
(T1
T2 )
1( k 1
2、气体的比热与状态参数有关
q c(t2 t1)
按定值比热计算
q cm12 (t2 t1)
按直线关系计算
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
yy 2 m 2 n mn 21 2 n 1n 22 2 n 2 n 23 2 n 3n
t qi ij x j
t q qV
xx cos 2 sin 2 xy yx ( ) cos sin yy sin 2 cos 2
xx cos 2 sin 2 xy yx ( ) cos sin yy sin 2 cos 2
作业：
1) 假设球坐标系的坐标轴为导热系数的主轴，推导球坐标系下的非稳态导热方程。
2) 推导：各向同性材料在球坐标系下的非稳态导热方程。
V 0
z
V
V
A
qd A
V
q3 H 2 dx2 H1dx1 q3 H 2 dx2 H1dx1
V
(q3 H 2 dx2 H1dx1 )dx3 ... x3
x3
x
y
(q3 H 2 dx2 H1dx1 )dx3 ... (q3 H 2 H1 )dx1dx2 dx3 ... q d A x x 3 3 V V H1 H 2 H 3dx1dx2 dx3 (q3 H 2 H1 ) ( q2 H 1 H 3 ) (q1 H 2 H 3 ) x x2 x1 q 3 H1 H 2 H 3
3) 证明：各向异性材料的导热系数张量λij是对称张量。
离散Fourier 展开
f(x) yi
n
C e
n
I
nπ x L
k N
Ck e
N
I
2kπ xi 2N1
k N
Ck e
N
I
2kπ iΔx 2N1
k N
Iθ i C e k
N
ε ψ(t)e
c
'ij im jnmn
xx 1m1n mn 111n1n 121n2n 131n3n xy 1m 2 n mn 11 2 n 1n 12 2 n 2 n 13 2 n 3n
yx 2 m1n mn 211n 1n 221n 2 n 231n 3n
t 2t 2t 2t 2t c xx 2 yx xy yy 2 qV x yx xy y t 2t 2t 2t 2 2 2 2 c ( cos sin ) 2 2( ) cos sin ( sin cos ) 2 qV x yx y
t x2
0 0 3
t x3
与该主值对应的坐标系称为主轴坐标系，在主轴坐标系内有：
t q'1 1 x1
q '2 2
q '3 3
a) 已知任一坐标系的导热系数，求主值和主轴坐标系： b) 已知主值和主轴坐标系，求任一坐标系的导热系数：
'ij im jnmn
c) 导热系数：
Q q d A t d A
A A
q t
J /( s m 2 ) W 单位： K /m K m
新材料、节能、导热系数 现行国家标准(GB 4272—92)规定：平 均温度在350℃以下，导热系数低于 0.12时，这种材料称为保温材料。
② 微分形式的方程
t c dV t d A qV dV t c dV n (t )dA qV dV
dA
n
q
V
A
c
t dV (t )dV q dV V
q t a 2t V c
x2 x1
c
t (t ) qV
(q3 H 2 H1 ) ( q2 H 1 H 3 ) (q1 H 2 H 3 ) x x2 x1 q 3 H1 H 2 H 3 t t t ( H 2 H1 ) ( H1 H 3 ) ( H2H3 ) x H 3 x3 x2 H 2 x2 x1 H1 x1 (t ) 3 H1 H 2 H 3 t t t ( H 2 H1 ) ( H1 H 3 ) ( H2H3 ) x2 H 2 x2 x1 H1 x1 t x3 H 3 x3 c qV H1 H 2 H 3
t 2t c ij qV xi x j
③ 坐标变换
z'
z
y'
e'i ij e j
ij cos( e'i , e j )
x
y
x'
根据张量定义，在不同坐标系中的张量有以下关系：
'ij im jnmn
根据张量性质，存在主值，使得：
1 0 'ij 0 2 0 0
t 如图二维平扳，已知主轴方向 的传热系数，推导导热微分方程式。假设为二维问题，t 在 z 方向上没有变化： 0 z
④ 例：
y
ij cos( e'i , e j )
x
cos ij sin 0 sin cos 0 0 0 1
通大学出版社 2000 72.54/4712-1.2 上海交
3 高等传热学 张靖周编著 科学出版社 2009 TK124/34 4 高等传热学
程俊国等编 重庆大学出版社 199172.54/2626
5 高等传热学:导热与对流的数理解析 孙德兴编著 中国建筑工业出版
社 2005 TK124/5
6 高等传热学.第2版 贾力, 方肇洪 高等教育出版社 2008
常数
（ 0 1 bt）
c) 导热系数：
各种物质的导热系数相差很大，原因在于不同的物质其导热机理存在着差异。 同一种物质的导热系数是物质温度和压力的函数。 工程计算采用的各种物质的导热系数都是用专门实验测定出来的，物质的导热 系数值可以查阅相关文献。
1.2 固体导热问题的数学描述
① 积分形式的方程
t t dx dA ( ) Adx 2h(t f t ) L 0 x A x x A cos
t dx ( A ) dx 2h(t f t ) L 0 x x cos
t L (A ) 2h(t f t ) 0 x x cos
y
c
t q qV
qi ij
t x j
x
qi 2t q ij xi xi x j
t 2t c ij qV xi x j
t 2t 2t 2t 2t c 11 21 12 22 qV x1x1 x2x1 x1x2 x2x2
高等传热传质学
1 2 3 4 5 6 7 8 9 10 11 12 13 导热理论和导热微分方程 稳态导热 非稳态导热 凝固和熔化时的导热 导热问题的数值解 对流换热基本方程 层流边界层的流动与换热 槽道内层流流动与换热 湍流流动与换热 自然对流 热辐射基础 辐射换热计算 复合换热
参考资料：
1 高等传热学 贾力等[著] 高等教育出版社 2003 72.54/1040 2 高等传热学:热传导和对流传热与传质 杨强生,浦保荣编著
静止时：
dA
ቤተ መጻሕፍቲ ባይዱ
n
q
V
A
U dV t d A qdV
静止的固体：
c
t dV t d A qdV
t c dV t d A qV dV
qV：单位时间、单位体积的固体通过辐射或者热源获得的热量
例：变截面直肋的导热微分方程
1 2t 1 t 2t 2 2 C a
常物性下的扩散方程
t c ( t ) q V dV 0
对超低温或极短时间 加热时的修正
t c (t ) qV 0
导热微分方程
t a 2t
t t t (r ) ( ) (r ) t z z r r r c qV r
柱坐标系中的导热微分方程
2t 1 2t 1 t (r ) 0 z 2 r 2 2 r r r
柱坐标系中的Laplace equation
2t qV
Fourier方程
c
t (t ) qV
0
Poisson equation Laplace equation
2t 0
x3
③ 曲线坐标系中的导热微分方程
c
t (t ) qV
dA
n
x1
q
x2
r
qd A q lim
2001 72.54/1216
TK124/28
7 高等传热学学习指导及典型题精解 张强编著 西安交通大学出版社
考核要求：
1 作业：40% 2 读书笔记：30% 3 论文：30%
Chapter 1 理想气体的热力过程
1.1 导热基本方程 1.2 固体导热问题的数学描述 1.3 各向异性材料中的导热
② 热流向量 q
0
x
1.3 各向异性材料中的导热
① 广义Fourier定律
q t
t qi ij x j
② 导热微分方程
根据张量识别定理，ij必定为二阶张量。
a) 直角坐标系下的导热微分方程：
c
t q qV
qi ij
t x j
qi 2t q ij xi xi x j
×
I iθ
0
t qi ij x j
t q qV
xx cos 2 sin 2 xy yx ( ) cos sin yy sin 2 cos 2
xx cos 2 sin 2 xy yx ( ) cos sin yy sin 2 cos 2
作业：
1) 假设球坐标系的坐标轴为导热系数的主轴，推导球坐标系下的非稳态导热方程。
2) 推导：各向同性材料在球坐标系下的非稳态导热方程。
V 0
z
V
V
A
qd A
V
q3 H 2 dx2 H1dx1 q3 H 2 dx2 H1dx1
V
(q3 H 2 dx2 H1dx1 )dx3 ... x3
x3
x
y
(q3 H 2 dx2 H1dx1 )dx3 ... (q3 H 2 H1 )dx1dx2 dx3 ... q d A x x 3 3 V V H1 H 2 H 3dx1dx2 dx3 (q3 H 2 H1 ) ( q2 H 1 H 3 ) (q1 H 2 H 3 ) x x2 x1 q 3 H1 H 2 H 3
3) 证明：各向异性材料的导热系数张量λij是对称张量。
离散Fourier 展开
f(x) yi
n
C e
n
I
nπ x L
k N
Ck e
N
I
2kπ xi 2N1
k N
Ck e
N
I
2kπ iΔx 2N1
k N
Iθ i C e k
N
ε ψ(t)e
c
'ij im jnmn
xx 1m1n mn 111n1n 121n2n 131n3n xy 1m 2 n mn 11 2 n 1n 12 2 n 2 n 13 2 n 3n
yx 2 m1n mn 211n 1n 221n 2 n 231n 3n
t 2t 2t 2t 2t c xx 2 yx xy yy 2 qV x yx xy y t 2t 2t 2t 2 2 2 2 c ( cos sin ) 2 2( ) cos sin ( sin cos ) 2 qV x yx y
t x2
0 0 3
t x3
与该主值对应的坐标系称为主轴坐标系，在主轴坐标系内有：
t q'1 1 x1
q '2 2
q '3 3
a) 已知任一坐标系的导热系数，求主值和主轴坐标系： b) 已知主值和主轴坐标系，求任一坐标系的导热系数：
'ij im jnmn
c) 导热系数：
Q q d A t d A
A A
q t
J /( s m 2 ) W 单位： K /m K m
新材料、节能、导热系数 现行国家标准(GB 4272—92)规定：平 均温度在350℃以下，导热系数低于 0.12时，这种材料称为保温材料。
② 微分形式的方程
t c dV t d A qV dV t c dV n (t )dA qV dV
dA
n
q
V
A
c
t dV (t )dV q dV V
q t a 2t V c
x2 x1
c
t (t ) qV
(q3 H 2 H1 ) ( q2 H 1 H 3 ) (q1 H 2 H 3 ) x x2 x1 q 3 H1 H 2 H 3 t t t ( H 2 H1 ) ( H1 H 3 ) ( H2H3 ) x H 3 x3 x2 H 2 x2 x1 H1 x1 (t ) 3 H1 H 2 H 3 t t t ( H 2 H1 ) ( H1 H 3 ) ( H2H3 ) x2 H 2 x2 x1 H1 x1 t x3 H 3 x3 c qV H1 H 2 H 3
t 2t c ij qV xi x j
③ 坐标变换
z'
z
y'
e'i ij e j
ij cos( e'i , e j )
x
y
x'
根据张量定义，在不同坐标系中的张量有以下关系：
'ij im jnmn
根据张量性质，存在主值，使得：
1 0 'ij 0 2 0 0
t 如图二维平扳，已知主轴方向 的传热系数，推导导热微分方程式。假设为二维问题，t 在 z 方向上没有变化： 0 z
④ 例：
y
ij cos( e'i , e j )
x
cos ij sin 0 sin cos 0 0 0 1
通大学出版社 2000 72.54/4712-1.2 上海交
3 高等传热学 张靖周编著 科学出版社 2009 TK124/34 4 高等传热学
程俊国等编 重庆大学出版社 199172.54/2626
5 高等传热学:导热与对流的数理解析 孙德兴编著 中国建筑工业出版
社 2005 TK124/5
6 高等传热学.第2版 贾力, 方肇洪 高等教育出版社 2008
常数
（ 0 1 bt）
c) 导热系数：
各种物质的导热系数相差很大，原因在于不同的物质其导热机理存在着差异。 同一种物质的导热系数是物质温度和压力的函数。 工程计算采用的各种物质的导热系数都是用专门实验测定出来的，物质的导热 系数值可以查阅相关文献。
1.2 固体导热问题的数学描述
① 积分形式的方程
t t dx dA ( ) Adx 2h(t f t ) L 0 x A x x A cos
t dx ( A ) dx 2h(t f t ) L 0 x x cos
t L (A ) 2h(t f t ) 0 x x cos
y
c
t q qV
qi ij
t x j
x
qi 2t q ij xi xi x j
t 2t c ij qV xi x j
t 2t 2t 2t 2t c 11 21 12 22 qV x1x1 x2x1 x1x2 x2x2
高等传热传质学
1 2 3 4 5 6 7 8 9 10 11 12 13 导热理论和导热微分方程 稳态导热 非稳态导热 凝固和熔化时的导热 导热问题的数值解 对流换热基本方程 层流边界层的流动与换热 槽道内层流流动与换热 湍流流动与换热 自然对流 热辐射基础 辐射换热计算 复合换热
参考资料：
1 高等传热学 贾力等[著] 高等教育出版社 2003 72.54/1040 2 高等传热学:热传导和对流传热与传质 杨强生,浦保荣编著
静止时：
dA
ቤተ መጻሕፍቲ ባይዱ
n
q
V
A
U dV t d A qdV
静止的固体：
c
t dV t d A qdV
t c dV t d A qV dV
qV：单位时间、单位体积的固体通过辐射或者热源获得的热量
例：变截面直肋的导热微分方程
1 2t 1 t 2t 2 2 C a
常物性下的扩散方程
t c ( t ) q V dV 0
对超低温或极短时间 加热时的修正
t c (t ) qV 0
导热微分方程
t a 2t
t t t (r ) ( ) (r ) t z z r r r c qV r
柱坐标系中的导热微分方程
2t 1 2t 1 t (r ) 0 z 2 r 2 2 r r r
柱坐标系中的Laplace equation
2t qV
Fourier方程
c
t (t ) qV
0
Poisson equation Laplace equation
2t 0
x3
③ 曲线坐标系中的导热微分方程
c
t (t ) qV
dA
n
x1
q
x2
r
qd A q lim
2001 72.54/1216
TK124/28
7 高等传热学学习指导及典型题精解 张强编著 西安交通大学出版社
考核要求：
1 作业：40% 2 读书笔记：30% 3 论文：30%
Chapter 1 理想气体的热力过程
1.1 导热基本方程 1.2 固体导热问题的数学描述 1.3 各向异性材料中的导热
② 热流向量 q
0
x
1.3 各向异性材料中的导热
① 广义Fourier定律
q t
t qi ij x j
② 导热微分方程
根据张量识别定理，ij必定为二阶张量。
a) 直角坐标系下的导热微分方程：
c
t q qV
qi ij
t x j
qi 2t q ij xi xi x j
×
I iθ
0