双曲线的简单几何性质练习题
- 格式:doc
- 大小:54.00 KB
- 文档页数:8

3.2.2双双双双双双双双双双(2)一、单选题1. 已知斜率为1的直线l 与双曲线2214x y -=的右支交于A ,B 两点,若||8AB =,则直线l 的方程为 ( )A. 21y x =B. 21y x =C. 35y x = D. 35y x =2. 已知圆223(1)4x y -+=的一条切线y kx =与双曲线2222:1(0,0)x y C a b a b -=>>没有公共点,则双曲线C 的离心率的取值范围是( )A. 3)B. (1,2]C. 3,)+∞D. [2,)+∞3. 设12,F F 是双曲线22:-=145x y C 的两个焦点,O 为坐标原点,点P 在C 上且||3OP =,则12PF F 的面积为( )A. 3B.72C.532D. 54. 已知1F ,2F 是双曲线C :22221(0,0)x y a b a b-=>>的两个焦点,12||23F F =,600(,)M x y 是双曲线C 上的一点,若120MF MF ⋅<,则0y 的取值范围是( )A. 33(B. 33(C. 2222(33-D. 2323( 5. 若直线2y x =与双曲线22221(0,0)x y a b a b-=>>有公共点,则双曲线的离心率的取值范围为( )A. 5)B. 5,)+∞C. 5]D. 5,)+∞6. 已知双曲线方程为2214y x -=,过(1,0)P 的直线L 与双曲线只有一个公共点,则L 的条数共有( )A. 4条B. 3条C. 2条D. 1条7. 已知双曲线C :2212x y -=,若直线l :(0)y kx m km =+≠与双曲线C 交于不同的两点M ,N ,且M ,N 都在以(0,1)A -为圆心的圆上,则m 的取值范围是( )A. 1(,0)(3,)3-⋃+∞B. (3,)+∞C. (,0)(3,)-∞⋃+∞D. 1(,3)3-二、多选题8. 已知双曲线C :22221(0,0)x y a b a b-=>>的左,右焦点分别为1F ,2F ,过2F 作垂直于渐近线的直线l 交两渐近线于A ,B 两点,若223||||F A F B =,则双曲线C 的离心率可能为( )A.141B.6 C. 3 D. 59. 已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为1F 、2F ,左、右顶点分别为A 、B ,O 为坐标原点.点P 为双曲线上任意一点(异于实轴端点),过点1F 作12F PF ∠的平分线的垂线,垂足为Q ,连接.OQ 则下列结论正确的有.( )A. 2//OQ PFB. ||OQ a =C. 22||||2PF PF b ⋅=D. 2max()ABQ Sa =三、填空题10. 若直线0x y m -+=与双曲线2212y x -=交于不同的两点A ,B ,且线段AB 的中点在圆225x y +=上,则m 的值为__________.11. 直线1y kx =+与双曲线2231x y -=相交于不同的两点,.A B 若点,A B 分别在双曲线的左、右两支上,则实数k 的取值范围为__________;若以线段AB 为直径的圆经过坐标原点,则实数k 的值为__________.12. 已知双曲线C :22145x y -=的右焦点为F ,过F 的直线l 与C 交于A 、B 两点,若||5AB =,则满足条件的l 的条数为__________.13. 已知双曲线22221(0,0)x y a b a b-=>>的离心率为2,1F ,2F 分别是双曲线的左、右焦点,点(,0)M a -,(0,)N b ,点P 为线段MN 上的动点,当12PF PF ⋅取得最小值和最大值时,12PF F 的面积分别为1S ,2S ,则21S S =__________. 四、解答题14. 设A ,B 分别为双曲线22221(0,0)x y a b a b-=>>的左,右顶点,双曲线的实轴长为43 3.(1)求双曲线的方程; (2)已知直线32y x =-与双曲线的右支交于M 、N 两点,且在双曲线的右支上存在点D ,使OM ON tOD +=,求t 的值及点D 的坐标.15. 如图,平面上,P 、Q 两地间距离为4,O 为PO 中点,M 处为一基站,设其发射的电波为直线,测量得60MOQ ︒∠=,且O 、M 间距离为23N 正在运行,它在运行过程中始终保持到P 地的距离比到Q 地的距离大2(P 、O 、M 、N 及电波直线均共面),请建立适当的平面直角坐标系.(1)求出机器人N 运行的轨迹方程;(2)为了使机器人N 免受M 处发射的电波的影响(即机器人接触不到过点M 的直线),求出电波所在直线斜率k 的取值范围.16. 已知双曲线E :22221(0,0)x y a b a b -=>>的两条渐近线方程为3y x =,且点(2,3)P 为E 上一点.(1)求E 的标准方程;(2)设M 为E 在第一象限的任一点,过M 的直线与E 恰有一个公共点,且分别与E 的两条渐近线交于点A ,B ,设O 为坐标原点,证明:AOB 面积为定值.17. 已知双曲线2222:1(0,0)x y C a b a b-=>>的离心率为2,过点且斜率为1的直线l 交双曲线C 于A ,B 两点.且 3.OA OB ⋅=(1)求双曲线C 的标准方程.(2)设Q 为双曲线C 右支上的一个动点,F 为双曲线C 的右焦点,在x 轴的负半轴上是否存在定点.M 使得2QFM QMF ∠=∠?若存在,求出点M 的坐标;若不存在,请说明理由.答案和解析1.【答案】B解:设直线l 的方程为y x m =+,,由2214y x m x y =+⎧⎪⎨-=⎪⎩得2238440x mx m +++=, 则212443m x x +=,1283m x x +=-,又因为||8AB =,且A 、B 是直线l 与双曲线2214x y -=右支的交点, 所以,且803m->, 即,且0m <,解得221m =,且0m <, 所以21m =-,所以直线l 的方程为21.y x =- 故选.B2.【答案】B解:由题意,圆心到直线的距离231d k ==+,3k ∴= 圆223(1)4x y -+=的一条切线y kx =与双曲线2222:1(0,0)x y C a b a b -=>>没有公共点,与其中一条渐近线by x a=斜率比较即可, 3b a∴,2214b a+,∴双曲线C 的离心率的取值范围是(1,2].故答案选:.B11(,)A x y3.【答案】D解:由已知得2, 3.a c == 设(,)P x y ,由||3OP =,得229x y +=, 所以229x y =-,代入22145x y -=,解得5.3y =± 所以1212115||||6||5223F F PSF F y ==⨯⨯±=, 故选.D4.【答案】A解:由题意,3c =2a =1b =,∴双曲线方程为22 1.2x y -=120MF MF ⋅<,220030x y ∴+-<, 220022x y =+, 20310y ∴-<,03333y ∴-<<, 故选:.A5.【答案】B解:双曲线22221(0,0)x y a b a b -=>>的渐近线方程为by x a=±,由双曲线与直线2y x =有交点, 则有2ba>, 即有22221()145c a b b e a a a+===+>+=则双曲线的离心率的取值范围为(5,).+∞ 故选:.B6.【答案】B解:由题意可得:双曲线2214y x -=的渐近线方程为:2y x =±, 点(1,0)P 是双曲线的右顶点,故直线1x =与双曲线只有一个公共点;过点(1,0)P 平行于渐近线2y x =±时,直线L 与双曲线只有一个公共点,有2条, 所以,过(1,0)P 的直线L 与双曲线只有一个公共点,这样的直线共有3条. 故选.B7.【答案】A解:设11(,)M x y ,22(,)N x y , 由,则①,且122412mkx x k+=-,21222(1)12m x x k -+=-, 设MN 的中点为00(,)G x y ,则02212km x k =-,0212my k=-, M ,N 在以A 为圆心的圆上,,G 为MN 的中点,AG MN ∴⊥,21212m k k km+-∴⋅=-,2231k m ∴=+②,由①②得103m -<<或3m >, 故选.A8.【答案】BC解:由题意得直线 l 垂直于渐近线by x a=,则2OA BF ⊥, 由双曲线性质得2||AF b =,||OA a =,由223||||F A F B =,得2||2||2AB AF b ==或2||4||4.AB AF b == 当2||2||2AB AF b ==时,如图:在Rt BOA 中,2tan b BOA a∠=, 由双曲线渐近线性质得21AOF BOF ∠=∠,2tan b AOF a∠=, 因此有22tan tan(2)tan(2)BOA AOF AOF π∠=-∠=-∠2222222tan 21tan 1bAOF b a b AOF a a⨯∠=-=-=-∠-,化简得2b a =,故离心率2213b e a=+=;当||4AB b =时,如图:在2Rt AOF 中,2tan b AOF a∠=,在Rt AOB 中,4tan b AOB a ∠=,因为22AOB AOF ∠=∠,利用二倍角公式,得2241()bb a b a a⨯=-, 化简得21()2b a =,故离心率2261.2b e a =+=综上所述,离心率e 的值为3或6.2故选.BC9.【答案】ABD解:如图所示:A 选项,延长1F Q 交2PF 于点C ,因为PQ 为12F PF ∠的平分线,1PQ F Q ⊥, 故Q 为1F C 的中点,1||||F Q QC =,又因为12||||FO F O =,即O 为12F F 的中点, 故OQ 为12F F C 的中位线, 所以2||2||F C OQ =,2//OQ F C , 又因为P 、2F 、C 共线, 故2//OQ PF ,故A 正确;B 选项,由定义可知12||||2PF PF a -=, 因为1||||F P PC =,而12||||2F P PF a -=, 故22||||||2PC PF F C a -==,而2||2||F C OQ =, 故1||22OQ a a =⨯=,故B 正确; C 选项,若212||||2PF PF b ⋅=,则222222212121212||||(||||)2||||444()PF PF PF PF PF PF a b c F F +=-+=+==,则1290F PF ∠=︒,题中无说明,故不成立,故C 错误; D 选项,因为||2AB a =,||OQ a =, 当OQ x ⊥轴时,2max1()22ABQ Sa a a =⨯⨯=,故D 正确.故选:.ABD10.【答案】1±解:设A ,B 两点的坐标分别为11(,)A x y ,22(,)B x y ,线段AB 的中点为00(,).M x y 由得22220(0)x mx m ---=∆>,则212122,2x x m x x m +==--,1202x x x m +∴==,002.y x m m =+= 点00(,)M x y 在圆225x y +=上,22(2)5m m ∴+=, 1.m ∴=±故答案为 1.±11.【答案】1±解:(1)由直线1y kx =+与双曲线2231x y -=,得22(3)220k x kx ---=, 因为A , B 在双曲线的左右两支上,所以230k -≠,2203k -<- 解得33;k -<<(2)假设存在实数k ,使得以线段AB 为直径的圆经过坐标原点,设11(,)A x y ,22(,)B x y ,则0OA OB ⋅=,即12120x x y y +=,1212(1)(1)0x x kx kx ∴+++=,即21212(1)()10k x x k x x ++++=,22222(1)1033kk k k k -∴+⋅+⋅+=--, 整理得21k =,符合条件,1.k ∴=±故答案为; 1.±12.【答案】3解:24a =,25b =,29c =,则(3,0)F ,若A 、B 都在右支上,当AB 垂直于x 轴时,将3x =代入22145x y -=得52y =±,则||5AB =,满足, 若A 、B 分别在两支上,2a =,∴两顶点的距离为2245+=<,∴满足||5AB =的直线有2条,且关于x 轴对称,综上满足条件的l 的条数为3. 故答案为:3.13.【答案】4解:离心率为2ce a==,即2c a =,3b a =, (,0)M a -,(0,)N b ,可得MN 的方程为0bx ay ab -+=,设(,)P m n ,1(,0)F c -,2(,0)F c ,可得22212(,)(,)PF PF c m n c m n m n c ⋅=---⋅--=+-, 由22222()m n m n +=+表示原点O 与P 的距离的平方, 显然OP 垂直于MN 时,||OP 最小, 由OP :ay x b=-,即33y x =-330x y a -+=, 可得33(,)44P a a -,即211332242S c a a =⋅⋅=, 当P 与N 重合时,可得||OP 最大, 可得2212232S c b a =⋅⋅=, 即有222123 4.3S a S a ==故答案为:4.14.【答案】解:(1)双曲线的渐近方程为by x a=±,焦点为(,0)F c ±, ∴焦点到渐近线的距离为,又243a =,23a ∴=,双曲线的方程为221.123x y -=(2)设点112200(,),(,),(,)M x y N x y D x y ,由得: 2163840x x -+=,1212123163,()4123x x y y x x ∴+=+=+-=, OM ON tOD +=,0,01212()(,)t x y x x y y ∴=++,有,又点00(,)D x y 在双曲线上, 2216312()()1123t t ∴-=,解得216t =,点D 在双曲线的右支上,0t ∴>,4t ∴=,此时点(43,3).D15.【答案】解:(1)如图所示,以点O 为坐标原点,以PQ 所在的直线为x 轴建立直角坐标系,则(2,0),(2,0)P Q -,设点(,)N x y ,则||||2||4NP NQ PQ -=<=, 所以动点N 是以点,P Q 为焦点的双曲线的右支, 由题得22,2,1a c a ===, 所以2413b =-=,所以动点N 的轨迹方程为221(1).3y x x -= (2)由题得点M 的坐标为3,3),设直线的方程为3(3)y k x -=,即:(3)3y k x =-+,联立直线和221(1)3y x x -=, 消去y 得2222(3)(236)633120k x k k x k k -+-+--=当230k -=时,若3k =当3k =当230k -≠时,由0∆<得2222(236)4(3)(63312)0k k k k k -----<,所以(3)(3)0k k --<, 32 3.k << 32 3.k <所以电波所在直线斜率k 的取值范围16.【答案】解:(1)当3ba =E 的标准方程为222213x y a a -=,代入(2,3),解得2 1.a =故E 的标准方程为221.3y x -=(2)直线斜率显然存在,设直线方程为y kx t =+,与2213y x -=联立得:222(3)230.k x ktx t -+++=由题意,3k ≠222244(3)(3)0k t k t ∆=--+=,化简得:2230.t k -+=设1122(,),(,)A x y B x y ,将y kx t =+与3y x =联立,解得13x k =-;与3y x =-联立,解得23x k=+ 212122113||||sin |2||2|sin1203|.22|3|AOBt S OA OB AOB x x x x k ︒∆=⋅⋅∠=⋅⋅==- 由2230t k -+=,3AOB S ∆∴AOB 3.17.【答案】解:(1)设双曲线C 的焦距为2c ,由双曲线C 的离心率为2知2c a =,所以223b c a a -=,从而双曲线C 的方程可化为222213x y a a-=,由得22226630x x a ---=,设11(,)A x y ,22(,)B x y , 因为,所以126x x +=,212332x x a ⋅=--, 因为3OA OB ⋅=,所以12121212(6)(6)3x x y y x x x x +=+=, 于是21212326()62(3)66632x x x x a ++=⨯--=,解得1a =, 所以双曲线C 的标准方程为2213y x -=; (2)假设存在,点(,0)(0)M t t <满足题设条件.由(1)知双曲线C 的右焦点为,设为双曲线C 右支上一点,当02x =时,因为290QFM QMF ︒∠=∠=, 所以45QMF ︒∠=,于是,所以 1.t =-当02x ≠时,00tan 2QF y QFM k x ∠=-=--,00tan QM y QMF k x t∠==-, 因为2QFM QMF ∠=∠,所以0002000221()y y x ty x x t⨯--=---, 将220033y x =-代入并整理得22200002(42)4223x t x t x tx t -++-=--++,所以,解得 1.t =-综上,满足条件的点M 存在,其坐标为。

2020-2021学年高中数学人教A版选修1-1配套作业:2.2.2 双曲线的简单几何性质含解析第二章2。
22。
2.2A级基础巩固一、选择题1.以椭圆错误!+错误!=1的顶点为顶点,离心率为2的双曲线方程为(C)A.错误!-错误!=1B.错误!-错误!=1C.错误!-错误!=1或错误!-错误!=1D.以上都不对[解析]当顶点为(±4,0)时,a=4,c=8,b=43,双曲线方程为错误!-错误!=1;当顶点为(0,±3)时,a=3,c=6,b=3错误!,双曲线方程为错误!-错误!=1。
2.双曲线2x2-y2=8的实轴长是(C)A.2B.2错误!C.4D.42[解析]双曲线2x2-y2=8化为标准形式为x24-y28=1,∴a=2,∴实轴长为2a=4。
3.(全国Ⅱ文,5)若a〉1,则双曲线x2a2-y2=1的离心率的取值范围是(C)A.(错误!,+∞) B.(错误!,2 )C.(1,错误!) D.(1,2)[解析]由题意得双曲线的离心率e=错误!.∴c2=a2+1a2=1+错误!.∵a>1,∴0〈错误!<1,∴1<1+错误!〈2,∴1〈e〈错误!.故选C.4.(2018·全国Ⅲ文,10)已知双曲线C:错误!-错误!=1(a>0,b>0)的离心率为错误!,则点(4,0)到C的渐近线的距离为(D) A. 2 B.2C.错误!D.2错误![解析]由题意,得e=错误!=错误!,c2=a2+b2,得a2=b2。
又因为a〉0,b>0,所以a=b,渐近线方程为x±y=0,点(4,0)到渐近线的距离为错误!=2错误!,故选D.5.(2019·全国Ⅲ卷理,10)双曲线C:错误!-错误!=1的右焦点为F,点P在C的一条渐近线上,O为坐标原点,若|PO|=|PF|,则△PFO的面积为(A)A.错误!B.错误!C.2错误!D.3错误![解析]双曲线错误!-错误!=1的右焦点坐标为(错误!,0),一条渐近线的方程为y=错误!x,不妨设点P在第一象限,由于|PO|=|PF|,则点P的横坐标为错误!,纵坐标为错误!×错误!=错误!,即△PFO 的底边长为错误!,高为错误!,所以它的面积为错误!×错误!×错误!=错误!。

双曲线专题一、学习目标:1.理解双曲线的定义;2.熟悉双曲线的简单几何性质;3.能根据双曲线的定义和几何性质解决简单实际题目.二、知识点梳理定 义1、到两个定点1F 与2F 的距离之差的绝对值等于定长(小于21F F )的点的轨迹2、到定点F 与到定直线l 的距离之比等于常数()1>e ee (>1)的点的轨迹标准方程-22a x 22b y =1()0,0>>b a -22a y 22bx =1()0,0>>b a 图 形性质范围a x ≥或a x -≤,R y ∈R x ∈,a y ≥或a y -≤对称性 对称轴: 坐标轴 ;对称中心: 原点渐近线x a by ±=x b a y ±=顶点 坐标 ()0,1a A -,()0,2a A ()b B -,01,()b B ,02 ()a A -,01,()a A ,02()0,1b B -,()0,2b B焦点 ()0,1c F -,()0,2c F()c F -,01,()c F ,02轴 实轴21A A 的长为a 2 虚轴21B B 的长为b 2离心率1>=ace ,其中22b a c += 准线准线方程是c a x 2±=准线方程是ca y 2±=三、课堂练习1、双曲线方程为2221x y -=,则它的右焦点坐标为( )A 、2,02⎛⎫ ⎪ ⎪⎝⎭B 、5,02⎛⎫⎪ ⎪⎝⎭C 、6,02⎛⎫⎪ ⎪⎝⎭D 、()3,01.解析:C2.设椭圆C 1的离心率为,焦点在x 轴上且长轴长为26,若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8,则曲线C 2的标准方程为( )A . ﹣=1B .﹣=1C .﹣=1D .﹣=12.解析A :在椭圆C 1中,由,得椭圆C 1的焦点为F 1(﹣5,0),F 2(5,0),曲线C 2是以F 1、F 2为焦点,实轴长为8的双曲线, 故C 2的标准方程为:﹣=1,故选A .3.已知F 1、F 2为双曲线C :x 2-y 2=2的左、右焦点,点P 在C 上,|PF 1|=2|PF 2|,则cos ∠F 1PF 2=( ) A.14 B.35 C.34 D.453.解析C :依题意得a =b =2,∴c =2. ∵|PF 1|=2|PF 2|,设|PF 2|=m ,则|PF 1|=2m .又|PF 1|-|PF 2|=22=m . ∴|PF 1|=42,|PF 2|=2 2. 又|F 1F 2|=4,∴cos ∠F 1PF 2=422+222-422×42×22=34.故选C.4.已知双曲线的两个焦点为F 1(﹣,0)、F 2(,0),P 是此双曲线上的一点,且PF 1⊥PF 2,|PF 1|•|PF 2|=2,则该双曲线的方程是( ) A.﹣=1 B.﹣=1 C.﹣y 2=1D.x 2﹣=14.解析C :解:设双曲线的方程为﹣=1. 由题意得||PF 1|﹣|PF 2||=2a ,|PF 1|2+|PF 2|2=(2)2=20.又∵|PF 1|•|PF 2|=2, ∴4a 2=20﹣2×2=16 ∴a 2=4,b 2=5﹣4=1.所以双曲线的方程为﹣y 2=1.故选C .5.已知双曲线C :x 2a 2-y 2b 2=1的焦距为10,点P (2,1)在C 的渐近线上,则C 的方程为( )A.x 220-y 25=1B.x 25-y 220=1C.x 280-y 220=1D.x 220-y 280=1 5.解析A :设焦距为2c ,则得c =5.点P (2,1)在双曲线的渐近线y =±ba x 上,得a =2b .结合c=5,得4b 2+b 2=25, 解得b 2=5,a 2=20,所以双曲线方程为x 220-y 25=1. 6.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB |=43,则C 的实轴长为( )A. 2 B .2 2 C .4 D .86.解析C :设等轴双曲线方程为x 2-y 2=a 2,根据题意,得抛物线的准线方程为x =-4,代入双曲线的方程得16-y 2=a 2,因为|AB |=43,所以16-(23)2=a 2,即a 2=4,所以2a =4,所以选C. 7.平面直角坐标系xOy 中,已知双曲线x 24-y 212=1上一点M 的横坐标为3,则点M 到此双曲线的右焦点的距离为________.7.解析:双曲线的右焦点(4,0),点M (3,15)或(3,-15),则点M 到此双曲线的右焦点的距离为4.8.以知F 是双曲线221412x y -=的左焦点,(1,4),A P 是双曲线右支上的动点,则PF PA + 的最小值为 。

双曲线的简单几何性质1.设双曲线x 2a 2-y 2b 2=1(a >0,b >0)的虚轴长为2,焦距为23,则双曲线的渐近线方程为( )A .y =± 2xB .y =±2xC .y =± 22xD .y =± 12x答案:C2.双曲线2x 2-y 2=8的实轴长是( )A .2B .2 2C .4D .4 2答案:C3.双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,则m 等于( )A .-14B .-4C .4D.14答案:A4.中心在原点,实轴在x 轴上,一个焦点在直线3x -4y +12=0上的等轴双曲线方程是( )A .x 2-y 2=8B .x 2-y 2=4C .y 2-x 2=8D .y 2-x 2=4答案:A5.已知A ,B 为双曲线E 的左、右顶点,点M 在E 上,△ABM 为等腰三角形,且顶角为120°,则E 的离心率为( ) A. 5 B .2 C. 3 D. 2答案:D6.已知双曲线x 2a 2-y 2=1(a >0)的一条渐近线为3x +y =0,则a =________. 答案:337.过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左焦点且垂直于x 轴的直线与双曲线相交于M ,N 两点,以MN 为直径的圆恰好过双曲线的右顶点,则双曲线的离心率为________.答案:28.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率e =2,且它的一个顶点到较近焦点的距离为1,则双曲线C 的方程为________.答案:x 2-y 23=1 10.设A ,B 分别为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右顶点,双曲线的实轴长为43,焦点到渐近线的距离为 3.(1)求双曲线的方程;(2)已知直线y =33x -2与双曲线的右支交于M 、N 两点,且在双曲线的右支上存在点D ,使OM→+ON →=tOD →,求t 的值及点D 的坐标. 解析:(1)由题意知a =23,∴一条渐近线为y =b23x ,即bx -23y =0,∴|bc |b 2+12=3, ∴b 2=3,∴双曲线的方程为x 212-y 23=1. (2)设M (x 1,y 1),N (x 2,y 2),D (x 0,y 0),则x 1+x 2=tx 0,y 1+y 2=ty 0,将直线方程代入双曲线方程得x 2-163x +84=0,则x 1+x 2=163,y 1+y 2=12,∴⎩⎪⎨⎪⎧ x 0y 0=433,x 2012-y 203=1,∴⎩⎪⎨⎪⎧x 0=43,y 0=3, ∴t =4,点D 的坐标为(43,3).[B 组 能力提升]1.(2016·高考全国Ⅰ卷)已知方程x 2m 2+n -y 23m 2-n =1表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是( )A .(-1,3)B .(-1,3)C .(0,3)D .(0,3)解析:根据双曲线的焦距,建立关于n 的不等式组求解.若双曲线的焦点在x 轴上,则⎩⎪⎨⎪⎧ m 2+n >0,3m 2-n >0.又∵(m 2+n )+(3m 2-n )=4,∴m 2=1,∴⎩⎪⎨⎪⎧ 1+n >0,3-n >0,∴-1<n <3.若双曲线的焦点在y 轴上,则双曲线的标准方程为y 2n -3m 2-x 2-m 2-n =1,即⎩⎪⎨⎪⎧ n -3m 2>0,-m 2-n >0,即n >3m 2且n <-m 2,此时n 不存在.故选A.答案:A2.已知F 1,F 2分别是双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,过F 1作垂直于x 轴的直线交双曲线于A 、B 两点,若△ABF 2为锐角三角形,则双曲线的离心率的范围是( )A .(1,1+2)B .(1+2,+∞)C .(1-2,1+2)D .(2,2+1)解析:由△ABF 2为锐角三角形得,b 2a 2c <tan π4=1,即b 2<2ac ,∴c 2-a 2<2ac , ∴e 2-2e -1<0,解得1-2<e <1+2,又e >1,∴1<e <1+ 2.答案:A3.已知F 是双曲线C :x 2-y 28=1的右焦点,P 是C 左支上一点,A ()0,66,当△APF 周长最小时,该三角形的面积为________.解析:由双曲线方程x 2-y 28=1可知,a =1,c =3,故F (3,0),F 1(-3,0).当点P 在双曲线左支上运动时,由双曲线定义知|PF |-|PF 1|=2,所以|PF |=|PF 1|+2,从而△APF 的周长=|AP |+|PF |+|AF |=|AP |+|PF 1|+2+|AF |.因为|AF |=32+(66)2=15为定值,所以当(|AP |+|PF 1|)最小时,△APF 的周长最小,由图象可知,此时点P 在线段AF 1与双曲线的交点处(如图所示).由题意可知直线AF 1的方程为y =26x +66,由⎩⎨⎧ y =26x +66,x 2-y 28=1,得y 2+66y -96=0,解得y =26或y =-86(舍去),所以S △APF =S △AF 1F -S △PF 1F=12×6×66-12×6×26=12 6.答案:12 64.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点为F (2,0),且双曲线的渐近线与圆(x -2)2+y 2=3相切,则双曲线的方程为________. 解析:由双曲线的渐近线y =±b ax 与圆(x -2)2+y 2=3相切 可知⎩⎪⎨⎪⎧⎪⎪⎪⎪⎪⎪±b a ×21+⎝ ⎛⎭⎪⎫b a 2=3,c =2,a 2+b 2=c 2,解得⎩⎪⎨⎪⎧ a =1,b = 3. 故所求双曲线的方程为x 2-y 23=1.答案:x 2-y 23=1 5.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为3,且a 2c =33.(1)求双曲线C 的方程;(2)已知直线x -y +m =0与双曲线C 交于不同的两点A ,B ,且线段AB 的中点在圆x 2+y 2=5上,求m 的值.解析:(1)由题意得⎩⎪⎨⎪⎧ a 2c =33,c a =3,解得⎩⎪⎨⎪⎧a =1,c = 3. 所以b 2=c 2-a 2=2.所以双曲线C 的方程为x 2-y 22=1.(2)设A ,B 两点的坐标分别为(x 1,y 1),(x 2,y 2),线段AB 的中点为M (x 0,y 0).由⎩⎨⎧ x -y +m =0,x 2-y 22=1,得x 2-2mx -m 2-2=0(判别式Δ>0).所以x 0=x 1+x 22=m ,y 0=x 0+m =2m .因为点M (x 0,y 0)在圆x 2+y 2=5上,所以m 2+(2m )2=5.故m =±1.6.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点是F 2(2, 0),离心率e =2.(1)求双曲线C 的方程;(2)若斜率为1的直线l 与双曲线C 相交于两个不同的点M ,N ,线段MN 的垂直平分线与两坐标轴围成的三角形的面积为4,求直线l 的方程.解析:(1)由已知得c =2,e =2,∴a =1,b = 3.∴所求的双曲线方程为x 2-y 23=1.(2)设直线l 的方程为y =x +m ,点M (x 1,y 1),N (x 2,y 2)的坐标满足方程组⎩⎨⎧ y =x +m , ①x 2-y 23=1, ②将①式代入②式,整理得2x2-2mx-m2-3=0.(*) 设MN的中点为(x0,y0),则x0=x1+x22=m2,y0=x0+m=3m2,所以线段MN垂直平分线的方程为y-3m2=-⎝⎛⎭⎪⎫x-m2即x+y-2m=0,与坐标轴的交点分别为(0,2m),(2m,0),可得12|2m|·|2m|=4,得m2=2,m=±2此时(*)的判别式Δ>0,故直线l的方程为y=x±2.。

第二章 2.2 2.2.2基础练习1.双曲线-=1的焦点到渐近线的距离为( )x 24y 212A .1 B . 3C .2 D .23【答案】D【解析】不妨取焦点(4,0)和渐近线y =x ,则所求距离d ==2.3|43-0|3+132.已知0<θ<,则双曲线C 1:-=1与C 2:-=1的( )π4x 2sin2θy 2cos2θy 2cos2θx 2sin2θA .实轴长相等B .虚轴长相等C .离心率相等D .焦距相等【答案】D【解析】对于双曲线C 1,a 1=sin θ,b 1=cos θ,c 1=1,则实轴长为2sin θ,虚轴长为2cos θ,离心率为,焦距为2;对于双曲线C 2,a 2=cos θ,b 2=sin θ,c 2=1,则实轴长为2cos θ,虚轴长为2sin1sin θθ,离心率为,焦距为2.故选D .1cos θ3.双曲线+=1的离心率e ∈(1,2),则实数k 的取值范围是( )x 24y 2k A .(-10,0)B .(-3,0)C .(-12,0)D .(-60,-12)【答案】C【解析】双曲线方程可变为-=1,则a 2=4,b 2=-k ,c 2=4-k ,e ==.又e ∈(1,2),x 24y 2-k c a 4-k 2则1<<2.解得-12<k <0.故选C .4-k24.双曲线C :-=1(a >0,b >0)的离心率e =,则它的渐近线方程为( )x 2a 2y 2b 2132A .y =±x B .y =±x 2332C .y =±x D .y =±x 9449【答案】B【解析】双曲线C :-=1(a >0,b >0)的离心率e =,可得=.∴+1=,可得=.x 2a 2y 2b 2132c 2a 2134b 2a 2134b a 32于是双曲线的渐近线方程为y =±x .故选B .325.(2019年河南郑州期末)已知双曲线-=1(a >0,b >0)的两个焦点分别为F 1,F 2,以线段F 1F 2y 2a 2x 2b 2为直径的圆与双曲线渐近线的一个交点是(4,3),则此双曲线的方程为__________________.【答案】-=1y 29x 216【解析】由题意,c ==5,∴a 2+b 2=c 2=25.① 又双曲线的渐近线为y =±x ,∴=.② 42+32ab a b 34由①②解得a =3,b =4.∴双曲线方程为-=1.y 29x 2166.设F 1,F 2是双曲线C :-=1(a >0,b >0)的两个焦点.若在C 上存在一点P ,使PF 1⊥PF 2x 2a 2y 2b 2且∠PF 1F 2=30°,则C 的离心率为________.【答案】+13【解析】由PF 1⊥PF 2,∠PF 1F 2=30°,|F 1F 2|=2c ,可得|PF 1|=2c cos 30°=c ,|PF 2|=2c sin 30°=c .3又||PF 1|-|PF 2||=2a ,∴c -c =2a ,则e ===+1.3c a 23-137.已知双曲线过点P (3,-),离心率e =,试求此双曲线的方程.252解:依题意,双曲线的焦点可能在x 轴上,也可能在y 轴上,分别讨论如下.若双曲线的焦点在x 轴上,设双曲线方程为-=1(a >0,b >0).x 2a 2y 2b 2由e =,得=.①52c 2a 254由点P (3,-)在双曲线上,得-=1.②29a 22b 2又a 2+b 2=c 2.③所以由①②③可得a 2=1,b 2=.14若双曲线的焦点在y 轴上,设双曲线方程为-=1(a >0,b >0).y 2a 2x 2b 2同理有=,-=1,a 2+b 2=c 2.c 2a 2542a 29b 2解得b 2=-(不合题意,舍去).172故双曲线的焦点只能在x 轴上,所求双曲线方程为x 2-4y 2=1.8.已知双曲线C :-=1(a >0,b >0)的离心率为,=.x 2a 2y 2b 23a 2c 33(1)求双曲线C 的方程;(2)已知直线x -y +m =0与双曲线C 交于不同的两点A ,B ,线段AB 的中点在圆x 2+y 2=5上,求实数m 的值.解: (1)∵=,=,∴a =1,c =.c a 3a 2c 333∴b 2=c 2-a 2=2.∴双曲线C 的方程为x 2-=1.y 22(2)设A (x 1,y 1),B (x 2,y 2),线段AB 的中点 M (x 0,y 0).由Error!得x 2-2mx -m 2-2=0(判别式Δ>0).∴x 0==m ,y 0=x 0+m =2m .x 1+x 22∵点M (x 0,y 0)在圆x 2+y 2=5上,∴m 2+(2m )2=5,解得m =±1.能力提升9.(2019年山东枣庄十六中模拟)已知双曲线C 1:-y 2=1,双曲线C 2:-=1(a >0,b >0)的x 24x 2a 2y 2b 2左、右焦点分别为F 1,F 2,点M 是双曲线C 2的一条渐近线上的点,且OM ⊥MF 2,O 为坐标原点,若S △OMF 2=16,且双曲线C 1,C 2的离心率相同,则双曲线C 2的实轴长是( )A .4 B .8C .16D .32【答案】C【解析】双曲线C 1:-y 2=1的离心率为,设F 2(c,0),双曲线C 2一条渐近线方程为y =x ,可x 2452b a 得|F 2M |==b ,即有|OM |==a .由S △OMF 2=16,得ab =16,即ab =32.又bc a 2+b 2c 2-b 212a 2+b 2=c 2,且=,解得a =8,b =4,c =4,∴双曲线的实轴长为16.c a 52510.(2019年江西南昌模拟)已知等腰梯形ABCD 中AB ∥CD ,AB =2CD =4,∠BAD =60°,双曲线以A ,B 为焦点,且与线段CD (包括端点C ,D )有两个交点,则该双曲线的离心率的取值范围是( )A .[,+∞) B .[,+∞)23C .[+1,+∞)D .[+1,+∞)23【答案】D【解析】当双曲线过点C ,D 时,由平面几何可知∠ACB =90°,AB =4,BC =2,AC =2,所以32c =4,|CA |-|CB |=2(-1)=2a ,即a =-1,c =2,此时==+1.若双曲线与线段CD 相33ca 23-13交,则双曲线的张口变大,离心率变大,即e ≥+1,故选D .311.已知双曲线E :-=1(a >0,b >0),若矩形ABCD 的四个顶点在E 上,AB ,CD 的中点为E x 2a 2y 2b 2的两个焦点,且2|AB |=3|BC |,则E 的离心率是________.【答案】2【解析】如图,由题意得|BC |=|F 1F 2|=2c .又2|AB |=3|BC |,∴|AF 1|=c .在Rt △AF 1F 2中,32|AF 2|===.|AF 1|2+|F 1F 2|2(32c )2+(2c )25c 2∴2a =|AF 2|-|AF 1|=c -c =c .∴e ==2.5232ca 12.已知双曲线的中心在原点,焦点F 1,F 2在坐标轴上,离心率为且过点(4,-),点210M (3,m )在双曲线上.(1)求双曲线方程;(2)求证:MF 1⊥MF 2;(3)求△F 1MF 2的面积.(1)解:∵e =,2∴可设双曲线方程为x 2-y 2=λ(λ≠0).∵双曲线过点(4,-),∴16-10=λ,解得λ=6.10∴双曲线方程为x 2-y 2=6.(2)证明:易知F 1(-2,0),F 2(2,0),33∴kMF 1=,kMF 2=.m 3+23m3-23∴kMF 1·kMF 2=·=-.m 3+23m 3-23m 23∵点M (3,m )在双曲线上,∴9-m 2=6,即m 2=3.∴kMF 1·kMF 2=-1.∴MF 1⊥MF 2.(3)解:S △F 1MF 2=|F 1F 2|·|m |=×4×=6.121233。

2.2.2 双曲线的简单几何性质基础梳理1.直线与双曲线的位置关系.一般地,设直线l :y =kx +m (m ≠0),①双曲线C :x 2a 2-y 2b2=1(a >0,b >0),② 把①代入②得(b 2-a 2k 2)x 2-2a 2mkx -a 2m 2-a 2b 2=0.(1)当b 2-a 2k 2=0,即k =±b a时,直线l 与双曲线的渐近线平行,直线与双曲线C 相交于一点.(2)当b 2-a 2k 2≠0,即k ≠±b a时,Δ=(-2a 2mk )2-4(b 2-a 2k 2)(-a 2m 2-a 2b 2). Δ>0⇒直线与双曲线有________公共点,此时称直线与双曲线相交;Δ=0⇒直线与双曲线有________公共点,此时称直线与双曲线相切;Δ<0⇒直线与双曲线________公共点,此时称直线与双曲线相离.想一想:直线和双曲线只有一个公共点,直线一定和双曲线相切吗?2.弦长公式.斜率为k (k ≠0)的直线l 与双曲线相交于A (x 1,y 1),B (x 2,y 2),则|AB |=1+k 2|x 1-x 2|=1+1k2(y 1+y 2)2-4y 1y 2.想一想:当直线的斜率k 不存在或为0时,如何求弦长?自测自评1.中心在坐标原点,离心率为53的双曲线的焦点在y 轴上,则它的渐近线方程为( ) A .y =±54x B .y =±45x C .y =±43x D .y =±34x 2.设F 1和F 2为双曲线x 2a 2-y 2b2=1(a >0,b >0)的两个焦点,若F 1,F 2,P (0,2b )是正三角形的三个顶点,则双曲线的离心率为( )A.32 B .2 C.52 D .33.已知双曲线方程为x 2-y 24=1,过P (1,0)的直线l 与双曲线只有一个公共点,则l 的条数为( )A .4条B .3条C .2条D .1条基础巩固1.设双曲线x 2a 2-y 2b 2=1(a >0,b >0)的虚轴长为2,焦距为23,则双曲线的渐近线方程为( ) A .y =±2x B .y =±2xC .y =±22xD .y =±12x 2.已知双曲线x 2a 2-y 2b 2=1的一条渐近线方程为y =43x ,则双曲线的离心率为( ) A.53 B.43 C.54 D.323.若圆x 2+y 2-4x -9=0与y 轴的两个交点A ,B 都在双曲线上,且A ,B 两点恰好将此双曲线的焦距三等分,则此双曲线的标准方程为( )A.x 29-y 272=1B.y 29-x 272=1 C.x 216-y 281=1 D.y 281-x 216=1 4.若双曲线的渐近线方程为y =±3x ,它的一个焦点是(10,0),则双曲线的方程是______________.能力提升5.若实数k 满足0<k <5,则曲线x 216-y 25-k =1与曲线x 216-k -y 25=1的( ) A .实半轴长相等 B .虚半轴长相等C .离心率相等D .焦距相等6.设a ,b 是关于t 的方程t 2cos θ+t sin θ=0的两个不等实根,则过A (a ,a 2),B (b ,b 2)两点的直线与双曲线x 2cos 2θ-y 2sin 2θ=1的公共点的个数为( ) A .0个 B .1个 C .2个 D .3个7.若双曲线x 24-y 2m =1的渐近线方程为y =±32x ,则双曲线的焦点坐标是__________. 8.已知双曲线x 2a 2-y 2b 2=1的离心率为2,焦点与椭圆x 225+y 29=1的焦点相同,那么双曲线的焦点坐标为__________,渐近线方程为__________.9.双曲线与椭圆有共同的焦点F 1(0,-5),F 2(0,5),点P (3,4)是双曲线的渐近线与椭圆的一个交点,试求双曲线方程与椭圆的方程.10.P (x 0,y 0)(x 0≠±a )是双曲线E :x 2a 2-y 2b 2=1(a >0,b >0)上一点,M ,N 分别是双曲线E 的左、右顶点,直线PM ,PN 的斜率之积为15. (1)求双曲线的离心率;(2)过双曲线E 的右焦点且斜率为1的直线交双曲线于A ,B 两点,O 为坐标原点,C 为双曲线上一点,满足OC →=λOA →+OB →,求λ的值.答 案基础梳理1.【答案】(2)两个 一个 没有想一想:【解析】不一定.当直线与双曲线的渐近线平行时,直线与双曲线相交,只有一个交点.2.想一想:【解析】把直线的方程直接代入双曲线方程,求出交点坐标,再求其弦长.自测自评1.【解析】依题意,得e =c a =53.设a =3k ,c =5k ,则b 2=c 2-a 2=25k 2-9k 2=16k 2,则b =4k .又双曲线焦点在y 轴上,∴其渐近线方程为y =±34x . 【答案】D2.【答案】B3.【解析】过P 与渐近线平行的直线与双曲线只有一个公共点,另外x =1与双曲线只有一个公共点,∴l 的条数是3.【答案】B基础巩固1.【解析】由题意得b =1,c =3,所以a =2,所以双曲线的渐近线方程为y =±b ax ,即y =±22x .故选C. 【答案】C2.【解析】双曲线焦点在x 轴,由渐近线方程可得b a =43,可得e =c a =32+423=53. 【答案】A3.【解析】因为圆x 2+y 2-4x -9=0与y 轴的两个交点A ,B 都在双曲线上,且A ,B 两点恰好将此双曲线的焦距三等分,所以A ,B 是双曲线的顶点.令x =0,则y =-3或y =3,A (0,-3),B (0,3),在双曲线中a =3,2c =3×2a =18,所以c =9,得b 2=81-9=72,因此,双曲线的标准方程是y 29-x 272=1.故选B. 【答案】B4.【解析】由渐近线方程知b a=3,又c =10, a 2+b 2=c 2⇒a 2+9a 2=10⇒a 2=1,b 2=9.【答案】x 2-y 29=1能力提升5.【解析】∵0<k <5,∴5-k >0,16-k >0.对于双曲线:x 216-y 25-k=1,其焦距是25-k +16=221-k ;对于双曲线:x 216-k -y 25=1,其焦距是216-k +5=221-k .故焦距相等. 【答案】D6.【解析】由方程t 2cos θ+t sin θ=0,解得t 1=0,t 2=-tan θ,不妨设点A (0,0),B (-tan θ,tan 2θ),则过这两点的直线方程为y =-x tan θ,该直线恰是双曲线x 2cos 2θ-y 2sin 2θ=1的一条渐近线,所以该直线与双曲线无公共点.故选A.【答案】A7.【解析】由渐近线方程为y =±m 2x =±32x ,得m =3,c =7,且焦点在x 轴上. 【答案】(±7,0)8.【解析】椭圆的焦点坐标为(4,0),(-4,0),故c =4,且满足c a=2,故a =2,b =c 2-a 2=23,所以双曲线的渐近线方程为y =±b ax =±3x . 【答案】(4,0),(-4,0) y =±3x9.【答案】解:由共同的焦点F 1(0,-5),F 2(0,5),可设椭圆方程为y 2a 2+x 2a 2-25=1(a 2>25); 双曲线方程为y 2b 2-x 225-b 2=1(0<b 2<25), 点P (3,4)在椭圆上,所以16a 2+9a 2-25=1,得a 2=40, 双曲线过点P (3,4)的渐近线为y =b 25-b 2x , 即4=b 25-b 2×3,b 2=16, 所以椭圆方程为y 240+x 215=1,双曲线方程为y 216-x 29=1. 10.【答案】解:(1)由点P 在双曲线x 2a 2-y 2b 2=1上,有x 20a 2-y 20b 2=1, 由题意又有y 0x 0-a ·y 0x 0+a =15, 可得a 2=5b 2,c 2=a 2+b 2=6b 2,则e =c a =305. (2)联立方程得⎩⎪⎨⎪⎧x 2-5y 2=5b 2,y =x -c ,得4x 2-10cx +35b 2=0, 设A (x 1,y 1),B (x 2,y 2),则⎩⎨⎧x 1+x 2=5c 2,x 1x 2=35b 24. 设OC →=(x 3,y 3),由OC →=λOA →+OB →得⎩⎪⎨⎪⎧x 3=λx 1+x 2,y 3=λy 1+y 2. 又C 为双曲线E 上一点,即x 23-5y 23=5b 2,有(λx 1+x 2)2-5(λy 1+y 2)2=5b 2,化简得:λ2(x 21-5y 21)+(x 22-5y 22)+2λ(x 1x 2-5y 1y 2)=5b 2,又A (x 1,y 1),B (x 2,y 2)在双曲线E 上,所以x 21-5y 21=5b 2,x 22-5y 22=5b 2. 又x 1x 2-5y 1y 2=x 1x 2-5(x 1-c )(x 2-c )=-4x 1x 2+5c (x 1+x 2)-5c 2=10b 2, 得:λ2+4λ=0,解出λ=0或λ=-4.。

双曲线一、单选题(共29题;共58分)1.已知双曲线的焦距为,则的离心率为()A. B. C. D.2.已知,是双曲线的两个焦点,以线段为边作正,若边的中点在双曲线上,则双曲线的离心率为()A. B. C. D.3.双曲线的渐近线方程为()A. B. C. D.4.双曲线的一个焦点到一条渐近线的距离为()A. 4B.C. 2D.5.实轴长为的双曲线上恰有个不同的点满足,其中,分别是双曲线的左、右顶点.则的离心率的取值范围为()A. B. C. D.6.双曲线方程为x2-2y2=1,则它的左焦点的坐标为( )A. (-,0)B. (-,0)C. (-,0)D. (-,0)7.已知双曲线的离心率,且其右焦点,则双曲线的方程为()A. B. C. D.8.已知双曲线的渐近线为,实轴长为,则该双曲线的方程为()A. B. 或C. D. 或9.双曲线的焦点坐标是( )A. B. C. D.10.已知双曲线(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线l与双曲线的右支有且只有一个交点,则此双曲线的离心率e的取值范围是()A. B. (1,2), C. D.11.设F1,F2是双曲线的两个焦点,P在双曲线上,当△F1PF2的面积为时,的值为()A. 2B. 3C. 4D. 612.已知双曲线的左、右焦点为、,在双曲线上存在点P满足,则此双曲线的离心率e的取值范围是()A. B. C. D.13.设为双曲线的右焦点,过坐标原点的直线依次与双曲线的左.右支交于点,若,则该双曲线的离心率为()A. B. C. D.14.已知双曲线:的离心率为,则的渐近线方程为()A. B. C. D.15.双曲线C的对称轴与坐标轴重合,两个焦点分别为F1,F2,虚轴的一个端点为A,若△AF1F2是顶角为120°的等腰三角形,则双曲线C的渐近线方程为()A. B. 或 C. D. 或16.若双曲线的一条渐近线被圆所截得的弦长为2,则的离心率为()A. 2B.C.D.17.过点,且与双曲线有相同渐近线的双曲线的方程是()A. B. C. D.18.若双曲线的实轴长、虚轴长、焦距成等差数列,则双曲线的渐近线方程是()A. B. C. D.19.设、分别为双曲线的左、右顶点,、是双曲线上关于轴对称的不同两点,设直线、的斜率分别为、,若,则双曲线的离心率是()A. B. C. D.20.双曲线的焦点坐标为()A. B. C. D.21.双曲线的渐近线方程是()A. B. C. D.22.已知双曲线:(,)的左右顶点分别为,,点,若三角形为等腰直角三角形,则双曲线的离心率为()A. B. C. 2 D. 323.已知中心在原点,对称轴为坐标轴的双曲线的一条渐近线方程为,则该双曲线的离心率是()A. B. C. 或 D. 或24.若双曲线与直线无交点,则离心率的取值范围()A. B. C. D.25.若双曲线的离心率大于2,则该双曲线的虚轴长的取值范围是()A. B. C. D.26.已知点为双曲线上一点,则它的离心率为()A. B. C. D.27.设双曲线的一个焦点为F,虚轴的一个端点为B,焦点F到一条渐近线的距离为d,若,则双曲线离心率的取值范围是()A. B. C. D.28.设点是双曲线上的一点,分别是双曲线的左、右焦点,已知,且,则双曲线的一条渐近线方程是()A. B. C. D.29.以原点为中心,焦点在y轴上的双曲线C的一个焦点为,一个顶点为,则双曲线C的方程为()A. B. C. D.二、填空题(共12题;共13分)30.设为曲线上一点,,,若,则________.31.已知双曲线的离心率为2,则点到的渐近线的距离为________.32.若点在双曲线上,它的横坐标与双曲线的右焦点的横坐标相同,则点与双曲线的左焦点的距离为________33.双曲线上的一点到一个焦点的距离等于1,那么点到另一个焦点的距离为________.34.已知双曲线的离心率为2,过右焦点且垂直于轴的直线与双曲线交于两点. 设到双曲线的同一条渐近线的距离分别为和,且,则双曲线的方程为________.35.双曲线- =1的渐近线方程是________,实轴长为________.36.已知双曲线C的中心在原点,焦点在x轴上,其渐近线方程为2x±3y=0,焦距为2 ,则双曲线C的标准方程为________.37.双曲线的一个焦点是,一条渐近线是,那么双曲线的方程是________38.已知双曲线(,)满足,且双曲线的右焦点与抛物线的焦点重合,则该双曲线的方程为________.39.设是双曲线上一点,双曲线的一条渐近线方程为,分别是双曲线的左、右焦点,若,则的值为________.40.双曲线的其中一个焦点坐标为,则实数________.41.已知分别为双曲线的左、右焦点,过与双曲线的一条渐近线平行的直线交双曲线于点,若,则双曲线的离心率为________.三、解答题(共5题;共55分)42.已知双曲线的中心在原点,焦点在坐标轴上,离心率为,且过点.(1)求双曲线的方程;(2)若点在双曲线上,求的面积.43.已知双曲线与椭圆有相同焦点,且经过点(4,6).(1)求双曲线方程;(2)若双曲线的左,右焦点分别是F1,F2,试问在双曲线上是否存在点P,使得|PF1|=5|PF2|.请说明理由.44.已知双曲线:的实轴长为2.(1)若的一条渐近线方程为,求的值;(2)设、是的两个焦点,为上一点,且,的面积为9,求的标准方程.45.已知双曲线的中心在原点,焦点,在坐标轴上,离心率为,且过点.(1)求双曲线的方程;(2)若点在双曲线上,求证:;(3)求的面积.46.双曲线x2﹣=1(b>0)的左、右焦点分别为F1、F2,直线l过F2且与双曲线交于A、B两点.(1)若l的倾斜角为,△F1AB是等边三角形,求双曲线的渐近线方程;(2)设b= ,若l的斜率存在,M为AB的中点,且=0,求l的斜率.答案解析部分一、单选题1.【答案】C【考点】双曲线的简单性质【解析】【解答】依题意可知,所以,故,所以,故答案为:C.【分析】根据求得的值,进而求得双曲线离心率.2.【答案】C【考点】双曲线的简单性质【解析】【解答】依题意可知双曲线的焦点为,,,三角形高是,,边的中点,,代入双曲线方程得:,整理得:,,,整理得,求得,,.故答案为:C.【分析】先根据双曲线方程求得焦点坐标的表达式,进而可求得三角形的高,则点的坐标可得,进而求得边的中点的坐标,代入双曲线方程求得,和的关系式化简整理求得关于的方程求得.3.【答案】D【考点】双曲线的简单性质【解析】【解答】令,整理得,所以双曲线的渐近线方程为.故答案为:D【分析】令双曲线的为,从而得到方程,化简后即得渐近线方程.4.【答案】C【考点】双曲线的简单性质【解析】【解答】双曲线的,,,一个焦点设为,,一条渐近线设为,可得一个焦点到一条渐近线的距离为.故答案为:C.【分析】求得双曲线的,,,可设一个焦点和一条渐近线方程,由点到直线的距离公式,可得所求值.5.【答案】A【考点】双曲线的简单性质【解析】【解答】依题意可得,,,设,则由,得,整理得.由,得,因为双曲线上恰有个不同的点满足,所以方程有两不等实根,所以只需,解得,则.故答案为:A【分析】先由题意,得到,,,设,根据,得,再与双曲线联立,消去,得到,根据双曲线上存在个不同的点满足,得到只需,求出,进而可求出离心率的范围.6.【答案】C【考点】双曲线的标准方程【解析】【解答】由,可得,,由得,所以左焦点坐标为(-,0)故答案为:C【分析】将双曲线化成标准式,再结合双曲线的关系式求解7.【答案】B【考点】双曲线的标准方程【解析】【解答】由双曲线的离心率,且其右焦点为,可得,所以,所求双曲线的方程为,故答案为:B.【分析】由已知双曲线的离心率,右焦点为列式,得到,即可求出双曲线的标准方程.8.【答案】B【考点】双曲线的标准方程,双曲线的简单性质【解析】【解答】当双曲线的焦点在轴上时, ,又,即,所以,所求双曲线的方程为: ;当双曲线的焦点在轴上时, ,又,即,所以,所以所求双曲线的方程为: .所以所求双曲线方程为: 或.故答案为:.【分析】根据双曲线的焦点所在位置分两种情况讨论: 当双曲线的焦点在轴上时, ; 当双曲线的焦点在轴上时, ,结合可解得.9.【答案】D【考点】双曲线的简单性质【解析】【解答】由得,故,故焦点坐标为故答案为:D【分析】将化简成标准方程再进行焦点坐标运算即可.10.【答案】A【考点】双曲线的简单性质【解析】【解答】已知双曲线的右焦点为,若过点且倾斜角为的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率,,离心率,,故答案为:.【分析】若过点且倾斜角为的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率.根据这个结论可以求出双曲线离心率的取值范围.11.【答案】C【考点】双曲线的简单性质【解析】【解答】双曲线的两个焦点坐标为,设的坐标为,则△的面积为,,,代入双曲线方程解得,不妨取,,,故答案为:.【分析】求得双曲线的焦点坐标,利用△的面积为,确定的坐标,运用两点的距离公式,即可求得结论.12.【答案】B【考点】双曲线的应用【解析】【解答】因为为的边的中线,可知,双曲线上存在点满足,则,由,可知,则。


双曲线的简单几何性质练习题班级 姓名 学号1.已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为( ) A.x 24-y 212=1B.x 212-y 24=1C.x 210-y 26=1D.x 26-y 210=1 2.(新课标卷Ⅰ)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为52,则C 的渐近线方程为( )A .y =±14xB .y =±13xC .y =±12x D .y =±x 3.下列双曲线中离心率为62的是( ) A.x 22-y 24=1 B.x 24-y 22=1C.x 24-y 26=1 D.x 24-y 210=1 4.中心在原点,实轴在x 轴上,一个焦点在直线3x -4y +12=0上的等轴双曲线方程是( )A .x 2-y 2=8B .x 2-y 2=4C .y 2-x 2=8D .y 2-x 2=45.已知双曲线x 2a 2-y 2b2=1的两条渐近线互相垂直,则双曲线的离心率为( ) A.3B.2C.52D.226.双曲线x 24+y 2k=1的离心率e ∈(1,2),则k 的取值范围是( ) A .(-10,0) B .(-12,0)C .(-3,0) D .(-60,-12)7.已知双曲线E 的中心为原点,F (3,0)是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为N (-12,-15),则E 的方程为( )A.x 23-y 26=1B.x 24-y 25=1C.x 26-y 23=1D.x 25-y 24=1 8.(江苏高考)双曲线x 216-y 29=1的两条渐近线的方程为________. 9.已知双曲线中心在原点,一个顶点的坐标是(3,0)且焦距与虚轴长之比为5∶4,则双曲线的标准方程为.10.过双曲线x 2-y 23=1的左焦点F 1,作倾斜角为π6的直线AB ,其中A ,B 分别为直线与双曲线的交点,则|AB |的长为________.11.过双曲线x 2a 2-y 2b2=1(a >0,b >0)的左焦点且垂直于x 轴的直线与双曲线相交于M ,N 两点,以MN 为直径的圆恰好过双曲线的右顶点,则双曲线的离心率为________.12.双曲线x 29-y 216=1的右顶点为A ,右焦点为F ,过点F 平行于双曲线的一条渐近线的直线与双曲线交于点B ,则△AFB 的面积为________.13.求适合下列条件的双曲线的标准方程:(1)过点(3,-2),离心率e=5 2;(2)已知双曲线的中心在原点,焦点F1,F2在坐标轴上,实轴长和虚轴长相等,且过点P(4,-10).14.已知双曲线C:x2a2-y2b2=1(a>0,b>0)的离心率为3,且a2c=33.(1)求双曲线C的方程;(2)已知直线x-y+m=0与双曲线C交于不同的两点A,B,且线段AB的中点在圆x2+y2=5上,求m的值.参考答案1.已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为( ) A.x 24-y 212=1B.x 212-y 24=1 C.x 210-y 26=1D.x 26-y 210=1 解析:选A 由题意知c =4,焦点在x 轴上, 所以⎝⎛⎭⎫b a 2+1=e 2=4,所以b a =3,又由a 2+b 2=4a 2=c 2=16,得a 2=4,b 2=12.所以双曲线方程为x 24-y 212=1. 2.(新课标卷Ⅰ)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为52,则C 的渐近线方程为( )A .y =±14xB .y =±13x C .y =±12x D .y =±x 解析:选C 因为双曲线x 2a 2-y 2b 2=1的焦点在x 轴上,所以双曲线的渐近线方程为y =±b ax .又离心率为e =c a =a 2+b 2a =1+⎝⎛⎭⎫b a 2=52,所以b a =12,所以双曲线的渐近线方程为y =±12x .3.下列双曲线中离心率为62的是( ) A.x 22-y 24=1 B.x 24-y 22=1 C.x 24-y 26=1 D.x 24-y 210=1 解析:选B 由e =62得e 2=32,∴c 2a 2=32, 则a 2+b 2a 2=32,∴b 2a 2=12,即a 2=2b 2.因此可知B 正确. 4.中心在原点,实轴在x 轴上,一个焦点在直线3x -4y +12=0上的等轴双曲线方程是( )A .x 2-y 2=8B .x 2-y 2=4C .y 2-x 2=8D .y 2-x 2=4 解析:选A 令y =0得,x =-4,∴等轴双曲线的一个焦点坐标为(-4,0),∴c =4,a 2=12c 2=12×16=8,故选A. 5.已知双曲线x 2a 2-y 2b 2=1的两条渐近线互相垂直,则双曲线的离心率为( ) A.3B. 2 C.52D.22解析:选B 由题意可知,此双曲线为等轴双曲线.等轴双曲线的实轴与虚轴相等,则a =b ,c = a 2+b 2=2a ,于是e =c a= 2. 6.双曲线x 24+y 2k=1的离心率e ∈(1,2),则k 的取值范围是( ) A .(-10,0)B .(-12,0)C .(-3,0)D .(-60,-12)解析:选B 由题意知k <0,∴a 2=4,b 2=-k .∴e 2=a 2+b 2a 2=4-k 4=1-k 4. 又e ∈(1,2),∴1<1-k 4<4,∴-12<k <0. 7.已知双曲线E 的中心为原点,F (3,0)是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为N (-12,-15),则E 的方程为( )A.x 23-y 26=1B.x 24-y 25=1 C.x 26-y 23=1 D.x 25-y 24=1 解析:选B 设双曲线的标准方程为x 2a 2-y 2b2=1(a >0,b >0),由题意知c =3,a 2+b 2=9, 设A (x 1,y 1),B (x 2,y 2)则有⎩⎨⎧ x 21a 2-y 21b 2=1,x 22a 2-y 22b 2=1,两式作差得y 1-y 2x 1-x 2=b 2(x 1+x 2)a 2(y 1+y 1)=-12b 2-15a 2=4b 25a2, 又AB 的斜率是-15-0-12-3=1, 所以4b 2=5a 2,代入a 2+b 2=9得a 2=4,b 2=5,所以双曲线标准方程是x 24-y 25=1. 8.(江苏高考)双曲线x 216-y 29=1的两条渐近线的方程为________. 解析:令x 216-y 29=0,解得y =±34x . 答案:y =±34x 9.已知双曲线中心在原点,一个顶点的坐标是(3,0)且焦距与虚轴长之比为5∶4,则双曲线的标准方程为________.解析:由题意得双曲线的焦点在x 轴上,且a =3,焦距与虚轴长之比为5∶4,即c ∶b =5∶4,解得c =5,b =4,∴双曲线的标准方程为x 29-y 216=1. 答案:x 29-y 216=1 10.过双曲线x 2-y 23=1的左焦点F 1,作倾斜角为π6的直线AB ,其中A ,B 分别为直线与双曲线的交点,则|AB |的长为________.解析:双曲线的左焦点为F 1(-2,0),将直线AB 方程:y =33(x +2)代入双曲线方程, 得8x 2-4x -13=0.显然Δ>0,设A (x 1,y 1),B (x 2,y 2),∴x 1+x 2=12,x 1x 2=-138, ∴|AB |=1+k 2·(x 1+x 2)2-4x 1x 2 =1+13×⎝⎛⎭⎫122-4×⎝⎛⎭⎫-138=3. 答案:311.过双曲线x 2a 2-y 2b2=1(a >0,b >0)的左焦点且垂直于x 轴的直线与双曲线相交于M ,N 两点,以MN 为直径的圆恰好过双曲线的右顶点,则双曲线的离心率为________.解析:由题意知,a +c =b 2a, 即a 2+ac =c 2-a 2,∴c 2-ac -2a 2=0,∴e 2-e -2=0,解得e =2或e =-1(舍去).答案:212.双曲线x 29-y 216=1的右顶点为A ,右焦点为F ,过点F 平行于双曲线的一条渐近线的直线与双曲线交于点B ,则△AFB 的面积为________.解析:双曲线x 29-y 216=1的右顶点A (3,0),右焦点F (5,0),渐近线方程为y =±43x . 不妨设直线FB 的方程为y =43(x -5),代入双曲线方程整理,得x 2-(x -5)2=9,解得x =175,y =-3215,所以B ⎝⎛⎭⎫175,-3215. 所以S △AFB =12|AF ||y B |=12(c -a )|y B |=12×(5-3)×3215=3215. 答案:3215. 13.求适合下列条件的双曲线的标准方程:(1)过点(3,-2),离心率e =52; (2)已知双曲线的中心在原点,焦点F 1,F 2在坐标轴上,实轴长和虚轴长相等,且过点P (4,-10).解:(1)若双曲线的焦点在x 轴上,设其标准方程为x 2a 2-y 2b2=1(a >0,b >0). 因为双曲线过点(3,-2),则9a 2-2b2=1.① 又e =c a =a 2+b 2a 2=52,故a 2=4b 2.② 由①②得a 2=1,b 2=14,故所求双曲线的标准方程为x 2-y 214=1. 若双曲线的焦点在y 轴上,设其标准方程为y 2a 2-x 2b 2=1(a >0,b >0).同理可得b 2=-172,不符合题意. 综上可知,所求双曲线的标准方程为x 2-y 214=1. (2)由2a =2b 得a =b ,∴e =1+b 2a2=2,所以可设双曲线方程为x 2-y 2=λ(λ≠0).∵双曲线过点P (4,-10),∴16-10=λ,即λ=6.∴双曲线方程为x 2-y 2=6.∴双曲线的标准方程为x 26-y 26=1. 14.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为3,且a 2c =33. (1)求双曲线C 的方程;(2)已知直线x -y +m =0与双曲线C 交于不同的两点A ,B ,且线段AB 的中点在圆x 2+y 2=5上,求m 的值.解:(1)由题意得⎩⎨⎧a 2c =33,c a =3,解得⎩⎪⎨⎪⎧a =1,c = 3. 所以b 2=c 2-a 2=2. 所以双曲线C 的方程为x 2-y 22=1. (2)设A ,B 两点的坐标分别为(x 1,y 1),(x 2,y 2),线段AB 的中点为M (x 0,y 0). 由⎩⎪⎨⎪⎧x -y +m =0,x 2-y 22=1,得x 2-2mx -m 2-2=0(判别式Δ>0).所以x 0=x 1+x 22=m ,y 0=x 0+m =2m . 因为点M (x 0,y 0)在圆x 2+y 2=5上,所以m 2+(2m )2=5.故m =±1.。

2.3.2 双曲线的简单几何性质自测自评1.双曲线x 24-y 29=1的渐近线方程是( )A .y =±23xB .y =±49xC .y =±32xD .y =±94x2.双曲线x 22-y 214=1的离心率为( ) A .2 B .2 2 C .3 D .43.中心在原点,实轴长为10,虚轴长为6的双曲线的标准方程是( ) A.x 225-y 29=1 B.x 225-y 29=1或y 225-x 29=1 C.x 2100-y 236=1 D.x 2100-y 236=1或y 2100-x 236=1 自测自评1.解析:a 2=4,b 2=9,焦点在x 轴上,∴渐近线方程为y =±b a x =±32x .答案:C2.解析:∵a 2=2,∴a = 2.又b 2=14,∴c 2=a 2+b 2=16.∴c =4.∴e =ca=2 2. 答案:B3.解析:考虑焦点在x 轴或y 轴两种情况,选B. 答案:B忽略标准方程与渐近线的对应关系致错. 基础巩固1.双曲线2x 2-y 2=8的实轴长是 ( ) A .2 B .2 2 C .4 D .4 21.解析:双曲线方程可变形为x 24-y 28=1,所以a 2=4,a =2,2a =4.故选C.答案:C2.双曲线的实轴长与虚轴长之和等于其焦距的2倍,且一个顶点的坐标为(0,2),则双曲线的标准方程为( )A.x 24-y 24=1B.y 24-x 24=1C.y 24-x 28=1 D.x 28-y 24=1 2.解析:2a +2b =22c ,即a +b =2c ,又a =2,且a 2+b 2=c 2,∴a =2,b =2. 答案:B3.已知双曲线x 2a 2-y 25=1的右焦点为(3,0),则该双曲线的离心率等于( )A.31414 B.324 C.32 D.433.解析:根据离心率的定义求解.由双曲线中a ,b ,c 的关系c 2=a 2+b 2,得32=a 2+5,∴a 2=4,∴e =c a =32.答案:C4.椭圆x 24+y 2a =1与双曲线x 2a -y 22=1有相同的焦点,则a 的值是________.4.解析:∵a >0,∴焦点在x 轴上,∴4-a =a +2,∴a =1. 答案:1 能力提升5.(2014·天津卷)已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的一条渐近线平行于直线l :y =2x+10,双曲线的一个焦点在直线l 上,则双曲线的方程为( )A.x 25-y 220=1B.x 220-y 25=1 C.3x 225-3y 2100=1 D.3x 2100-3y225=1 5.解析:由题意知,双曲线的渐近线为y =±b a x ,∴b a=2.∵双曲线的左焦点(-c ,0)在直线l 上,∴0=-2c +10,∴c =5.又∵a 2+b 2=c 2,∴a 2=5,b 2=20,∴双曲线的方程为x 25-y 220=1.答案:A6.(2014·重庆卷)设F 1,F 2分别为双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点,双曲线上存在一点P ,使得|PF 1|+|PF 2|=3b ,|PF 1|·|PF 2|=94ab ,则该双曲线的离心率为( )A.43B.53C.94D .3 6.解析:不妨设P 为双曲线右支上一点,根据双曲线的定义有|PF 1|-|PF 2|=2a ,联立|PF 1|+|PF 2|=3b ,平方相减得|PF 1|·|PF 2|=9b 2-4a 24,则由题设条件,得9b 2-4a 24=94ab ,整理得b a =43(负值舍去),∴e =ca=1+(ba)2=1+(43)2=53.答案:B7.在平面直角坐标系xOy 中,若双曲线x 2m -y 2m 2+4=1的离心率为5,则m 的值为________.7.解析:由题意得m >0,所以a =m ,b =m 2+4,c =m 2+m +4,由e =c a =5得m 2+m +4m=5,解得m =2.答案:28.双曲线C 1与椭圆C 2:x 29+y 225=1共焦点,且C 1与C 2的离心率之和为145,则双曲线C 1的标准方程为______________.8.解析:椭圆的焦点是(0,4),(0,-4),所以c =4,e =45,所以双曲线的离心率等于145-45=2,所以4a=2,所以a =2,所以b 2=42-22=12.所以双曲线的标准方程为y 24-x 212=1.答案:y 24-x 212=19.设F 1,F 2是双曲线x 29-y 216=1的两个焦点,点P 在双曲线上,且∠F 1PF 2=60°,求△F 1PF 2的面积.9.解析:双曲线x 29-y 216=1中a =3,c =5,不妨设|PF 1|>|PF 2|,则|PF 1|-|PF 2|=2a =6, |F 1F 2|2=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|cos 60°, 而|F 1F 2|=2c =10,得|PF 1|2+|PF 2|2-|PF 1|·|PF 2|= (|PF 1|-|PF 2|)2+|PF 1|·|PF 2|=100, 即|PF 1|·|PF 2|=64,S =12|PF 1|·|PF 2|sin 60°=16 3.10.已知双曲线的中心在原点,焦点F 1,F 2在坐标轴上,离心率为2,且过点P (4,-10).(1)求双曲线的方程;(2)若点M (3,m )在双曲线上,求证:MF 1→·MF 2→=0; (3)求△F 1MF 2的面积.10.解析:(1)因为e =2,所以可设双曲线方程为x 2-y 2=λ(λ≠0).因为双曲线过点P (4,-10),所以16-10=λ,即λ=6. 所以双曲线方程为x 2-y 2=6. (2)由(1)可知,双曲线中a =b =6,所以c =23,所以F 1(-23,0),F 2(23,0), 所以kMF 1=m 3+23,kMF 2=m3-23,所以kMF 1·kMF 2=m 29-12=-m 23,因为点M (3,m )在双曲线上, 所以9-m 2=6,得m 2=3.故kMF 1·kMF 2=-1,所以MF 1⊥MF 2,所以MF 1→·MF 2→=0. (3)△F 1MF 2的底边|F 1F 2|=43,底边F 1F 2上的高h =|m |=3, 所以S △F 1MF 2=6.。
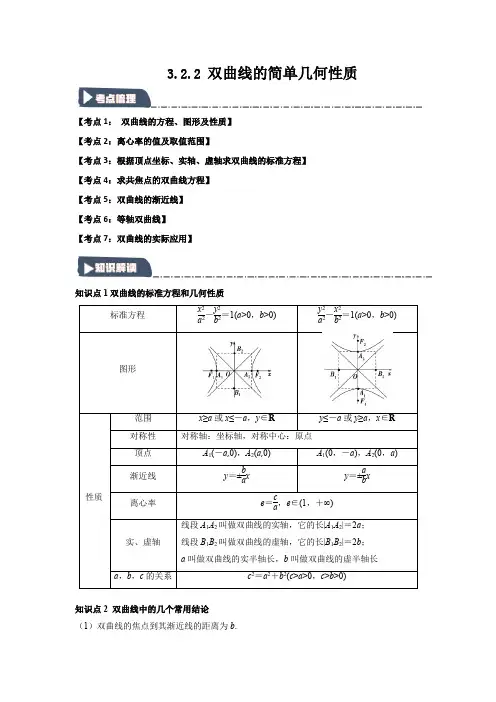
3.2.2 双曲线的简单几何性质【考点1:双曲线的方程、图形及性质】【考点2:离心率的值及取值范围】【考点3:根据顶点坐标、实轴、虚轴求双曲线的标准方程】【考点4:求共焦点的双曲线方程】【考点5:双曲线的渐近线】【考点6:等轴双曲线】【考点7:双曲线的实际应用】知识点1双曲线的标准方程和几何性质x≥a或x≤-a,y∈R y≤-a或y≥a,x∈R知识点2 双曲线中的几个常用结论(1)双曲线的焦点到其渐近线的距离为b.(2)若P 是双曲线右支上一点,F 1,F 2分别为双曲线的左、右焦点,则|PF 1|min =a +c ,|PF 2|min =c -a .(3)同支的焦点弦中最短的为通径(过焦点且垂直于长轴的弦),其长为2b 2a ,异支的弦中最短的为实轴,其长为2a .(4)设P ,A ,B 是双曲线上的三个不同的点,其中A ,B 关于原点对称,直线P A ,PB 斜率存在且不为0,则直线P A 与PB 的斜率之积为b 2a2.(5)P 是双曲线上不同于实轴两端点的任意一点,F 1,F 2分别为双曲线的左、右焦点,则,其中θ为∠F 1PF 2.(6)等轴双曲线①定义:中心在原点,以坐标轴为对称轴,实半轴长与虚半轴长相等的双曲线叫做等轴双曲线.②性质:a =b ;e =2;渐近线互相垂直;等轴双曲线上任意一点到中心的距离是它到两焦点距离的等比中项. (7)共轭双曲线①定义:若一条双曲线的实轴和虚轴分别是另一条双曲线的虚轴和实轴,那么这两条双曲线互为共轭双曲线.②性质:它们有共同的渐近线;它们的四个焦点共圆;它们的离心率的倒数的平方和等于1.【考点1: 双曲线的方程、图形及性质】【典例1】双曲线9x 2−4y 2=36的一个焦点坐标为( ) A .(√13,0)B .(0,√13)C .(√5,0)D .(0,√5)【变式11】已知双曲线C:x 25−y 2b 2=1的焦距为6,则双曲线C 的焦点到渐近线的距离为( )A .√3B .2C .4D .√31【变式12】若双曲线x 2m 2+1−y 2=1的实轴长为4,则正数m =( ) A .√3 B .2C .94D .72【考点2:离心率的值及取值范围】【典例2】已知双曲线x2−y2=4,则其离心率是()A.2B.√2C.√3D.√5【变式21】已知双曲线的两个焦点分别为(0,4),(0,−4),点(−6,4)在该双曲线上,则该双曲线的离心率为()A.4B.3C.2D.√2【变式22】已知双曲线x 2a2−y2b2=1(a>0,b>0)的一条渐近线的倾斜角为π3,则此双曲线的离心率e为()A.2B.2√33C.2或2√33D.√3或2【变式23】若双曲线x 2a2−y2=1(a>0)的离心率为√2,则a=()A.2B.√2C.1D.√22【考点3:根据顶点坐标、实轴、虚轴求双曲线的标准方程】【典例3】已知双曲线C经过点(0,1),离心率为√2,则C的标准方程为()A.x2−y2=1B.x2−y23=1C.y2−x2=1D.y2−x23=1【变式31】双曲线C的中心在原点,焦点在x轴上,离心率e=2,且点P(√6,3)在双曲线C上,则双曲线C的标准方程为()A.x24−y212=1B.x22−y26=1C.x23−y29=1D.x2−y23=1【变式32】已知双曲线x 2a2−y2b2=1的虚轴长为4,离心率为√2,则该双曲线的方程为()A.x2−y24=1B.x24−y2=1C.x24−y24=1D.x22−y22=1【变式33】以椭圆x 28+y24=1的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为()A.x24−y24=1B.x28−y24=1C.x24−y2=1D.x28−y2=1【考点4:双曲线的渐近线】【典例4】已知双曲线C:y 2a2−x2b2=1(a>0,b>0)的离心率为√6,则双曲线C的渐近线方程为()A.y=±√5x B.y=±√6x C.y=±√55x D.y=±√66x【变式41】双曲线x 23m −y26m=1的渐近线方程为()A.y=±√2x B.y=±√22xC.y=±2x D.y=±12x【变式42】双曲线y 24m −x22m=1的渐近线方程为()A.y=±√22x B.y=±√2x C.y=±2x D.y=±12x【变式43】已知双曲线C1:x2+y2m=1(m≠0)与C2:x2−y2=2共焦点,则C1的渐近线方程为().A.x±y=0B.√2x±y=0C.x±√3y=0D.√3x±y=0【变式44】双曲线x 24−y25=1的渐近线方程为.【考点5:等轴双曲线】【典例5】已知等轴双曲线C的对称轴为坐标轴,且经过点A(4√2,2),则双曲线C的标准方程为()A.x236−y236=1B.y236−x236=1C.x228−y228=1D.y228−x228=1【变式51】等轴双曲线的渐近线方程为()A.y=±√2x B.y=±√3x C.y=±x D.y=±√5x【变式52】若双曲线C:x 2m +y2m2−2=1为等轴双曲线,其焦点在y轴上,则实数m=()A.1B.−1C.2D.−2【变式53】中心在原点,实轴在x轴上,一个焦点在直线x−4y+2√2=0上的等轴双曲线方程是()A.x2−y2=8B.x2−y2=4C.y2−x2=8D.y2−x2=4【考点6:共焦点的双曲线】【典例6】多选题过点(3,2)且与椭圆x 28+y23=1有相同焦点的圆锥曲线方程为()A.x225+y220=1B.x215+y210=1C.x23−y22=1D.x22−y23=1【变式61】过点(2,3)且与椭圆5x2+9y2=45有相同焦点的双曲线的标准方程为()A.x2−y23=1B.x29−y2=1C.x22−y29=1D.x29−y25=1【变式62】与双曲线x 216−y24=1有公共焦点,且过点(3√2,2)的双曲线方程为.【考点7:双曲线的实际应用】【典例7】3D打印是快速成型技术的一种,它是一种以数字模型文件为基础,运用粉末状金属或塑料等可粘合材料,通过逐层打印的方式来构造物体的技术,如图所示的塔筒为3D 打印的双曲线型塔筒,该塔筒是由离心率为√10的双曲线的一部分围绕其旋转轴逐层旋转打印得到的,已知该塔筒(数据均以外壁即塔筒外侧表面计算)的上底直径为6√2cm,下底直径为9√2cm,喉部(中间最细处)的直径为8cm,则该塔筒的高为()A.272cm B.18cm C.27√22cm D.18√2cm【变式71】单叶双曲面是最受设计师青睐的结构之一,它可以用直的钢梁建造,既能减少风的阻力,又能用最少的材料来维持结构的完整.如图1,俗称小蛮腰的广州塔位于中国广州市,它的外形就是单叶双曲面,可看成是双曲线的一部分绕其虚轴旋转所形成的曲面.某市计划建造类似于广州塔的地标建筑,此地标建筑的平面图形是双曲线,如图2,最细处的直径为100m,楼底的直径为50√22m,楼顶直径为50√6m,最细处距楼底300m,则该地标建筑的高为()A.350m B.375m C.400m D.450m【变式72】祖暅是我国南北朝时期伟大的科学家,他于5世纪末提出了“幂势既同,则积不容异”的体积计算原理,即“夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等”.某同学在暑期社会实践中,了解到火电厂的冷却塔常用的外形可以看作是双曲线的一部分绕其虚轴旋转所形成的曲面(如图).现有某火电厂的冷却塔设计图纸,其外形的双曲线方程为x2−y24=1(−2≤y≤1),内部虚线为该双曲线的渐近线,则该同学利用“祖暅原理”算得此冷却塔的体积为.【变式73】青花瓷,中华陶瓷烧制工艺的珍品,是中国瓷器的主流品种之一.如图是一个落地青花瓷,其外形称为单叶双曲面,且它的外形左右对称,可以看成是双曲线的一部分绕其虚轴旋转所形成的曲面.若该花瓶横截面圆的最小直径为16cm,上瓶口圆的直径为20cm,上瓶口圆与最小圆圆心间的距离为12cm,则该双曲线的离心率为.一、单选题1.已知等轴双曲线C的对称轴为坐标轴,且经过点A(4√2,2),则双曲线C的标准方程为()A.x236−y236=1B.y236−x236=1C.x228−y228=1D.y228−x228=12.等轴双曲线的渐近线方程为()A.y=±√2x B.y=±√3x C.y=±x D.y=±√5x3.若双曲线C:x2m +y2m2−2=1为等轴双曲线,其焦点在y轴上,则实数m=()A.1B.−1C.2D.−24.中心在原点,实轴在x轴上,一个焦点在直线x−4y+2√2=0上的等轴双曲线方程是()A.x2−y2=8B.x2−y2=4C.y2−x2=8D.y2−x2=45.设双曲线E的中心为O,一个焦点为F,过F作E的两条渐近线的垂线,垂足分别为A、B.若|BF|=√2|OA|,则E的离心率等于()A.√62B.√2C.√3D.36.若双曲线x25+y2m=1的离心率为2,则m的值为()A.−5B.−10C.−15D.−207.已知双曲线C:y2a2−x2b2=1(a>0,b>0)的实半轴长为√3,其上焦点到双曲线的一条渐近线的距离为3,则双曲线C的渐近线方程为()A.y=±√3x B.y=±√33x C.y=±√32x D.y=±2√33x8.双曲线E:x29−y236=1的渐近线方程为()A.y=±14x B.y=±12x C.y=±2x D.y=±4x9.已知双曲线C:x24−y23=1,以右顶点A为圆心,r为半径的圆上一点M(M不在x轴上)处的切线与C交于S、T两点,且M为ST中点,则r的取值范围为()A.r>2√217B.0<r<4√57C.r>67D.r>110.已知双曲线C:x2a2−y2b2=1(a>0,b>0),点B的坐标为(0,b),若C上存在点P使得|PB|<b成立,则C的离心率取值范围是()A.[√2+12,+∞)B.[√5+32,+∞)C.(√2,+∞)D.(√5+12,+∞)11.双曲线y23−x26=1的焦点坐标为()A.(±√3,0)B.(0,±√3)C.(±3,0)D.(0,±3)12.已知点A为双曲线x24−y2=1的左顶点,点B和点C在双曲线的左支上,若△ABC是等腰直角三角形,则△ABC的面积是()A.4B.89C.169D.329二、填空题13.双曲线x29−y27=1的右焦点坐标为.14.如果双曲线关于原点对称,它的焦点在y轴上,实轴的长为8,焦距为10.则双曲线的标准方程为.15.已知双曲线的左右焦点分别为F1,F2,过F1的直线与左支交于A,B两点,若|AB|=5,且双曲线的实轴长为8,则△ABF2的周长为.三、解答题16.已知双曲线C:x2a2−y2b2=1(a>0,b>0)的焦距为10,F为双曲线的右焦点,且点F到渐近线的距离为4.(1)求双曲线C的方程;(2)若点A(12,0),点P为双曲线C左支上一点,求|PA|+|PF|的最小值.17.已知双曲线C与椭圆x24+y2=1有公共焦点,其渐近线方程为y=±√22x.(1)求双曲线C的标准方程;(2)若直线y=x+m与双曲线C交于A,B两点,且|AB|=4√2,求实数m的值.。
2024学年高二数学重难点和易错点专项(双曲线的简单几何性质)练习重难点1已知方程求焦距、实轴、虚轴1.已知12,F F 是双曲线2221(0)3y x a a-=>的两个焦点,若双曲线的左、右顶点和原点把线段12F F 四等分,则该双曲线的焦距为( ) A .1 B .2C .3D .42.双曲线221x y m-=的实轴长是虚轴长的3倍,则m 的值为( )A .9B .-9C .19D .19-3.已知双曲线C :()222210,0x y a b a b-=>>的左顶点为A ,右焦点为F ,焦距为6,点M 在双曲线C 上,且MF AF ⊥,2MF AF =,则双曲线C 的实轴长为( )A .2B .4C .6D .84.如图,这是一个落地青花瓷,其外形被称为单叶双曲面,可以看成是双曲线C :22221x y a b -=的一部分绕其虚轴所在直线旋转所形成的曲面.若该花瓶横截面圆的最小直径为8cm ,瓶高等于双曲线C 的虚轴长,则该花瓶的瓶口直径为( )A.cm B .24cm C .32cmD .cm5.若实数m 满足05m <<,则曲线221155x y m -=-与曲线221155x y m -=-的( )A .离心率相等B .焦距相等C .实轴长相等D .虚轴长相等6.等轴双曲线2221(0)x y a a -=>的焦距为 .7.已知椭圆22122:1(0)x y C a b a b +=>>的左、右焦点分别为1F ,2F ,M 是1C 上任意一点,12MF F △的面积的1C 的焦距为2,则双曲线22222:1y x C a b -=的实轴长为 .重难点2已知方程求双曲线的渐近线8.双曲线()22102y x a a a-=≠的渐近线方程为( )A .2y x =±B .12y x =±C .y =D .2y x =±9.已知双曲线22221(0,0)x y a b a b-=>>的离心率为e ,若点(与点(),2e 都在双曲线上,则该双曲线的渐近线方程为( )A .y x =±B .y =C .y =D .2y x =±10.双曲线22139x y -=的两条渐近线的夹角为( )A .30︒B .45︒C .60︒D .120︒11.在平面直角坐标系xOy 中,双曲线2221x y -=的渐近线方程为( )A .2y x =± B .y =C .y x =±D .4y x =±12.已知双曲线()2222:10,0x y C a b a b-=>>的一个焦点是F ,点F 到C 的渐近线的距离为d ,则d ( )A .与a 有关B .与a 无关C .与b 有关D .与b 无关13.双曲线2221(0)36x y a a -=>的渐近线方程为2y x =±,则=a .14.已知双曲线()22:10y C x n n-=>的一条渐近线为0nx =,则C 的离心率为 .重难点3由双曲线的几何性质求标准方程15.已知双曲线2222:1y x C a b-=的一条渐近线斜率为2-,实轴长为4,则C 的标准方程为( )A .2214x y -=B .221416y x -=C .2214y x -=D .221164y x -=16倍,且一个顶点的坐标为()2,0,则双曲线的标准方程为( )A .22144x y -=B .22144-=y xC .2214y x -=D .2214x y -=17.已知双曲线2222:1(0,0)x y C a b a b-=>>的焦点到渐近线的距离为4,实轴长为6,则C 的方程为( )A .22149x y -=B .22194x y -=C .221169x y -=D .221916x y -=18.求双曲线以椭圆22185x y +=的焦点为顶点,且以椭圆的顶点为焦点,则双曲线的方程是 ( )A .22135x y -=B .22153x y -=C .22135y x -=D .22153y x -=19.已知双曲线C :22221x y a b-=(0a >,0b >)的实轴长为4.若点()P m 是双曲线C位于第一象限内的一点,则m =( )A .2B .1CD20.双曲线()2210,0x y m n m n -=>>的渐近线方程为y x =,实轴长为2,则m n -为( )A .14-B .1C .12D .12-21.如果中心在原点,对称轴在坐标轴上的等轴双曲线的一个焦点为()10,6F -,那么此双曲线的标准方程为 .重难点4求共渐近线的双曲线方程22.若双曲线C 与双曲线2211612x y -=有相同的渐近线,且经过点(,则双曲线C 的标准方程是 .23.与双曲线221169x y -=渐近线相同,且一个焦点坐标是()0,5的双曲线的标准方程是 .24.若双曲线C 与2219x y -=有共同渐近线,且与椭圆2214020x y +=有相同的焦点,则该双曲线C 的方程为 .25.双曲线22:12y C x -=,写出一个与双曲线C 有共同的渐近线但离心率不同的双曲线方程 .26.求与双曲线22143y x -=有共同的渐近线,且经过点()3,2M -的双曲线的标准方程.27.已知双曲线E 与双曲线221169x y -=共渐近线,且过点()3A -,若双曲线M 以双曲线E 的实轴为虚轴,虚轴为实轴,试求双曲线M 的标准方程.28.已知双曲线()2222:10,0x y C a b a b-=>>的两个焦点分别为()1F ,)2F ,且过点)2P.(1)求双曲线C 的虚轴长;(2)求与双曲线C 有相同渐近线,且过点()3,6Q -的双曲线的标准方程.重难点5根据,,a b c 齐次式关系求渐近线方程29.过原点的直线l 与双曲线E :()222210,0x y a b a b-=>>交于A ,B 两点(点A 在第一象限),AC x ⊥交x轴于C 点,直线BC 交双曲线于点D ,且1AB AD k k ⋅=,则双曲线的渐近线方程为( )A .2y x =±B .12y x =±C .y =D .y x =30.双曲线2222:1(0,0)x y E a b a b-=>>,点A ,B 均在E 上,若四边形OACB 为平行四边形,且直线OC ,AB的斜率之积为3,则双曲线E 的渐近线的倾斜角为( )A .π3B .π3或2π3C .π6D .π6或5π631.已知双曲线2222:1(0,0)x y C a b a b-=>> )A .12y x =±B .2y x =±C .y =D .y =32.设12,F F 分别是双曲线22221x y a b-=()0,0a b >>的左、右焦点,若双曲线右支上存在一点P 满足212PF F F =,且124cos 5PF F ∠=,则双曲线的渐近线方程为( ) A .340x y ±= B .430x y ±= C .350x y ±= D .540x y ±=33.已知F 为双曲线C :22221x y a b-=(0a >,0b >)的右焦点,过点F 作x 轴的垂线与双曲线及它的渐近线在第一象限内依次交于点A 和点B .若A B A F =,则双曲线C 的渐近线方程为( )A 0y ±=B .0x =C 0y ±=D .0x =34.如图,已知1F ,2F 为双曲线()222210,0x y a b a b-=>>的焦点,过2F 作垂直于x 轴的直线交双曲线于点P ,且1230PF F ∠=︒,则双曲线的渐近线方程为 .35.过双曲线2222:1-=y W x a b 的右焦点F 作x 轴的垂线,与两条渐近线的交点分别为A ,B ,若OAB 为等边三角形,则W 的渐近线方程为 ,W 的离心率为 .重难点6求双曲线的离心率36.设12,F F 是双曲线2222:1(0,0)x y C a b a b -=>>的左、右焦点,过点1F 作双曲线的一条渐近线的垂线,垂足为M .若2MF ,则双曲线C 的离心率为( )AB C .3 D37.已知F 为双曲线C :()222210,0x y a b a b-=>>的右焦点,平行于x 轴的直线l 分别交C 的渐近线和右支于点A ,B ,且90OAF ∠=︒,OBF OFB ∠=∠,则C 的离心率为( )A .2B C .32D38.设1F 、2F 分别为双曲线22221(0,0)x y a b a b-=>>的左右焦点,O 为坐标原点,过左焦点1F 作直线1F P 与圆222x y a +=切于点E ,与双曲线右支交于点P ,且121||2OP F F =,则双曲线的离心率为( )AB .2C D39.已知双曲线2222>:1(00,)>x y C a b a b -=的左右焦点12F F ,,点2F 关于一条渐近线的对称点在另一条渐近线上,则双曲线C 的离心率是( )AB C .2D .340.若0m >,双曲线1C :2212x y m -=与双曲线2C :2218x y m-=的离心率分别为1e ,2e ,则( )A .12e e 的最小值为94B .12e e 的最小值为32C .12e e 的最大值为94D .12e e 的最大值为3241.已知双曲线2222:1(0,0)y x C a b a b-=>>,过其上焦点F 的直线与圆222x y a +=相切于点A ,并与双曲线C的一条渐近线交于点(,B A B 不重合).若25FB FA =,则双曲线C 的离心率为 .42.已知双曲线C :22221(0,0)x y a b a b-=>>的右焦点为F ,过F 分别作C 的两条渐近线的平行线与C 交于A ,B 两点,若||AB =,则C 的离心率为43.已知双曲线()2222:10,0x y C a b a b-=>>的右顶点为A ,左、右焦点分别为1F ,2F ,渐近线在第一象限的部分上存在一点P ,且1OP OF =,直线1PF ,则该双曲线的离心率为 .重难点7求双曲线离心率的取值范围44.过双曲线22221(0,0)x y a b a b-=>>的左焦点且垂直于x 轴的直线与双曲线交于,A B 两点,D 为虚轴上的一个端点,且ADB ∠为钝角,则此双曲线离心率的取值范围为( )A .(B .C .)2D .)+∞45.已知1F ,2F 是双曲线()222210,0x y a b a b-=>>的左、右焦点,若双曲线上存在点P 满足2212PF PF a ⋅=- ,则双曲线离心率的最小值为( )AB C .2 D46.已知双曲线22221E y x a b-=:(0a >,0b >)的离心率为e ,若直线2y x =±与E 无公共点,则e 的取值范围是 .47.已知双曲线2222:1(0,0),x y C a b F a b-=>>为双曲线的右焦点,过点F 作渐近线的垂线()0MN MN k <,垂足为M ,交另一条渐近线于N ,若()2NM MF λλ=≥,则双曲线C 的离心率的取值范围是( )A .)+∞ B .(C .D .3⎡⎫+∞⎪⎢⎣⎭48.双曲线2221y x b-=的左焦点为F ,()0,A b -,M 为双曲线右支上一点,若存在M ,使得5FM AM +=,则双曲线离心率的取值范围为( )A .(B .(C .)+∞D .)+∞49.如图为陕西博物馆收藏的国宝——唐ꞏ金筐宝钿团化纹金杯,杯身曲线内收,玲珑娇美,巧夺天工,是唐朝金银细作的典范之作.该杯的主体部分可以近似看作是双曲线C :()222210,0x y a b a b -=>>的部分的旋转体.若该双曲线右支上存在点P ,使得直线P A ,PB (点A ,B 为双曲线的左、右顶点)的斜率之和为83,则该双曲线离心率的取值范围为 .50.已知双曲线C :22221x y a b -=(0a >,0b >)的左、右焦点分别为1F ,2F ,若在C 上存在点P (不是顶点),使得21123PF F PF F ∠∠=,则C 的离心率的取值范围为 .重难点8根据离心率求参数51.已知有公共焦点的椭圆与双曲线的中心为原点,焦点在x 轴上,左右焦点分别为1F ,2F ,且它们在第一象限的交点为P ,12PF F △是以1PF 为底边的等腰三角形.若110PF =,双曲线的离心率的取值范围为(1,2),则该椭圆的焦距的取值范围是( )A .55,32⎛⎫ ⎪⎝⎭B .205,3⎛⎫ ⎪⎝⎭C .10,53⎛⎫ ⎪⎝⎭D .510,23⎛⎫ ⎪⎝⎭52.设双曲线2222:1y x C a b-=(0,0)a b >>的上、下焦点分别为12,F F P 是C 上一点,且12PF PF ⊥.若12PF F △的面积为4,则=a ( )A .8B .4C .2D .153.设k 为实数,已知双曲线2214x y k-=的离心率(2,3)e ∈,则k 的取值范围为54.已知1F ,2F 是双曲线C 的两个焦点,P 为C 上一点,且1260F PF ∠=︒,()121PF PF λλ=>,若C 的离2,则λ的值为 .55.已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别是1F ,2F ,P 是双曲线右支上一点,2120PF F F ⋅= ,O为坐标原点,过点O 作1F P 的垂线,垂足为点H ,若双曲线的离心率e =存在实数m 满足1OH m OF =,则m = .56.已知双曲线22:113x y C m m-=+-m 的取值范围是( )A .()1,1-B .()1,3-C .(),1-∞D .()0,157.点P 是双曲线C :()222210,0x y a b a b-=>>右支上一点,1F ,2F 分别是双曲线C 的左,右焦点,M 为12PF F △的内心,若双曲线C 的离心率32e =,且121MPF MPF MF F S S S λ=+ 2,则λ=( ) A .12 B .34C .1D .23重难点9双曲线的实际应用58.某中心接到其正东、正西、正北方向三个观测点的报告;正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其它两观测点晚2s ,已知各观测点到该中心的距离是680m ,则该巨响发生在接报中心的( )处(假定当时声音传播的速度为340m/s ,相关各点均在同一平面上) A .西偏北45°方向,距离B .东偏南45°方向,距离C .西偏北45°方向,距离D .东偏南45°方向,距离59.如图,B 地在A 地的正东方向4km 处,C 地在B 地的北偏东30︒方向2km 处,河流的沿岸PQ (曲线)上任意一点到A 的距离比到B 的距离远2km .现要在曲线PQ 上选一处M 建一座码头,向B 、C 两地转运货物.经测算,从M 到B 、C 两地修建公路的费用分别是a 万元/km 、2a 万元/km ,那么修建这两条公路的总费用最低是( )A .2)a 万元B .5a 万元C .1)a 万元D .3)a +万元60.如图是等轴双曲线形拱桥,现拱顶离水面5m ,水面宽30m AB =. 若水面下降5m ,则水面宽是 .(结果精确到0.1m )61.如图,一个光学装置由有公共焦点12,F F 的椭圆C 与双曲线C '构成,一光线从左焦点1F 发出,依次经过C '与C 的反射,又回到点1F .,历时m 秒;若将装置中的C '去掉,则该光线从点1F 发出,经过C 两次反射后又回到点1F 历时n 秒,若C '的离心率为C 的离心率的4倍,则mn= .62.如图1,北京冬奥会火种台以“承天载物”为设计理念,创意灵感来自中国传统青铜礼器一尊的曲线造型,基座沉稳,象征“地载万物”,顶部舒展开阔,寓意迎接纯洁的奥林匹克火种.如图2,一种尊的外形近似为某双曲线的一部分绕着虚轴旋转所成的曲面,尊高63cm ,上口直径为40cm ,底部直径为26cm ,最小直径为24cm ,则该双曲线的渐近线与实轴所成锐角的正切值为 .63.(多选)我国首先研制成功的“双曲线新闻灯”,如图,利用了双曲线的光学性质:1F ,2F 是双曲线的左、右焦点,从2F 发出的光线m 射在双曲线右支上一点P ,经点P 反射后,反射光线的反向延长线过1F ;当P 异于双曲线顶点时,双曲线在点P 处的切线平分12F PF ∠.若双曲线C 的方程为221916x y -=,则下列结论正确的是( )A .射线n 所在直线的斜率为k ,则44,33k ⎛⎫∈- ⎪⎝⎭B .当m n ⊥时,1232PF PF ⋅=C .当n 过点()7,5Q 时,光线由2F 到P 再到Q 所经过的路程为13D .若点T 坐标为()1,0,直线PT 与C 相切,则212PF =64.如图1所示,双曲线具有光学性质:从双曲线右焦点发出的光线经过双曲线镜面反射,其反射光线的反向延长线经过双曲线的左焦点.若双曲线E:22221x ya b-=(0a>,0b>)的左、右焦点分别为1F,2F,从2F发出的光线经过图2中的A,B两点反射后,分别经过点C和D,且5tan12CAB∠=-,AB BD⊥,则双曲线E的离心率为.参考答案重难点1已知方程求焦距、实轴、虚轴1.已知12,F F 是双曲线2221(0)3y x a a-=>的两个焦点,若双曲线的左、右顶点和原点把线段12F F 四等分,则该双曲线的焦距为( )A .1B .2C .3D .4【答案】D【详细分析】根据题意列出方程组222243c a c a ⎧=⎨=+⎩进行求解即可. 【答案详解】因为12,F F 是双曲线2221(0)3y x a a-=>的两个焦点,若双曲线的左、右顶点和原点把线段12F F 四等分,所以24c a =,即2c a =,即224c a =, 又因为223c a =+,解得2214a c ⎧=⎨=⎩,所以c =2,所以该双曲线的焦距为2224c =⨯=.故选:D2.双曲线221x y m-=的实轴长是虚轴长的3倍,则m 的值为( )A .9B .-9C .19D .19-【答案】C【详细分析】根据双曲线的方程,求得1,a b ==,结合题意,列出方程,即可求解.【答案详解】由双曲线221x y m-=,可得0m >,且1,a b ==,因为双曲线的实轴长是虚轴长的3倍,可得3a b =,即1=19m =. 故选:C.3.已知双曲线C :()222210,0x y a b a b-=>>的左顶点为A ,右焦点为F ,焦距为6,点M 在双曲线C 上,且MF AF ⊥,2MF AF =,则双曲线C 的实轴长为( )A .2B .4C .6D .8【答案】A【详细分析】运用代入法,结合已知等式进行求解即可.【答案详解】把x c =代入22221x y a b -=中,得2b y a =±,即2bMF a=,因为AF a c =+,2MF AF =, 所以()22b a c a=+⇒22222c a ac a -=+,又3c =,所以2230a a +-=,解得1a =,3a =-舍去,则22a =. 故选:A4.如图,这是一个落地青花瓷,其外形被称为单叶双曲面,可以看成是双曲线C :22221x y a b -=的一部分绕其虚轴所在直线旋转所形成的曲面.若该花瓶横截面圆的最小直径为8cm ,瓶高等于双曲线C 的虚轴长,则该花瓶的瓶口直径为( )A .cmB .24cmC .32cmD .cm【答案】D【详细分析】求出4a =,设出(),M r b ,代入双曲线方程,求出r =. 【答案详解】因为该花瓶横截面圆的最小直径为8cm ,所以4a =.设M 是双曲线C 与瓶口截面的一个交点,该花瓶的瓶口半径为r ,则(),M r b ,所以222214r b b -=,解得r =2r =.故选:D5.若实数m 满足05m <<,则曲线221155x y m -=-与曲线221155x y m -=-的( )A .离心率相等B .焦距相等C .实轴长相等D .虚轴长相等【答案】B【详细分析】根据双曲线的性质逐一详细分析判断即可. 【答案详解】因为05m <<,所以50,150m m ->->,所以曲线221155x y m -=-与曲线221155x y m -=-都是焦点在x 轴上的双曲线,15520155m m m +-=-=-+,所以两曲线的焦点和焦距都相同,故B 正确; 因为20201515m m m--≠-,所以离心率不相等,故A 错误; 因为1515m ≠-,所以实轴长不相等,故C 错误; 因为55m -≠,所以虚轴长不相等,故D 错误. 故选:B.6.等轴双曲线2221(0)x y a a-=>的焦距为 .【答案】【详细分析】根据等轴双曲线定义得到221a b ==,进而求出c =.【答案详解】由题意得,221a b ==,故2222c a b =+=,故c =2c =.故答案为:7.已知椭圆22122:1(0)x y C a b a b +=>>的左、右焦点分别为1F ,2F ,M 是1C 上任意一点,12MF F △的面积的1C 的焦距为2,则双曲线22222:1y x C a b-=的实轴长为 .【答案】4【详细分析】根据椭圆焦点三角形的性质即可列方程求解2,a b =⎧⎪⎨=⎪⎩,进而可求解.【答案详解】由于12MF F △的面积为122M c y cb ⨯⨯≤,由题意知22222,,c b c a b c ⎧⋅=⎪=⎨⎪=+⎩所以2,a b =⎧⎪⎨=⎪⎩故双曲线2C 的方程为22143y x -=,则2C 的实轴长为4.故答案为:4重难点2已知方程求双曲线的渐近线8.双曲线()22102y x a a a-=≠的渐近线方程为( )A .2y x =±B .12y x =±C.y =D.2y x =±【答案】C【详细分析】利用双曲线渐近线方程定义计算即可.【答案详解】由题意可得:双曲线()22102y x a a a -=≠渐近线斜率为k ==则其渐近线方程为:y =. 故选:C9.已知双曲线22221(0,0)x y a b a b-=>>的离心率为e,若点(与点(),2e 都在双曲线上,则该双曲线的渐近线方程为( ) A .y x =± B.y = C.y =D .2y x =±【答案】B【详细分析】根据给定条件,列出方程组,结合离心率的意义求出,a b 作答.【答案详解】由点,2)e 在双曲线22221x y a b -=上,得2222241461e a b a b ⎧-=⎪⎪⎨⎪-=⎪⎩,则222420e a b --=,即2222214b e e a==--,整理得42560e e -+=,解得22e =或23e =, 当22e =时,22a b =,此时方程22461a b -=无解, 当23e =时,222b a =,而22461a b -=,解得1,a b ==,所以该双曲线的渐近线方程为y =. 故选:B10.双曲线22139x y -=的两条渐近线的夹角为( )A .30︒B .45︒C .60︒D .120︒【答案】C【详细分析】根据题意求得双曲线的渐近线方程,进而求得其夹角.【答案详解】由双曲线22139x y -=,可得3a b =,所以双曲线的渐近线的方程为by x a=±=,所以两渐近线y =的夹角为60︒. 故选:C.11.在平面直角坐标系xOy 中,双曲线2221x y -=的渐近线方程为( )A.2y x =± B.y = C .y x =±D.4y x =±【答案】B【详细分析】化简双曲线的方程为标准方程,求得,a b 的值,结合双曲线的几何性质,即可求解. 【答案详解】由双曲线2221x y -=,可得其标准方程为22112x y -=,所以,12a b ==,则双曲线的渐近线方程为by x a=±=. 故选:B.12.已知双曲线()2222:10,0x y C a b a b-=>>的一个焦点是F ,点F 到C 的渐近线的距离为d ,则d ( )A .与a 有关B .与a 无关C .与b 有关D .与b 无关【答案】BC【详细分析】根据双曲线标准方程可求得焦点坐标,再利用点到直线距离即可求出d b =,便可得出结论. 【答案详解】设双曲线C 的焦距为2c ,不妨取右焦点F 的坐标为(),0c ,如下图所示:双曲线C 的渐近线方程是by x a=±,即bx ay ±=0,所以===bcd b c, 所以d 与a 无关,与b 有关. 故选:BC.13.双曲线2221(0)36x y a a -=>的渐近线方程为2y x =±,则=a .【答案】3【详细分析】根据双曲线的渐近线方程即可求解.【答案详解】2221(0)36x y a a -=>的渐近线方程为6y x a =±,所以623a a =⇒=,故答案为:314.已知双曲线()22:10y C x n n-=>的一条渐近线为0nx =,则C 的离心率为.2n =⇒=,进而求出双曲线的离心率.【答案详解】双曲线的一条渐近线方程为0nx =,即y =,2n =⇒=,故双曲线22:12y C x -=,所以双曲线的离心率为1e ==重难点3由双曲线的几何性质求标准方程15.已知双曲线2222:1y x C a b-=的一条渐近线斜率为2-,实轴长为4,则C 的标准方程为( )A .2214x y -=B .221416y x -=C .2214y x -=D .221164y x -=【答案】C【详细分析】根据双曲线的基本量关系,结合渐近线方程求解即可.【答案详解】由题意双曲线2222:1y x C a b-=的焦点在y 轴上,则24a =,2a =,又2a b -=-,则1b =,故C 的标准方程为2214y x -=.故选:C16倍,且一个顶点的坐标为()2,0,则双曲线的标准方程为( )A .22144x y -=B .22144-=y xC .2214y x -=D .2214x y -=【答案】A【详细分析】根据条件列关于a ,b ,c 的方程组求解即可.【答案详解】设双曲线的标准方程为22221x y a b-=,由已知得222222a b a a b c ⎧+=⎪=⎨⎪+=⎩,解得22a b =⎧⎨=⎩, 所以双曲线的标准方程为22144x y -=故选:A.17.已知双曲线2222:1(0,0)x y C a b a b-=>>的焦点到渐近线的距离为4,实轴长为6,则C 的方程为( )A .22149x y -=B .22194x y -=C .221169x y -=D .221916x y -=【答案】D【详细分析】由距离公式得出4b =,进而由双曲线的性质得出方程. 【答案详解】右焦点2(,0)F c 到渐近线0bx ay -=4b ==,因为实轴长为26a =,所以3a =,即C 的方程为221916x y -=.故选:D18.求双曲线以椭圆22185x y +=的焦点为顶点,且以椭圆的顶点为焦点,则双曲线的方程是 ( )A .22135x y -=B .22153x y -=C .22135y x -=D .22153y x -=【答案】A【详细分析】根据椭圆22185x y +=方程,可得出其焦点坐标、顶点坐标,进而得到双曲线的焦点坐标、顶点坐标,即可得到双曲线的方程.【答案详解】在椭圆22185x y +=中,c =,椭圆的焦点坐标为,(,左右顶点坐标分别为,()-,则双曲线的顶点坐标为,(,焦点坐标为,()-,且双曲线的焦点在x 轴上,所以a =c =222835b c a =-=-=,所以双曲线的方程为:22135x y -=.故选:A.19.已知双曲线C :22221x y a b-=(0a >,0b >)的实轴长为4.若点()P m 是双曲线C位于第一象限内的一点,则m =( )A.2 B .1CD 【答案】B【详细分析】根据已知条件求得,a b ,从而求得双曲线的方程,代入P 点坐标,由此求得m 的值. 【答案详解】法一:双曲线的几何性质由题知22224,2,a c e abc a =⎧⎪⎪==⎨⎪⎪=-⎩,解得21a b c ⎧=⎪=⎨⎪=⎩,所以双曲线C :2214x y -=.又点()P m 是双曲线C 位于第一象限内的一点, 所以2814m -=(0m >),解得1m =. 法二:由题知24a c e a =⎧⎪⎨===⎪⎩21a b =⎧⎨=⎩, 所以双曲线C :2214x y -=.又点()P m 是双曲线C 位于第一象限内的一点, 所以2814m -=(0m >),解得1m =.故选:B20.双曲线()2210,0x y m n m n -=>>的渐近线方程为2y x =±,实轴长为2,则m n -为( )A .14- B.1C .12 D.1【答案】A【详细分析】根据渐近线方程、实轴长求得,m n ,由此求得m n -.【答案详解】依题意222222a m ab n a m ⎧⎪⎪=⎪=⎨⎪⎪==⎪⎝⎭⎩,解得511,,44m n m n ==-=-. 故选:A21.如果中心在原点,对称轴在坐标轴上的等轴双曲线的一个焦点为()10,6F -,那么此双曲线的标准方程为 .【答案】2211818y x -=【详细分析】根据焦点坐标及题意,设方程为22221(0)y x a a a-=>,根据焦点坐标,可求得2a ,即可得答案.【答案详解】因为一个焦点是()10,6F -,所以6c =,且焦点在y 轴,所以设等轴双曲线方程为22221(0)y x a a a-=>,所以22236c a a =+=,解得218a =,所以双曲线标准方程为2211818y x -=,故答案为:2211818y x -=.重难点4求共渐近线的双曲线方程22.若双曲线C 与双曲线2211612x y -=有相同的渐近线,且经过点(,则双曲线C 的标准方程是 . 【答案】221912y x -=【详细分析】设双曲线C 的方程为221612x y λ-=,根据双曲线C 经过的点求得λ,从而求得双曲线C 的标准方程.【答案详解】由双曲线C 与双曲线2211612x y -=有相同的渐近线,可设双曲线C 的方程为221612x y λ-=,又C 过点(,所以34λ=-,22316124x y -=-,整理得双曲线C 的标准方程是221912y x -=.故答案为:221912y x -=23.与双曲线221169x y -=渐近线相同,且一个焦点坐标是()0,5的双曲线的标准方程是 .【答案】221916y x -=【详细分析】设所求双曲线的方程为22221y x a b -=,由题意有2225a b +=且34a b =,解出22,a b 即可.【答案详解】双曲线221169x y -=的渐近线方程为34y x =?,由焦点坐标是()0,5,可设所求双曲线的方程为22221y x a b-=(0,0)a b >>,得2225a b +=,双曲线渐近线的方程为a y x b =±,由题意有34a b =, 解得29a =,216b =,所以双曲线的方程为221916y x -=.故答案为:221916y x -=.24.若双曲线C 与2219x y -=有共同渐近线,且与椭圆2214020x y +=有相同的焦点,则该双曲线C 的方程为 . 【答案】221182x y -=【详细分析】根据双曲线与椭圆的标准方程,求得渐近线方程与焦点坐标,由双曲线标准方程,建立方程,可得答案.【答案详解】由方程2219x y -=,则其渐近线方程为13y x =±,由椭圆2214020x y +=,则其焦点为()±,由题意可知,双曲线C 的标准方程设为22221x y a b -=,则221320b a a b ⎧=⎪⎨⎪+=⎩,解得22182a b ⎧=⎨=⎩,则双曲线C 的标准方程为221182x y -=,故答案为:221182x y -=.25.双曲线22:12y C x -=,写出一个与双曲线C 有共同的渐近线但离心率不同的双曲线方程 .【答案】2212y x -=(答案不唯一)【详细分析】根据有共同渐近线的双曲线方程的性质进行求解即可.【答案详解】与双曲线C 有共同的渐近线的双曲线方程可设为222y x λ-=,当1λ=-时,得到双曲线方程为2212y x -=,显然该双曲线与双曲线C 有共同的渐近线但离心率不同,故答案为:2212y x -=26.求与双曲线22143y x -=有共同的渐近线,且经过点()3,2M -的双曲线的标准方程.【答案】22168x y -=【详细分析】利用待定系数法即可得到所求双曲线的标准方程.【答案详解】与双曲线22143y x -=有相同的渐近线的双曲线可设为22(0)43y x λλ-=≠又所求双曲线过点()3,2M -,则()222343λ--=,则2λ=- 则所求双曲线的方程为22243y x -=-,即22168x y -=.27.已知双曲线E 与双曲线221169x y -=共渐近线,且过点()3A -,若双曲线M 以双曲线E 的实轴为虚轴,虚轴为实轴,试求双曲线M 的标准方程.【答案】221944x y -= 【详细分析】设双曲线E 的方程为()220169-=≠x y t t ,代入点A 可得双曲线E 的标准方程,从而得到双曲线双曲线M 的标准方程.【答案详解】由题意,设双曲线E 的方程为()220169-=≠x y t t ,∵点()3A -在双曲线E上,∴(()223169--=t ,∴14t =-,∴双曲线E 的标准方程为221944y x -=, 又双曲线M 以双曲线E 的实轴为虚轴,虚轴为实轴,∴双曲线M 的标准方程为221944x y -=. 28.已知双曲线()2222:10,0x y C a b a b-=>>的两个焦点分别为()1F,)2F,且过点)2P.(1)求双曲线C 的虚轴长;(2)求与双曲线C 有相同渐近线,且过点()3,6Q -的双曲线的标准方程. 【答案】(1)(2)221189y x -= 【详细分析】(1)由双曲线的定义可知,12||||2PF PF a -=,又222+=a b c,求得b =即可.(2)设与双曲线C 有相同渐近线的双曲线的方程为22(0)2y x λλ-=≠,将点()3,6Q -的坐标代入上述方程得λ即可.【答案详解】(1)由题意,易知22PF =,12F F =212PF F F ⊥.在21Rt PF F △中,14PF ==由双曲线的定义可知,122PF PF a -=,22a =,即1a =. ∵双曲线C的两个焦点分别为()1F,)2F,∴c =又∵222+=a b c,∴b = 故双曲线C的虚轴长为(2)由(1)知双曲线C 的方程为2212y x -=.设与双曲线C 有相同渐近线的双曲线的方程为()2202y x λλ-=≠将点()3,6Q -的坐标代入上述方程,得9λ=-故所求双曲线的标准方程为221189y x -=重难点5根据,,a b c 齐次式关系求渐近线方程29.过原点的直线l 与双曲线E :()222210,0x y a b a b-=>>交于A ,B 两点(点A 在第一象限),AC x ⊥交x轴于C 点,直线BC 交双曲线于点D ,且1AB AD k k ⋅=,则双曲线的渐近线方程为( )A .2y x =±B .12y x =±C.y = D.2y x =±【答案】D【详细分析】由题可设,000011(,),(,),(,)A x y B x y D x y --,0(,0)C x ,分别表示出,,AB BC AD k k k ,逐步转化,即可求得本题答案.【答案详解】因为,A B 直线过原点,所以,A B 关于原点对称,设000011(,),(,),(,)A x y B x y D x y --, 因为AC 与x 轴垂直,所以0(,0)C x , 设123,,AB BC AD k k k k k k ===, 则00121001,22y y k k k x x ===, 而222222210101012232222222101010101(1)(1)y y y y y y x x b k k b b x x x x x x x x a a a⎡⎤+--⋅=⋅==---=⎢⎥+---⎣⎦所以,213232221b k k k k a⋅=⋅==,所以,222,a b a ==所以渐近线方程为y =. 故选:D30.双曲线2222:1(0,0)x y E a b a b -=>>,点A ,B 均在E 上,若四边形OACB 为平行四边形,且直线OC ,AB的斜率之积为3,则双曲线E 的渐近线的倾斜角为( )A .π3B .π3或2π3 C .π6D .π6或5π6【答案】B【详细分析】利用点差法,结合双曲线渐近线方程、平行四边形的性质、中点坐标公式进行求解即可.【答案详解】设()()1122,,,A x y B x y ,显然线段AB 的中点坐标为1212,22x x y y ++⎛⎫⎪⎝⎭,因为四边形OACB 为平行四边形,所以线段OC 的中点坐标和线段AB 的中点坐标相同,即为1212,22x x y y ++⎛⎫⎪⎝⎭,因此C 点坐标为()1212,x x y y ++, 因为直线OC ,AB 的斜率之积为3,所以221212122212121233y y y y y y x x x x x x +--⋅=⇒=+--, 因为点A ,B 均在E 上,所以2222112222221,1x y x y a b a b-=-=,两式相减得:22212222123y y b bx x a a-==⇒=- 所以两条渐近线方程的倾斜角为π3或2π3, 故选:B【点睛】关键点睛:本题的关键是应用点差法和平行四边形的性质.31.已知双曲线2222:1(0,0)x y C a b a b-=>> )A .12y x =±B .2y x =±C .y =D .3y x =±【答案】B【详细分析】由离心率求得ba即得渐近线方程.【答案详解】c e a ==,222225c a b a a +==,2b a =, 故选:B32.设12,F F 分别是双曲线22221x y a b -=()0,0a b >>的左、右焦点,若双曲线右支上存在一点P 满足212PF F F =,且124cos 5PF F ∠=,则双曲线的渐近线方程为( ) A .340x y ±= B .430x y ±= C .350x y ±=D .540x y ±=【答案】B【详细分析】结合双曲线的定义,以及条件,得到425a c c +=,再根据222c ab =+,即可求解双曲线渐近线的斜率.【答案详解】作21F Q PF ⊥于点Q ,如图所示,因为122F F PF =,所以Q 为1PF 的中点,由双曲线的定义知|122PF PF a -=,所以122PF a c =+,故1FQ a c =+,因为124cos 5PF F ∠=,所以11212cos FQ PF F F F =∠,即425a c c +=,得35c a =,所以5a =,得43b a =,故双曲线的渐近线方程为43y x =±,即430x y ±=. 故选:B33.已知F 为双曲线C :22221x y a b -=(0a >,0b >)的右焦点,过点F 作x 轴的垂线与双曲线及它的渐近线在第一象限内依次交于点A 和点B .若A B A F =,则双曲线C 的渐近线方程为( )A 0y ±=B .0x =C 0y ±=D .0x =【答案】B【详细分析】分别求出点A,B 的坐标,利用线段相等建立方程求出ba即可得解. 【答案详解】由题意得(),0F c ,双曲线C 的渐近线方程为by x a=±.设点A ,B 的纵坐标依次为1y ,2y ,因为221221c y a b -=,所以21b y a =,所以2b AF a =.因为2bc y a=,所以bcBF a =.因为A B A F =,所以22bc ba a=,得2c b =,所以a =,故b a =C 的渐近线方程为y x =,即0x =, 故选:B .34.如图,已知1F ,2F 为双曲线()222210,0x y a b a b-=>>的焦点,过2F 作垂直于x 轴的直线交双曲线于点P ,且1230PF F ∠=︒,则双曲线的渐近线方程为 .【答案】y =【详细分析】利用点在双曲线上及直角三角形中30︒所对的直角边等于斜边的一半,结合双曲线的定义和渐近线方程即可求解.【答案详解】设()()2,00F c c >,()0,P c y ,则220221y c a b -=,解得20b y a=±,∴22b PF a=.在21Rt PF F △中,1230PF F ∠=︒,则122PF PF =①. 由双曲线的定义,得122PF PF a -=②. 由①②得22PF a =.∵22b PF a =,∴22b a a=,即222b a =.∴ba=∴双曲线的渐近线方程为y =.故答案为:y =.35.过双曲线2222:1-=y W x a b 的右焦点F 作x 轴的垂线,与两条渐近线的交点分别为A ,B ,若OAB 为等边三角形,则W 的渐近线方程为 ,W 的离心率为 .【答案】 3y x =±3【详细分析】根据图形则得到tan 30b a== ,再利用离心率公式即可. 【答案详解】双曲线渐近线方程为by x a =±,因为OAB 是等边三角形,则tan 30b a== y =,即3e ===,故答案为:3y x =±重难点6求双曲线的离心率36.设12,F F 是双曲线2222:1(0,0)x y C a b a b -=>>的左、右焦点,过点1F 作双曲线的一条渐近线的垂线,垂足为M .若2MF ,则双曲线C 的离心率为( )AB C .3 D 【答案】A【详细分析】根据题意,先求得焦点1F 到渐近线的距离为b ,在直角1MOF △中,求得1cos bOF M c∠=,再在12MF F △中,利用余弦定理求得222343b c b =-,结合222b c a =-和离心率的定义,即可求解.【答案详解】由双曲线2222:1(0,0)x y C a b a b -=>>,可得1(,0)F c -,渐近线方程为b y x a=±,如图所示,则焦点1F 到渐近线by x a =-的距离为1MF b ==, 在直角1MOF △中,可得111cos MF bOF M OF c∠==, 在12MF F △中,由余弦定理得222212112112cos MF F F MF F F MF OF M =+-∠,即22222342243bb c b cb c b c=+-⨯⨯=-,所以2223c b =, 又由222b c a =-,所以22223()c c a =-,可得223c a =,所以双曲线的离心率为==ce a. 故选:A.。
高三数学双曲线试题1.若双曲线:与抛物线的准线交于两点,且,则的值是()A.1B.C.4D.13【答案】【解析】抛物线的准线为,代人解得,所以,由双曲线的对称性得,.选.【考点】1、抛物线的几何性质;2、双曲线的几何性质.2.已知双曲线的右焦点为F,若过点F且倾斜角为的直线与双曲线右支有且仅有一个交点,则此双曲线的离心率的取值范围是( )A.B.C.D.【答案】C【解析】其中一条渐近线斜率,,故选C.3.已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于,在双曲线C的方程是( ) A.B.C.D.【答案】B【解析】依题意c=3,e=,所以a=2,从而,故选B.4.如图,分别是双曲线C:的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交与点M,若|MF2|=|F1F2|,则C的离心率是()A.B.C.【答案】B【解析】由题意知直线的方程为:y=x+b,联立方程组得点Q(,);联立方程组得点P (-,)所以PQ的中点坐标为(,),即PQ的垂直平分线方程为:y-=-(x-)令,得x=c(1+),所以c(1+)=3c,所以,即,所以e=,故选B.5.已知双曲线的离心率为,一个焦点与抛物线的焦点相同,则双曲线的渐近线方程为()A.B.C.D.【答案】A【解析】抛物线的焦点坐标为,因此,双曲线的离心率为,所以,因此双曲线的渐近线方程为,故选A.【考点】双曲线与抛物线的几何性质6.过双曲线的右焦点作直线l交双曲线于A、B两点,若满足的直线l共有3条,则实数 .【答案】4【解析】当的倾斜角为时,;当的倾斜角为时,.结合图形可知,当适当倾斜时,还可作出两条长度为4的直线,故.【考点】直线与双曲线.7.已知双曲线的离心率为,且它有一个焦点与抛物线的焦点相同,那么双曲线的渐近线方程为()A.B.C.D.【解析】由于抛物线的焦点坐标为,因此双曲线的焦点也在轴上,不妨设双曲线的方程为,则,离心率为,,因此双曲线的方程为,其渐近线方程为,故选D.【考点】双曲线与抛物线的几何性质8.已知双曲线的虚轴长是实轴长的倍,则此双曲线的离心率为()A.B.C.D.【答案】D【解析】由题意知,因此该双曲线的离心率,故选D.【考点】1.双曲线的几何性质;2.双曲线的离心率9.已知抛物线的准线过双曲线的左焦点且与双曲线交于A、B两点,O为坐标原点,且△AOB的面积为,则双曲线的离心率为()A.B.4C.3D.2【答案】D【解析】解:抛物线的准线方程为:,由题意知,双曲线的左焦点坐标为,即且,因为△AOB的面积为,所以,,即:所以,,解得:,故应选D.【考点】1、抛物线的标准方程;2、双曲线的标准方程及简单几何性质.10.双曲线x2-y2=1的顶点到其渐近线的距离等于()A.B.C.1D.【答案】B【解析】双曲线x2-y2=1的渐近线方程为x±y=0,双曲线x2-y2=1的顶点坐标为(±1,0),顶点到渐近线的距离为.故选B.11.已知抛物线y2=2px(p>0)上的一点M(1,m)(m>0)到其焦点的距离为5,双曲线-y2=1的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a的值为()A.B.C.D.【解析】由已知得1+=5,∴p=8.∴y2=16x,又M(1,m)在y2=16x上,∴m2=16(m>0),∴m=4,∴M(1,4).又双曲线-y2=1的左顶点A(-,0),一条渐近线为y=x=x.又kAM=,∴=,解得a=.12.己知抛物线的焦点F恰好是双曲线的右焦点,且两条曲线的交点的连线过点F,则该双曲线的离心率为()A.+1B.2C.D.-1【答案】A【解析】由题意得抛物线上的点在双曲线上,而,所以点在双曲线上,因此又因为,所以.【考点】抛物线通径的应用13.已知双曲线=1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是()A.|OA|>|OB|B.|OA|<|OB|C.|OA|=|OB|D.|OA|与|OB|大小关系不确定【答案】C【解析】由于点Q为三角形PF1F2内切圆的圆心,故过点F2作PQ的垂线并延长交PF1于点N,易知垂足B为F2N的中点,连接OB,则|OB|=|F1N|=(|F1P|-|F2P|)=a,又设内切圆与PF1,PF2分别切于G,H,则由内切圆性质可得|PG|=|PH|,|F1G|=|F1A|,|F2A|=|F2H|,故|F1P|-|F2P|=|F1A|-|F2A|=2a,设|OA|=x,则有x+c-(c-x)=2a,解得|OA|=a,故有|OA|=|OB|=a,故选C.14.设P是双曲线=1左支上一点,该双曲线的一条渐近线方程是3x+4y=0,F1,F2分别是双曲线的左、右焦点,若|PF1|=10,则|PF2|等于()A.2B.2或18C.18D.16【答案】C【解析】由渐近线方程得y=-x,∴=,a=4.又P是双曲线=1左支上一点,∴|PF2|-|PF1|=2a=8,∴|PF2|=18,故选C.15.已知双曲线的左、右焦点分别为,过作双曲线的一条渐近线的垂线,垂足为,若的中点在双曲线上,则双曲线的离心率为()A.B.C.2D.3【答案】A【解析】由题意可知,一渐近线方程为,则的方程为 y-0=k(x-c),代入渐近线方程可得的坐标为,故的中点,根据中点在双曲线上,∴,解得,故,本题求出的中点的坐标是解题的关键.【考点】双曲线的简单性质.16.已知圆x2+y2-4x-9=0与y轴的两个交点A,B都在某双曲线上,且A,B两点恰好将此双曲线的焦距三等分,则此双曲线的标准方程为________.【答案】=1【解析】在方程x2+y2-4x-9=0中,令x=0,得y=±3,不妨设A(0,-3),B(0,3).设题中双曲线的标准方程为=1(a>0,b>0).∵点A在双曲线上,∴=1.∵A,B两点恰好将此双曲线的焦距三等分,∴双曲线的焦点为(0,-9),(0,9).a2+b2=81.∴a2=9,b2=72.∴此双曲线的标准方程为=1.17.已知双曲线=1(a>0,b>0)的一个焦点与抛物线y2=4x的焦点重合,且双曲线的离心率等于,则该双曲线的方程为________.【答案】5x2-y2=1.【解析】由于抛物线y2=4x的焦点为F(1,0),即c=1,又e==,可得a=,结合条件有a2+b2=c2=1,可得b2=,又焦点在x轴上,则所求的双曲线的方程为5x2-y2=1.18.若双曲线=1(a>0,b>0)与直线y=x无交点,则离心率e的取值范围是().A.(1,2)B.(1,2]C.(1,)D.(1,]【答案】B【解析】因为双曲线的渐近线为y=±x,要使直线y=x与双曲线无交点,则直线y=x应在两渐近线之间,所以有≤,即b≤a,所以b2≤3a2,c2-a2≤3a2,即c2≤4a2,e2≤4,所以1<e≤2.19.已知分别为双曲线的左、右焦点,P为双曲线右支上一点,满足,直线与圆相切,则该双曲线的离心率为()A.B.C.D.2【答案】C【解析】因为过0作直线的垂线,垂足为A,则,过点作直线的垂线,垂足为B.由于点O为的中点. ,所以点B是线段的中点,.又因为,.所以.所以在直角三角形中可得.所以可得.故选C.【考点】1.圆锥曲线的定义.2.等腰三角形的性质.3.直线与圆相切的性质.4.方程的思想.20.点P是双曲线左支上的一点,其右焦点为,若为线段的中点, 且到坐标原点的距离为,则双曲线的离心率的取值范围是 ( )A.B.C.D.【答案】B【解析】设左焦点为,则,设,则有,即,由定义有:,∴,由得.【考点】1.双曲线的定义;2.焦点三角形求离心率的方法.21.已知双曲线的一个焦点与抛物线的焦点重合,且双曲线的离心率等于,则该双曲线的方程为( )A.B.C.D.【答案】D【解析】由已知得,双曲线的焦点为,所以,则有,解得.【考点】1.双曲线的标准方程;2.双曲线的性质;3.抛物线的性质22.若抛物线的焦点与双曲线的右焦点重合,则的值为.【答案】6【解析】双曲线的右焦点是抛物线的焦点,所以,,.【考点】双曲线的焦点.23.设F1,F2是双曲线C, (a>0,b>0)的两个焦点。
课时作业16 双曲线的简单几何性质(1)知识点一由双曲线的标准方程研究几何性质1.若直线x =a 与双曲线x 24-y 2=1有两个交点,则a 的值可以是( )A.4B.2C.1D.-2答案 A解析 ∵双曲线x 24-y 2=1中,x ≥2或x ≤-2,∴若x =a 与双曲线有两个交点,则a >2或a <-2,故只有A 选项符合题意. 2.双曲线x 24-y 212=1的焦点到渐近线的距离为( )A.2 3B.2C. 3D.1答案 A解析 不妨取焦点(4,0)和渐近线y =3x ,则所求距离d =|43-0|3+1=2 3.故选A.3.求双曲线4x 2-y 2=4的顶点坐标、焦点坐标、实半轴长、虚半轴长、离心率和渐近线方程.解 把方程化为标准形式为x 212-y 222=1,由此可知,实半轴长a =1,虚半轴长b =2. 顶点坐标是(-1,0),(1,0).c =a 2+b 2=12+22=5,∴焦点坐标是(-5,0),(5,0). 离心率e =c a=5,渐近线方程为x 1±y2=0,即y =±2x .知识点二求双曲线的离心率 4.下列方程表示的曲线中离心率为62的是( ) A.x 22-y 24=1 B.x 24-y 22=1 C.x 24-y 26=1 D.x 24-y 210=1 答案 B解析 ∵e =c a,c 2=a 2+b 2,∴e 2=c 2a 2=a 2+b 2a 2=1+b 2a 2=⎝ ⎛⎭⎪⎫622=32.故b 2a 2=12,观察各曲线方程得B 项系数符合,应选B. 5.已知F 1,F 2是双曲线x 2a 2-y 2b2=1(a >0,b >0)的两个焦点,PQ 是经过F 1且垂直于x 轴的双曲线的弦,如果∠PF 2Q =90°,求双曲线的离心率.解 设F 1(c,0),将x =c 代入双曲线的方程得c 2a 2-y 2b 2=1,∴y =±b 2a.由|PF 2|=|QF 2|,∠PF 2Q =90°, 知|PF 1|=|F 1F 2|,∴b 2a=2c .∴b 2=2ac . ∴c 2-2ac -a 2=0. ∴⎝ ⎛⎭⎪⎫c a 2-2·c a-1=0. 即e 2-2e -1=0.∴e =1+2或e =1-2(舍去). 所以所求双曲线的离心率为1+ 2. 知识点三由双曲线的几何性质求标准方程6.已知中心在原点的双曲线C 的右焦点为F (3,0),离心率等于32,则C 的方程是( )A.x 24-y 25=1 B.x 24-y 25=1 C.x 22-y 25=1 D.x 22-y 25=1 答案 B解析 由右焦点为F (3,0)可知c =3,又因为离心率等于32,所以c a =32,所以a =2.由c2=a 2+b 2知b 2=5,故双曲线C 的方程为x 24-y 25=1,故选B.7.已知双曲线x 24-y 2b2=1(b >0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A ,B ,C ,D 四点,四边形ABCD 的面积为2b ,则双曲线的方程为( )A.x 24-3y 24=1B.x 24-4y 23=1C.x 24-y 24=1 D.x 24-y 212=1答案 D解析 根据圆和双曲线的对称性,可知四边形ABCD 为矩形.双曲线的渐近线方程为y=±b 2x ,圆的方程为x 2+y 2=4,不妨设交点A 在第一象限,由y =b 2x ,x 2+y 2=4得x A =44+b 2,y A =2b4+b2,故四边形ABCD 的面积为4x A y A =32b 4+b 2=2b ,解得b 2=12,故所求的双曲线方程为x 24-y 212=1,选D.一、选择题1.双曲线2x 2-y 2=8的实轴长是( ) A.2 B.2 2 C.4 D.4 2答案 C解析 双曲线方程可变形为x 24-y 28=1,所以a 2=4,a =2,从而2a =4,故选C.2.若双曲线的实轴长、虚轴长、焦距成等差数列,则它的离心率为( ) A.43 B.53 C.2 D.3 答案 B解析 不妨设双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0),则2·2b =2a +2c ,即b =a +c2.又b 2=c 2-a 2,则⎝ ⎛⎭⎪⎫a +c 22=c 2-a 2,所以3c 2-2ac -5a 2=0,即3e 2-2e -5=0,注意到e >1,得e =53. 故选B.3.若中心在坐标原点,离心率为53的双曲线的焦点在y 轴上,则它的渐近线方程为( )A.y =±54xB.y =±45xC.y =±43xD.y =±34x答案 D解析 设双曲线的标准方程为y 2a 2-x 2b 2=1(a >0,b >0).因为c a =53,所以a 2+b 2a 2=259,所以b a =43.所以双曲线的渐近线方程为y =±a b x ,即双曲线的渐近线方程为y =±34x ,故选D. 4.设直线l 过双曲线C 的一个焦点,且与C 的一条对称轴垂直,l 与C 交于A ,B 两点,|AB |为C 的实轴长的2倍,则C 的离心率为( )A. 2B. 3C.2D.3答案 B解析 设双曲线C 的方程为x 2a 2-y 2b 2=1,焦点F (-c,0),将x =-c 代入x 2a 2-y 2b 2=1可得y2=b 4a 2,所以|AB |=2·b 2a=2·2a . ∴b 2=2a 2,c 2=a 2+b 2=3a 2,∴e =ca= 3.5.若点O 和点F (-2,0)分别为双曲线x 2a2-y 2=1(a >0)的中心和左焦点,点P 为双曲线右支上的任意一点,则OP →·FP →的取值X 围为( )A.[3-23,+∞)B.[3+23,+∞)C.⎣⎢⎡⎭⎪⎫-74,+∞ D.⎣⎢⎡⎭⎪⎫74,+∞答案 B解析 因为F (-2,0)是已知双曲线的左焦点,所以a 2+1=4,即a 2=3,所以双曲线方程为x 23-y 2=1.设点P (x 0,y 0)(x 0≥3),则x 203-y 20=1(x 0≥3),可得y 20=x 203-1(x 0≥3),易知FP →=(x 0+2,y 0),OP →=(x 0,y 0),所以OP →·FP →=x 0(x 0+2)+y 2=x 0(x 0+2)+x 203-1=4x 23+2x 0-1,此二次函数对应的图象的对称轴为x 0=-34.因为x 0≥3,所以当x 0=3时,OP →·FP →取得最小值43×3+23-1=3+23,故OP →·FP →的取值X 围是[3+23,+∞).二、填空题6.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的一条渐近线为2x +y =0,一个焦点为(5,0),则a =________;b =________.答案 1 2解析 由题意知,渐近线方程为y =-2x ,由双曲线的标准方程以及性质可知b a=2,由c =5,c 2=a 2+b 2,可得b =2,a =1.7.中心在原点,实轴在x 轴上,一个焦点为直线3x -4y +12=0与坐标轴的交点的等轴双曲线方程是________.答案 x 2-y 2=8解析 由双曲线的实轴在x 轴上知其焦点在x 轴上,直线3x -4y +12=0与x 轴的交点坐标为(-4,0),故双曲线的一个焦点为(-4,0),即c =4.设等轴双曲线方程为x 2-y 2=a 2,则c 2=2a 2=16,解得a 2=8,所以双曲线方程为x 2-y 2=8.8.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的渐近线与圆x 2+y 2-4x +2=0有公共点,则该双曲线离心率的取值X 围是________.答案 (1,2]解析 将圆的方程配方,得(x -2)2+y 2=2.双曲线的渐近线方程为bx ±ay =0.由于双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线与圆x 2+y 2-4x +2=0有公共点,所以|2b ±0|a 2+b 2≤ 2.又c 2=a 2+b 2,所以c 2≤2a 2,即e ≤2,所以离心率的取值X 围为(1,2].三、解答题9.根据下列条件,求双曲线的标准方程: (1)一个顶点是(0,6),且离心率是1.5;(2)与双曲线x 29-y 216=1有共同渐近线,且过点(-3,23).解 (1)∵顶点为(0,6),设所求双曲线方程为y 2a 2-x 2b2=1,∴a =6.又∵e =1.5,∴c =a ×e =6×1.5=9,b 2=c 2-a 2=45. 故所求的双曲线方程为y 236-x 245=1.(2)解法一:双曲线x 29-y 216=1的渐近线为y =±43x ,令x =-3,y =±4,因23<4,故点(-3,23)在射线y =-43x (x ≤0)及x 轴负半轴之间,∴双曲线焦点在x 轴上.设双曲线方程为x 2a 2-y 2b2=1,(a >0,b >0),则⎩⎪⎨⎪⎧b a =43,-32a 2-232b 2=1,解之得⎩⎪⎨⎪⎧a 2=94,b 2=4.∴双曲线方程为x 294-y 24=1.解法二:设双曲线方程为x 29-y 216=λ(λ≠0),∴-329-23216=λ.∴λ=14,∴双曲线方程为x 294-y24=1.10.中心在原点,焦点在x 轴上的一椭圆与一双曲线有共同的焦点F 1,F 2,且|F 1F 2|=213,椭圆的半长轴长与双曲线半实轴长之差为4,离心率之比为3∶7.(1)求这两曲线方程;(2)若P 为这两曲线的一个交点,求△F 1PF 2的面积.解 (1)设椭圆方程为x 2a 2+y 2b 2=1,双曲线方程为x 2m 2-y 2n 2=1(a ,b ,m ,n >0,且a >b ),则⎩⎪⎨⎪⎧a -m =4,7×13a =3×13m ,解得a =7,m =3,所以b =6,n =2,所以椭圆方程为x 249+y 236=1,双曲线方程为x 29-y 24=1.(2)不妨设F 1,F 2分别为左、右焦点,P 是第一象限的一个交点,则|PF 1|+|PF 2|=14,|PF 1|-|PF 2|=6,所以|PF 1|=10,|PF 2|=4,所以cos ∠F 1PF 2=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1|·|PF 2|=45,所以S △F 1PF 2=12|PF 1|·|PF 2|·sin∠F 1PF 2=12×10×4×35=12.。
《双曲线的简单几何性质》同步练习一、选择题1.已知P是双曲线2221(0)16x yaa-=>上一点,双曲线的一条渐近线方程为2x-y=0,F1,F2分别是双曲线的左、右焦点,若PF1⊥F1F2,则|PF2|=( )A.12B.16C.18D.202.已知双曲线221(0)6x ymm m-=>+的虚轴长是实轴长的2倍,则双曲线的标准方程为( )A.221 24x y-=B.221 48x y-=C.2218yx-=D.221 28x y-=3.已知双曲线C的离心率e=2,一个焦点坐标为(0,2),则双曲线C的标准方程为( )A.2213yx-=B.2215yx-=C.2215xy-=D.2213xy-=二、填空题4.已知双曲线221x my+=的虚轴长是实轴长的2倍,则实数m=______.5.若双曲线的渐近线方程为3y x=±,它的一个焦点坐标为),则双曲线的标准方程为______.6.已知双曲线22221(0)(3)x yaa a-=>+的渐近线方程为y=±2x,则a=______.三、解答题7.已知双曲线的一条渐近线方程是x+2y=0,且经过点(2,2),求双曲线的标准方程.8.过双曲线22221(0,0)x ya ba b-=>>的一个焦点F作一条渐近线的垂线,若垂足恰在线段OF(O为原点)的垂直平分线上,求双曲线的离心率.9.已知双曲线的方程是224936x y-=.(1)求双曲线的焦点坐标、离心率和渐近线方程;(2)设F1和F2是双曲线的左、右焦点,点P在双曲线上,且1216PF PF=,求∠F1PF2的大小.参考答案1.答案:A解析:因为双曲线222116x y a -=的一条渐近线方程为20x y -=,所以42a=,即a =2,所以双曲线的标准方程221416x y -=,所以()1F -,所以点P的横坐标为-,代入双曲线的标准方程可得点P 的纵坐标为±8,所以1218,212PF PF a PF ==+=. 2.答案:D解析:由题意可得22,6a m b m ==+,则实轴长为,虚轴长为,所以2=,解得m =2,代入2216x y m m -=+可得双曲线的标准方程为22128x y -=. 3.答案:D解析:由离心率c e a =,可得2c a=,又因为一个焦点坐标为(0,2),所以c =2,所以a =1,所以b ==.又因为焦点在y 轴上,故双曲线C 的标准方程为2213x y -=. 4.答案:14- 解析:将双曲线方程化为标准方程得2211y x m -=-,则1,a b ==依题意得可知b =2a 2= 解得14m =-. 5. 答案:2219y x -= 解析:由双曲线的渐近线方程可知3b a =.①因为它的一个焦点坐标为),所以c =.② 又222c a b =+③,联立①②③,解得a 2=1,b 2=9,所以双曲线的标准方程为2219y x -=. 6.答案:3解析:因为双曲线22221(0)(3)x y a a a -=>+的渐近线方程为3a y x a +=,所以32a a+=,解得a =3.7.答案:见解析解析:由题意可设双曲线的方程为()2240x y λλ-=≠,因为双曲线经过点(2,2),所以λ=-12,故双曲线的标准方程为221312y x -=. 8.答案:见解析解析:如图所示,不妨设F 为右焦点,过F 作FP 垂直于一条渐近线,垂足为P ,过P 作PM ⊥OF 于M .由已知得M 为OF 的中点, 由射影定理知2||PF FM FO =.又F (c ,0),渐近线OP 的方程为bx -ay =0,所以PF b ==,于是22c b c =⋅, 即22222b c a b ==+,因此22a b =,故c e a ===9.答案:见解析解析:(1)由224936x y -=,得22194x y -=, 所以a =3,b=2,c ==, 所以焦点坐标为())12,F F ,离心率为e =, 渐近线方程为23y x =±. (2)由双曲线的定义可知126PF PF -=, 所以22212121212||||cos 2PF PF F F F PF PF PF +-=∠2212121122()2|||2PF PF PF PF F F F PF P -+-=3632521322+-== 所以∠F 1PF 2=60°.。
课时作业(十一)[学业水平层次]一、选择题1.等轴双曲线的一个焦点是F 1(-6,0),则它的标准方程是( ) -x 218=1 -y 218=1 -y 28=1-x 28=1【解析】 设等轴双曲线方程为x 2a 2-y 2a 2=1(a >0),∴a 2+a 2=62,∴a 2=18,故双曲线方程为x 218-y218=1.【答案】 B2.(2014·天水高二考试)已知双曲线方程为x 2-y24=1,过P (1,0)的直线l 与双曲线只有一个公共点,则共有l ( )A .4条B .3条C .2条D .1条【解析】 因为双曲线方程为x 2-y24=1,所以P (1,0)是双曲线的右顶点,所以过P (1,0)并且和x 轴垂直的直线是双曲线的一条切线,与双曲线只有一个公共点,另外还有两条就是过P (1,0)分别和两条渐近线平行的直线,所以符合要求的共有3条,故选B.【答案】 B3.(2014·大纲全国卷)双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,焦点到渐近线的距离为3,则C 的焦距等于( )A .2B .2 2C .4D .42【解析】 由已知得e =c a =2,所以a =12c ,故b =c 2-a 2=32c ,从而双曲线的渐近线方程为y =±ba x =±3x ,由焦点到渐近线的距离为3,得32c =3,解得c =2,故2c =4,故选C.【答案】 C4.(2014·广东高考)若实数k 满足0<k <5,则曲线x 216-y 25-k =1与曲线x 216-k -y 25=1的( )A .实半轴长相等B .虚半轴长相等C .离心率相等D .焦距相等【解析】 若0<k <5,则5-k >0,16-k >0,故方程x 216-y 25-k =1表示焦点在x 轴上的双曲线,且实半轴的长为4,虚半轴的长为5-k ,焦距2c =221-k ,离心率e =21-k 4;同理方程x 216-k -y 25=1也表示焦点在x 轴上的双曲线,实半轴的长为16-k ,虚半轴的长为5,焦距2c =221-k ,离心率e =21-k16-k .可知两曲线的焦距相等,故选D.【答案】 D 二、填空题5.(2014·南京高二检测)在平面直角坐标系xOy 中,若双曲线x 2m -y 2m 2+4=1的离心率为5,则m 的值为________. 【解析】 ∵c 2=m +m 2+4,∴e 2=c 2a 2=m +m 2+4m=5, ∴m 2-4m +4=0,∴m =2. 【答案】 26.(2013·辽宁高考)已知F 为双曲线C :x 29-y 216=1的左焦点,P ,Q 为C 上的点.若PQ 的长等于虚轴长的2倍,点A (5,0)在线段PQ 上,则△PQF 的周长为________.【解析】 由双曲线方程知,b =4,a =3,c =5,则虚轴长为8,则|PQ |=16.由左焦点F (-5,0),且A (5,0)恰为右焦点,知线段PQ 过双曲线的右焦点,则P ,Q 都在双曲线的右支上.由双曲线的定义可知|PF |-|PA |=2a ,|QF |-|QA |=2a ,两式相加得,|PF |+|QF |-(|PA |+|QA |)=4a ,则|PF |+|QF |=4a +|PQ |=4×3+16=28,故△PQF 的周长为28+16=44.【答案】 447.(2014·浙江)设直线x -3y +m =0(m ≠0)与双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线分别交于点A ,B ,若点P (m,0)满足|PA |=|PB |,则该双曲线的离心率是________.【解析】由⎩⎨⎧x -3y +m =0,y =b a x ,得点A 的坐标为⎝ ⎛⎭⎪⎫am 3b -a ,bm 3b -a ,由⎩⎨⎧x -3y +m =0,y =-b a x ,得点B 的坐标为⎝⎛⎭⎪⎫-am 3b +a ,bm 3b +a , 则AB 的中点C 的坐标为⎝ ⎛⎭⎪⎫a 2m 9b 2-a 2,3b 2m 9b 2-a 2,∵k AB =13,∴k CP =3b 2m 9b 2-a 2a 2m 9b 2-a 2-m=-3,即3b 2a 2-9b 2-a 2=-3,化简得a 2=4b 2, 即a 2=4(c 2-a 2),∴4c 2=5a 2, ∴e 2=54,∴e =52.【答案】 52 三、解答题8.双曲线与椭圆x 216+y 264=1有相同的焦点,它的一条渐近线为y =x ,求双曲线的标准方程和离心率.【解】由椭圆x 216+y 264=1,知c 2=64-16=48,且焦点在y 轴上, ∵双曲线的一条渐近线为y =x , ∴设双曲线方程为y 2a 2-x 2a 2=1. 又c 2=2a 2=48,∴a 2=24. ∴所求双曲线的方程为y 224-x 224=1.由a 2=24,c 2=48,得e 2=c2a 2=2,又e >0,∴e = 2.9.(2014·玉溪高二检测)已知双曲线x 23-y 2b 2=1的右焦点为(2,0). (1)求双曲线的方程;(2)求双曲线的渐近线与直线x =-2围成的三角形的面积. 【解】 (1)∵双曲线的右焦点坐标为(2,0),且双曲线方程为x 23-y 2b 2=1,∴c 2=a 2+b 2=3+b 2=4,∴b 2=1,∴双曲线的方程为x 23-y 2=1. (2)∵a =3,b =1,∴双曲线的渐近线方程为y =±33x , 令x =-2,则y =±233,设直线x =-2与双曲线的渐近线的交点为A 、B ,则|AB |=433,记双曲线的渐近线与直线x =-2围成的三角形面积为S ,则S =12×433×2=43 3.[能力提升层次]1.(2014·山东省实验中学高二检测)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线均与C :x 2+y 2-6x +5=0相切,则该双曲线离心率等于( )【解析】 圆的标准方程为(x -3)2+y 2=4,所以圆心坐标为C (3,0),半径r =2,双曲线的渐近线为y =±b a x ,不妨取y =ba x ,即bx -ay =0,因为渐近线与圆相切,所以圆心到直线的距离d =|3b |a 2+b 2=2,即9b 2=4(a 2+b 2),所以5b 2=4a 2,b 2=45a 2=c 2-a 2,即95a 2=c 2,所以e 2=95,e =355,选A.【答案】 A2.(2014·北京市东城区)设F 1,F 2分别为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点.若在双曲线右支上存在点P ,满足|PF 2|=|F 1F 2|,且F 2到直线PF 1的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( )A .3x ±4y =0B .3x +5y =0C .5x ±4y =0D .4x ±3y =0【解析】 由题意可知|PF 2|=|F 1F 2|=2c ,所以△PF 1F 2为等腰三角形,所以由F 2向直线PF 1作的垂线也是中线,因为F 2到直线PF 1的距离等于双曲线的实轴长2a ,所以|PF 1|=24c 2-4a 2=4b ,又|PF 1|-|PF 2|=2a ,所以4b -2c =2a ,所以2b -a =c ,两边平方可得4b 2-4ab +a 2=c 2=a 2+b 2,所以3b 2=4ab ,所以4a =3b ,从而b a =43,所以该双曲线的渐近线方程为4x ±3y =0,故选D.【答案】 D3.过双曲线x 2-y 23=1的左焦点F 1,作倾斜角为π6的直线AB ,其中A 、B 分别为直线与双曲线的交点,则|AB |的长为________.【解析】 双曲线的左焦点为F 1(-2,0), 将直线AB 方程y =33(x +2)代入双曲线方程, 得8x 2-4x -13=0.显然Δ>0, 设A (x 1,y 1)、B (x 2,y 2), ∴x 1+x 2=12,x 1x 2=-138, ∴|AB |=1+k 2·x 1+x 22-4x 1x 2 =1+13×⎝ ⎛⎭⎪⎫122-4×⎝ ⎛⎭⎪⎫-138=3. 【答案】 34.(2014·安徽师大)已知中心在原点的双曲线C 的右焦点为(2,0),右顶点为(3,0).(1)求双曲线C 的方程;(2)若直线l :y =kx +2与双曲线C 恒有两个不同的交点A 和B ,且OA →·OB →>2,其中O 为原点,求k 的取值范围.【解】 (1)设双曲线C 的方程为x 2a 2-y 2b 2=1(a >0,b >0),由已知得a =3,c =2.又因为a 2+b 2=c 2,所以b 2=1, 故双曲线C 的方程为x 23-y 2=1. (2)将y =kx +2代入x 23-y 2=1中,得(1-3k 2)x 2-62kx -9=0, 由直线l 与双曲线交于不同的两点得⎩⎪⎨⎪⎧1-3k 2≠0,Δ=-62k 2+361-3k 2>0,即k 2≠13且k 2<1.①设A (x A ,y A ),B (x B ,y B ),则x A +x B =62k1-3k 2,x A x B =-91-3k 2,由OA →·OB →>2得x A x B +y A y B >2,而x A x B +y A y B =x A x B +(kx A +2)(kx B +2) =(k 2+1)x A x B +2k (x A +x B )+2=(k 2+1)·-91-3k 2+2k ·62k 1-3k 2+2=3k 2+73k 2-1,于是3k 2+73k 2-1>2,解此不等式得13<k 2<3.②由①②得13<k 2<1.故k 的取值范围是⎝ ⎛⎭⎪⎫-1,-33∪⎝ ⎛⎭⎪⎫33,1.。