线型分析-练习作业

线性模型练习题(含答案)练题一设有线性回归模型：$ y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_3 $，其中 $x_1$、$x_2$ 和 $x_3$ 是自变量，$y$ 是因变量。

已知模型的参数估计值如下：$ \hat{\beta}_0 = 2.5 $$ \hat{\beta}_1 = 0.8 $$ \hat{\beta}_2 = -1.2 $$ \hat{\beta}_3 = 1.3 $请判断以下哪个自变量与因变量的关系最为显著：A. $x_1$B. $x_2$C. $x_3$D. 无法确定答案：B. $x_2$练题二下面是一个简单的线性回归模型：$ y = 3x_1 + 4x_2 + 2x_3 + 1 $已知模型的参数估计值如下：$ \hat{\beta}_1 = 2.1 $$ \hat{\beta}_2 = 1.8 $$ \hat{\beta}_3 = 0.9 $请根据模型参数估计值计算预测值 $ \hat{y} $，当 $x_1 = 2$，$x_2 = 3$，$x_3 = 1$ 时的结果。

答案：$ \hat{y} = 3(2) + 4(3) + 2(1) + 1 = 23 $练题三某研究人员运用线性回归模型分析了一个因变量 $y$ 和四个自变量 $x_1$、$x_2$、$x_3$ 和 $x_4$ 的关系，得到模型方程如下：$ y = 2.6x_1 + 1.9x_2 - 1.4x_3 + 0.5x_4 - 1 $已知 $x_1 = 3$，$x_2 = 2$，$x_3 = 4$，$x_4 = 1$，请计算对应的预测值 $ \hat{y} $。

答案：$ \hat{y} = 2.6(3) + 1.9(2) - 1.4(4) + 0.5(1) - 1 = 2.9 $练题四以下是一个多元线性回归模型的参数估计值摘录：$ \hat{\beta}_0 = 1.2 $$ \hat{\beta}_1 = -0.8 $$ \hat{\beta}_2 = 0.5 $$ \hat{\beta}_3 = 1.0 $$ \hat{\beta}_4 = 0.3 $$ \hat{\beta}_5 = -0.6 $请写出该线性回归模型的方程。

解线性方程组专项练习及测试(含专练60
道)
解线性方程组专项练及测试（含专练60道）
简介
本文档旨在提供一套解线性方程组的专项练及测试，包含60
道题目。

通过这些练和测试，你将能够加深对线性方程组的理解，
熟练掌握解决线性方程组的方法和技巧。

练题目
以下是60道解线性方程组的练题目，请你根据题目要求解答。

1. 题目1
2. 题目2
3. ...
...
60. 题目60
说明
首先，根据题目给出的线性方程组，你可以使用多种方法求解，包括代入法、减法法、矩阵法等。

请根据实际情况选择合适的方法
进行求解。

其次，每道题目都有唯一的解或无穷多解。

请根据题目给出的
信息判断线性方程组的解的情况，并给出解的形式。

最后，当你完成所有题目时，请仔细检查答案，并核对解的正
确性。

如果有任何疑问或不明确的地方，请不要犹豫，随时向老师
或同学寻求帮助。

重要提示
请注意，本文档中的题目仅供练和测试使用，不作为正式考试
的题目。

完成这些题目将有助于你巩固知识点和提高解决线性方程
组问题的能力。

祝你考试顺利，取得好成绩！
参考答案
以下是练题目的参考答案，供你参考。

1. 答案1
2. 答案2
3. ...
...
60. 答案60。

思考题4.1 为了考察城镇商品房市场的特征，有人建立了如下的模型：ii i i i Z P X Y εαααα++++=3210ln ln 其中：i Y 为第i 个城镇的商品房销售面积，i X 为该城镇居民的人均可支配收入，i P 为商品房均价，i Z 为常住人口数量。

（1）分别解释系数1α和2α的经济含义。

（2）有人认为，中国商品房市场存在严重的炒房现象，导致价格越高，商品房的销售量越火爆，你如何检验这种观点？写出你的原假设、备选假设、检验统计量和判定规则。

（3）有人认为，商品房市场存在严重泡沫，商品房的销售量已经与居民收入、人口规模严重脱节，你如何检验这种观点？写出你的原假设、备选假设、检验统计量和判定规则。

（4）如果样本中既有大城市，也有小城镇，你如何检验大小城市的商品房市场是否具有相同的特征。

4.2. 在分析变量Y 的影响因素时，学生甲建立了如下的多元回归方程： t t t t X X Y εααα+++=22110。

学生乙也在研究同样的经济问题，她只学习了一元回归模型。

为了考察在X 2不变时，X 1对Y 的影响，学生乙进行了如下的三步回归分析： t t t X Y 1210εββ++= （a ） t t t X X 22101εγγ++= （b ）t t t 3211ˆˆεελε+= （c ）其中：t t 21ˆ,ˆεε分别是回归方程（a ）、（b ）的残差项。

（1）参数1α和参数1λ有什么样的关系？解释你的理由。

（2）参数2α和参数1β是同一个参数吗？解释你的理由。

（3）回归方程（c ）为什么没有截距项？4.3. 在基于受约束和无约束回归方程的估计结果检验规线性约束时，需要建立F 检验统计量。

有同学在相关文献中看到了如下的F 检验统计量：)1,(~)1/(/)(222-----=K N q F K N R qR R F ur r ur 。

（1）说明该F 统计量的形式是如何得到的。

线性分析测试题及答案一、选择题（每题5分，共20分）1. 线性方程组的解法中，使用高斯消元法的步骤不包括以下哪一项？A. 将方程组写成增广矩阵的形式B. 将矩阵进行行变换C. 将矩阵的列进行交换D. 将矩阵的行进行交换答案：C2. 线性相关和线性无关的概念中，以下说法正确的是？A. 线性相关是指一组向量中至少有一个向量可以由其他向量线性表示B. 线性无关是指一组向量中没有一个向量可以由其他向量线性表示C. 线性相关和线性无关是相同的概念D. 线性相关是指一组向量中所有向量都可以由其他向量线性表示答案：B3. 在线性代数中，以下哪个矩阵是可逆的？A. 对角矩阵B. 零矩阵C. 奇异矩阵D. 单位矩阵答案：D4. 线性空间的基具有以下性质？A. 基是线性空间中的一组线性无关的向量B. 基是线性空间中的一组线性相关的向量C. 基是线性空间中的一组向量，但不一定线性无关D. 基是线性空间中的一组向量，但不一定线性无关答案：A二、填空题（每题5分，共20分）1. 若线性方程组的系数矩阵的秩等于增广矩阵的秩，且等于未知数的个数，则该方程组有________解。

答案：唯一2. 线性方程组中，若系数矩阵的秩小于增广矩阵的秩，则该方程组有________解。

答案：无3. 线性空间的维数是指基中向量的个数，也称为线性空间的________。

答案：维度4. 若向量组α1, α2, ..., αn线性无关，则它们构成的矩阵的行列式________。

答案：不为零三、简答题（每题10分，共20分）1. 请简述线性方程组解的存在性与系数矩阵的秩之间的关系。

答案：线性方程组的解的存在性与系数矩阵的秩密切相关。

如果系数矩阵的秩等于增广矩阵的秩，并且等于未知数的个数，则方程组有唯一解；如果系数矩阵的秩小于增广矩阵的秩，则方程组无解；如果系数矩阵的秩等于增广矩阵的秩但小于未知数的个数，则方程组有无穷多解。

2. 什么是线性空间？请给出一个例子。

线性考试题库及答案解析1. 线性代数中，矩阵的秩是指什么？答案：矩阵的秩是指矩阵中线性无关的行（或列）的最大数目。

2. 请解释线性方程组的解集。

答案：线性方程组的解集是指所有满足方程组的未知数的集合。

3. 什么是特征值和特征向量？答案：对于一个方阵A，如果存在一个非零向量v和标量λ，使得Av = λv，则称λ为矩阵A的特征值，v为对应的特征向量。

4. 矩阵的可逆性是什么？答案：如果一个方阵存在逆矩阵，则称该矩阵是可逆的。

5. 请解释什么是正交矩阵。

答案：正交矩阵是指一个矩阵的转置矩阵与其自身的乘积等于单位矩阵的矩阵。

6. 如何判断一个矩阵是否为正定矩阵？答案：一个实对称矩阵是正定的，如果它的所有特征值都是正的。

7. 线性空间的基是什么？答案：线性空间的基是构成该空间的一组线性无关的向量，且这组向量可以线性表出空间中的任意向量。

8. 请解释什么是线性变换。

答案：线性变换是指在两个线性空间之间，保持向量加法和数乘运算不变的映射。

9. 什么是线性方程组的齐次解？答案：线性方程组的齐次解是指方程组中所有方程的系数都为零时的解。

10. 请解释什么是矩阵的迹。

答案：矩阵的迹是指矩阵对角线元素之和。

11. 什么是向量的范数？答案：向量的范数是指衡量向量大小的非负实数。

12. 请解释什么是投影矩阵。

答案：投影矩阵是指将一个向量投影到另一个向量上得到的向量。

13. 什么是线性方程组的非齐次解？答案：线性方程组的非齐次解是指方程组中至少有一个方程的系数不为零时的解。

14. 什么是矩阵的行列式？答案：矩阵的行列式是一个标量值，它提供了矩阵是否可逆的信息。

15. 请解释什么是矩阵的伴随矩阵。

答案：矩阵的伴随矩阵是由原矩阵的代数余子式组成的矩阵的转置。

线性优化练习题线性优化是数学中的一个分支，用于解决优化问题。

通过线性优化，我们可以找到最优的解决方案，从而提高效率和效果。

下面是几个线性优化的练习题，帮助你更好地理解和应用线性优化。

问题一：生产计划问题某公司生产两类产品A和B，产品A每件利润为500元，产品B每件利润为300元。

生产一件产品A需要2个工时，生产一件产品B需要3个工时。

每天工厂总共有120个工时可用。

假设工厂每天最多能生产100件产品，且产品A和产品B的产量之和不能超过100。

问应该生产多少件产品A和产品B，才能使得总利润最大化？解答：设生产产品A件数为x，生产产品B件数为y。

则有以下线性规划问题：目标函数：maximize 500x + 300y约束条件：2x + 3y ≤ 120x + y ≤ 100x, y ≥ 0问题二：货物运输问题一家物流公司需要将货物从仓库A运送到仓库B、C和D。

运输费用如下表所示：| 仓库 | 仓库B | 仓库C | 仓库D ||---------|--------|--------|--------|| 仓库A | 100 | 200 | 300 |公司需要确定每个仓库的货物运输量，以使得总运输费用最低。

解答：设仓库A向仓库B的运输量为x，仓库A向仓库C的运输量为y，仓库A向仓库D的运输量为z。

则有以下线性规划问题：目标函数：minimize 100x + 200y + 300z约束条件：x + y + z ≤ 容量（仓库A的货物最大运输量）x, y, z ≥ 0问题三：投资问题小明有100万元用于投资，他考虑将资金分配到股票、债券和黄金三种投资渠道。

已知股票每万元投资可以获得8%的收益，债券每万元投资可以获得6%的收益，黄金每万元投资可以获得4%的收益。

小明希望利息最大化，但他的投资组合必须满足以下条件：1. 股票和债券的投资额总和不能超过80万元；2. 黄金的投资额至少为20万元。

问小明应该如何分配投资才能最大化利息？解答：设小明投资于股票的金额为x万元，债券的金额为y万元，黄金的金额为z万元。

高中线性分析练习题及讲解# 高中线性分析练习题及讲解## 一、选择题1. 题目：已知线性方程组：\[\begin{cases}x + y = 5 \\2x - y = 1\end{cases}\]求 \( x \) 和 \( y \) 的值。

选项：A. \( x = 2, y = 3 \)B. \( x = 3, y = 2 \)C. \( x = 1, y = 4 \)D. \( x = 4, y = 1 \)2. 题目：线性方程 \( ax + by = c \) 中，若 \( a \), \( b \), \( c \) 都不是0，且 \( a \) 和 \( b \) 不相等，那么此方程：选项：A. 有唯一解B. 有无穷多解C. 无解D. 解的情况不确定## 二、填空题1. 题目：若线性方程组：\[\begin{cases}3x - y = 4 \\2x + y = 1\end{cases}\]的解为 \( x = k \) 和 \( y = m \)，求 \( k \) 和 \( m \)的值。

答案： \( x = \_\_\_\_\_\_\_ , y = \_\_\_\_\_\_\_\_ \)2. 题目：线性方程 \( 2x + 5y = 10 \) 可以表示为 \( y =\_\_\_\_\_\_\_\_ \) 的形式。

## 三、解答题1. 题目：解线性方程组：\[\begin{cases}x + 2y + 3z = 6 \\2x + y + z = 4 \\x - y + z = 2\end{cases}\]并求出 \( x \), \( y \), \( z \) 的值。

2. 题目：已知线性方程 \( 3x - 4y = 5 \)，求当 \( x = 2 \) 时，\( y \) 的值。

## 四、应用题1. 题目：某工厂生产两种产品，A产品每件成本为10元，利润为5元；B产品每件成本为15元，利润为10元。

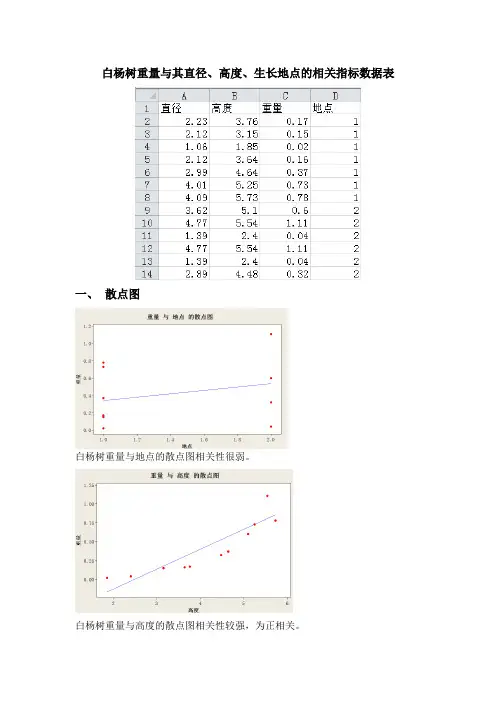
白杨树重量与其直径、高度、生长地点的相关指标数据表一、散点图白杨树重量与地点的散点图相关性很弱。

白杨树重量与高度的散点图相关性较强，为正相关。

白杨树重量与直径的散点图相关性很强，为正相关。

二、检验（统计-回归-回归）回归分析: 重量与直径, 高度, 地点回归方程为：重量= - 0.185 + 0.513 直径- 0.210 高度+ 0.0019 地点自变量系数系数标准误T P常量-0.18477 0.07859 -2.35 0.043直径0.51276 0.04428 11.58 0.000高度-0.21012 0.04172 -5.04 0.001地点0.00193 0.02861 0.07 0.948S = 0.0469198 R-Sq = 98.9% R-Sq（调整）= 98.6%方差分析来源自由度SS MS F P回归 3 1.85328 0.61776 280.61 0.000残差误差9 0.01981 0.00220合计12 1.87309来源自由度Seq SS直径 1 1.78807高度 1 0.06520地点 1 0.00001异常观测值拟合值标准化观测值直径重量拟合值标准误残差残差2 2.12 0.1500 0.2423 0.0224 -0.0923 -2.24RR 表示此观测值含有大的标准化残差因地点的P值大于0.05，无法通过回归方程检验，故剔除自变量“地点”。

回归分析: 重量与直径, 高度回归方程为：重量= - 0.181 + 0.514 直径- 0.211 高度自变量系数系数标准误T P常量-0.18114 0.05432 -3.33 0.008直径0.51395 0.03851 13.35 0.000高度-0.21116 0.03682 -5.74 0.000S = 0.0445233 R-Sq = 98.9% R-Sq（调整）= 98.7%方差分析来源自由度SS MS F P回归 2 1.85327 0.92663 467.45 0.000残差误差10 0.01982 0.00198合计12 1.87309来源自由度Seq SS直径 1 1.78807高度 1 0.06520异常观测值拟合值标准化观测值直径重量拟合值标准误残差残差2 2.12 0.1500 0.2433 0.0162 -0.0933 -2.25RR 表示此观测值含有大的标准化残差1.拟合优度检验：由于R-Sq（调整）= 98.7%，故数据之间拟合度很好，通过检验。

第10章 简单线性回归分析思考与练习参考答案一、最佳选择题1．如果两样本的相关系数21r r =，样本量21n n =，那么（ D ）。

A. 回归系数21b b = B ．回归系数12b b < C. 回归系数21b b > D ．t 统计量11r b t t = E. 以上均错2．如果相关系数r =1，则一定有（ C ）。

A ．总SS =残差SSB ．残差SS =回归SSC ．总SS =回归SSD ．总SS ＞回归SS E.回归MS =残差MS3．记ρ为总体相关系数，r 为样本相关系数，b 为样本回归系数，下列（ D ）正确。

A ．ρ=0时，r =0B ．|r |＞0时，b ＞0C ．r ＞0时，b ＜0D ．r ＜0时，b ＜0 E. |r |=1时，b =14．如果相关系数r =0，则一定有（ D ）。

A ．简单线性回归的截距等于0B ．简单线性回归的截距等于Y 或XC ．简单线性回归的残差SS 等于0D ．简单线性回归的残差SS 等于SS 总E ．简单线性回归的总SS 等于05．用最小二乘法确定直线回归方程的含义是（ B ）。

A ．各观测点距直线的纵向距离相等B ．各观测点距直线的纵向距离平方和最小C ．各观测点距直线的垂直距离相等D ．各观测点距直线的垂直距离平方和最小E ．各观测点距直线的纵向距离等于零二、思考题1．简述简单线性回归分析的基本步骤。

答：① 绘制散点图，考察是否有线性趋势及可疑的异常点；② 估计回归系数；③ 对总体回归系数或回归方程进行假设检验；④ 列出回归方程，绘制回归直线；⑤ 统计应用。

2．简述线性回归分析与线性相关的区别与联系。

答：区别：（1）资料要求上，进行直线回归分析的两变量，若X 为可精确测量和严格控制的变量，则对应于每个X 的Y 值要求服从正态分布；若X 、Y 都是随机变量，则要求X 、Y 服从双变量正态分布。

直线相关分析只适用于双变量正态分布资料。