2015-2016学年度高二年级第二学期期中考试成绩
- 格式:xlsx
- 大小:41.19 KB
- 文档页数:23

2015~2016学年度第二学期期中考试高二年级数学(理)试题一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位......置上... 1.已知复数i z -=2 (i 是虚数单位),则=z ▲ .2.的值为则若x C C x x ,1288-= ▲ .3. 复数,1z z i=-则的共轭复数为 ▲ . 4. a b a b θ设向量与的夹角为,定义与的“向量积”:a b ⨯是一个向量,它的模 ||=||||sin ,(1,0),(1,1),||=a b a b a b a b θ⨯⋅⋅==⨯若则 ▲ .5.用0,1,2,3这四个数字,可以组成没有重复数字的3位数,其中奇数的个数 为 ▲ .6.观察下列式子:1+122<32,1+122+132<53,1+122+132+142<74,……,根据以上式子可以猜想:<++++2222016131211 ▲ . 7. 21,z z i i i z -=+已知复数满足()则的虚部为 ▲ . 8. 利用数学归纳法证明“)(2131211n p n =+⋅⋅⋅⋅⋅⋅+++”,从k n =推导1+=k n 时原等式的左边应增加的项的个数为 ▲ 个(用含有k 的代数式表示).注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求 1.本试卷共4页,包含填空题(第1题~第14题)、解答题(第15题~第20题).本卷满分160分,考试时间为120分钟.考试结束后,请将答题卡交回.2.答题前,请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请在答题卡上按照顺序在对应的答题区域内作答,在其他位置作答一律无效.作答必须用0.5毫米黑色墨水的签字笔.请注意字体工整,笔迹清楚.4.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.5.请保持答题卡卡面清洁,不要折叠、破损.一律不准使用胶带纸、修正液、可擦洗的圆珠笔.9.4名男生和2名女生站成一排照相,要求男生甲不站在最左端,女生乙不站在最右端, 有 ▲ 种不同的站法.(用数字作答)10.已知ABC △的周长为l ,面积为S ,则ABC △的内切圆半径为2sr l=.将此结论类比到空间,已知四面体ABCD 的表面积为S ,体积为V ,则四面体ABCD 的内切球的半径R ▲ .11.已知复数z 满足243=--i z ,则z 的最大值为 ▲ . 12.若多项式975311010991010,)1()1()1(a a a a a x a x a x a a x+++++++++++=则= ▲ .(用数字作答)13.A 、B 、C 、D 、E 五人住进编号为1,2,3,4,5的五个房间,每个房间只住一人,则B 不住2号房间,且B 、C 两人不住编号相邻房间的住法种数为 ▲ . 14.已知函数1()3x f x x =+,(0)x >,对于*n N ∈,定义11()[()]n n f x f f x +=,则函数()n f x 的值域为 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本题满分14分)已知复数)()65()67(22R a i a a a a z ∈--++-=.(1)若复数z 为纯虚数,求实数a 的值;(2)若复数z 在复平面内的对应点在第四象限,求实数a 的取值范围.16.(本题满分14分)(1)证明:当2a ><; (2)证明:532,, 不可能是同一个等差数列中的三项.17.(本题满分14分)从5名女同学和4名男同学中选出4人参加四场不同的演讲,每场一人,分别按下列要求,各有多少种不同方法?(1)男、女同学各2名; (2)男、女同学分别至少有1名;(3)男、女同学分别至少有1名且男同学甲与女同学乙不能同时选出.18.(本题满分16分)已知nx m x ⎪⎭⎫ ⎝⎛+展开式的二项式系数之和为256.(1)求n ;(2)若展开式中常数项为835,求m 的值;(3)若展开式中系数最大项只有第6项和第7项,求m 的值.19.(本题满分16分)已知椭圆方程是22143x y +=,12,F F 是它的左、右焦点,A ,B 为它的左、右顶点, l 是椭圆的右准线,P 是椭圆上一点,P A 、PB 分别交准线l 于M ,N 两点. (1)若(0,3)P ,求12MF NF ⋅的值;(2)若00(,)P x y 是椭圆上任意一点,求12MF NF ⋅的值;(3)能否将问题推广到一般情况,即给定椭圆方程是22221(0)x y a b a b +=>>,00(,)P x y 是椭圆上任意一点,问12MF NF ⋅是否为定值?证明你的结论.20.(本题满分16分) 设函数21()1+f x px qx=+(其中220p q +≠),且存在公差不为0的无穷等差数列{}n a ,使得函数在其定义域内还可以表示为212()1n n f x a x a x a x =+++++.(1)求,1a 2a 的值(用,p q 表示); (2)求{}n a 的通项公式;(3)当*N n ∈且2≥n 时,比较n an a )(1-与1)(-n a n a 的大小.高二数学理科试题参考答案1. 52. 1或33. i -14. 15.86.7. 18. 2k9. 50410.S V 3 11.7 12. -512 13. 60 14. 2(0,)31n -15. 解:(1)由题设知:⎩⎨⎧≠--=+-06506722a a a a ………………3分解之得,a =1……………………………7分(2)由题设知:⎩⎨⎧<-->+-06506722a a a a ………………10分解之得,⎩⎨⎧<<-><6161a a a 或 …………… 12分所以实数a 的取值范围是 -1<a <1 …………14分16. 证明: (1)要证222a a a ++-<,只要证22)2()22(a a a <-++, ---------------------2分只要证a a a 44222<-+, 只要证a a <-42,----------------4分由于2a >,只要证224a a <-, -----------------------------------------6分222a a a +-<………7分(其它方法酌情给分) (2)(反证法)假设3,5是同一个等差数列中的三项,分别设为,,m n p a a a ,----8分则23m n a a d m n --==-------------------------------------10分 又253m p a a d m p m p m p---===---为有理数----------------------12分所以产生矛盾,假设不成立,即3,5不可能是同一个等差数列中的三项. -------14分17. 解:620131401440)1(442425=A C C --------------------4分2880))(2(44444549=--A C C C --------------------8分504)3(4427=A C --------------------------11分 23765042880=-----------------12分 答:略----------------------------------14分18. 解(1)二项式系数之和为2n=256,可得 8=n ; ---------4分(2)设常数项为第r +1项,则rr r rrrr x m C x m xC T 288881--+=⎪⎭⎫ ⎝⎛=, -------5分 故8-2r =0,即r =4, ---------------------------6分 则835448=m C ,解得21±=m .---------------------9分(3)易知m >0,设第r+1项系数最大. ----------------10分则⎪⎩⎪⎨⎧≥≥++--.,11881188r r r r r r r r m C m C m C m C 化简可得19118+≤≤+-m m r m m . -------13分 由于只有第6项和第7项系数最大,所以⎪⎪⎩⎪⎪⎨⎧<+≤≤+-<.7196,51184m m m m ,即⎪⎪⎩⎪⎪⎨⎧<≤≤<.272,245m m ------15分所以m 只能等于2. ---------------16分(若由第6项和第7项系数相等得出m=2,则需要验证.不验证仅给3分. )19. 解: (1)22121,(2,0),(2,0),(1,0),(1,0):443x y A B F F l x +=--=椭圆方程为,P 又22PA y x =+故所在直线方程为:(),=4(4x M 与联立得N 同理可得----------------------2分12(5,33),(MF NF ∴=--=-121596MF NF ⋅=-=------------------------4分(2) 2222000000(,),1=3-434x y x P x y y +=则,即(1) 00022y PA y x x x =+≠+所在直线方程为:(),(-2) 006=4(4,),2y x M x +与联立得-----------------------------------------------6分 002(4,).2y N x -同理可得-----------------------------------------------------8分 00120062(5,),(3,)22y y MF NF x x ∴=--=--+- 2020*********(1)1241515644x y MF NF x x ⨯-⋅=+=+=--------------------------10分 (3) 2122()MF NF b ⋅=定值,下证之--------------------------------------------11分22212221,(,0),(,0),(,0),(,0):x y a A a B a F c F c l x a b c+=--=证明:椭圆方程为,22222000000222(,),1=-x y x P x y y b a b a +=设则,即(1)00y PA y x a x a x a=+≠+所在直线方程为:(),(-) 22200()=(,),a a y a a c x M c c x a ++与联立得2200()(,).a a y a c N c x a --同理可得--------------14分 2222001200()()(,),(,).a a a y a y a a c c MF c NF c c x a c x a+-∴=---=--+- 4224022122220()a a y ac MF NF c c x a -⋅=-+-2224222()2()a c b b b c c+=-=定值--------------------------------16分20.解:(1)由题意,得2212(1)(1)1n n px qx a x a x a x +++++++=,显然2,x x 的系数为0,所以121+0++0a p a a p q =⎧⎨=⎩,从而1a p =-,22a p q =-.………………………4分(2)考虑(3)nx n ≥的系数,则有120n n n a pa qa --++=,……………5分因数列{}n a 是等差数列,所以1220n n n a a a ---+=,所以12(2+)(1)n n p a q a --=-对一切3n ≥都成立,……………7分若0n a =,则0p q ==,与220p q +≠矛盾,若数列{}n a 是等比数列,又据题意{}n a 是等差数列,则{}n a 是常数列,这与数列{}n a 的公差不为零矛盾,所以210p q +=-=,即2,1p q =-=,……………9分 由(1)知12a =,23a =,所以1n a n =+.……………10分(其他方法:根据题意可以用p 、q 表示出1a ,2a ,3a ,4a ,由数列{}n a 为等差数列,利用2132a a a =+,3242a a a =+解方程组也可求得.其它解法酌情给分.)(3)111,(1).n n a a n nn n a n a n -+-==+由(2)可知,()() 2121321212228,39,a a a a n a a a a =====∴<时,11-13(1).n n a a n n n n n n n a a -+≥>+>当时,,即()()下用数学归纳法证明.……………12分4333=81,4=64,8164,n =>1)当时,结论成立.13,(1)k k n k k k N k k +=≥∈>+2)设当时()时,结论成立,即有①. ……………13分1n k =+下面证明当时,结论也成立.由①得1211.(1)(2),,(1)21k kk k k k k k k k k ++>+>+>+++又因为即 221+1+11(1)(2)=()1,(2)2212(1)k k k k k kk k k k k k k k k k k k k +++++⋅>⋅=>++++++()所以()21+1+2,1k k k k n k ++>=+即()()所以结论在时也成立. 1-11)2)(3,).n n a a n n n n n N a a -≥∈>综合、,对任何结论成立,即()()……………16分。

北京师大附中2015—2016学年度第二学期期中考试高二物理试题考试时间100分钟,满分100分一、单项选择题1.对光的本性认识过程中,波动说和微粒说是两个重要的观点,下面科学家中不支持波动说的是()A.惠更斯B.菲涅耳C.托马斯·杨D.牛顿2.下列现象中由干涉产生的是A.天空出现彩虹B.肥皂泡在阳光下呈现彩色条纹C.阳光通过三棱镜形成彩色光带D.水中气泡看起来很亮3.“泊松亮斑”是下面的哪个图形?()A.第一个B.B第二个C.第三个D.第四个4.如图,只含黄、紫光的复色光束PO,沿半径方向射入空气中的玻璃半圆柱后,被分成两光束OA和OB沿如图方向射出.则()A.OA为黄光,OB为紫光B.OA为紫光,OB为黄光C.OA为黄光,OB为复色光D.OA为紫光,OB为复色光5. 如图所示,绕在铁芯上的线圈与电源、滑动变阻器和电键组成闭合回路,在铁芯的右端套有一个表面绝缘的铜环A,下列各种情况中铜环A中没有感应电流的是()A.线圈中通以恒定的电流B.通电过程中,使变阻器的滑片P作匀速移动C.通电过程中,使变阻器的滑片P作加速移动D.将电键突然断开的瞬间6.在磁感应强度为B、方向如图所示的匀强磁场中,金属杆PQ在的平行金属导轨上向右匀速滑动,PQ中产生的感应电动势为E1;若磁感应强度增为2B,其它条件不变,所产生的感应电动势大小变为E2,则E1与E2之比及金属杆两端电势高低是()A.2∶1,φP>φQ B.1∶2,φP>φQC.2∶1,φP<φQ D.1∶2,φP<φQ7.如图所示,三只完全相同的灯泡a、b、c分别与电阻R、电感L、电容C串联,再将三者并联,接在220V,50Hz的交变电压两端,三只灯泡亮度相同。
若接在220V,60Hz的交变电压两端,则()A.三只灯泡亮度都不变B.三只灯泡都将变亮C.a亮度不变,b变亮,c变暗D.a亮度不变,b变暗,c变亮8.如图所示,有一个铜盘,轻轻拨动它,能长时间地绕轴自由转动。

2015-2016年高二化学下学期期中试题(有答案)201-2016学年度下学期半期校联考高二化学试题考试时间:100分钟总分:100分出题人:付银燕审题人:幸孙剑可能用到的原子量:H—1,—16,I—3,—12,a—40,u—64第Ⅰ卷(选择题共40分)一、选择题:(共20题,每小题2分,共40分,每题只有一个答案符合题意。
)1、据报道,199年我国科研人员在兰州首次合成了镤元素的一种同位素镤-239,其原子核内有148个中子。
现有A元素的一种同位素,比镤—239的原子核内少4个质子和100个中子,则A元素在周期表中的位置是:()A.第3周期第ⅠA族B.第4周期第ⅠA族.第周期第ⅠA族D.第3周期第ⅡA族2、下列化学用语的书写正确的是:()A.基态g离子的核外电子排布图:B.过氧化氢的电子式:.As原子的简化电子排布式:[Ar]4s24p3D.羟基的电子式:3、下列各组元素都属于p区的是:()A.原子序数为1,6,7的元素B.,S,P.Fe,u,l D.Na,Li,g4、下列大小比较不正确的是:()A.熔沸点:Si2>Nal>S>2 B.酸性:HN2<HN3;H3P4<H2S4.还原性:H2S>HI>HBr>Hl D.键长:—H<N—H<—H 、现有四种元素的基态原子的电子排布式如下:①[Ne]3s23p4;②1s22s22p63s23p3;③1s22s22p。
则下列有关比较中正确的是:()A.最高正化合价:③>②>①B.单质氧化性:③>①>②.电负性:③>②>①D.原子半径:③>②>①6、下列对分子及其性质的解释中,不正确的是:()A.碘易溶于四氯化碳,甲烷难溶于水都可用相似相溶原理解释B.乳酸[H3H(H)H]中存在一个手性碳原子.许多过渡金属离子对多种配体具有很强的结合力,因而,只有过渡金属才能形成配合物D.已知酸性:H3P4>Hl,是因为H3P4分子中有1个非羟基氧原子而Hl为07、下面有关晶体的叙述中,不正确的是:()A.金刚石为空间网状结构,由共价键形成的碳原子环上,最小的环上有6个碳原子B.氯化钠晶体中,每个Na+周围距离相等的Na+共有6个.氯化铯晶体中,每个s+周围紧邻8个l-D.干冰晶体中,每个2分子周围紧邻12个2分子8、向盛有硫酸铜水溶液的试管里加入氨水,首先形成难溶物,继续添加氨水,难溶物溶解得到深蓝色的透明溶液。


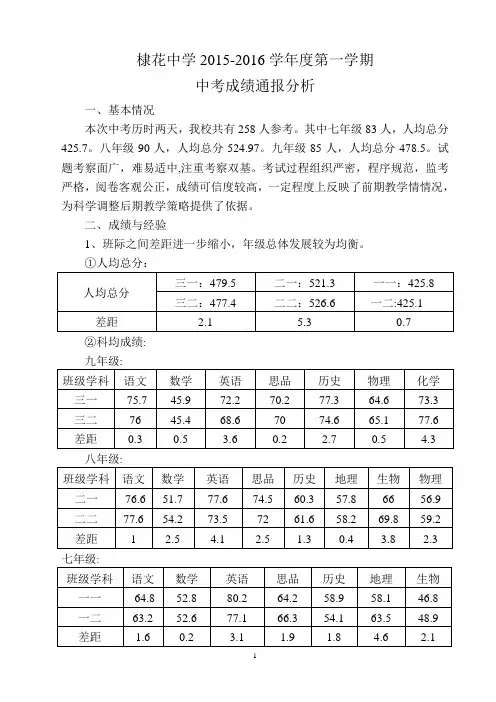
棣花中学2015-2016学年度第一学期中考成绩通报分析一、基本情况本次中考历时两天,我校共有258人参考。
其中七年级83人,人均总分425.7。
八年级90人,人均总分524.97。
九年级85人,人均总分478.5。
试题考察面广,难易适中,注重考察双基。
考试过程组织严密,程序规范,监考严格,阅卷客观公正,成绩可信度较高,一定程度上反映了前期教学情情况,为科学调整后期教学策略提供了依据。
二、成绩与经验1、班际之间差距进一步缩小,年级总体发展较为均衡。
②科均成绩:九年级:八年级:七年级:③年级前40名各班人数:从以上数据,班级间人均总分差距最大为八年级,二班比一班多5.3分;最小为七年级,一班比二班高0.7分。
科均分差距最大为九年级化学,二班比一班高4.3分;最小为九年级思品、七年级数学,一班比二班高0.2分;年级前40名中,差距最大为九年级,一班比二班多4人;差距最小为七年级,二班比一班多2人。
2、全优生人数增多。
像九年级的韩娇、张琦、李金萍、李盈、陈合欢等同学,八年级的张明博、牛卫卫、李芬芬、雷一凡、张煜等同学,七年级的张雨彤、张肖梅、张夏波、许宇泉、张思妙等同学,他们胸有大志,学习自觉,学科均衡,成绩优异,成为其他同学赶超的对象。
3、学习标兵继续领跑。
像九年级的赵子琨、雷龙泉、李雨强、韩兰兰、李博、雷雨萌、张鹏杰、张晨阳、姜雨溪,八年级的李红红、王程毅、许志强、贾程皓、张璟、贾旭阳、李娜、姜孟莉、余倩、姜晨晓,七年级的雷雨林、陈晨、张明乐、赵琳、孙阳阳、周欣怡、代靖靖、雷育嘉、刘月定、付延玉,他们不畏困难,学有目标,踏实勤奋,为其他同学树立了学习的榜样。
4、中等生潜力巨大。
像九年级总分在499-420之间的林丹红、张侨兴等23名同学,八年级总分在540-480之间的赵洋、李涵宇、吕玉娇等14名同学,七年级总分在499-420之间的张智远、李明青、张雯雯等26名同学,只要在个别薄弱学科上有所突破,就完全可以挤入优生行列,成为未来重点高中的有力竞争者。

深圳市高级中学2015—2016学年第二学期期中测试高二物理命题人:朱立光审题人:钟早鸣本试卷由两部分组成.第一卷,共65分;第二卷,共35分.全卷由第Ⅰ卷和第Ⅱ卷两部分构成,第Ⅰ卷为1~8题,第Ⅱ卷为9~13题.全卷满分:100分.考试时间:90分钟.注意事项:1、答第一卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2、每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动用橡皮擦干净后,再涂其它答案,不能答在试题卷上.3、考试结束,监考人员将答题卡按座位号、页码顺序收回.第Ⅰ卷(高二上学期及以前基础知识和能力,共65分)一、单项选择题:(本题共4小题;每小题5分,共20分.)1.两相邻的匀强磁场区域的磁感应强度大小不同,方向平行.一速度方向与磁感应强度方向垂直的带电粒子(不计重力),从较强磁场区域进入到较弱磁场区域,粒子的:A.轨道半径减小,角速度增大B.轨道半径减小,角速度减小C.轨道半径增大,角速度增大D.轨道半径增大,角速度减小2.如图所示,一物块在拉力F T作用下沿水平方向做匀速运动.则拉力F T与摩擦力F f的合力的方向为:A.可能向上偏右B.可能向上偏左C.一定竖直向上D.无法判定3.如图所示,在同一轨道平面上的几个人造地球卫星A、B、C 绕地球做匀速圆周运动,某一时刻它们恰好与地球在同一直线上,下列说法中正确的是:A.根据v=错误!可知,运行速度满足v A>v B>v CB.运转角速度满足ωA>ωB>ωCC.向心加速度满足a A<a B<a CD.此后,A最先回到图示位置4.目前世界上输送功率最大的直流输电工程--哈(密)郑(州)特高压直流输电工程已正式投入运行.高压直流输电具有无感抗、无容抗、无同步问题等优点.已知某段直流输电线长度L=200 m,通有从西向东I=4 000 A的恒定电流,该处地磁场的磁感应强度B=5×10—5T,磁倾角(磁感线与水平面的夹角)为5°(sin 5°≈0。

深圳市高级中学2015-2016学年第二学期期中测试高二(理科)数学命题人: 审题人:本试卷由二部分组成.第一部分:本学期以前所学内容基础知识和能力考查(共96分);第二部分:本学期知识内容考查(共54分)。
全卷共计150分,考试时间为120分钟. 注意事项: 1、答题前,考生务必将自己的姓名、考号、座位号涂写在答题卡上。
2、选择题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动用橡皮擦干净后,再涂其它答案,不能答在试题卷上。
3、考试结束,监考人员将答题卡收回。
第一部分 一.选择题:共10小题,每小题5分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的一项.1。
若复数z 满足201520161z i i i=++ i 为虚数单位),则复数z=( B )A .1B .2C .iD .2i ) (17cos 17sin 347sin 2.2=-DA .3-B .—1C .3D .13。
给出下列三个命题: (1)“若0322≠-+x x,则1≠x ”为假命题;(2)命题02,:>∈∀xR x P :,则02,:≤∈∃⌝ x R x P ; (3)“)(2Z k k ∈+=ππφ”是“函数)2sin(φ+=x y 为偶函数”的充要条件; 其中正确的个数是( C )A. 0B. 1 C 。
2 D. 34。
双曲线M :2222x y a b-=1(a>0,b 〉0)的左、右焦点为F 1,F 2,抛物线N :y 2=2px( p>0)的焦点为F 2,点P 为双曲线M 与抛物线N 的一个交点,若线段PF 1的中点在y 轴上,则该双曲线的离心率为(B ) A .3+1 B .2+1C .312+ D .212+ 5.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺313寸,容纳米2000斛(1丈=10尺,l 尺=10寸,斛为容积单位,l 斛≈1。
62立方尺,π≈3),则圆柱底圆周长约 为( B )A. l 丈3尺 B 。

湖北省枣阳市阳光中学高二年级2015-2016学年度下学期期中考试数学(文科)试题时间:120分钟 分值150分 第I 卷(选择题共60分)一、选择题(本大题12小题,每小题5分,共60分) 1.若R a ∈,则“2a =”是“()()240a a -+=”的( ) A .充要条件 B .充分不必要条件 C .必要不充分条件 D .既不充分也不必要条件2.已知以F 为焦点的抛物线y 2=4x 上的两点A 、B 满足AF =3FB ,则弦AB 的中点到准线的距离为( )A .B .C .2D .1 3.设非零向量a 与b 的夹角为θ,则(,)2πθπ∈是0a b ⋅<的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 4.设曲线y =在点(3,2)处的切线与直线ax +y +3=0垂直,则a 等于( )A .2B .C .-2D .- 5.已知()()32213af x x a x=+-+,若()18f '-=,则()1f -= ( )A .4B .5C .2-D .3-6.在ABC ∆中,“060A ∠=”是“sin 2A =”的( ) A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件7.命题“2,220x x x ∃∈++≤R ”的否定是( ) A .2,220x x x ∀∈++>RB .2,220x x x ∀∈++≤RC .2,220x x x ∃∈++>RD .2,220x x x ∃∈++≥R8.命题“2,0x R x ∀∈>”的否定是( ) A.2,0x R x ∀∈≤ B.2,0x R x ∃∈> C.2,0x R x ∃∈< D.2,0x R x ∃∈≤ 9.函数已知时取得极值,则的值等于( )A.2B.3C.4D.510.已知直线1y x =+与曲线ln()y x a =+相切,则a 的值为( ) A.1 B.2 C.1- D.2- 11.“1x >”是“12log (2)0x +<”的 ( )A 、充要条件B 、充分不必要条件C 、必要不充分条件D 、既不充分也不必要条件12.定义域为R 的可导函数()x f y =的导函数为()x f ',满足()()x f x f '>,且(),10=f 则不等式()1<xe xf 的解集为( )A .()0,∞-B .()+∞,0C .()2,∞-D .()+∞,2第II 卷(非选择题)二、填空题(本大题共4个小题,每题5分,满分20分)13.双曲线2214x y m-=的虚轴长是实轴长的2倍,则m 的值= . 14.若不等式|x -m |<1成立的充分不必要条件是13<x <12,则实数m 的取值范围是________.15.直线1y kx =+与曲线3y x ax b =++相切于点()1,3A ,则b 的值为 .16.已知椭圆C :22143x y +=,点M 与C 的焦点不重合.若M 关于C 的焦点的对称点分别为A ,B ,线段MN 的中点在C 上,则||||AN BN += . 三、解答题(70分) 17.(本题12分)已知命题[]2:2,4,220p x x x a ∀∈--≤恒成立,命题()2:1q f x x ax =-+在区间1,2⎡⎫+∞⎪⎢⎣⎭上是增函数. 若p q ∨为真命题,p q ∧为假命题,求实数a 的取值范围.18.(本小题满分12分) 已知函数f (x )=6ln x +x 2-8x , g (x )=P x+x 2(p ∈R) (1)求函数f (x )的单调递增区间;(2)若在区间上至少存在一点x 0,使f (x 0)>g (x 0)成立,求实数p 的取值范围.19.(本题12分)已知二次函数2()f x ax bx c =++满足(1)()2f x f x x +-=且(0)1f =. (1)求()f x 的解析式;(2)当[1,1]x ∈-时,方程()2f x x m ≥+恒成立,求实数m 的范围.20.(本题12分)(本小题满分l2分)(注意:在试题卷上作答无效.........) 已知函数f (x )=x 3+bx 2+ax +d 的图象过点P (0,2),且在点M (-1,f (-1))处的切线方程为6x -y +7=0.(1)求函数y =f (x )的解析式; (2)求函数y =f (x )的单调区间.21.(本题12分)已知双曲线与椭圆共焦点,且以为渐近线,求双曲线方程.1244922=+y x x y 34±=22.(本题10分)已知函数3()f x ax bx c =++在2x =处取得极值为16c -(1)求a 、b 的值; (2)若()f x 有极大值28,求()f x 在[3,3]-上的最小值.参考答案1.B 【解析】试题分析:若“2a =”,则“()()240a a -+=”;反之 “()()240a a -+=”,则2,a =或4a =-.故“2a =”是“()()240a a -+=”的充分不必要条件.考点:充分、必要条件的判断.2.A 【解析】试题分析:抛物线的焦点为()1,0F ,准线方程为1x =- 设()()1122,,,A x y B x y ,直线AB 的方程为:()1y k x =-由()241y x y k x ⎧=⎪⎨=-⎪⎩消法x 得:2440y y k --= (*)由题设知:12,y y 是方程的两根,所以124y y ⋅=- (1) 又因为AF =3FB ,所以123y y =- (2)解由方程(1)(2)组成的方程组得:12y y == 所以22121213,443y y x x ==== 设弦AB 的中点为C ()00,x y , 则120523x x x +==,所以C 到准线的距离()0581133d x =--=+= 故选A.考点:1、抛物线的标准方程与几何性质;2、直线与抛物线的位置关系. 3.A 【解析】试题分析:因为当θ为钝角或平角时0a b ⋅<均成立,所以(,)2πθπ∈是0a b ⋅<的充分不必要条件,故选A .考点:1、充分条件与必要条件的判定;2、平面向量的夹角. 4.C 【解析】试题分析:,,由导数的几何意义可得曲线在处的切线斜率为,又直线的斜率为,依题意可得,解得.故C 正确.考点:1导数的几何意义;2直线垂直. 5.A 【解析】试题分析:()()()()()32''22221362118a a f x x a f x x f x x=+-+∴=++-=1a ∴=()()()3221314f x x f x∴=+-+∴-= 考点:函数导数及函数求值 6.A 【解析】试题分析:若060A ∠=,则sin sin 60A =︒=;若sin A =,则60360,A k k z ∠=︒+⋅︒∈;故“060A ∠=”是“sin A =”的充分不必要条件.考点:充分、必要条件的判断.【方法点睛】充分不必要条件、必要不充分条件、既不充分也不必要条件的判断的一般方法:①充分不必要条件:如果p q ⇒,且p q ⇐/,则说p 是q 的充分不必要条件; ②必要不充分条件:如果p q ⇒/,且p q ⇐,则说p 是q 的必要不充分条件; ③既不充分也不必要条件:如果p q ⇒/,且p q ⇐/,则说p 是q 的既不充分也不必要条件. 7.A 【解析】试题分析:由特称命题和全称命题的关系可知“2,220x x x ∃∈++≤R ”的否定为2,220x x x ∀∈++>R 。
湖北省枣阳市第二中学高二年级2015-2016学年度下学期期中考试数学(文科)试题★ 祝考试顺利 ★时间:120分钟 分值150分_第I 卷(选择题共60分)一、选择题(本大题12小题,每小题5分,共60分) 1.“0,0a b >>”是“2b aa b+≥”的( A .充分不必要条件 B .必要不充分条件C .充要条件 D .既不充分也不必要条件2) xyAOxyBOxyCOxyDO3.设双曲线22221(0,0)y x a b a b-=>>的左焦点(,0)F c -,圆222x y c +=与双曲线的一条渐近线交于点A ,直线AF 交另一条渐近线于点B ,若12FB FA =,则双曲线的离心率为( )A .2B .3C .32D 4.函数'()y f x =是函数()y f x =的导函数,且函数()y f x =在点00(,())p x f x 处的切线为000:()'()()(),()()()l y g x f x x x f x F x f x g x ==-+=-,如果函数()y f x =在区间[,]a b 上的图像如图所示,且0a x b <<,那么( )A .00'()0,F x x x ==是()F x 的极大值点B .0'()F x =00,x x =是()F x 的极小值点C .00'()0,F x x x ≠=不是()F x 极值点D .00'()0,F x x x ≠=是()F x 极值点5,若)5(),4(),3(f c f b f a ===则( ) A. a< b < c B. c < b < a C. c < a < b D. b < a < c 6.已知命题:,25xp x R ∀∈=,则p ⌝为( ) A 、,25xx R ∀∉= B 、,25xx R ∀∈≠C 、00,25x x R ∃∈= D 、00,25x x R ∃∈≠7.下列命题中的说法正确的是A .若向量b a //,则存在唯一的实数λ使得b a λ=;B .命题“若12=x ,则1=x ”的否命题为“若12=x ,则1≠x ”;C .命题“R x ∈∃0,使得01020<++x x ”的否定是:“R x ∈∀,均有012>++x x ”; D .“5≠a 且5-≠b ”是“0≠+b a ”的不充分也不必要条件;8.设R a ∈,若函数x a x y ln +=在区间) , 1(e e有极值点,则a 取值范围为( )A .) , 1(e eB .)1 , (e e --C .) , ()1 , (∞+-∞e e UD .) , 1() , (∞+---∞ee U9.()f x 与()g x 是定义在R 上的两个可导函数,若()f x ,()g x 满足''()()f x g x =,则()f x 与()g x 满足A .()f x =()g xB .()f x -()g x 为常数函C.()f x =()0g x = D.()f x +()g x 为常数函数10.设A(x 1,y 1),B(x 2,y 2)是抛物线y 2=2px(p>0)上的两点,并且满足OA ⊥OB. 则y 1y 2等于A – 4p 2B 4p 2C – 2p 2D 2p 211.已知椭圆C 的方程为222116x y m +=(m >0),如果直线y x 与椭圆的一个交点M 在x 轴上的射影恰好是椭圆的右焦点F ,则m 的值为( )A .2B .C .8D . 12.已知函数21()43ln 2f x x x x =-+-在[,1]t t +上不单调,则t 的取值范围是( ) A .(0,1)(2,3)⋃ B .(0,2) C .(0,3) D .(0,1][2,3)⋃二、填空题(题型注释)13.已知函数f (x )=x 3-3ax -1,a ≠0.若f (x )在x =-1处取得极值,直线y =m 与y =f (x )的图象有三个不同的交点,则m 的取值范围是 .14.过抛物线)0(22>=p py x 的焦点作斜率为1的直线与该抛物线交于A 、B 两点,A 、B 在x 轴上的正射影分别为D 、C 。
2015-2016学年第二学期高二期中考试数学学科(文科)试题一、填空题:本大题共14小题,每小题5分,共70分1.命题0)(),2,0(:<∈∀x f x p π,则p ⌝: .2.已知复数i Z 43+= (i 为虚数单位),则Z = . 3.设全集{}3,2,1,0,1{},42-=≤≤-∈=A x Z x U ,若A C B U ⊆,则集合B 的个数是 .4.已知复数i Z i Z 34,221-=+= 在复平面内的对应点分别为点A 、B ,则A 、B 的中点所对应的复数是 .5.已知11)1(+=x x f ,那么)(x f 的解析式为 . 6.已知ni i+=-112,其中i R n ,∈ 是虚数单位,则n = . 7.函数)3lg(1)(2x x x f --=的定义域为 .8. 函数⎪⎩⎪⎨⎧>+-≤=0,10,2)(2x x x x f x 的值域为 . 9.若函数2+-=x b x y 在)2)(6,(-<+b a a 上的值域为),2(+∞,则=+b a . 10.若命题“存在04,2≤++∈a x ax R x ”为假命题,则实数a 的取值范围是 .11. 已知函数⎩⎨⎧≥<+-=-1,21,3)21()(1x x a x a x f x 的值域为R ,则实数a 的取值范围是 . 12. 记12x x -为区间],[21x x 的长度.已知函数)0](,2[,2≥-∈=a a x y x,其值域为],[n m ,则区间],[n m 的长度的最小值是 .13.观察下列各式9﹣1=8,16﹣4=12,25﹣9=16,36﹣16=20…,这些等式反映了自然数间的某种规律,设n 表示自然数,用关于n 的等式表示为 . 14.设][x 表示不超过x 的最大整数,如2]5.1[,1]5.1[-=-=.若函数x xaa x f +=1)( )1,0(≠>a a ,则]21)-([]21)([)(-+-=x f x f x g 的值域为 . 二、解答题:(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)15.(本小题满分14分) 已知}42{},71{},9{2<-=≤<-=≥=x x C x x B x x A .(1)求A ∩B 及A ∪C ;(2)若U=R ,求A ∩∁U (B ∩C )16.(本小题满分14分)已知复数Z 满足:Z i Z -+=31,求Zi i 2)43()1(2++的值.17.(本小题满分15分)设a 为实数,给出命题:p 关于x 的不等式a x ≥-1)21(的解集为φ,命题:q 函数]89)2(lg[)(2+-+=x a ax x f 的定义域为R ,若命题""q p ∨为真,""q p ∧为假,求实数a 的取值范围.18.(本小题满分15分)“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度v (单位:千克/年)是养殖密度x(单位:尾/立方米)的函数.当x 不超过4尾/立方米时,v 的值为2千克/年;当204≤<x 时,v 是x 的一次函数,当x 达到20尾/立方米时,因缺氧等原因,v 的值为0千克/年.(1)当200≤<x 时,求v 关于x 的函数表达式;(2)当养殖密度x 为多大时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.19.(本小题满分16分)若)(x f 为二次函数,1-和3是方程04)(=--x x f 的两根,1)0(=f(1)求)(x f 的解析式;(2)若在区间]1,1[-上,不等式m x x f +>2)(有解,求实数m 的取值范围.20.(本小题满分16分)已知函数0(2log )(>-+=a x m x x f a且)1≠a 的定义域为2{>x x 或}2-<x . (1)求实数m 的值;(2)设函数)2()(xf xg =,对函数)(x g 定义域内任意的21,x x ,若021≠+x x ,求证:)1()()(212121x x x x g x g x g ++=+; (3)若函数)(x f 在区间),4(r a -上的值域为),1(+∞,求r a -的值.2015-2016学年第二学期高二期中考试数学试题(文科)参考答案一、填空题: 1. 0)(),2,0(≥∈∃x f x π2. 53. 44. i -35. xx x f +=1)( 6. 1 7. 5]30[-2,(), 8. ]1,(-∞ 9. 10- 10. ),(∞+2 11. )21,0[ 12. 3 13. )(),1(4)2(*22N n n n n ∈+=-+ 14. 1}-{0,二、解答题:15.解:(1)集合A 中的不等式解得:x≥3或x≤﹣3,即A={x|x≥3或x≤﹣3};--2分 集合C 中的不等式解得:﹣2<x <6,即C={x|﹣2<x <6},-------- -------------4分 ∴A∩B={x|3≤x≤7},----------------------- ------------------------------6分 A∪C={x|x≤﹣3或x >﹣2};-----------------------------------------------8分(2)∵B∩C={x|﹣1<x <6},-----------------------------------------------10分 全集U=R ,∴∁U (B∩C)={x|x≤﹣1或x≥6},--------------------------------12分 则A∩∁U (B∩C)={x|x≥6或x≤﹣3}.--------------------------------------14分16.解:设z=a+bi (a ,b ∈R ),---------------------------------------------2分 而|z|=1+3i ﹣z ,即,-------------------------------4分 则-----------------------------------------------------6分 解得,z=﹣4+3i ,--------------------------------------------------8分 ∴==1.-------------14分17.解:命题p :|x ﹣1|≥0,∴,∴a>1;---------------------4分命题q :不等式的解集为R ,∴,解得;---------------------------------------------------------------8分若命题“p∨q”为真,“p∧q”为假,则p,q一真一假;----------------------10分p真q 假时,,解得a≥8;----------------------------------12分p假q 真时,,解得;-----------------------------------14分∴实数a 的取值范围为:.----------------------------15分18.解(1)由题意得当0<x≤4时,v=2; ----------------------------------2分当4<x≤20时,设v=ax+b,由已知得:,解得:,所以v=﹣x+,---------------------4分故函数v=;-------------------------------------------6分(2)设年生长量为f(x)千克/立方米,依题意并由(1)可得f(x)=-----------------------8分当0<x≤4时,f(x)为增函数,故f(x)max=f(4)=4×2=8;-----------------10分当4<x≤20时,f(x)=﹣x2+x=﹣(x2﹣20x)=﹣(x﹣10)2+,f(x)max=f(10)=12.5.--------------------------------------------------12分所以当0<x≤20时,f(x)的最大值为12.5.-------------------------------14分即当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值为12.5千克/立方米.--------------------------------------------------------------------15分19. 解:(1)设二次函数f(x)=ax2+bx+c,(a≠0),由f(0)=1可得c=1,------------------------------------------------------2分故方程f(x)﹣x﹣4=0可化为ax2+(b﹣1)x﹣3=0,∵﹣1和3是方程f(x)﹣x﹣4=0的两根,∴由韦达定理可得﹣1+3=﹣,﹣1×3=,解得a=1,b=﹣1,故f(x)的解析式为f(x)=x2﹣x+1;----------------------------------------8分(2)∵在区间[﹣1,1]上,不等式f(x)>2x+m有解,∴m<x2﹣3x+1在区间[﹣1,1]上有解,--------------------------------------10分故只需m小于函数g(x)=x2﹣3x+1在区间[﹣1,1]上的最大值,由二次函数可知当x=﹣1时,函数g(x)取最大值5,--------------------------14分∴实数m的取值范围为(﹣∞,5)------------------------------------------16分20.解:(1)m=2时,解得,x>2,或x<﹣2;∴m=2;-----------------1分(2)证明:,;------------2分∴g(x1)+g(x2)==;=;∴;------------------------------------6分(3);∴①若a>1,f(x)在(a﹣4,r)上单调递减;∴;∴;∴;∴;-----------------------------12分②若0<a<1,f(x)在(a﹣4,r)上单调递增;∴;∴;∴,或(舍去);∴.-----------------16分。