数学培训计算方法资料
- 格式:ppt
- 大小:4.59 MB
- 文档页数:7

七年级数学新课标培训资料数学作为一门重要的学科,是培养学生逻辑思维、数学思维和分析解决问题能力的重要途径。
近年来,随着国家教育改革的推进,新课标的实施对于培养学生的数学素养、创新意识以及实际应用能力都提出了更高的要求。
因此,为了帮助七年级学生更好地适应新课标要求和提高数学水平,本文将以新课标为指导,为大家准备了一份七年级数学的培训资料。
一、数的概念与运算在七年级数学课程中,数的概念与运算是基础中的基础,也是其他数学知识的基石。
为了帮助同学们更好地掌握这一部分知识,我们将从以下几个方面进行讲解和练习。
1. 自然数与整数的认识与运算自然数和整数是我们在日常生活中接触最多的数,对于它们的认识和运算是十分重要的。
在这部分内容中,我们将介绍自然数和整数的概念,以及加法、减法的运算规则和性质,并通过一些实际问题进行练习。
2. 分数的认识与运算分数是表示小于1的有理数,它可以用来表示几次相等的部分。
在这部分内容中,我们将介绍分数的概念,以及分数的四则运算规则和性质,并通过练习题来巩固所学知识。
3. 小数的认识与运算小数是表示大于或等于1的有理数,它是分数的一种特殊形式。
在这部分内容中,我们将介绍小数的概念,以及小数的加减乘除运算规则和性质,并给出一些实际应用题供同学们练习。
二、代数与方程代数是数学的一个重要分支,它研究的是用字母表示数的规律和性质。
在七年级数学中,代数与方程是一个相对较难的部分,需要同学们具备一定的逻辑推理和转化能力。
为了更好地掌握这一部分知识,我们将从以下几个方面进行讲解和练习。
1. 代数式的认识与转化代数式是由数字和字母以及运算符号组成的式子,它用来表示数或数之间的关系。
在这部分内容中,我们将介绍代数式的概念,以及代数式的运算规则和性质,并通过练习题来加深理解。
2. 方程的认识与解法方程是用等号连接的两个代数式,它表示两个量相等的关系。
在这部分内容中,我们将介绍方程的概念,以及方程的解法和解的意义,并通过一些实际问题来应用所学知识。

四年级数学简便计算:乘除法篇一、乘法:1.因数含有25和125的算式:例如①:25×42×4我们牢记25×4=100,所以交换因数位置,使算式变为25×4×42. 同样含有因数125的算式要先用125×8=1000。
例如②:25×32此时我们要根据25×4=100将32拆成4×8,原式变成25×4×8。
例如③:72×125 我们根据125×8=1000将72拆成8×9,原式变成8×125×9。
重点例题:125×32×25 =(125×8)×(4×25)2.因数含有5或15、35、45等的算式:例如:35×16我们根据需要将16拆分成2×8,这样原式变为35×2×8。
因为这样就可以先得出整十的数,运算起来比较简便。
3.乘法分配律的应用:例如:56×32+56×68我们注意加号两边的算式中都含有56,意思是32个56加上68个56的和是多少,于是可以提出56将算式变成56×(32+68)如果是56×132—56×32 一样提出56,算是变成56×(132-32)注意:56×99+56 应想99个56加上1个56应为100个56,所以原式变为56×(99+1) 或者56×101-56=56×(101-1)另外注意综合运用,例如:36×58+36×41+36=36×(58+41+1)47×65+47×36-47 =47×(65+36-1)4.乘法分配律的另外一种应用:例如:102×47我们先将102拆分成100+2 算式变成(100+2)×47 然后注意将括号里的每一项都要与括号外的47相乘,算式变为:100×47+2×47 例如:99×69 我们将99变成100-1算式变成(100-1)×69然后将括号里的数分别乘上69,注意中间为减号,算式变成:100×69-1×69二、除法:1.连续除以两个数等于除以这两个数的乘积:例如:32000÷125÷8 我们可以将算式变为32000÷(125×8)=32000÷10002.例如:630÷18 我们可以将18拆分成9×2 这时原式变为630÷(9×2)注意要加括号,然后打开括号,原式变成630÷9÷2=70÷2三、乘除综合:例如6300÷(63×5)我们需要打开括号,此时要将括号里的乘号变为除号,原式变为6300÷63÷5四年级数学简便计算:加减法篇一、加法:1.利用加法交换律例如:254+158+246我们首先观察发现254与246相加可以凑成整百,于是交换158和246两个加数的位置,变成254+246+158。

小学五年级数学上册教材培训资料一、整体内容分布:(一)数与代数(三)统计与概率1.小数乘法统计与可能性2.小数除法(四)数学思想方法3.简易方程数学广角――数字编码(二)空间与图形(五)综合应用1.观察物体(二)1.量一量找规律2.多边形的面积2.铺一铺第一单元小数乘法教学内容小数乘法积的近似值有关小数乘法的两步计算整数乘法运算定律推广到小数二、教学目标1.自主探索小数乘法的计算方法,能正确进行笔算,并能对其中的算理做出合理的解释。
2.会用“四舍五入”法截取积是小数的近似值。
3.理解整数乘法运算定律对于小数同样适用,并会运用这些定律进行一些小数的简便运算,进一步发展学生的数感。
4.体会小数乘法是解决生产、生活中实际问题的重要工具。
三、编排特点1.选择“进率是十的常见量”作为学习素材,引入小数乘法的学习。
对于五年级学生的生活经验而言,“元、角、分”“米、分米、厘米”是他们熟悉不过的计量单位了。
根据学生已有的这些知识基础,教材从丰富多彩的校内外活动中,选择“买风筝”(与元、角有关)、“换玻璃”(与米、分米有关)的活动为背景,引入小数乘法的学习。
这样的生活背景,不但能激发童心童趣,而且能促成学生利用元、角之间、米、分米之间的十进关系顺利沟通小数乘法与整数乘法的联系,利于学生将新知纳入到已有的认知系统中。
2.淡化小数乘法意义的教学,突出计算方法的教学。
小数实质上是十进分数,要让学生理解小数乘法的意义,应从分数乘法的意义入手。
但考虑到学生已有的知识经验和认知水平,根据小数与整数的密切联系,教材先教学小数乘法,再教学分数乘法。
与原义务教材比,淡化了小数乘法意义的教学,把重点放在计算的算理和方法的总结上,引导学生利用因数的变化引起积的变化规律来解释小数乘法的算理,并由此总结小数乘法的一般方法。
3.应用转化和对比,概括小数乘法的计算方法。
小数的书写方式,进位规则均与整数相同,教材紧扣两者的密切联系,引导学生:①用转化的方法,将小数乘法转化为整数乘法。

数学计算方法1.十几乘十几:口诀:头乘头,尾加尾,尾乘尾。
例:12×14=?解: 1×1=12+4=62×4=812×14=168注:个位相乘,不够两位数要用0占位。
2.头相同,尾互补(尾相加等于10):口诀:一个头加1后,头乘头,尾乘尾。
例:23×27=?解:2+1=32×3=63×7=2123×27=621注:个位相乘,不够两位数要用0占位。
3.第一个乘数互补,另一个乘数数字相同:口诀:一个头加1后,头乘头,尾乘尾。
例:37×44=?解:3+1=44×4=167×4=2837×44=1628注:个位相乘,不够两位数要用0占位。
4.几十一乘几十一:口诀:头乘头,头加头,尾乘尾。
例:21×41=?解:2×4=82+4=61×1=121×41=8615.11乘任意数:口诀:首尾不动下落,中间之和下拉。
例:11×23125=?解:2+3=53+1=41+2=32+5=72和5分别在首尾11×23125=254375注:和满十要进一。
6.十几乘任意数:口诀:第二乘数首位不动向下落,第一因数的个位乘以第二因数后面每一个数字,加下一位数,再向下落。
例:13×326=?解:13个位是33×3+2=113×2+6=123×6=1813×326=4238注:和满十要进一。
各种图形计算公式(给孩子留着)。



⼩学数学计算⽅法合集(14种⽅法+27条原则+37个顺⼝溜)14 种⼩学数学计算⽅法技巧1、20 以内进位加法表,让孩⼦更轻松掌握加法运算。
看⼤数,分⼩数,凑整⼗,加零头。
(掌握“凑⼗法”,提倡“递推法”)20 以内进位加减法被加数相同2、20 以内退位减法,让⼝算该去更简单。
20 以内退位减,⼝算⽅法和简单。
⼗位退⼀,个加补,⼜准⼜快写得数。
20 以内退位减法表减数相同3、加法意义,竖式计算,⽅法巧妙,⽅便掌握。
两数合并⽤加法,加的结果叫做和。
数位对其从右起,逢⼗进⼀别忘记。
例:435+697=4 3 5+ 6 9 71 1 3 24、减法的重要意义,提倡竖式计算。
从⼤去⼩⽤减法,减的结果叫做差。
数位对齐从右起,不够减时前位拿。
例: 756-569=7 5 6- 5 6 91 8 75、两位数乘法,⽅法技巧需牢记!两位数乘法并不难,计算过程有三点:乘数个位要先算,再⽤⼗位乘⼀遍,乘积末位是关键,要和⼗位来对端;两次乘积相加完,层层计算记⼼间。
例: 15x24=1 5× 2 43 6 06、两位数除法,⽅法技巧需牢记!除数两位看两位,两位不够除三位。
除到那位商那位,余数要⽐除数⼩,然后再除下⼀位,试商⽅法要灵活,掌握“四含五⼊”法,还有“同商⽐较法”了解“折半定商法”,不⾜除数商九,⼋。
(包括:同头。
⾼位少1)例:84÷24=3.57、混合运算,⽅法技巧需牢记!拿到式题认真看,先算乘除后加碱。
遇到括号要先算,运⽤规律要改变。
- -些数据要记牢,技能技巧掌握好。
例: (13+24)×35÷25=8、⼩数加减法,⽅法技巧需牢记!⼩数加减计算题,以点对准好对齐。
算法如同算整数,算毕把点往下移。
例: 3.24+7.83=3.2 4+ 7.8 31 1.0 79、⼩数乘法,⽅法技巧需牢记!⼩数乘⼩数,法则同整数。
定积⼩数位,因数共同凑。
例:0.45×2.5=0.4 5×2.51.1 2 510、分数乘除法,⽅法技巧需牢记!分数乘法易学懂,分⼦分母分别乘。


数学快速计算方法1.快速计算乘法:-在两个两位数相乘时,将个位数和十位数对齐,然后将十位数相乘,个位数相乘。
最后将两个结果相加就是最终答案。
-对于乘以11的倍数的乘法,将该数的个位数和十位数相加,然后将结果复制,即为最终答案。
例如:23x11=253-对于两个整数相乘,其中一个数接近10的倍数,可以通过分配律来简化计算。
例如:7x18=7x(20-2)=(7x20)-(7x2)=140-14=1262.快速计算除法:-除以整数10的倍数时,可以将被除数向右移动相应的位数,即去掉小数点的整数部分。
-如果除数是2的幂次方,可以通过右移二进制位来完成除法运算。
例如:36÷4=36÷(2^2)=36>>2=93.快速计算平方和平方根:-计算一个整数的平方,可以通过著名的“平方公式”来简化。
例如:52=(5x5)=25-计算一个数的平方根时,可以使用二分法逼近。
首先猜测一个数作为答案,然后用该数除以猜测答案,将商和猜测答案的平均值作为新的猜测答案。
重复此过程直到找到一个接近真正答案的解。
4.快速计算百分比和利息:-计算一个数的百分之几时,可以直接将该数除以100,得到结果。
-计算一个数的百分之几的增加或减少量时,可以先计算出该数的百分之一,然后将其乘以相应的百分比。
-计算利息时,可以使用百分数和本金相乘的方法。
例如:1000元以5%的利率存款1年,则利息为1000x0.05=50元。
5.大数和小数的快速估算:-当需要计算大数的和或积时,可以对其中的一些数进行适当的近似处理来简化计算。
例如,将大数取整,然后在最后结果上进行修正。
-当需要计算小数的和或积时,可以将小数近似到一个更易计算的形式,如将小数化为分数或百分数,然后进行相应的运算。
以上是一些常用的数学快速计算方法。
通过熟练掌握这些技巧,你可以更高效地进行数学计算,省去了一些繁琐的步骤。
同时,还可以提高你的数学思维和解题能力。

数学计算技巧同头尾合十数学计算技巧-同头尾合十今天看到一篇文章里面提到了“同头尾合十法”,我竟然长这么大都没有听说过,赶快Google了一下,长见识呀。
一、同头尾合十所谓“同头尾合十”,是指两位数乘两位数的算式中十位上的数相同,个位上的数字之和是10。
解答时可把尾数相乘的积作为后两位数,把十位相乘的积作为前两位数。
(十位相乘的积再加一个该数,作为前两位数)例1:53×57 解:53×57 =(5×6)(3×7) =3021二、同尾头合十所谓“同尾头合十”,是指两位数乘两位数的算式中个位上的数相同,十位上的数字之和是10。
解答时将十位上的数相乘加上个位数字后扩大100倍,再加上个位数乘个位数的积。
例2:48×68 解:48×68 =(4×6+8)×100+8×8 = 3200+64 = 3264三、去一添补所谓“去一添补”,是指一个两位数与99、999等由9组成的多位数相乘时,即把两位数去1放在前面,同时在末两位写上两位数的补数,数较多时中间添9。
例3:36×99 解:36×99 =(36-1)(100-36) = 3564 例4:36×999 解:36×999 =(36-1)9(100-36) = 35964四、两头拉,中间加所谓“两头拉,中间加”,是指一个两位数与11相乘时,取两位数的十位,个位分别作积的最高位和最低位,把十位、个位数字作为中间数,满十向头上加“1”。
例5:52×11 解:52×11 =5(5+2)2 =572 例6:89×11 解:89×11 =8(8+9)9 =979。
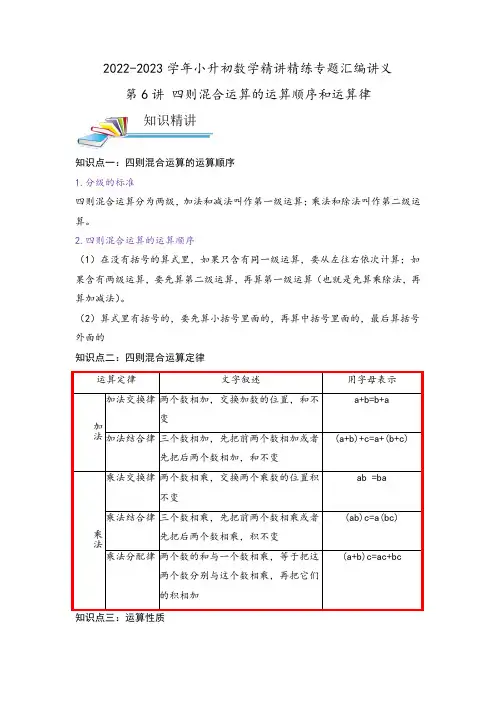
2022-2023学年小升初数学精讲精练专题汇编讲义第6讲四则混合运算的运算顺序和运算律知识点一:四则混合运算的运算顺序1.分级的标准四则混合运算分为两级,加法和减法叫作第一级运算;乘法和除法叫作第二级运算。
2.四则混合运算的运算顺序(1)在没有括号的算式里,如果只含有同一级运算,要从左往右依次计算;如果含有两级运算,要先算第二级运算,再算第一级运算(也就是先算乘除法,再算加减法)。
(2)算式里有括号的,要先算小括号里面的,再算中括号里面的,最后算括号外面的知识点二:四则混合运算定律运算定律文字叙述用字母表示加法加法交换律两个数相加,交换加数的位置,和不变a+b=b+a加法结合律三个数相加,先把前两个数相加或者先把后两个数相加,和不变(a+b)+c=a+(b+c)乘法乘法交换律两个数相乘,交换两个乘数的位置积不变ab =ba乘法结合律三个数相乘,先把前两个数相乘或者先把后两个数相乘,积不变(ab)c=a(bc)乘法分配律两个数的和与一个数相乘,等于把这两个数分别与这个数相乘,再把它们的积相加(a+b)c=ac+bc知识点三:运算性质知识精讲1.减法的性质:a-b-c=a-(b+c) a-b+c=a-(b-c)2.除法的性质(除数不等于0): a÷(b×c)=a÷b÷c a÷b÷c=a÷c÷b3.商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商不变。
a÷b=(a×m)÷(b×m)(m≠0,b≠0) a÷b=(a÷m)÷(b÷m)(m≠0,b≠0)重点提示:在利用减法和除法的运算性质进行简便计算时,等式的两边可以颠倒过来,要根据算式的特点灵活地进行去括号或添括号。
知识点四:四则混合运算中的速算技巧:1.加减法中的速算与巧算(1)分组凑整法.把几个互为“补数”的减数先加起来,再从被减数中减去,或先减去那些与被减数有相同尾数的减数.(“补数”就是两个数相加,如果恰好凑成整十、整百、整千……,就把其中的一个数叫做另一个数的“补数”)(2)加补凑整法.有些算式中直接凑整不明显,这时可“借数”或“拆数”凑整.(3)数值原理法:先把加在一起为整十、整百、整千…的数相加,再与其它的数相加.(4)“基准数”法,基准当几个数比较接近于某一整数的数相加时,选这个整数为“基准数”(要注意把多加的数减去,把少加的数加上)2.乘法凑整技巧:先把能凑成整十、整百、整千的几个乘数结合在一起,最后再与前面的数相乘,使得运算简便。
2023考研数学复习资料:计算行列式方法4,加边法1500字计算行列式是数学中的一项重要内容,也是考研数学中常见的题型之一。
在考研数学复习中,熟练掌握计算行列式的方法对提高解题效率和正确率非常重要。
本文将介绍数学复习资料中的计算行列式方法之一——加边法。
加边法是一种通过增加边和顶点的方法,将原始的行列式转化为一些已知的行列式,从而简化计算过程的方法。
下面将介绍加边法的具体步骤和应用示例。
加边法的基本步骤如下:步骤一:将原始的行列式的每一行或每一列上方添加一行(或一列)相等的元素,并且该行(或列)元素只在后面加边的行列式中出现。
步骤二:根据加边后的行列式的性质,进行一系列行列式的变换,使其转化为已知的行列式。
步骤三:根据已知的行列式的性质,求解最终的行列式。
下面通过一个具体的示例来说明加边法的应用:例题:计算行列式$$D = \\left| \\begin{array}{cccc}1 &2 &3 &4 \\\\5 &6 &7 &8 \\\\9 & 10 & 11 & 12 \\\\13 & 14 & 15 & 16 \\\\\\end{array} \\right|$$解:根据加边法的步骤,我们可以进行如下操作:步骤一:在每一行上方添加一行相等的元素,添加的行为$(13,14,15,16)$。
$$\\left| \\begin{array}{cccc}1 &2 &3 &4 \\\\5 &6 &7 &8 \\\\9 & 10 & 11 & 12 \\\\13 & 14 & 15 & 16 \\\\\\end{array} \\right|$$步骤二:对加边后的行列式进行一系列的变换。
①将第3行乘以-1加到第1行上,得到$$\\left| \\begin{array}{cccc}10 & 12 & 14 & 16 \\\\5 &6 &7 &8 \\\\9 & 10 & 11 & 12 \\\\13 & 14 & 15 & 16 \\\\\\end{array} \\right|$$②将第4行乘以-1加到第2行上,得到$$\\left| \\begin{array}{cccc}10 & 12 & 14 & 16 \\\\-1 & -8 & -9 & -8 \\\\9 & 10 & 11 & 12 \\\\13 & 14 & 15 & 16 \\\\\\end{array} \\right|$$③将第4行乘以-1加到第3行上,得到$$\\left| \\begin{array}{cccc}10 & 12 & 14 & 16 \\\\-1 & -8 & -9 & -8 \\\\0 & -4 & -4 & -4 \\\\13 & 14 & 15 & 16 \\\\\\end{array} \\right|$$步骤三:根据已知的行列式的性质,求解最终的行列式。
自学资料一、解直角三角形【知识探索】1.解直角三角形的类型与解法:类型一︰已知一边一角(角为两锐角之一)第1页共11页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训类型二︰已知两边(两直角边或一条直角边与斜边)【解题技巧】计算边时,可以用以下口诀来解题:有斜求对乘正弦,有斜求邻乘余弦,无斜求对乘正切,无斜求邻乘余切.【错题精练】例1.在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=()A. 3sin40°B. 3sin50°C. 3tan40°D. 3tan50°第2页共11页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训第3页 共11页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训例2.如图,△ABC 中,∠ACB =90°,sinA =45,BC =8,D 是AB 中点,过点B 作直线CD 的垂线,垂足为点E .(1)求线段CD 的长; (2)求cos∠ABE 的值.例3.某楼梯的侧面如图所示,其中∠A =Rt∠BAC ,测得AB =2.5米,AC =6米,则tan∠ACB 等于( )A. 513; B. 1213; C.125; D. 512.例4.如图,AD 是△ABC 的中线,tanB =13,cosC =√22,AC =√2.求:(1)BC 的长;(2)尺规作图(保留作图痕迹,不写作法):作出△ABC 的外接圆,并求外接圆半径.例5.如图,四边形ABCD 中,∠ABC =Rt∠,已知∠A =α,外角∠DCE =β,BC =a ,CD =b ,则下列结论错误的是( )A. ∠ADC =90∘−α+β;B. 点D 到BE 的距离为b ⋅sinβ;C. AD=a+b⋅cosB;cosαD. 点D到AB的距离为a+bcosβ.例6.如图,AB是⊙O的直径,BE⊥CD于E.(1)求证:AB⋅BE=BC⋅BD;(2)若AB=26,CD=24,求sin∠CBD.【举一反三】1.在△ABC中,∠BAC=120°,AB=AC,∠ACB的平分线与∠BAC的外角平分线交于点D,连结BD,则tan∠BDC的值是(); B. √3;A. √33C. √2; D. 1.22.如图,一根长为10米的竹竿AB斜靠在垂直于地面的墙上(∠O=90∘),竹竿AB的倾斜角为α.当竹竿的顶端A下滑到点A′时,竹竿的另一端B向右滑到了点B′,此时倾斜角为β,则线段AA′的长为10(sinα−sinβ)米.当竹竿AB滑到A′B′位置时,AB的中点P滑到了A′B′的中点P′位置,则点P所经过的路线长为米.(两空格均用含α、的式子表示)3.在Rt△ABC中,∠C=90∘,若AB=4,sinA=3,则斜边AB边上的高CD的长为.5第4页共11页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训4.如图,cosB=,sinC=,AC=10,则△ABC的面积是()A. 42B. 43C. 44D. 455.△ABC中,AB=AC,且AB=10,BC=12,则sin∠ABC=()A. 43; B. 34;C. 45; D. 35.6.如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.(1)求每个小矩形的长与宽;(2)在矩形网格中找出所有的格点E,使△ABE为直角三角形;(描出相应的点,并分别用E1,E2…表示)(3)求sin∠ACB的值.二、锐角三角函数的定义【知识探索】1.对于锐角的每一个确定的值,有唯一确定的值与它对应,所以是的函数.同样地,、也是的函数.的正弦、余弦、正切都是的锐角三角函数(trigonometric function of acute angle).【错题精练】第5页共11页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训例1.如图,△ABC的顶点都在方格纸的格点上,则sinA的值是()A.B.C.D.例2.在正方形网格中,∠α的位置如图所示,则tanα的值是()A.B.C.D. 2例3.已知,在Rt△ABC中,∠C=90°,AB=,AC=1,那么∠A的正切tanA等于()A.B. 2C.D.【举一反三】1.在Rt中,°,AC=12,BC=5,则sinA的值为__________ 。
小学数学“加、减、乘、除”速算技巧掌握良好的速算技巧,是让孩子们在最短的时间内,提高数学成绩的关键之处,所以,家长要善于引导孩子们发现和使用速算技巧,并且多多将这些技巧进行验证,让这些技巧好好为孩子服务。
下面就让我们一起学习加减乘除除法的速算技巧吧。
加法的神奇速算法一、加大减差法1、口诀前面加数加上后面加数的整数,减去后面加数与整数的差等于和。
2、例题1376+98=1474 计算方法:1376+100-23586+898=4484 计算方法:3586+1000-1025768+9897=15665 计算方法:5768+10000-103二、求只是数字位置颠倒两个两位数的和1、口诀一个数的十位数加上它的个位数乘以11等于和2、例题47+74=121 计算方法:(4+7)x 11=12168+86=154 计算方法:(6+8)x 11=15458+85=143 计算方法:(5+8)x 11=143三、一目三行加法1、口诀提前虚进一,中间弃9,末位弃102、例题365427158644785963+742334452———————1752547573方法:从左到右,提前虚进1;第1列:中间弃9(3和6)直接写7;第2列:6+4-9+4=5 以此类推...最后1列:末位弃10(8和2)直接写3 注意:中间不够9的用分段法,直接相加,并要提前虚进1;中间数字和大于19的,弃19,前边多进1,末位数字和大于19的,弃20,前边多进1 减法的神奇速算法一、减大加差法1、例题321-98=223计算方法:减100,加28135-878=7257计算方法:减1000,加12291321-8987= 82334计算方法:减10000,加10132、总结被减数减去减数的整数,再加上减数与整数的差,等于差。
二、求只是数字位置颠倒两个两位数的差1、例题74-47=27计算方法:(7-4)x9=2783-38=45计算方法:(8-3)x9=4592-29=63计算方法:(9-2)x9=63被减数的十位数减去它的个位数乘以9,等于差。
- 1 -第1讲 定义新运算一、知识要点定义新运算是指运用某种特殊符号来表示特定的意义,从而解答某些算式的一种运算。
解答定义新运算,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。
定义新运算是一种人为的、临时性的运算形式,它使用的是一些特殊的运算符号,如:*、△、⊙等,这是与四则运算中的“+、-、×、÷”不同的。
新定义的算式中有括号的,要先算括号里面的。
但它在没有转化前,是不适合于各种运算定律的。
二、精讲精练【例题1】假设a*b=(a+b)+(a-b),求13*5和13*(5*4)。
【思路导航】这题的新运算被定义为:a*b 等于a 和b 两数之和加上两数之差。
这里的“*”就代表一种新运算。
在定义新运算中同样规定了要先算小括号里的。
因此,在13*(5*4)中,就要先算小括号里的(5*4)。
练习1:1.将新运算“*”定义为:a*b=(a+b)×(a-b).。
求27*9。
2.设a*b=a2+2b ,那么求10*6和5*(2*8)。
3.设a*b=3a -b ×1/2,求(25*12)*(10*5)。
【例题2】设p 、q 是两个数,规定:p △q=4×q-(p+q)÷2。
求3△(4△6)。
【思路导航】根据定义先算4△6。
在这里“△”是新的运算符号。
练习2:1.设p 、q 是两个数,规定p △q =4×q -(p+q )÷2,求5△(6△4)。
2.设p 、q 是两个数,规定p △q =p2+(p -q )×2。
求30△(5△3)。
3.设M 、N 是两个数,规定M*N =M/N+N/M ,求10*20-1/4。
【例题3】如果1*5=1+11+111+1111+11111,2*4=2+22+222+2222,3*3=3+33+333,4*2=4+44,那么7*4=________;210*2=________。
第一讲 速算与巧算同学们,我们又在奥数网见面了!一提到“数学”,大家第一个想到的大多都会是计算。
计算是数学的“地基”,只有打牢这个“地基”,我们的数学大厦才能建高、建好!在数学计算中有许多好的方法技巧和规律,我们如果能理解掌握、灵活运用,“数学大厦”的地基就会为你的成长提供最好的帮助!呵呵!下面就让我们一起来看看吧!加减法中的巧算小朋友们,你知道“凑整”的思想么?在速算、巧算中我们常常为了方便计算而采用“凑整”的思想,它大大加快了我们的计算速度和正确率 。
【例1】 用你的好办法算出下式结果: (1)1350+49+68+51+32+1650(2)33+105+18+95+57+56+12+114 (3)378+26+609 (4)66+218+79+87分析:(1)先观察算式,找能凑整的数,一般找能凑整的数看个位就可以了。
如右图,我们可以先把能凑整的数标出来,能“凑整”的先算,写成算式时一定要看清是不是每个数都写进去了,故有:(1)式=(1350+1650)+(49+51)+(68+32)=3000+100+100=3200(2)式 =(33+57)+(105+95)+(18+12)+(56+114)= 90+200+30+170 = 290+200 = 490分析:在许多情况下,我们没有如例1那么理想的“凑整”状态,这个时候我们可以自己创造条件,变成理想的“凑整”状态,而后进行计算。
(3)原式=(378+22)+(609+1)+(26-22-1)=400+610+3=1013或,原式=(378+2)+(26+4)+(609-2-4)=380+30+603=410+603=1013(4)原式=(66+4)+(218+2)+(87+3)+(79-4-2-3) =70+220+90+70=450方法不唯一,以上仅供参考!可鼓励学生多方位凑整求和。
【例2】 用你的好办法算出下式结果: (1)356+(84-36) (2)376-(87-24) (3)1000-90-80-20-10 (4)178-33-16-29 去括号和添括号的法则:在只有加减运算的算式里,如果括号前面是“+”号,则不论去掉括号或添上括号,括号里面的运算符号都不变;如果括号前面是“-”号,则不论去掉括号或添上括号,括号里面的运算符号都要改变,“+”变“-”,“-”变“+”,即: a +(b +c +d )= a +b +c +d a -(b +a +d )= a -b -c -d a -(b -c )= a -b +c分析:(1)原式=356+84-36=356-36+84=320+84=404注意:在加减运算中,改变运算顺序时要带着符号搬家。
第三章习题答案1.分别用梯形公式、Simpson公式、Cotes公式计算积分1,I=⎰并估计误差。
解:1)用梯形公式有:()()110.51[10.5]10.42678242f f⎛-≈+=+≈⎝⎭⎰()()()333333220.512.6042107.36571012124Tb aE f fηηη-----⎛⎫''=-=--=⨯≤⨯⎪⎝⎭事实上,()()()()()()110.430964410.50.510.4267767210.50.510.00418772Tf x II f fE f f f===-≈+=⎡⎤⎣⎦-∴=-+=⎡⎤⎣⎦⎰⎰2)Simpson公式()110.53111410.43093 64212f f f⎛-⎡⎤⎛⎫⎛⎫≈++=+=⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎝⎭⎰[]()()44744211111522 1.1837710180218028Sb a b aE f fηη--⎛⎫--⎪⎛⎫--⎛⎫=-=--≤⨯⎪ ⎪⎪⎝⎭⎝⎭⎪⎝⎭()312()''()48T f fb aE h=?--事实上,()()()110.50.510.5410.000030462SE f f f f-⎡+⎤⎛⎫=-++=⎪⎢⎥⎝⎭⎣⎦⎰3)由Cotes公式有:()() ()111537270.5321232719084814.9497525.2982210.3923029.9332670.43096180f f f f f-⎡⎤⎛⎫⎛⎫⎛⎫≈++++⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=++++=⎰17)180+++()6116211294522 2.697410945464C E f η--⎛⎫⨯ ⎪⎛⎫=-⨯-≤⨯ ⎪ ⎪⎝⎭⎪⎝⎭()7(6)945*4()()82Cf b a E f h =?-- 事实上,()0.0000003C E f =2.证明Simpson 公式()2.8具有三次代数精度。